Решение целых и дробно рациональных неравенств
Продолжаем разбирать способы решения неравенств, имеющих в составе одну переменную. Мы уже изучили линейные и квадратные неравенства, которые представляют из себя частные случаи рациональных неравенств. В этой статье мы уточним, неравенства какого типа относятся к рациональным, расскажем, на какие виды они делятся (целые и дробные). После этого покажем, как правильно их решать, приведем нужные алгоритмы и разберем конкретные задачи.
Понятие рациональных равенств
Когда в школе изучают тему решения неравенств, то сразу берут рациональные неравенства. На них приобретаются и оттачиваются навыки работы с этим видом выражений. Сформулируем определение данного понятия:
Определение 1Рациональное неравенство представляет из себя такое неравенство с переменными, которое содержит в обоих частях рациональные выражения.
Отметим, что определение никак не затрагивает вопрос количества переменных, значит, их может быть сколь угодно много.
Следовательно, возможны рациональные неравенства с 1, 2, 3 и более переменными. Чаще всего приходится иметь дело с выражениями, содержащими всего одну переменную, реже две, а неравенства с большим количеством переменных обычно в рамках школьного курса не рассматривают вовсе.
Таким образом, мы можем узнать рациональное неравенство, посмотрев на его запись. И с правой, и с левой стороны у него должны быть расположены рациональные выражения. Приведем примеры:
x>4 x3+2·y≤5·(y−1)·(x2+1)2·xx-1≥1+11+3x+3·x2
А вот неравенство вида 5+x+1<x·y·z не относится к рациональным, поскольку слева у него есть переменная под знаком корня.
Все рациональные неравенства делятся на целые и дробные.
Определение 2Целое рациональное равенство состоит из целых рациональных выражений (в обеих частях).
Определение 3Дробно рациональное равенство – это такое равенство, которое содержит дробное выражение в одной или обеих своих частях.
Например, неравенства вида 1+x-11322+23+211-2·13·x-1>4-x4 и 1-235-y>1×2-y2 являются дробно рациональными, а 0,5·x≤3·(2−5·y) и 1:x+3>0 – целыми.
Мы разобрали, что из себя представляют рациональные неравенства, и выделили их основные типы. Можем переходить дальше, к обзору способов их решения.
Как решать целые неравенства
Допустим, что нам требуется найти решения целого рационального неравенства r(x)<s(x), которое включает в себя только одну переменную x. При этом r(x) и s(x) представляют собой любые целые рациональные числа или выражения, а знак неравенства может отличаться. Чтобы решить это задание, нам нужно преобразовать его и получить равносильное равенство.
Начнем с перенесения выражения из правой части в левую. Получим следующее:
вида r(x)−s(x) <0 (≤,>, ≥)
Мы знаем, что r(x)−s(x)
Зачастую такого простого преобразования будет достаточно для решения неравенства, поскольку в итоге может получиться линейное или квадратное неравенство, значение которого вычислить несложно. Разберем такие задачи.
Пример 1Условие:
Решение
Начнем с переноса выражения из правой части в левую с противоположным знаком.
x·(x+3) +2·x−(x+1)2−1≤0
Теперь, когда мы выполнили все действия с многочленами слева, можно переходить к линейному неравенству 3·x−2≤0, равносильному тому, что было дано в условии. Решить его несложно:
3·x≤2 x≤23
Ответ: x≤23.
Пример 2Условие: найдите решение неравенства (x2+1)2−3·x2> (x2−x) ·(x2+x).
Решение
Переносим выражение из левой части в правую и выполняем дальнейшие преобразования с помощью формул сокращенного умножения.
(x2+1)2−3·x2−(x2−x)·(x2+x)>0x4+2·x2+1−3·x2−x4+x2>01>0
В итоге наших преобразований мы получили неравенство, которое будет верным при любых значениях x, следовательно, решением исходного неравенства может быть любое действительное число.
Ответ: любое действительно число.
Пример 3Условие: решите неравенство x+6+2·x3−2·x·(x2+x−5)>0.
Решение
Из правой части мы ничего переносить не будем, поскольку там 0. Начнем сразу с преобразования левой части в многочлен:
x+6+2·x3−2·x3−2·x2+10·x>0−2·x2+11·x+6>0.
Мы вывели квадратное неравенство, равносильное исходному, которое легко решить несколькими методами. Применим графический способ.
Начнем с вычисления корней квадратного трехчлена −2·x2+11·x+6:
D=112-4·(-2)·6=169×1=-11+1692·-2, x2=-11-1692·-2×1=-0,5, x2=6
Теперь на схеме отметим все необходимые нули. Поскольку старший коэффициент меньше нуля, ветви параболы на графике будут смотреть вниз.
Нам будет нужна область параболы, расположенная над осью абсцисс, поскольку в неравенстве у нас стоит знак >. Нужный интервал равен (−0,5, 6)
Ответ: (−0,5, 6).
Бывают и более сложные случаи, когда слева получается многочлен третьей или более высокой степени. Чтобы решить такое неравенство, рекомендуется использовать метод интервалов. Сначала мы вычисляем все корни многочлена h(x), что чаще всего делается с помощью разложения многочлена на множители.
Пример 4Условие: вычислите (x2+2) ·(x+4) <14−9·x.
Решение
Начнем, как всегда, с переноса выражения в левую часть, после чего нужно будет выполнить раскрытие скобок и приведение подобных слагаемых.
(x2+2)·(x+4)−14+9·x<0x3+4·x2+2·x+8−14+9·x<0x3+4·x2+11·x−6<0
В итоге преобразований у нас получилось равносильное исходному равенство, слева у которого стоит многочлен третьей степени.
Применим метод интервалов для его решения.
Сначала вычисляем корни многочлена, для чего нам надо решить кубическое уравнение x3+4·x2+11·x−6=0. Имеет ли оно рациональные корни? Они могут быть лишь в числе делителей свободного члена, т.е. среди чисел ±1, ±2, ±3, ±6. Подставим их по очереди в исходное уравнение и выясним, что числа 1, 2 и 3 будут его корнями.
Значит, многочлен x3+4·x2+11·x−6 может быть описан в виде произведения (x−1) ·(x−2) ·(x−3), и неравенство x3+4·x2+11·x−6<0 может быть представлено как (x−1) ·(x−2) ·(x−3) <0. С неравенством такого вида нам потом будет легче определить знаки на промежутках.
Далее выполняем оставшиеся шаги интервального метода: рисуем числовую прямую и точки на ней с координатами 1, 2, 3. Они разбивают прямую на 4 промежутка, в которых нужно определить знаки. Заштрихуем промежутки с минусом, поскольку исходное неравенство имеет знак <.
Нам осталось только записать готовый ответ: (−∞, 1) ∪ (2, 3).
Ответ: (−∞, 1) ∪ (2, 3).
В некоторых случаях выполнять переход от неравенства r(x)−s(x) <0 (≤,>, ≥) к h(x) <0 (≤,>, ≥), где h(x) – многочлен в степени выше 2, нецелесообразно. Это распространяется на те случаи, когда представить r(x)−s(x) как произведение линейных двучленов и квадратных трехчленов проще, чем разложить h(x) на отдельные множители. Разберем такую задачу.
Пример 5Условие: найдите решение неравенства (x2−2·x−1) ·(x2−19) ≥2·x·(x2−2·x−1).
Решение
Данное неравенство относится к целым. Если мы перенесем выражение из правой части влево, раскроем скобки и выполним приведение слагаемых, то получим
Решить такое неравенство непросто, поскольку придется искать корни многочлена четвертой степени. Оно не имеет ни одного рационального корня (так, 1, −1, 19 или −19не подходят), а искать другие корни сложно. Значит, воспользоваться этим способом мы не можем.
Но есть и другие способы решения. Если мы перенесем выражения из правой части исходного неравенства в левую, то сможем выполнить вынесение за скобки общего множителя x2−2·x−1:
(x2−2·x−1)·(x2−19)−2·x·(x2−2·x−1)≥0(x2−2·x−1)·(x2−2·x−19)≥0.
Мы получили неравенство, равносильное исходному, и его решение даст нам искомый ответ. Найдем нули выражения в левой части, для чего решим квадратные уравнения
Согласно рисунку, ответом будет -∞,1-25∪1-25, 1+2∪1+25, +∞.
Ответ: -∞,1-25∪1-25, 1+2∪1+25, +∞.
Добавим, что иногда нет возможности найти все корни многочлена h(x), следовательно, мы не можем представить его в виде произведения линейных двучленов и квадратных трехчленов. Тогда решить неравенство вида h(x) <0 (≤,>, ≥) мы не можем, значит, решить исходное рациональное неравенство тоже нельзя.
Как решать дробно рациональные неравенства
Допустим, надо решить дробно рационально неравенств вида r(x)<s(x) (≤,>, ≥), где r(x) и s(x) являются рациональными выражениями, x – переменной. Хотя бы одно из указанных выражений будет дробным. Алгоритм решения в этом случае будет таким:
- Определяем область допустимых значений переменной x.
- Переносим выражение из правой части неравенства налево, а получившееся выражение r(x)−s(x) представляем в виде дроби. При этом где p(x) и q(x) будут целыми выражениями, которые являются произведениями линейных двучленов, неразложимых квадратных трехчленов, а также степеней с натуральным показателем.
- Далее решаем полученное неравенство методом интервалов.
- Последним шагом является исключение точек, полученных в ходе решения, из области допустимых значений переменной x, которую мы определили в начале.
Это и есть алгоритм решения дробно рационального неравенства.
Большая часть его понятна, небольшие пояснения требуются только для п.2. Мы перенесли выражение из правой части налево и получили r(x)−s(x) <0 (≤,>, ≥), а как потом привести его к виду p(x)q(x) <0 (≤,>, ≥)?
Сначала определим, всегда ли можно выполнить данное преобразование. Теоретически, такая возможность имеется всегда, поскольку в рациональную дробь можно преобразовать любое рациональное выражение. Здесь же у нас есть дробь с многочленами в числителе и знаменателе. Вспомним основную теорему алгебры и теорему Безу и определим, что любой многочлен n-ной степени, содержащий одну переменную, может быть преобразован в произведение линейных двучленов. Следовательно, в теории мы всегда можем преобразовать выражение таким образом.
На практике разложение многочленов на множители зачастую оказывается довольно трудной задачей, особенно если степень выше 4. Если мы не сможем выполнить разложение, то не сможем и решить данное неравенство, однако в рамках школьного курса такие проблемы обычно не изучаются.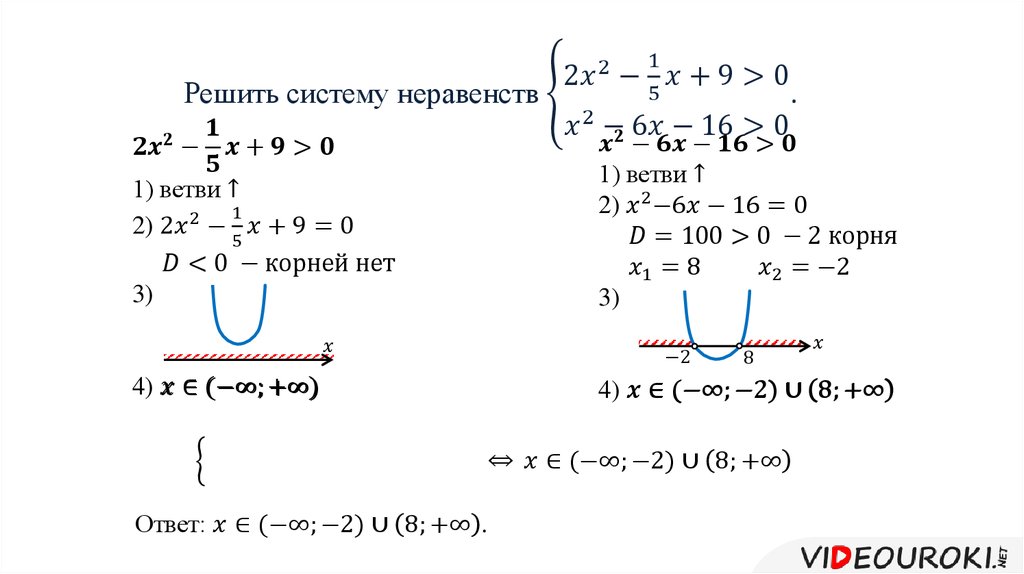
Далее нам надо решить, будет ли полученное неравенство p(x)q(x) <0 (≤,>, ≥) равносильным по отношению к r(x)−s(x) <0 (≤,>, ≥) и к исходному. Есть вероятность, что оно может оказаться и неравносильным.
Равносильность неравенства будет обеспечена тогда, когда область допустимых значений p(x)q(x) совпадет с областью значений выражения r(x)−s(x). Тогда последний пункт инструкции по решению дробно рациональных неравенств выполнять не нужно.
Но область значений для p(x)q(x) может оказаться шире, чем у r(x)−s(x), например, за счет сокращения дробей. Примером может быть переход от x·x-13x-12·x+3 к x·x-1x+3. Либо это может происходить при приведении подобных слагаемых, например, здесь:
x+5x-22·x-x+5x-22·x+1x+3 к 1x+3
Для таких случаев и добавлен последний шаг алгоритма. Выполнив его, вы избавитесь от посторонних значений переменной, которые возникают из-за расширения области допустимых значений. Возьмем несколько примеров, чтобы было более понятно, о чем идет речь.
Условие: найдите решения рационального равенства xx+1·x-3+4x-32≥-3·xx-32·x+1.
Решение
Действуем по алгоритму, указанному выше. Сначала определяем область допустимых значений. В данном случае она определяется системой неравенств x+1·x-3≠0x-32≠0x-32·(x+1)≠0, решением которой будет множество (−∞, −1)∪(−1, 3)∪(3, +∞).
Далее нам надо сделать так, чтобы в правой части неравенства получился 0. Выполняем перенос выражения из правой части влево с противоположным знаком и получаем неравенство, равносильное исходному:
xx+1·x-3+4(x-3)2+3·x(x-3)2·(x+1)≥0
После этого нам нужно преобразовать его так, чтобы было удобно применить метод интервалов. Первым делом приводим алгебраические дроби к наименьшему общему знаменателю (x−3)2·(x+1):
xx+1·x-3+4(x-3)2+3·x(x-3)2·(x+1)==x·x-3+4·x+1+3·xx-32·x+1=x2+4·x+4(x-3)2·(x+1)
Сворачиваем выражение в числителе, применяя формулу квадрата суммы:
x2+4·x+4x-32·x+1=x+22x-32·x+1
Областью допустимых значений получившегося выражения является (−∞,−1) ∪ (−1, 3) ∪ (3, +∞).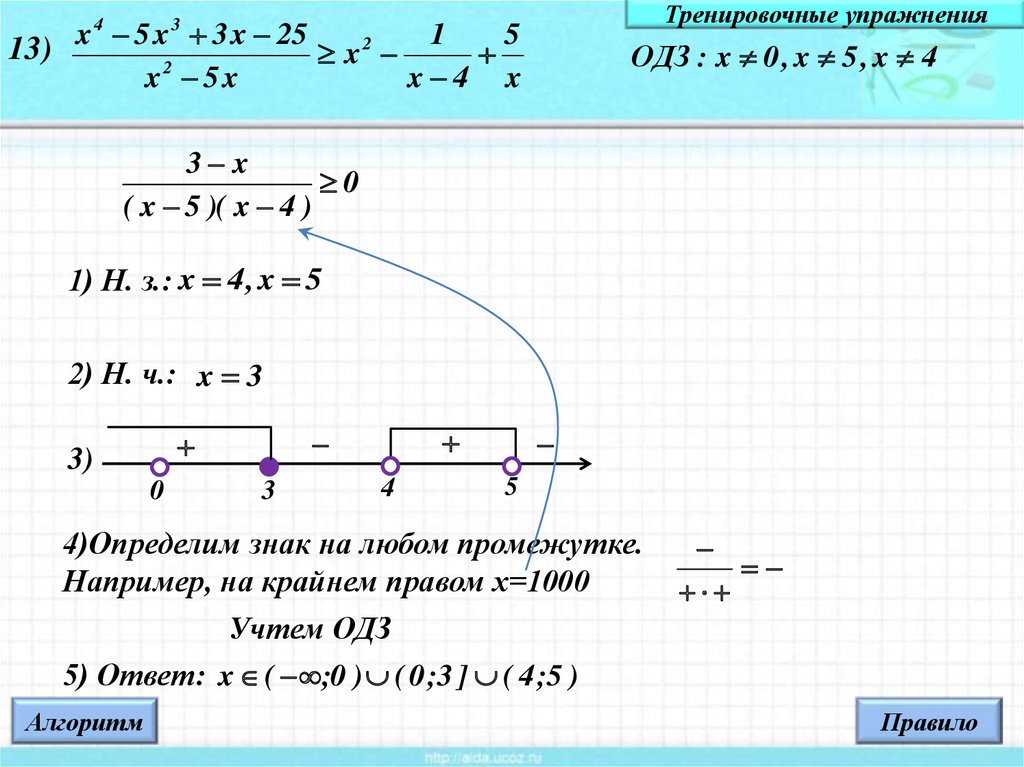
Мы видим, что она аналогична той, что была определена для исходного равенства. Заключаем, что неравенство x+22x-32·x+1≥0 является равносильным исходному, значит, последний шаг алгоритма нам не нужен.
Используем метод интервалов:
Видим решение {−2}∪(−1, 3)∪(3, +∞), которое и будет решением исходного рационального неравенства xx+1·x-3+4x-32≥-3·x(x-3)2·(x+1).
Ответ: {−2} ∪ (−1, 3) ∪ (3, +∞).
Пример 7Условие: вычислите решение x+3x-1-3xx+2+2x-1>1x+1+2·x+2×2-1.
Решение
Определяем область допустимых значений. В случае с этим неравенством она будет равна всем действительным числам, кроме −2,−1, 0 и 1.
Переносим выражения из правой части в левую:
x+3x-1-3xx+2+2x-1-1x+1-2·x+2×2-1>0
Далее выполняем преобразование левой части. Сначала преобразуем первую дробь:
x+3x-1-3xx+2=x+3-x-3xx+2=0xx+2=0x+2=0
Учитывая получившийся результат, запишем:
x+3x-1-3xx+2+2x-1-1x+1-2·x+2×2-1==0+2x-1-1x+1-2·x+2×2-1==2x-1-1x+1-2·x+2×2-1==2x-1-1x+1-2·x+2(x+1)·x-1==-x-1(x+1)·x-1=-x+1(x+1)·x-1=-1x-1
Для выражения -1x-1 областью допустимых значений будет множество всех действительных чисел, за исключением единицы.
Мы видим, что область значений расширилась: в нее были добавлены −2, −1 и 0. Значит, нам нужно выполнить последний шаг алгоритма.
Поскольку мы пришли к неравенству -1x-1>0, можем записать равносильное ему 1x-1<0. С помощью метода интервалов вычислим решение и получим (−∞, 1).
Исключаем точки, которые не входят в область допустимых значений исходного равенства. Нам надо исключить из(−∞, 1) числа −2, −1 и 0. Таким образом, решением рационального неравенства x+3x-1-3xx+2+2x-1>1x+1+2·x+2×2-1 будут значения (−∞, −2)∪(−2, −1)∪(−1, 0)∪(0, 1).
Ответ: (−∞, −2) ∪ (−2, −1) ∪ (−1, 0) ∪ (0, 1).
В заключение приведем еще один пример задачи, в котором окончательный ответ зависит от области допустимых значений.
Пример 8Условие: найдите решение неравенства 5+3x2x3+1×2-x+1-x2-1x-1≥0.
Решение
Область допустимых значений неравенства, заданного в условии, определяет система x2≠0x2-x+1≠0x-1≠0x3+1×2-x+1-x2-1x-1≠0.
Решений у этой системы нет, поскольку
x3+1×2-x+1-x2-1x-1==(x+1)·x2-x+1×2-x+1-(x-1)·x+1x-1==x+1-(x+1)=0
Значит, исходное равенство 5+3x2x3+1×2-x+1-x2-1x-1≥0 не имеет решения, поскольку нет таких значений переменной, при которой оно имело бы смысл.
Ответ: решений нет.
Графические калькуляторы разрешены на уроках математики по ФГОС, но школы отказываются их использовать. Эта проблема требует скорейшего решения.
Мы неоднократно писали, что российская система образования многое теряет, отказываясь от использования графических калькуляторов на уроках в школе. Оказывается, Министерство образования и науки понимает необходимость использования дополнительных средств для решения задач по математике! Это ясно из Федерального государственного образовательного стандарта для среднего общего образования (ФГОС). Так, в разделе, посвященном математике и информатике, мы читаем, какими навыками должны обладать ученики. Уже для базового уровня там значится «владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств».
Чуть ниже читаем, что школьникам обязаны привить «навыки использования готовых компьютерных программ при решении задач«.
Давайте вспомним, что такое ФГОС. Основываясь на этом стандарте составляются образовательные программы, организуется образовательный процесс, проводятся аттестации педагогов и проверки учащихся. ФГОС — документ, обязательный для использования во всех школах. Помимо всего прочего, этот стандарт обеспечивает преемственность ступеней образования: знания, полученные в старших классах, должны помочь ученикам с легкостью осваивать университетскую программу.
В теории — и на практике
Итак, что мы имеем. Министерство образования требует, чтобы учителя математики внедряли готовые компьютерные программы для решения и иллюстрации уравнений и неравенств. Но при этом ни разу не конкретизирует, что за программы разрешено использовать. Логично, что школы идут по самому простому пути — игнорируют этот раздел ФГОС. Ни обучению «навыкам использования готовых компьютерных программ», ни проверкам этих навыков на экзаменах нет места в системе российского образования.
Получается, что ФГОС нарушается повсеместно — и на это не обращают внимания ни школы, ни разработавшее стандарты Минобрнауки.
В ФГОС есть и еще одна интересная формулировка: так, говорится о том, что у школьников должны сформироваться представления «о способах описания на математическом языке явлений реального мира«, а также развиться умение «моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат«. Эти аспекты, как нам кажется, в данный момент практически исключены из современной системы школьного образования: учащиеся знают теорию, умеют решать отвлеченные задачи, но их не учат применять знания на практике.
Решение — на поверхности: используем графические калькуляторы
Сам факт, что в ФГОС предписывает обучать навыкам использования специальных устройств для решения и графического отображения задач, радует. Это значит, что чиновники понимают: без умения быстро и безошибочно выполнять сложные расчеты с использованием программ сегодня специалистам не обойтись.
К этому постулату уже давно пришли в США, Японии, Китае, странах Европы: здесь у каждого школьника в рюкзаке обязательно есть графический калькулятор.
|
|
Почему именно графические калькуляторы мы считаем идеальным воплощением «готовых компьютерных программ»?
- Графические калькуляторы идеально соответствуют ФГОС, обладая всем необходимым функционалом для решения обозначенных в стандарте задач и графического отображения уравнений и неравенств. Более того, их возможностей хватит и на освоение программирования (языки Basic, Assembler, C, Lua и другие) и высшей математики.
- Графические калькуляторы разрешены к использованию на экзаменах SAT, AP, PSAT/NMQT, ACT, IB Diploma, Advanced Placement Test, Praxi. Более того: без умения ими пользоваться сдать эти экзамены будет во много раз сложнее.
- Калькуляторы удобны в использовании.
Графические модели серьезно отличаются от офисных, поскольку имеют большой экран и специальные кнопки для тригонометрических, логарифмических и других функций, построения графиков и т.д. Производить вычисления не только проще, но и существенно быстрее. - Графические калькуляторы недорого стоят. Ими может оснастить класс любая общеобразовательная школа — цена вопроса от 6 тыс. р. Согласитесь, это совсем немного, особенно если сравнивать со стоимостью ПК или планшетов (которые намного хуже подходят для решения математических задач и требуют установки лицензированного программного обеспечения). Приобрести калькуляторы для решения задач дома будет необременительно и для семей школьников, притом устройства пригодятся при обучении в высших учебных заведениях на любой технической или естественнонаучной специальности.
- Графические калькуляторы очень практичны. Они весят совсем немного, имеют компактные размеры, а время автономной работы составляет от двух недель до шести месяцев. Современные модели имеют прочный корпус и снабжаются защитными чехлами, поэтому беспроблемно служат многие годы.
- Графические калькуляторы — основа STEM-образования, предполагающего объединение дисциплин и решение практических задач на школьных уроках. К калькуляторам можно подключить до 60 датчиков для проведения опытов! Несколько устройств легко объединяются в сеть, чтобы школьники могли делиться вычислениями или отправлять задания на проверку преподавателю. Графические калькуляторы позволяют создать цифровую лабораторию, которая поможет в освоении физики, биологии, географии, программирования.
Графические модели серьезно отличаются от офисных, поскольку имеют большой экран и специальные кнопки для тригонометрических, логарифмических и других функций, построения графиков и т.д. Производить вычисления не только проще, но и существенно быстрее.
Современные модели имеют прочный корпус и снабжаются защитными чехлами, поэтому беспроблемно служат многие годы.Добиться соблюдения ФГОС в наших силах
Графические калькуляторы не только удовлетворят требования ФГОС в пункте «использования готовых компьютерных программ при решении задач», но и помогут приблизить математику к жизни! Именно на практических занятиях в цифровых лабораториях американские школьники выполняют сложные расчеты для опытов, пишут программы для управления роботами, разбирают основы экономики на реальных примерах.
Подтянуться к международным стандартам обучения математике будет непросто: придется изменить формулировки в ФГОС, напрямую указав на использование калькуляторов, обучить учителей навыкам использования современных вычислительных технологий, разработать новые программы обучения и добавить соответствующие задания в учебники, внедрить проверку навыков работы с вычислительными программами в ЕГЭ. Однако это практически единственная возможность заполнить пробел в системе российского образования и сделать обучение математике соответствующим современным реалиям.
Давайте будем откровенны: в XXI веке специалисты не могут позволить себе тратить время на расчеты в уме, и навыкам работы с программируемыми калькуляторами нужно обучать на всех ступенях образовательной лестницы — от средней школы до ВУЗа. Пока мы будем замалчивать проблему, система образования будет еще больше отставать от Запада.
Давайте попробуем вместе изменить положение дел: настаивайте, чтобы в школах на уроках математики использовали программируемые калькуляторы.
Теперь вы знаете, что это разрешено по ФГОСтам, поэтому учителя не имеют права вам отказать. Мы же в ближайшее время подготовим Единый список программируемых калькуляторов, которые соответствуют требованиям ФГОС и могут использоваться в школах, а также выложим примеры заданий и уроков.
Автор: Анна Питер
Calculators-Online.ru
примеров алгебры | Неравенства | Рациональные неравенства
Шаг 1
Вычтите из обеих частей неравенства.
Шаг 2
Упрощение .
Нажмите, чтобы увидеть больше шагов…
Шаг 2.1
Чтобы записать дробь с общим знаменателем, умножьте на .
Шаг 2.2
Объединить и .
Шаг 2.3
Приведите числители к общему знаменателю.
Шаг 2.4
Вычесть из .
Шаг 3
Найдите все значения, при которых выражение переключается с отрицательного на положительное, установив каждый коэффициент равным и решив.
Шаг 4
Вычтите из обеих частей уравнения.
Шаг 5
Решите для каждого фактора, чтобы найти значения, при которых выражение абсолютного значения переходит от отрицательного к положительному.
Шаг 6
Консолидация решений.
Шаг 7
Найдите домен .
Нажмите, чтобы увидеть больше шагов…
Шаг 7.1
Установите знаменатель равным, чтобы найти, где выражение не определено.
Шаг 7.2
Домен — это все значения, которые определяют выражение.
Шаг 8
Используйте каждый корень для создания тестовых интервалов.
Шаг 9
Выберите тестовое значение из каждого интервала и подставьте это значение в исходное неравенство, чтобы определить, какие интервалы удовлетворяют неравенству.
Нажмите, чтобы увидеть больше шагов…
Шаг 9.1
Проверить значение на интервале, чтобы убедиться, что оно соответствует неравенству.
Нажмите, чтобы увидеть больше шагов.
..
Шаг 9.1.1
Выберите значение на интервале и посмотрите, соответствует ли это значение исходному неравенству.
Шаг 9.1.2
Заменить на в исходном неравенстве.
Шаг 9.1.3
Левая часть больше правой, значит данное утверждение всегда истинно.
Верно
Шаг 9.2
Проверить значение на интервале, чтобы убедиться, что оно соответствует неравенству.
Нажмите, чтобы увидеть больше шагов…
Шаг 9.2.1
Выберите значение на интервале и посмотрите, соответствует ли это значение исходному неравенству.
Шаг 9.2.2
Заменить на в исходном неравенстве.
Шаг 9.2.3
Левая часть не больше правой, значит данное утверждение неверно.
Ложь
Шаг 9.3
Проверить значение на интервале, чтобы убедиться, что оно соответствует неравенству.
Нажмите, чтобы увидеть больше шагов…
Шаг 9.3.1
Выберите значение на интервале и посмотрите, соответствует ли это значение исходному неравенству.
Шаг 9.3.2
Заменить на в исходном неравенстве.
Шаг 9.3.3
Левая часть больше правой, значит данное утверждение всегда истинно.
Верно
Шаг 9.4
Сравните интервалы, чтобы определить, какие из них удовлетворяют исходному неравенству.
Верно
Ложно
Верно
Верно
Ложно
Верно
Шаг 10
Решение состоит из всех истинных интервалов.
или
Шаг 11
Результат может отображаться в нескольких формах.
Форма неравенства:
Обозначение интервала:
Шаг 12
Введите СВОЮ задачу
Я купил ваш продукт Algebrator и могу честно сказать, что это причина, по которой я сдаю уроки математики! 
Leave A Comment