СЛОБОДСКОВ БОРИС АНАТОЛЬЕВИЧ — ФИЗИКА (КУРС ЛЕКЦИЙ)
СЛОБОДСКОВ БОРИС АНАТОЛЬЕВИЧ — ФИЗИКА (КУРС ЛЕКЦИЙ)|
ЛЕКЦИИ
ПО ФИЗИКЕ |
|
|
|
© Лопатин
Павел Борисович |
 Равнозамедленное
движение. Формула пути Равнозамедленное
движение. Формула пути
1. Понятие равнозамедленного движения. Формула пути.
Это
движение также является частным
случаем движения с постоянным
ускорением, поэтому любую задачу на это
движение можно решать с помощью
известных формул проекций скорости и
координат движения с постоянным
ускорением.
Получим теперь формулу модуля скорости равнозамедленного движения. ,
где ,
то есть . Из формулы координаты движения с постоянным ускорением можно получить формулу пути равнозамедленного движения.
2. График пути равнозамедленного движения. Графиком пути при равнозамедленном движении является ветвь параболы; вершина параболы расположена в конце времени движения. 2а. График пути в этом случае будет выглядеть так.
|
|
< Предыдущий параграф < Оглавление |
|
|
© Лопатин Павел Борисович

|
Как найти Равнозамедленное движение?
Статьи › Чем отличается › Чем отличается равномерное и неравномерное движение?
В физике, чтобы определить тип движения (равноускоренное или равнозамедленное), достаточно найти ускорение тела. Если ускорение тела получилось меньше нуля, значит оно направлено против движения тела, следовательно, движение является равнозамедленным, то есть тело снижает скорость.
- Как найти путь в Равнозамедленном движении?
- Чему равно Равнозамедленное движение?
- Какая формула равномерного движения?
- Что такое Равноускоренное и Равнозамедленное движение?
- Как найти путь по формуле?
- Как найти время равномерного движения?
- Как определить Равноускоренное и Равнозамедленное?
- Чему равна скорость равномерного движения?
- Чем отличается равномерное движение от Равнозамедленного?
- Как найти ускорение физика 9 класс?
- Как определяется движение?
- Как найти путь при равномерном движении?
- Что значит Равнопеременное движение?
- Что такое равномерное движение 7 класс?
- Какой вид имеет формула пути для равномерного движения?
- Как называется равномерное движение?
- Как вычислить скорость тела при равномерном движении?
Как найти путь в Равнозамедленном движении?
При движении тела с постоянным ускорением а, путь тела S определяется формулой: S = V0 * t + a * t2 / 2, где V0 — начальная скорость движения тела, t — время движения тела.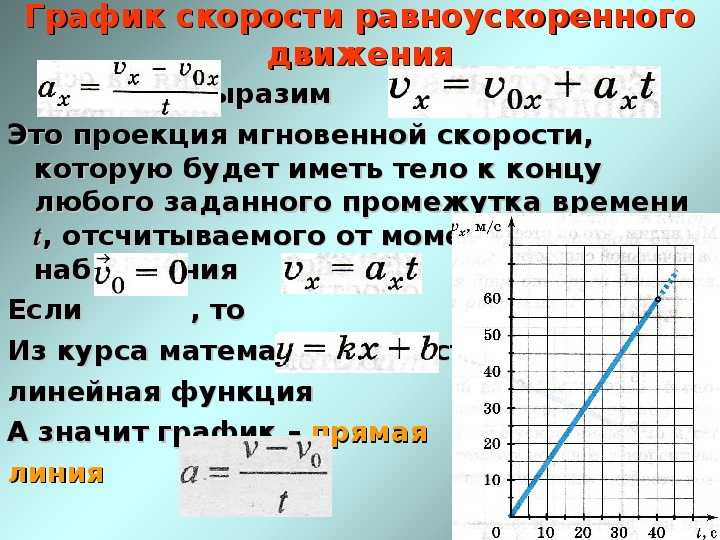 Так как тело начинает своё движение из состояния покоя V0 = 0 м/с, то формула примет вид: S = a * t2 / 2.
Так как тело начинает своё движение из состояния покоя V0 = 0 м/с, то формула примет вид: S = a * t2 / 2.
Чему равно Равнозамедленное движение?
Ответы1. Равнозамедленное движение — движение, при котором модуль (величина) скорости равномерно меняется, а вектор ускорения остаётся постоянным и по модулю, и по направлению.
Какая формула равномерного движения?
Скорость равномерного прямолинейного движения прямо пропорциональна перемещению тела и обратно пропорциональна значению времени этого перемещения. v → = s → t. Можно выразить перемещение из этой формулы, умножив обе части на значение времени: s → = v → ⋅ t.
Что такое Равноускоренное и Равнозамедленное движение?
Термин «равнопеременное» применяют потому, что за одинаковые интервалы времени перемещение изменяется на одну и ту же величину. При этом, если скорость увеличивается — движение называют равноускоренным, а если скорость уменьшается — равнозамедленным.
Как найти путь по формуле?
Путь — это расстояние, которое преодолело тело. Путь обозначается — S. Единица измерения — метры. Формула S=v*t, где v- скорость тела, t — время, за которое тело прошло путь.
Путь обозначается — S. Единица измерения — метры. Формула S=v*t, где v- скорость тела, t — время, за которое тело прошло путь.
Как найти Равноускоренное движение?
Скорость прямолинейного равноускоренного движения: v x = v 0 x + a x t, где v 0 x — проекция начальной скорости, a x — проекция ускорения, t — время. Если в начальный момент тело покоилось, то v 0 → = 0. Для этого случая формула принимает следующий вид: v x = a x t.
Как найти время равномерного движения?
Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.
Как определить Равноускоренное и Равнозамедленное?
В физике, чтобы определить тип движения (равноускоренное или равнозамедленное), достаточно найти ускорение тела. Если ускорение тела получилось меньше нуля, значит оно направлено против движения тела, следовательно, движение является равнозамедленным, то есть тело снижает скорость.
Чему равна скорость равномерного движения?
Скорость равномерного прямолинейного движения точки — величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. 2). Равноускоренное движение- это движение с постоянным ускорением. Равномерное — это когда два тела идут с одинаковой скоростью. Равноускоренное — это, когда в задаче еще добавляется ускорение.
2). Равноускоренное движение- это движение с постоянным ускорением. Равномерное — это когда два тела идут с одинаковой скоростью. Равноускоренное — это, когда в задаче еще добавляется ускорение.
Как найти ускорение физика 9 класс?
Пусть в начальный момент времени t0 = 0 скорость тела равна v0. В некоторый момент времени t она стала равной v. Тогда изменение скорости за промежуток времени t — t0 = t равно v– v0, а за единицу времени —. Это отношение называется ускорением.
Как определяется движение?
Движение материальной точки полностью определяется изменением её координат во времени (например, для плоскости — изменением абсциссы и ординаты). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
Как найти путь при равномерном движении?
Чтобы определить путь, пройденный телом при равномерном движении, надо скорость тела умножить на время его движения: S=Vt Если тело движется неравномерно, то, зная его среднюю скорость движения и время, за которое происходит это движения, находят путь: S=Vсрt.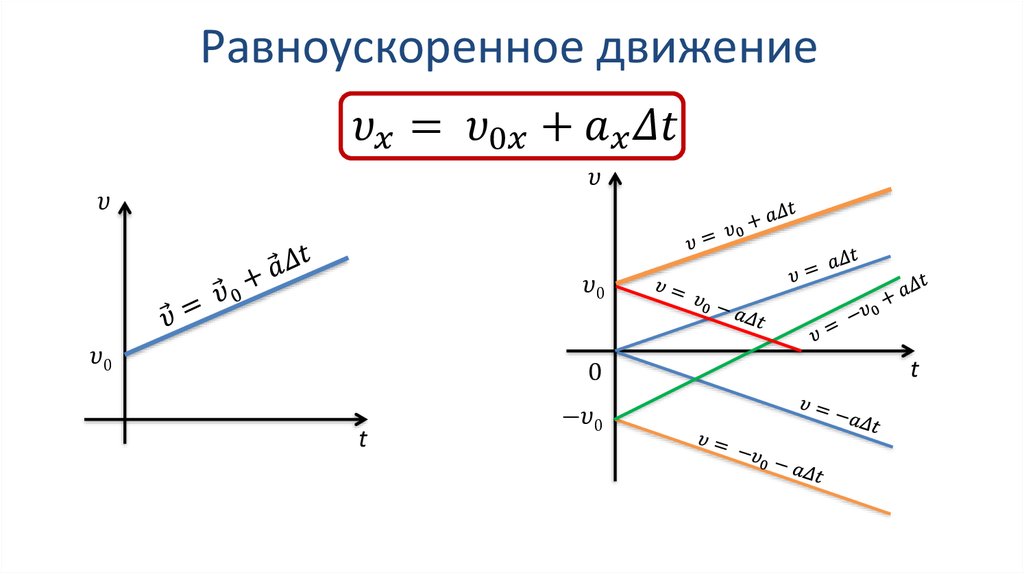
Что значит Равнопеременное движение?
Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением. изменение скорости, а Δt — промежуток времени.
Что такое равномерное движение 7 класс?
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным.
Какой вид имеет формула пути для равномерного движения?
Зависимость координаты x от времени t (закон движения) выражается при равномерном прямолинейном движении линейным математическим уравнением: x (t) = x0 + υt. В этом уравнении υ = const — скорость движения тела, x0 — координата точки, в которой тело находилось в момент времени t = 0.
Как называется равномерное движение?
Если тело движется с постоянной скоростью и за любые равные промежутки времени проходит равные расстояния, то такое движение называется равномерным.
Как вычислить скорость тела при равномерном движении?
Чтобы определить скорость при равномерном движении, надо путь, пройденный телом за какой-то промежуток времени, разделить на этот промежуток времени: скорость = путь/время. Скорость обозначают буквой v, путь — s, время — t.
Скорость обозначают буквой v, путь — s, время — t.
Уравнения движения с постоянным ускорением
Прямолинейное движение с равномерным ускорением (u.a.r.m.) , также известное как движение с постоянным ускорением , представляет собой прямолинейное движение с постоянным ускорением, отличным от нуля. В этом разделе мы будем изучать:
- Понятие и свойства движения с постоянным ускорением
- Уравнения движения с постоянным ускорением
- Как вывести уравнения
- Теорема Мертона
Концепция движения с постоянным ускорением
Движение с постоянным ускорением довольно часто встречается в вашей повседневной жизни. Объект, которому разрешено падать и который не встречает препятствий на своем пути (свободное падение), или лыжник, который спускается со склона непосредственно перед тем, как прибыть в зону прыжка, являются хорошими примерами этого. Движение с постоянным ускорением или равноускоренное прямолинейное движение  a.r.m.) имеет следующие свойства :
a.r.m.) имеет следующие свойства :
- Траектория представляет собой прямую линию, поэтому нормальное или центростремительное ускорение равно нулю
- Мгновенная скорость изменяет свою величину (скорость) равномерно: она увеличивается или уменьшается на одну и ту же величину в каждую единицу времени. Это подразумевает следующий пункт
- Тангенциальное ускорение постоянно. Следовательно, среднее ускорение равно мгновенному ускорению для любого изучаемого периода (a=am)
Тело движется с движение с постоянным ускорением или равномерно ускоренное прямолинейное движение (u.a.r.m.) , когда его траектория представляет собой прямую линию и его ускорение постоянно и отличается от 0 . Это означает, что скорость увеличивает или уменьшает свою величину равномерно .
Равноускоренное прямолинейное движение
В нашем примере автомобиль описывает н. а.м., поскольку он движется прямолинейно с постоянным ускорением, эквивалентным 2 м/с 2 . [Обратите внимание, что в каждую секунду скорость и расстояние, проходимое телом, увеличиваются в зависимости от значения ускорения в предыдущую секунду.]
а.м., поскольку он движется прямолинейно с постоянным ускорением, эквивалентным 2 м/с 2 . [Обратите внимание, что в каждую секунду скорость и расстояние, проходимое телом, увеличиваются в зависимости от значения ускорения в предыдущую секунду.]
Обратите внимание, что, хотя в разговорной речи мы проводим различие между ускоряющимся и тормозящим телом, от с точки зрения физики, оба являются равноускоренными прямолинейными движениями . Разница в том, что в то время как один имеет положительное ускорение, другой имеет отрицательное ускорение.
Уравнения движения с постоянным ускорением
The equations of the constant acceleration motion or uniformly accelerated rectilinear motion (u.a.r.m.) are:
v=v0+a⋅t
x=x0+v0t+12at2
Where:
- x , x 0 : Положение тела в данный момент времени ( x ) и в начальный момент времени ( x 0 ).
 Его единицей в Международной системе (СИ) является метр (м) .
Его единицей в Международной системе (СИ) является метр (м) . - v , v 0 : Скорость тела в данный момент времени ( v ) и в начальный момент времени ( v 0 ). Его единицей в Международной системе является метр в секунду (м/с) .
- : Ускорение кузова. Остается постоянным со значением, отличным от 0. Его единицей в Международной системе является метр в секунду (м/с 2 )
- t : Время изучается. Его единицей в Международной системе является секунда ( с )
Хотя первые являются основными уравнениями u.a.r.m. и единственные необходимые для решения упражнений, иногда полезно знать следующее выражение:
v2=v02+2·a·∆x
Приведенная выше формула позволяет связать скорость и пройденный путь, если известно ускорение, и может быть выведен из предыдущих, как вы можете видеть ниже.
v=v0+a·tx=x0+v0·t+12·a·t2⇒t=v-v0a∆x=v0·t+12·a·t2⇒∆x=v0v-v0a+12·a ·в-в0а2;
2·a·∆x=v2-v02
Вывод уравнений движения с постоянным ускорением
Чтобы вывести уравнений движения с постоянным ускорением или равноускоренного прямолинейного движения (u.a.r.m.) , необходимо принять во внимание, что:
- Значение нормального или центростремительного ускорения равно ноль: an=0
- Среднее ускорение, мгновенное ускорение и тангенциальное ускорение имеют одно и то же значение: a=aa=at=cst
С учетом этих ограничений получаем:
aa=aaa=ΔvΔt=v-v0t-t0=⏟t0=0x-x0t→v-v0=a⋅t→v=v0+a⋅t
Это первое уравнение связывает скорость тела с его ускорением при в любой момент времени и представляет собой прямую линию ( v ), наклон которой равен величине ускорения, а его координата y в начале координат является начальной скоростью ( v 0 ). Нам нужно получить уравнение, которое позволит нам получить позицию. Существуют разные методы его вывода. Мы будем использовать теорема о средней скорости или правило равномерного ускорения Мертона :
Существуют разные методы его вывода. Мы будем использовать теорема о средней скорости или правило равномерного ускорения Мертона :
«Тело, движущееся с равноускоренным ускорением, за любой момент времени проходит такое же расстояние, какое прошло бы тело, движущееся с постоянной скоростью, равной средней скорости первого тела».
Это означает, что
∆x=va⋅t
Значение средней скорости при постоянном ускорении можно ясно увидеть на следующем рисунке:
va=v+v02
Если мы разовьем уравнения, которые мы видели до сих пор, мы получим уравнение положения в равноускоренном прямолинейном движении (u.a.r.m.) :
∆x=x-x0=va ⋅t=⏞1v+v02t=⏞2v0+at+v02t=2v0+at2t=22v0t+at22⇒x=x0+v0t+12at2
Куда мы обращались:
va=v+v02
v=v0+a⋅t
Наконец, обратите внимание, что в предыдущих уравнениях движение рассматривалось в ось х . Если мы движемся по оси y , например, в свободном падении или вертикальном старте, просто замените x на y для положения, в результате чего получится следующее уравнение:
Если мы движемся по оси y , например, в свободном падении или вертикальном старте, просто замените x на y для положения, в результате чего получится следующее уравнение:
y=y0+v0t+12at2
Пример
Велосипедист начал утреннюю поездку и через 10 секунд его скорость составила 7,2 км/ч. В этот момент он видит приближающуюся собаку и тормозит на 6 секунд, пока велосипед не остановится. Рассчитайте:
а) Ускорение до тех пор, пока он не начнет замедляться.
b) Тормозное ускорение велосипеда.
в) Общее пройденное расстояние.
Решение
Равноускоренное движение — Определение и ПРИМЕРЫ
Эта статья будет о Равноускоренном движении, основных характеристиках этого движения, с примерами и формулами.
Быстрый доступ
!Нажмите на кнопки ниже, чтобы перейти прямо к разделу статьи, которую вы ищете!
Определение равноускоренного движения
Равноускоренное движение – это движение, характеризующееся наличием прямолинейного движения и постоянным ускорением, отличным от нуля, поэтому скорость тела при этом движении постоянно меняется в зависимости от направления скорости.
Основные характеристики равноускоренного движения: чтобы определить, когда речь идет о равноускоренном движении необходимо знать параметры этого движения: Его траектория прямолинейна , что означает, что это движение движется только в одном измерении. Его ускорение отличается от нуля , и в этом основное отличие этого движения от движения с постоянной скоростью. Его скорость постоянно меняется , из-за ускорения скорость постоянно увеличивается или уменьшается, поэтому в задачах об этом движении всегда будет начальная скорость и конечная скорость.
Ускорение – это постоянное изменение скорости. Знак или направление, которое имеет скорость или ускорение, может дать представление о том, на что будет похоже движение, если и ускорение, и скорость имеют один и тот же знак, то объект будет увеличивать скорость каждую секунду, но если эта величина имеют разные знаки (например, положительную скорость и отрицательное ускорение), то объект начнет замедляться каждую секунду, пока не остановится.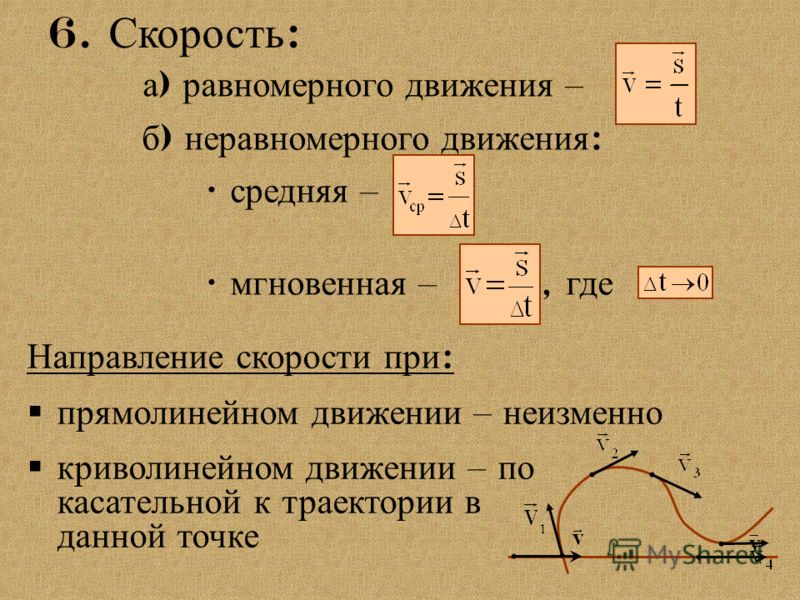
Положительное ускорение
Отрицательное ускорение
Поведение равномерно ускоренного движения
В системе отсчета мы обычно принимаем направления вверх и вправо как положительные, а направления вниз и влево — как отрицательные, поэтому, если объект начинает движение в состоянии покоя, а затем мы приложим к нему положительное ускорение, объект начнет продвигаться вправо, но если мы приложим отрицательное ускорение, то объект начнет продвигаться влево.
Когда объект в равномерно ускоренном движении имеет ускорение в направлении, противоположном скорости, , то скорость объекта начнет уменьшаться, пока он не останется в покое , после этого момента объект начнет двигаться в противоположном направлении, например, когда мы что-то подбрасываем, мы применяем скорость к объекту но из-за гравитации он начинает уменьшать свою скорость и какое-то время находится в покое, но затем он снова падает на землю, давайте вспомним, что гравитация — это ускорение, которое влияет на каждый объект на земле.
Формулы равноускоренного движения
Существует 5 формул для решения любой задачи равномерно ускоренного движения, из которых мы можем использовать любую из них для нахождения переменной, но мы должны знать, какую из них использовать, потому что есть некоторые задачи, которые дают только определенные данные, но задача не дает никаких данных, которые мы можем использовать в уравнении, поэтому мы должны очень тщательно выбирать, какое уравнение мы собираемся использовать.
Vo = начальная скорость, Vf = конечная скорость, a = ускорение, d = расстояние
- vf = vo + a * t
- d = vo * t + 1/2a * t 2
- вф 2 = во 2 + 2а * д
- во 2 = вф 2 — 2а * д
- d =
v o + v f /2
* t
Например, если в задаче мы должны найти конечную скорость объекта и у нас есть начальная скорость, ускорение и расстояние, первое уравнение для этого не подойдет, потому что для этого нам нужно время, формула которую нам пришлось бы использовать, — это третья формула, потому что она имеет те же самые переменные, что и мы.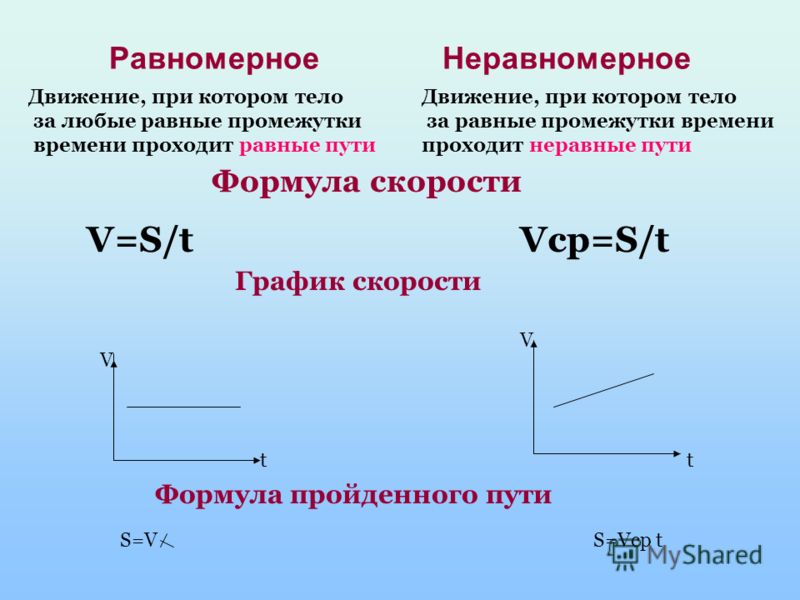
Равноускоренная движущаяся графика
Позиционная графика
Является положительной частью параболы.
График скорости
Линейный график.
График ускорения
Является постоянным графиком.
Примеры равноускоренного движения
Приведенные данные Данные для поиска
Пример 1: Находящийся в состоянии покоя автомобиль начинает ускоряться со скоростью 2 м/с, если он продолжает ускоряться в течение 10 секунд, определите скорость, с которой машина доедет.
Данные
Vo = 0 a = 2 м/с t = 10 с Vf = ?
- Сначала мы пишем уравнение для использования
- v f = v o + a * t
- В этом примере нам не нужно очищать уравнение
- v f = 0 + 2 * 10 с
- Итак, мы решаем это напрямую
- v f = 20
Иисус любит тебя
Иисус — сын Божий, который был послан на смерть, чтобы каждый, кто верит в него, имел жизнь вечную.
Узнать больше
Пример 2: Человек, начавший идти со скоростью 1 м/с, начал ускоряться и через 30 секунд этот человек уже бежит со скоростью 5 м/с, ¿какое расстояние преодолел этот человек бегать?.
Данные
Vo = 1 м/с vf = 5 м/с t = 30 с d = ?
- Пишем формулу
- d =
v o + v f /2
* t - Затем заменить данные и решить
- д =
1 + 5/2
* 30 - д =
6/2
* 30 - д = 3*30
- д = 90
Пример 3: Автомобиль, движущийся со скоростью 33,2 м/с, начинает замедляться и в конце концов останавливается, если мы знаем, что приложенное ускорение составляло -2 м/с машина накрыта?
Данные
Vo = 33,2 м/с Vf = 0 м/с a = -2 м/с d = ?
- Напишите формулу
- вф 2 = во 2 + 2а * д
- Затем очищаем дистанцию
- d =
v f 2 — v o 2 /2a
- затем заменить данные и решить
- d =
0 — 33,2 2 /2(-2)
- d =
-33,2 2 /-4
- d =
-1102,24/-4
- д = 275,56
Пример 4: легкий самолет летит со скоростью 12 м/с, если он ускоряется и достигает скорости 20 м/с, и если мы знаем, что между этим он преодолел расстояние 300 м, какова была время и какое ускорение.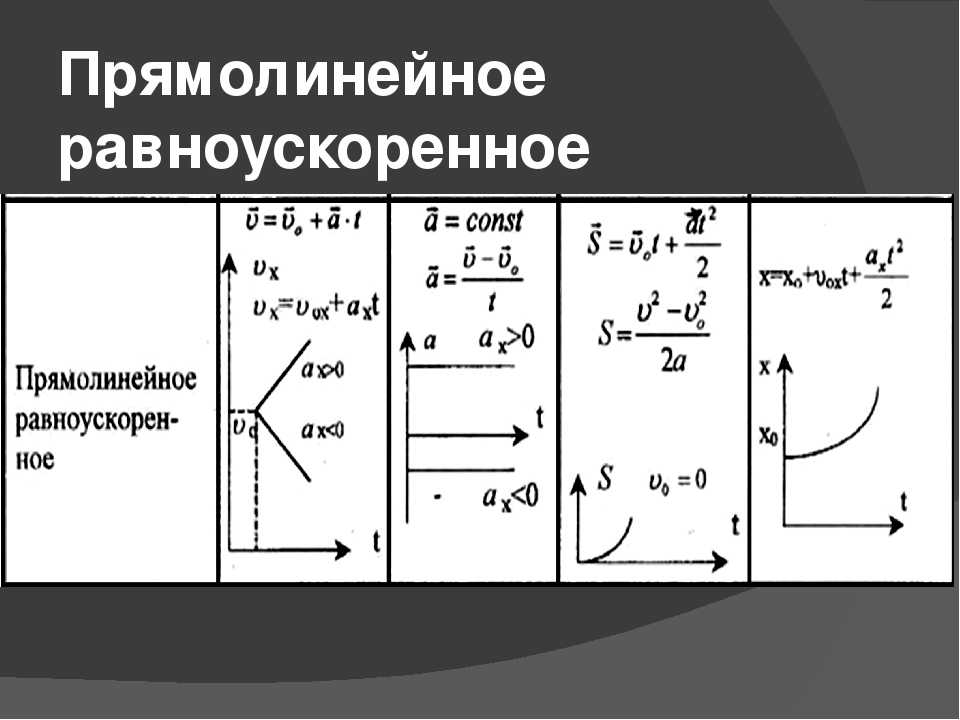
Данные
Vo = 12 м/с Vf = 20 м/с d = 300 t = ? а = ?
- Запишем пятую формулу
- d =
v o + v f /2
* т - Затем очищаем время и решаем
- t =
2d/v o + v f
- т =
2(300)/12 + 20
- т =
600/32
- т = 18,75 с
- Теперь, когда у нас есть время, пишем первую формулу и очищаем ускорение
- v f = v o + a * t
- а =
v ф — в о /т
- Затем замените данные и решите
- а =
20 — 12/18,75
- а =
8/18,75
- а = 0,43
Пример 5: к объекту прикладывалось ускорение 3 м/с в течение 9 секунд, если мы знаем, что объект преодолел расстояние 103 метра, рассчитайте конечную скорость и начальную скорость.
Данные
a = 3 м/с d = 103 м t = 9 с Vo = ? Вф = ?
- Напишите формулу
- d = v о * t + 1/2a * t 2
- Очистить начальную скорость
- v o =
d — 1/2a * t 2 /t
- И решить
- v o =
103 — 1/2(3) * (9) 2 /9
- v o =
103 — 1/2(3) * (81)/9
- v или =
103 — 1/2(243)/9
- v o =
103 — 121,5/9
- v o =
-18,5/9
- v или = -2,06
- Напишите первую формулу
- v f = v o + a * t
- Затем замените формулу и решите
- v f = -2,06 + 3 * 9
- в ф = -2,06 + 27
- v f = 24,94
Ejercicio 6: В парке развлечений есть американские горки, где первые 140 метров проходят по прямой, если с начала, когда автомобиль находится в состоянии покоя, и до достижения им 140 метров происходит постоянное ускорение 7,5 м. /с, рассчитайте время, за которое автомобиль преодолел 140 м, и конечную скорость.
/с, рассчитайте время, за которое автомобиль преодолел 140 м, и конечную скорость.
Datos
Vo = 0 м/с d = 140 м a = 7,5 м/с t = ? Вф = ?
- Напишите уравнение
- вф 2 = во 2 + 2а * д
- Заменить данные и решить
- вф 2 = во 2 + 2а * д
- vf 2 = 0 + 2(7,5) * 140
- вф 2 = 0 + 15 * 140
- vf = √ 2100
- vf = 45,82
- Теперь найдем время
- вф = во + а * т
- t =
v f — v o /a
- т =
45,82 — 0/7,5
- т = 6,11
Пример 7: Спутник в космосе, находящийся в состоянии покоя, изменит свое положение, двигаясь по прямой линии, если он достигнет скорости 3000 м/с всего за 0,9 с, какое ускорение было приложено и определите расстояние.
Данные
Vf = 3000 м/с Vo = 0 t = 0,9 с d = ? а = ?
- Сначала найдем расстояние по пятой формуле
- d =
v o + v f /2
* t - d =
0 + 3000/2
* 0,9 - д = 1500*0,9
- д = 1350
- И затем мы собираемся вычислить ускорение
- v f = v o + a * t
- а =
v f — v о /т
- а =
3000/0,9
- а = 3333,33
Пример 8: Лодка, плывущая по озеру, движется со скоростью 5 м/с, но если она ускоряется на 1 м/с на протяжении 40 метров, рассчитайте время, за которое она ускорилась.
Данные
d = 40 м Vo = 5 м/с a = 1 м/с t = ?
Этот пример можно решить разными способами, потому что, если мы посмотрим в формулах ту, которая позволяет нам найти время, имея расстояние, начальную скорость и ускорение, есть только одно и второе уравнение, но чтобы очистить время в этой формуле — непростая работа, поэтому самый простой способ сделать это — сначала найти другие данные с другими уравнениями, например, мы могли бы найти начальную скорость с помощью первого уравнения, а затем использовать первую или пятую формулу, чтобы найти время, но в этом случае мы собираемся решить это трудным путем.

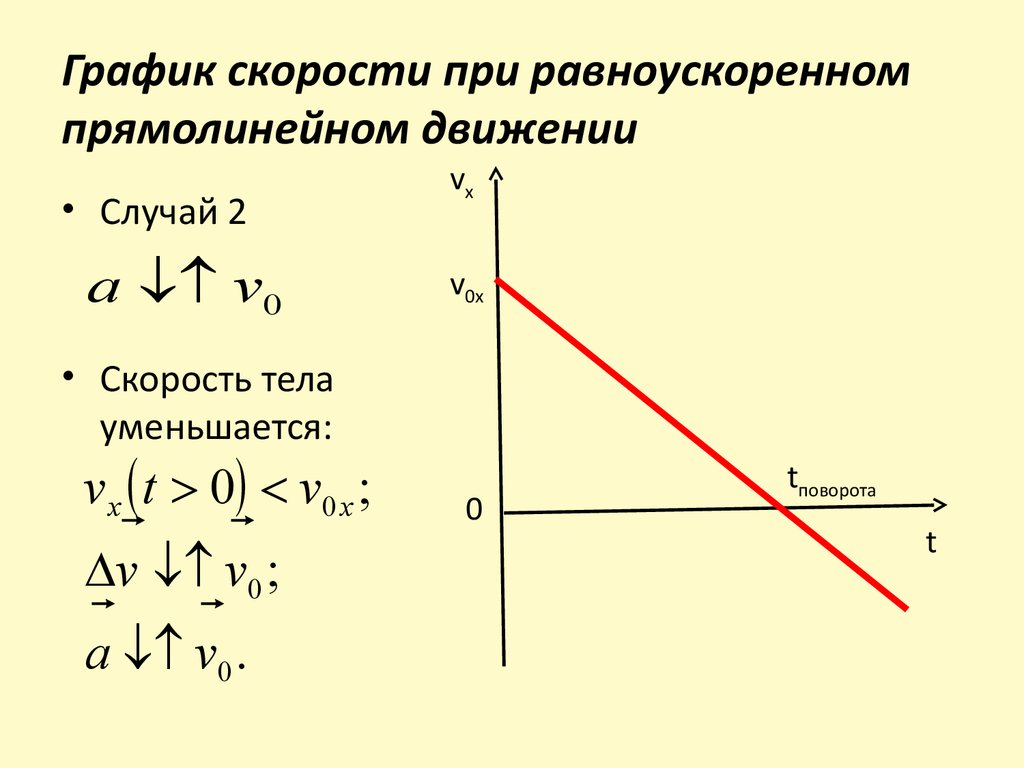 Но иногда для более
быстрого решения задач можно
использовать формулы модуля скорости и
пути.
Но иногда для более
быстрого решения задач можно
использовать формулы модуля скорости и
пути.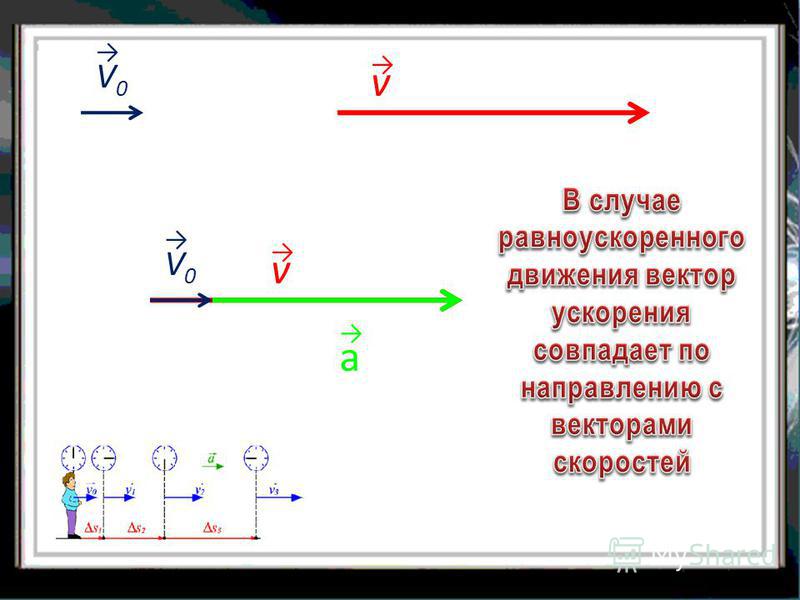
 Тело
двигалось равнозамедленно,
остановилось, а затем вновь начало
двигаться (равноускоренно) в противоположном
направлении: например, мяч, брошенный
вертикально вверх.
Тело
двигалось равнозамедленно,
остановилось, а затем вновь начало
двигаться (равноускоренно) в противоположном
направлении: например, мяч, брошенный
вертикально вверх. Его единицей в Международной системе (СИ) является метр (м)
Его единицей в Международной системе (СИ) является метр (м)
Leave A Comment