Равнобедренном треугольнике abc с основанием ac внешний угол при вершине c равен 123: В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° Найдите…

2011 Срочно плиз дам 50баллов

Математика

21 секунд назад

Для визначення поверхневого натягу води десятикласник використав піпетку, діаметр вихідного отвору якої дорівнює 2 мм. Яке значення поверхневого натягу одержав юнак. якщо в ході досліду він з’ясував, що об’єм 40 краплин води дорівнює 2 мл?

Математика

5 минут назад

алгебра , срочно! 90 балллов! ТОЛЬКО ЧЕТНЫЕ НОМЕРА! тема — площадь криволинейной трапеции и интеграл

Математика

5 минут назад

8. Реши задачу. Закладка и карандаш сколько раз карандаш закладка стоит 5 тг? вместе стоят 50 тг. Во дороже закладки, если​

Математика

5 минут назад

Задание 4. Реши задачу: Два ученика решили 437 примеров на умножение. Один из них работал 9 минут, а другой 10 минут. Сколько примеров решил каждый ученик? СРОЧНО ФОТО БЕЗ ФОТО НЕТ​

Математика

5 минут назад

17. Определите треугольник с наибольшим периметром. b) a) 3 cm 4,2 cm 3 cm 2 cm 6,3 cm 6 cm 3 cm 6,5 cm 6 cm​

Математика

5 минут назад

Запишите выражение в виде дроби: 6:7​

Математика

6 минут назад

Подарок упакован в коробку, которая имеет форму прямоугольного параллелепипеда. Длина двух сторон грани основания — 8 см и 12 см, длина бокового ребра коробки — 18 см.

Сколько бумаги потребуется для упаковки подарка?

Математика

10 минут назад

запишите выражение в виде дроби: а÷7​

Математика

15 минут назад

6. Реши задачу по схеме. В магазин до обеда привезли 22 книги, а после обеда 14 книг. Из них 9 книг продали. Сколько книг осталось?​

Математика

15 минут назад

б) Мастер за 6 часов сделал 210 дет., а его ученик за 8 часов 224 дет. У кого производительность больше и на сколько ?

Математика

15 минут назад

запишите выражение в виде дроби: k:45​

Математика

25 минут назад

Practice просто на смог уделить.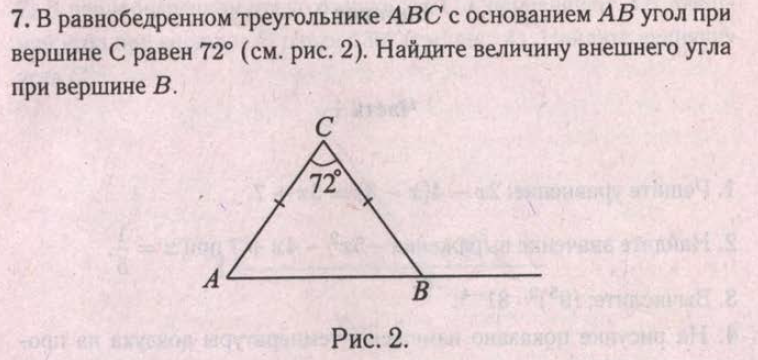 Отдаю много баллов!!!

Математика

30 минут назад

1. Вычислите: — 21 + 84 : 14 с решением

Математика

30 минут назад

Запиши у вигляді неправильного дробу

Все предметы

Выберите язык и регион

English

United States

Polski

Polska

Português

Brasil

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Русский

Россия

How much to ban the user?

1 hour 1 day 100 years

Равнобедренный треугольник определение рисунок.

Углы возле основания равнобедренного треугольника равны между собой

Равнобедренный треугольник — это треугольник , в котором две стороны равны между собой по длине. Равные стороны называются боковыми, а последняя — основанием. По определению, правильный треугольник также является равнобедренным, но обратное утверждение неверно.

Свойства

• Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Также равны биссектрисы , медианы и высоты , проведённые из этих углов.
• Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой. Центры вписанной и описанной окружностей лежат на этой линии.
• Углы, противолежащие равным сторонам, всегда острые (следует из их равенства).

Пусть a — длина двух равных сторон равнобедренного треугольника,

b — длина третьей стороны, α и β — соответствующие углы, R — радиус описанной окружности , r — радиус вписанной .

Стороны могут быть найдены следующим образом:

Углы могут быть выражены следующими способами:

Периметр равнобедренного треугольника может быть вычислен любым из следующих способов:

Площадь треугольника может быть вычислена одним из следующих способов:

(формула Герона).

Признаки

• Два угла треугольника равны.
• Высота совпадает с медианой.
• Высота совпадает с биссектрисой.
• Биссектриса совпадает с медианой.
• Две высоты равны.
• Две медианы равны.
• Две биссектрисы равны (теорема Штейнера — Лемуса).

См. также

Wikimedia Foundation . 2010 .

Смотреть что такое «Равнобедренный треугольник» в других словарях:

РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК, ТРЕУГОЛЬНИК, имеющий две равные по длине стороны; углы при этих сторонах также равны … Научно-технический энциклопедический словарь

И (прост.) трёхугольник, треугольника, муж. 1. Геометрическая фигура, ограниченная тремя взаимно пересекающимися прямыми, образующими три внутренних угла (мат.

). Тупоугольный треугольник. Остроугольный треугольник. Прямоугольный треугольник.… … Толковый словарь Ушакова

РАВНОБЕДРЕННЫЙ, ая, ое: равнобедренный треугольник имеющий две равные стороны. | сущ. равнобедренность, и, жен. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

треугольник — ▲ многоугольник имеющий, три, угол треугольник простейший многоугольник; задается 3 точками, не лежащими на одной прямой. треугольный. остроугольник. остроугольный. прямоугольный треугольник: катет. гипотенуза. равнобедренный треугольник. ▼… … Идеографический словарь русского языка

треугольник — ТРЕУГОЛЬНИК1, а, м чего или с опр. Предмет, имеющий форму геометрической фигуры, ограниченной тремя пересекающимися прямыми, образующими три внутренних угла. Она перебирала письма мужа пожелтевшие фронтовые треугольники. ТРЕУГОЛЬНИК2, а, м… … Толковый словарь русских существительных

У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия

Треугольник (многоугольник) — Треугольники: 1 остроугольный, прямоугольный и тупоугольный; 2 правильный (равносторонний) и равнобедренный; 3 биссектрисы; 4 медианы и центр тяжести; 5 высоты; 6 ортоцентр; 7 средняя линия. ТРЕУГОЛЬНИК, многоугольник с 3 сторонами. Иногда под… … Иллюстрированный энциклопедический словарь

Энциклопедический словарь

треугольник — а; м. 1) а) Геометрическая фигура, ограниченная тремя пересекающимися прямыми, образующими три внутренних угла. Прямоугольный, равнобедренный треуго/льник. Вычислить площадь треугольника. б) отт. чего или с опр. Фигура или предмет такой формы.… … Словарь многих выражений

А; м. 1. Геометрическая фигура, ограниченная тремя пересекающимися прямыми, образующими три внутренних угла. Прямоугольный, равнобедренный т.

Вычислить площадь треугольника. // чего или с опр. Фигура или предмет такой формы. Т. крыши. Т.… … Энциклопедический словарь

Тема урока

Равнобедренный треугольник

Цель урока

Познакомить учеников с равнобедренным треугольником;
Продолжать формировать навыки построения прямоугольных треугольников;
Расширить знания школьников о свойствах равнобедренных треугольников;
Закрепить теоретические знания при решении задач.

Задачи урока

Уметь формулировать, доказывать и использовать теорему о свойствах равнобедренного треугольника в процессе решения задач;
Продолжать развитие сознательного восприятия учебного материала, логического мышления, навыков самоконтроля и самооценки;
Вызвать познавательный интерес к урокам математики;
Воспитывать активность, любознательность и организованность.

План урока

1. Общие понятия и определения о равнобедренном треугольнике.
2. Свойства равнобедренного треугольника.
3. Признаки равнобедренного треугольника.
4. Вопросы и задания.

Равнобедренный треугольник

Равнобедренный треугольник — это треугольник, имеющий две равные стороны, которые называются боковыми сторонами равнобедренного треугольника, а его третья сторона называется основанием.

Вершиной данной фигуры есть та, которая расположена напротив его основания.

Угол, который лежит напротив основания называется углом при вершине этого треугольника, а два других угла называются углами при основании равнобедренного треугольника.

Виды равнобедренных треугольников

Равнобедренный треугольник, как и другие фигуры, может иметь разные виды. Среди равнобедренных треугольников встречаются остроугольные, прямоугольные, тупоугольные и равносторонние.

Остроугольный треугольник имеет все острые углы.
У прямоугольного треугольника угол его вершины прямой, а при основании расположены острые углы.
Тупоугольный имеет тупой угол при вершине, а при его основании углы острые.
У равностороннего все его углы и стороны равны.

Свойства равнобедренного треугольника

Противолежащие углы в отношении равных сторон равнобедренного треугольника, равны между собой;

Биссектрисы, медианы и высоты, проведённые из углов, противолежащих равным сторонам треугольника, равны между собой.

Биссектриса, медиана и высота, направлена и проведена к основанию треугольника, совпадают между собой.

Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, (они совпадают) проведенных к основанию.

Противолежащие равным сторонам равнобедренного треугольника углы, всегда острые.

Данные свойства равнобедренного треугольника применяются при решении задач.

Домашнее задание

1. Дайте определение равнобедренного треугольника.
2. В чем особенность этого треугольника?
3. Чем отличается равнобедренный треугольник от прямоугольного?
4. Назовите известные вам свойства равнобедренного треугольника.
5. Как вы думаете, можно ли на практике проверить равенство углов при основании и как это сделать?

Задание

А теперь давайте проведем небольшой блиц-опрос и узнаем, как вы усвоили новый материал.

Послушайте внимательно вопросы и ответьте верно ли такое утверждение, что:

1. Треугольник можно считать равнобедренным, если у него две стороны равны?
2. Биссектрисой называют отрезок, который соединяет вершину треугольника с серединой противоположной стороны?
3. Биссектрисой является отрезок, который делит угол, который соединяет вершину с точкой противоположной стороны пополам?

Советы относительно решения задач о равнобедренном треугольнике:

1. Для определения периметра равнобедренного треугольника достаточно умножить длину боковой стороны на 2 и сложить это произведение с длиной основы треугольника.
2. Если в задаче известны периметр и длина основы равнобедренного треугольника, то для нахождения длины боковой стороны достаточно отнять длину основы от периметра и найденную разницу разделить на 2.
3. А чтобы найти длину основы равнобедренного треугольника, зная и периметр, и длину боковой стороны, необходимо всего лишь умножить боковую сторону на два и отнять это произведение от периметра нашего треугольника.

Задачи:

1. Среди треугольников на рисунке определите один лишний и объясните свой выбор:

2. Определите, какие из изображенных на рисунке треугольников являются равнобедренными, назовите их основы и боковые стороны, а так же рассчитайте их периметр.

3. Периметр равнобедренного треугольника равен 21 см. Найдите стороны этого треугольника, если одна из них больше на 3 см. Какое количество решений может иметь данная задача?

4. Известно, что если боковая сторона и противолежащий основе угол одного равнобедренного треугольника равен боковой стороне и углу другого, то эти треугольники будут равны. Докажите это утверждение.

5. Подумайте и скажите, является ли любой равнобедренный треугольник равносторонним? И будет ли любой равносторонний треугольник равнобедренным?

6. Если стороны равнобедренного треугольника равны 4 м и 5 м, то каков будет его периметр? Сколько решений может иметь эта задача?

7. Если один из углов равнобедренного треугольника равен 91 градусу, то чему равны остальные углы?

8. Подумайте и ответьте, какие углы должны быть у треугольника, чтобы он одновременно был и прямоугольным, и равнобедренным?

А кто из вас знает, что такое треугольник Паскаля? Задачку на построение треугольника Паскаля часто задают для проверки навыков элементарного программирования. Вообще треугольник Паскаля относиться к комбинаторике и теории вероятности. Так что же это за такой треугольник?

Треугольник Паскаля — это бесконечный арифметический треугольник или таблица в форме треугольника, которая сформирована при помощи биномиальных коэффициентов. Простыми словами, вершиной и сторонами этого треугольника являются единицы, а сам он заполнен суммами двух чисел, которые расположены выше. Складывать такой треугольник можно до бесконечности, но если его очертить, то мы получим равнобедренный треугольник с симметричными строками относительно его вертикальной оси.

Подумайте, а где в повседневной жизни вам приходилось встречать равнобедренные треугольники? Не правда ли, крыши домов и древних архитектурных сооружений очень напоминают их? А вспомните, какая основа у египетских пирамид? Где еще вам встречались равнобедренные треугольники?

Равнобедренные треугольники с древних времен выручали греков и египтян при определении расстояний и высот. Так, например, древние греки определяли с его помощью издалека расстояние до корабля в море. А древние египтяне определяли высоту своих пирамид благодаря длине отбрасываемой тени, т.к. она представляла собой равнобедренный треугольник.

Начиная с древних времен, люди уже тогда оценили красоту и практичность этой фигуры, так как формы треугольников нас окружают всюду. Передвигаясь по разным селениям, мы видим крыши домов и других сооружений, которые напоминают нам о равнобедренном треугольнике, зайдя в магазин, мы нам встречаются пакеты с продуктами и соками треугольной формы и даже некоторые человеческие лица имеют форму треугольника. Эта фигура настолько популярна, что ее можно встретить на каждом шагу.

Предмети > Математика > Математика 7 класс

Треугольник, у которого две стороны равны между собой, называется равнобедренным. Эти его стороны называют боковыми, а третью сторону называют основанием. В этой статье мы расскажем Вам о том, какие бывают свойства равнобедренного треугольника.

Теорема 1

Углы возле основания равнобедренного треугольника равны между собой

Доказательство теоремы.

Допустим, мы имеем равнобедренный треугольник ABC, основание которого AB. Давайте рассмотрим треугольник BAC. Эти треугольники, по первому признаку, равны между собой. Так и есть, ведь BC = AC, AC = BC, угол ACB = углу ACB. Отсюда вытекает, что угол BAC = углу ABC, ведь это соответствующие углы наших равных между собой треугольников. Вот Вам и свойство углов равнобедренного треугольника.

Теорема 2

Медиана в равнобедренном треугольнике, которую провели к его основанию, является также высотой и биссектрисой

Доказательство теоремы.

Допустим, мы имеем равнобедренный треугольник ABC, основание которого AB, а CD — это медиана, которую мы провели к его основанию. В треугольниках ACD и BCD угол CAD = углу CBD, как соответствующие углы при основании равнобедренного треугольника (Теореме 1). А сторона AC = стороне BC (по определению равнобедренного треугольника). Сторона AD = стороне BD, Ведь точка D делит отрезок AB на равные части. Отсюда выходит, что треугольник ACD = треугольнику BCD.

Из равенства этих треугольников мы имеем равенство соответствующих углов. То есть угол ACD = углу BCD и угол ADC = углу BDC. Из равенства 1 выходит, что CD — это биссектриса. А угол ADC и угол BDC — смежные углы, и из равенства 2 выходит, что они оба прямые. Получается, что CD — это высота треугольника. Это и есть свойство медианы равнобедренного треугольника.

А теперь немного о признаках равнобедренного треугольника.

Теорема 3

Если в треугольнике два угла равны между собой, то такой треугольник равнобедренный

Доказательство теоремы.

Допустим, мы имеем треугольник ABC, в котором угол CAB = углу CBA. Треугольник ABC = треугольнику BAC по второму признаку равенства между треугольниками. Так и есть, ведь AB = BA; угол CBA = углу CAB, угол CAB = углу CBA. Из такого равенства треугольников мы имеем равенство соответствующих сторон треугольника — AC = BC. Тогда выходит, что треугольник ABC равнобедренный.

Теорема 4

Если в любом треугольнике его медиана является также и его высотой, то такой треугольник равнобедренный

Доказательство теоремы.

В треугольнике ABC мы проведем медиану CD. Она также будет являться и высотой. Прямоугольный треугольник ACD = прямоугольному треугольнику BCD, так как катет CD общий для них, а катет AD = катету BD. С этого следует, что их гипотенузы равны между собой, как соответственные части равных треугольников. Это значит, что AB = BC.

Теорема 5

Если три стороны треугольника равны трем сторонам другого треугольника, то эти треугольники равны

Доказательство теоремы.

Допустим, мы имеем треугольник ABC и треугольник A1B1C1 такие, в которых стороны AB = A1B1, AC = A1C1, BC = B1C1. Рассмотрим доказательство этой теоремы от противного.

Допустим, что эти треугольники не равны между собой. Отсюда имеем, что угол BAC не равен углу B1A1C1, угол ABC не равен углу A1B1C1, угол ACB не равен углу A1C1B1 одновременно. В противном случае, эти треугольники были бы равны по вышерассмотренному признаку.

Допустим, что треугольник A1B1C2 = треугольнику ABC. У треугольника вершина C2 лежит с вершиной C1 относительно прямой A1B1 в одной полуплоскости. Мы предположили, что вершины C2 и C1 не совпадают. Допустим, что точка D — это середина отрезка C1C2. Так мы имеем равнобедренные треугольники B1C1C2 и A1C1C2, у которых есть общее основание C1C2. Выходит, что их медианы B1D и A1D — это также и их высоты. А это значит, что прямая B1D и прямая A1D перпендикулярны прямой C1C2.

B1D и A1D имеют разные точки B1 и A1, и соответственно, не могут совпадать. Но ведь через точку D прямой C1C2 мы можем провести всего одну перпендикулярную ей прямую. У нас получилось противоречие.

Теперь Вы знаете, какие бывают свойства равнобедренного треугольника!

Свойства равнобедренного треугольника выражают следующие теоремы.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Докажем одну из них, например теорему 2.5.

Доказательство. Рассмотрим равнобедренный треугольник ABC с основанием ВС и докажем, что ∠ В = ∠ С. Пусть AD — биссектриса треугольника ABC (рис.1). Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD — общая сторона, ∠ 1 = ∠ 2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠ В = ∠ С. Теорема доказана.

С использованием теоремы 1 устанавливается следующая теорема.

Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (рис. 2).

Замечание. Предложения, установленные в примерах 1 и 2, выражают свойства серединного перпендикуляра к отрезку. Из этих предложений следует, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке .

Пример 1. Доказать, что точка плоскости, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.

Решение. Пусть точка М равноудалена от концов отрезка АВ (рис. 3), т. е. AM = ВМ.

Тогда Δ АМВ равнобедренный. Проведем через точку М и середину О отрезка АВ прямую р. Отрезок МО по построению есть медиана равнобедренного треугольника АМВ, а следовательно (теорема 3), и высота, т. е. прямая МО, есть серединный перпендикуляр к отрезку АВ.

Пример 2. Доказать, что каждая точка серединного перпендикуляра к отрезку равноудалена от его концов.

Решение. Пусть р — серединный перпендикуляр к отрезку АВ и точка О — середина отрезка АВ (см. рис. 3).

Рассмотрим произвольную точку М, лежащую на прямой р. Проведем отрезки AM и ВМ. Треугольники АОМ и ВОМ равны, так как у них углы при вершине О прямые, катет ОМ общий, а катет ОА равен катету ОВ по условию. Из равенства треугольников АОМ и ВОМ следует, что AM = ВМ.

Пример 3. В треугольнике ABC (см. рис. 4) АВ = 10 см, ВС = 9 см, АС = 7 см; в треугольнике DEF DE = 7 см, EF = 10 см, FD = 9 см.

Сравнить треугольники ABC и DEF. Найти соответственно равные углы.

Решение. Данные треугольники равны по третьему признаку. Соответственно равные углы: А и Е (лежат против равных сторон ВС и FD), В и F (лежат против равных сторон АС и DE), С и D (лежат против равных сторон АВ и EF).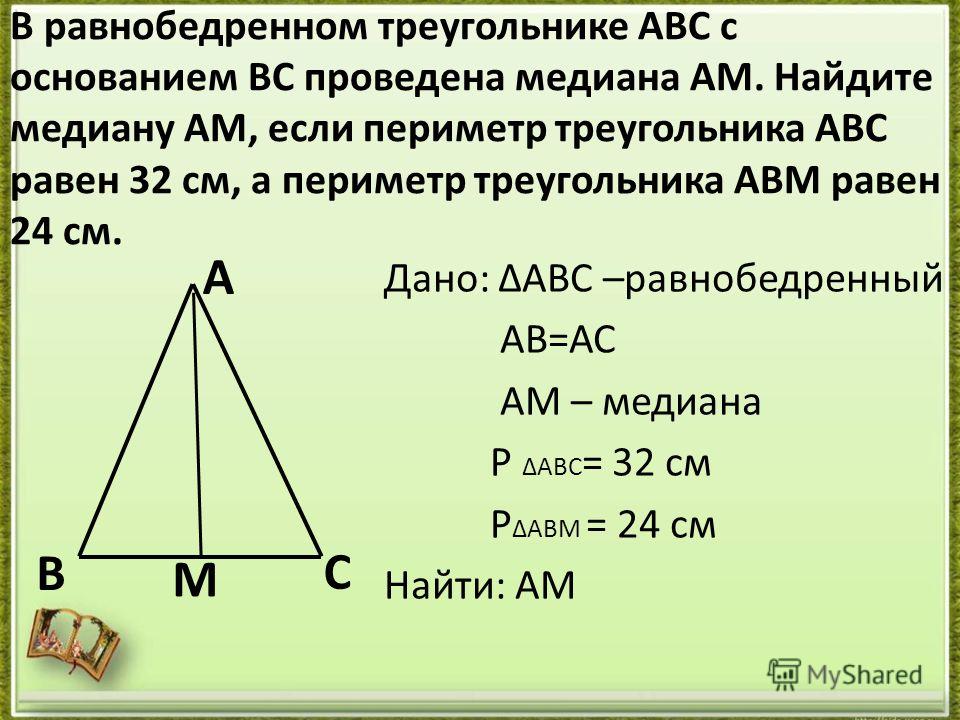

Пример 4. На рисунке 5 АВ = DC, ВС = AD, ∠B = 100°.

Найти угол D.

Решение. Рассмотрим треугольники ABC и ADC. Они равны по третьему признаку (АВ = DC, ВС = AD по условию и сторона АС — общая). Из равенства этих треугольников следует, что ∠ В = ∠ D, но угол В равен 100°, значит, и угол D равен 100°.

Пример 5. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC . Ответ дайте в градусах.

Видео-решение.

На данном уроке будет рассмотрена тема «Равнобедренный треугольник и его свойства». Вы узнаете, как выглядят и чем характеризуются равнобедренный и равносторонний треугольники. Докажете теорему о равенстве углов при основании равнобедренного треугольника. Рассмотрите также теорему о биссектрисе (медиане и высоте), проведенной к основанию равнобедренного треугольника. В конце урока вы разберете две задачи с использованием определения и свойств равнобедренного треугольника.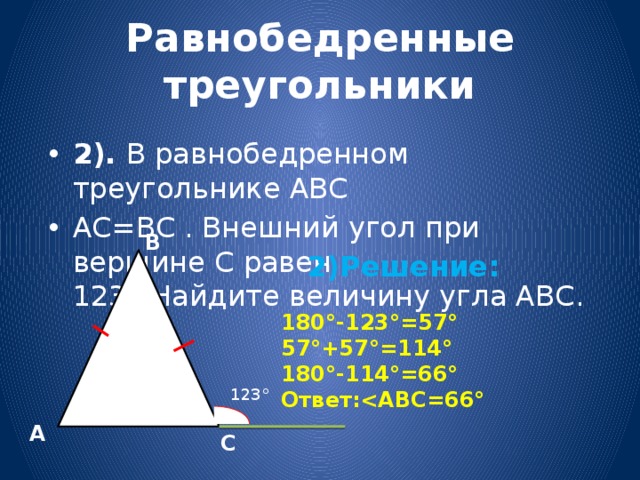

Определение: Равнобедренным называется треугольник, у которого равны две стороны.

Рис. 1. Равнобедренный треугольник

АВ = АС — боковые стороны. ВС — основание.

Площадь равнобедренного треугольника равна половине произведения его основания на высоту.

Определение: Равносторонним называется треугольник, у которого все три стороны равны.

Рис. 2. Равносторонний треугольник

АВ = ВС = СА.

Теорема 1: В равнобедренном треугольнике углы при основании равны.

Дано: АВ = АС.

Доказать: ∠В =∠С.

Рис. 3. Чертеж к теореме

Доказательство: треугольник АВС = треугольнику АСВ по первому признаку (по двум равным сторонам и углу между ними). Из равенства треугольников следует равенство всех соответствующих элементов. Значит, ∠В = ∠С, что и требовалось доказать.

Теорема 2: В равнобедренном треугольнике биссектриса , проведенная к основанию, является медианой и высотой .

Дано: АВ = АС, ∠1 = ∠2.

Доказать: ВD = DC, AD перпендикулярно BC.

Рис. 4. Чертеж к теореме 2

Доказательство: треугольник ADB = треугольнику ADC по первому признаку (AD — общая, АВ = АС по условию, ∠BAD = ∠DAC). Из равенства треугольников следует равенство всех соответствующих элементов. BD = DC, так как они лежат против равных углов. Значит, AD является медианой. Также ∠3 = ∠4, поскольку они лежат против равных сторон. Но, к тому же, они в сумме равняются . Следовательно, ∠3 = ∠4 = . Значит, AD является высотой треугольника, что и требовалось доказать.

В единственном случае a = b = . В этом случае прямые АС и ВD называются перпендикулярными.

Поскольку биссектрисой, высотой и медианой является один и тот же отрезок, то справедливы и следующие утверждения:

Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

Пример 1: В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметр равен 50 см. Найдите стороны треугольника.

Дано: АВ = АС, ВС = AC. Р = 50 см.

Найти: ВС, АС, АВ.

Решение:

Рис. 5. Чертеж к примеру 1

Обозначим основание ВС как а, тогда АВ = АС = 2а.

2а + 2а + а = 50.

5а = 50, а = 10.

Ответ: ВС = 10 см, АС = АВ = 20 см.

Пример 2: Докажите, что в равностороннем треугольнике все углы равны.

Дано: АВ = ВС = СА.

Доказать: ∠А = ∠В = ∠С.

Доказательство:

Рис. 6. Чертеж к примеру

∠В = ∠С, так как АВ=АС, а ∠А = ∠В, так как АС = ВС.

Следовательно, ∠А = ∠В = ∠С, что и требовалось доказать.

Ответ: Доказано.

На сегодняшнем уроке мы рассмотрели равнобедренный треугольник, изучили его основные свойства. На следующем уроке мы порешаем задачи по теме равнобедренного треугольника, на вычисление площадт равнобедренного и равностороннего треугольника.

1. Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. — М.: Просвещение.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. — М.: Просвещение.
3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. — М.: Просвещение, 2010.

1. Словари и энциклопедии на «Академике» ().
2. Фестиваль педагогической идеи «Открытый урок» ().
3. Кaknauchit.ru ().

1. № 29. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. — М.: Просвещение, 2010.

2. Периметр равнобедренного треугольника равен 35 см, а основа втрое меньше боковой стороны. Найдите стороны треугольника.

3. Дано: АВ = ВС. Докажите, что ∠1 = ∠2.

4. Периметр равнобедренного треугольника равен 20 см, одна из его сторон в два раза больше другой. Найдите стороны треугольника. Сколько решений имеет задача?

Математическая задача: Равнобедренная 64774 — практическая математическая задача, планиметрия

На рисунке показана равнобедренная трапеция CDEF. Величина угла α равна 73 градусам. Вычислите величину угла β в градусах.

Правильный ответ:

β =  107 °

Пошаговое объяснение:

α=73 ∘  ∠FED=180−α=180−73=107 ∘ ∠CFE=∠FED=107=107 ∠ =∠CFE=107=107∘

Нашли ошибку или неточность? Не стесняйтесь

пишите нам

. Спасибо!

You need to know the following knowledge to solve this word math problem:

• planimetrics
• trapezoid

Units of physical quantities:

• angle

Grade of the word problem:

• Практика для 12-летних
• Практика для 13-летних

 

Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1

• Равнобедренная трапеция
  Трапеция ЮЭБ (Ю||ЭБ) равнобедренная. Величина угла при вершине U равна 49 градусов. Вычислите величину угла при вершине B.
• Остаток 25441
  Равнобедренный треугольник имеет размер углов при основании альфа = бета = 34 градуса 34 минуты. Вычислите величину угла при оставшейся вершине треугольника в градусах и минутах.
• В треугольнике
  В треугольнике ABC величина внутреннего угла гамма равна одной трети угла альфа. Размер угла бета на 80 градусов больше размера угла гамма. Вычислите величины внутренних углов треугольника ABC.
• Трапеция ISO
  Вычислите площадь равнобедренной трапеции с основанием 95°, катетом 27° и углом между основанием и катетом 70°.
• Внутренние углы
  Величина внутреннего угла при центральной вершине C равнобедренного треугольника ABC равна 72°. Прямая p, параллельная основанию этого треугольника, делит треугольник на трапецию и меньший треугольник. Насколько велики внутренние углы трапеций
• Вычислить 48073
  Вычислить площадь равнобедренной трапеции ABCD, если a = 14 см, c = 8 см, а величина угла DAB равна 52°.
• Трапеция ABCD
  На рисунке показана трапеция ABDC, в которой AB || CD. Отрезки RN и LM проведены параллельно AB так, что AJ=JK=KP. Если AB=0,5 м и AP=BQ=1,8 м, найдите длины AC, BD, RN и LM. угол D=угол C=60
• Равнобедренная трапеция v3
  В равнобедренной трапеции ABCD величина угла β = 123° Определить величину углов α, γ и δ.
• Равнобедренный 65784
  Равнобедренный треугольник имеет угол при основании 78°20′. Вычислите величину угла между плечами.
• Четыре стороны трапеции
  В трапеции ABCD |AB| = 73,6 мм; |БК| = 57 мм; |CD| = 60 мм; |ОБЪЯВЛЕНИЕ| = 58,6 мм. Вычислите величину его внутренних углов.
• Трапеция v3
  Равнобедренная трапеция имеет угол при первом основании на 40 градусов меньше угла при втором основании. Какие большие углы имеет эта трапеция?
• Угол
  Прямая линия p, заданная уравнением y = (-8)/(6) x +78. Вычислите величину угла в градусах между линией p и осью y.
• Вычислить 80358
  Треугольник имеет внутренние углы 58º 20′ и 83º 40′. Вычислите величину терции в градусах угла.
• Равнобедренная трапеция
  Вычислите длину окружности и площадь равнобедренной трапеции, если известны размеры оснований 8 и 12 см, а размер плеч 5 см.
• Строительство 6411
  Нарисуйте равнобедренную трапецию ABDC, если a = 6 см, v = 5 см, бета = 60 градусов. / эскиз, процедура, конструкция /
• Углы внутренние и внешние
  Вычислите оставшиеся внутренние и внешние углы треугольника, если вы знаете, что внутренний угол γ (гамма) = 34 градуса, а один внешний угол равен 78 градусам и 40′. Определите, что это за треугольник, по величине его углов.
• Параллелограмм 65954
  В параллелограмме ABCD AB = 8, BC = 5, BD = 7. Вычислить модуль угла α = ∠DAB (в градусах).

unit-4-test-study-guide-congruent-triangles — Googlesuche

AlleBilderVideosBücherMapsNewsShopping

suchoptionen

[PDF] Учебное пособие по тесту, Модуль 4 (конгруэнтные треугольники)

msjungmath. weebly.com › Geometry_chapter_2_review_answers

Учебное пособие по тесту, модуль 4. (равные треугольники). Тема 1: Классификация треугольников. 1. Классифицируйте каждый треугольник по его углам и сторонам. а. MBE: правильно, разносторонний.

Тема 4 Конгруэнтные треугольники: Учебное пособие — YouTube

www.youtube.com › смотреть

16.11.2020 · Тема 4 Конгруэнтные треугольники: Учебное пособие. Посмотреть позже. Делиться. Копировать ссылку. Информация. Покупка товаров. Нажмите, чтобы…
Dauer: 1:01:07
Прислан: 16.11.2020

Геометрия. Учебное пособие №4. Конгруэнтные треугольники. Quizlet

quizlet.com многоугольники, жесткие движения, угол и многое другое.

Геометрия Раздел 4 Учебное пособие | Математика — Викторина

quizizz.com › admin › викторина › геометрия-единица-4-стад…

Сыграйте в эту игру, чтобы повторить математику. Классифицируйте треугольник ABE по его углам и сторонам.

Учебное пособие по тесту Geometry Unit 4 | Course Hero — Course Hero

www.coursehero.com › file › Geometry-Unit-4-Test…

Geometry Unit 4 Test Study Guide Свойства треугольников 1. … 22 — 25: Определить, является ли сторона длины могут образовать треугольник. Обоснуйте свой ответ с помощью …

image.jpg — Учебное пособие по тесту Раздела 4 (Конгруэнтные треугольники) Имя

www.coursehero.com › file › imagejpg

View image.jpg из ALGEBRA 123 в Alcorn Central High School . Учебное пособие по тесту, Модуль 4 (Конгруэнтные треугольники) Имя: Маккензи Виллэм Дата: 15.02.22 Тема …

Ähnliche Fragen

Каковы 4 признака конгруэнтности в треугольнике?

Как вы изучаете конгруэнтные треугольники?

Является ли тест AAAA на соответствие треугольников?

Каковы 5 критериев конгруэнтности в треугольнике?

[PDF] Междунар. Geometry Unit 4 Test Review 1

Washingtonlee.