Банк ЕГЭ | Открытый банк заданий
Банк ЕГЭ Банк решенных | ЕГЭ по математике В1 ● В2 ● В3 ● В4 ● В5 ● В6 ● В7 |
Полезные советы | Лента задачек | |
| С4Дан параллелограмм $ABCD$, сторона которого $AB=13$. Из углов $А$ и $В$ проведены биссектрисы, которые пересекаются в точке $O$. Расстояние от точки $O$ до отрезка АВ равно $\frac{60}{13}$. В7Найдите, если $\operatorname{tg}\alpha=-4$ [посмотреть решение] |
wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье.
Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее.
Задание 7 ЕГЭ по математике (профиль) часть 3
Тренажер задания 7 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 7 — задачи на иррациональные, показательные и логарифмические функции. Это задание на применение математических знаний при решении прикладных задач. Номер заданий соответствует номеру заданий в базе mathege.ru.
27982 Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a км/ч2. Скорость V вычисляется по формуле где l — пройденный автомобилем путь.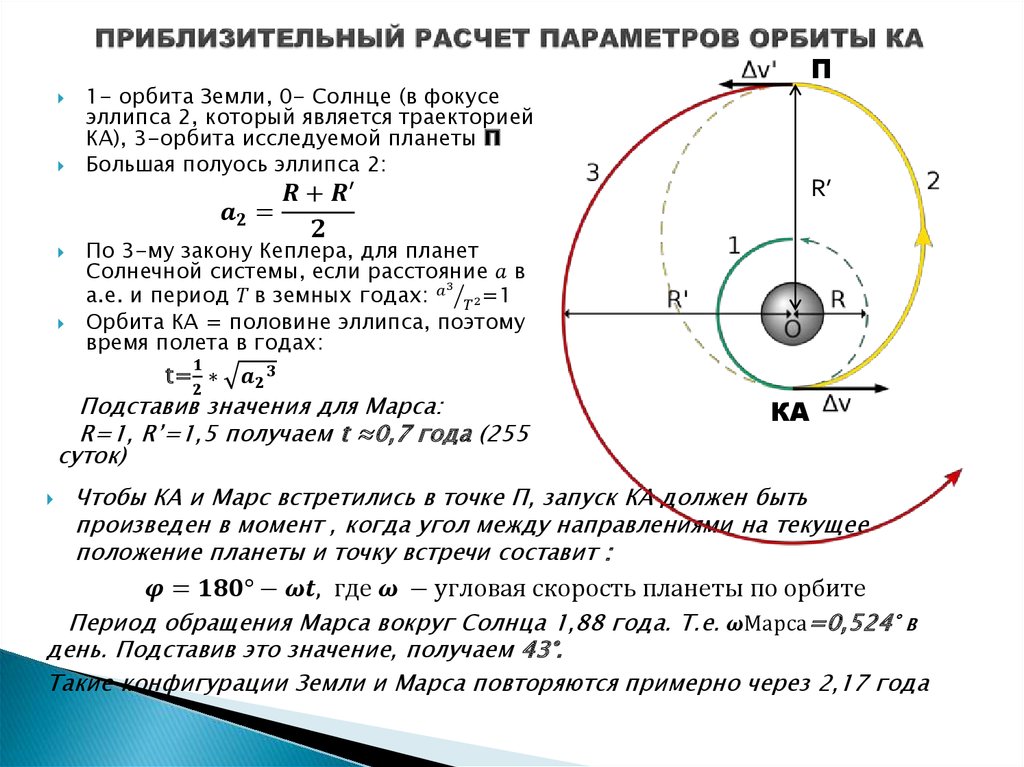
Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость 100 км/ч. Ответ выразите в км/ч2.
27983 При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону:
где l0 = 5 м — длина покоящейся ракеты, c = 3 · 105 км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с.
27984 Наблюдатель находится на высоте h, выраженной в метрах. Расстояние от наблюдателя до до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле:
где R = 6400 км — радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 4 километров? Ответ выразите в метрах.
27985 Расстояние от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле:
где R = 6400 км — радиус Земли.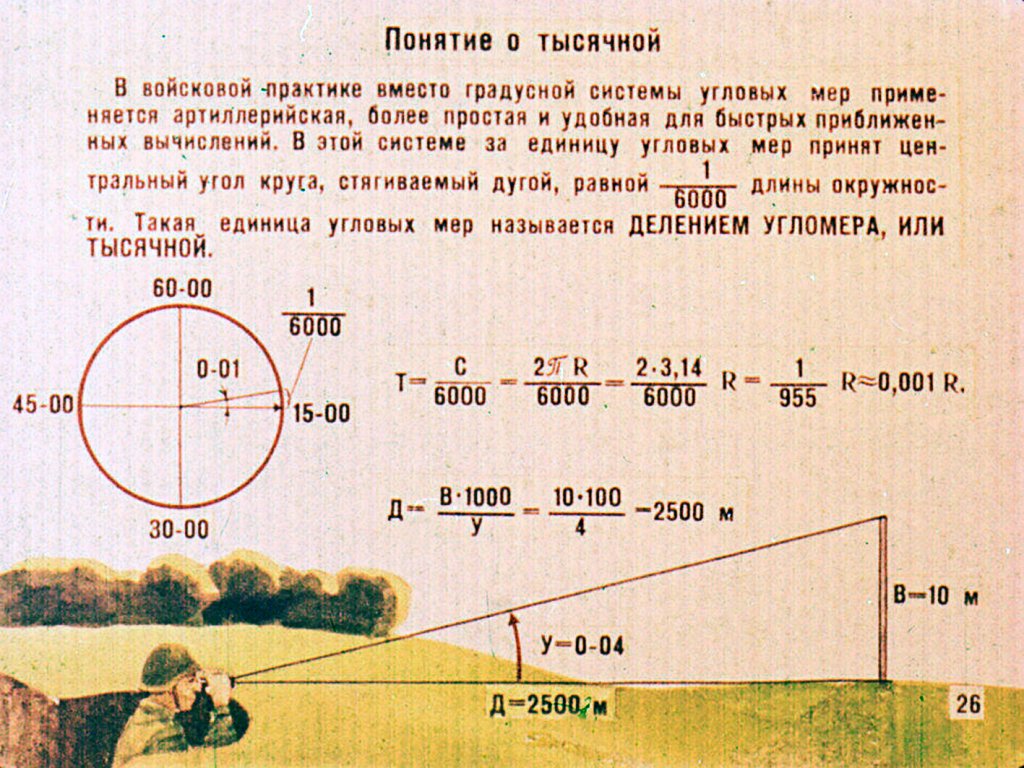
Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?
27986 Расстояние от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле:
где R = 6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?
27987 Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a = 5000 км/ч2. Скорость v вычисляется по формуле где l — пройденный автомобилем путь. Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 100 км/ч.
27990 При адиабатическом процессе для идеального газа выполняется закон pVk = 105 Па · м5, где p — давление в газе в паскалях, V — объeм газа в кубических метрах, k = 5/3.
Найдите, какой объем V (в куб.м) будет занимать газ при давлениях p, равном 3,2 · 106 Па?
27993 Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объeм и давление связаны соотношением , где p1 и р2 — давление в газе(в атм.), V1 и V2 — объeм газа (в литрах) в начальном и конечном состояниях. Изначально объeм газа равен 1,6 л, а давление газа равно одной атмосфере. До какого объема нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах.
27991 В ходе распада радиоактивного изотопа его масса уменьшается по закону:
где m0 — начальная масса изотопа, t — время, прошедшее от начального момента, T— период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг?
27992 Уравнение процесса, в котором участвовал газ, записывается в виде pVa = const, где p (Па) — давление в газе, V — объeм газа в кубических метрах, a — положительная константа.
При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
27994 В телевизоре емкость высоковольтного конденсатора C = 2 · 10-6 Ф. Параллельно с конденсатором подключeн резистор с сопротивлением R = 5 · 106 Ом. Во время работы телевизора напряжение на конденсаторе U0 = 16 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением:
(с), где α = 0,7 — постоянная. Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло 21 с. Ответ дайте в киловольтах.
27995 Для обогрева помещения, температура в котором поддерживается на уровне Tп = 20º C, через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды m = 0,3 кг/с.
Проходя по трубе расстояние x, вода охлаждается от начальной температуры Tв = 60º C до температуры T, причём:
где c = 4200 Вт·с/кг· ºC — теплоёмкость воды, γ = 21 Вт/м · ºC — коэффициент теплообмена, а α =0,7 — постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 84 м.
27996 Водолазный колокол, содержащий в начальный момент времени υ= 3 моля воздуха объeмом V1=8 л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма V2. Работа, совершаемая водой при сжатии воздуха, определяется выражением:
где α = 5,75 Дж/моль·К — постоянная, а T = 300 К — температура воздуха. Найдите, какой объeм V2 (в литрах) станет занимать воздух, если при сжатии воздуха была совершена работа в 10350 Дж.
27997 Водолазный колокол, содержащий υ = 2 моля воздуха при давлении p1 = 1,5 атмосферы, медленно опускают на дно водоeма.
При этом происходит изотермическое сжатие воздуха до конечного давления р2. Работа, совершаемая водой при сжатии воздуха, определяется выражением (Дж), где α = 5,75 Дж/моль · К — постоянная, T = 300 К — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 6900 Дж.
Понравилось это:
Нравится Загрузка…
Правильная длина
Правильная длинаПравильная длина
Проблема:
Решение:
- Концепты:
Лоренцево сокращение - Рассуждение:
Для наблюдателя, находящегося в движении относительно объекта, размеры объекта сокращаются в 1/γ раз в направлении движения. - Детали расчета:
L’ = L 0 /γ, γ = (1 — v 2 /c 2 ) -½ .
По данным, приведенным для автомобиля, вычисляем γ = 5/3.
Проблема:
Радиус галактики 3*10 20 м, измеренный в собственном покое
рамка.
(а) Если время, необходимое космическому кораблю, чтобы пересечь всю галактику, составляет 300 лет.
измеряется в системе покоя космического корабля, какова относительная скорость космического корабля
а галактика?
(b) Сколько времени проходит на Земле во время этого путешествия?
Решение:
- Концепты:
Релятивистская кинематика, собственный интервал времени, Лоренцево сокращение - Рассуждение:
Нам задан собственный интервал времени между двумя событиями и пространство координата этих двух событий в другом кадре. - Детали расчета:
(а) τ = 300 лет. Это интервал времени между моментами, когда противоположные края галактики передать космический корабль.
L = L 0 /γ – диаметр галактики в кадре космический корабль.
L 0 = 6*10 20 м = 6,34*10 4 св.
v = L/τ = L 0 /(γτ).
v 2 = (1 — v 2 /c 2 )L 0 2 /τ 2 , v 2 /c 2 = L 0 2 /(c 2 τ 2 + L 0
v/c = 0,99998 с.
(б) t = L 0 /v = 6,34*10 4 лет.
Задача:
Космический корабль имеет правильную длину 100 метров. Он проходит недалеко от
Поверхность Земли с постоянной скоростью 0,8 с. Земные наблюдатели решили
измерить длину корабля, возведя две башни, совпадающие с
концы корабля одновременно (в системе отсчета Земли) при его прохождении.
(а)
На каком расстоянии друг от друга наблюдатели на Земле строят башни?
(b) Как долго
говорят ли земные наблюдатели, что нос корабля должен пройти от
башня А в башню Б?
(c) Как долго, согласно измерениям в
каркас космического корабля, нужно ли носу корабля переместиться из башни А в
башня Б?
(e) В кадре космического корабля, сколько времени требуется луч света, идущий от передней части космического корабля к задней?
(ф) Сколько времени, по мнению земных наблюдателей, требуется для луча свет, чтобы путешествовать от передней к задней части движущегося космического корабля?
(Дать числовые ответы!)
Решение:
- Понятия:
Релятивистская кинематика - Рассуждение:
Нас просят вычислить различные пространственные и временные интервалы в разных инерциальных системах отсчета. - Детали расчета:
(a) Сокращение длины: L = L 0 /γ, γ = (1 — v 2 /с 2 ) — ½ = 1/0,6 = 1,667.
л = 60 м — расстояние между башнями.
(б) t = L/v = (60 м)/(2,4*10 8 м/с) = 2,5*10 -7 с.
(в) τ = t/γ = 1,5*10 -7 с. В космические корабли, обрамляющие два события, имеют одинаковые пространственные координаты, τ равно нужное время.
(г) d с = vτ = (2,4*10 8 м/с)(1,5*10 -7 с) = 36 м.
(д) т с = (100 м)/(3*10 8 м/с) = 3,33*10 -7 с.
(е) ct e = 60 m — vt
Проблема:
Предположим, что радиус покоя Земли равен 6400 км. а его орбитальная скорость вокруг солнца 30 км/с, сколько диаметр Земли кажутся укороченными вдоль направления движения для наблюдателя на Солнце?
Решение:
- Концепты:
Лоренцево сокращение - Рассуждение:
Для наблюдателя, находящегося в движении относительно объекта, размеры объекта сокращаются в 1/γ раз в направлении движения. - Детали расчета:
β = v/c = (30 км/с)/(3*10
1/γ = (1 − β 2 ) ½ ~ (1 — ½β 2 )
ΔL = L 0 − Л = Л 0 − L 0 /γ = Л 0 − Л 0 (1 — ½β 2 ) = ½ л 0 β 2 = ½ * 6,4*10 6 м * 10 -8 = 3,2 см
Диаметр Земли уменьшился в 3,2 раза. см в направлении его движения.
Задача:
Космический корабль имеет правильную длину 100 метров. Он путешествует
вблизи поверхности Земли с постоянной скоростью 0,8 с. Земные наблюдатели
решите измерить длину корабля, возведя две башни, совпадающие
одновременно с концами корабля (в системе отсчета Земли) при его прохождении.
(б) Сколько времени, по мнению земных наблюдателей, требуется, чтобы нос корабля добраться из башни А в башню Б?
(c) Как долго, согласно измерениям в корпусе космического корабля, принять за нос корабля для путешествия из башни А в башню Б?
(d) По измерениям пассажиров космического корабля, насколько далеко друг от друга находятся два башни?
(д) В кадре космического корабля, сколько времени требуется лучу света, чтобы путешествовать от передней до задней части космического корабля?
(е) Сколько времени, по мнению наблюдателей на Земле, требуется для того, чтобы луч света, чтобы пройти от передней к задней части движущегося космического корабля?
(Дайте числовые ответы!)
Решение:
- Концепты:
Релятивистская кинематика - Рассуждение:
Нас просят вычислить различные пространственные и временные интервалы в различных инерционные рамки. - Детали расчета:
(а) Сокращение длины: L = L 0 /γ, γ = (1 — v 2 /c 2 ) -½ = 1/0,6 = 1,667.
L = 60 м — расстояние между башнями.
(б) t = L/v = (60 м)/(2,4*10 8 м/с) = 2,5*10 -7 с.
(в) τ = t/γ = 1,5*10 -7 с. В космических кораблях обрамляют два события имеют одинаковые пространственные координаты, τ — собственное время.
(г) d с = vt = (2,4*10 8 м/с)(1,5*10 -7 с) = 36 м.
(e) t с = (100 м)/(3*10 8 м/с) = 3,33*10 -7 с.
(f) vt e + ct e = 60 м, t e = (60 м)/(1,8*3*10 8 м/с) = 1,11*10 -7 с.
Проблема:
Стержень длиной L 0 наклонен под углом θ к оси x в своей
кадр отдыха. Найдите угол наклона стержня, измеренный наблюдателем.
движется с релятивистской скоростью «v» в направлении x.
Решение:
- Концепты:
Релятивистская кинематика, Лоренцево сокращение - Рассуждение:
Для наблюдателя, находящегося в движении относительно объекта, размеры объекта сокращаются в 1/γ раз в направлении движения. - Детали расчета:
В опорной раме стержней: L x = L 0 cosθ, L y = L 0 sinθ.
В раме отдыха наблюдателей L x ‘ = L x /γ, L y ‘ = L y . Здесь γ = (1 — v 2 /c 2 ) — ½ .
tanθ’ = L y ‘/L x ‘ = γ tanθ.
Проблема:
Прямоугольная пластина размерами a × b движется с релятивистской скоростью В = V i , как показано на рисунке. В остальной рамке прямоугольника сторона a составляет угол θ по отношению к оси x.
(a) Нарисуйте форму пластины, измеренную наблюдателем в
лабораторный каркас.
Запишите выражения для длин всех сторон и
значения всех внутренних углов через β = V/c, γ = (1 — β 2 ) -½ ,
и θ.
(b) Оцените свои выражения для случая θ = π/4 и V = (2/3) ½ c.
Решение:
- Концепты:
Лоренцево сокращение - Рассуждение:
Наблюдатель в лабораторной системе отсчета будет измерять длины, параллельные оси x. с коэффициентом γ -1 .
γ = (1 — β 2 ) — ½ , β = В/c. Длины, перпендикулярные ось абсцисс не сжата. - Детали расчета:
Из тригонометрии:
tanΦ 1 = γtanθ, tanΦ 2 = γ -1 tanθ,
а’ = а(γ -2 cos 2 θ + sin 2 θ) ½ = a(1 — β 2 cos 2 θ) ½ ,
b’ = b(γ -2 sin 2 θ + cos 2 θ) ½ = a(1 — β 2 sin 2 θ) ½ ,
Χ 1 = ½π + тангенс -1 (γtanθ) — тангенс -1 (γ -1 тангенс θ),
Χ 2 = ½π — тангенс -1 (γtanθ) — тангенс -1 (γ -1 тангенс θ).(б) Для случая θ = π/4 и V = (2/3) ½ c имеем γ = (3) ½ .
Φ 1 = π/3, Φ 2 = π/6, Χ 1 = 2π/3, Χ 2 = π/3.
Это дает a’ = (2/3) ½ a, b’ = (2/3) ½ b.
Проблема:
Палка длиной l закреплена под углом θ к оси x 1 в своей системе покоя K. Рассмотрим наблюдателя в системе K′, движущегося вдоль
ось x 1 со скоростью v. Что измеряет этот наблюдатель для
(а) длина стержня и
(б) угол стержня
относительно оси x 1 ‘?
Решение:
- Понятия:
Релятивистская кинематика - Рассуждение:
Наблюдатель в системе K’ измерит проекцию длина, параллельная оси x, контактирует с коэффициентом γ -1 . - Детали расчета:
(a) В системе отсчета K l x = lcosθ, l г = lsinθ.
В системе отсчета K’ l’ x = l x /γ = lcosθ/γ, l’ y = l y = lsinθ.
l’ = (l’ x 2 + l’ y 2 ) ½ = l(cos 2 θ/γ 2 + sin 2 θ) ½ = l(1 — cos 2 θ*v 2 /c 2 2) 9002 2 .
(b) tanθ’ = l y ‘/l x ‘ = γtanθ.
Как далеко я могу видеть? – The Math Doctors
Мы рассматривали вопросы о круглости Земли, начиная с общего факта, а затем определяя размер Земли. Очень распространен вопрос о том, как эта округлость влияет на то, что мы можем видеть, иногда как вызов («Если я могу это видеть, то как Земля может быть круглой?»), а гораздо чаще из любопытства («Как далеко может Я вижу, если…?). Здесь мы рассмотрим несколько последних вопросов.
В поисках горизонта
Этот вопрос, не первый в своем роде, с 1999 года:
Расстояние до горизонта Как далеко горизонт?
Это требует уточнения! Доктор FWG предложил конкретную настройку:
Дорогой Роберт! Спасибо, что прислали этот интересный вопрос.
Однако точно ответить трудно, поскольку необходимо указать определенные условия, независимо от того, существуют они или нет. Например, одну оценку расстояния до горизонта можно сделать, если предположить, что идеально гладкая поверхность для земли и наблюдателя, смотрящего на горизонт своими глазами на уровне ровно 5,28 фута (или «ч») над поверхностью земли (эта высота произвольна, но используемое для нее значение повлияет на окончательный ответ). Ближайшее приближение к этому состоянию может существовать для невысокого человека, стоящего в весельной лодке, плывущей посреди очень большого (спокойного) озера . Поскольку высота глаза над поверхностью будет разной, а радиус земли нужно искать вверх (и будет варьироваться в зависимости от того, как его интерпретирует источник, поскольку земля не является точной сферой), лучше всего использовать для них переменные. И поскольку мы делаем ряд предположений, любой ответ, который мы даем, будет приблизительным.
Предполагаемая высота глаз 5,28 фута выбрана по причине, которую мы скоро увидим, но не безосновательной. Поскольку Земля не является точной сферой, ее радиус варьируется; это 3963 мили на экваторе. Средний радиус рассчитывается как 3958,7613 миль, но в любом конкретном месте и направлении он может варьироваться от 3936 до 3977 миль (от 6335 до 6400 км). Здесь мы приблизимся примерно на 4000 миль.
Если теперь предположить, что расстояние от центра Земли до «идеально сферической» поверхности Земли составляет ровно 4000 миль (или «R») и что расстояние от центра Земли до уровня глаз невысокого человека равно 4000 миль плюс 5,28 фута (или R + H), вы можете оцените расстояние до горизонта (при условии отсутствия других проблем, таких как преломление или отклонение света, идущего от горизонта к глазам наблюдателя). Пусть «s» обозначает фактическое расстояние между глазами наблюдателя и горизонтом. Вам также необходимо предположить, что лучи света, идущие от горизонта к глазам наблюдателя, составляют прямой угол с радиус-вектором Земли на горизонте.
Другими словами, световые лучи, идущие от точки горизонта к глазам наблюдателя, касаются земной «поверхности» в точке горизонта 9.0534 . Вы можете игнорировать реальную кривизну земли и предположить, что «s» и фактическое расстояние между наблюдателем и горизонтом вдоль искривленной части земной поверхности эквивалентны. Из этих условий и приближений можно нарисовать «прямоугольный» треугольник, а затем использовать теорему Пифагора для оценки расстояния до видимого горизонта. 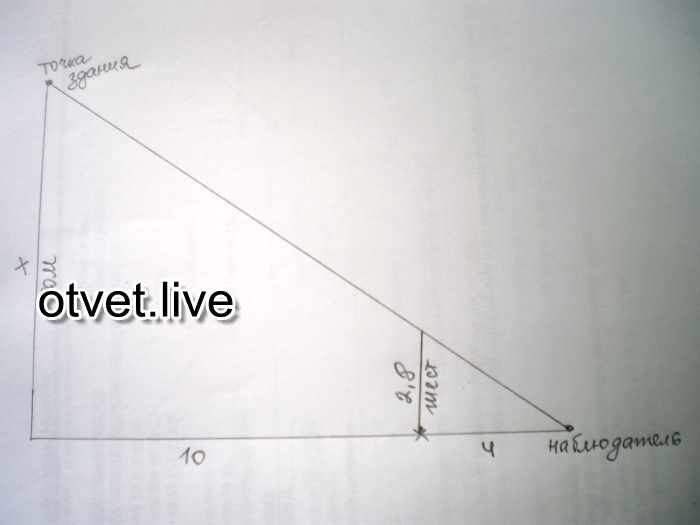Вот картинка для иллюстрации (сильно преувеличена, чтобы мы могли ее увидеть):
Здесь C — центр земли, E — ваш глаз, F — ваша нога, а H — точка на горизонте; s — расстояние по прямой до горизонта, d — пройденное расстояние до горизонта, h — ваш рост, R — радиус Земли. На картинке х не очень мало по сравнению с R ; это очень высокая башня! Если бы h было намного меньше, вы можете видеть, что s и d были бы практически одинаковыми.
Мы воспользуемся этим фактом. 92 = 2Rh.
Это дало нам точную формулу $$s = \sqrt{h(2R + h)},$$ и приблизительную, но более простую формулу $$s = \sqrt{2Rh}$$, которая применима, пока наша высота значительно меньше диаметра Земли.
Теперь мы можем применить это к предполагаемым измерениям, постаравшись перевести все в одну и ту же единицу, в данном случае мили:
Следовательно: s = Sqrt(2Rh) = Sqrt[2(4000 миль)(5,28 футов/5280 футов/миль)] = Квадрат[(8000)(0,001)] = Sqrt[8] = Sqrt[(4)(2)] = 2[Sqrt(2)] = 2(1,414) = 2,8 мили. Итак, для этих условий расстояние до горизонта составляет около 2,8 мили. Я надеюсь, что это было полезно.
Теперь вы можете видеть, откуда взялась эта предполагаемая высота 5,28 фута! Он был выбран для получения простых чисел после преобразования в мили.
Что, если бы мы использовали точную формулу? $$s = \sqrt{h(2R + h)} = \sqrt{\frac{5.28}{5280}\left(2(4000) + \frac{5.28}{5280}\right)} = \sqrt{ 0,001(2(4000) + 0,001)} = \sqrt{8,000001} \приблизительно 2,828\text{миль}$$ Как видите, разницы нет.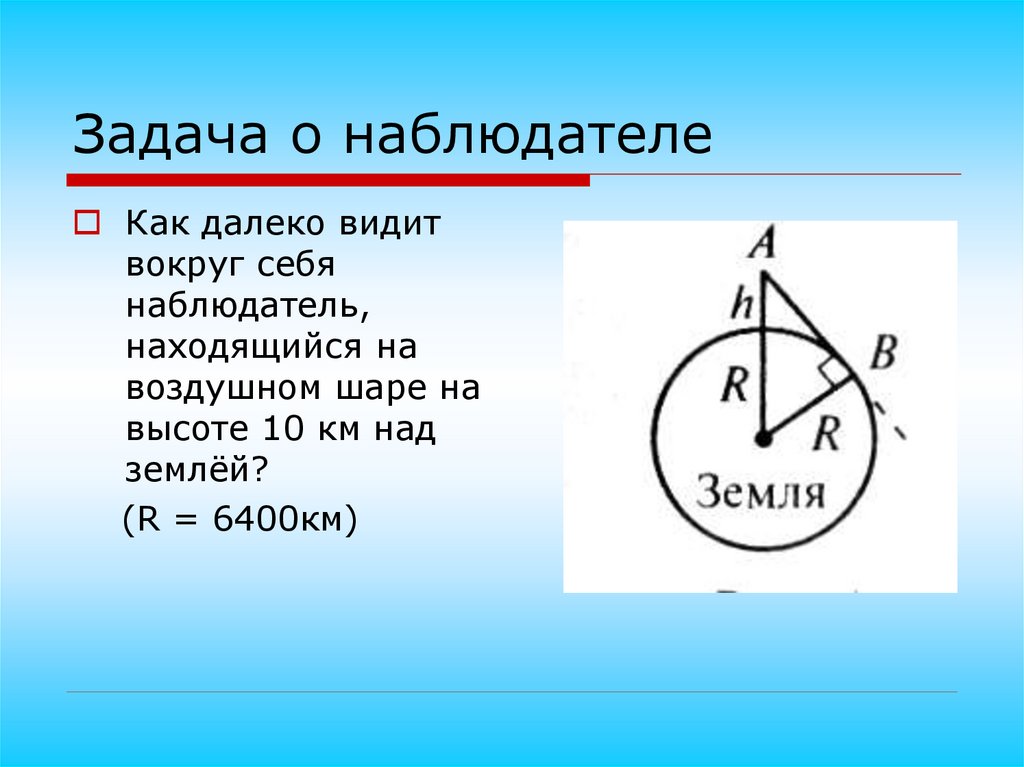
Вот почему приближение вполне разумно.
Что, если бы мы стояли на вершине утеса так, чтобы наши глаза были на высоте 100 футов над водой? $$s = \sqrt{2Rh} = \sqrt{2(4000)\left(\frac{100}{5280}\right)} = 12,3\text{миль}$$
За горизонтом
Следующий вопрос из 2005 года и касается не горизонта (видение объекта прямо на поверхности), а высокого объекта за горизонтом. То есть первый вопрос касается того, чтобы увидеть ватерлинию лодки, а это может быть вершина мачты.
Расстояние прямой видимости между двумя объектами Морскую буровую установку буксируют в море. На каком максимальном расстоянии наблюдатель, стоящий у береговой линии, может видеть навигационные огни? высота глаза наблюдателя составляет 5 футов 9 дюймов, а самый верхний навигационный огонь находится на высоте 225 футов над водой. Ответ дайте в милях. Я в замешательстве, потому что считаю, что не хватает прямой информации, чтобы узнать точный ответ, как кривизна земли.
Это должно сыграть роль, но я в этом не уверен. Какую роль это играет, и есть ли формула для определения момента потери прямой видимости? Я знаю, что радиус Земли составляет 3959 миль. Поскольку свет находится над уровнем воды, мы сможем увидеть его за горизонтом. На самом деле, самое дальнее, что мы можем увидеть, будет касаться горизонта по касательной к земле. Таким образом, мы можем использовать то же самое мышление здесь:
Доктор Джерри ответил:
Привет Кеннет-- Спасибо, что написали доктору Математику. Представьте себе сектор круга, который представляет собой Землю (как кусок пирога). На одном конце дуги сектора возведите башню высотой H, а на другом конце возведите башню высотой h. Их вершины — это точки, между которыми мы хотим определить самое длинное расстояние прямой видимости. Нарисуйте линию, соединяющую вершины. Мы хотим настроить размер сектора так, чтобы эта линия обзора касалась окружности в точке между двумя основаниями. Если две башни были дальше друг от друга, они не могли видеть друг друга.Высокий, с триггером
Давайте рассмотрим еще один вопрос, похожий на последний, из 2001 года:
Вершина башни Учитывая башню высотой 300 миль на земле, как далеко вы можете уйти от нее, прежде чем вершина исчезнет за горизонтом ? (Предполагается неограниченная видимость.) Мы нарисовали диаграммы и треугольники, чтобы попытаться понять это с помощью тригонометрии, но мы ищем уравнения, которые помогут нам получить ответ.На этот раз мы не сможем использовать аппроксимацию малой высоты, не так ли?
С земли
Доктор Ян ответил, начав с простого случая, когда вы находитесь на горизонте башни:
Привет, Эшли! На клавиатуре сложно нарисовать круг, но давайте представим, что это земля: . . . . . . . . . . . . Кроме того, давайте представим, что Земля — это сфера , и что это идеально гладкое , хотя ни то, ни другое не соответствует действительности. Если ваш глаз в какой-то момент находится на уровне земли , то вы можете смотреть по касательной к земле: <------------------ . . . . . . . . . . . Если вершина башни высотой h как раз пересекает линию вашего взгляда, <-----------.------ . . . . . час . . . . . . . тогда вы можете образовать прямоугольный треугольник с вами, центром земли и верхушкой башни по углам: А С <-----------.Это тот самый треугольник, который мы использовали для определения расстояния до горизонта. Но он собирается использовать тригонометрию, а не только теорему Пифагора, и по уважительной причине: с такой высокой башней расстояние прямой видимости не то же самое, что расстояние ходьбы!
Если радиус Земли (в милях) равен r, то АВ = р ВС = г + ч и р потому что (АВС) = ----- r + hЭто отношение «прилегающего катета» к «гипотенузе».
На сфере расстояние вдоль поверхности (s), соответствующее центральному углу тета, равно с = г * тета Таким образом, расстояние, которое вам придется пройти от точки А до основания башни, будет равно с = г * тета р = r * arccos( ----- ) р + ч Для г = 39{-1}\frac{r}{r+h}$$ Расстояние прямой видимости от нашего первого ответа будет равно $$s = \sqrt{h(2R + h)} = \sqrt{300(2 (3950) + 300)} = 1568\text{ми},$$, что значительно больше.Проверка реальностью: Sears Tower
Это кажется довольно большим расстоянием! Это разумно? Трудно представить что-то высотой 300 миль. Давайте подумаем о чем-то более реалистичном, например, о Sears Tower. Башня Sears имеет высоту 1450 футов, что составляет около 0,275 мили. Таким образом, наше уравнение говорит, что мы должны быть в состоянии увидеть его до 3950 s = 3950 * arccos( -------- ) 3950,275 = 46,6 миль Это означает, что вы могли бы просто увидеть башню Sears из государственного парка Indiana Dunes — если бы вы лежали на земле. Я точно знаю, что оттуда его видно стоя , потому что я вырос рядом с ним.Имеется в виду, конечно, видя вершину башни.
Многие вопросы, которые нам задают в пользу плоской Земли, основаны на личном опыте или фотографиях зданий с большого расстояния. Иногда кажется, что их наблюдения зависят от плохой памяти или атмосферного искривления света, но главный ответ для таких людей состоит в том, что если бы Земля была плоской, вы могли бы видеть база любого здания с любого расстояния …
С земли
Это был легкий случай.
Хорошо, а если ты _не_ лежишь на земле? Ну подумайте над этой проблемой. Если ваш глаз находится на высоте h' над землей, какую самую дальнюю точку вы можете видеть? А' | час' | . . . . . . . С' . . . . . Б . . . . . Теперь у нас есть другой прямоугольный треугольник (A'C'B - прямой угол), и мы знаем, что р потому что (A'BC') = ------ г + ч ' Это выглядит знакомо, не так ли? 9{-1}\frac{r}{r+h}$$Больше реальности
Давайте еще раз проверим это для Sears Tower. Если ваш рост 6 футов, это примерно 0,0011 мили, поэтому 3950 3950 s = 3950 * [arccos( --------- ) + arccos( -------- )] 3950.0011 3950.275 = 49,6 миль что не большая разница.
2
Все это можно увидеть здесь:
92 + 2hr}.$$ Мы могли бы также использовать приблизительную форму, если высота не слишком велика (измеряется, скажем, в футах, а не в милях): $$D \ приблизительно \sqrt{2Hr} + \sqrt{2hr }.$$ Используя последний для примера, мы получаем тот же результат: = 0,001089\текст{ми}\\H = 225\текст{фут} = \frac{225}{5280}\текст{ми} = 0,04261\текст{ми}\\D \приблизительно \sqrt{2(0,04261) (3959)} + \sqrt{2(0,001089)(3959)} = 18,4 +2,9 = 21,3\text{ми}.$$ Мы видим, что наш горизонт равен 2,9миль, а у света 18,4 мили. 
------
. . . .
. . . час
. .
. . .
Б
. .
. .
. 
Насколько изменится, если вы встанете (или подниметесь на вершину утеса, или здания, или чего-то еще)? Мы уже знаем, что делать, не так ли?
Leave A Comment