Все формулы для радиуса вписанной окружности
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :


Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :


2. Радиус вписанной окружности ромба, равен половине его высоты

a — сторона ромба
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Напомним определение биссектрисы угла.
Определение 1. Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла). Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).

Рис. 1
Доказательство. Рассмотрим произвольную точку D, лежащую на биссектрисе угла BAC, и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE, а гипотенуза AD – общая. Следовательно,
DF = DE,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1). Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).

Рис. 2

что и требовалось доказать.
Определение 2. Окружность называют окружностью, вписанной в угол, если она касается касается сторон этого угла.
Доказательство. Пусть точка D – центр окружности, вписанной в угол BAC, а точки E и F – точки касания окружности со сторонами угла (рис.3).

Рис.3
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности), а гипотенуза AD – общая. Следовательно
AF = AE,
что и требовалось доказать.
Замечание. Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных, проведенных к окружности из одной точки, равны.
Напомним определение биссектрисы треугольника.
Определение 3. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4. В любом треугольнике все три биссектрисы пересекаются в одной точке.

Рис. 4
Опустим из точки O перпендикуляры OD, OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC, то в силу теоремы 1 справедливо равенство:
OD = OE,
Поскольку точка O лежит на биссектрисе угла ACB, то в силу теоремы 1 справедливо равенство:
OD = OF,
Следовательно, справедливо равенство:
OE = OF,
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC. Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4. Окружностью, вписанной в треугольник, называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности.

Рис. 5
Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности, удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения |
| Произвольный треугольник |  |
Посмотреть вывод формулы | a, b, c – стороны треугольника,
|
Посмотреть вывод формулы | |||
| Равнобедренный треугольник |  |
Посмотреть вывод формулы | a – боковая сторона равнобедренного треугольника, |
| Равносторонний треугольник |  |
Посмотреть вывод формулы | a – сторона равностороннего треугольника, |
| Прямоугольный треугольник |  |
Посмотреть вывод формул | a, b – катеты прямоугольного треугольника, |
| Произвольный треугольник | |
 |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы | |
| Равнобедренный треугольник | |
 |
где Посмотреть вывод формулы |
| Равносторонний треугольник | |
 |
где Посмотреть вывод формулы |
| Прямоугольный треугольник | |
 |
где Посмотреть вывод формул |
| Произвольный треугольник |

где Посмотреть вывод формулы |

где Посмотреть вывод формулы |
| Равнобедренный треугольник |

где Посмотреть вывод формулы |
| Равносторонний треугольник |

где Посмотреть вывод формулы |
| Прямоугольный треугольник |

где Посмотреть вывод формулы |
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство

где a, b, c – стороны треугольника, r – радиус вписанной окружности, – полупериметр (рис. 6).
– полупериметр (рис. 6).

Рис. 6
Доказательство. Из формулы

с помощью формулы Герона получаем:



что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство

где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).

Рис. 7
Доказательство. Поскольку для произвольного треугольника справедлива формула

где

то, в случае равнобедренного треугольника, когда


получаем

что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство

где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).

Рис. 8
Доказательство. Поскольку для равнобедренного треугольника справедлива формула

то, в случае равностороннего треугольника, когда
b = a,
получаем


что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство


где a, b – катеты прямоугольного треугольника, c – гипотенуза, r – радиус вписанной окружности.
Доказательство. Рассмотрим рисунок 9.

Рис. 9
Поскольку четырёхугольник CDOF является прямоугольникомпрямоугольником, у которого соседние стороны DO и OF равны, то этот прямоугольник – квадратквадрат. Следовательно,
СD = СF= r,
В силу теоремы 3 справедливы равенства


Следовательно, принимая также во внимание теорему Пифагора, получаем


что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Радиус вписанной окружности | Треугольники
Удобно, когда все формулы, по которым можно найти радиус вписанной в треугольник и в многоугольник окружности, размещены на одной странице.
Радиус вписанной в многоугольник окружности
Если в многоугольник можно вписать окружность, то формула для вычисления радиуса вписанной окружности:
где p — полупериметр, то есть полусумма длин всех сторон этого многоугольника.
Например, для пятиугольника со сторонами a, b, c, d, e радиус вписанной окружности находится по формуле
откуда
По этой же формуле ищут радиус вписанной в треугольник окружности.
Радиус вписанной в треугольник окружности
Формула для нахождения радиуса вписанной в треугольник окружности (верна для треугольника любого вида)
где p — полупериметр,
где a, b, c — стороны треугольника.
Радиус вписанной в прямоугольный треугольник окружности
Формула для нахождения радиуса окружности, вписанной в прямоугольный треугольник
где a и b — катеты, c — гипотенуза.
Радиус окружности, вписанной в правильный многоугольник
Формула радиуса вписанной в правильный многоугольник окружности
где a — сторона многоугольника, n — количество сторон.
Частные случаи — правильный (равносторонний) треугольник, правильный четырехугольник (квадрат) и правильный шестиугольник.
Радиус окружности, вписанной в правильный треугольник
Формула радиуса вписанной окружности для правильного треугольника:
В правильном треугольнике радиус вписанной окружности вдвое меньше радиуса описанной окружности:
Радиус окружности, вписанной в квадрат
Формула радиуса вписанной в квадрат окружности:
где a — сторона квадрата.
Радиус окружности, вписанной в правильный шестиугольник
Формула радиуса вписанной в правильный шестиугольник окружности:
где a — сторона правильного шестиугольника.
Для любого многоугольника центр вписанной окружности лежит в точке пересечения его биссектрис.
Равносторонний (правильный) треугольник | matematicus.ru
Равносторонний или правильный треугольник — треугольник, у которого три стороны равны. Все углы равностороннего треугольника равны.
Равносторонним треугольником называется такой треугольник, у которого все стороны равны, то есть АВ = ВС = АС (рис. 1)

Рисунок 1
Свойства равностороннего (правильного) треугольника
- Все углы равностороннего треугольника равны по 60°
∠А=∠С=∠В=60°
- Биссектрисы треугольника являются медианами и высотами, то есть равны и точка их пересечения, является центром вписанной окружности (рис. 2).

Рисунок 2
Из (рис. 2) обозначения:
h — высота=биссектриса=медиана
R — радиус описанной окружности
r — радиус вписанной окружности
a — стороны правильного треугольника
Формула периметра равностороннего треугольника:
P=3·a
Формула площади правильного треугольника:
Формула высоты (или медианы или биссектрисы) равностороннего треугольника:

Радиус вписанной окружности в равносторонний треугольник:

Радиус описанной окружности в равносторонний треугольник:

Окружность, вписанная в правильный треугольник
Окружность, вписанная в правильный треугольник, помимо свойств вписанной в произвольный треугольник окружности, обладает своими собственными свойствами.
1) Центр вписанной в треугольник окружности — точка пересечения его биссектрис.
Поскольку в равностороннем треугольнике биссектрисы, медианы и высоты совпадают, то центр вписанной в правильный треугольник окружности является точкой пересечения не только его биссектрис, но также медиан и высот.
Например, в правильном треугольнике ABC AB=BC=AC=a
точка O — центр вписанной окружности.
AK, BF и CD — биссектрисы, медианы и высоты треугольника ABC.
2) Расстояние от центра вписанной окружности до точки касания её со стороной треугольника равно радиусу. Так как центр вписанной в правильный треугольник окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус вписанной в равносторонний треугольник окружности равен одной третьей длины медианы:
Таким образом, формула для радиуса вписанной в правильный треугольник окружности
Обратно, сторона равностороннего треугольника через радиус вписанной окружности:
3) Так как формула для нахождения площади равностороннего треугольника через сторону
можем найти площадь через r:
Таким образом, формула площади правильного треугольника через радиус вписанной окружности —
3) Все отрезки, на которые стороны равностороннего треугольника делятся точками касания вписанной окружности, равны половине его стороны:
4) Центр вписанной в правильный треугольник окружности является также центром описанной около него окружности.
5) Радиус вписанной в равносторонний треугольник окружности в два раза меньше радиуса описанной окружности:
Радиус вписанной в треугольник окружности
Радиус вписанной в треугольник окружности можно найти по одной общей формуле.
Кроме того, для правильного и прямоугольного треугольников существуют дополнительные формулы.
Радиус вписанной в треугольник окружности для произвольного треугольника
Формула для нахождения радиуса окружности, вписанной в произвольный треугольник:
где S — площадь треугольника, p — его полупериметр.
Для треугольника со сторонами a, b, c полупериметр
и формулу можно записать так:
Если нужно найти радиус вписанной в треугольник окружности по его сторонам, то площадь треугольника ищут по формуле Герона, соответственно, формула для нахождения радиуса треугольника по трем сторонам имеет вид:
Радиус вписанной в прямоугольный треугольник окружности
Формула для нахождения радиуса вписанной в прямоугольный треугольник окружности:
где a, b — длины катетов, c — длина гипотенузы.
Радиус окружности, вписанной в правильный (то есть равносторонний) треугольник
Формула для нахождения радиуса окружности, вписанной в правильный треугольник:
или (без иррациональности в знаменателе):
где a -длина стороны правильного треугольника.
В правильном треугольнике радиус вписанной окружности также можно найти через радиус описанной окружности:
Радиус вписанной окружности, формулы, задачи.
Окружность, вписанная в треугольник
Существование окружности, вписанной в треугольник
Напомним определение биссектрисы угла.
Определение 1. Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла). Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
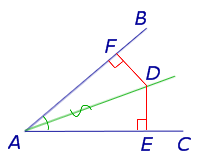
Рис. 1
Доказательство. Рассмотрим произвольную точку D, лежащую на биссектрисе угла BAC, и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE, а гипотенуза AD – общая. Следовательно,
DF = DE,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1). Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
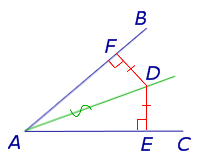
Рис. 2
Доказательство. Рассмотрим произвольную точку D, лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE, а гипотенуза AD – общая. Следовательно,
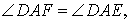
что и требовалось доказать.
Определение 2. Окружность называют окружностью, вписанной в угол, если она касается сторон этого угла.
Теорема 3. Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство. Пусть точка D – центр окружности, вписанной в угол BAC, а точки E и F – точки касания окружности со сторонами угла (рис.3).
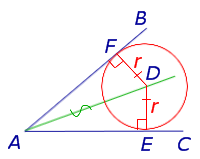
Рис.3
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности), а гипотенуза AD – общая. Следовательно
AF = AE,
что и требовалось доказать.
Замечание. Теорему 3 можно сформулировать и по-другому: отрезки касательных, проведенных к окружности из одной точки, равны.
Напомним определение биссектрисы треугольника.
Определение 3. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4. В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство. Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC, и обозначим точку их пересечения буквой O (рис. 4).
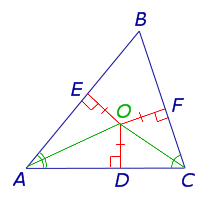
Рис. 4
Опустим из точки O перпендикуляры OD, OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC, то в силу теоремы 1 справедливо равенство:
OD = OE,
Поскольку точка O лежит на биссектрисе угла ACB, то в силу теоремы 1 справедливо равенство:
OD = OF,
Следовательно, справедливо равенство:
OE = OF,
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC. Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Фигура
Рисунок
Формула
Обозначения
Произвольный треугольник
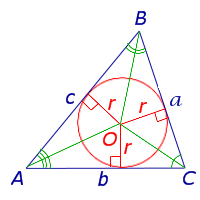
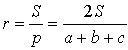
Посмотреть вывод формулы
a, b, c – стороны треугольника, S –площадь,
r – радиус вписанной окружности, p – полупериметр
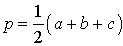 .
.
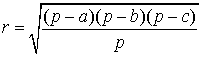
Посмотреть вывод формулы
Равнобедренный треугольник
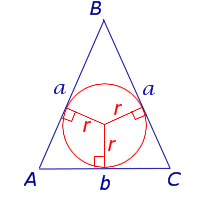
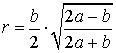
Посмотреть вывод формулы
a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности
Равносторонний треугольник
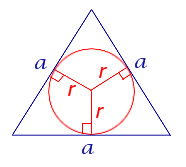
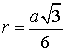
Посмотреть вывод формулы
a – сторона равностороннего треугольника, r – радиус вписанной окружности
Прямоугольный треугольник
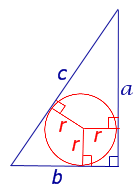
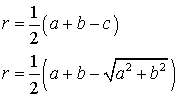 Посмотреть вывод формул
Посмотреть вывод формул
a, b – катеты прямоугольного треугольника, c – гипотенуза, r – радиус вписанной окружности
Определение 4. Окружностью, вписанной в треугольник, называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности. 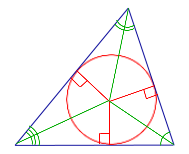
Рис. 5
Следствие. В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности, удобно представить в виде следующей таблицы.
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
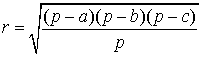 ,
,
где a, b, c – стороны треугольника, r – радиус вписанной окружности,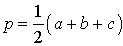 – полупериметр (рис. 6).
– полупериметр (рис. 6).

Рис. 6
Доказательство. Из формулы
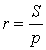
с помощью формулы Герона получаем:
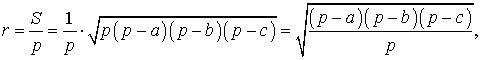
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
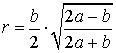 ,
,
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).

Рис. 7
Доказательство. Поскольку для произвольного треугольника справедлива формула
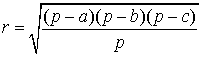 ,
,
где
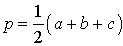 ,
,
то, в случае равнобедренного треугольника, когда
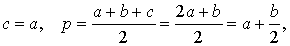
получаем
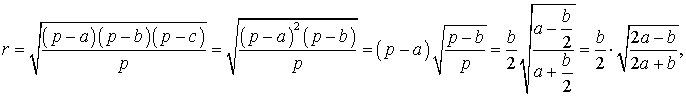
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
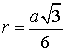
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).

Рис. 8
Доказательство. Поскольку для равнобедренного треугольника справедлива формула
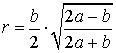 ,
,
то, в случае равностороннего треугольника, когда
b = a,
получаем
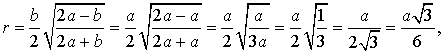
что и требовалось.
Замечание. Я рекомендую вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
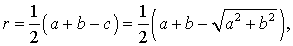
где a, b – катеты прямоугольного треугольника, c – гипотенуза, r – радиус вписанной окружности.
Доказательство. Рассмотрим рисунок 9.
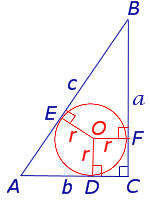
Рис. 9
Поскольку четырёхугольник CDOF является прямоугольником, у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат. Следовательно,
СВ = СF= r,
В силу теоремы 3 справедливы равенства
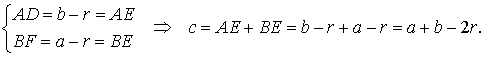
Следовательно, принимая также во внимание теорему Пифагора, получаем
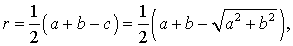
что и требовалось.
Подборка задач по теме «Окружность, вписанная в треугольник».
1.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
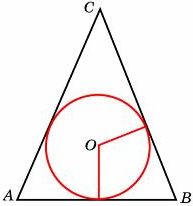
2.
Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

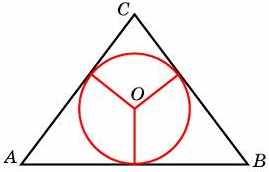
3
В треугольнике ABC АС=4, ВС=3, угол C равен 90º. Найдите радиус вписанной окружности.
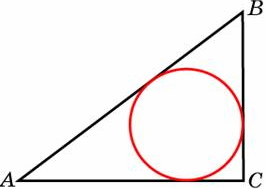
4.
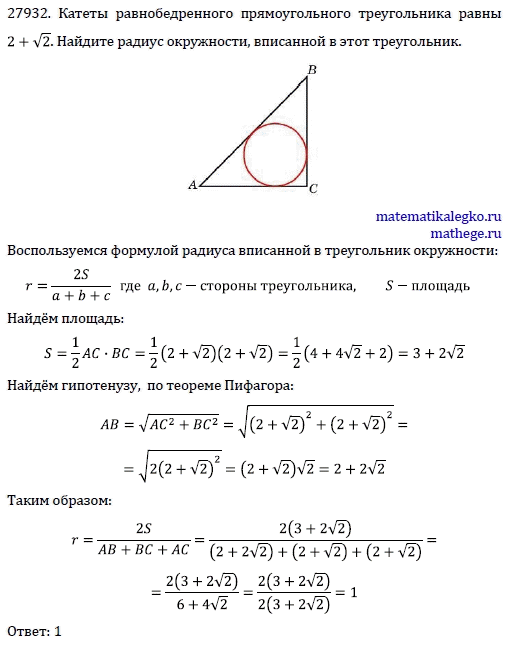
Катеты равнобедренного прямоугольного треугольника равны 2+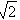 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.
5.
Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу c этого треугольника. В ответе укажите с(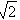 –1).
–1).

Приведем ряд задач из ЕГЭ с решениями.
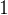 . Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 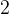 . Найдите гипотенузу c этого треугольника. В ответе укажите
. Найдите гипотенузу c этого треугольника. В ответе укажите 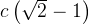 .
.
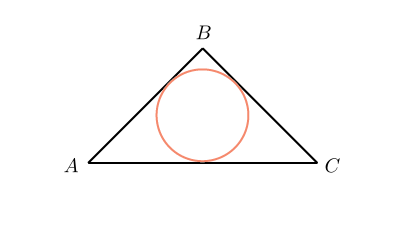
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен 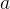 . Тогда гипотенуза равна
. Тогда гипотенуза равна 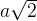 .
.
Запишем площадь треугольника АВС двумя способами:
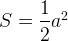
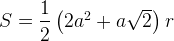
Приравняв эти выражения, получим, что 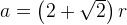 . Поскольку
. Поскольку 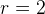 , получаем, что
, получаем, что 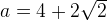 . Тогда
. Тогда 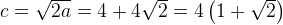 .
.
В ответ запишем 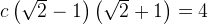 .
.
Ответ: 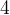 .
.
Задача 2.

Задача 3.
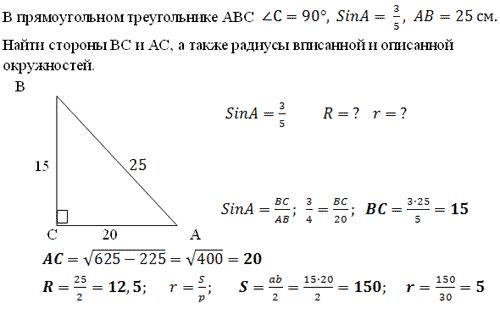
Задача 4.
1. В произвольном 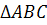 две боковые стороны 10см и 6см (AB и BC).
две боковые стороны 10см и 6см (AB и BC). 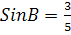 Найти радиусы описанной и вписанной окружностей
Найти радиусы описанной и вписанной окружностей
Задача решается самостоятельно с комментированием.
Решение:
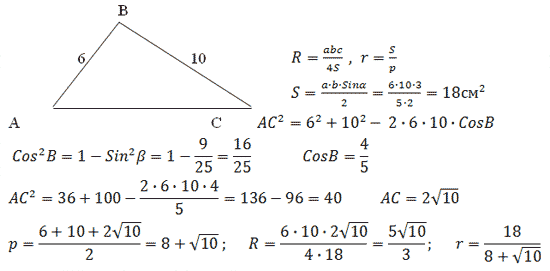
Задача 5.
В 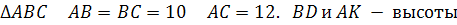 .
.
1) Найти: 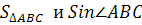
2) Доказать: 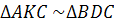 и найти СK
и найти СK
3) Найти: радиусы описанной и вписанной окружностей
Решение:
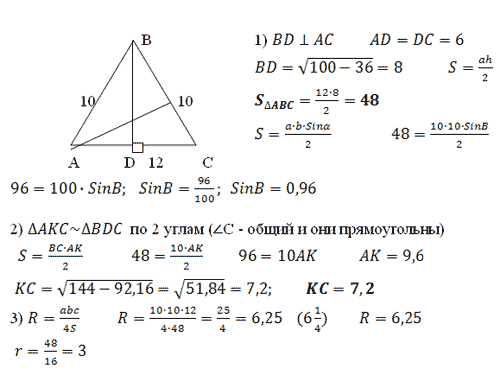
Задача 6.
Радиус окружности вписанной в квадрат равен 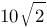 . Найти радиус окружности описанной около этого квадрата.
. Найти радиус окружности описанной около этого квадрата.
Дано:
Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.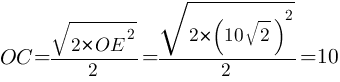
Задача 7.
Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу с этого треугольника. В ответе укажите 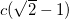 .
.
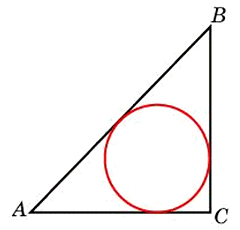
Воспользуемся формулой радиуса окружности вписанной в треугольник:
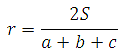
где a, b, c – стороны треугольника
S – площадь треугольника
Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна:
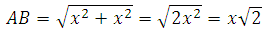
А площадь треугольника будет равна 0,5х2.
Значит
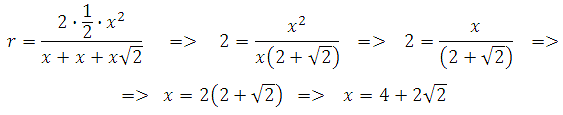
Таким образом, гипотенуза будет равна:
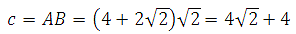
В ответе требуется записать:
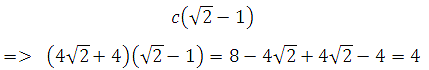
Ответ: 4
Задача 8.
В треугольнике ABC АС = 4, ВС = 3, угол C равен 900. Найдите радиус вписанной окружности.
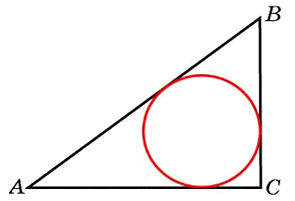
Воспользуемся формулой радиуса окружности вписанной в треугольник:
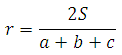
где a, b, c – стороны треугольника
S – площадь треугольника
Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.
По теореме Пифагора:
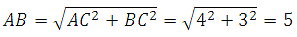
Найдём площадь:
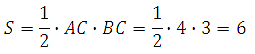
Таким образом:
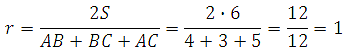
Ответ: 1
Задача 9.
Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
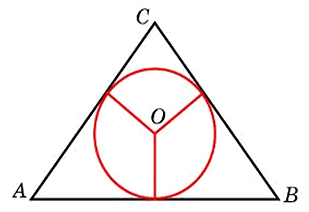
Воспользуемся формулой радиуса окружности вписанной в треугольник:
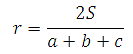
где a, b, c – стороны треугольника
S – площадь треугольника
Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:
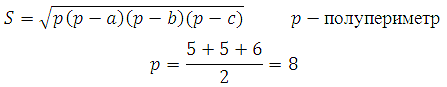
Тогда
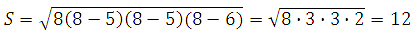
Таким образом:
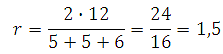
Ответ: 1,5
Задача 10. (Из банка ЕГЭ)

Задача 11. (Из банка ЕГЭ)

Задача 12. (Из банка ЕГЭ)

Задача 13. (Из банка ЕГЭ)
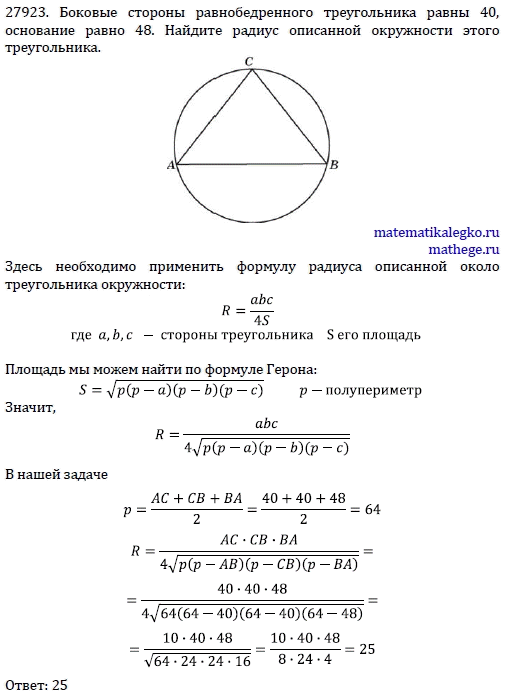
Задача 14. (Из банка ЕГЭ)
Задача 15.
Найдите радиусы окружностей, вписанной в правильный треугольник и описанный около него, если их разность равна 4см.
Сторона правильного треугольника вычисляется по формуле a = R√3, где R – радиус описанной окружности, и a = 2r√3 , где r – радиус вписанной окружности, приравняем стороны R√3 = 2·r√3 , отсюда R = 2r, сдругой сторони по условию задачи R – r = 4 cм, отсюда r = 4 см, тогда R = 2·4 см = 8 см
Ответ: 4 см, 8 см
Задача 16.
Катеты прямоугольного треугольника равны 12 и 5. Найти:
а) радиусы вписанной окружности;
б) радиусы описанной окружности;
в) расстояние от центра вписанной окружности до вершины наименьшего угла.
Решение:
1. По теореме Пифагора
2. О – центр описанной окружности, 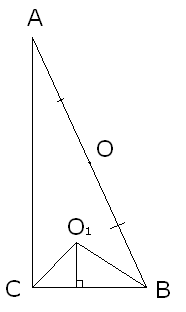
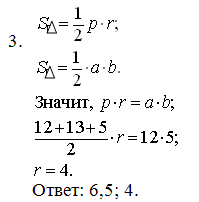
Задача 17.
В треугольнике с углами 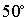 и
и 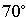 вписана окружность. Найти углы треугольника, вершинамикоторого являются точки касания окружности со сторонами треугольника.
вписана окружность. Найти углы треугольника, вершинамикоторого являются точки касания окружности со сторонами треугольника.
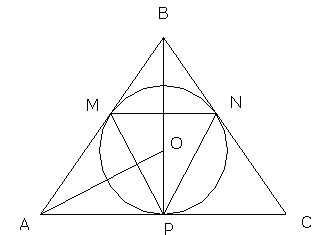
Дано: 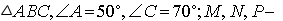 точки касания вписанной окружности.
точки касания вписанной окружности.
Найти: 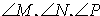
Решение:
1.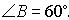
2. Из 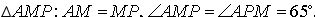
3. Из 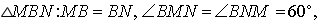
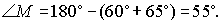
4. Из 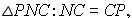
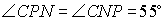
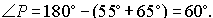
5.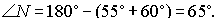
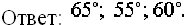
Задача 18.
В равнобедренную трапецию с основаниями 1 и 9 вписана окружность. Найти: а) боковую сторону; б) радиус вписанной окружности; в) высоту; г) диагональ.

Приведу пример возможной самостоятельной работы по теме «Вписанная и описанная окружность».

Карточки с задачами.
1) В 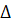 ABC AB = 8, BC = 10,
ABC AB = 8, BC = 10, 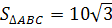 . Найти высоту, опущенную из вершины B и
. Найти высоту, опущенную из вершины B и 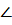 BAC.
BAC.
2) В 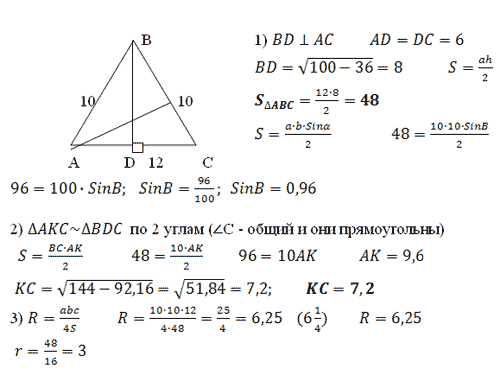 ABC AB=12
ABC AB=12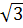 , BC = 9. Площадь треугольника 9
, BC = 9. Площадь треугольника 9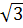 . Найти радиусы вписанной и описанной окружностей.
. Найти радиусы вписанной и описанной окружностей.
Пример математического диктанта.
I. Математический диктант
I вариант
1. В любой треугольник можно вписать окружность? (Да/Нет)
2. Центр вписанной в треугольник окружности является …
3. Вокруг любого треугольника можно описать окружность? (Да/Нет)
4. Центр окружности описанной около треугольника является …
5. Если центр вписанной и описанной окружности совпадают, то это треугольник …
6. Центр окружности, описанной около прямоугольного треугольника, совпадает с …
7. Если в трапецию можно вписать окружность, то …
8. Если вокруг трапеции можно описать окружность, то …
9. Если центр окружности, описанной около треугольника находится вне его, то этот треугольник …
10. Если центр окружности, описанной около треугольника, находится внутри его, то треугольник …
Использовать взаимопроверку, заготовить заранее ответы на доске. Анализ ошибок.
| ПРИМЕЧАНИЕ. Шаги с 1 по 7 такие же, как для построения шестиугольника, вписанного в круг. В случае вписанного равностороннего треугольника мы используем все остальные точки на окружности. | ||
| 1 | A, B, C, D, E, F все лежат в центре круга O | По строительству. |
| 2 | AB = BC = CD = DE = EF | Все они были нарисованы с одинаковой шириной компаса. |
| Из (2) мы видим, что пять сторон равны по длине, но последняя сторона FA не была нарисована с компасами. Это было «оставшееся» пространство, когда мы обошли круг и остановились у F. Таким образом, мы должны доказать, что это соответствует другим пяти сторонам. | ||
| 3 | OAB — равносторонний треугольник | AB был нарисован с шириной компаса, установленной в OA, и OA = OB (оба радиуса круга). |
| 4 | m∠AOB = 60 ° | Все внутренние углы равностороннего треугольника 60 °. |
| 5 | m∠AOF = 60 ° | Как и в (4) m∠BOC, m∠COD, m∠DOE, m∠EOF — все & 60deg; Так как все центральные углы составляют 360 °, m∠AOF = 360 — 5 (60) |
| 6 | треугольник BOA, AOF конгруэнтны | SAS См. Проверка на конгруэнтность, сторона-сторона-сторона. |
| 7 | AF = AB | CPCTC — Соответствующие части конгруэнтных треугольников конгруэнтны |
| Итак, теперь мы можем доказать, что BDF является равносторонним треугольником | ||
| 8 | Все шесть центральных углов (∠AOB, ∠BOC, ∠COD, ODOE, ∠EOF, ∠FOA) совпадают | Из (4) и путем повторения для остальных 5 углов все шесть углов имеют меру 60 ° |
| 9 | Углы ∠BOD, ∠DOF, ∠BOF совпадают | Из (8) — каждый из них представляет собой сумму двух углов 60 ° |
| 10 | Треугольники BOD, DOF и BOF являются конгруэнтными. | Все стороны равны радиусам окружности, и из (9) включенные углы являются конгруэнтными. См. Проверка на соответствие, сторона-сторона-сторона |
| 11 | BDF — равносторонний треугольник. | Из (10) BD, DF, FB являются конгруэнтными. CPCTC — Соответствующие части конгруэнтных треугольников конгруэнтны. Это в свою очередь удовлетворяет определению равносторонний треугольник. |
| 12 | BDF — равносторонний треугольник, вписанный в данный круг | Из (11) и всех трех вершин B, D, F лежат на заданной окружности. |
Центр окружности, называемый вписанный, это пересечение из угол биссектрисы.Биссектрисы показаны в виде пунктирных линий на рисунке выше.
Построение окружности треугольника
Можно построить вписанный треугольник, используя компас и линейку. Видеть Построение вписанного треугольника.Атрибуты
| Incenter | Расположение центра вкрапления. Точка, где встречаются угловые биссектрисы. |
| Inradius | Радиус окружности.Радиус определяется по формуле: где: а — площадь треугольника. В приведенном выше примере мы знаем все три стороны, поэтому Формула цапли используется. р — периметр треугольника, сумма его сторон. |
Корпус равностороннего треугольника
Для частного случая равностороннего треугольника Inradius также дается формулой где S — длина стороны.
Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Треугольный центр
Конгруэнтность и Сходство
Решение треугольников
Тесты по треугольнику и упражнения
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
- Подробнее
- Написано администратором

1.Найти радиус вписанного круга, если вы знаете сторону и угол у основания

 — равные стороны треугольника
— равные стороны треугольника
 — сторона (основа)
— сторона (основа)
 — угол у основания
— угол у основания
 — центр окружности
— центр окружности



2.Найти радиус вписанного круга, если вы знаете сторону и высоту

 — равные стороны треугольника
— равные стороны треугольника
 — сторона (основа)
— сторона (основа)
 — высота
— высота
 — центр окружности
— центр окружности


,
Вписанный угол окружности
Вписанный угол круга — Math Open Reference Определение: Угол в точке на окружности двумя заданными точками на окружности. Попробуйте это Перетащите любую оранжевую точку. Обратите внимание, что при перемещении точки P вписанный угол постоянен пока это в главная дуга образованный A, B.Для двух точек A и B прямые от них до третьей точки P образуют вписанный угол ∠APB. Перетаскивая точку P выше, обратите внимание, что вписанный угол постоянен.Это зависит только от положения A и B.
Перетаскивая P по кругу, вы увидите, что вписанный угол постоянен. Но когда P находится в малой дуге (самая короткая дуга между A и B), угол все еще постоянен, но является дополнением к обычной мере. То есть это 180-м, где м — это обычная мера.
Формула для вписанного угла
Если вы знаете длину малой дуги и радиус, вписанный угол определяется по формуле ниже.
где:L — длина малой (самой короткой) дуги AB
R — радиус окружности
π — это Пи, приблизительно 3,142
Формула верна для точек на главной дуге. Если точка находится на малой дуге, то результат будет дополнением к правильному результату, но длина малой дуги все равно должна использоваться в формуле.
Дуги и Аккорды
Две точки A и B могут быть изолированными точками или конечными точками дуга или аккорд.Когда они являются конечными точками дуги, этот угол иногда называют периферийным углом дуги.Центральный угол
 Похожая концепция — центральный угол. Это угол, образованный в центре круга двумя заданными точками.
См. Определение центрального угла
Похожая концепция — центральный угол. Это угол, образованный в центре круга двумя заданными точками.
См. Определение центрального углаЦентральный угол всегда вдвое больше вписанного угла. См. Теорему о центральном угле.
Связь с теоремой Фалеса
Обратитесь к рисунку выше. Если две точки A, B образуют диаметр круга, вписанный угол будет равен 90 °, что Теорема Фалеса.Вы можете убедиться в этом сами, решив приведенную выше формулу, используя длину дуги, равную половине окружности круга.
Вы также можете перемещать точки A или B выше, пока вписанный угол не станет точно 90 °. Вы увидите, что точки A и B диаметрально противоположны друг другу.
Другие темы круга
General
Уравнения окружности
Углы по кругу
дуг
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены




Leave A Comment