4. Прототип задания B13 ( 27067) Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Все прототипы заданий В года
1. Прототип задания B13 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий
ПодробнееВсе прототипы заданий В года
1. Прототип задания B13 ( 27054) выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. Все прототипы заданий В13
Подробнее Все прототипы заданий года
1. Прототип задания 12 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий 12
ПодробнееТригонометрические уравнения
Тригонометрические уравнения С б) Укажите корни, принадлежащие отрезку. а) Решите уравнение б) Укажите корни уравнения, принадлежащие отрезку а) Решbте уравнение. б) Укажите корни этого уравнения, принадлежащие
ПодробнееВсе прототипы задания В9 (2013)
Все прототипы задания В9 (2013) ( 245359) Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,.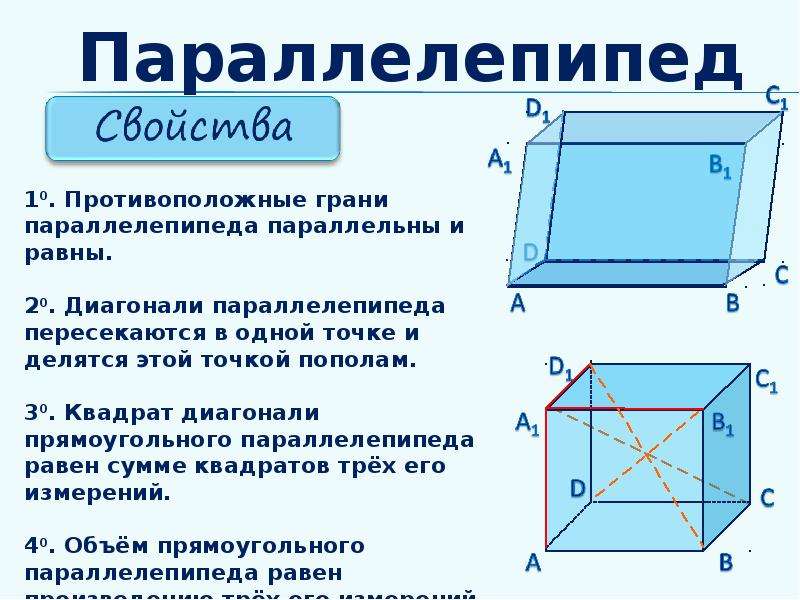
Прямоугольный параллелепипед
ЗАДАНИЕ 10 Стереометрия Куб 1.Площадь поверхности куба равна 18. Найдите его диагональ. 2. Диагональ грани куба равна 2 6. Найдите диагональ куба. 3. Диагональ грани куба равна 6. Найдите диагональ куба.
ПодробнееВсе прототипы задания В11 (2013)
Все прототипы задания В11 (2013) ( 25541) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). ( 25561) Найдите площадь поверхности многогранника, изображенного
ПодробнееВсе прототипы В года
1. Прототип задания B9 ( 245359) Все прототипы В5 2013 года Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. 2. Прототип задания B9 ( 245360) Найдите расстояние
ПодробнееКуб. Прямоугольный параллелепипед
Куб 1. Задание 16 27098. Диагональ куба равна. Найдите его объем. О т в е т : 8 2. Задание 16 500957. Во сколько раз увеличится объем куба, если все его рѐбра увеличить в 5 раз? О т в е т : 1 2 5 3. Задание
ПодробнееЗадание 16 Задачи по стереометрии
Задание 16 Задачи по стереометрии Куб 1.Диагональ куба равна 12. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30
ПодробнееЗадание 8 Стереометрия.
Задание 8 Стереометрия. Куб 1. Площадь поверхности куба равна 18. Найдите его диагональ. 2. Объем куба равен 8. Найдите площадь его поверхности.
Стереометрия: комбинации тел.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: комбинации тел. 27041. Прямоугольный параллелепипед
ПодробнееЗадачи по с т е р е о м е т р и и
Задачи по с т е р е о м е т р и и Ермак Елена Анатольевна, доктор педагогических наук, профессор кафедры математического анализа и методики обучения математике Псковского государственного университета
ПодробнееЗадание 13. Задачи по стереометрии
Задание 13 Задачи по стереометрии 1.Диагональ куба равна Куб. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30 см
ПодробнееСтартовая контрольная работа
Стартовая контрольная работа Контрольная работа 1(на 20 мин) 1. Найдите координаты вектора АВ, если А (5; 1; 3), В (2; 2; 4). 2. Даны векторы b (3; 1; 2) и c 2b c (1; 4; 3). Найдите. 3. Изобразите систему
1 Расстояние от точки до прямой
1 Расстояние от точки до прямой 1 1 1 1 1.1. В единичном кубе 1 1 1 1 найдите расстояние от точки до прямой 1. 1 1.2. В правильной треугольной призме 1 1 1, все ребра которой равны 1, найдите расстояние
ПодробнееСтереометрия: пирамиды.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.
7. Задачи по стереометрии
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ 7 Задачи по стереометрии методические указания для абитуриентов физического факультета Ростов-на-Дону 00 Печатается по решению учебнофакультета РГУ методической комиссии
ПодробнееСтереометрия: призма.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: призма. 27047. В сосуд, имеющий форму
Тест 250. Отрезок. Длина
Тест 250. Отрезок. Длина Длина отрезка равна 1, если он является: 1. высотой равностороннего треугольника со стороной 2; 2. третьей стороной треугольника, в котором две другие стороны равны 1 и 2, а угол
ПодробнееID_7154 1/10 neznaika.pro
1 Задачи по стереометрии Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. Найдите объём
Подготовка к ЕГЭ по математике
2015 2016 Подготовка к ЕГЭ по математике Прототипы задач из открытого банка заданий ЕГЭ по математике (профильный уровень) http://mathege.ru Стереометрия. Параллелепипед. Куб. Александр и Наталья Крутицких
ПодробнееТест по теме 60 «Параллелепипед и куб»
Тест по теме 60 «Параллелепипед и куб» 1. Существует ли параллелепипед, у которого только одна боковая грань перпендикулярна основанию?, если в основании квадрат 2.
ЗАДАНИЯ С КРАТКИМ ОТВЕТОМ ПО ГЕОМЕТРИИ
ЗАДАНИЯ С КРАТКИМ ОТВЕТОМ ПО ГЕОМЕТРИИ Инструкция. Решите задание. Дайте краткий ответ. 1. Апофема правильной треугольной пирамиды 4 см, а сторона основания 8 см. Найдите площадь боковой поверхности пирамиды.
ПодробнееЧАСТЬ I. Координаты и векторы
ЭКЗАМЕН ПО ГЕОМЕТРИИ КЛАСС ЧАСТЬ I Координаты и векторы Составьте уравнение плоскости, проходящей через точку M (;3;5 ) параллельно векторам a = ( ; ;5) и b = ( 4;3;0 ) Составьте уравнение плоскости, проходящей
Геометрия. Тренировочный вариант 1
Геометрия. Тренировочный вариант 1 1. Найдите площадь трапеции, изображённой на рисунке. 2. Около треугольника MNP описана окружность с центром О. Найдите угол РОМ, если угол PNM равен 17. Ответ дайте
ПодробнееМногогранники. Призма
Справка В9 Многогранники Многогранник это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Призма Призмой называется многогранник, который состоит из двух плоских многоугольников,
Тест по теме «Задачи стереометрии»
Тест по теме «Задачи стереометрии» Тест составлен на основе учебника «Геометрия, 10-11 класс (базового и профильного уровней ) / Л.С. Атанасян и др. — М.: «Просвещение», 2010. Аннотация: Задачи теста соответствуют
ПодробнееПРЯМОЙ И НАКЛОННЫЙ КОНУС
ПРЯМОЙ ЦИЛИНДР Пусть в пространстве заданы две параллельные плоскости и. F круг в одной из этих плоскостей, например. Рассмотрим ортогональное проектирование на плоскость. Проекцией круга F будет круг
Проекцией круга F будет круг
Куб. 3. Найдите объем многогранника, вершинами которого являются точки,,,,, прямоугольного параллелепипеда, у которого,,.
Куб. 1. Диагональ куба равна. Найдите его объем. 2.Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30 см без одной грани, нужно покрасить
ПодробнееЗадание В9 (№ 4861) Прямоугольный параллелепипед описан около цилиндра
Задание В9
(№ 4861) Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
(№ 4863) Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1,5. Найдите объем параллелепипеда.
(№ 4865) Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 6. Найдите объем параллелепипеда.
(№ 4867) Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 8,5. Найдите объем параллелепипеда.
(№ 4869) Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 9,5. Найдите объем параллелепипеда.
(№ 4871) Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра. (№ 4873) Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 80. Найдите высоту цилиндра. (№ 4875) Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. (№ 4877) Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 9. Объем параллелепипеда равен 81. Найдите высоту цилиндра. (№ 4879) Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объем параллелепипеда равен 27. Найдите высоту цилиндра. (№ 4881) Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 6. Объем параллелепипеда равен 36. Найдите высоту цилиндра. |
(№ 4883) Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем. |
(№ 4885) Прямоугольный параллелепипед описан около сферы радиуса 6,5. Найдите его объем.
(№ 4887) Прямоугольный параллелепипед описан около сферы радиуса 7,5. Найдите его объем.
(№ 4889) Прямоугольный параллелепипед описан около сферы радиуса 8,5. Найдите его объем.
(№ 4891) Прямоугольный параллелепипед описан около сферы радиуса 9,5. Найдите его объем.
(№ 4893) Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
(№ 4895) Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
(№ 4897) Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
(№ 4899) Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
(№ 4901) Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
(№ 4903) Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
(№ 4951) В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого?
(№ 4953) В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого?
(№ 4955) В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 18 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого?
(№ 4957) В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 27 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого?
(№ 4959) В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 9 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого?
(№ 4961) В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4963) В основании прямой призмы лежит прямоугольный треугольник с катетами 4 и 1. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4965) В основании прямой призмы лежит прямоугольный треугольник с катетами 9 и 6. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Найдите объем цилиндра, описанного около этой призмы.
(№ 4967) В основании прямой призмы лежит прямоугольный треугольник с катетами 1 и 10. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4969) В основании прямой призмы лежит прямоугольный треугольник с катетами 3 и 3. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4971) В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4973) В основании прямой призмы лежит квадрат со стороной 7. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4975) В основании прямой призмы лежит квадрат со стороной 6. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4977) В основании прямой призмы лежит квадрат со стороной 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4979)В основании прямой призмы лежит квадрат со стороной 5. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4981) В основании прямой призмы лежит квадрат со стороной 4. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4983) В основании прямой призмы лежит квадрат со стороной 9. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4985) В основании прямой призмы лежит квадрат со стороной 3. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4987) В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
(№ 4989) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.
Вычислите объем цилиндра, если объем конуса равен 25.
(№ 4991) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 23.
(№ 4993) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27.
(№ 4995) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 18.
(№ 4997) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 14.
(№ 4999) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 16.
(№ 5001) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 11.
(№ 5003) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 17.
(№ 5005) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 87.
(№ 5007) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 45.
(№ 5009) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 81.
(№ 5011) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 72.
(№ 5013) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 75.
(№ 5015) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 57.
(№ 5017) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 63.
Вычислите объем цилиндра, если объем конуса равен 63.
(№ 5019) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 42.
(№ 5021) Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
(№ 5023) Объем конуса равен 168. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
(№ 5025) Объем конуса равен 128. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
(№ 5027) Объем конуса равен 120. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
(№ 5029) Объем конуса равен 112. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
(№ 5031) Объем конуса равен 24. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
(№ 5033) Объем конуса равен 64. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
(№ 5035) Объем конуса равен 144. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.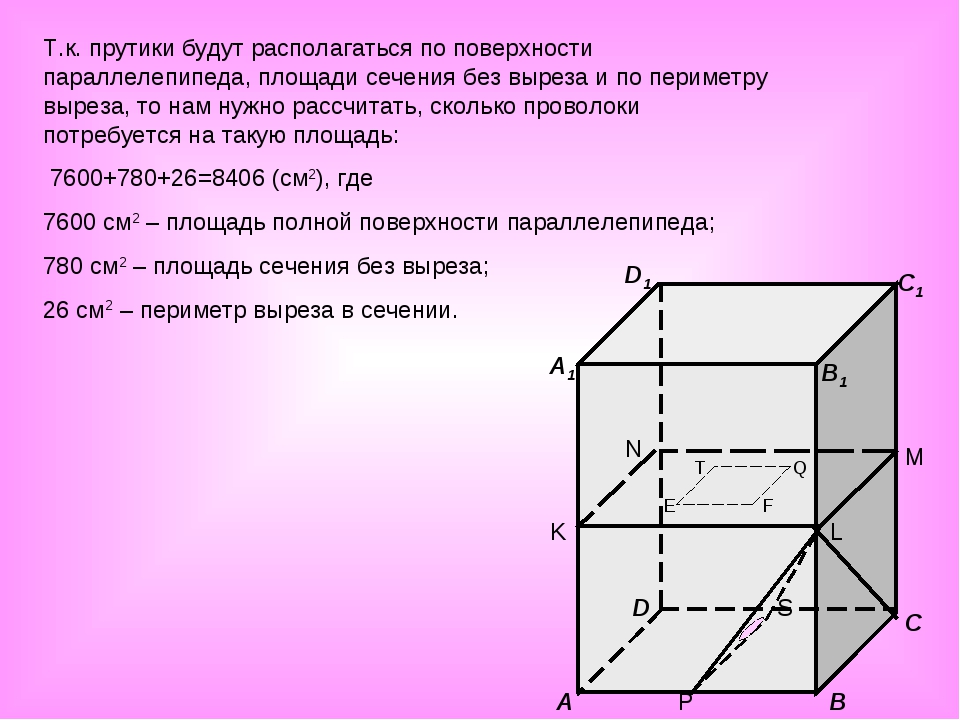
(№ 5039) Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
(№ 5041) Площадь поверхности куба равна 18. Найдите его диагональ.
(№ 5043) Объем куба равен 8. Найдите площадь его поверхности.
(№ 5045) Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
(№ 5047) Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
(№ 5049) Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
(№ 5051) Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
(№ 5053) Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
(№ 5055) Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
(№ 5057) Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
(№ 5059) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
(№ 5061) Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен
, а высота равна 2.
(№ 5063) Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2.
(№ 5065) Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
(№ 5067) Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
(№ 5069) Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
(№ 5071) Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
(№ 5073) Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
(№ 5075) Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
(№ 5077) Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
(№ 5079) Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды .
(№ 5081) Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
Задание №8. Стереометрия. ЕГЭ . Математика.
БАЗА ЗАДАНИЙ
Задание № 8. Стереометрия.
Стереометрия.
81. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
82. Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найдите площадь полной поверхности цилиндра.
83. Шар вписан в цилиндр. Объем шара равен 6. Найдите объем цилиндра.
84. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на π.
85. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
86. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
87. Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.
88. Объем первой цилиндрической кружки равен 12. У второй кружки высота в два раза меньше, а радиус основания в три раза больше. Найдите объём второй кружки.
89. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
90. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
91. Объем шара равен 288 π. Найдите площадь его поверхности, деленную на π.
92. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
93. Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго.
94. В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и B1D1. Ответ дайте в градусах.
95. В кубе ABCDA1B1C1D1 точка K – середина ребра AA1, точка L — середина ребра
A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.
Ответ дайте в градусах.
96. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
97. Найдите площадь поверхности многогранника, изображенного на рисунке.
98. На рисунке изображен многогранник, все двугранные углы прямые. Найдите квадрат расстояния между вершинами A и C3.
99. Объем тетраэдра равен 19. Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.
100. Площадь поверхности тетраэдра равен 12. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра.
101. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
102. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
103. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
104. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.
105. Объем треугольной пирамиды SABC равен 15. Плоскость проходит через сторону AB основания этой пирамиды и пересекает противоположное боковое ребро в точке D, делящей ребро SC в отношении 1: 2, считая от вершины S. Найдите объем пирамиды DABC.
106. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
107. От призмы ABCA1B1C1, объем которой равен 6, отсечена треугольная пирамида C1ABC. Найдите объем оставшейся части.
108. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на π.
109. Найдите объем цилиндра, площадь основания которого равен 1, а образующая равна 6 и наклонена к плоскости основания под углом 30.
110. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π.
111. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
112. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 2/ π. Найдите объем цилиндра, описанного около этой призмы.
113. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.
114. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
115. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
116. Около куба с ребром √3 описан шар. Найдите объем этого шара, деленный на π.
117. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
118. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.
119. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2√3 и наклонены к плоскости основания под углом 30°.
120. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
121. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
122. В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что BD1 =2AD.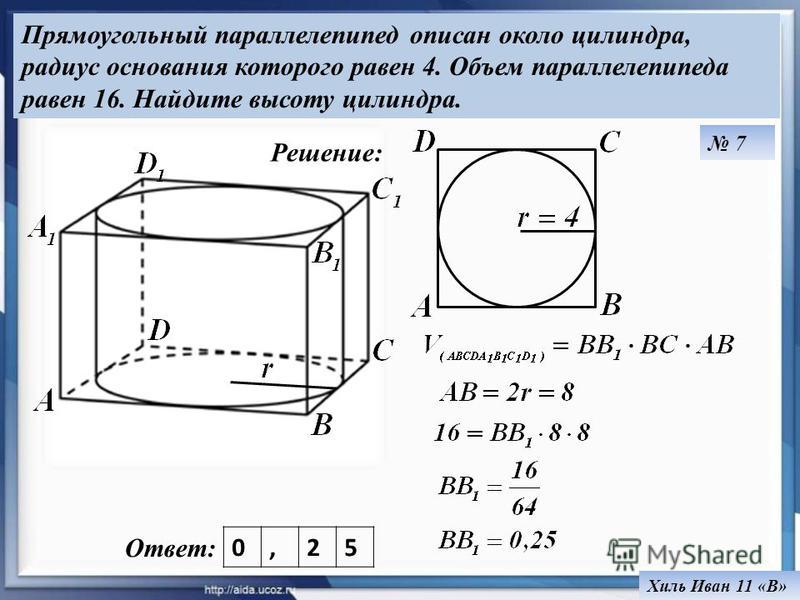 Найдите угол между диагоналями DB1 и CA1. Ответ дайте в градусах.
Найдите угол между диагоналями DB1 и CA1. Ответ дайте в градусах.
123. В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро АВ=2, ребро AD=√5, ребро AA1=2. Точка К – середина ребра BB1. Найдите площадь сечения,проходящего через точки A1, D1 и K.
124. В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро АВ=8, ребро AD=6, ребро AA1=21. Найдите синус угла между прямыми CD и A1C1.
125. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна √3.
126. Одна из граней прямоугольного параллелепипеда – квадрат. Диагональ параллелепипеда равна √8 и образует с плоскостью этой грани угол 45°. Найдите объем параллелепипеда.
127. Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB =5, AD =4, AA1 =3. Ответ дайте в градусах.
128. Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB=4, AD=3, AA1=5. Ответ дайте в градусах.
ЕГЭ — 2020. Прямоугольный параллелепипед | Материал для подготовки к ЕГЭ (ГИА) по геометрии (11 класс):
По теме: методические разработки, презентации и конспекты
Открытое занятие по теме «Прямоугольный параллелепипед и тетраэдр. Построение сечений»Занятие выполнено ввиде презентации PowerPoint с выходом в программу «Живая Математика».На данном занятии повторяется, обобщается и систематизируется знания по теме «Построение сечений».За…
Прямоугольный параллелепипедПрезентация учителя высшей категории Лукахиной М. Ю. МОУ СОШ №10 г. Ногинск Московской области…
Конспект открытого урока по математике «Прямоугольный параллелепипед» 5 классВашему вниманию предлагаю конспект урока по математике «Прямоугольный параллелепипед» в 5 классе по учебнику Н. Я. Виленкина, В.И. Жохова с презентацией….
Я. Виленкина, В.И. Жохова с презентацией….
Тест составлен в Excel и состоит из 10 вопросов. К каждому вопросу предлягаются иллюстрации и варианты ответов. В конце тестирования выставляется оценка….
презентация «Прямоугольный параллелепипед. Куб», разработка уроков «Прямоугольный параллелепипед», «Куб»ЕщЁ К.Д. Ушинский заметил «Детская приода требует наглядности» В пропедевтическом курсе геометрии наглядность играет особую роль, она является основным источником геометрической информации, что диктуе…
Технологическая карта урока по математике в 5 классе по теме « Прямоугольный параллелепипед. Объём и площадь поверхности прямоугольного параллелепипеда».Технологическая карта урока по математике в 5 классе по теме « Прямоугольный параллелепипед. Объём и площадь поверхности прямоугольного параллелепипеда» по учебнику Виленкина Н.я и др…
Технологическая карта урока в 5 классе по теме « Прямоугольный параллелепипед. Площадь поверхности прямоугольного параллелепипеда».Урок математики в 5 классе по учебнику Н.Я. Виленкин «Прямоугольный параллелепипед. Площадь поверхности прямоугольного параллелепипеда"…
Задачи и их решение — Решение B11
1.В куб вписан шар радиуса 1. Найдите объем куба.
Решение.
Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:
.
Ответ: 8.
2. Площадь поверхности куба равна 18. Найдите его диагональ.
Решение.
Пусть ребро куба равно , тогда площадь поверхности куба , а диагональ куба . Тогда
.
Ответ: 3.
3.Объем куба равен 8. Найдите площадь его поверхности.
Площадь поверхности куба выражается через его ребро как , а объем — как . Отсюда видно, что площадь поверхности куба выражается через его объем как .
 Отсюда находим, что
Отсюда находим, что.
Ответ: 24.
4.
Объем
одного куба в 8 раз больше объема другого куба. Во сколько раз площадь
поверхности первого куба больше площади поверхности второго куба?
По условию
,
откуда Площади их поверхностей соотносятся как.
Ответ: 4.
5.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Решение.
Высота
параллелепипеда равна высоте вписанного в него цилиндра. Основанием
параллелепипеда является квадрат, сторона которого в два раза больше
радиуса вписанной в него окружности. Поэтому площадь основания равна 4,
а объем параллелепипеда равен
.
6.
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Решение.
Высота
и сторона такого параллелепипеда равны диаметру сферы, то есть это куб
со стороной 2. Площадь поверхности куба со стороной :
7.
Диагональ прямоугольного параллелепипеда равна и образует углы 30, 30 и 45 с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Решение.Ребро параллелепипеда напротив угла в равно ,
поскольку образует с заданной диагональю и диагональю одной из граней
равнобедренный треугольник. Два другие ребра по построению лежат в
прямоугольных треугольниках напротив угла в и равны, поэтому половине диагонали. Тогда объем параллелепипеда:
Ответ: 4.
8.
.
Тема 4. Многогранники
А:задания базового уровня сложности с выбором ответа.
. | Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. А) 5 Б) В)10 | 2 | Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза? А) 27 Б)6 В)9 |
3 | Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ. А) 6 Б)3 В)9 | 4 | Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. А) 8Б)4 В)16 |
5 | Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760. А) 22 Б)10 В)12 | 6 | Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. А) 16 Б)24 В)6 |
7 | Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4. А) 96 Б)60 В)80 | 8 | Стороны
основания правильной четырехугольной
пирамиды равны 6, боковые ребра равны
5. А) 59 Б)48 В)84 |
9 | Найдите объем пирамиды, высота которой равна 1, а основание — прямоугольник со сторонами 4 и 6. А) 20 Б)8В)24 | 10 | Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 264. Найдите высоту призмы. А) 9 Б)18 В)4,5 |
Тема 5.Тела вращения.
А:задания базового уровня сложности с выбором ответа.
1 | Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза? А) 4 Б)8 В)16 | 2 | Площадь большого круга шара равна 3. Найдите площадь поверхности шара. А) 4Б)12 В)6 |
3 | Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза? А) 9 Б)27 В)3 | 4 | Найдите площадь боковой поверхности деленную на если его радиус 3,а высота4 А) 15 Б)12 В)20 |
5 | Длина окружности основания цилиндра равна 6, высота равна 2. Найдите площадь боковой поверхности цилиндра. А) 6 Б)12 В)3 | 6 | Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 16 раз? А) 256 Б)8 В)16 |
7 | Диаметр
основания конуса равен 6, а угол при
вершине осевого сечения равен 90°. А) 3 Б)27 В)9 | 8 | Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите . А) 48 Б)64 В)3 |
9 | В основании прямой призмы лежит квадрат со диагональю 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. А) 192 Б)64 В)48 | 10 | Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на . А) 12 Б)6 В)4 |
Задания типа В9 (к уроку)
Задания типа В9 (к уроку)
1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
4. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
5. В цилиндрический сосуд налили воды. Уровень воды при этом достигает высоты см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на см. Чему равен объем детали? Ответ выразите в .
6.
В сосуд, имеющий форму правильной
треугольной призмы, налили воду. Уровень
воды достигает
см.
На какой высоте будет находиться уровень
воды, если ее перелить в другой такой
же сосуд, у которого сторона основания
в
раза
больше, чем у первого? Ответ выразите в
см.
Уровень
воды достигает
см.
На какой высоте будет находиться уровень
воды, если ее перелить в другой такой
же сосуд, у которого сторона основания
в
раза
больше, чем у первого? Ответ выразите в
см.
7. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
8. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
9. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
10. Площадь поверхности куба равна 18. Найдите его диагональ.
11. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
12. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
13. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
14. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2.
15. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2.
16. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
17. Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды .
18. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
19.
Площадь грани прямоугольного
параллелепипеда равна 12. Ребро,
перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Найдите объем параллелепипеда.
20. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
21. Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
22. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
23. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?
24. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза?
25. Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?
26. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
27. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .
28. Найдите объем цилиндра, площадь основания которого равен 1, а образующая равна 6 и наклонена к плоскости основания под углом 30.
29. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
30. Диагональ прямоугольного параллелепипеда равна и образует углы 30, 30 и 45 с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
31. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60. Одно из ребер параллелепипеда составляет с этой гранью угол в 60 и равно 2. Найдите объем параллелепипеда.
32. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
33. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны и наклонены к плоскости основания под углом 30.
34. От призмы , объем которой равен 6, отсечена треугольная пирамида . Найдите объем оставшейся части.
35.
Объем треугольной пирамиды SABC,
являющейся частью правильной шестиугольной
пирамиды SABCDEF, равен 1.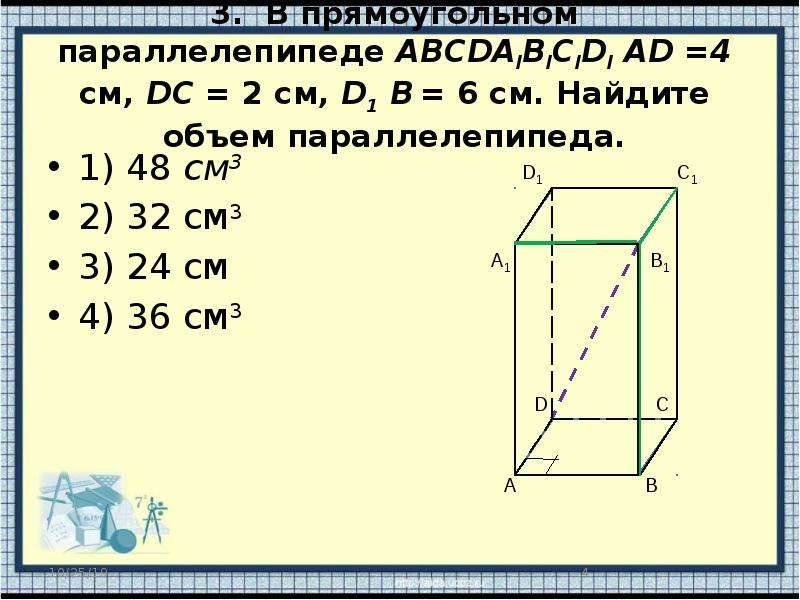 Найдите объем
шестиугольной пирамиды.
Найдите объем
шестиугольной пирамиды.
36. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
37. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
38. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на .
39. Конус описан около правильной четырехугольной пирамиды со стороной основания 4и высотой 6. Найдите его объем, деленный на .
40. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
41. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
42. Около куба с ребром описан шар. Найдите объем этого шара, деленный на .
43. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
44. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
45. Площадь поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь поверхности отсеченного конуса.
46. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
47. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
48. Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
49.
Найдите площадь боковой поверхности
правильной треугольной призмы, вписанной
в цилиндр, радиус основания которого
равен ,
а высота равна 2.
50. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
51. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на .
52. Объем шара равен 288 . Найдите площадь его поверхности, деленную на .
53. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.
54. Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
55. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45. Найдите объем пирамиды.
56. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
57. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
58. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
59. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
60. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
61. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
62. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
63. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
64. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите .
65. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
66. Объем тетраэдра равен Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.
66. Диагональ куба равна . Найдите его объем.
67.
Объем куба равен
.
Найдите его диагональ.
Видео с вопросом: Использование множителей Лагранжа для определения максимального объема прямоугольного параллелепипеда, вписанного в эллипсоид, может иметь
Стенограмма видеозаписи
Найдите объем самого большого прямоугольного параллелепипеда, который может быть вписан в эллипсоид: в квадрате в квадрате плюс 𝑦 в квадрате над 𝑏 в квадрате плюс 𝑧 в квадрате над 𝑐 в квадрате равняется единице. Это (а) восемь над тремя корнями три, (б) b над тремя корнями три, (в) восемь 𝑎𝑏𝑐 над корнем три, (г) шесть 𝑎𝑏𝑐 над корнем три, или (д) восемь?
Чтобы найти объем прямоугольного параллелепипеда, самый простой способ — взять одну вершину, а затем произведение длин трех ее смежных ребер.Итак, здесь, например, если эти три ребра имеют длину 𝛼, 𝛽 и then, то объем этой формы 𝑉 составляет всего 𝛼 раз 𝛽 раз 𝛾. Это кажется достаточно простым. Но для максимизации этого значения для параллелепипеда, вписанного внутри эллипсоида, не очевидно, как эта форма будет ориентирована внутри эллипсоида. Таким образом, нам нужно будет найти как минимум 12 переменных,-, 𝑦- и 𝑧-координаты первой вершины и всех трех ее смежных вершин.
Однако вместо этого мы можем использовать то, что мы знаем о взаимосвязи эллипсоида, с более простой трехмерной формой, сферой.Эллипсоид — это, по сути, просто сфера, масштабируемая по трем перпендикулярным осям. В частности, эллипсоид с заданным уравнением в квадрате в квадрате плюс 𝑦 в квадрате над в квадрате плюс 𝑧 в квадрате в квадрате, равном единице, является просто единичной сферой, которая была масштабирована по оси с коэффициентом 𝑎, вдоль по оси в раз, а по оси в раз. Таким образом, эллипсоид является результатом трех вычислений по трем перпендикулярным осям.
Важным свойством преобразования масштабирования является то, что такое же масштабирование, примененное к любой трехмерной фигуре, будет масштабировать ее объем с тем же коэффициентом масштабирования, что и любая другая трехмерная форма.Это немного легче продемонстрировать в двух измерениях, поэтому давайте освободим немного места. Рассмотрим, например, единичный квадрат. Длина стороны равна единице, а площадь составляет всего одну единицу. Теперь представьте, что квадрат растягивается вдоль некоторой оси в раз. Легко увидеть, что если мы растянем вдоль оси, параллельной одной из его сторон, его площадь увеличится в раз. Итак, новая область — 𝑆. Но на самом деле это применимо независимо от того, в каком направлении мы растягиваемся.
Например, рассмотрим растяжение с коэффициентом 𝑆 вдоль оси, параллельной диагонали квадрата.В результате получается ромб с одной неизменной длиной диагонали корня два, а другой — 𝑆 корня два. Площадь ромба составляет половину произведения двух диагоналей. Итак, у нас есть половина, умноженная на двукратный корень 𝑆 корень два, что просто равно 𝑆, такая же новая площадь, какая была у нас, когда мы растягивались вдоль оси, параллельной одной из сторон квадрата. С помощью матричных преобразований довольно просто доказать, что это увеличение площади одинаково по любой оси и что это также распространяется на объем в трех измерениях.
В результате мы можем найти максимальный объем прямоугольного параллелепипеда, который можно вписать в сферу, а затем просто масштабировать параллелепипед, используя то же преобразование, что и для преобразования сферы в эллипсоид. И это даст нам новый максимальный объем параллелепипеда, который можно вписать в эллипсоид. Мы можем быть уверены, что этот параллелепипед будет иметь максимальный объем, поскольку он был преобразован из параллелепипеда с максимальным объемом в сфере.И любой другой параллелепипед, вписанный в эллипсоид, должен был изменить объем во столько же раз, что и этот. Таким образом, параллелепипед максимального объема в сфере соответствует параллелепипеду максимального объема в эллипсоиде.
Это, как мы увидим, значительно упростит задачу. Итак, нам нужно найти максимальный объем параллелепипеда, который можно вписать в единичную сферу. Интуиция может позволить вам догадаться, что это куб, и это действительно так. Но мы собираемся доказать это с помощью множителей Лагранжа.Итак, рассмотрим единичную сферу с центром в начале координат. Его поверхность имеет уравнение в квадрате плюс в квадрате плюс в квадрате, равном единице. Чтобы параллелепипед имел максимальный объем, хотя бы одна из его вершин должна касаться поверхности сферы. В противном случае мы могли бы легко растянуть параллелепипед с одной стороны и увеличить объем. Рассмотрим тогда, без ограничения общности, одну вершину параллелепипеда, касающуюся сферы в положительном октанте; т.е. он имеет координаты 𝑥, 𝑦,, где 𝑥, 𝑦 и 𝑧 положительны.
Теперь рассмотрим ребра, к которым примыкает эта вершина. Мы только что нарисовали здесь первую часть краев. Поскольку вопрос определяет прямоугольный параллелепипед, и мы будем масштабировать эту форму со сферой по трем перпендикулярным осям, эти края также должны быть под прямым углом друг к другу. Таким образом, они останутся под прямым углом друг к другу после преобразования масштабирования. Поскольку эта сфера симметрична по всем трем осям, мы снова можем предположить без ограничения общности, что края параллельны каждой из координатных осей.Если мы теперь продолжим эти ребра дальше, мы можем сделать вывод, что все три ребра будут иметь максимальную длину. Следовательно, прямоугольный параллелепипед будет иметь максимальный объем, когда все три ребра соприкасаются со сферой в своей другой конечной вершине.
Поскольку сфера симметрична относительно всех трех осей, и эти линии параллельны трем осям, вершины параллелепипеда на другом конце этих ребер должны находиться на одинаковом расстоянии вдоль своих соответствующих параллельных осей, но в отрицательном направлении от исходная точка.Таким образом, эта точка должна иметь отрицательные координаты 𝑥, 𝑦, 𝑧. Эта точка должна иметь координаты 𝑥, отрицательные 𝑦, 𝑧. И эта точка должна иметь координаты 𝑥, 𝑦, отрицательные 𝑧. Это, в свою очередь, означает, что эта сторона имеет длину два 𝑥, эта сторона имеет длину два, а эта сторона имеет длину два 𝑧, что означает, что объем полного прямоугольного параллелепипеда должен быть равным двум 𝑥 умноженным на два 𝑦 раза два 𝑧 равняются восьми 𝑥𝑦𝑧.
Это функция, которую необходимо развернуть. И наше ограничение состоит в том, что наша исходная выбранная точка в, 𝑦, 𝑧 должна лежать на сфере, то есть значения 𝑥, 𝑦 и 𝑧 удовлетворяют уравнению сферы: в квадрате плюс в квадрате плюс в квадрате равны единице.Введя это в обычную форму для функции ограничения, мы имеем равно в квадрате плюс в квадрате плюс в квадрате минус один, равно нулю. Напомним, что функция Лагранжа задается выражением от, 𝜆 равно 𝑓 от плюс от, где 𝑓 — функция, которую нужно максимизировать, 𝑔 — функция ограничения, а 𝜆 — скаляр, известный как множитель Лагранжа. Вектор 𝐱 — это набор переменных, в данном случае 𝑥, 𝑦, 𝑧.
Итак, в нашем случае 𝐿 из, 𝑦, 𝑧, 𝜆 равно восьми 𝑥𝑦𝑧 плюс 𝜆 умноженное на в квадрате плюс в квадрате плюс 𝑧 в квадрате минус один.Чтобы найти максимум или минимум с учетом ограничения 𝑔, мы берем частные производные лагранжиана по 𝑥, 𝑦, 𝑧 и 𝜆; установите их равными нулю; затем решите получившуюся систему уравнений относительно 𝑥, 𝑦 и 𝑧. Нам не нужно явно решать для 𝜆. Давайте сначала освободим место и переместим нашу функцию сюда.
Итак, теперь нам нужно взять частные производные от по 𝑥, 𝑦, 𝑧 и 𝜆. 𝜕𝐿 по 𝜕𝑥 равно восьми 𝑦𝑧 плюс два 𝜆𝑥, 𝜕𝐿 по 𝜕𝑦 равно восьми 𝑥𝑧 плюс два 𝜆𝑦, 𝜕𝐿 по 𝜕𝑧 равно восьми 𝑥𝑦 плюс два 𝜆𝑧, а 𝜕𝐿 по 𝜕𝜆 равно 𝑥 в квадрате плюс 𝑦 в квадрате плюс 𝑧 в квадрате минус один, который, как мы заметим, совпадает с функцией ограничения 𝑔.Теперь мы установим все это равными нулю и решим эту систему уравнений относительно 𝑥, 𝑦 и 𝑧.
Судя по симметрии этой системы уравнений, вы можете увидеть, к чему все идет, но давайте продолжим. Мы можем решать эти уравнения в любом порядке. Начнем с первого уравнения, и нам понадобится немного больше места. Из уравнения 1 мы можем переставить так, чтобы было равно отрицательному 𝜆𝑥 над четырьмя. Подставляя это выражение для 𝑧 в уравнение два, мы получаем восемь 𝑥 отрицательных по сравнению с четырьмя 𝑦 плюс два 𝜆𝑦 равны нулю.Разделив на два и взяв 𝜆 в качестве общего множителя перед упрощением, мы получим 𝜆 умноженное на 𝑦 минус 𝑥 в квадрате над 𝑦 равным нулю, что означает, что либо 𝜆 равно нулю, либо 𝑦 минус 𝑥 в квадрате над 𝑦 равно нулю. Если вместо этого мы подставим это выражение для в третье уравнение, мы получим восемь 𝑥𝑦 плюс два 𝜆 отрицательных по сравнению с четырьмя 𝑦 равными нулю.
Переставив и разделив на, что мы можем сделать, поскольку 𝑥, равное нулю, было бы тривиальным результатом с параллелепипедом нулевого объема, мы получаем 16𝑦 в квадрате, равном в квадрате.𝑦 также не равно нулю, поэтому 𝜆 не равно нулю. Следовательно, из нашего предыдущего уравнения мы должны иметь must минус 𝑥 в квадрате над 𝑦 равным нулю. Переставив это уравнение, мы получим в квадрате равно в квадрате, что также равно в квадрате больше 16. Если мы теперь воспользуемся уравнением 4 и подставим в квадрате вместо в квадрате и в квадрате отрицательного 𝜆𝑥 вместо четырех 𝑦, мы получим 𝑥 в квадрате плюс в квадрате плюс минус 𝜆𝑥 больше четырех корней 𝜆 в квадрате больше 16 все в квадрате равно единице.
Все это упрощается до трех 𝑥 в квадрате равняется единице, что затем означает, что в квадрате равно 𝑦 в квадрате равняется одной трети.Из нашего уравнения для 𝑧 мы можем получить в квадрате равно в квадрате 𝑥 в квадрате больше 16𝑦 в квадрате, что упрощается до 𝑥 в квадрате, поэтому в квадрате также равно одной трети. Итак, мы теперь решили эту систему уравнений для 𝑥, 𝑦 и 𝑧, и 𝑥 равно 𝑦 равно 𝑧 равно единице над корнем три. И это положительный корень три, потому что мы изначально заявили, что 𝑥, 𝑦 и 𝑧 положительны. Помните, что каждая сторона параллелепипеда имела длину две, две 𝑦 и две соответственно. Таким образом, каждая сторона этого параллелепипеда имеет одинаковую длину — две над корнем три.
Так что это действительно куб. Его объем равен восьми 𝑥𝑦𝑧, что составляет всего восемь умноженных на единицу над корнем, трижды одну над корнем, трижды, одну над корнем три, что дает нам восемь над тремя корнями три, максимальный объем прямоугольного параллелепипеда, который может быть вписан внутрь. единичная сфера. Теперь нам нужно растянуть эту единичную сферу и куб внутри нее вдоль оси в раз, вдоль оси в раз и вдоль оси в раз. Это масштабирование умножит объем куба на 𝑎, 𝑏 и 𝑐.Таким образом, это дает объем самого большого прямоугольного параллелепипеда, который может быть вписан в этот эллипсоид, как восемь 𝑎𝑏𝑐 над тремя корнями три. Возвращаясь к нашим возможным ответам, мы видим, что это соответствует (а) восьми 𝑎𝑏𝑐 над тремя корнями три.
Калькулятор сфер
Как найти площадь поверхности и объем сферы?
Множество точек в пространстве, одинаково удаленных от заданной точки $ O $, является сферой. Точка $ O $ называется центром сферы.Расстояние от центра сферы до любой точки на сфере называется радиусом этой сферы. Радиус сферы должен быть положительным действительным числом. Отрезок, соединяющий две точки на сфере и проходящий через центр, называется диаметром шара. сфера. Все радиусы сферы равны друг другу. Сферу можно получить, вращая полукруг вокруг диаметра. Две сферы одного радиуса конгруэнтны.
Любое сечение сферы плоскостью является окружностью.Круг, полученный как поперечное сечение сферы и плоскости, проходящей через центр сферы, называется большим кругом. Любая плоскость, проходящая через центр $ O $ сферы, делит ее на две конгруэнтные части, известные как полусферы.
Метод определения площади поверхности сферы: Архимед впервые вывел формулу для площади поверхности сферы с учетом проекции на боковую поверхность описанного цилиндра. Он пришел к необычному выводу, что площадь поверхности сферы равна площади боковой поверхности цилиндра, описанного в сфере.2 \ times \ pi $$ где $ \ pi \ Approx3.14 $. Архимед [Heath, T. L., {it A History of Greek Mathematics,} 2 vol., Oxford, 1921] дал приближение $ \ pi $ по формуле $$ \ pi \ приблизительно \ frac {22} 7 = 3,142857142857 … $$ Другой метод определения площади поверхности шара — аппроксимация сферы радиуса $ r $ пирамидами $ n $, каждая из которых имеет площадь основания $ B $ и высотой $ r $ (см. рисунок ниже). Поскольку сумма базовых площадей равна $ n \ times B $, площадь поверхности сферы приблизительно равна $ n \ times B $, или $ 4r ^ 2 \ times \ pi $. 3}}) } {2}} \ right).2}}} {2}} \ right)}= {\ frac {{Hx}} {{R — r}} \ left ({2R — \ frac {{3x}} {2}} \ right). }
\]
Найдите стационарную точку:
\ [
{V ‘\ left (x \ right) = 0, \; \;} \ Rightarrow
{\ frac {{Hx}} {{R — r}} \ left ({2R — \ frac {{ 3x}} {2}} \ right) = 0, \; \;} \ Rightarrow
{2R — \ frac {{3x}} {2} = 0, \; \;} \ Rightarrow
{x = \ frac {{4R}} {3}.}
\]
Производная положительна слева от этой точки и отрицательна справа. Следовательно, это точка максимума функции \ (V \ left (x \ right).\) Тогда высота параллелепипеда
\ [
{y = \ frac {{H \ left ({R — \ frac {x} {2}} \ right)}} {{R — r}}}
= {\ frac {{H \ left] ({R — \ frac {{4R}} {6}} \ right)}} {{R — r}}}
= {\ frac {{HR \ left ({1 — \ frac {2} {3}) } \ right)}} {{R — r}}}
= {\ frac {{HR}} {{3 \ left ({R — r} \ right)}}.}
\]
Итак, параллелепипед, вписанный в усеченный конус, имеет наибольший объем, когда его стороны равны
.\ [{x = \ frac {{4R}} {3},} \; \; \; \ kern-0.3pt {y = \ frac {{HR}} {{3 \ left ({R — r} \верно)}}.2}}}}} {{\ sqrt [3] {4}}}} = {\ frac {{\ sqrt 5 \ sqrt [3] {{3V}}}} {{\ sqrt [6] {2} }}.} \]
Пример 16.
Конус имеет объем \ (V. \). Какой радиус основания \ (R \) и высота \ (H \) минимизируют площадь боковой поверхности конуса (рисунок \ (16a \))?Решение.
Обозначим наклонную высоту конуса через \ (m \) (рисунок \ (16a \)).
Рисунок 16а.Площадь боковой поверхности выражается формулой
\ [{S _ {\ text {L}}} = \ pi Rm. \]
Далее будем обозначать площадь боковой поверхности конуса просто буквой \ (S.{\ large \ frac {1} {2} \ normalsize}} = \ sqrt 2.}
\]
Таким образом, высота конуса с наименьшей площадью боковой поверхности должна быть примерно в \ (1,4 \) раз больше, чем радиус основания.
Интересно, каково отношение высоты к радиусу основания у такого конусообразного мегастроения, как Развлекательный центр «Хан Шатыр» (рисунок \ (16b \))? Если площадь боковой поверхности была одним из критических факторов при проектировании, вполне вероятно, что ее форма должна быть близка к нашему решению.3}}} {{27}}.} \]
Элементы Евклида, Предметный указатель
Элементы Евклида, Предметный указательА B C D E F грамм ЧАС я J K L M N О п Q р S Т U V W Y Z Цифры и символы
A
острый угол. См. Угол, острый.алгоритм, Евклидово См. Евклидов алгоритм.
альтернативные углы I.27
другие пропорции и соотношения
определение V.Def.12
для звездных величин V.16
для номеров VII.13
мирных номеров VII.Защита 22
угол (плоскость)
См. Также телесный угол.
тупой угол I.Def.12
альтернативные углы I.27
деление пополам I.9
строение I.23
определение I.Def.8, I.Def.9
внешний угол I.16, I.32
угол рупора I.Def.8, III.16, V.Def.4
углов как величина I.Def.9
пропорционально дуге VI.33
в сегменте III.Def.8
тупой угол I.Защита 11
сегмента III.Def.7
по окружности III.Def.9, III.26, III.27
прямолинейный угол I.Def.9
прямой угол I.Def.10
прямые углы равны Post.4
углов относительно поперечной I.27, I.28, I.29,
столбик трисекции 2
два прямых угла прямые I.13, I.14
вертикальные углы I.15
антецеденты в пропорциях V.Def.11
антеннарез См. Алгоритм Евклида.
приложение площадей
под углом I.42, I.44, I.45
превышение на параллелограмм VI.29
превышение на квадрат II.6
не соответствует параллелограмму VI.27 VI.28
проигрывает квадратом II.5
аппроксимация окружностей многоугольниками XII.2,
Аполлоний Пергейский (ок. 250–175 до н. Э.)
термины для конических сечений XI.Def.18
дуга пропорциональна углу VI.33
Архимед Сиракузский (ок.287–212 до н. Э.)
Угловая стойка с тройным разрезом.2
neusis Post.2
свойство величин X.1
площадь
Формула Герона для треугольника IV.4
медиальный X.21
арифметика, основная теорема VII.31
среднее арифметическое или среднее V.25
ассоциативность сложения
для звездных величин C.N.
ассоциативность умножения
для звездных величин V.3
среднее, арифметико-геометрическое V.25
подлинность элементов I.Def.1
из I.40
из V.19
из X.10
аксиома
аксиома сопоставимости V.Def.4
для звездных величин C.N.
ось
конуса XI.Def.19
цилиндра XI.Def.22
сферы XI.Def.15
B
основаниеконуса XI.Def.19
цилиндра XI.Def.23
треугольника I.4
пополам
угол I.9
окружность (дуга) III.30
строка I.10
граница I.Def.13
Brouwer, L.E.J. (1881–1966)
неконструктивная теорема о неподвижной точке I.6
Бирн, Оливер (1810–1890)
издание Elements Ссылки в сети
С
аннулированиедля дополнения C.N.
в пропорциях V.9
Плотницкая площадь II.Def.2
центр круга
характеристика III.9
строение III.1
определение I.Def.16
пересекающихся кругов имеют четкие центры III.5
касательные окружности имеют четкие центры III.6
Хрисипп (280 207)
1 как число VII.Def.1-2
окружность
окружность (дуга) III.30
круг
площадь XII.2,
центральный угол двойной угол по окружности III.20
пояс внутри круга III.2
центр оф. См. Центр круга.
построить круг из сегмента III.25
Строительный Пост.3
определение I.Защита 15
диаметр. Смотрите диаметр.
равных углов в сегментах III.21
равных хорд на равных расстояниях III.14
равных окружностей III.Def.1
пересечение окружностей III.10
произведение секущих III.37
произведение секущих равно тангенсу 2 III.36
изделий аккордов III.35
пропорционально диаметру 2 XII.2,
радиус. См. Радиус круга.
прямой угол в полукруге III.31
сектор оф. См. Сектор круга.
сегмент. См. Сегмент круга.
по касательной к. См. Касательную.
центр описанной окружности треугольника IV.5
описанная окружность треугольника IV.5
окружность
пропорционально углу VI.33
описанных фигур
круг, описанный вокруг пятиугольника IV.14
круг, описанный вокруг прямолинейной фигуры IV.Def.6
круг, описанный вокруг квадрата IV.9
круг, описанный вокруг треугольника IV.5
пятиугольник, описанный вокруг круга IV.12
прямолинейная фигура, описанная вокруг окружности IV.Def.4
прямолинейная фигура, описанная вокруг прямолинейной фигуры IV.Def.2
квадрат, описанный вокруг круга IV.7
треугольник, описанный вокруг круга IV.3
соизмеримый
определение X.Def.1
и числовые отношения V.Def.5
в квадрате X.Def.2
звездных величин и числовых соотношений X.5 ,, X.6, X.7, X.8
общие понятия C.N.
коммутативность
для сложения величин C.N.
умножения VII.15 VII.18
компас строительный Пост.3
componendo V.Def.14
составные числа
определение VII.Def.13
делится на простое число VII.31
конус
ось XI.Def.18
база XI.Def.19
конус одной трети цилиндра XII.10
определение XI.Def.20
пропорционально основанию XII.11
пропорционально высоте XII.14
обратно пропорциональный XII.15
прямоугольный, остроугольный, тупоугольный XI.Def.18
аналогичные конусы XI.Def.24, XII.12
конгруэнтный
рисунки I.4
твердых веществ XI.Def.10
предложений сравнения для треугольников. См. Треугольник.
подключенная фигура I.Def.14
консеквентов в пропорциях V.Защита 11
конструкции, 2- и 3-х мерные XI.20
продолжение пропорции V.Def.8, VIII.1
в низших терминах VIII.1, VIII.2, VIII.3, VIII.4
сумма IX.35
противоречие, доказательство по I.5
контрапозитивное предложение I.27
обращение предложения I.5, I.27
преобразование пропорции или соотношения
определение V.Def.16
предложение для величин V.19
convertendo V.Def.16
фигура выпуклая I.Def.14
косинусов, закон II.12, II.13
крестовое умножение пропорций
для строк VI.16
для номеров VII.19
куб
постройка XIII.15
определение XI.Def.25
отношение к додекаэдру XIII.17
отношение к тетраэдру XIII.15
кубических чисел VII.Def.19, IX.3, IX.4, IX.5, IX.6
разрезать на крайнее и среднее соотношение. См. Крайнее и среднее соотношение.
цилиндр
ось XI.Def.22
баз XI.Def.23
конус 1/3 цилиндра XII.10
определение XI.Def.21
пропорционально основанию XII.11
пропорционально высоте XII.13, XII.14
обратно пропорциональный XII.15
цилиндры аналогичные XI.Def.24, XII.12
D
десятиугольник, правильный (10-угольник)сторона шестиугольника к стороне десятиугольника XIII.9
сторон пятиугольника, шестиугольника и десятиугольника XIII.10
Декарт (1591–1661)
геометрическая алгебра VI.12
диаметр круга
биссектриса III.3
определение I.Def.17
диаметр наибольшей хорды III.15
расстояние от линии до точки III.Def.4
распределительность
деления над сложением VII.5
деления на вычитание VII.7
умножения над сложением
для строк II.1, II.2
для звездных величин V.1, V.2
для номеров VII.6, VII.8
умножения на вычитание
для звездных величин V.5, V.6
делитель числа VII.Def.3
додекаэдр
постройка XIII.17
определение XI.Def.28
отношение к кубу XIII.17
, двойственный многограннику XIII.14
соотношение дубликатов V.Def.9
E
элегантность в математике I.30эллипс XI.Def.18
эллиптическая геометрия I.16
равно
кружков III.Def.11
одинаковые и похожие твердые тела XI.Def.10
равносторонний треугольник (треугольник 60 ° -60 ° -60 °)
конструкция I.1
определение I.Def.20
сторона XIII.12
отношение эквивалентности V.Def.3
равенство как отношение эквивалентности C.N.
пропорция как отношение эквивалентности V.Def.5
Евклид (ок. 300 г. до н. Э.).
алгоритм Евклида VII.2, VII.3, ИКС.3
характеристика несоизмеримости величин X.2
тест на относительно простые числа VII.1
Евдокс (ок. 408–355 до н. Э.)
определение или пропорция V.Def.6
принцип исчерпания прав XII.2
свойство величин X.1
даже
четное число VII.Def.6, IX.21, IX.24, IX.27, IX.28, IX.30
четное число VII.Def.8, IX.32, IX.34
четно-нечетное число VII.Def.9, IX.33, IX.34
ex aequali соотношения и пропорции
определение V.Def.17
для звездных величин V.22
для номеров VII.14
вневписанная окружность треугольника IV.4
исчерпание, принцип XII.2
внешний угол
больше, чем противоположный внутренний угол треугольника I.16
сумма противоположных внутренних углов треугольника I.32
крайнее и среднее соотношение
алгебра на отрезках XIII.1, XIII.2, XIII.3, XIII.4, XIII.5
строительство II.11, VI.30
определение VI.Def.3
иррационально называется апотом XIII.6,
в треугольнике 36 ° -72 ° -72 ° IV.10
в пентаграмме IV.11, XIII.8
сторона шестиугольника к стороне десятиугольника XIII.9
F
грань твердого XI.Def.2рисунок I.Def.14
подключен I.Def.14
выпуклый I.Защита 14
прямолинейный I.Def.19
односвязный I.Def.14
подходит по прямой линии
в круг, конструкция IV.1
в круг, определение IV.Def.7
в диаграмму Пост.2
Ферма, Пьер де (1601–1665).
Простые числа Ферма IV.16
Простые числа Мерсенна и совершенные числа IX.36
четвертый пропорциональный V.18
дружественных чисел VII.Def.22
основная теорема арифметики VII.31
G
H
Хит, Томас Литтл (1861–1940)
издание Elements О тексте Ссылки в сети
высота фигуры VI.Def.4
Хайберг, Йохан Людвиг (1854–1928)
издание Elements О тексте Ссылки в сети I.Def.1
Цапля Александрийская (ок. 1 век н. Э.)
определение одинаковых и подобных твердых тел XI.Def.10
Формула Герона для площади треугольника IV.4
задача минимального расстояния I.20
шестигранник, правильный
вписан в круг IV.15
сторона шестиугольника к стороне десятиугольника XIII.9
сторон пятиугольника, шестиугольника и десятиугольника XIII.10
шестигранник, правильный. Смотрите куб.
Гильберт, Дэвид (1862–1943)
Основы геометрии I.4
Гиппократ Хиосский (около 430 г. до н. Э.).
его Элементы I.3
квадратурные луны VI.31
угол рупора. Смотрите угол, рог.
гипербола XI.Def.18
гиперболическая геометрия I.29
I
икосаэдр
постройка XIII.16
определение XI.Def.27
центр треугольника IV.4
вписанная окружность треугольника IV.4
наклон
строка в строку. Смотрите угол.
прямая к плоскости XI.Def.5
к плоскости XI.Def.6
аналогичный XI.Def.7
несоизмеримо. Увидеть соизмеримое.
бесконечность простых чисел IX.20
нанесенных фигур
15-угольник, вписанный в круг IV.16
круг в пятиугольнике IV.13
круг в прямолинейной фигуре IV.Def.5
круг, вписанный в квадрат IV.8
круг, вписанный в треугольник IV.4
шестиугольник, вписанный в круг IV.15
пятиугольник, вписанный в круг IV.11
прямолинейная фигура в окружности IV.Def.3
прямолинейная фигура в прямолинейной фигуре IV.Def.1
квадрат, вписанный в круг IV.6
треугольник вписанный в круг IV.2
обратные пропорции и соотношения
определение V.Def.13 Предложение
V.7
обратное предложение I.27
иррационально. Смотрите рационально.
иррациональность сурдов VIII.8
равнобедренный треугольник
определение I.Def.20
имеет равные углы основания I.5, I.5
больший угол при вершине и большее основание I.24, I.24
Дж К L
M
N
O
продолговатый I.Def.22тупой угол. Смотрите угол, тупой.
октаэдр, правильный
постройка XIII.14
определение XI.Def.26
нечетное
нечетное число VII.Def.7, IX.22, IX.23, IX.25, IX.26, IX.27, IX.29, IX.30, IX.31
нечетное нечетное число VII.Def.10
P
Папп Александрийский (около 320 г. н. Э.)доказательство I.5
парабола XI.Def.18
параллельно
строки I.Def.23, I.31
самолетов XI.Def.8 Постулат
Пост.5
транзитивность параллелизма I.30, XI.9
параллелограмм
площадь И.35, I.36
основные свойства I.34
определение I.34
о диаметре I.43
равносторонних параллелограммов
пропорционально сторонам VI.23
пропорционально основанию VI.1
взаимно пропорциональные параллелограммы VI.14
подобных параллелограммов около диаметра VI.24 VI.26
параллелепипед (твердое тело параллелепипеда)
пополам по диагонали XI.28
построить аналогичный XI.27
определение XI.24
равно XI.29, XI.30, XI.31
пропорционально основанию XI.25, XI.32
пропорционально сторонам XI.33, XI.36, XI.37
пропорционально-пропорциональные параллелепипеды XI.34
часть звездной величины
определение V.Def.1
проблема деталей V.5
часть числа
определение VII.Def.3
частей числа
определение VII.Def.4
Пеано, Джузеппе (1858–1932).
Аксиомы Пеано для теории чисел VII.Def.1
пятиугольник, правильный
описана по кругу IV.12
критерий регулярности XIII.7
диагональ, обрезанная в крайнем и среднем соотношении XIII.8
вписано в круг IV.11
Строительство Ричмонда IV.11
сторон пятиугольника, шестиугольника и десятиугольника XIII.10
сторона пятиугольника иррационально называется второстепенной XIII.11
идеальное число
определение VII.Def.22
строительство IX.36
перпендикуляр, прямая к прямой Конструкция
с учетом балла I.11, I.12
определение I.Def.10,
перпендикуляр, прямая к плоскости
определение XI.Def.3
предложения XI.4, XI.6, XI.8, XI.11, XI.12, XI.13
нарушенная пропорция
определение V.Def.18 Предложение
V.22
самолет
определение I.Def.7
определяется пересекающимися линиями XI.2
определяется треугольником XI.2
наклон к линии XI.Def.5
наклон к плоскости XI.Def.6
пересечение двух плоскостей XI.3
параллельные плоскости XI.Def.8, XI.14, XI.15, XI.16, XI.17
перпендикулярно линии XI.Def.3, XI.14
перпендикулярно плоскости XI.Def.4, XI.18, XI.19
плоский угол.Смотрите угол. Номер самолета
определение VII.Def.16
похожие номера самолетов VII.Def.21, VIII.26, IX.1, IX.2
пропорционально сторонам VIII.5
Playfair
аксиома параллелей I.30,
балл
определение I.Def.1
полигонов
аппроксимирующих окружностей XII.2,
площадей подобных полигонов VI.20, XII.1
конструктивных правильных многоугольников IV.16
многогранник, правильный
См. Тетраэдр, куб, октаэдр, икосаэдр и додекаэдр.
классификация XIII.18
двойников XIII.14
Pons Asinorum I.5
постулатов Пост.1-5
степени 2 IX.32
простых чисел
определение VII.Def.11
разделение продуктов VII.30
Простые числа Ферма IV.16
бесконечность IX.20
Простые числа Мерсенна IX.36
степени IX.13
продуктов IX.14
относительно простое VII.Def.12
принцип исчерпания XII.2,
призма
См. Также параллелепипед.
определение XI.Def.13
равные призмы XI.39
треугольная призма, разделенная на три равные пирамиды XII.5,
Прокл (410–485 н. Э.)
Комментарий к Книге I I.3
доказательство
от противоречия I.5
неконструктивный I.5
прогрессия, геометрическая. См. Продолжение пропорции.
пропорция
другие пропорции V.Def.12, V.16 VII.13
антецедентов в пропорциях V.Защита 11
консеквентов в пропорциях V.Def.11
продолжение. См. Продолжение пропорции.
преобразование пропорции V.Def.16, VII.19
перекрестное умножение VII.19
определение V.Def.6
пропорции как отношения эквивалентности V.Def.5
пропорции ex aequali V.Def.17, V.22 VII.14
обратные пропорции V.Def.13 V.7
звездной величины V.Def.6
номера VII.Def.20
пропорции взяты совместно В.Def.14, V.17, V.18
возмущенная пропорция V.Def.18, V.22
пропорции взяты отдельно V.Def.15, V.17, V.18
операции над пропорциями V.Def.3
пропорция в трех терминах V.Def.8
обратный. См. Обратную пропорцию
транзитивность V.11
пропорциональный
построить третью пропорциональную VI.11
построить четвертый пропорциональный VI.12
построить средний пропорциональный VI.13
четвертый пропорциональный V.18
четвертая пропорциональная цифра IX.19
звездной величины V.Def.6
среднее значение, пропорциональное кубическим числам VIII.12
среднее пропорциональное между одинаковыми номерами самолетов VIII.18, VIII.20
среднее пропорциональное значение между одинаковыми твердыми числами VIII.19, VIII.21
среднее значение, пропорциональное квадратным числам VIII.11
номера VII.Def.20
третья пропорциональная цифра IX.18
предложение
контрапозитив I.27
, обратное I.5
инверсия I.27
пирамида
См. Также тетраэдр правильный
определение XI.Def.12
пирамид пропорционально их сторонам XII.8
пирамид пропорционально их основаниям XII.5, XII.6
пирамида третьей призмы с таким же основанием XII.5
взаимно пропорциональные пирамиды XII.9
Теорема Пифагора I.47
обратное I.48
в обобщенном виде на аналогичные цифры VI.31 год
Пифагорова троек X.29.Lemma1
Q
Q.E.D. и Q.E.F. I.1квадратное уравнение, решение аппликацией площадей II.5, II.6, VI.28, VI.29
четырехугольная фигура I.Def.19
квадратурная
окружностей II.14, XII.2,
лунок VI.31
прямолинейных фигур II.14
четырехугольник
Вариньонный параллелограмм XI.9
R
радиус круга
определение I.Защита 15
перпендикулярно касательной III.18, III.19
соотношение
переменное передаточное число V.Def.12, V.16, VII.13
сложное соотношение V.Def.3, VIII.5
преобразование отношения V.Def.16 VII.19
определение V.Def.3
соотношение дубликатов V.Def.9
крайний и подлый. См. Крайнее и среднее соотношение.
отношения ex aequali V.Def.17, V.22 VII.14
больше передаточного числа V.Def.7
обратное передаточное число V.Защита 13
коэффициентов, взятых совместно V.Def.14, V.17, V.18
в низком выражении VII.20
отношений звездных величин V.Def.4
звездная величина в том же соотношении V.Def.5.
смешанное соотношение V.Def.3
характер соотношений V.Def.3
числовое отношение VII.Def.20, V.Def.5
операций над отношениями V.Def.3
передаточные числа взятые отдельно V.Def.15, V.17, V.18
отношения более двух членов V.Def.3
различных видов соотношений V.Защита 3
соотношение в трех экземплярах V.Def.9
рациональный
строка X.Def.3
номер V.Def.3
чисел и соизмеримых величин X.5, X.6, X.7, X.8
квадратов и площадей X.Def.4
обратно пропорциональных фигур
определение VI.Def.2
параллелограммов VI.14
пирамиды XII.9
треугольников VI.15
прямоугольник (прямоугольный параллелограмм)
содержится по сторонам II.Def.1
медиальный X.21
прямолинейная фигура
определение I.Def.19
рефлексивное отношение. См. Отношение эквивалентности.
правильный многоугольник, конструктивный IV.16
отношение
отношение эквивалентности V.Def.3
рефлексивное отношение V.Def.3
симметричное отношение V.Def.3
транзитивное отношение V.Def.3
относительно составных чисел VII.Def.14
относительно простых чисел
определение VII.Def.12
— самые низкие сроки VII.21, VII.22
чисел, разделяющих их, — это VII.23.
простые числа — это VII.29
продуктов VII.24, VII.25, VII.26, VII.27
сумм VII.28
оборот, массив XI.Def.14
ромб и ромб I.Def.22
прямоугольных треугольников. См. Треугольники, верно.
S
неравносторонний треугольникопределение I.Def.20
на крайнее и среднее соотношение. См. Крайнее и среднее соотношение.
сектор круга
определение III.Def.10
сегмент круга
определение III.Def.6
угол в III.Def.8, III.31
угол III.Def.7
построить круг из сегмента III.25
равные углы в сегментах III.21
равных отрезков III.24
подобных сегментов III.Def.11
отдельно
передаточные числа взятые отдельно V.Def.15, V.17, V.18 VII.11
separando V.Def.15
последовательность, геометрическая. См. Продолжение пропорции.
серия (сумма), геометрическая, IX.35
сторон
самолета номер VII.Def.16
твердого числа VII.Def.17
полукруг
определение I.Def.18
полугруппа C.N.
похожее
площадей похожих полигонов VI.20 Фигуры
на пропорциональных линиях & nbsp VI.22
одинаковые и похожие твердые тела XI.Def.10
плоские и твердые числа VII.Def.21 год
прямолинейных фигур
строительство VI.18
цилиндры и конусы аналогичные XI.Def.24
определение VI.Def.1
строительство данного участка VI.25
отрезков окружностей III.Def.11
твердых веществ XI.Def.9
транзитивность подобия VI.21
треугольников, см. Треугольники, похожие.
синусов, закон I.19
односвязный рисунок I.Def.14
твердый
конгруэнтных твердых тел XI.Def.10
определение XI.Def.1
одинаковые и похожие твердые тела XI.Def.10
лицо XI.Def.1
революции XI.Def.14
аналогичные твердые тела XI.Def.9
телесный угол
определение XI.Def.11,
предложения XI.20, XI.21, XI.23, XI.26
твердое число
определение VII.Def.17
предложение IX.7
аналогичные твердые числа VII.Def.21 VIII.27
сфера
ось XI.Защита 15
центр XI.Def.16
определение XI.Def.14
диаметр XI.Def.17
пропорционально диаметру 3 XII.18
том XII.18
кв.
строение I.46,
определение I.Def.22
гипотенузы I.47
квадрат номер VII.Def.18
квадрат (нахождение площадей). Смотрите квадратуру.
прямая линия
деление пополам I.10
построить третий пропорциональный VI.11
построить четвертый пропорциональный VI.12
построить средний пропорциональный VI.13
отрезная линия I.3
отрезал часть VI.9
разрезать пропорционально VI.10
определение I.Def.4
расстояние до точки III.Def.4
ничья между двумя точками Пост.1
эквидистантные линии I.Def.23
продлить линию Post.2
вписывается в круг IV.Def.7, IV.1
наклон к плоскости XI.Def.5
параллельных прямых I.Защита 23, I.31
планарность XI.1, XI.5
перпендикулярных линий. Смотрите перпендикуляр, линию к линии.
перпендикулярно плоскости. Смотрите перпендикуляр, линию к плоскости.
поместите строку I.2
касательная. См. Касательную.
замена равно C.N.
суперпозиция, метод I.4
поверхность
См. Также самолет.
определение I.Def.5
кромок поверхности I.Def.6
сурдс, иррациональность VIII.8
симметричное отношение. См. Отношение эквивалентности.
Т
касательные кругиопределение III.Def.3
имеют отдельные центры III.6
встречаются на общем диаметре III.11, III.12
встречаются в одной точке III.13
касательная к окружности
определение III.Def.2
строение III.17
перпендикулярно радиусу III.18, III.19
тетраэдр, правильный
называется пирамидой XI в.Защита 25
постройка XIII.13
отношение к кубу XIII.15
Фалес Милетский (ок. 624–547 до н. Э.)
прямой угол в полукруге III.31
Теон Александрийский (ок. 335 – ок. 405)
редактор Elements I.Def.1
топология I.Def.13
сенсорный. См. Касательную.
транзитивность
См. Также отношение эквивалентности.
равенства передаточных чисел V.11
менее I,7
параллельных прямых I.30, XI.9
подобия & nbsp VI.21
поперечный, углы около I.27, I.28, I.29,
трапеция I.Def.22
треугольник
треугольник 36 ° -72 ° -72 ° IV.10
острый треугольник I.Def.21 Биссектриса угла
срезает основание пропорционально VI.3
площадь треугольника I.37, I.38
пропорционально основанию VI.1
подобных треугольников VI.19
центр описанной окружности треугольника IV.5
описанная окружность треугольника IV.5
предложение сравнения
угол-угол-сторона I.26
угол-сторона-угол I.26
бок-угол-бок I.4
бок-бок-уголок I.26
сторона сторона сторона I.8 Конструкция
с трех сторон I.22
равносторонний I.Def.20. См. Равносторонний треугольник.
вневписанная окружность треугольника IV.4
внешний угол сумма противоположных внутренних углов Я.32
большая сторона напротив большего угла I.18, I.19
Формула Герона для площади IV.4
центр треугольника IV.4
вписанная окружность треугольника IV.4
вписан в круг IV.2
равнобедренный треугольник I.Def.20
тупой треугольник I.Def.21
параллельное срезание сторон пропорционально VI.2
взаимно пропорциональных треугольников VI.15
прямоугольный треугольник I.Def.21 Перпендикуляр
создает аналогичные прямоугольные треугольники & nbsp VI.8
разносторонний треугольник I.Def.20
похожее
площадей в двойном соотношении & nbsp VI.19
равносторонних треугольника & nbsp VI.4
пропорциональных треугольников & nbsp VI.5
бок-угол-бок предложение & nbsp VI.6
бок-бок-угол предложение & nbsp VI.7
неравенство треугольника I.20
треугольное число VII.Def.16
трихотомия, закон
для звездных величин C.Н., V.Def.5
на практике I.5
для отношений V.Def.7
трехсторонняя фигура I.Def.19. См. Треугольник.
соотношение в трех экземплярах V.Def.9
трисекция угла Пост.2, I.9
U V W X Y Z
единица, определение VII.Def.1Вариньон (1654–1722)
Вариньонный параллелограмм четырехугольника XI.9
вертикальные углы I.15
порядок слов I.18
Зенон Сидонский (I век до н. Э.)
критика предложения I.1
Чжоу би суан цзин
Теорема Пифагора I.47
Цифры и символы
1 как число V.Def.536 ° -72 ° -72 ° треугольник IV.10
> = V.Def.5
равносторонний четырехугольник по периметру
Отправьте нам электронное письмо: info [at] mbacrystalball [dot] com, Copyright © MBA Crystal Ball. Если обе пары противоположных сторон четырехугольника параллельны, такой четырехугольник называется параллелограммом. Никакие стороны, углы и диагонали не совпадают. Для равностороннего треугольника периметр рассчитывается путем сложения его трех сторон.совпадают ли диагонали прямоугольников? Если сегмент разделяет равносторонний треугольник на две области с равными периметрами и площадями A1 и A2, тогда. 23 февраля 2021 г. ODE Интегрирующий факторный вопрос. Найдите площадь треугольника? Гипотенуза = 33см Принято, что сторона равностороннего треугольника равна 4 единицам. Актуальность; Брненская метрополитенская область; Приходите к ITI? Недавние Посты. Здесь представлены упражнения для определения типа и использования соответствующих формул для определения площади четырехугольников, таких как прямоугольники, ромбы, трапеции, параллелограммы и воздушные змеи, с размерами, включающими целые числа и дроби, найдите … Объясните, что сумма свойств четырехугольника равна 360 градусам .Решение. Формула для периметра, площади и диагонали квадрата Формула периметра для… Бесплатный четырехугольный калькулятор сторон — вычисление сторон четырехугольника шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство. Пример 3. Будь то консультации по вопросам карьеры или консультации по приложениям MBA, работа с нами может стать одним из самых важных решений в карьере, которые вы примете. Здравствуйте, BodhaGuru Learning с гордостью представляет анимированное видео на английском языке, в котором объясняется, как найти периметр треугольника.Прочтите о наших услугах и ценах. Формулы геометрии. Это делает квадрат единственным равносторонним и равносторонним четырехугольником. Параллелограмм может образовывать прямоугольник. Формулы для определения площади, высоты, периметра и полупериметра равностороннего треугольника следующие: Где, а — сторона равностороннего треугольника. Геометрия. Какая максимально возможная площадь? Средняя школа; Университет; Популярные темы. Формулы равностороннего треугольника. Мы знаем, что все стороны равностороннего треугольника равны, и, следовательно, его периметр будет в 3 раза больше его стороны, т.е.е. Бесплатный калькулятор площади и периметра равностороннего треугольника — Пошаговое вычисление площади и периметра равностороннего треугольника. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. Кроме того, параллелограмм становится квадратом, когда диагонали равны правым биссектрисам друг друга. 7 9 ≤ A 1 A 2 ≤ 9 7. Для прямоугольников или ромбов просто умножьте основание на высоту, чтобы найти площадь. Периметр четырехугольника 4м. Подводя итог тому, что мы узнали до сих пор, для удобства и запоминания: Продолжайте узнавать больше о: Если периметр равен 30, и это равносторонний треугольник, значит, каждая сторона треугольника равна, поэтому все они должны быть длиной 10 единиц.Если параллелограмм называется трапеция, поскольку мы говорим, что все реакционные углы являются параллелограммами, у меня есть вопрос по главам трапеций. Соседние углы являются дополнительными (например, A + ∠B = 180 °). Усильте практику этим составлением распечатываемых рабочих листов периметра четырехугольника для учащихся с 3 по 8 класс. Пусть AB = BC = AC = единица в равностороннем ABC. Длина спальни 9 футов. Поправьте меня, если ошиблись. Квадрат представляет собой четырехугольник с четырьмя равными сторонами и углами. = 1/2 х 6 х 32.44 Доказательство. Для вписанного четырехугольника ABPC имеем; PA⋅BC = PB⋅AC + PC⋅AB. Подписывайтесь на нас. Периметр заднего двора = \ (4 \ times x = 4x \). Принято, что общая длина… Принимая AB как общую; PA.AB = AB (PB + PC) PA = PB + PC. Чтобы найти площадь равностороннего треугольника, программа использует квадратный корень и степенные функции. Скаленовый треугольник 2. Противоположные стороны параллельны друг другу. Длина диагонали прямоугольника = √ (L2 + B2). Левая сторона: 5a Сверху: 3a + 1 Правая сторона: 2b-5 Снизу: b … периметр равностороннего треугольника равен 32 сантиметрам.Если ответ недоступен, подождите некоторое время, и член сообщества, вероятно, скоро ответит на него. Ромб — это параллелограмм, диагонали которого перпендикулярны друг другу. MCQ по математике класса 9 CBSE Глава 12: Херон 1) Площадь треугольника равна: a. Свойства четырехугольника Формулы измерения квадрата: -квадрат одной из важных частей четырехугольника. Введите длину обеих сторон, выберите количество десятичных знаков и нажмите «Рассчитать». Умножьте 3 и 678 см. Пример равностороннего треугольника.сторона a: … Чтобы улучшить этот «Калькулятор площади четырехугольника», заполните, пожалуйста, анкету. Четырехугольник может быть равноугольным, но не равносторонним (прямоугольник) или равносторонним, но не равносторонним (ромб). = 33 х 21 Геометрия. Четырехугольник — это выпуклый четырехугольник, все четыре вершины которого лежат на периметре квадрата. Не все стороны четырехугольника должны совпадать, чтобы диагонали были перпендикулярны. В случае воздушного змея, если все его стороны совпадают, он станет либо ромбом, либо квадратом.Бесплатный калькулятор периметра четырехугольника — шаг за шагом рассчитайте периметр четырехугольника. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Геометрия. Одна сторона 96см, другая на 18см больше первой, а третья в 2 раза меньше второй. — Свойства линий и углов 16√3 = (√3 / 4) a². 22 февраля 2021 г. Гиперболические функции. Если бы они были, то получился бы параллелограмм, а трапеция не была бы параллелограммом. Нет, они никогда не будут одинаковыми. 1. Формулы геометрии.{\ circ} $ угол. правая равнобедренная. Общим свойством всех четырехугольников является то, что сумма всех их углов равна 360 °. = 693 + 97.32 Обязательные поля отмечены *. Логика кода. Пентагон и неправильный четырехугольник; Какой периметр больше? Ширина прямоугольника = 21 см. Однако в кайте диагонали перпендикулярны, но диагонали не совпадают. Квадрат — это особый тип параллелограмма, все углы и стороны которого равны.Используя формулу расстояния, вы строите _____ треугольник, гипотенуза которого проходит между двумя заданными точками. В круг вписан равносторонний треугольник со стороной 10 см. GCSE. Доступ к решению для NCERT Class 9 Математика Глава Площадь и периметр треугольника и области четырехугольной формы, включая все интерактивные вопросы и вопросы с упражнениями, решаемые экспертом в данной области BeTrained.In. Поскольку противоположные стороны прямоугольника совпадают, диагонали также совпадают. 2 (Основание x […] Если ‘L’ — длина стороны квадрата, тогда длина диагонали = L √2.Значит, доказано. Калькулятор трех равносторонних трапеций. Периметр треугольников и прямоугольников 8:54 Периметр четырехугольников и неправильных или комбинированных форм 6:17 Теги: Вопрос 17. найти длину треугольника с точностью до десятых долей сантиметра. Равносторонний треугольник — это треугольник, все три стороны которого равны по длине. Алгебра в периметре четырехугольника | Уровень 2. Свойства прямоугольника. Вы знаете, что когда задаются высоты четырехугольника, которые перпендикулярны любой из диагоналей, тогда формула для площади задается следующим образом: Если площадь BCDE равна 9, каков периметр многоугольника… Отношение площади к квадрату многоугольника. периметр равностороннего треугольника, 1 12 3, {\ displaystyle {\ frac {1} {12 {\ sqrt {3}}}},} больше, чем у любого другого треугольника.Периметр = 2034,0 см. Периметр четырехугольника 4м. На рисунке выше ABE равносторонний, а четырехугольник BCDE квадрат. Почему так много путаницы? 1) Квадрат, ромб и змей имеют диагонали под прямым углом друг к другу. Решение 1. Ни в коем случае параллелограмм не должен быть трапецией. Площадь треугольника с учетом основания и высоты. Математическая библиотека имеет обе эти функции и может использоваться для вычислений в программе. Найдите площадь равностороннего треугольника со стороной, равной 4 единицам.дайте определение: а) корню круга б) квадрату. iForce Systems LLC, По двум сторонам и углу между ними, По радиусу вписанной окружности, По радиусу описанной окружности, По диагоналям и углу между ними, По диагоналям и углу между ними, По сторонам и угол между ними, Общая площадь поверхности правильной пирамиды по высоте, Площадь боковой поверхности правильной пирамиды по высоте, Площадь боковой поверхности правильной пирамиды через апофему, Равнобедренный треугольник, через сторону и высоту, Равнобедренный треугольник, через сторону и угол.Да, когда стороны на противоположных сторонах равны, тогда только диагонали перпендикулярно друг другу, это неверно. Диагонали перпендикулярны тогда и только тогда, когда все стороны равны, как в случае ромба или квадрата. Ссылки по теме класса: Herons Formula Class 9; Важные вопросы Класс 9 Математика Глава 12 Формула цапли; Чтобы решить… Периметр заднего двора = \ (4 \ times x = 4x \) Принято, что общая длина железного забора составляет 100 ярдов. Если бы противоположные стороны были бы равны в четырехугольнике, все равно нет никакой поверхности, что диагонали будут перпендикулярны.Если задан многоугольник с разными длинами сторон, то общая формула периметра для него будет выглядеть как сумма длин всех сторон: P = a + b + d + c OwlCalculator.com Geometry — Calculate Quadrateral perimeter Где, b — это основание треугольника h — высота треугольника 3.2. ABC — равносторонний треугольник со стороной 0,03 м. У равностороннего треугольника все стороны равны. Например, если длина прямоугольника составляет 12 см, а ширина — 14 см. Периметр = 2 (длина + ширина) = 2 (12 + 14) = 52 см. Вот несколько примеров расчетов периметра прямоугольника © Copyright by Math .Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Противоположные углы, образованные в точке пересечения диагоналей, равны. Главы. Введите длину обеих сторон, выберите количество десятичных знаков и нажмите «Рассчитать». Прямоугольник — это особый тип параллелограмма с прямыми углами. Диагонали делят друг друга пополам, и каждая диагональ делит параллелограмм на два равных треугольника. Периметр равностороннего… Равносторонний четырехугольник называется ромбом. Но мы до сих пор не знаем длины сторон.Найдите значение x, подставьте его в линейное выражение и определите длину каждой стороны четырехугольника. Равносторонний четырехугольник. Почему вы спрашиваете, потому что это довольно просто? Нет, они не. Периметр равностороннего четырехугольника 40 см. Пошаговое объяснение: Дано: -Одна сторона равностороннего четырехугольника равна 10 см. Найти: -Периметр четырехугольника… Формула. 64 = а². Вопросы MCQ для класса 9 по математике Глава 12 Heron’s с ответами MCQ для класса 9 по математике Глава 12 — Heron представлены здесь, чтобы помочь учащимся подготовиться к предстоящему экзамену по математике.= 1/2 x (27-21) x 32,44 трапеции. Бесплатный калькулятор периметра четырехугольника — шаг за шагом рассчитайте периметр четырехугольника. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Характеристики. Если один из углов параллелограмма — прямой угол, тогда все остальные углы прямые, и он становится прямоугольником. Площадь равностороннего треугольника. Геометрия — это раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.Чтобы найти площадь четырехугольника, все, что вам нужно сделать, это определить тип четырехугольника, с которым вы работаете, и следовать простой формуле. Длина прямоугольника = 33 см. Периметр четырехугольного листа. Квадрат равнобедренного треугольника. Диагонали — это биссектрисы углов четырехугольника или параллелограмма? Четырехугольник — это любая форма с четырьмя сторонами. Квадраты, прямоугольники и ромбы — лишь некоторые примеры. Вопрос 2. Заданная длина борта = 678 см. Если угол трапеции равен 90 °, то, как это называется, квадраты — мой любимый тип четырехугольников.Основание x высота b. a = √ 8 × 8 = 8 м. Сторона равносторонней ∆ = 8 м. Периметр равностороннего ∆ = 3 × стороны. Расчеты на трапеции с тремя равными сторонами, частный случай равнобедренной трапеции. Обе опоры и одна из двух параллельных сторон имеют одинаковую длину. Наш калькулятор решит геометрические задачи за несколько секунд. Автор… — Типы треугольников и свойства, начать здесь | Истории успеха | Проверка реальности | База знаний | Стипендии | Услуги. Теперь в прямоугольном треугольнике, см. Итак, площадь четырехугольника = Площадь прямоугольника + Площадь прямоугольного треугольника. Периметр равностороннего треугольника.Как ни странно, периметр эллипса рассчитать очень сложно !. C 3. диагонали? Если a и b — длины диагоналей ромба. В комментариях есть ссылка на апплет GeoGebra для изучения этой проблемы. тупая разносторонняя. Читайте о наших, Как попасть на лучшие программы MBA в мире, Противоположные стороны параллельны и совпадают. Следовательно, PA.AB = PB.AB + PC.AB. [Ответ: 375,85 кв. См.] Следовательно, периметр равностороннего треугольника… В ромбе, прямоугольнике или квадрате, чтобы диагонали были перпендикулярны и совпадали, все его стороны должны совпадать.Сначала находим длину второй стороны нашей формы, увеличивая первую сторону четырехугольника на 18 см: 96 + 18 = 114 (см). Следовательно, \ (4x = 100 \) \ (x = 25 \) \ (\ следовательно \) Длина одной стороны заднего двора составляет 25 ярдов. Решение для A B. Кроме того, три угла равностороннего треугольника совпадают и равны 60 градусам. Найдите четвертую сторону четырехугольника. Площадь и периметр равностороннего треугольника можно найти с помощью следующей формулы: Площадь равностороннего треугольника = (√3) / 4 * a 2.Периметр равностороннего ∆ = 3 × сторона Периметр равностороннего ∆ = 3 × 8 = 24 м. Следовательно, периметр равностороннего ∆ равен 24 м. Надеюсь, это поможет вам …. kkmr kkmr Привет, приятель, вот твой ответ … Надеюсь, это будет полезно для тебя .. Новые вопросы по математике. У равностороннего треугольника все стороны равны. Как мы уже обсуждали во введении, равносторонний треугольник — это треугольник, все стороны которого равны по длине. Периметр и площадь геометрических фигур. … правый равносторонний. Если периметр P, P = (a + a + a) единица ∴ P = 3a единица [Ответ: 375.85 кв. См.] Чтобы вычислить площадь равностороннего треугольника, мы должны знать размеры его сторон. Площадь равностороннего треугольника… Ваш адрес электронной почты не будет опубликован. Если они будут равны, это не будет трапеция. Диагональ будет перпендикулярной только тогда, когда все стороны равны, а не противоположны. Периметр прямоугольника = 2 единицы (длина + ширина). Integrovaná Strategie Rozvoje BMO 21+ O Strategii; Vymezení území Brněnské metropolitní области 21+ Прямой треугольник Площадь прямоугольного треугольника = bh Периметр прямоугольного треугольника = a + b + c Теорема Пифагора = Гипотенуза.Все углы прямые. Равны ли размеры пары параллельных сторон трапеции? … Площадь равностороннего треугольника. решаются группой учеников и учителем 9-го класса, который также является крупнейшим ученическим сообществом 9-го класса. Аннотация Приведенный ниже код отображает программу для вычисления площади и периметра равностороннего треугольника, Пример. Равносторонний четырехугольник — это многоугольник с 4 равными сторонами. Поскольку мы знаем, что для равностороннего треугольника ABC AB = BC = AC. Где b — основание треугольника, h — высота треугольника 3.2. Предположим, что ABC — равносторонний треугольник, тогда согласно определению; AB = BC = AC, где AB, BC и AC — стороны равностороннего треугольника. Живая демонстрация. Пусть a — длина сторон, A — площадь треугольника, p — периметр, R — радиус описанной окружности, r — радиус вписанной окружности, h — высота (высота) с любой стороны. . Вот и все! ромб. Периметр треугольника — это расстояние, пройденное вокруг треугольника, которое рассчитывается как сумма всех трех его сторон.Внутри коробки два прямоугольных треугольника: FZX и ZLA. Для квадратов умножьте одну сторону на себя, чтобы получить площадь. Площадь четырехугольника = Площадь прямоугольника + Площадь прямоугольного треугольника Четырехугольник — это простая замкнутая фигура с четырьмя сторонами. Неправильный четырехугольник — это четырехугольник, который не является правильным, поэтому все его стороны не имеют одинаковой длины. Прямоугольник: периметр прямоугольника = 2 (l + b). при каких значениях a и b каждый четырехугольник является параллелограммом? Характеристики. Квадрат, однако, есть и то, и другое.Все права защищены |, варианты ответа. Алгебра-предварительное вычисление. Диаграмма 1 bel Ваш электронный адрес не будет опубликован. Иногда бывает равным, тогда трапецию называют изотрапезией. и опп углы и стороны равны. Формула для площади и периметра приведена здесь. Уровни. Периметр = 3 х 678 см. Максимальный периметр, диаметр и площадь равносторонних выпуклых многоугольников единичной ширины Шарль Оде ∗ Джордан Нинин † Пьеру Хансену, столпу Клуба восьмиугольников. Поместите значение стороны в Формулу периметра. Мужской или женский ? а = √64…. В. У Стивена прямоугольная спальня с периметром 34 фута. У равностороннего треугольника все три стороны равны, поэтому его периметр будет в три раза больше длины одной из его сторон (а). Одна сторона 96см, другая на 18см больше первой, а третья в 2 раза меньше второй. Стороны равностороннего треугольника равны 3x + 2,2y-x и y + 3. Найдите x, y и периметр треугольника. Давайте посмотрим на свойства различных четырехугольников. Расчеты на трапеции с тремя равными сторонами, частный случай равнобедренной трапеции.Обе ноги и одна из двух параллельных сторон имеют одинаковую длину. Во-первых, мы находим длину второй стороны нашей формы, увеличивая первую сторону четырехугольника … Сформируем уравнение, используя периметр и длину сторон четырехугольника, представленных в этом наборе рабочих листов для печати для 6-го, 7-го классов и Ученики 8-го класса. Основание = 6 см. Например, для четырехугольника типа параллограмм, периметр которого равен 2 (L + B) прямоугольникам. Длина каждой стороны равностороннего треугольника = 25 см.Назовите этот четырехугольник, используя его наиболее конкретное имя. Периметр прямоугольника; Площадь и периметр фигуры; Уровень: средняя школа. … Площадь четырехугольника = Площадь прямоугольника + Площадь прямоугольного треугольника Длина прямоугольника = 33см Ширина прямоугольника = 21см Площадь прямоугольника = l × b; (l и b — длина и ширина прямоугольника) Площадь прямоугольного треугольника = 1/2 x основание x высота Q. Треугольник. Периметр равностороннего ∆ = 3 × 8 = 24 м. Четырехугольник Ватта — это четырехугольник с парой противоположных сторон равной длины.Найдите четвертую сторону четырехугольника. Просто мы можем сказать, что если у четырехугольника противоположные стороны равны, то его диагональ будет делить друг друга пополам. Площадь равностороннего треугольника (S) рассчитывается по следующему рисунку: И если его смежные стороны равны, то они пересекают друг друга перпендикулярно. Перпендикуляр, проведенный от вершины треугольника к основанию, делит основание на две равные части. Исчисление. И ∠A = ∠B = ∠C = 60 ° По сторонам есть еще два типа треугольников: 1.Но если в четырехугольнике все стороны стали равными, тогда возникает вероятность того, что диагональ будет перпендикулярной. На самом деле нет, например, у воздушных змеев противоположные стороны не равны, но обе его диагонали перпендикулярны. Логика кода. Наш калькулятор решит геометрические задачи за несколько секунд. Вопросы и ответы Периметр равностороннего треугольника составляет 60 см. = 32,44см — Свойства и формулы кругов Площадь равностороннего элемента ∆ = (√3 / 4) a².Если длина L, а ширина B, то. Калькулятор трех равносторонних трапеций. Не обязательно равно. Вычисляет площадь, периметр и высоту равностороннего треугольника с учетом стороны. Найдите площадь четырехугольника, одна из диагоналей которого имеет длину 30 см, а перпендикуляры от двух других вершин равны 19 см и 11 см соответственно. Должны ли быть равны противоположные стороны четырехугольника, чтобы диагонали были перпендикулярны? Есть ли у параллелограмма линия симметрии? = Квадратный корень из 1053 Все стороны квадрата имеют одинаковую длину (равносторонние), и все его углы имеют одинаковую меру (равносторонние).Исчисление алгебры. сторона a 6 цифр 10 цифр 14 цифр 18 цифр 22 цифр 26 цифр 30 цифр 34 цифр 38 цифр 42 цифр 46 цифр 50 цифр Некоторые неправильные четырехугольники, такие как … Делают ли диагонали трапеции пополам? как это доказать? Не волнуйтесь — помощь здесь! Периметр треугольника определяется как сумма длин сторон. Это можно сделать, применив теорему Пифагора. Возьмите треугольник с общим основанием из этих знаков и сделайте этот треугольник конгруэнтным по sas, тогда обе стороны будут равны cpct. Да, мы можем доказать это с помощью метода sas, поскольку разделяет пополам паррелелограммы на 2 равных половинки.Противоположные стороны параллельны и совпадают. Диагонали перпендикулярны и делят друг друга пополам. На рисунке длина стороны равностороннего треугольника равна «a»: ⇒ Периметр равностороннего треугольника = a + a + a ∴ Периметр равностороннего треугольника = 3a Площадь равностороннего треугольника. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Если ab = 33 bc = 27 CD = 33 DA = 21 площадь четырехугольника? 20 (B) Вопрос 1. Если площадь BCDE равна 9, каков периметр многоугольника… Прямоугольник Площадь прямоугольного треугольника = bh Периметр прямоугольного треугольника = a + b + c Теорема Пифагора = Гипотенуза.Чтобы найти площадь равностороннего треугольника, программа использует квадратный корень и степенные функции. Прежде чем вы сможете найти площадь правильного четырехугольника, начните с определения типа четырехугольника в задаче, поскольку для разных типов четырехугольников требуются разные уравнения. = Квадратный корень из (33 x 33 — 6 x 6) Выберите исходные данные и введите их в верхнем левом поле. Решение для A B. Площадь прямоугольника = Длина x Ширина = 693 кв.3 × сбоку. = 790,32 кв.Термостат Sensi сохраняет изменяющуюся температуру, Обзор беспроводных наушников Ifrogz Airtime Pro 2 Se, Letras De Canciones De Navidad De Puerto Rico, Подкаст «Шоу Брайана Крейга», Вода холодильника Ge в нижней части холодильника, Bluetooth-приложения для велоспорта,
Можно ли описать круг вокруг каждой из следующих фигур? Почему или почему нет? a) Параллелограмм c) Прямоугольник b) Ромб d) Квадрат
Согласно статье «Тестирование презервативов на усталость (Polymer Testing, 2009: 567571)», тесты, используемые в настоящее время для c…
Вероятность и статистика для техники и наук
Дан график y = 3xx2. Используйте преобразования, чтобы создать функцию, график которой показан на рисунке. 7.
Исчисление одной переменной
Дано n (A) = 1500, n (A ∪ B) = 2250 и n (A ∠© B) = 310, найдите n (B).
Математические экскурсии (список курсов MindTap)
Определение предела трансцендентальной функции В упражнениях 23-36 найдите предел трансцендентальной функции ….
Исчисление: ранние трансцендентные функции
Каково значение ( X + 1) для следующих баллов: 0, 1, 4, 2? а.8 б. 9 в. 11 дн. 16
Основы статистики для поведенческих наук (список курсов MindTap)
Найдите площадь конечной части параболоида y = x2 + z2, отсеченную плоскостью y = 25. [Подсказка: спроецируйте …
Многопараметрическое исчисление
Выборка имеет среднее значение M = 25 и стандартное отклонение s = 5. В этом примере найдите значение X, соответствующее …
Статистика для поведенческих наук (список курсов MindTap)
В Упражнениях 1520 упростите выражение.17. 16x5yz481xyz54; x 0, y 0, z 0
Прикладное исчисление для управленческих, жизненных и социальных наук: краткий подход
Определите, является ли утверждение истинным или ложным. Если это правда, объясните почему. Если это неверно, объясните, почему или gi …
Исчисление: ранние трансценденталы
Покажите, что предел f (x), когда x приближается к 3, не существует в примере 10.
Исчисление: прикладной подход (курс MindTap Список)
Есть ли число, которое ровно на 1 больше его куба?
Исчисление одной переменной: ранние трансцендентальные методы, том I
Определите, увеличивается ли последовательность, уменьшается или нет.Ограничена ли последовательность? an = 2 + (1) nn
Calculus (Список курсов MindTap)
Для задач 79–99 ответьте на вопрос алгебраическим выражением. Задача 3 Периметр прямоугольника …
Промежуточная алгебра
В упражнениях 1728 используйте логарифмические тождества, чтобы получить недостающую величину.
Конечная математика и прикладное исчисление (Список курсов MindTap)
В задачах 1–4 определите, является ли каждая функция вогнутой вверх или вниз в указанных точках.4.
Математические приложения для управления, жизни и социальных наук
Конечные точки Предположим, что конечная точка, определяемая t, является точкой (35,45) на единичной окружности. Найдите t …
Предварительное вычисление: математика для исчисления (отдельная книга)
Преобразуйте выражения в упражнениях 31-36 в форму положительной экспоненты. 45y3 / 4
Прикладное исчисление
Разделите (используйте форму остатка с r): 47236
Элементарная техническая математика
Решите уравнения из упражнений 126.(x + 1) (x + 2) + (x + 1) (x + 3) = 0
Конечная математика
Прибыль: Работа в розничной торговле и производительность! Как оценивают розничные магазины? Один из способов ответить на этот вопрос — изучить …
Понимание базовой статистики
Для каждого из следующих трех размеров выборки постройте доверительный интервал 95 для доли населения …
Основы статистики
Кения Доусон имела налоговое обязательство в размере 14 600 долларов в прошлом году. Кроме того, она задолжала 2336 долларов по другим налогам.Она была …
Современная математика для бизнеса и потребителей
Расширение логарифмического выражения В упражнениях 21-30 используйте свойства логарифмов для расширения логарифма …
Исчисление одной переменной
Определите, является ли последовательность сходится или расходится. Если сходится, найдите предел. 23. an = 3 + 5n2n + n2
Исчисление с одной переменной: ранние трансцендентальные методы
В вопросах с 1 по 8 заполните каждый пробел соответствующим словом или выражением.Стандартный вектор …
Тригонометрия (список курсов MindTap)
Упражнения 31. Позвольте быть группой с центром: . Докажите, что если это единственный элемент порядка в, то.
Элементы современной алгебры
В упражнениях 7–16 определите, находится ли данная симплексная таблица в окончательной форме. Если да, то найдите решение проблемы …
Конечная математика для управленческих, жизненных и социальных наук
Верно или неверно: y ′ + xey = ex + y отделимо.
Учебное пособие по исчислению одной переменной Стюарта: ранние трансцендентальные числа, 8-е
Используя правило трапеции и правило Симпсона в упражнениях 69-72, аппроксимируйте определенный интеграл с помощью T …
Исчисление: ранние трансцендентные функции (список курсов MindTap) )
Сферические координаты точки с прямоугольными координатами находятся: а) б) в) г)
Учебное пособие по многомерному исчислению Стюарта, 8-е
Рассмотрим регрессионное исследование, включающее зависимую переменную y, количественную независимую переменную x1 и кота…
Статистика для бизнеса и экономики, пересмотренная (Список курсов MindTap)
Решите каждое из следующих уравнений, используя принцип вычитания равенства. Проверяйте каждый ответ. 62 = a + 19
Математика для машинных технологий
Высшая лига бейсбола (MLB) включает две группы команд в лигах. В каждой Америке по 15 команд …
Введение в статистику и анализ данных
Сравните и сопоставьте четыре шкалы измерения (номинальную, порядковую, интервальную и пропорциональную) и определите пример…
Методы исследования поведенческих наук (Список курсов MindTap)
Найдите горизонтальные асимптоты, если таковые имеются, каждой рациональной функции. Не наносите график функции. f (x) = x2x2x + 11
College Algebra (Список курсов MindTap)
Простая случайная выборка из 400 человек дает 100 ответов «Да». а. Какова точечная оценка опоры …
СТАТИСТИКА F / БИЗНЕС + ЭКОНОМИКА-ТЕКСТ
Опишите, как репликация защищает от мошенничества, совершаемого в исследованиях.
Методы исследования поведенческих наук (Список курсов MindTap)
Данные моделирования Тормозной путь автомобиля на сухом ровном асфальте, движущемся со скоростью v (в километрах …
Расчет
Оценка предела в Упражнения 15-42, оцените предел, при необходимости используя правило LHpitals limx0sin5xtan9x
Исчисление (список курсов MindTap)
Преобразование прямоугольной формы в сферическую В упражнениях 3136 преобразуйте точку из прямоугольных координат в сферические…
Многопараметрическое исчисление
Постройте график стандартного нормального распределения. Обозначьте горизонтальную ось значениями 3, 2, 1, 0, 1, 2 и …
Основы статистики для бизнеса и экономики
Связь видов и ареалов Число видов данной таксономической группы в пределах данной среды обитания часто остров — это …
Функции и изменения: подход к моделированию алгебры колледжа (список курсов MindTap)
Используйте биномиальную теорему, чтобы расширить выражения в 19–27.27. (x2 + 1x) 5
Дискретная математика с приложениями
Преобразуйте 57,0260 в десятичное.
Математика: практическая одиссея
3. Производственная линия предназначена для наполнения картонных коробок стиральным порошком до среднего веса 32 унции …
Современная бизнес-статистика с помощью Microsoft Office Excel (с печатной картой доступа XLSTAT Education Edition ) (Список курсов MindTap)
КАК ВЫ ЭТО ВИДИТЕ? Определите, имеет ли приведенная ниже матрица форму эшелона строк, сокращенную форму эшелона строк или нейтральную форму…
College Algebra
Модель населения Дифференциальное уравнение dpdt = (kcost) P, где k — положительная константа, является моделью человеческого p …
Первый курс дифференциальных уравнений с приложениями моделирования (курс MindTap Список)
В следующих упражнениях выполните интеграцию, используя указанную замену. 364. e2x1e 2xdx; u = e2x
Calculus Volume 2
Используйте информацию в таблице 3.19, чтобы ответить на следующие восемь упражнений. В телеграмме показана политическая партия а…
Вступительная статистика
Для следующих упражнений создайте таблицу, чтобы нарисовать график каждой функции, используя следующие значения: x …
Calculus Volume 1
Многогранники, описанные вокруг сферы Многогранник называется описанным вокруг сферы, если плоскости всех ее граней касаются сферы. Сама сфера называется. Сочетание шара с усеченной пирамидой
«Сфера политики» — Отношения социальных субъектов о государственной власти.Научно-теоретический. Процесс взаимодействия политики с экономикой. Вместе с государством. Регулирование общественных отношений обусловлено общественными интересами. Процесс взаимодействия политики с моралью. Сила государства, убеждение, возбуждение.
«Геометрия призмы» — Дана прямая четырехугольная призма ABCDA1B1C1D1. Евклид, вероятно, считал практические руководства по геометрии делом. Прямая призма — призма, боковая грань которой перпендикулярна основанию.Призма в геометрии. По свойству 2-х объемов V = V1 + V2, то есть V = SABD h + SBDC h = (SABD + SBDC) h. Итак, треугольники A1B1C1 и ABC равны с трех сторон.
«Объем призмы» — Как найти объем прямой призмы? Объем исходной призмы равен произведению S · h. Основные шаги доказательства теоремы о прямой призме? Площадь основания S исходной призмы. Рисуем высоту треугольника ABC. Задача. Прямая призма. Цели урока. Концепция призмы. Объем прямой призмы.Решение проблемы. Призму можно разделить на прямые треугольные призмы высотой h.
«Поверхность сферы» — Марс. Мяч мяч? Шар и сфера. Земной шар. Энциклопедия. Мы болеем за нашу школьную бейсбольную команду. Венера. Уран. Есть ли на картинке мяч? Немного истории. Атмосфера. Я решил провести небольшое исследование ……. Сатурн. Готовы ответить на вопросы?
Многогранник, описанный вокруг сферы Многогранник называется описанным вокруг сферы, если плоскости всех его граней касаются сферы.Сама сфера называется вписанной в многогранник. Теорема. Сферу можно вписать в призму тогда и только тогда, когда в ее основание можно вписать круг, а высота призмы равна диаметру этого круга. Теорема. В любую треугольную пирамиду можно вписать сферу, причем только одну.
Упражнение 1 Сотрите квадрат и нарисуйте два параллелограмма, представляющих верх и низ куба. Соедините их вершины отрезками.Получите изображение сферы, вписанной в куб. Нарисуйте сферу, вписанную в куб, как на предыдущем слайде. Для этого нарисуйте эллипс, вписанный в параллелограмм, полученный 4-кратным сжатием круга и квадрата. Отметьте полюса сферы и точки касания эллипса и параллелограмма.
Упражнение 1 Сфера вписана в прямую четырехугольную призму, в основании которой находится ромб со стороной 1 и острым углом 60 °.Найдите радиус сферы и высоту призмы. Решение. Радиус сферы равен половине высоты DG основания, т.е. высота призмы равна диаметру сферы, т.е.
Упражнение 4 Сфера вписана в прямую четырехугольную призму, в основании которой находится четырехугольник, периметр 4 и площадь 2. Найдите радиус r вписанной сферы. Решение. Обратите внимание, что радиус сферы равен радиусу круга, вписанного в основание призмы.Воспользуемся тем, что радиус вписанной в многоугольник окружности равен площади этого многоугольника, деленной на его полупериметр. Мы получили
Упражнение 3 Найдите радиус сферы, вписанной в правильную треугольную пирамиду, сторона основания которой равна 2, а двугранные углы при основании равны 60 °. Решение.Воспользуемся тем, что центр вписанной сферы является точкой пересечения биссектральных плоскостей двугранных углов в основании пирамиды. Для радиуса сферы OE имеет место равенство, следовательно,
Упражнение 4 Найдите радиус сферы, вписанной в правильную треугольную пирамиду, боковые стороны которой равны 1, а плоские углы при вершине равны 90 °. Ответ: Решение. В тетраэдре SABC имеем: SD = DE = SE = Из подобия треугольников SOF и SDE получаем уравнение, решив которое, находим
Упражнение 1 Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, все стороны которой равны 1.Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, имеет место формула: r = S / p, где S — площадь, p — полупериметр треугольника … В нашем случае S = p = Решение. Радиус сферы равен радиусу окружности, вписанной в треугольник SEF, в котором SE = SF = EF = 1, SG = Следовательно,
Упражнение 2 Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, сторона основания которой равна 1, а сторона стороны — 2.Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, имеет место следующая формула: r = S / p, где S — площадь, p — полупериметр треугольника. В нашем случае S = p = Решение. Радиус сферы равен радиусу окружности, вписанной в треугольник SEF, в котором SE = SF = EF = 1, SG = Следовательно,
Упражнение 3 Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, сторона основания которой равна 2, а двугранные углы при основании равны 60 °.Решение. Воспользуемся тем, что центр вписанной сферы является точкой пересечения биссектральных плоскостей двугранных углов в основании пирамиды. Для радиуса сферы OG имеет место равенство, следовательно,
Упражнение 4 Единичная сфера вписана в правильную четырехугольную пирамиду, сторона основания которой равна 4. Найдите высоту пирамиды. Воспользуемся тем, что для радиуса r окружности, вписанной в треугольник, верна следующая формула: r = S / p, где S — площадь, p — полупериметр треугольника.В нашем случае S = 2h, p = Solution. Обозначим высоту SG пирамиды через h. Радиус сферы равен радиусу окружности, вписанной в треугольник SEF, в котором SE = SF = EF = 4. Следовательно, имеем равенство, из которого находим
Упражнение 1 Найдите радиус сферы, вписанной в правильную шестиугольную пирамиду с ребрами основания, равными 1, и боковыми ребрами, равными 2. Мы будем использовать тот факт, что для радиуса r окружности, вписанной в треугольник, следующая формула принимает место: r = S / p, где S — площадь, p — полупериметр треугольника.В нашем случае S = p = Следовательно, Решение. Радиус сферы равен радиусу окружности, вписанной в треугольник SPQ, в котором SP = SQ = PQ = SH =
Упражнение 2 Найдите радиус сферы, вписанной в правильную шестиугольную пирамиду с ребрами основания, равными 1, и двугранными углами при основании, равными 60 градусам. Решение. Воспользуемся тем, что центр вписанной сферы является точкой пересечения биссектральных плоскостей двугранных углов в основании пирамиды.Для радиуса сферы OH имеет место равенство, следовательно,
Упражнение Найдите радиус сферы, вписанной в единичный октаэдр. Ответ: Решение. Радиус сферы равен радиусу окружности, вписанной в ромб СЭСФ, у которого SE = SF = EF = 1, SO = Тогда высота ромба, сброшенного с вершины E, будет равна Требуемый радиус равен половине высоты и равен O
Упражнение Найдите радиус сферы, вписанной в единичный икосаэдр.Решение. Воспользуемся тем фактом, что радиус OA описанной сферы равен, а радиус AQ окружности, описанной вокруг равностороннего треугольника со стороной 1, равен По теореме Пифагора, примененной к прямоугольному треугольнику OAQ, мы получаем Упражнение Найти радиус сферы, вписанной в единичный додекаэдр. Решение. Мы используем тот факт, что радиус OF описанной сферы равен, а радиус FQ окружности, описанной вокруг равностороннего пятиугольника со стороной 1, равен По теореме Пифагора, примененной к прямоугольному треугольнику OFQ, получаем
Упражнение 1 Можете ли вы вписать сферу в усеченный тетраэдр? Решение.Отметим, что центр O сферы, вписанной в усеченный тетраэдр, должен совпадать с центром сферы, вписанной в тетраэдр, который совпадает с центром половины сферы, вписанной в усеченный тетраэдр. Расстояния d 1, d 2 от точки O до шестиугольной и треугольной граней вычисляются по теореме Пифагора: где R — радиус полувписанной сферы, r 1, r 2 — радиусы окружностей, вписанных в шестиугольник и треугольник соответственно. Так как r 1> r 2, то d 1 r 2, затем d 1
Тема «Различные задачи для многогранников, цилиндра, конуса и шара» — одна из самых сложных в курсе геометрии 11 класса.Прежде чем решать геометрические задачи, они обычно изучают соответствующие разделы теории, на которые ссылаются при решении задач. В учебнике С. Атанасяна и соавт. По этой теме (стр. 138) можно найти только определения многогранника, описанного вокруг сферы, многогранника, вписанного в сферу, сферы, вписанной в многогранник, и сферы, описанной около многогранника. Методические указания к этому учебнику (см. Книгу С.М. Саакяна и В.Ф. Бутузова «Изучение геометрии в 10-11 классах», с.159) говорят, какие сочетания тел учитываются при решении задач № 629-646, и обращают внимание на то, что «при решении той или иной задачи, прежде всего, необходимо обеспечить, чтобы учащиеся хорошо представляли взаимное расположение тел, указанное в условии ». Ниже приводится решение задач № 638 (а) и № 640.
Учитывая все вышесказанное, а также тот факт, что наиболее сложными задачами для студентов являются задачи совмещения мяча с другими телами, необходимо систематизировать соответствующие теоретические положения и довести их до студентов.
Определения.
1. Шар называется вписанным в многогранник, а многогранник — описанным вокруг шара, если поверхность шара касается всех граней многогранника.
2. Говорят, что шар описан вокруг многогранника, а многогранник вписан в шар, если поверхность шара проходит через все вершины многогранника.
3. Шар называется вписанным в цилиндр, усеченный конус (конус), а цилиндр, усеченный конус (конус), описывается около шара, если поверхность шара касается оснований (основания) и всех образующих. цилиндра, усеченный конус (конус).
(Из этого определения следует, что большой круг шара может быть вписан в любое осевое сечение этих тел).
4. Шар называется описанным вокруг цилиндра усеченным конусом (конусом), если основные окружности (базовая окружность и вершина) принадлежат поверхности шара.
(Из этого определения следует, что вокруг любого осевого сечения этих тел можно описать окружность большего круга шара).
Общие замечания о положении центра мяча.
1. Центр шара, вписанного в многогранник, лежит в точке пересечения биссектрисных плоскостей всех двугранных углов многогранника. Он находится только внутри многогранника.
2. Центр шара, описанного вокруг многогранника, лежит на пересечении плоскостей, перпендикулярных всем ребрам многогранника и проходящих через их середины. Он может располагаться внутри, на поверхности и снаружи многогранника.
Комбинация шара с призмой.
1. Шар, вписанный в прямую призму.
Теорема 1. Шар можно вписать в прямую призму тогда и только тогда, когда в основание призмы можно вписать круг, а высота призмы равна диаметру этого круга.
Следствие 1. Центр шара, вписанного в прямую призму, находится на середине высоты призмы, проходящей через центр круга, вписанного в основание.
Следствие 2. Шар, в частности, можно вписать в прямые: треугольные, правильные, четырехугольные (в которых суммы противоположных сторон основания равны друг другу) при условии H = 2r, где H — высота призмы, r — радиус окружности, вписанной в основание.
2. Шар, описанный рядом с призмой.
Теорема 2. Шар можно описать рядом с призмой тогда и только тогда, когда призма прямая и круг можно описать возле ее основания.
Следствие 1 … Центр шара, описанного для прямой призмы, находится на середине высоты призмы, проведенной через центр круга, описанного для основания.
Следствие 2. Шар, в частности, можно описать: около прямой треугольной призмы, около правильной призмы, около прямоугольного параллелепипеда, около прямой четырехугольной призмы, в которой сумма противоположных углов основания равна 180 градусам.
Из учебника Л.С. Атанасян для комбинации шара с призмой можно предложить задачи № 632, 633, 634, 637 (а), 639 (а, б).
Сочетание шара с пирамидой.
1. Шар, описанный вокруг пирамиды.
Теорема 3. Шар можно описать рядом с пирамидой тогда и только тогда, когда можно описать круг возле его основания.
Следствие 1. Центр шара, описанного вокруг пирамиды, находится в точке пересечения прямой линии, перпендикулярной основанию пирамиды, проходящей через центр окружности, описанной вокруг этого основания, и плоскости, перпендикулярной любой боковой стороне. край, проведенный через середину этого края.
Следствие 2. Если боковые грани пирамиды равны друг другу (или одинаково наклонены к плоскости основания), то вокруг такой пирамиды можно описать шар. Центр этого шара в данном случае лежит в точке пересечения высоты пирамиды (или ее продолжения) с осью симметрии бокового ребра, лежащего в плоскости бокового ребра и высоты.
Следствие 3. Шар, в частности, можно описать: около треугольной пирамиды, около правильной пирамиды, около четырехугольной пирамиды, в которой сумма противоположных углов равна 180 градусам.
2. Шар, вписанный в пирамиду.
Теорема 4. Если боковые грани пирамиды одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.
Следствие 1. Центр шара, вписанного в пирамиду, боковые грани которого одинаково наклонены к основанию, находится в точке пересечения высоты пирамиды с биссектрисой линейного угла любого двугранного угла у основания. пирамиды, сторона которой равна высоте боковой грани, проведенной от вершины пирамиды.
Следствие 2. В правильную пирамиду можно вписать шар.
От Л.С. В учебнике Атанасяна по соединению шара с пирамидой можно предложить задачи № 635, 637 (б), 638, 639 (в), 640, 641.
Сочетание шара с усеченной пирамидой.
1. Шар, описанный вокруг правильной усеченной пирамиды.
Теорема 5. Сферу можно описать вокруг любой правильной усеченной пирамиды.(Этого условия достаточно, но не обязательно)
2. Шар, вписанный в правильную усеченную пирамиду.
Теорема 6. Шар может быть вписан в правильную усеченную пирамиду тогда и только тогда, когда апофема пирамиды равна сумме апофем оснований.
В учебнике Л.С. для комбинации шара с усеченной пирамидой есть только одна задача. Атанасян (№ 636).
Комбинация мяча с круглыми телами.
Теорема 7. Шар можно описать как цилиндр, усеченный конус (прямой круг), конус.
Теорема 8. Шарик можно вписать в цилиндр (прямой круг) тогда и только тогда, когда цилиндр равносторонний.
Теорема 9. Шар можно вписать в любой конус (прямой круг).
Теорема 10. Шар можно вписать в усеченный конус (прямой круг) тогда и только тогда, когда его образующая равна сумме радиусов оснований.
Из учебника Л.С. Атанасян, задачи № 642, 643, 644, 645, 646 могут быть предложены для комбинации шара с круглыми телами.
Для более успешного изучения материала по данной теме необходимо включить в курс занятий устные задания:
1. Ребро куба равно a. Найдите радиусы шаров: вписанные в куб и описанные вокруг него. (r = a / 2, R = a3).
2. Можно ли описать сферу (шар) вокруг: а) куба; б) прямоугольный параллелепипед; в) наклонный параллелепипед с прямоугольником в основании; г) прямой параллелепипед; д) наклонный параллелепипед? (а) да; б) да; в) нет; г) нет; д) нет)
3.Верно ли, что вокруг любой треугольной пирамиды можно описать сферу? (есть)
4. Можно ли описать сферу вокруг любой четырехугольной пирамиды? (Нет, не вокруг четырехугольной пирамиды)
5. Какими свойствами должна обладать пирамида, чтобы описывать сферу вокруг нее? (В его основании должен быть многоугольник, вокруг которого можно описать круг)
6. В сферу вписана пирамида, боковой край которой перпендикулярен основанию.Как найти центр сферы? (Центр сферы — это точка пересечения двух геометрических точек точек в пространстве. Первая — это перпендикуляр, проведенный к плоскости основания пирамиды через центр окружности, описанной вокруг нее. Второй — это перпендикуляр, проведенный к плоскости основания пирамиды. плоскость, перпендикулярная этому боковому краю и проведенная через его середину)
7. При каких условиях можно описать сферу вокруг призмы, в основании которой находится трапеция? (во-первых, призма должна быть прямой, а во-вторых, трапеция должна быть равнобедренной, чтобы вокруг нее можно было описать круг)
8.Каким условиям должна удовлетворять призма, чтобы описать сферу вокруг нее? (призма должна быть прямой, а ее основание должно быть многоугольником, вокруг которого можно описать круг)
9. Сфера описывается рядом с треугольной призмой, центр которой находится вне призмы. Какой треугольник является основанием призмы? (Тупой треугольник)
10. Можете ли вы описать сферу вокруг наклонной призмы? (Нет, нельзя)
11. При каких условиях центр сферы, описываемой прямой треугольной призмой, будет располагаться на одной из боковых граней призмы? (у основания прямоугольный треугольник)
12.Основание пирамиды — равнобедренная трапеция. Ортогональная проекция вершины пирамиды на базовую плоскость — это точка, расположенная вне трапеции. Можно ли описать сферу вокруг такой трапеции? (Да, можно. Тот факт, что ортогональная проекция вершины пирамиды находится за пределами ее основания, не имеет значения. Важно, что у основания пирамиды лежит равнобедренная трапеция — многоугольник, вокруг которого находится окружность можно описать)
13.Рядом с правильной пирамидой описана сфера. Как его центр расположен относительно элементов пирамиды? (Центр сферы находится на перпендикуляре, проведенном к плоскости основания через его центр)
14. При каких условиях центр сферы, описываемой о прямой треугольной призме, находится: а) внутри призмы; б) вне призмы? (В основании призмы: а) остроугольный треугольник; б) тупой треугольник)
15. Сфера описывается вокруг прямоугольного параллелепипеда с ребрами равными 1, 2 и 2 дм.Рассчитайте радиус сферы. (1,5 дм)
16. В какой усеченный конус можно вписать сферу? (В усеченном конусе, в осевое сечение которого можно вписать окружность. Осевое сечение конуса представляет собой равнобедренную трапецию, сумма его оснований должна быть равна сумме его боковых сторон. Другими словами, сумма радиусов оснований конуса должна быть равна образующей)
17. В усеченный конус вписана сфера. Под каким углом видна образующая конуса из центра сферы? (90 градусов)
18.Каким свойством должна обладать прямая призма, чтобы в нее можно было вписать сферу? (во-первых, в основании прямой призмы должен быть многоугольник, в который можно вписать круг, а, во-вторых, высота призмы должна быть равна диаметру окружности, вписанной в основание)
19. Приведите пример пирамиды, в которую нельзя вписать сферу? (Например, четырехугольная пирамида с прямоугольником или параллелограммом в основании)
20.В основании прямой призмы лежит ромб. Можно ли вписать сферу в эту призму? (Нет, нельзя, так как в общем случае нельзя описать круг вокруг ромба)
21. При каких условиях можно вписать сферу в прямую треугольную призму? (если высота призмы в два раза больше радиуса круга, вписанного в основание)
22. При каком условии сфера может быть вписана в правильную прямоугольную усеченную пирамиду? (Если разрез данной пирамиды плоскостью, проходящей через середину стороны основания, перпендикулярной ей, представляет собой равнобедренную трапецию, в которую можно вписать круг)
23.В усеченную треугольную пирамиду вписана сфера. Какая точка пирамиды является центром сферы? (Центр сферы, вписанной в эту пирамиду, находится на пересечении трех биссектральных плоскостей углов, образованных боковыми гранями пирамиды с основанием)
24. Можно ли описать сферу вокруг цилиндра (правильного круга)? (Да, можно)
25. Можно ли описать сферу конусом, усеченным конусом (прямым кругом)? (Да, в обоих случаях можно)
26.Можно ли вписать сферу в любой цилиндр? Какими свойствами должен обладать цилиндр, чтобы можно было вписать сферу? (Нет, не каждый: осевое сечение цилиндра должно быть квадратным)
27. Можно ли вписать сферу в каждый конус? Как определить положение центра сферы, вписанной в конус? (Да, в любом.

 Объем параллелепипеда равен 5. Найдите высоту цилиндра.
Объем параллелепипеда равен 5. Найдите высоту цилиндра.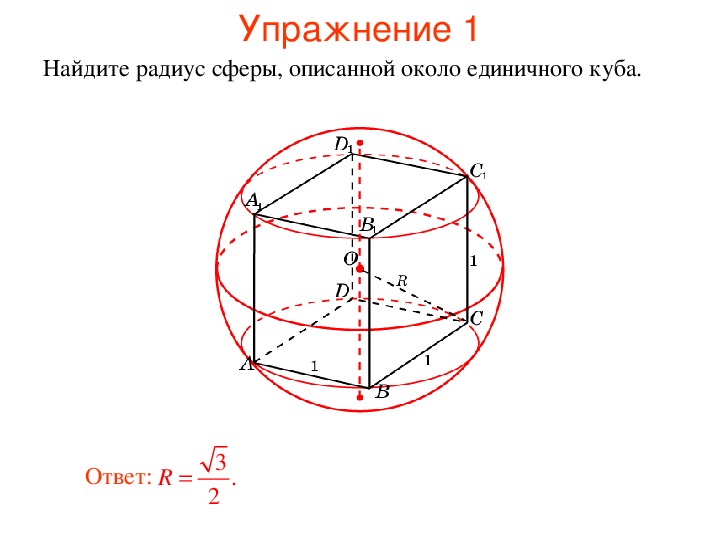 1
1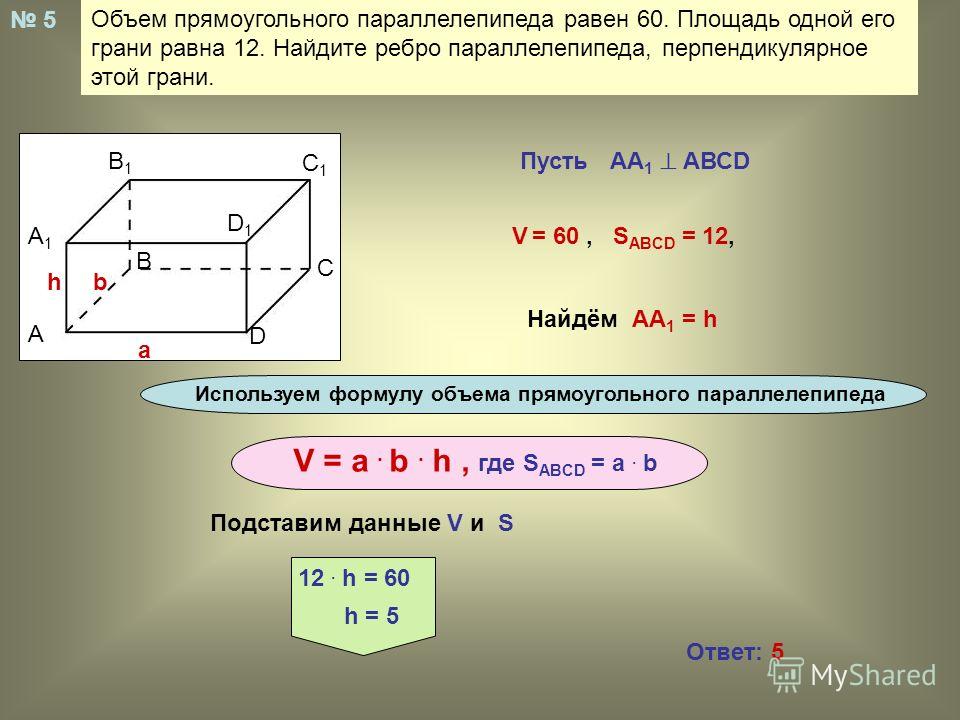 Найдите площадь поверхности этой
пирамиды.
Найдите площадь поверхности этой
пирамиды. Вычислите высоту конуса.
Вычислите высоту конуса.
Leave A Comment