Ответов пока нет | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Главная → Видеоуроки → ОГЭ (ГИА) по математике. Задача 24. Описание видеоурока: Условие задачи: Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=35, BC=21, CF:DF=5:2. 00:10:17 Валерий Волков 36 05.02.2015 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
линейная алгебра — Трапеция нахождение длины разделительной линии
Задавать вопрос
спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 6к раз
$\begingroup$
Дана трапеция с основаниями $437\mathrm{m}$ и $57\mathrm{m}$ со сторонами $300\mathrm{m}$ и $350\mathrm{m}$
, он должен быть разделен на две части в соотношении $2:3$ линией, параллельной параллельным сторонам, причем $\color{brown}{\text{большая часть примыкает к меньшей параллельной стороне}}$.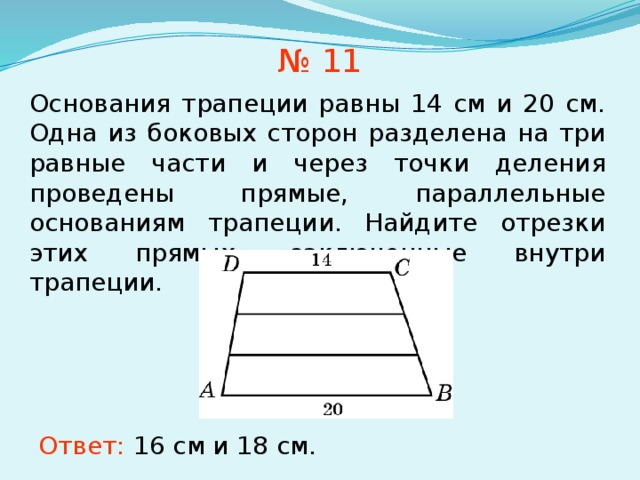 2$ двух треугольников, образованных, когда линия проведена параллельно основаниям. Итак, найдены необходимые переменные для $\text{area}(149782,072\mathrm{m})$.
2$ двух треугольников, образованных, когда линия проведена параллельно основаниям. Итак, найдены необходимые переменные для $\text{area}(149782,072\mathrm{m})$.
Я не знаю, что использовать для определения разделительной линии. Я знаю, что площадь может быть пропорциональна $ 2: 3 $, но, учитывая третье основание (разделительную линию) и разную высоту двух полученных трапеций, мне нужно было бы сначала найти две высоты. Как я смогу это сделать? Или есть более простой способ?
- линейная алгебра
- площадь
- четырехугольник
$\endgroup$
$\begingroup$
(1) После построения пунктирной параллельной линии, как показано, у нас есть два // грамма со сторонами длины = 437.
(2) Длина основания большего треугольника = 138
(3) Длина основания меньшего треугольника = 138*(3/5)=x, скажем.
(4) Требуемое = х + 437.
$\endgroup$
2
$\begingroup$
Назовем $h$ высотой трапеции.
Назовем $A,B,C,D$ вихрем трапеции с меньшим основанием $AB$ и более длинным $CD$.
Назовем $I,J$ пересечением разделительной линии и двух сторон $AD$ и $BC$.
Обозначим $h’$ высоту верхней трапеции (примыкающей к меньшему основанию), а $h»$ высоту нижней.
$ABJI=\frac 23 ABCD$ и $JCDI=\frac 13 ABCD$
$ABJI=(AB+JI)*h’/2=(AB+CD)*h/3$
Вы можете выразить $h’$ с точки зрения остальных.
$JCDI=(CD+IJ)*h»/2=(AB+CD)*h/6$
Аналогично $h»$.
Но $h’+h»=h$ Таким образом, вы получили квадратное выражение в $IJ$, которое можете решить и получить ответ.
$\endgroup$
Объяснение урока: Площадь трапеции
В этом объяснении мы научимся находить площадь трапеции с помощью формулы и применять ее для нахождения площади в реальной жизни.
Мы начнем с обсуждения различных существующих типов трапеций. Трапеция – это четырехугольник, у которого ровно одна пара параллельных сторон. Мы называем эти стороны основаниями и часто обозначаем их длины буквами 𝑎 и 𝑏. Перпендикулярное расстояние
между двумя основаниями называется высотой трапеции и обычно обозначается ℎ. Две другие стороны трапеции
(непараллельные противоположные стороны) известны как ноги.
Мы называем эти стороны основаниями и часто обозначаем их длины буквами 𝑎 и 𝑏. Перпендикулярное расстояние
между двумя основаниями называется высотой трапеции и обычно обозначается ℎ. Две другие стороны трапеции
(непараллельные противоположные стороны) известны как ноги.
Равнобедренная трапеция — это трапеция, катеты которой имеют одинаковую длину. Все равнобедренные трапеции имеют линию симметрии, проходящую через середины их оснований.
A правая трапеция – это трапеция, у которой один из катетов перпендикулярен двум параллельным основаниям.
Теперь рассмотрим, как найти площадь трапеции, у которой высота обозначена через ℎ, а длины основания по 𝑎 и 𝑏.
Допустим, мы проводим диагональ трапеции, соединяющую две противоположные вершины. Это делит трапецию на два треугольника, как показано на рисунке ниже.
Площадь каждого треугольника можно найти по формуле
площадьоснованиятреугольникаперпендикулярвысота=×2.
Перпендикулярная высота каждого треугольника равна ℎ. Верхний треугольник имеет основание длиной 𝑎 единиц, а нижний треугольник имеет основание длины 𝑏 единиц. Следовательно, площадь трапеции равна площадь трапецииплощадь верхнего треугольникаплощадь цветкатреугольник=+=𝑎×ℎ2+𝑏×ℎ2=(𝑎+𝑏)ℎ2.
Заметим, что (𝑎+𝑏) есть сумма длин параллельных оснований трапеции. Неформально мы можем думать о площадь трапеции как «половина суммы параллельных оснований, умноженная на высоту».
Формула: Площадь трапеции
Площадь трапеции равна половине суммы длин параллельных оснований, умноженных на высоту.
Для трапеции с высотой ℎ и длинами оснований 𝑎 и 𝑏 площадь определяется выражением площадь трапеции=12(𝑎+𝑏)ℎ.
В нашем первом примере мы покажем, как применить эту формулу, чтобы найти площадь трапеции, зная ее высоту и длины ее оснований.
Пример 1. Нахождение площади трапеции
Длины параллельных сторон трапеции равны 82 и 70. Если высота равна 100, какова площадь трапеции?
Если высота равна 100, какова площадь трапеции?
Ответ
Напомним, что площадь трапеции определяется выражением площадь трапеции=12(𝑎+𝑏)ℎ, где 𝑎 и 𝑏 представляют длины оснований или параллельных сторон трапеции. и ℎ представляет его перпендикулярную высоту. Нам дана каждая из этих длин в вопросе.
Замена 𝑎=82, 𝑏=70 и ℎ=100, а затем вычисление дает площадь трапеции=12(82+70)×100=12×152×100=76×100=7600.
Следовательно, площадь трапеции равна 7 600 квадратных единиц.
Теперь мы рассмотрели пример того, как вычислить площадь трапеции, зная ее высоту и длины параллельных сторон. Теперь рассмотрим проблему это, по сути, обратное: вычисление высоты трапеции по ее площади и длинам ее оснований.
Пример 2. Нахождение высоты трапеции по ее площади
Площадь этой трапеции составляет 30 000 ярдов 2 . Какова его высота?
Ответ
Начнем с того, что вспомним, что площадь трапеции можно вычислить, умножив половину суммы длин параллельных оснований на высоту перпендикуляра.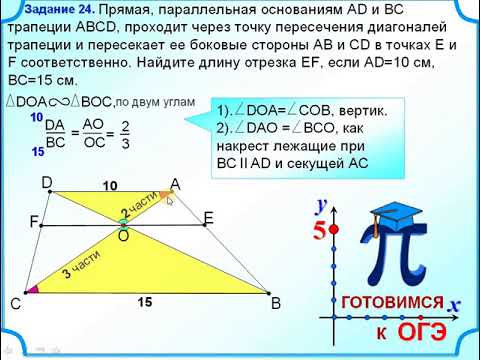
Из рисунка видно, что параллельные основания трапеции имеют длины 80 ярдов и 295 ярдов. Нам также известна длина одного из катетов трапеции. (232 ярда), но это не относится к нашему расчету, так как это не перпендикулярная высота трапеции.
Мы можем использовать данную площадь трапеции и длины двух параллельных оснований, чтобы составить уравнение, где ℎ представляет собой неизвестную высоту трапеции: 12(80+295)ℎ=30000.
Теперь решим это уравнение, чтобы определить значение ℎ. Упрощение левой части дает 3752ℎ=30000.
Умножение обеих частей уравнения на 2375 (множительное обратное 3752) дает ℎ=30000×2375=60000375=160.
Следовательно, высота трапеции равна 160 ярдам.
В примере, который мы только что видели, нам дали больше информации, чем нужно на рисунке. Длина катета трапеции не требовалась для того, чтобы
вычислить его площадь. Понимание измерений, необходимых для применения конкретной формулы, и возможность выбрать соответствующую информацию на диаграмме или
словесное описание является важным навыком при решении геометрических задач.
В нашем следующем примере мы рассмотрим, как найти длину одной из параллельных сторон трапеции, зная ее площадь, высоту, и длину другой параллельной стороны.
Пример 3. Нахождение длины основания трапеции по ее площади
Площадь трапеции равна 1 760, а расстояние между ее параллельными сторонами равно 40. Если одна параллельная сторона равна 39, чему равна другая сторона?
Ответ
Напомним, что площадь трапеции с параллельными сторонами (или основаниями) длин 𝑎 и 𝑏 единиц а высота ℎ единиц определяется выражением площадь трапеции=12(𝑎+𝑏)ℎ.
Нам известно, что эта трапеция имеет площадь 1 760 квадратных единиц. Расстояние между параллельными сторонами, иначе говоря, высота
трапеции, составляет 40 единиц, а длина одной параллельной стороны или основания трапеции составляет 39единицы измерения. Подставляя каждое из этих значений в формулу
выше дает уравнение, которое мы можем решить, чтобы определить длину другой параллельной стороны:
1760=12(39+𝑏)×40.
Начнем с упрощения правой части уравнения, уменьшив коэффициент 2: 1760=20(39+𝑏).
Деление обеих частей уравнения на 20 дает 88=39+𝑏.
Наконец, вычитание 39 из каждой части уравнения дает 49=𝑏.
Следовательно, длина другой параллельной стороны (или основания) трапеции равна 49единицы измерения.
Теперь рассмотрим альтернативный способ задания формулы площади трапеции. Неформально мы сказали, что эту формулу можно рассматривать как «половина суммы параллельных оснований, умноженная на высоту». На самом деле «половина суммы параллельных оснований» имеет геометрическое значение. которые мы определяем ниже.
Определение: среднее основание трапеции
Среднее основание трапеции — это отрезок, концы которого являются серединами катетов трапеции. Среднее основание трапеции параллельна двум основаниям трапеции.
Длина среднего основания трапеции 𝑚 равна среднему арифметическому длин оснований 𝑎 и 𝑏:
𝑚=𝑎+𝑏2.
Другими словами, длина среднего основания трапеции равна «половине суммы длин параллельных оснований». Формула для Следовательно, площадь трапеции может быть эквивалентно выражена как площадь трапециидлина середины основаниявысота=×.
Формула: Площадь трапеции через длину ее среднего основания
Площадь трапеции равна произведению длины ее среднего основания на ее высоту.
Для трапеции с высотой ℎ и средним основанием длины 𝑚 площадь определяется выражением площадь трапеции=𝑚ℎ.
Теперь рассмотрим два примера, в которых мы используем эту версию формулы площади для решения двух задач, касающихся площади трапеции.
Пример 4. Использование среднего основания для определения площади трапеции
Найдите площадь показанной трапеции.
Ответ
Изучив схему, мы видим, что 𝑋𝑌 делит каждый из катетов трапеции,
𝐴𝐷 и 𝐵𝐶, на два отрезка равной длины. Следовательно,
𝑋𝑌 соединяет середины катетов трапеции и, следовательно, является средним основанием трапеции.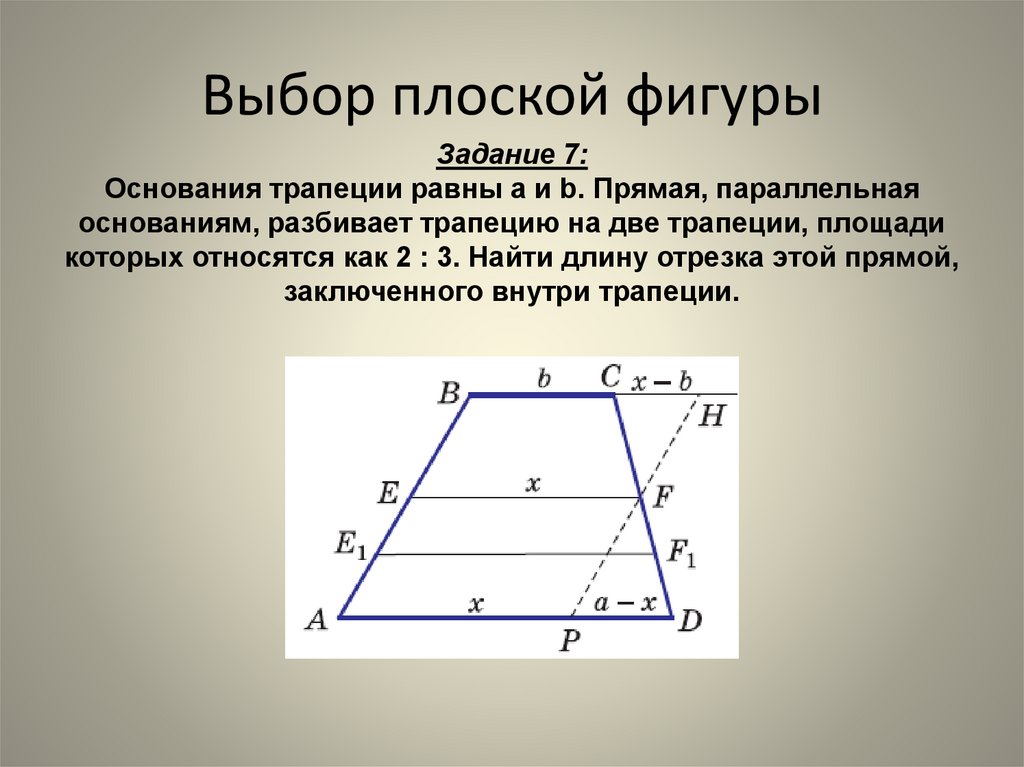
Напомним, что площадь трапеции можно вычислить из длины ее среднего основания и высоты по формуле площадь трапециидлина середины основаниявысота=×.
Замена 19 мм длины среднего основания и 8 мм на высоту трапеции дает areaoftrapezoidmm=19×8=152.
Пример 5. Вычисление длины срединного основания трапеции по ее площади и высоте
Найдите длину срединного основания трапеции, площадь которой равна 28 см 2 и высотой 4 см.
Ответ
Напомним, что площадь трапеции можно вычислить по формуле площадь трапециидлина середины основаниявысота=×.
Нам известны площадь и высота трапеции, поэтому мы можем составить уравнение. Подстановка 28 для площади и 4 для высоты дает 28=×4.lengthofmiddlebase
Чтобы найти длину среднего основания, разделим обе части уравнения на 4: длина среднего основания = 284 = 7.
Среднее основание данной трапеции равно 7 см.
Методы, которые мы разработали в этом объяснении, также могут быть применены к реальным задачам, связанным с трапециями. Теперь рассмотрим последний пример связанные с измерениями полей фермера, одно из которых имеет форму трапеции.
Пример 6. Использование площадей трапеций для решения реальной задачи
Фермер владеет двумя полями одинаковой площади: одно в форме ромба и одно в форме трапеции, как показано на рисунке. Вычислите длину среднего основания трапециевидного поля.
Ответ
Начнем с рассмотрения поля слева на рисунке. Это поле имеет форму ромба, потому что длины его четырех сторон равны. Нам даны длины двух диагоналей ромба: они равны 100 м и 90 м. Вспомним, что площадь ромба равна площадь ромба=𝑑𝑑2, где 𝑑 и 𝑑 представляют длины его диагоналей. Следовательно, у нас есть площадь ромба=100×902=
=4500.
Далее рассмотрим поле справа на рисунке. Это поле имеет форму трапеции, потому что это четырехугольник с одной парой параллельных сторон. Нам дана высота трапеции (25 м) и теперь мы знаем, что ее площадь, равная площади
другого поля, составляет 4 500 м 2 .
Нам дана высота трапеции (25 м) и теперь мы знаем, что ее площадь, равная площади
другого поля, составляет 4 500 м 2 .
Поскольку мы хотим вычислить длину среднего основания трапеции, вспомним формулу площади трапеции, включающую эту меру: площадь трапециидлина середины основаниявысота=×.
Подстановка известной площади трапеции (4 500 м 2 ) и известной высоты (25 м) дает уравнение, которое мы можем решить, чтобы определить длину среднего основания: 4500=×25.длина среднего основания
Разделив обе части этого уравнения на 25, получим длина среднего основания m=450025=180.
Длина среднего основания поля в форме трапеции 180 м.
Давайте закончим, повторив некоторые ключевые моменты.
Ключевые точки
- Площадь трапеции с высотой ℎ и параллельными основаниями длин 𝑎 и 𝑏 определяется выражением площадь трапеции=12(𝑎+𝑏)ℎ.
- Неформально мы можем думать об этом как
площадь трапеции равна половине суммы параллельных основанийвысота=×.



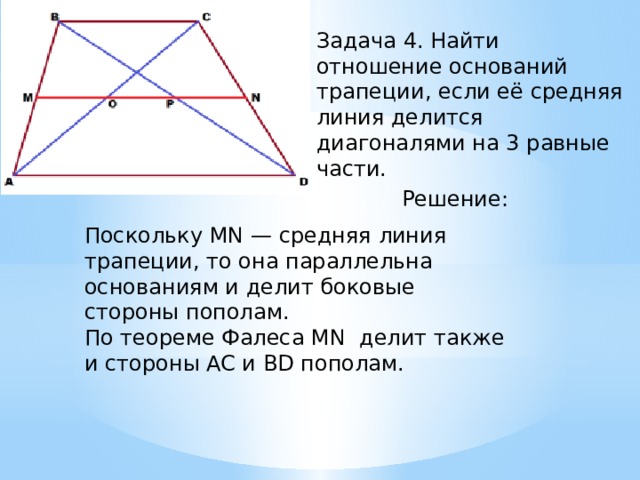
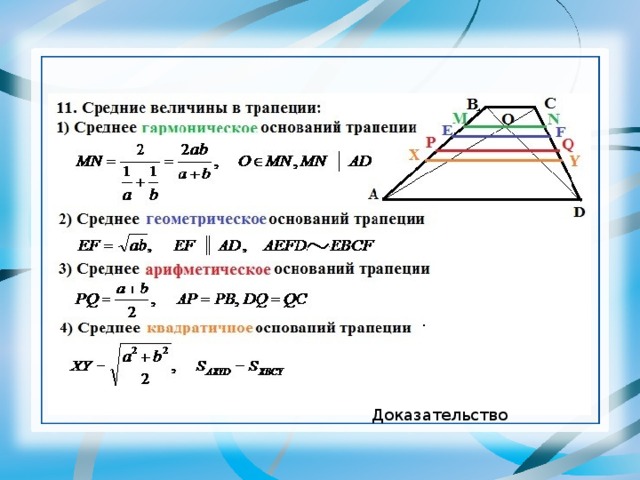
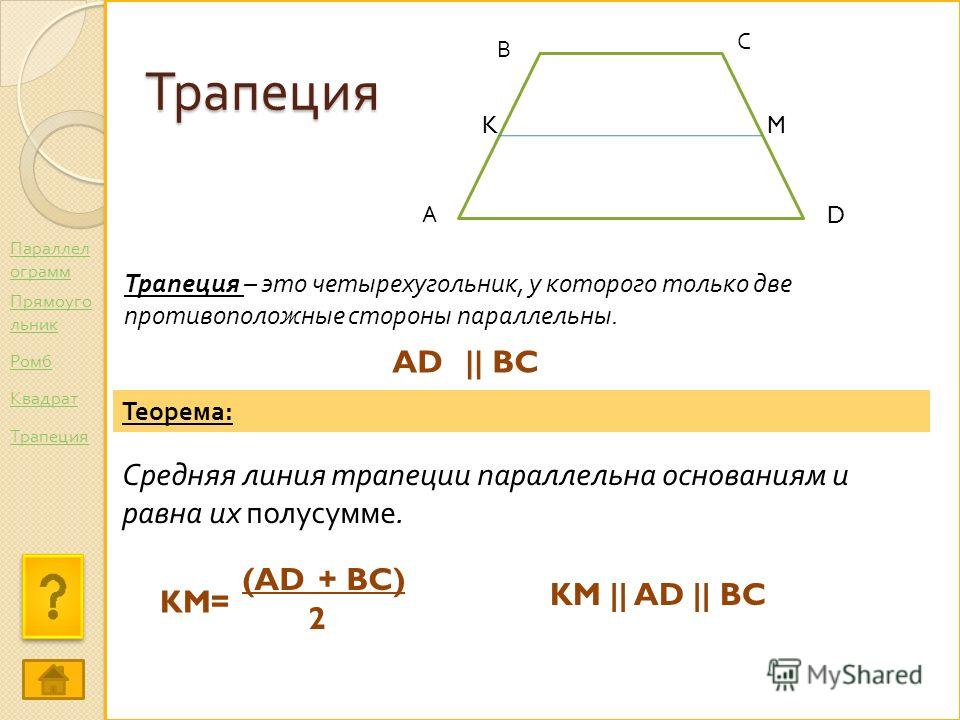 Решение задачи 24. Задача про трапецию.
Решение задачи 24. Задача про трапецию.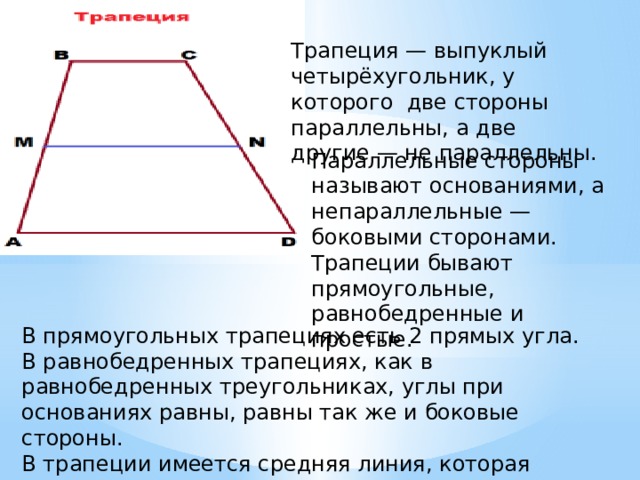 5 класс.
5 класс. 10 — 11 класс.
10 — 11 класс.
Leave A Comment