Приведите пример квадратичной функции график которой касается прямой y=3 с абсциссой 6 — Знания.site
Последние вопросы
Алгебра
3 минуты назад
один із коренів рівняння x2+12x+c=0 дорівнює 0. Знайти другий корінь та число cАлгебра
8 минут назад
Скільки складів з двох букв, перша буква якого позначає приголосний звук, а друга — голосний, можна скласти з букв слова «Дев’ятикласник»?Алгебра
8 минут назад
Запишіть в квадратному рівнянні його коефіцієнтиx²+3x-10=0Алгебра
13 минут назад
Поезд, двигаясь равномерно со скоростью 90 км/ ч, проезжает мимо лесополосы, длина которой равна 500 метров, за 45 секунд.

Умооооллляяяяюююю!!!
Алгебра
13 минут назад
Алгебра 7 класс уравнениеАлгебра
13 минут назад
cos a= -2/3 , 180градусовАлгебра
13 минут назад
2) Функцію задано формулою у =-0,6-0,3x, де х i-3< x < 2. Задайте цю функцію таблицею. ДАЮ 40 БАЛЛОВ!!СРОЧНОАлгебра
28 минут назад
Помогите с алгеброй пожалуйстаАлгебра
28 минут назад
Решение задачи Коли для дифференциального уравнения1 час назад
Дайте повну відповідь та малюнок, даю 75 балівАлгебра
1 час назад
Свойства степени. 3пж пж ответьте
3пж пж ответьте Алгебра
1 час назад
добуток двох послідовних натуральних чисел на 71 більший за їх суму. Знайдіть ці числа.
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Indonesia
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
Квадратичная функция, как построить параболу
Поможем понять и полюбить математику
Начать учиться
394. 4K
4K
Большинство явлений в нашей жизни можно описать математическим языком. И функция — отличный в этом помощник. Давайте рассмотрим ее квадратичную форму.
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило, в соответствии с которым каждому значению аргумента соответствует единственное значение функции. Вот какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.

- Словесный способ.
График функции — это объединение всех точек координатной плоскости, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0.
График квадратичной функции — парабола, которая имеет следующий вид для y = x2 в частном случае при b = 0, c = 0:
Точки, обозначенные фиолетовыми кружками, называют 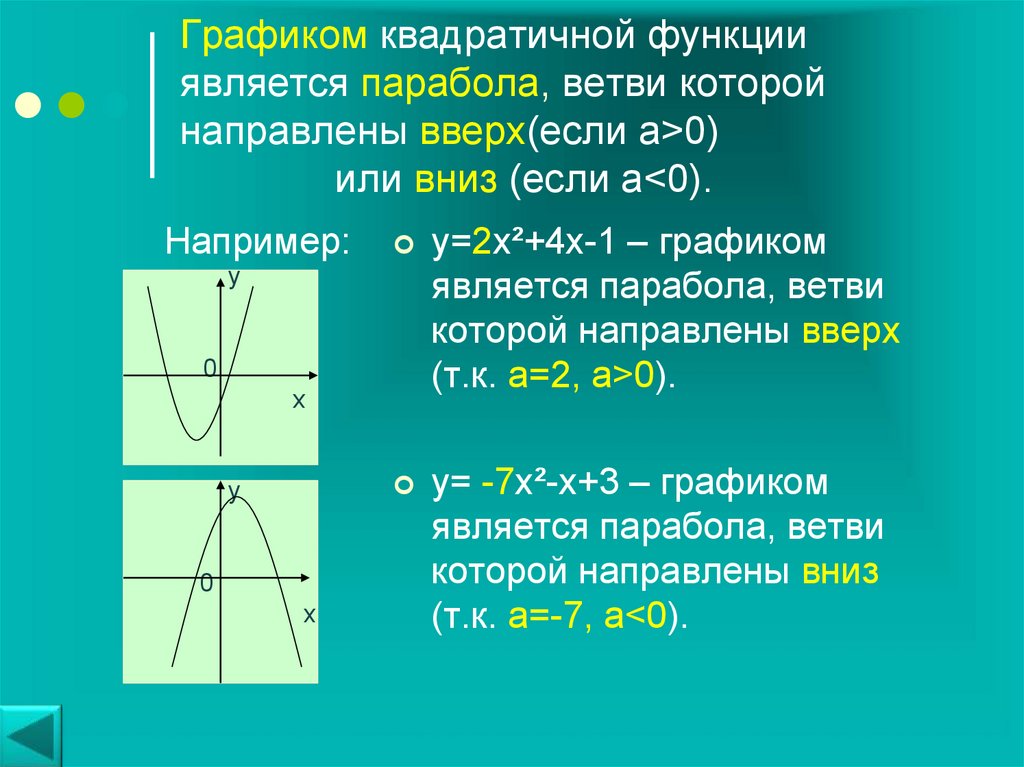 Чтобы найти их координаты для функции y = x2, нужно составить таблицу:
Чтобы найти их координаты для функции y = x2, нужно составить таблицу:
x | −2 | −1 | 0 | 1 | 2 |
y | 4 | 1 | 0 | 1 | 4 |
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов. При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.
При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.
График функции y = –x2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x | −2 | −1 | 0 | 1 | 2 |
y | −4 | −1 | 0 | −1 | −4 |
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ.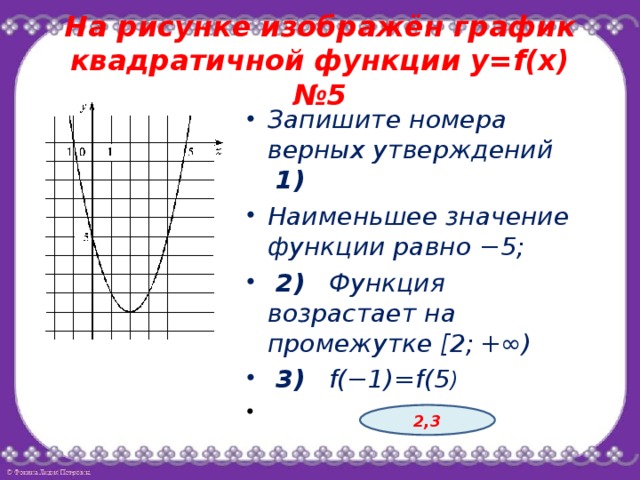 Отметим важные выводы:
Отметим важные выводы:
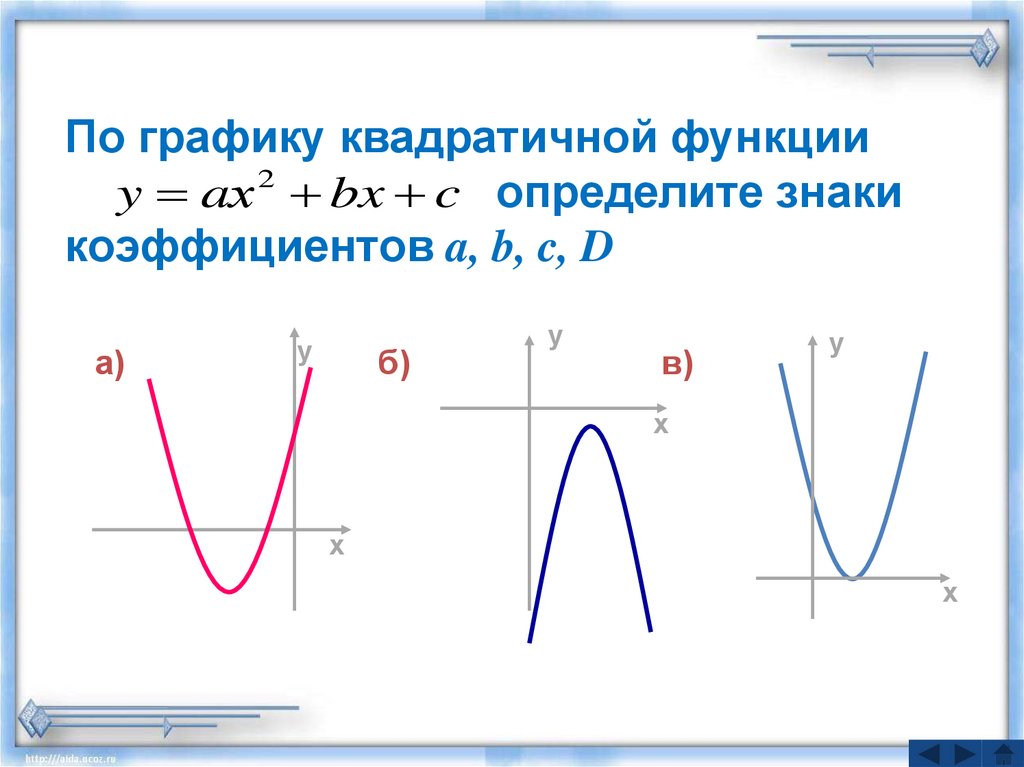
- Если старший коэффициент больше нуля (a > 0), то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля (a < 0), то ветви параболы напрaвлены вниз.
Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.
Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.
Для наглядности возьмем функцию y = ax2 + bx + c. Чтобы найти точки пересечения с осью Ox, нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.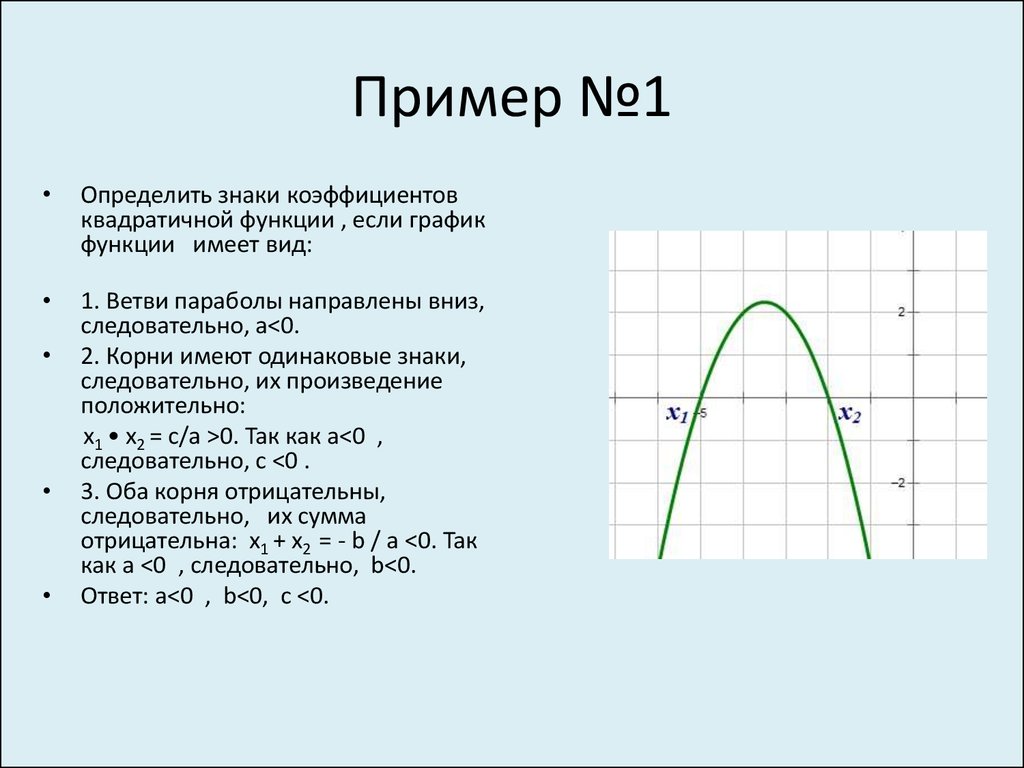
Рассмотрим три случая:
- Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
Теперь понятно, что, зная направление ветвей параболы и знак дискриминанта, мы можем схематично представить график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.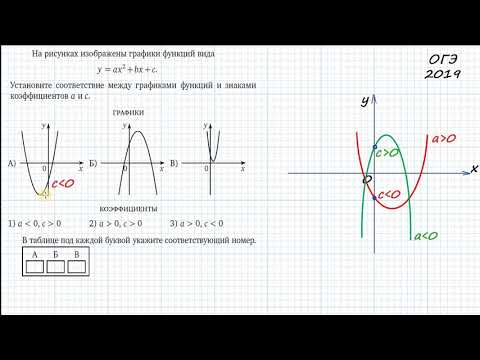
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax
2 + bx + c.Разберем общий алгоритм на примере y = 2x2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.

- Найдем дискриминант квадратного трехчлена 2x2 + 3x — 5.
D = b2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
√D = 7
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x2 + 3x — 5 = 0
,
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) относительно оси симметрии.
Нанесем эти точки на координатную плоскость и построим график параболы:
Уравнение квадратичной функции имеет вид y = a * (x — x₀)
2 + y₀Зная координаты вершины параболы и старший коэффициент, можно записать уравнение квадратичной функции в виде у = a(x − x0) + y0, где x0, y0 — координаты вершины параболы.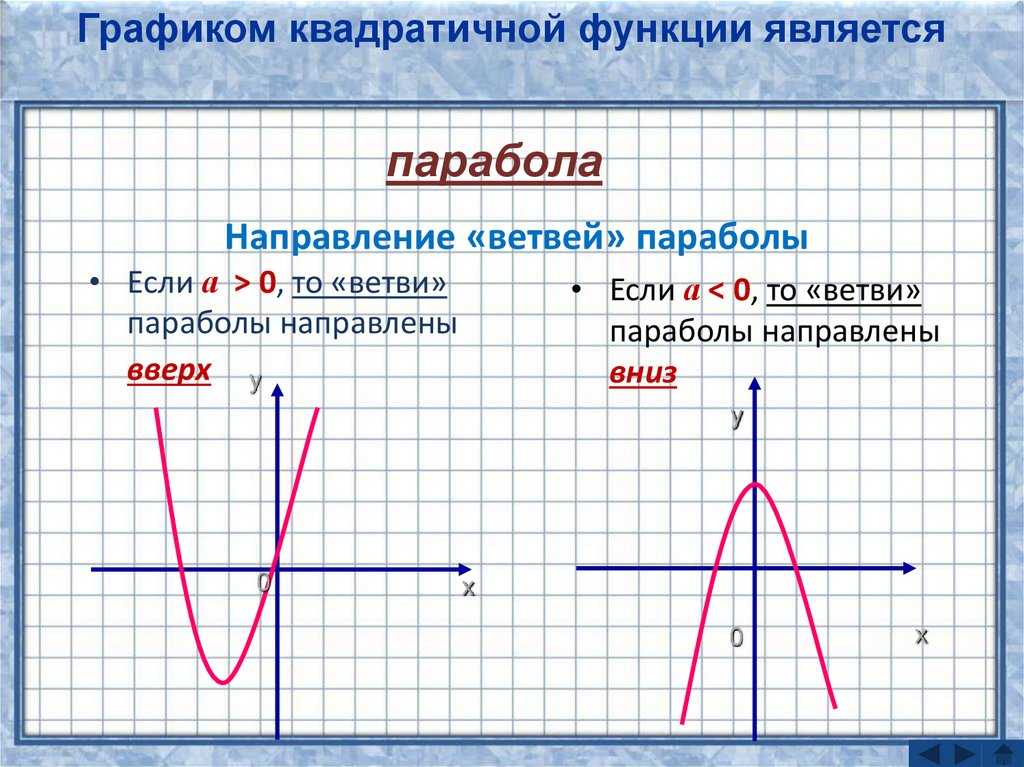
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x — 1)2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить график функции y = x2,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
Построить график параболы для каждого случая.
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).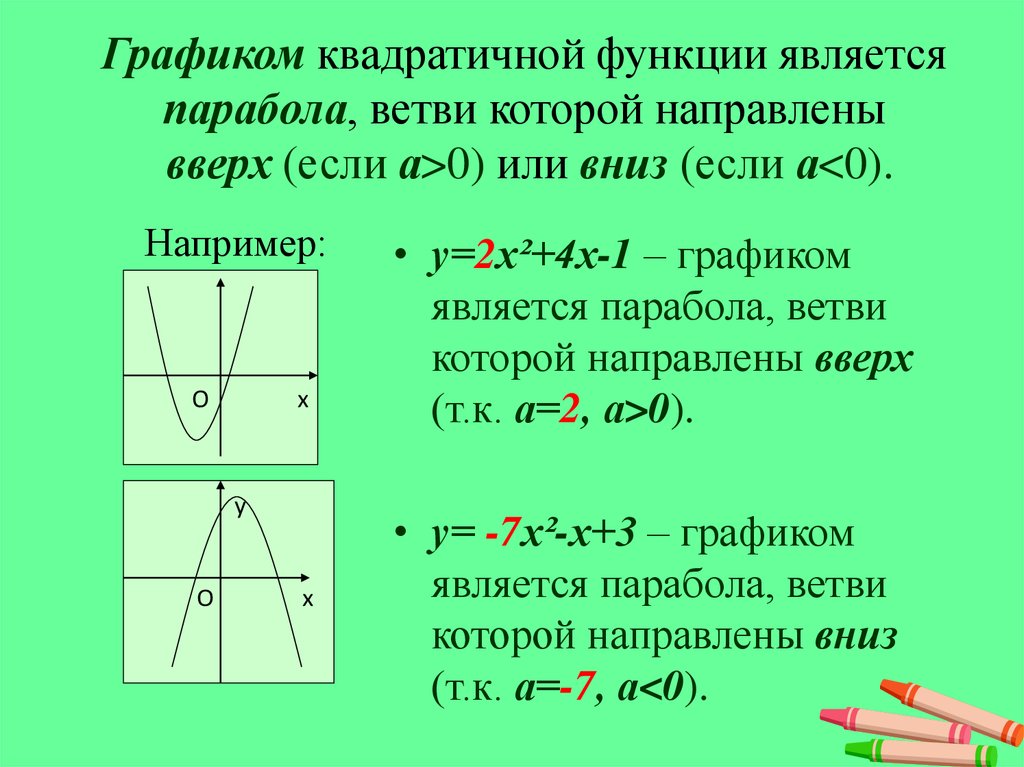
Как строим:
Данный вид функции позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная относительно оси симметрии параболы.
Отметим эти точки на координатной плоскости и соединим плавной прямой линией.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
123.2K
Решение линейных неравенств
К следующей статье
319. 3K
3K
Модуль числа
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Квадратичные функции
Квадратичные функции
|
Содержание : Эта страница соответствует § 3.1 (стр. 244) текста.
Предполагаемые проблемы из текста:
р.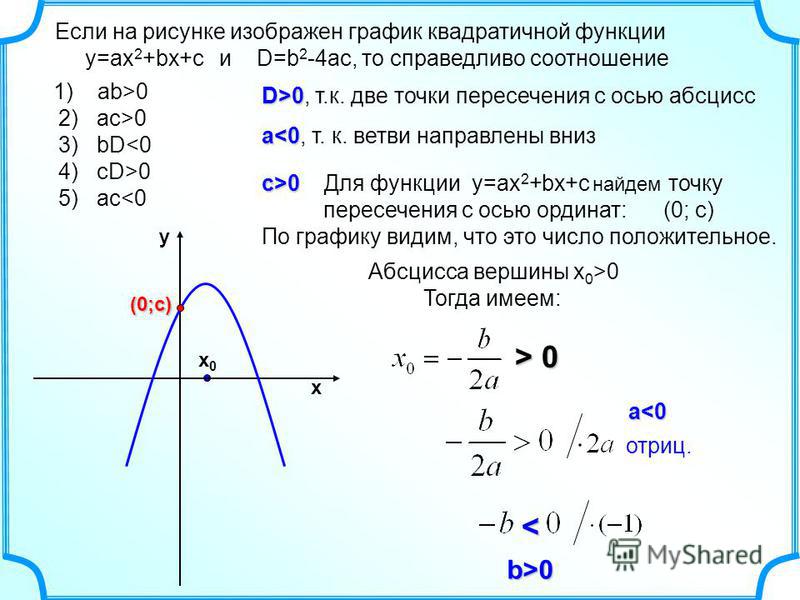 251 #1-8, 10, 11, 15, 16, 18, 19, 21, 23, 24, 30, 33, 37, 38, 75
251 #1-8, 10, 11, 15, 16, 18, 19, 21, 23, 24, 30, 33, 37, 38, 75
Графики
Стандартная форма
приложений
Графики
А квадратичная функция имеет вид f(x) = ax 2 + bx + c , где a , b и c — это числа, где a не равны нулю.
График квадратичной функции представляет собой кривую, называемую параболой . Параболы могут раскрываться вверх или вниз и различаются по «ширине» или «крутизне», но все они имеют одинаковую основную форму «U». На рисунке ниже показаны три графика, и все они являются параболами.
Все параболы симметричны относительно линии, называемой осью симметрии . Парабола пересекается его ось симметрии в точке, называемой вершиной параболы.
Вы знаете, что две точки определяют прямую.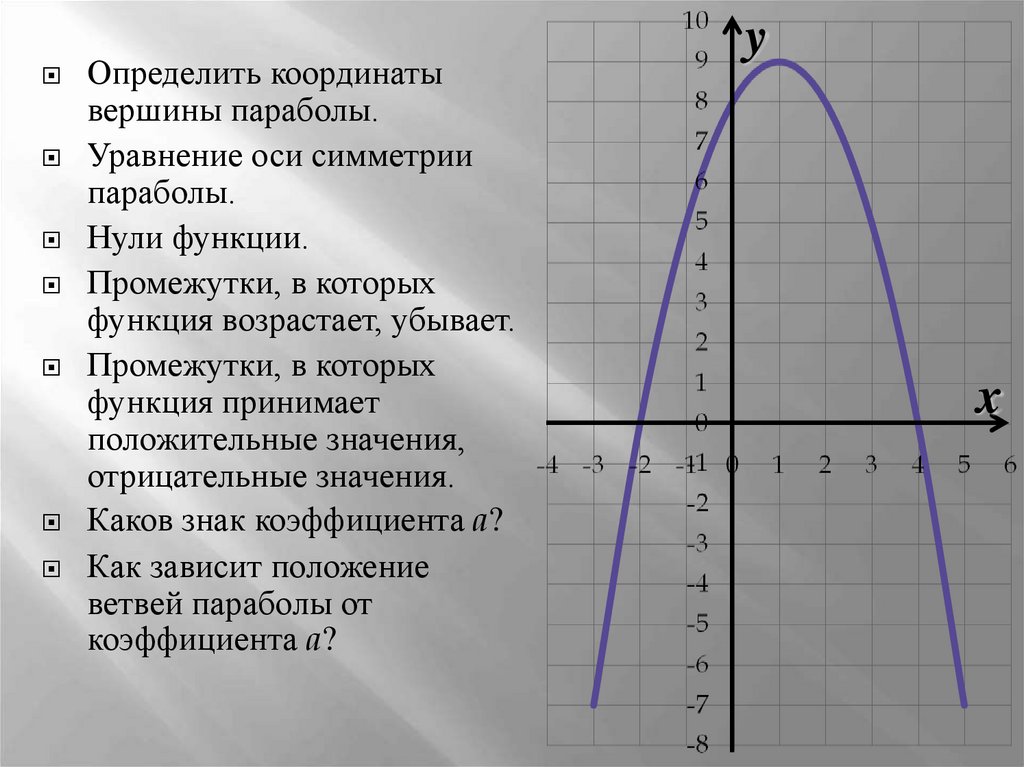 Это означает, что если вам даны любые две точки на плоскости, то
существует одна и только одна линия, содержащая обе точки. Аналогичное утверждение можно сделать о точках и квадратичных
функции.
Это означает, что если вам даны любые две точки на плоскости, то
существует одна и только одна линия, содержащая обе точки. Аналогичное утверждение можно сделать о точках и квадратичных
функции.
Даны три точки на плоскости, которые имеют разные первые координаты и не лежат на одной прямой. одну квадратичную функцию f, график которой содержит все три точки. Апплет ниже иллюстрирует этот факт. График содержит три точки и параболу, проходящую через все три. Соответствующая функция показана в тексте поле под графиком. Если перетащить любую из точек, то функция и парабола обновятся.
Многие квадратичные функции можно легко изобразить вручную, используя методы растяжения/сжатия и сдвига. (перевод) парабола y = x 2 . (См. раздел об управлении графики.)
Пример 1 .
Нарисуйте график y = x 2 /2. Начиная с графика y = x 2 , мы уменьшаем его в множитель из одной половины.
Это означает, что для каждой точки на графике y = x 92 — 5. Начнем с графика y = x 2 , сдвинем вправо на 4 единицы, затем 5 единиц вниз.
Упражнение 1 :
(a) Нарисуйте график y = (x + 2) 2 — 3. Ответ
(b) Нарисуйте график y = -(x — 5) 2 + 3. Ответ
Вернуться к содержанию
Стандартная форма
Функции в частях (a) и (b) упражнения 1 являются примерами квадратичных функций в стандартной форме . Когда квадратичная функция имеет стандартную форму, ее график легко начертить, отражая, сдвигая и растяжение/сжатие параболы y = x 2 .
Говорят, что квадратичная функция f(x) = a(x — h) 2 + k, не равная нулю, имеет стандартную форму . Если а положительное, то график открывается вверх, а если а отрицательное, то открывается вниз.
линия симметрии — вертикальная линия x = h, а вершина — точка (h,k).
Любая квадратичная функция может быть переписана в стандартной форме с помощью , дополняющего квадрат . (см. раздел о решая уравнения алгебраически, чтобы просмотреть завершение квадрата.) Шаги, которые мы используем в этом разделе для заполнения квадрата, будут выглядеть немного иначе, потому что наш главный цель здесь не решение уравнения.
Обратите внимание, что, когда квадратичная функция находится в стандартной форме, также легко найти ее нули по квадратному корню. принцип.
Пример 3 .
Запишите функцию f(x) = x 2 — 6x + 7 в стандартной форме. Нарисуйте график функции f и найдите ее нули. и вершина.
f(x) = x 2 — 6x + 7.
= (x 2 — 6x )+ 7. Сгруппируйте x 2 и х членов и затем завершите квадрат на этих условиях.
= (х 2 — 6х + 9 — 9) + 7.
Нам нужно прибавить 9, потому что это квадрат половины коэффициента x, (-6/2) 2 = 9. Когда мы решали уравнение, мы просто прибавляли 9 к обеим частям уравнения. В этой настройке мы добавляем и вычитаем 9 так что мы не меняем функцию.
= (х 2 — 6x + 9) — 9 + 7. Мы видим, что x 2 — 6x + 9 — полный квадрат, а именно (x — 3) 2 .
f(x) = (x — 3) 2 — 2. Это стандартная форма .
Из этого результата легко найти вершину графа функции f (3, -2).
Чтобы найти нули f, мы приравняем f к 0 и найдем x.
(х — 3) 2 — 2 = 0,
(х — 3) 2 = 2.
(х — 3) = ± квадратный сантиметр (2).
х = 3 ± квадрат (2).
Чтобы начертить график f, сдвинем график y = x 2 на три единицы вправо и на две единицы вниз.
Если коэффициент при х 2 не равен 1, то мы должны вынести этот коэффициент из х 2 и х терминов, прежде чем продолжить.
Пример 4 .
Запишите f(x) = -2x 2 + 2x + 3 в стандартной форме и найдите вершину графика f.
f(x) = -2x 2 + 2x + 3.
= (-2x 2 + 2x) + 3.
= -2(х 2 — х) + 3.
= -2(х 2 — х + 1/4 — 1/4) + 3.
Мы прибавляем и вычитаем 1/4, потому что (-1/2) 2 = 1/4, а -1 — коэффициент при x.
= -2(х 2 — х + 1/4) -2(-1/4) + 3.
Обратите внимание, что все в скобках умножается на -2, поэтому, когда мы удаляем -1/4 из скобок, мы надо умножить на -2.
= -2(х — 1/2) 2 + 1/2 + 3.
= -2(х — 1/2) 2 + 7/2.
Вершина — это точка (1/2, 7/2). Поскольку график открывается вниз (-2 < 0), вершина является самой высокой точкой на графике.
Упражнение 2 :
Запишите f(x) = 3x 2 + 12x + 8 в стандартной форме. Нарисуйте график функции f, найдите его вершину и найдите нули f. Ответ
Альтернативный метод нахождения вершины
В некоторых случаях завершение квадрата — не самый простой способ найти вершину параболы. Если график квадратичная функция имеет две точки пересечения с х, тогда линия симметрии — это вертикальная линия, проходящая через середину x-перехватов.
Х-пересечения на графике выше находятся в точках -5 и 3. Линия симметрии проходит через -1, что является средним
из -5 и 3. (-5 + 3)/2 = -2/2 = -1. Как только мы знаем, что линия симметрии равна x = -1, мы знаем первую координату
вершины равно -1.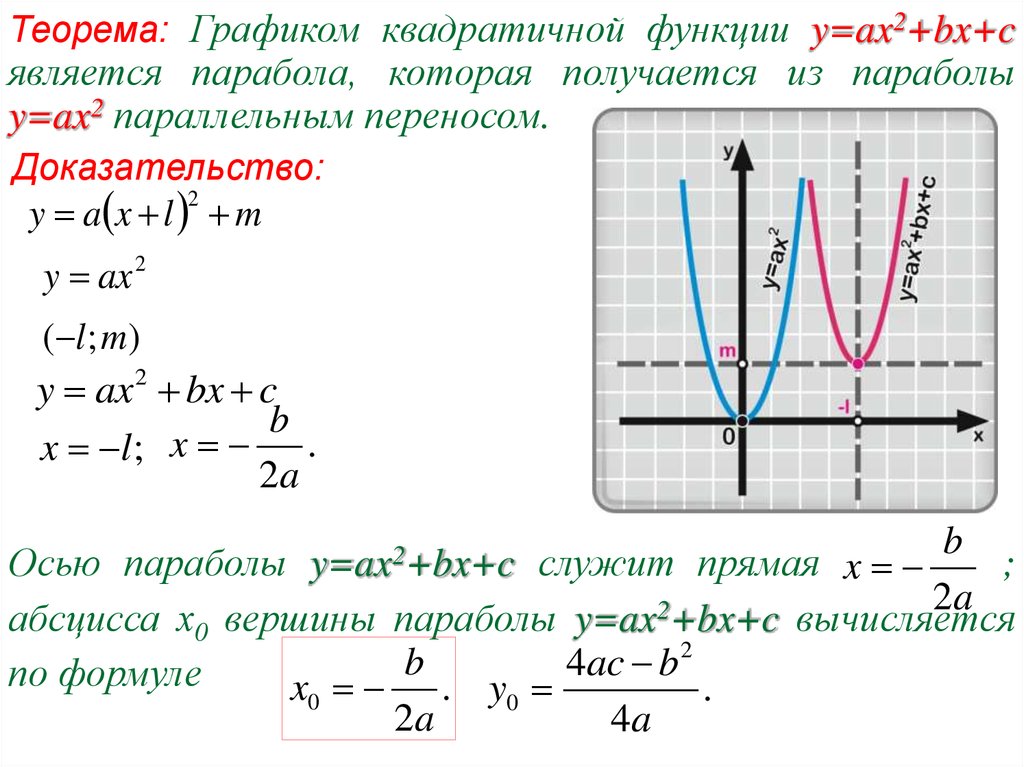 Вторую координату вершины можно найти, вычислив функцию при x = -1.
Вторую координату вершины можно найти, вычислив функцию при x = -1.
Пример 5 .
Найдите вершину графика функции f(x) = (x + 9)(х — 5).
Поскольку формула для f факторизуется, нули легко найти: -9 и 5.
Среднее значение нулей равно (-9 + 5)/2 = -4/2 = -2. Итак, линия симметрии равна x = -2, а первая координата вершины равно -2.
Вторая координата вершины: f(-2) = (-2 + 9)(-2 — 5) = 7*(-7) = -49.
Следовательно, вершина графика функции f равна (-2, -49).
Вернуться к содержанию
Приложения
Пример 6 .
Владелец ранчо имеет 600 метров забора, чтобы оградить прямоугольный загон с другим забором, разделяющим его посередине. как на схеме ниже.
Как показано на схеме, четыре горизонтальные секции забора будут иметь длину по x метров, а три каждая вертикальная секция будет иметь длину y метров.
Цель владельца ранчо — использовать весь забор и ограждать как можно большую площадь .
Каждый из двух прямоугольников имеет площадь xy, поэтому у нас есть
общая площадь: A = 2xy.
Мы мало что можем сделать с величиной А, пока она выражается как произведение двух переменных. Однако, тот факт, что у нас есть только 1200 метров забора, приводит к уравнению, которому x и y должны удовлетворять.
3у + 4х = 1200,
3г = 1200 — 4х.
г = 400 — 4x/3.
Теперь у нас есть выражение y как функция x, и мы можем подставить это выражение вместо y в формулу для общего район А.
А = 2xy = 2x (400 -4x/3).
Нам нужно найти значение x, при котором A будет как можно больше. A является квадратичной функцией x, и график открывается вниз, поэтому самая высокая точка на графике A является вершиной. Поскольку A факторизуется, самый простой способ найти вершина состоит в том, чтобы найти x-перехваты и среднее значение.
2x (400 -4x/3) = 0,
2x = 0 или 400 -4x/3 = 0.
х = 0 или 400 = 4х/3.
х = 0 или 1200 = 4х.
х = 0 или 300 = х.
Следовательно, линия симметрии графика A равна x = 150, среднее значение 0 и 300.
Теперь, когда мы знаем значение x, соответствующее наибольшей площади, мы можем найти значение y, вернувшись назад. к уравнению, связывающему x и y.
у = 400 — 4х/3 = 400 -4(150)/3 = 200.
Вернуться к содержанию
|


 3пж пж ответьте
3пж пж ответьте 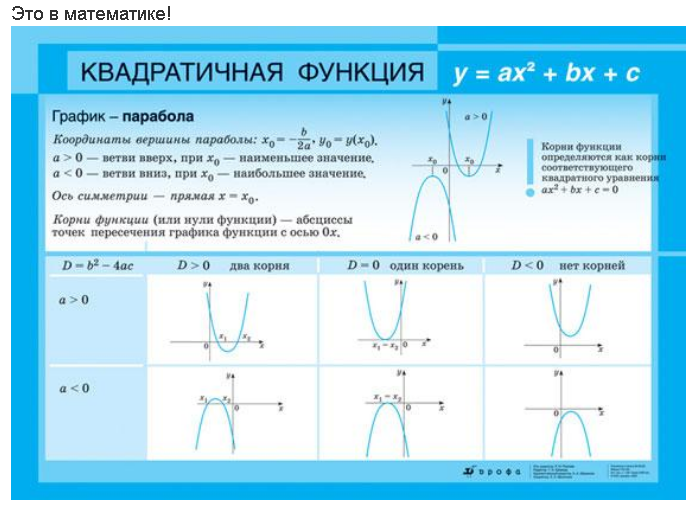
 Это означает, что для каждой точки на графике y = x 92 — 5. Начнем с графика y = x 2 , сдвинем вправо на 4 единицы, затем
5 единиц вниз.
Это означает, что для каждой точки на графике y = x 92 — 5. Начнем с графика y = x 2 , сдвинем вправо на 4 единицы, затем
5 единиц вниз.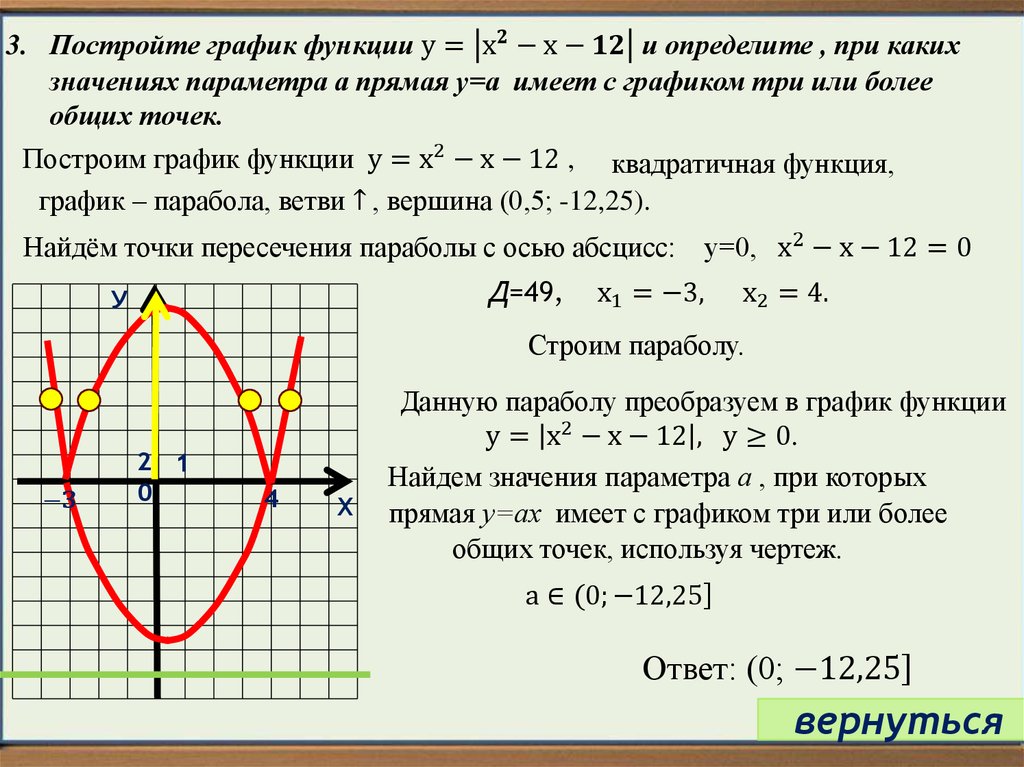 линия симметрии — вертикальная линия x = h, а вершина — точка (h,k).
линия симметрии — вертикальная линия x = h, а вершина — точка (h,k).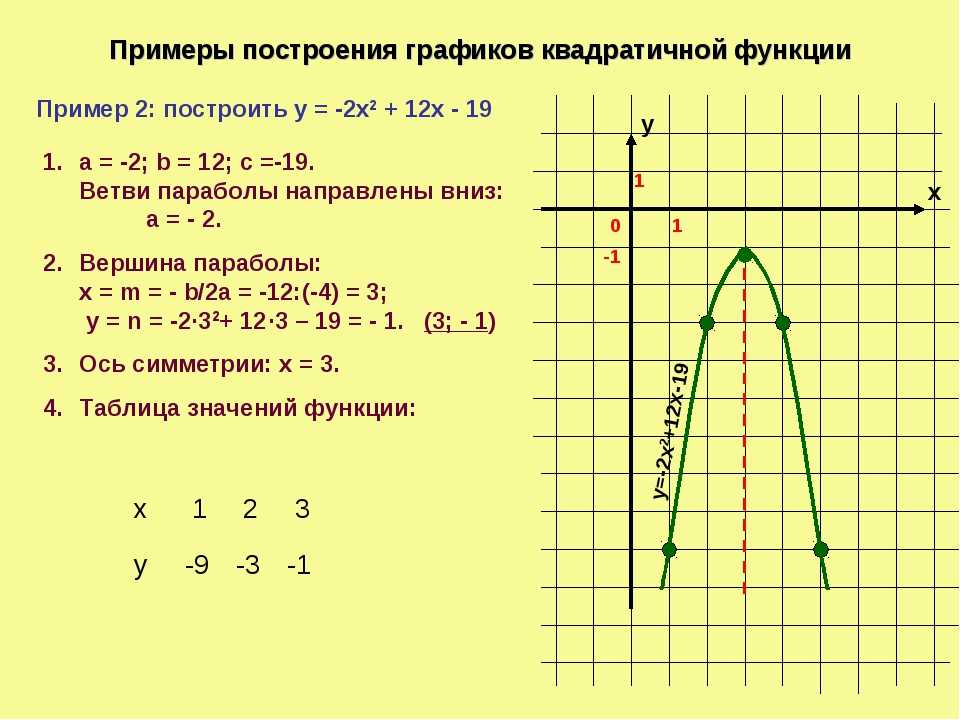
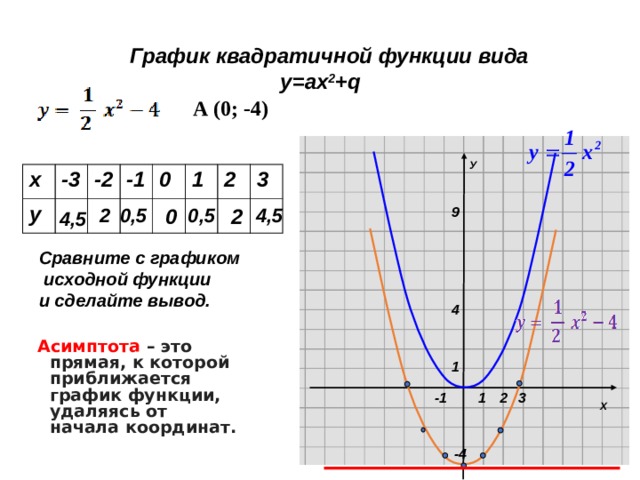
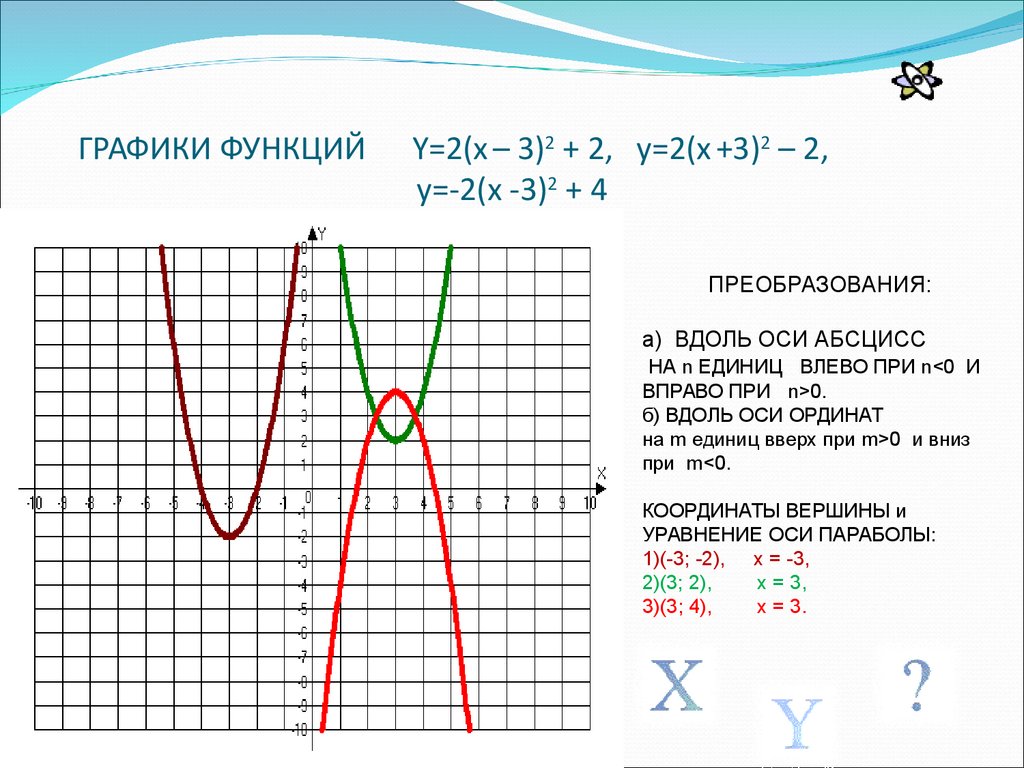
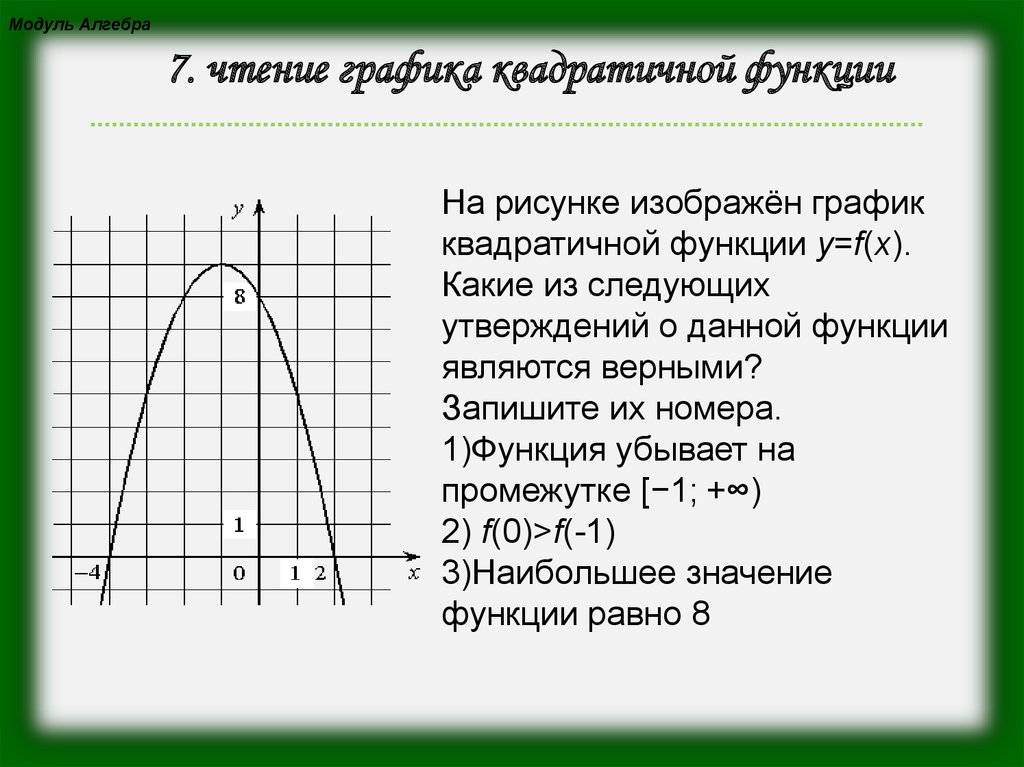
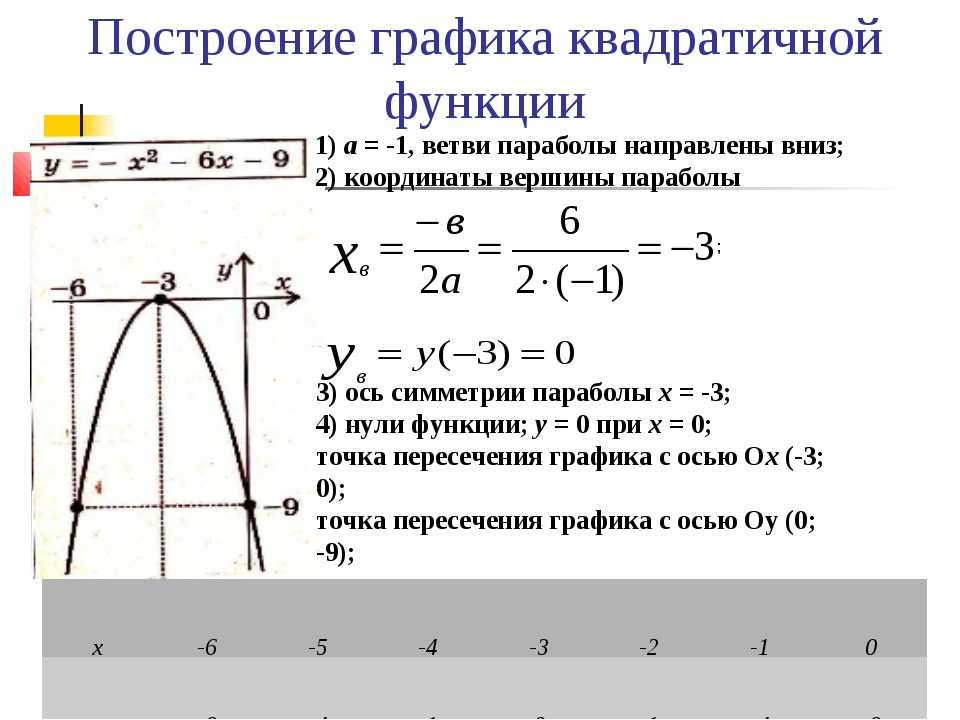
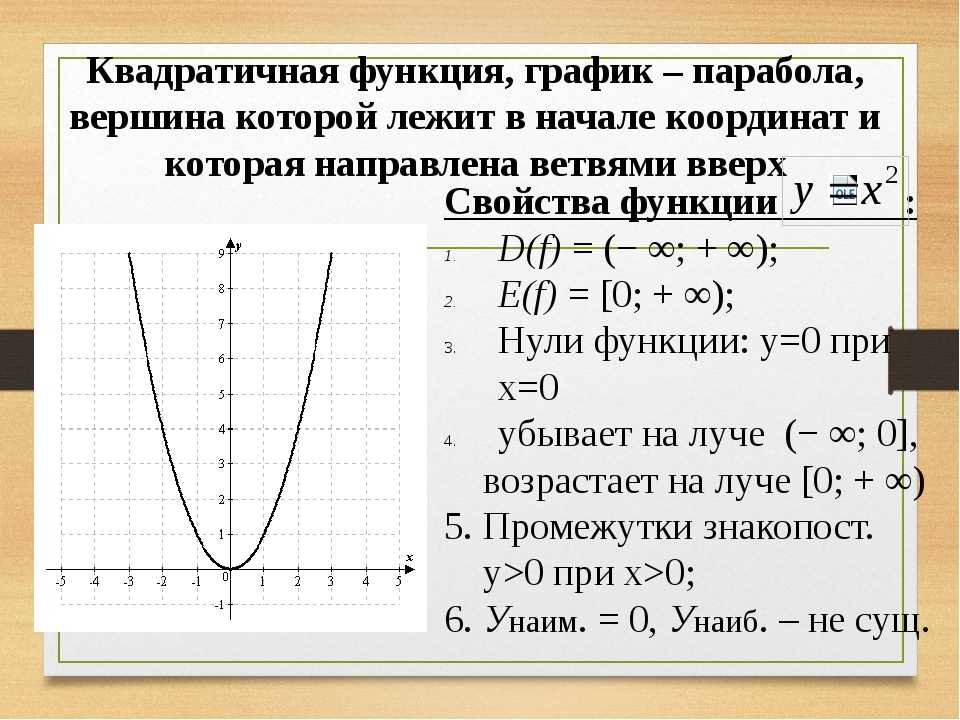
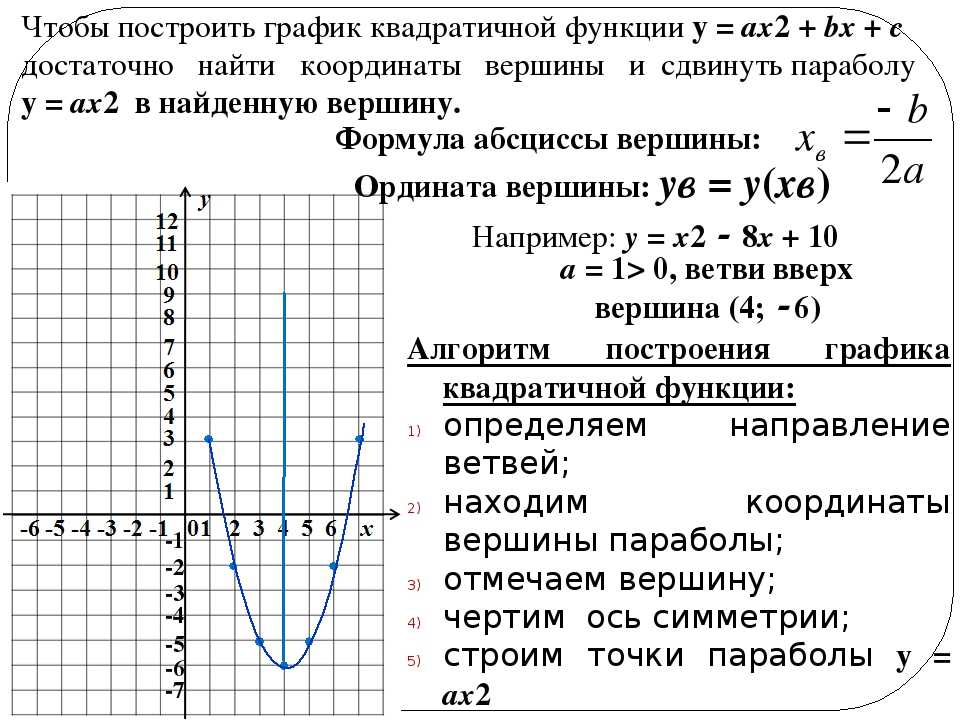 Корни также называют х — точками пересечения или нулями. Квадратичная функция графически изображается параболой с вершиной, расположенной в начале координат ниже оси x или выше оси x . Следовательно, квадратичная функция может иметь один, два или нулевые корни.
Корни также называют х — точками пересечения или нулями. Квадратичная функция графически изображается параболой с вершиной, расположенной в начале координат ниже оси x или выше оси x . Следовательно, квадратичная функция может иметь один, два или нулевые корни.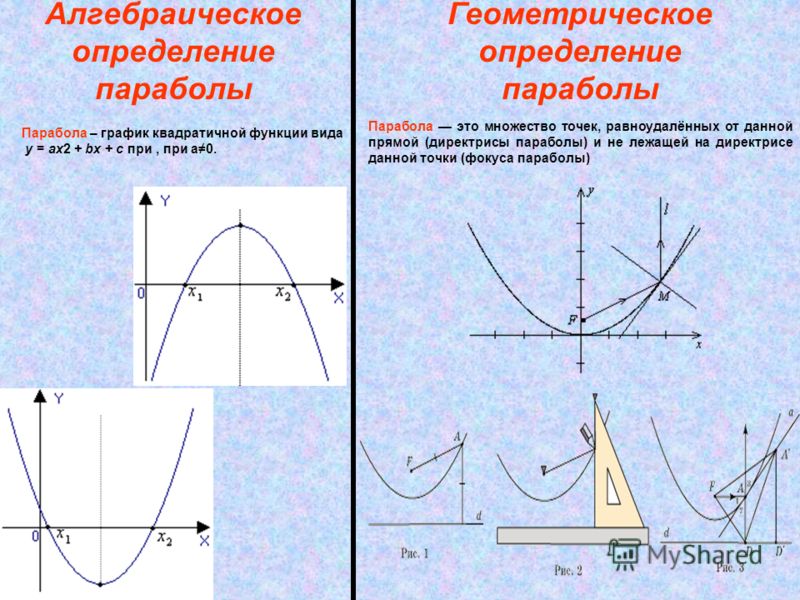
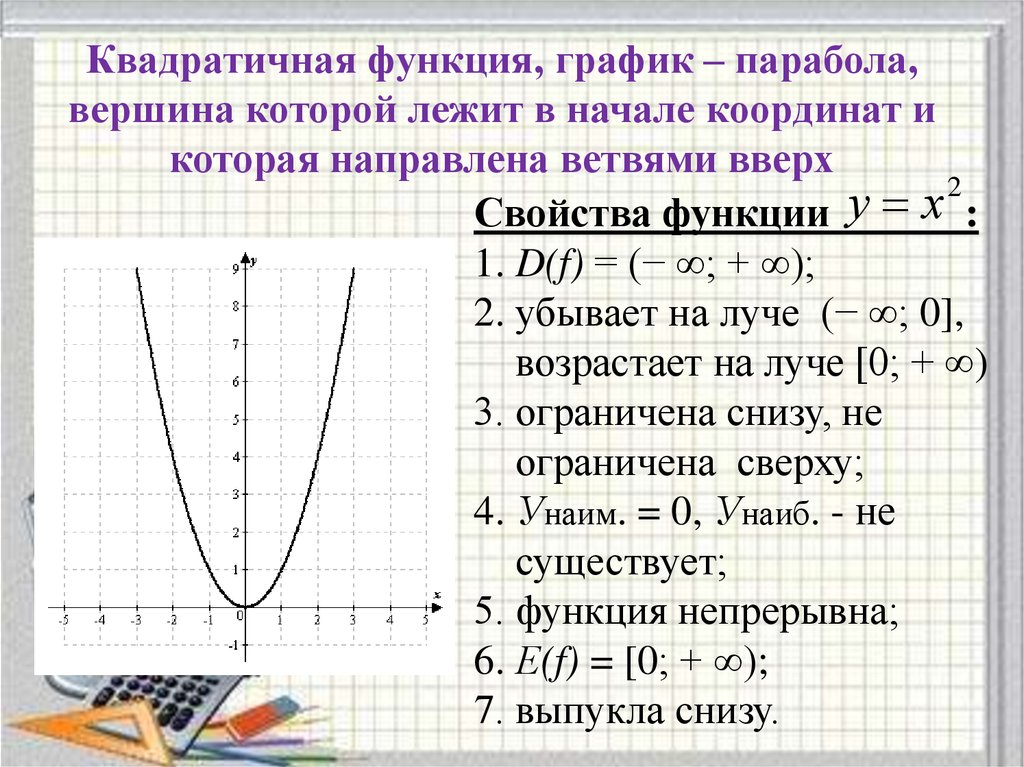
 Чтобы увидеть это, мы устанавливаем b 2 −4 ac = 0 в квадратичной формуле, чтобы получить
Чтобы увидеть это, мы устанавливаем b 2 −4 ac = 0 в квадратичной формуле, чтобы получить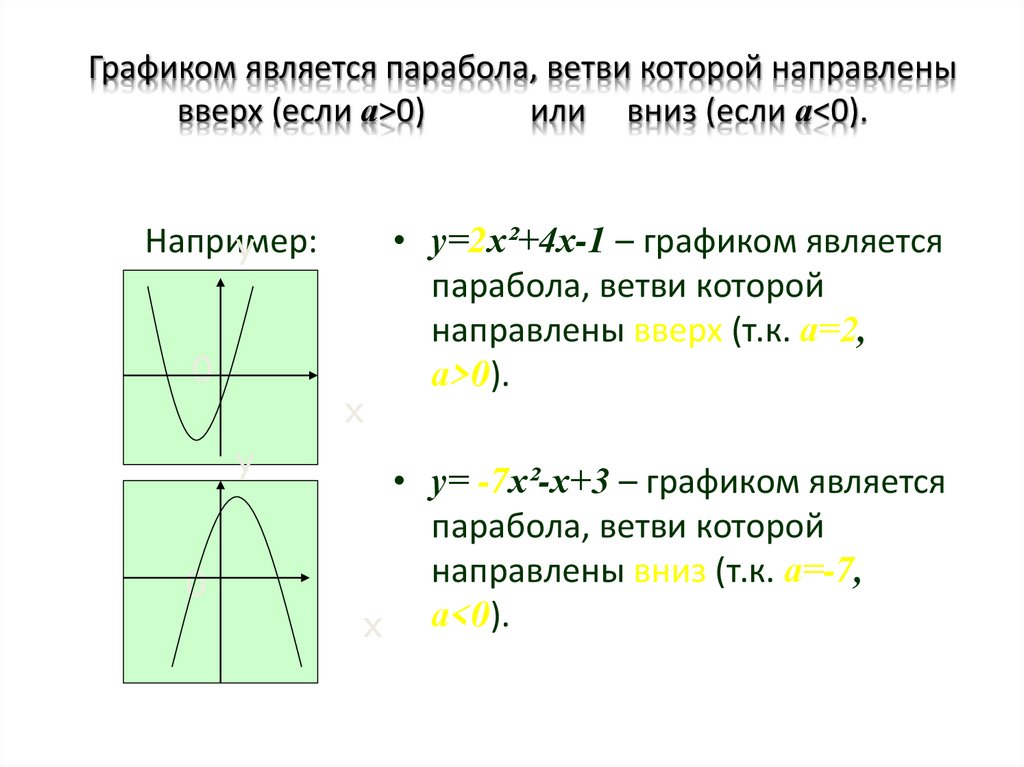 Таким образом, график пересекает ось x ровно в одной точке (т.е. имеет один корень), как показано ниже,
Таким образом, график пересекает ось x ровно в одной точке (т.е. имеет один корень), как показано ниже,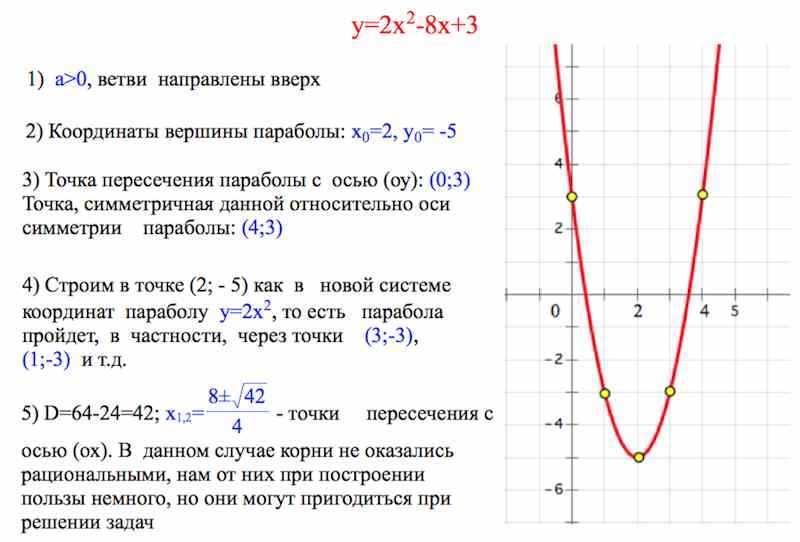
Leave A Comment