Урок алгебры в 11 классе «Преобразование иррациональных выражений «

учащиеся будут знать определение  и  свойства  корня п-й  степени для преобразования иррациональных выражений;   применять при   преобразование иррациональных выражений:  внесение множителя под знак корня,  извлечение  множителя из- под знака корня, переход от корней к степеням, избавление от иррациональности в знаменателе.

Просмотр содержимого документа
«Урок алгебры в 11 классе «Преобразование иррациональных выражений «»

Раздел

11.2.А Степени и корни. Степенная функция

Ф.И.О (при его наличии) педагога

Альжанова К.Е

Класс 11А

Количество присутствующих

Количество отсутствующих

Тема урока

Преобразование иррациональных выражений

Цели обучения в соответствии с учебной программой

11. 2.1.5. Применять свойства корня п-й степени для преобразования иррациональных выражений, знать и применять формулу сложного радикала

Цели урока

Все усвоят определение и свойства корня п-й степени для преобразования иррациональных выражений; будут применять при преобразование иррациональных выражений: внесение множителя под знак корня, извлечение множителя из под знака корня, переход от корней к степеням, избавление от иррациональности в знаменателе.

Большинство будут уметь: применять свойства корня п-й степени и формулы сокращенного умножения для преобразования иррациональных выражений, знать и применять формулу сложного радикала;

Некоторые смогут: аргументировать свое решение; наблюдать, сравнивать, обобщать, классифицировать, анализировать математические ситуации.

Ход урока

Этап урока/ Время

Действия педагога

Действия ученика

Оценивание

Ресурсы

Начало урока

2 мин

Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. Цель: организация начала урока.

Приветствие. Проверка готовности учащихся к уроку. .

чтобы хорошо работать на уроке, нужен настрой.

Начнем с задания на внимание.

Все учащиеся включаются в деловой ритм урока

Учащиеся записывают тему урока.

Презентация

Начало урока

2 мин

+

3 мин

Цель: определение «зоны ближайшего развития», актуализация опорных знаний.

Для целеполагания используется

Пробное действие.

Что знаете? Что надо узнать?

На интерактивной доске появится выражение. Спросить у учащихся что это за выражение.

Иррациональными выражениями называют выражения, содержащие операцию извлечения корня. Основные виды преобразований иррациональных выражений.

При преобразовании иррациональных выражений, как и при преобразовании любых других выражений, надо учитывать область допустимых значений (ОДЗ) и не допускать ее сужения.

С иррациональными выражениями, как и с выражениями других видов, можно проводить любые из основных тождественных преобразований:

  • раскрытие скобок

  • группировка и приведение подобных слагаемых

  • сокращение дроби

  • Применение ФСУ, свойств степени и корня

только с иррациональными выражениями следующие преобразования:

  • внесение под знак корня

  • извлечение из-под знака корня

  • избавление от иррациональности в знаменателе

  • упрощение выражений.

Упростить выражение:

Предположим, что под корнем стоит полный квадрат.

Тогда

Так как сумма квадратов не может равняться иррациональному числу, то в нашем случае сумма квадратов равна четырнадцати,

; предположим, что и проверяем

Вычислите: 

    =

       

Упростите вы­ра­же­ния: 

Упростите вы­ра­же­ния: 

Упростите вы­ра­же­ния: 

избавьтесь от иррациональности в знаменателе : 

Устно дают ответы на задания.

Записывают формулы у доски.

Самооценивание

Разноцветные стикеры (дл яделения на группы).

Маркеры, мини-доски или ламинированные листы А4.

Презентация

Цель: деятельность по формированию методов преобразования  через анализ, обработку материала, исследование, практическую работу.

Разделение на команды пары (4 – 6 учащихся) . (Возможно в группах будут по два учащегося, то есть пары (парная работа))

(Совместная, групповая, парная  деятельность)

Каждой группе предлагается четыре вида задании на преобразование иррациональных выражений несложного типа.

Время выполнения —   10 – 12 минут

Инструкция для групповой работы:

1.      Соблюдать тайм менеджмент

2.

      В группах разделится на пары (могут рассматривать также индивидуально)

3.      Вы можете разделить задания между собой

4.      Обсуждение результатов

5.      

Внимательно слушают, делают конспект.

Решают задания.

ФО тест в тестпаде

QR КОД или ссылка

https://onlinetestpad.com/5cjd2bascgzse

Решают задания у доски.

Обобщают изученный материал.

Отвечают на вопросы.

Делают вывод.

Записывают в дневники домашнее задание.

Найдите целое число, равное разности

При условии, что a242

1

Найдите значение выражения:

2

Избавьтесь от иррациональности в знаменателе:

3

Извлечь из- под знака корня: 

Вариант 1

1

Найдите значение выражения:

2

Избавьтесь от иррациональности в знаменателе:

3

Извлечь из- под знака корня: 

Вариант 1

1

Найдите значение выражения:

2

Избавьтесь от иррациональности в знаменателе:

3

Извлечь из- под знака корня: 

Вариант 1

1

Найдите значение выражения:

2

Избавьтесь от иррациональности в знаменателе:

3

Извлечь из- под знака корня: 

Вариант 1

1

Найдите значение выражения:

2

Избавьтесь от иррациональности в знаменателе:

3

Извлечь из- под знака корня: 

Вариант 1

1

Найдите значение выражения:

2

Избавьтесь от иррациональности в знаменателе:

3

Извлечь из- под знака корня: 

Вариант №2

1

Найдите значение выражения:

2

Избавьтесь от иррациональности в знаменателе:

3

Найдите целое число, равное разности

При условии, что a242

4

Вычислите:

Вариант №2

1

Найдите значение выражения:

2

Избавьтесь от иррациональности в знаменателе:

3

Найдите целое число, равное разности

При условии, что a242

4

Вычислите:

Вариант №2

1

Найдите значение выражения:

2

Избавьтесь от иррациональности в знаменателе:

3

Найдите целое число, равное разности

При условии, что a242

4

Вычислите:

Вариант №2

1

Найдите значение выражения:

2

Избавьтесь от иррациональности в знаменателе:

3

Найдите целое число, равное разности

При условии, что a242

4

Вычислите:

              

Преобразование ⭐ иррациональных выражений: формулы, примеры решения задач

Что такое иррациональные выражения

Из уроков алгебры известно, что существует несколько классов математических выражений: числовые и буквенные, одночлены и многочлены, дробные, рациональные, иррациональные и другие.

Определение 1

Иррациональными называют числовые или буквенные выражения, в которых присутствуют радикалы (корни).

Определение 2

Арифметическим корнем числа x называют такое неотрицательное число n, которое при возведении в степень m дает число x.

Формула 

xm=n ⇒ nm=x

Переменную x называют подкоренным выражением, переменную m — показателем корня, n — корнем числа x.

Как видно из определения, понятие арифметического корня и степени числа являются взаимообратными операциями.

Преобразование иррациональных выражений

Преобразование и вычисление простых иррациональных выражений не вызывает трудностей.

Пример 

25×2=5x;9·16=12;(x-5y+7)33=x-5y+7.

Более сложные выражения требует дополнительных операций и преобразований. В этом случае используют специальные тождества и формулы:

  1. Приведение подобных в подкоренном выражении. Пример: 5x+y3-x+8y33=(5x-x)+(y3+8y3)3=4x+9y33.
  2. Вынесение общего множителя в подкоренном выражении. Пример: 6x-4y2+y+9×2+3×35=3x·(2+3x+x2)-y·(4y-1)5.
  3. Операции с дробями, содержащимися в подкоренном выражении. Сюда можно отнести сложение и вычитание дробей, а также сокращение числителя и знаменателя на общий множитель. Пример: 23x-y2x2+2×6=2·2x3x·2x-y2·6×2·6+2x·x6·x=4x-6y2+2x26x2;3x3x2-3y3x-9y93=9x-9yx-9yx29x23=9x(1-y-yx)9×23=1-y-yxx3..
  4. Если выражение содержит несколько корней с одинаковыми или различными показателями корня, применяют свойства корней. Формула:xknm=xmnk;xm·xk=xm+k;xm÷xk=xm-k;xm·ym=xym;xm÷ym=xym.. Пример: 4×2+2xy6÷2xy-2×223=4×2+2xy6÷2xy-2×26=4×2+2xy2xy-2×26=2x·(2x+y)2x·(y-x)6=2x+yy-x6.
  5. Внесение общего множителя под корень. При этом вносимый множитель возводят в степень, равную показателю корня. Формула: n·xm=nm·xm.Пример:x·4y2x2-3xx2+2yx2=x·4y-6x+4y2x2=x2·(8y-6x)2×2=2×2·(4y-3x)2×2=4y-3x.
  6. Вынесение общего множителя из-под знака корня. При вынесении из множителя извлекают корень того же показателя, что и показатель общего выражения. Формула: n·xm=nm·xm. Пример: 4x2y+8x4y22x=4×2·(y+2x2y2)2x=4×2·y+2x2y22x=2x·y+2x2y22x=y+2x2y2.
  7. Замена иррационального выражения на степенное выражение. При этом показатель корня заменяют дробным показателем степени и используют свойства степени. Способ удобен, когда в подкоренном выражении находится степенное выражение. Формула: xnm=xnm.Пример:(5×2-7xy3)43·(5×2-7xy3)106=(5×2-7xy3)43+106=(5×2-7xy3)186=(5×2-7xy3)3.
Примечание 

Отметим, что при решении задач чаще используют комплексный подход, когда последовательно применяются несколько правил преобразований иррациональных выражений.

Примеры решения задач

Упражнение 1

Не используя калькулятора, найдите значение выражения: (20-5)20.

Решение:

Сначала умножим разность на общий множитель, получим:

(20-5)20=20·20-5·20.

Воспользуемся свойством корней с одинаковым показателем:

20·20-5·20=20·20-5·20=400-100.

Подкоренные выражения представляют собой квадраты чисел 20 и 10, тогда:

400-100=20-10=10.

Ответ: 10.

Упражнение 2

Не используя калькулятор, вычислить значение выражения: (6·5)26.

Решение:

Выполним преобразование и найдем значения выражения:

(6·5)26=62·(5)26=6·512·2=6·5=30.

Ответ: 30.

Упражнение 3

Выполнить преобразование выражения: 2x+63+2xy+6y3(x+3)43·x+33.

Решение:

Выполним преобразование выражения:

2x+63+2xy+6y3(x+3)43·x+33=2(x+3)2+2y(x+3)3(x+3)43+13=(x+3)·(1+2y)3(x+3)53=x+33·1+2y3(x+3)53.

Далее воспользуемся свойствами степеней:

(x+3)13-53·1+2y3=1+y(x+3)43 .

Ответ: 1+y(x+3)43.

Упражнение 4

Преобразовать выражение: 2x·5y+3xy-y24x2+24x2y3.

Решение:

Внесем множитель 2x под корень и выполним дальнейшие преобразования:

2x·5y+3xy-y24x2+24x2y3=4×2·(5y+3xy-y2)4×2+24x2y3=4×2·(5y+3xy-y2)4×2(1+6y3)=5y+3xy-y21+6y3.

Ответ: 5y+3xy-y21+6y3.

Задания для самостоятельной работы

Для закрепления материала предлагаем самостоятельно решить представленные ниже задания. Для проверки в конце каждого задания даны ответы.

Задача 1

Вычислить значение выражения: (2+12)27+24.

Ответ: 2.

Задача 2

Упростите выражение: 16x4y2+32x5y+x242x8(x+y)48.

Ответ: 1.

Задача 3

Преобразовать выражение: x22+y2·5y+6x312x-8xy2x33.

Ответ: x2+2y218.

9.2 – Подкоренные выражения и рациональные показатели

Цели обучения

  • (9.2.1) – Определение и идентификация подкоренного выражения
  • (9.2.2) — Преобразование радикалов в выражения с рациональными показателями
  • (9.2.3) — Преобразование выражений с рациональными показателями в их радикальные эквиваленты
  • (9.2.4) – Рациональные показатели, числитель которых не равен единице
  • (9.2.5) — Упрощение подкоренных выражений
    • Упрощение подкоренных выражений с помощью факторизации 9{\tfrac{1}{2}}}[/латекс].

      Не можете представить себе возведение числа в рациональную степень? К ним может быть трудно привыкнуть, но рациональные показатели могут помочь упростить некоторые задачи. {4 }}y}[/латекс] 9{\tfrac{1}{2}}}[/латекс] 10

      Давайте рассмотрим еще несколько примеров, но на этот раз с кубическими корнями. Помните, что кубирование числа возводит его в степень три. Обратите внимание, что в примерах в таблице ниже знаменатель рационального показателя степени равен 3.

      Радикальная форма

      Форма экспонента

      Основной корень

      [латекс] \sqrt[3]{8}[/латекс] 98\hspace{-0.1in} \sqrt{\,\,\,}[/латекс].

      Помните, что показатели степени относятся только к количеству непосредственно слева от них, если не используется символ группировки. Приведенный ниже пример очень похож на предыдущий с одним важным отличием — здесь нет круглых скобок! Посмотрите, что происходит.

      Гибкость

      Мы можем записывать радикалы с рациональными показателями, и, как мы увидим, упрощая более сложные радикальные выражения, это может упростить задачу. Наличие различных способов выражения и записи алгебраических выражений позволяет нам иметь гибкость при их решении и упрощении. Это похоже на тезаурус, когда вы пишете, вы хотите иметь варианты для самовыражения!

      Пример

      Запишите [латекс] \sqrt[4]{81}[/латекс] как выражение с рациональным показателем степени.

      Показать раствор

      Все числители дробных степеней в приведенных выше примерах равны 1. Вы можете использовать дробные степени, числители которых отличны от 1, для выражения корней, как показано ниже.

      93}[/латекс]

      Показать решение

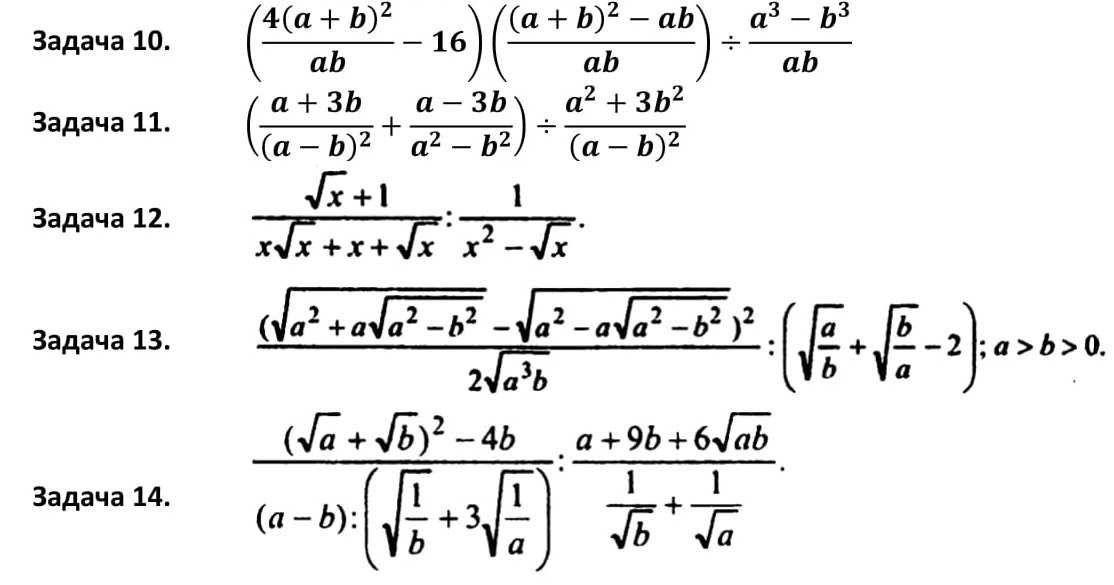      В нашем последнем примере мы перепишем выражения с рациональными показателями как радикалы. Эта практика поможет нам, когда мы будем упрощать более сложные радикальные выражения, и когда мы научимся решать радикальные уравнения. Обычно легче упростить, когда мы используем рациональные показатели степени, но это упражнение предназначено для того, чтобы помочь вам понять, как числитель и знаменатель показателя степени являются показателем степени подкоренного и индексом подкоренного. 9{\ гидроразрыва {4} {7}} [/латекс]

      Показать ответ

      В следующем видео мы покажем больше примеров написания подкоренных выражений с рациональными показателями и выражений с рациональными показателями в качестве подкоренных выражений.

      Мы будем использовать это обозначение позже, поэтому вернитесь к практике, если вы забудете, как писать радикал с рациональным показателем.

      Основные выражения — это выражения, содержащие радикалы. Радикальные выражения бывают разных форм, от простых и знакомых, таких как [латекс] \sqrt{16}[/латекс], до довольно сложных, таких как [латекс] \sqrt[3]{250{{x}^{4 }}y}[/латекс]. 9{\frac{1}{2}}}[/latex]

      А поскольку вы знаете, что возведение числа в степень [latex] \frac{1}{2}[/latex] равносильно возведению в квадрат корень этого числа, вы также можете записать его таким образом.

      [латекс] \sqrt{3x}=\sqrt{3}\cdot \sqrt{x}[/latex]

      Посмотрите на это — любое число под радикалом можно представить как произведение отдельных множителей , каждый под своим радикалом.

      Продукт, преобразованный в степенное правило или иногда называемый квадратный корень из правила продукта

      Для любых действительных чисел [латекс]а[/латекс] и [латекс]b[/латекс], [латекс] \sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex].

      Например: [латекс] \sqrt{100}=\sqrt{10}\cdot \sqrt{10}[/латекс] и [латекс] \sqrt{75}=\sqrt{25}\cdot \sqrt {3}[/latex]

      Это правило важно, потому что оно помогает вам думать об одном радикале как о произведении нескольких радикалов. Если вы можете идентифицировать правильные квадраты внутри радикала, как в случае [латекс] \sqrt{(2\cdot 2)(2\cdot 2)(3\cdot 3})[/latex], вы можете переписать выражение как произведение из нескольких идеальных квадратов: [латекс] \sqrt{{{2}^{2}}}\cdot \sqrt{{{2}^{2}}}\cdot \sqrt{{{3}^{2}} }[/латекс].

      Квадратный корень из правила произведения поможет нам упростить несовершенные корни, как показано в следующем примере.

      Упрощение подкоренных выражений с помощью разложения на множители

      Пример

      Упрощение. [латекс] \sqrt{63}[/латекс]

      Показать решение

      Окончательный ответ [латекс] 3\sqrt{7}[/латекс] может показаться немного странным, но он в упрощенной форме. Вы можете прочитать это как «три радикальных семи» или «три умножить на квадратный корень из семи».

      В следующем видеоролике показаны другие примеры упрощения квадратных корней, не имеющих идеальных квадратных корней. 9{2}}[/латекс]

      Радикальный

      Экспонента

      [латекс] \sqrt{9}[/латекс] [латекс]\влево|х\вправо|[/латекс]
      [латекс]−5[/латекс] 25 5 5
      [латекс]−2[/латекс] 4 2 2
      0 0 0 0
      6 36 6 6
      10 100 10 10 9{2}}}=4\left|xy\right|[/latex]

      Мы объединим это с квадратным корнем правила произведения в нашем следующем примере, чтобы упростить выражение с тремя переменными в подкоренной части. 2-6x+9}[/латекс].

      Показать ответ

      В следующем примере мы начнем с выражения, записанного с рациональным показателем. Вы увидите, что вы можете использовать аналогичный процесс — разложение членов на множители и сортировку по квадратам — для упрощения этого выражения.

      Вот еще один пример с идеальными квадратами.

      Упрощение кубических корней

      Мы можем использовать те же методы, которые мы использовали для упрощения квадратных корней, для упрощения корней более высокого порядка. Например, чтобы упростить кубический корень, цель состоит в том, чтобы найти множители под радикалом, которые являются идеальными кубами , чтобы вы могли извлечь их кубический корень. Нам больше не нужно беспокоиться о том, определили ли мы главный корень, поскольку теперь мы находим кубические корни. Сосредоточьтесь на поиске идентичных трио факторов по мере упрощения. 9{5}}}[/latex]

      Показать решение

      Помните, что из отрицательного выражения можно извлечь кубический корень. В следующем примере мы упростим кубический корень с отрицательным подкоренным числом.

      Вы также можете пропустить шаг разложения отрицательного числа на множители, когда освоитесь с определением кубов.

      В следующем видео мы покажем больше примеров упрощения кубических корней.

      Упрощение корней четвертой степени

      Теперь давайте перейдем к упрощению корней четвертой степени. Независимо от того, какой корень вы упрощаете, применяется одна и та же идея: найдите кубы для кубических корней, степени четырех для четвертых корней и т. д. Вспомните, что когда ваше упрощенное выражение содержит четный индексированный радикал и переменный множитель с нечетным показателем, вам нужно применить абсолютное значение.

      Упрощение подкоренных выражений с использованием рациональных показателей и законов показателей.

      Альтернативный метод разложения на множители состоит в том, чтобы переписать выражение с рациональными показателями, а затем использовать правила показателей для упрощения. Вы можете обнаружить, что предпочитаете один метод другому. В любом случае приятно иметь варианты. Мы снова покажем последний пример, используя эту идею.

      В следующем видео мы покажем еще один пример того, как упростить корень четвертой и пятой степени.

      9{4}}}}[/латекс] . В этом выражении две переменные, дробь и радикал. Давайте рассмотрим это шаг за шагом и посмотрим, может ли использование дробных показателей помочь нам упростить его.
      Мы начнем с упрощения знаменателя, так как именно здесь находится подкоренной знак. Напомним, что показатель степени в знаменателе или дроби можно переписать как отрицательный показатель степени.

      Ну, это заняло некоторое время, но вы сделали это. Вы применили свои знания о дробных показателях, отрицательных показателях и правилах показателей, чтобы упростить выражение. 9{n}}}=\влево| х \право|[/латекс]. (Абсолютное значение учитывает тот факт, что если x является отрицательным и возводится в четную степень, это число будет положительным, как и n -й главный корень этого числа.)

      ГЛАВА 1: Функции и отношения

      Уровень 110470 Глава 1: Функции и преобразования

      Ожидания

      1. Демонстрируйте понимание функций, их представления и их контакты и создания связей между Algebrebraics и создания конт. графическое представление функций с помощью преобразований;
      2. Определение нулей и максимума или минимума квадратичной функции и решение задач, связанных с квадратичными функциями, включая задачи, возникающие в реальных приложениях;
      3. Продемонстрировать понимание эквивалентности в том, что касается упрощения полиномиальных, радикальных и рациональных выражений

      6 февраля


      День 1. Повторение навыков, которые вам понадобятся на протяжении всего курса

      1 — РАЗДАТОЧНЫЙ МАТЕРИАЛ
      Скачать файл

      1 — РЕШЕНИЯ
      Скачать файл

      8 февраля


      День 2 — Функции и отношения

      2 — РАЗДАТОЧНЫЙ МАТЕРИАЛ
      Скачать файл

      2 — РЕШЕНИЯ
      Скачать файл

      1 — ДОМАШНЕЕ ЗАДАНИЕ
      Скачать файл