Диагональ правильного шестиугольника найти онлайн, формулы и примеры
Шестиугольник представляет собой геометрическую фигуру, многоугольник, который имеет шесть углов и шесть сторон.
Также существует правильный шестиугольник. Он обладает следующим свойством: все ребра и углы равны. Каждый угол составляет 120 градусов. А также он состоит из шести правильных и равных треугольников.
- Длинная диагональ правильного шестиугольника через площадь
- Котроткая диагональ правильного шестиугольника через площадь
- Длинная диагональ правильного шестиугольника через сторону
- Короткая диагональ правильного шестиугольника через сторону
Длинная диагональ через площадь
Длинной диагональю на рисунке являются отрезки ВЕ, AD и CF.
D = √((S / 3√3) * 8)
где S — площадь правильного шестиугольника.
Площадь (S):
мм²см²дм²м²
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Сторона шестиугольника равна 6 см. Тогда площадь: S = (6 * 6 * √3 * 6) / 4 = 54√3 см. D = √((54√3 / 3√3) * 8) = 12 см.
Короткая диагональ через площадь
Короткими диагоналями можно назвать BD, BF, AE или же DF. Для нахождения неизвестной стороны также,
как и в прошлой ситуации, понадобится площадь фигуры, которую возможно найти по следующей формуле:
S = (a * a * √3 * 6) / 4.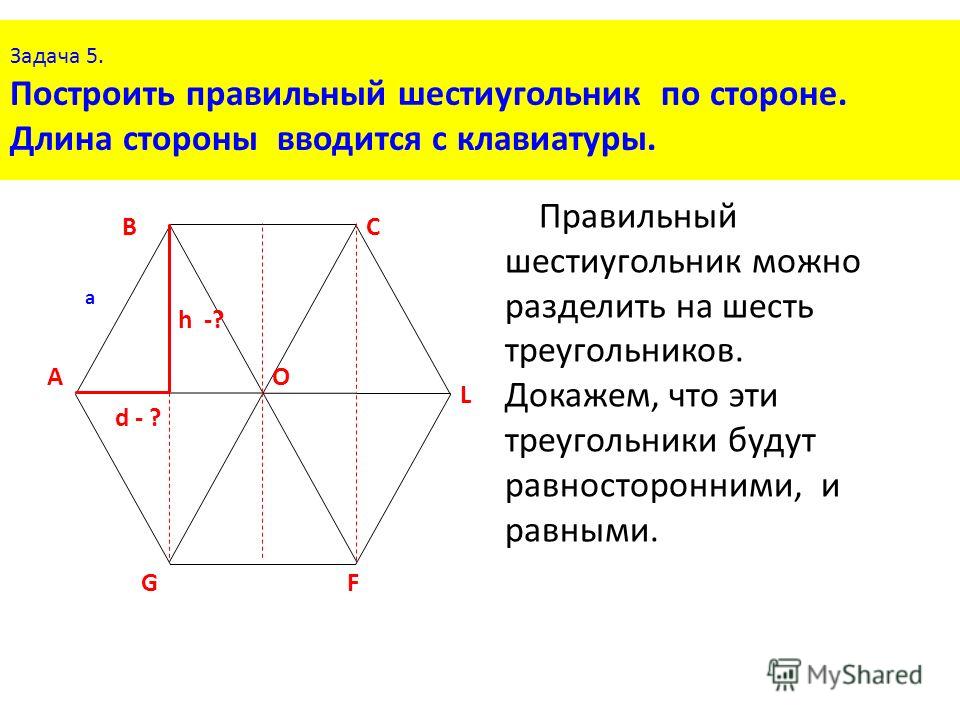 После этого найденная величина подставляется в
готовую формулу:
После этого найденная величина подставляется в
готовую формулу:
D = √((S / √3) * 2)
где S — площадь правильного многоугольника.
Площадь (S):
мм²см²дм²м²
012345678910Результат в: ммсмдмм
Пример. Как и в прошлой задаче, ребро равно 6 см. Тогда площадь правильного шестиугольника = 54√3 см. Далее можно находить и искомую диагональ: D = √((54√3 / √3) * 2) = 6√3
Длинная диагональ через сторону
Длинной диагональю на рисунке являются отрезки ВЕ, AD и CF. Длинную диагональ правильно шестиугольника можно вычислить и без нахождения площади. Для выполнения математических действий и нахождения неизвестной переменной надо знать лишь ребро многоугольника:
D = 2a
где a — сторона правильного шестиугольника.
Сторона (a):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Длинная диагональ состоит из двух сторон треугольников, прилегающих друг к другу, поэтому сторону
умножаем на 2.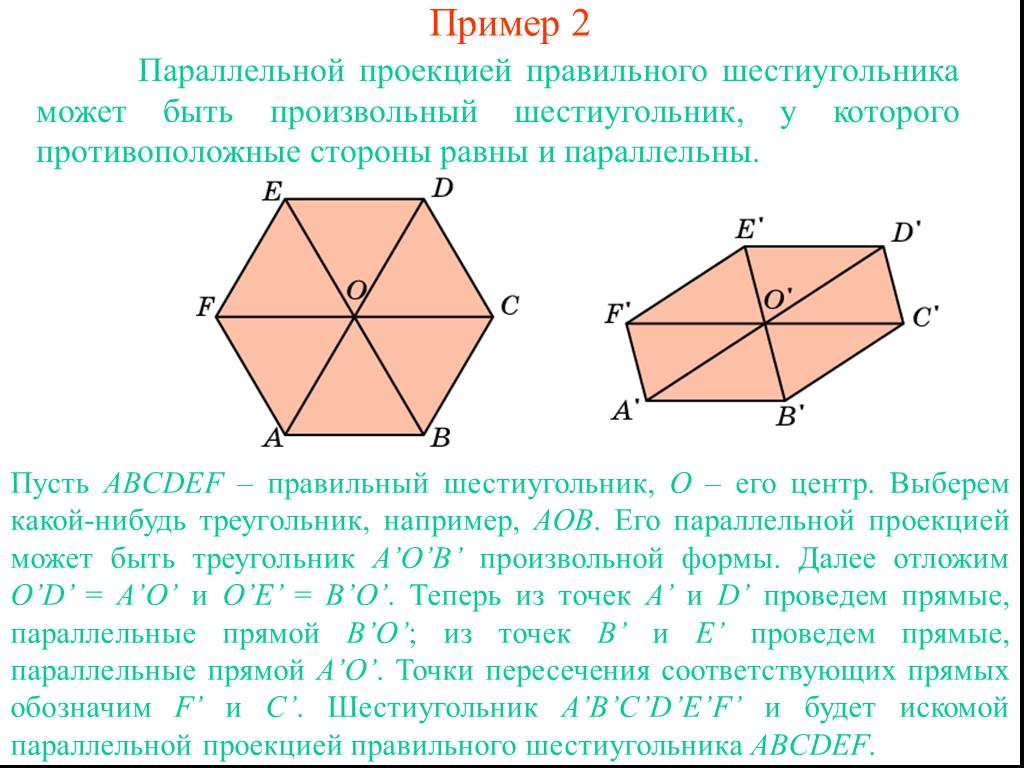
Пример. В задаче дан правильный шестиугольник. Его ребро равно 3 см. Тогда длинная диагональ равна 6 см.
Короткая диагональ через сторону
Также существует и другой способ нахождения короткой диагонали, равностороннего шестиугольника. Например, диагонали BD. Для нахождения достаточно лишь знание стороны фигуры:
D = √(3 * a * a)
где a — сторона правильного шестиугольника.
Сторона (a):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Сторона АВ равна 10 см. Тогда BD = D = √(3 * 10 * 10) = 10√3 см = 17 см.
Для более простого понимания такой темы, как вычисление диагонали правильного шестиугольника, стоит
для начала увидеть, что данный многоугольник состоит из шести равносторонних и равных между собой
треугольников.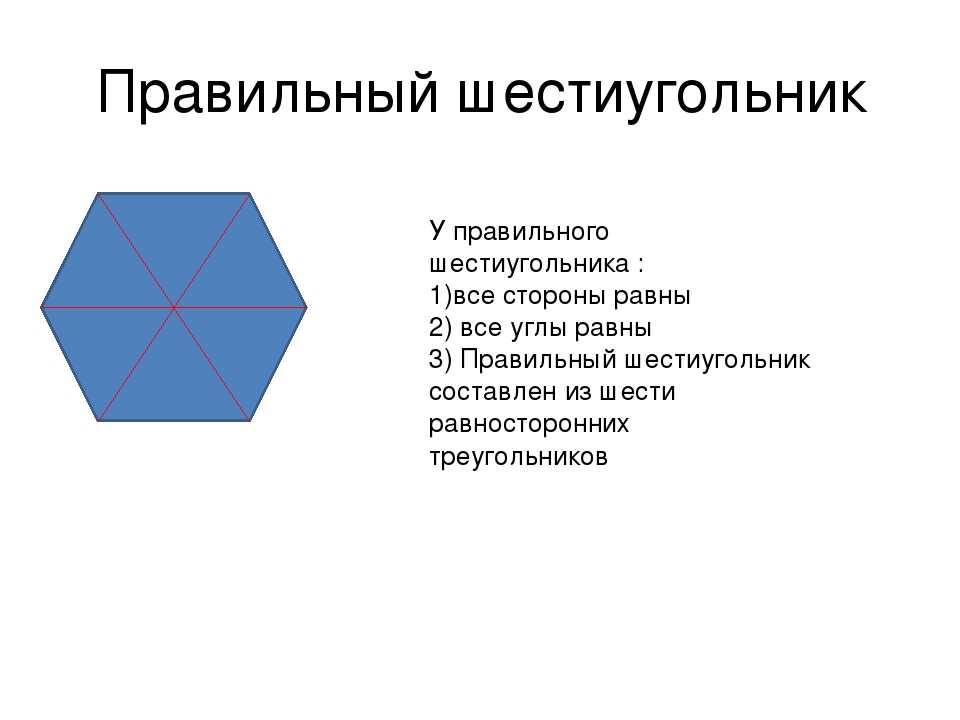
Однако существует и более сложный метод – через нахождение площади фигуры. Данную формулу запомнить просто: S = (a * a * √3) / 4 – она необходима, чтобы вычислить площадь равностороннего треугольника, где величина а является стороной. А вышеупомянутая фигура состоит из шести таких геометрических фигур, поэтому конечная формула будет выглядеть так: S = (a * a * √3 * 6) / 4
Таким образом, шестиугольник является не такой уж и сложной фигурой, как кажется на первый взгляд.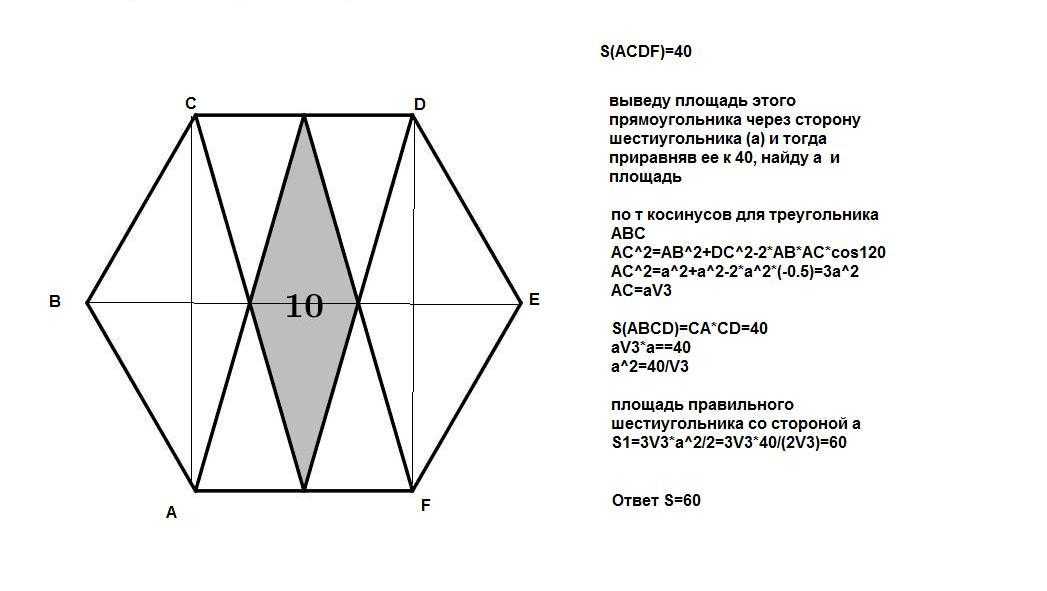 Достаточно изучить элементарные свойства и запомнить их.
Достаточно изучить элементарные свойства и запомнить их.
чему равна сторона и периметр
Содержание:
- Что такое правильный шестиугольник
- Основные свойства правильного шестиугольника
-
Нахождение радиуса вписанной окружности
- Классическая формула для нахождения радиуса вписанной окружности правильного многоугольника
- Периметр правильного шестиугольника
Содержание
- Что такое правильный шестиугольник
- Основные свойства правильного шестиугольника
-
Нахождение радиуса вписанной окружности
- Классическая формула для нахождения радиуса вписанной окружности правильного многоугольника
- Периметр правильного шестиугольника
Что такое правильный шестиугольник
Правильный шестиугольник или гексагон — выпуклый шестиугольник, у которого все стороны и углы равны.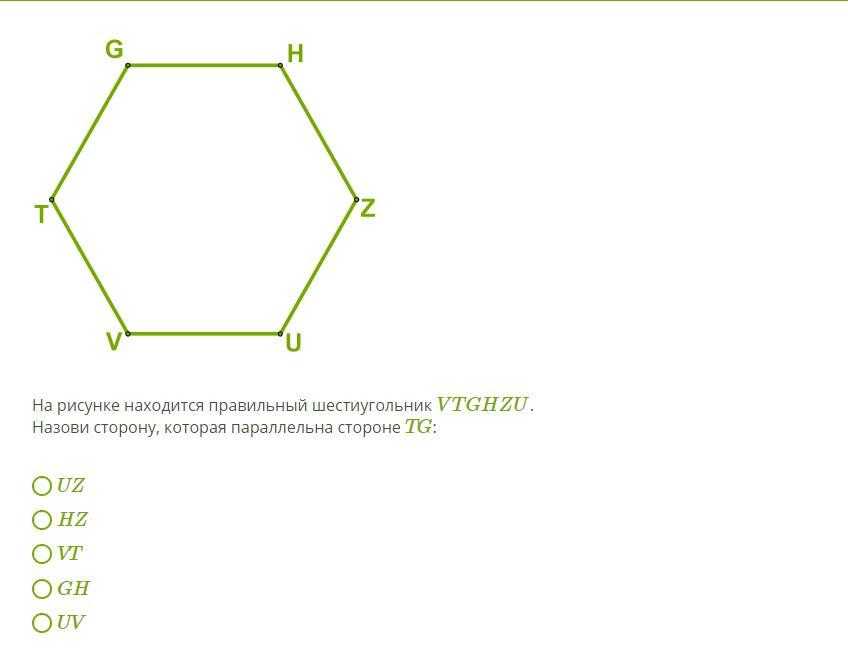
Сумма всех углов n–угольника равна 180°(n−2). Каждый угол правильного n–угольника равен \(α_n=\frac{\left(n-2\right)}n180°\). Следовательно углы правильного шестиугольника равны \(\frac{\left(6-2\right)}6180°=120°\).
Основные свойства правильного шестиугольника
- У гексагона все внутренние углы равны между собой.
- Каждый внутренний угол правильного шестиугольника равен 120°.
- Все стороны гексагона равны между собой.
- Радиус окружности, описанной около правильного шестиугольника, равен его стороне.
- Большая диагональ правильного шестиугольника равна диаметру описанной около него окружности или сумме двух его сторон.
- Меньшая диагональ правильного шестиугольника в \(\sqrt3\) раз больше его стороны.
- Меньшая диагональ правильного шестиугольника и две его противолежащие стороны перпендикулярны друг другу.
- Меньшая диагональ правильного шестиугольника равна удвоенному радиусу вписанной в него окружности.

- Правильный шестиугольник замещает плоскость, это значит заполняет ее без пробелов и наложений.
- Диагонали правильного шестиугольника пересекаются в одной точке и делят его на 6 равных равносторонних треугольников. Высота этих треугольников равна радиусу вписанной в правильный шестиугольник окружности.
- При поворотах относительно центра на угол, кратный 60°, правильный шестиугольник переходит в себя.
- Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями — прямоугольный. Гипотенузой такого треугольника является большая диагональ. Его острые углы равны 30° и 60°.
У изображенного правильного шестиугольника ∠А=∠В=∠С=∠D=∠Е=∠F=120°. Стороны равны между собой АВ=ВС=СD=DE=EF=FA. Точка О — центр пересечения диагоналей. Большая диагональ AD=2АВ. Меньшая диагональ \(СА=\sqrt3·АВ\).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления).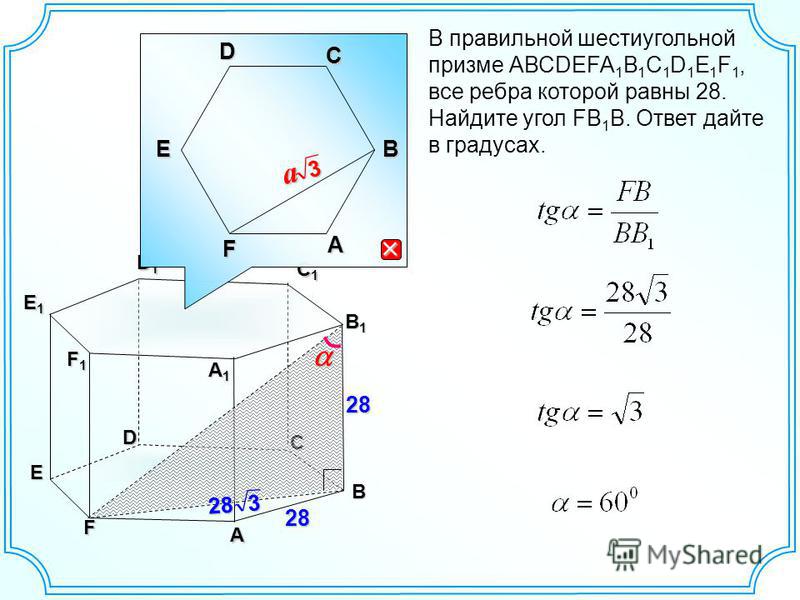 0=\frac1{\sqrt3}\), то \(r=\frac{\sqrt3}2·a\). То есть, получаем формулу, найденную выше.
0=\frac1{\sqrt3}\), то \(r=\frac{\sqrt3}2·a\). То есть, получаем формулу, найденную выше.
Периметр правильного шестиугольника
Если известен радиус вписанной окружности, то периметр правильного шестиугольника можно найти по формуле:
Формула 3
\(Р=4\sqrt3r\)
где Р — периметр правильного шестиугольника,
r — радиус вписанной в него окружности.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Диагональ шестиугольника — формула, свойства, примеры
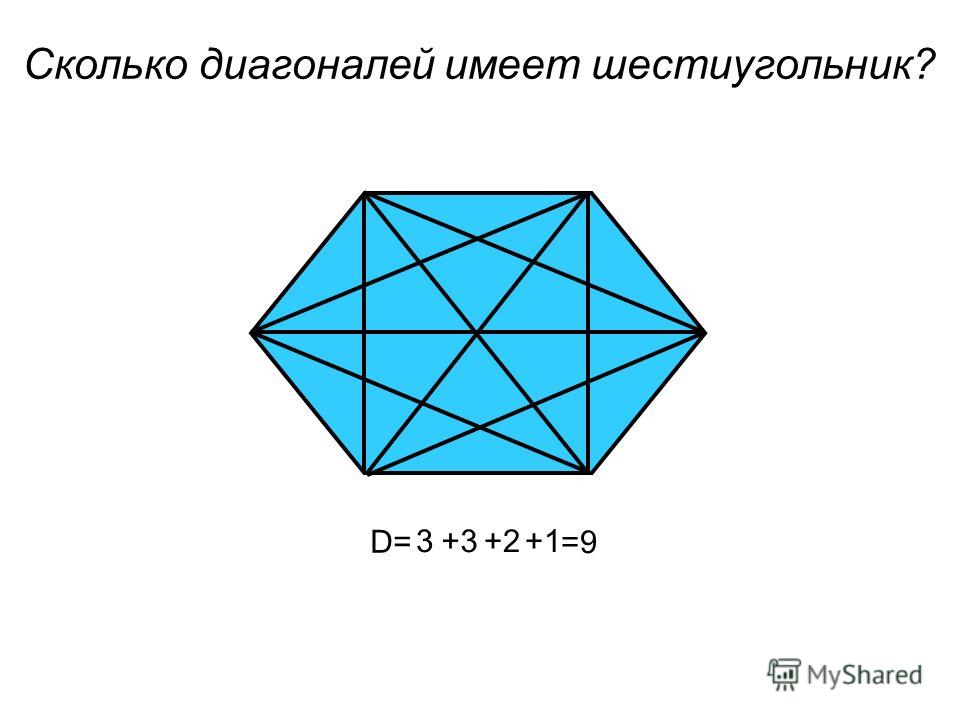
Диагонали шестиугольника строятся путем соединения любых двух несмежных вершин шестиугольника. Всего в шестиугольнике можно составить 9 диагоналей. Давайте узнаем больше о диагоналях шестиугольника на этой странице.
| 1. | Что такое диагональ шестиугольника? |
| 2. | Количество диагоналей в шестиугольнике |
| 3. | Правильные шестигранные диагонали |
| 4. | Диагональ шестиугольника Формула |
| 5. | Часто задаваемые вопросы о диагонали шестиугольника |
Что такое диагональ шестиугольника?
Диагональ шестиугольника — это отрезок, соединяющий несмежные вершины. Одна единственная вершина может образовывать 3 диагонали, а в шестиугольнике 6 вершин. Обратите внимание на рисунок, приведенный ниже, чтобы увидеть диагонали шестиугольника.
Количество диагоналей в шестиугольнике
В шестиугольнике 9 диагоналей. Если мы возьмем любые 3 последовательные вершины шестиугольника и начнем соединять их с другими несмежными вершинами, мы получим всего 9 диагоналей.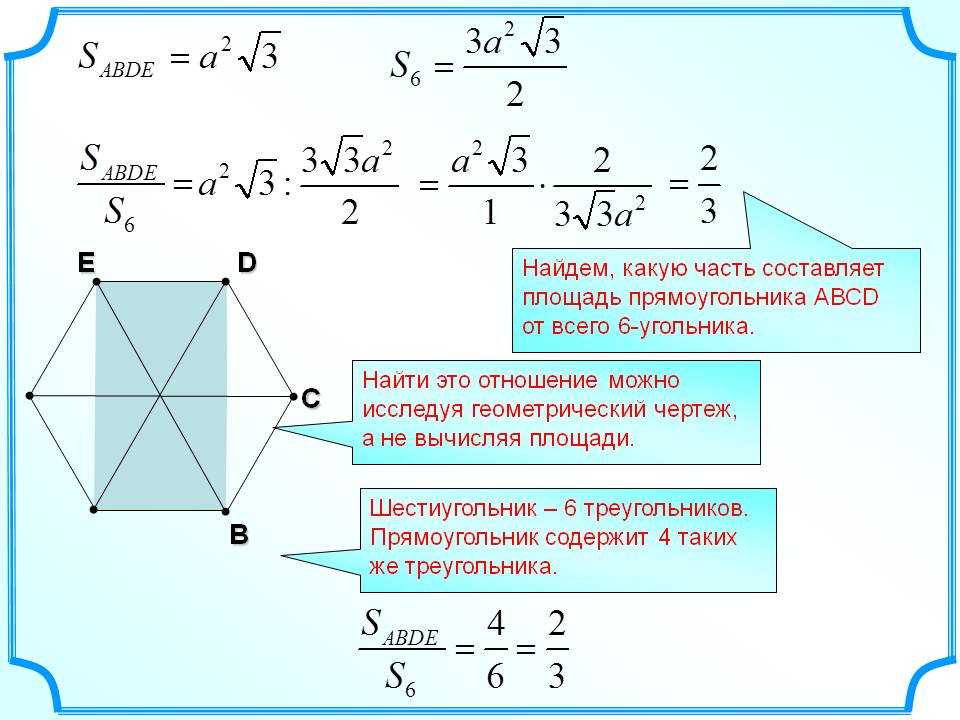 Например, на приведенном выше рисунке возьмем вершины D, E и F и соединим их с другими несмежными с ними вершинами. Это сформирует диагонали следующим образом.
Например, на приведенном выше рисунке возьмем вершины D, E и F и соединим их с другими несмежными с ними вершинами. Это сформирует диагонали следующим образом.
- Диагонали от вершины D: DF, DA, DB
- Диагонали от вершины E: EA, EB, EC
- Диагонали от вершины F: FB, FC
- Диагональное соединение вершин A и C: AC
Правильный шестигранник по диагонали
Правильный шестиугольник — это шестиугольник, у которого все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую величину. Это означает, что каждый внутренний угол правильного шестиугольника равен 120°. Теперь количество диагоналей, которые можно провести в правильном шестиугольнике, равно 9.. Их можно сформировать, соединив несмежные вершины, как показано на рисунке выше.
Диагональ шестиугольника Формула
Количество диагоналей, которые могут быть образованы в многоугольнике, можно рассчитать по формуле: Количество диагоналей в многоугольнике = 1/2 × n × (n-3), где n = количество сторон в многоугольнике.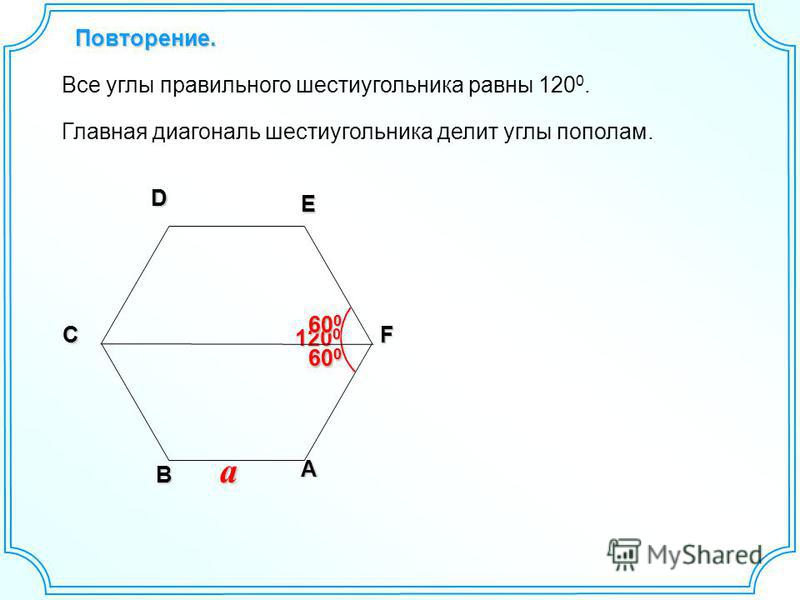 Здесь n = 6. После подстановки этого значения n = 6 в формулу получаем, Количество диагоналей в многоугольнике: 1/2 × n × (n-3) = 1/2 × 6 × (6 – 3) = 9. Следовательно, в шестиугольнике можно провести 9 диагоналей.
Здесь n = 6. После подстановки этого значения n = 6 в формулу получаем, Количество диагоналей в многоугольнике: 1/2 × n × (n-3) = 1/2 × 6 × (6 – 3) = 9. Следовательно, в шестиугольнике можно провести 9 диагоналей.
Длина диагонали шестиугольника с длиной стороны
Длину диагонали шестиугольника можно рассчитать, если известна длина стороны правильного шестиугольника. Мы знаем, что внутри правильного шестиугольника можно составить 6 равносторонних треугольников. Этот факт помогает найти длину диагонали шестиугольника, когда мы знаем одну сторону правильного шестиугольника.
Пример: Найдите длину диагонали шестиугольника, если длина стороны правильного шестиугольника равна 3 см.
Решение: Поскольку это правильный шестиугольник, мы знаем, что внутри него можно составить 6 равносторонних треугольников. Это означает, что длину диагонали можно вычислить, если известна длина стороны правильного шестиугольника. Обратите внимание на приведенный ниже рисунок, чтобы увидеть правильный шестиугольник с 6 равносторонними треугольниками.
Это означает, что диагональ будет в два раза длиннее стороны шестиугольника. Здесь длина стороны = 3 см, поэтому длина диагонали правильного шестиугольника = 2 × длина стороны = 2 × 3 = 6 см
Следовательно, длина диагонали шестиугольника равна 6 см.
☛ Статьи по теме
- Диагонали прямоугольника
- Диагональ куба Формула
- Диагональ формулы параллелограмма
- Диагональ многоугольника Формула
- Диагональ ромба
Примеры диагонали шестиугольника
Пример 1: Найдите длину диагонали шестиугольника со стороной 6 единиц.
Решение: Длину диагонали шестиугольника можно рассчитать по формуле Длина диагонали правильного шестиугольника = 2 × длина стороны. После подстановки значения длины стороны получаем, Длина диагонали правильного шестиугольника = 2 × длина стороны = 2 × 6 = 12 единиц. Следовательно, длина диагонали шестиугольника равна 12 единицам.

Пример 2: Какова длина диагонали шестиугольника, если периметр правильного шестиугольника равен 42 см?
Решение: Периметр правильного шестиугольника = 42 см. Следовательно, длина стороны шестиугольника = 42/6 = 7 см. Теперь мы можем использовать формулу Длина диагонали правильного шестиугольника = 2 × длина стороны. После подстановки значения длины стороны получаем, Длина диагонали правильного шестиугольника = 2 × длина стороны = 2 × 7 = 14 см. Следовательно, длина диагонали шестиугольника равна 14 см.
Пример 3: Укажите истинное или ложное значение.
а.) В шестиугольнике 9 диагоналей.
б.) Диагональ шестиугольника — это отрезок, соединяющий все его вершины.
Решение:
а) Верно, что в шестиугольнике 9 диагоналей.
б.) Неверно, диагональ шестиугольника — это отрезок, соединяющий несмежные вершины.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по диагонали шестиугольника
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о диагонали шестиугольника
Какие диагонали у шестиугольника?
Отрезки, соединяющие несмежные вершины шестиугольника, известны как диагоналей шестиугольника . Всего в шестиугольнике можно составить 9 диагоналей.
Что такое диагональ формулы шестиугольника?
Формула для определения количества диагоналей в шестиугольнике: Количество диагоналей в многоугольнике = 1/2 × n × (n-3), где n = количество сторон в многоугольнике. Здесь n = 6. После подстановки этого значения n = 6 в формулу получаем, Количество диагоналей в многоугольнике: 1/2 × n × (n-3) = 1/2 × 6 × (6 – 3) = 9. Следовательно, в шестиугольнике можно провести 9 диагоналей.
Какое максимальное количество различных диагоналей в шестиугольнике?
Максимальное количество различных диагоналей, которые могут быть образованы в шестиугольнике, равно 9. Они строятся путем соединения несмежных вершин.
Как найти количество диагоналей в шестиугольнике?
Чтобы найти количество диагоналей шестиугольника, можно использовать следующие методы.
- Количество диагоналей в многоугольнике = 1/2 × n × (n-3), где n = количество сторон в многоугольнике. Здесь n = 6. После подстановки этого значения n = 6 в формулу получаем, Количество диагоналей в многоугольнике: 1/2 × n × (n-3) = 1/2 × 6 × (6 – 3) = 9. Следовательно, в шестиугольнике можно провести 9 диагоналей.
- Возьмите любые 3 вершины и соедините их с другими несмежными вершинами без повторения и соедините любые оставшиеся вершины. Это также приведет к 9 диагоналей.
Как найти длину диагонали правильного шестиугольника?
Правильный шестиугольник — это тот, у которого все стороны имеют одинаковую длину и внутри него можно составить 6 равносторонних треугольников. Это означает, что длину диагонали можно вычислить, если известна длина стороны правильного шестиугольника. Например, если длина стороны правильного шестиугольника равна 7 см, найдем длину наибольшей диагонали шестиугольника. В данном случае мы знаем, что внутри правильного шестиугольника можно составить 6 равносторонних треугольников, это значит, что диагональ будет в два раза больше длины стороны шестиугольника. Здесь длина стороны = 7 см, поэтому длина диагонали = 2 × 7 = 14 см.
Это означает, что длину диагонали можно вычислить, если известна длина стороны правильного шестиугольника. Например, если длина стороны правильного шестиугольника равна 7 см, найдем длину наибольшей диагонали шестиугольника. В данном случае мы знаем, что внутри правильного шестиугольника можно составить 6 равносторонних треугольников, это значит, что диагональ будет в два раза больше длины стороны шестиугольника. Здесь длина стороны = 7 см, поэтому длина диагонали = 2 × 7 = 14 см.
Как найти диагональ шестиугольника, зная периметр?
Длину диагонали правильного шестиугольника можно вычислить, зная его периметр. Например, если периметр правильного шестиугольника равен 48 см, найдем длину его диагонали, выполнив следующие действия.
- Шаг 1: Поскольку это правильный шестиугольник, и мы знаем периметр, длину одной стороны можно рассчитать по формуле: Периметр правильного шестиугольника = 6 × сторона.
- Шаг 2: После подстановки значений в формулу получаем Периметр правильного шестиугольника = 6 × сторона.
 48 = 6 × сторона. Итак, сторона = 48/6 = 8 см.
48 = 6 × сторона. Итак, сторона = 48/6 = 8 см. - Шаг 3: Теперь, когда известна длина стороны, можно рассчитать длину диагонали, поскольку мы знаем, что внутри правильного шестиугольника можно сформировать 6 равносторонних треугольников, это означает, что длина диагонали будет в два раза больше длины стороны шестиугольника. Здесь длина стороны = 8 см, поэтому длина диагонали = 2 × 8 = 16 см.
Какова длина диагонали шестиугольника со стороной 4 единицы?
Если известна длина стороны правильного шестиугольника, то можно вычислить длину диагонали. Следует отметить, что внутри правильного шестиугольника можно составить 6 равносторонних треугольников. Это означает, что длина диагонали будет вдвое больше длины стороны шестиугольника. В этом случае длина стороны = 4 единицы, поэтому длина диагонали = 2 × 4 = 8 единиц. Следовательно, длина диагонали шестиугольника равна 8 единицам.
Скачать БЕСПЛАТНЫЕ учебные материалы
Диагональ шестиугольника
Как найти длину диагонали шестиугольника
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство по AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
Справка по математике для старших классов » Геометрия » Плоская геометрия » Шестиугольники » Как найти длину диагонали шестиугольника
Какова длина диагонали правильного шестиугольника с длиной стороны?
Возможные ответы:
Правильный ответ:
Пояснение:
Правильные шестиугольники состоят из шести равносторонних треугольников; в нашем вопросе каждый из этих треугольников имеет длину стороны 4 (см. диаграмму).
диаграмму).
Длина диагонали в два раза больше длины стороны. В этом случае ответ равен 8,9.0005
Сообщить об ошибке
Сколько диагоналей в правильном шестиугольнике?
Возможные ответы:
Правильный ответ:
Объяснение:
Диагональ — это отрезок, соединяющий две несмежные вершины многоугольника. Правильный шестиугольник имеет шесть сторон и шесть вершин. Одна вершина имеет три диагонали, поэтому шестиугольник будет иметь три диагонали, умноженные на шесть вершин, или 18 диагоналей. Разделите это число на 2, чтобы учесть повторяющиеся диагонали между двумя вершинами. Формула количества вершин в многоугольнике:
где .
Сообщить об ошибке
Сколько диагоналей в правильном шестиугольнике?
Возможные ответы:
18
10
6
3
Правильный ответ:
Объяснение:
Диагональ соединяет две непоследовательные вершины многоугольника.

 48 = 6 × сторона. Итак, сторона = 48/6 = 8 см.
48 = 6 × сторона. Итак, сторона = 48/6 = 8 см.
Leave A Comment