Сила трения Физика Касьянов 10 класс 180 – Рамблер/класс
Сила трения Физика Касьянов 10 класс 180 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Всем привет !!!!!!!!!подскажите решение, ответ:
Найдите массу стального бруска, равномерно скользящего по горизонтальной стальной поверхности под действием силы F = 20 Н.
Лучший ответ
Приветики!!!!
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
Звуковые волны Физика Касьянов 10 класс 602
Добрый день! Укажите примерные размеры источников, генерирующих инфразвуковые, звуковые и ультразвуковые волны.
ГДЗФизикаКасьянов В.А.10 класс
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
ГДЗ Тема 21 Физика 7-9 класс А.
В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Сила трения
Сила трения
|
|
|
Зная силу тяги F=157 кН при равномерном движении, найдите коэффициент качения.| Реклама на astronom-ntl.narod.ru | Закрыть [x] |
Объяснение урока: Центр тяжести однородных стержней
В этом объяснении мы узнаем, как найти центр тяжести однородных стержней.
В однородном поле массы центр тяжести является единственной точкой, из которой действует сила веса объекта. Другими словами, мы можем фактически предположить, что масса объекта сосредоточена в центре тяжести, как если бы это была частица.
Если мы поддерживаем твердое тело в его центре тяжести, то оно будет идеально сбалансировано в этой единственной точке.
В твердом теле с постоянной плотностью центр тяжести расположен в геометрическом центре тела. Однородный стержень представляет собой линейный объект с постоянной линейной плотностью, а его центр тяжести находится в его средней точке.
Как видно из приведенной выше диаграммы, однородный стержень идеально сбалансирован в своей средней точке.
Определение: Центр тяжести однородного стержня
Центр тяжести однородного стержня находится в его средней точке.
Отсюда можно считать, что масса однородного стержня сосредоточена в центре тяжести, расположенном в его середине. Другими словами, мы можем рассматривать массу однородного стержня как частицу, находящуюся в его середине. Имея дело с системой масс, включающей однородный стержень, мы можем найти центр тяжести системы, рассматривая однородный стержень как частицу и находя центр тяжести полученной системы частиц.
Вспомним формулу нахождения центра тяжести системы частиц в системе координат.
Теорема: Центр тяжести системы частиц
Центр тяжести системы частиц — это среднее положение частицы, взвешенное в соответствии с ее массой. Другими словами, для заданной массы 𝑚 с координатами (𝑥,𝑦), 𝑥- и 𝑦-координаты центра тяжести, обозначаемые COG и COG соответственно, определяются как COGCOG=∑𝑚𝑥∑𝑚,=∑𝑚𝑦∑𝑚.
В первом примере мы найдем центр тяжести однородного стержня, если сложить массы на обоих концах стержня.
Пример 1. Нахождение центра тяжести однородного стержня с присоединенными массами
𝐴𝐵 — однородный стержень длиной 4 см и массой 4 кг. Масса магнитудой 5 кг зафиксирована в точке 𝐴, а другая масса магнитудой 1 кг зафиксирована в точке 𝐵. Найдите расстояние от центра тяжести системы до 𝐴.
Ответ
Поскольку однородный стержень имеет постоянную плотность, центр тяжести однородного стержня расположен в его середине. Можно считать, что масса однородного стержня 4 кг сосредоточена в середине 𝐴𝐵, а массы величин 5 кг и 1 кг сосредоточены в 𝐴 и 𝐵 соответственно.
Используя сантиметры в качестве единицы длины и поместив точку 𝐴 в начало координат, мы можем провести координатную линию, чтобы указать положение этих масс.
Координата средней точки представляет собой среднее значение координат для 𝐴 и 𝐵, которое определяется как 0+42=2. Итак, масса однородного стержня сосредоточена в середине. Using the coordinates of all three masses, we construct the following table:
| Position | 0 | 2 | 4 |
|---|---|---|---|
| Mass | 5 kg | 4 kg | 1 kg |
Напомним, что если система частиц имеет массу 𝑚 в положении 𝑥, то положение ее центра тяжести, обозначаемое COG, определяется выражением COG=∑𝑚𝑥∑𝑚.
Другими словами, центр тяжести — это среднее значение положения каждой частицы, взвешенное с учетом ее массы. Используя нашу таблицу, построенную выше, мы можем умножить по столбцу и просуммировать произведения, чтобы получить числитель дроби:
𝑚𝑥=0×5+2×4+4×1=12⋅.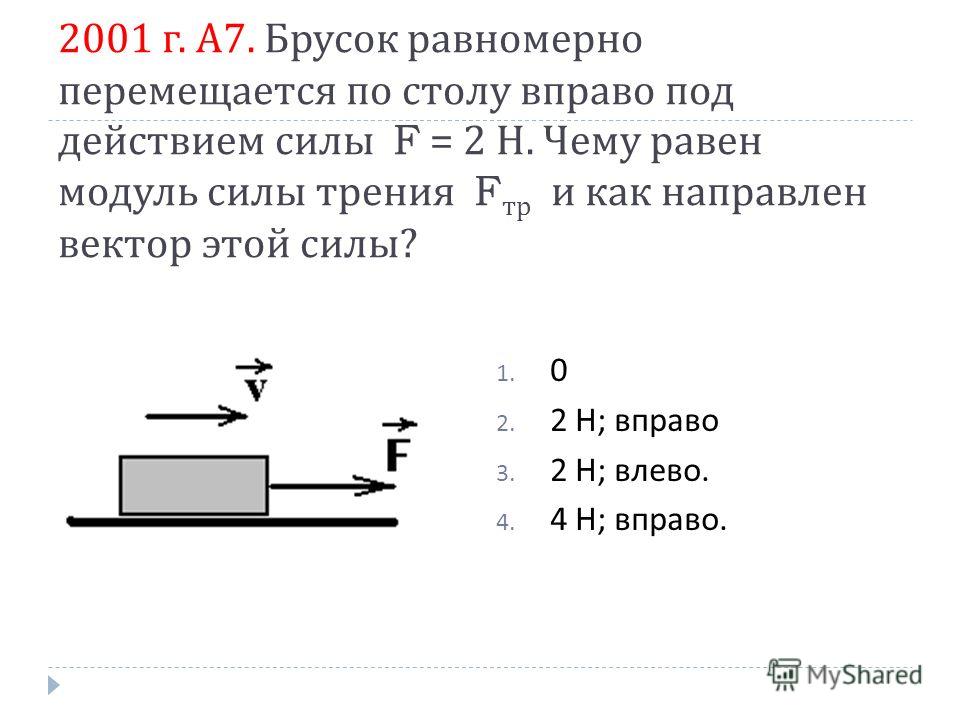
Знаменатель COG – это полная масса системы, которая получается суммированием по второй строке нашей таблицы. Следовательно, 𝑚=5+4+1=10,кг
Подставив эти значения в формулу для COG, COG=∑𝑚𝑥∑𝑚=1210=1,2.
Следовательно, координата центра тяжести равна 1,2.
Поскольку точка 𝐴 находится в начале координат, а единицей длины являются сантиметры, расстояние между точкой 𝐴 и центром тяжести составляет 1,2 см.
В предыдущем примере мы рассмотрели систему масс, состоящую из однородного стержня с двумя массами на обоих концах. Мы смогли определить центр тяжести этой системы, считая, что масса однородного стержня сосредоточена в его середине.
Мы можем использовать ту же стратегию, когда у нас есть система из нескольких одинаковых стержней. Когда несколько однородных стержней соединены вместе, они образуют твердое тело, называемое каркасом. Мы можем найти центр тяжести каркаса, считая массу каждого стержня сосредоточенной в его средней точке.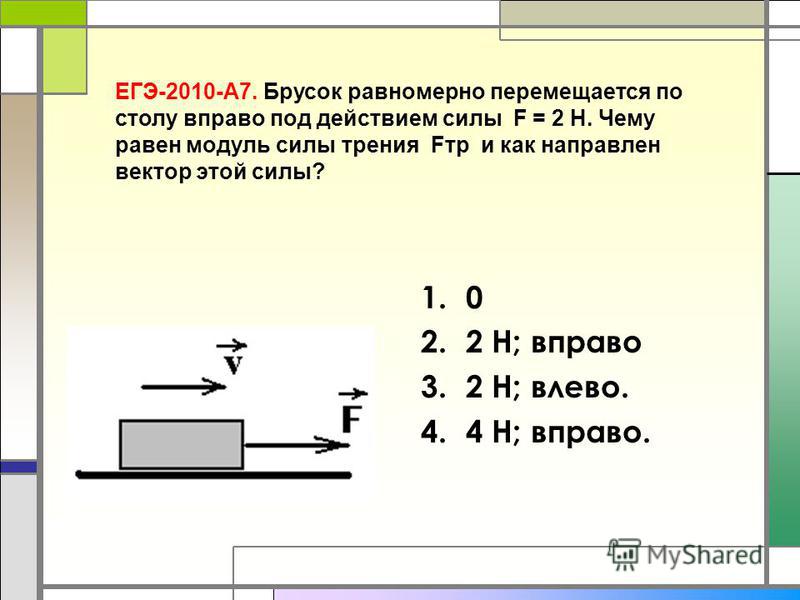
Это приводит к системе частиц, центр тяжести которых совпадает с центром тяжести каркаса.
Если каждый стержень каркаса имеет одинаковую плотность, то значение этого плотность не влияет на центр тяжести. Мы продемонстрируем это для 𝑥-координата центра тяжести, обозначаемая ЦОГ. Пусть однородные стержни каркаса имеют длину 𝐿. Обозначая линейную плотность однородного стержня 𝜌, масса 𝑚 однородного стержня равна 𝑚=𝐿×𝜌.
Подстановка этого выражения в формулу для COG приводит к COG=∑𝑚𝑥∑𝑚=∑𝐿𝜌𝑥∑𝐿𝜌=𝜌∑𝐿𝑥𝜌∑𝐑𝐑=∑𝐿𝜌∑𝐑
Заметим, что полученное выражение не зависит от линейной плотности 𝜌. Ясно, что 𝑦-координата COG также не будет зависеть от 𝜌. По этой причине плотность или точный вес однородных стержней часто в примерах не указывается. Для упрощения вычислений мы можем установить линейную плотность равной 1, чтобы масса однородного стержня определялась его длиной.
В следующем примере мы найдем центр тяжести системы однородных стержней, в частности Z-образного каркаса, расположенного в декартовой плоскости координат.
Пример 2: Нахождение координат центра тяжести однородного Z-образного провода
На рисунке показан однородный провод 𝐴𝐵𝐶𝐷 длиной 10 см, где 𝐴𝐵=𝐵𝐶=2𝐶𝐷=4см. Найдите координаты центра тяжести проволоки относительно осей 𝐵𝐴 и 𝐵𝐶.
Ответ
Напомним, что центр тяжести однородного стержня расположен в его середине. Данная система масс составлена из трех однородных стержней. Поскольку мы можем определить центр тяжести каждого стержня в его средней точке, мы можем эффективно рассматривать его как систему трех частиц, масса которых сосредоточена в трех центрах тяжести.
Поскольку однородный стержень имеет постоянное распределение массы, масса каждого стержня пропорциональна его длине. Значение плотности не влияет на расположение центра тяжести, поэтому мы можем установить линейную плотность равной 1 кг/см. Тогда масса каждого стержня определяется его длиной: массакгмассакгмассакг𝐴𝐵=4,𝐵𝐶=4,𝐶𝐷=4×12=2.
Поскольку центр тяжести каждого стержня находится в его средней точке, мы можем думать, что эти массы эффективно сосредоточены в соответствующих средних точках.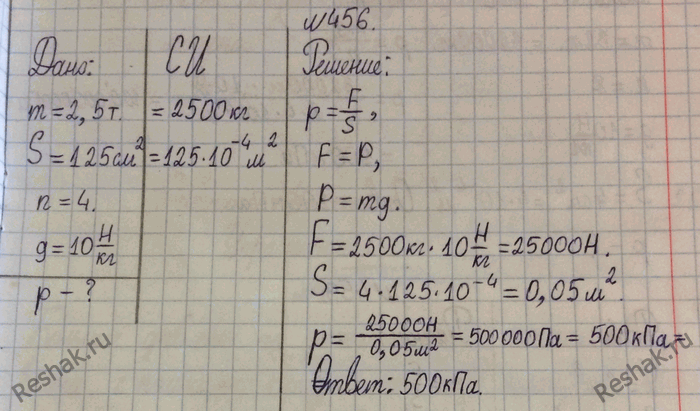
Другими словами, мы можем думать об этом каркасе как о системе частиц, расположенных в середине каждого стержня, как показано на диаграмме ниже.
Используя сантиметры в качестве единицы длины в системе координат, мы можем вычислить координаты каждой точки: 𝐴=(0,4),𝐵=(0,0),𝐶=(4,0),𝐷=(4,−2).
Координаты средней точки каждого стержня представляют собой средние значения координат соответствующих конечных точек: середина середины середины 𝐴𝐵=0,0+42=(0,2),𝐵𝐶=0+42,0=(2,0),𝐶𝐷=4,0−22=(4,−1).
Следовательно, мы можем построить таблицу координат и масс.
| Стержни | 𝐴𝐵 | 𝐵𝐶 | 𝐶𝐷 |
|---|---|---|---|
| 𝑥-Coordinate | 0 | 2 | 4 |
| 𝑦-Coordinate | 2 | 0 | −1 |
| Mass | 4 kg | 4 кг | 2 кг |
Напомним, что если система частиц имеет массу 𝑚 в положении (𝑥,𝑦), то 𝑥- и 𝑦-координаты ее центра тяжести, обозначаемые COG и COG соответственно
COGCOG=∑𝑚𝑥∑𝑚,=∑𝑚𝑦∑𝑚.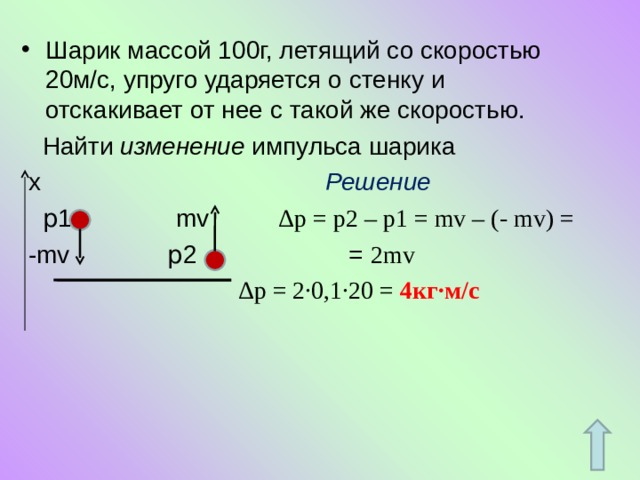
Другими словами, каждая координата центра тяжести является средним значением координаты каждой частицы, взвешенной с ее массой. Используя нашу таблицу выше, мы можем умножить каждую координату на массу в том же столбце и просуммировать произведения, чтобы получить 𝑚𝑥=0×4+2×4+4×2=16⋅,𝑚𝑦=2×4+0×4+(−1)×2=6⋅.kgcmkgcm
Знаменатель 𝑚 как в 𝑥-, так и в 𝑦-координатах — это полная масса системы, которая получается суммированием по последней строке нашей таблицы. Следовательно, 𝑚=4+4+2=10,кг
Подставив эти значения в формулу COG, COGCOG=∑𝑚𝑥∑𝑚=1610=85,=∑𝑚𝑦∑𝑚=610=35.
Отсюда координаты центра тяжести 85,35.
В следующем примере мы найдем центр тяжести системы однородных стержней на координатной плоскости, где плотности однородных стержней различны.
Пример 3. Определение координат центра тяжести неоднородной трапециевидной рамы
Тонкая стальная рама имеет форму трапеции 𝐴𝐵𝐶𝐷, в которой 𝐴𝐷=22см, 𝐶𝐷=33см, 𝐵𝐝, а =66см =𝑚∠𝐷=90∘.
Фрейм расположен в декартовой плоскости так, что 𝐴 находится в начале координат, а 𝐷 находится на оси 𝑥. Секция 𝐴𝐷 изготовлена из металла, плотность которого вдвое больше плотности металла, используемого в остальной части рамы. Определить координаты центра тяжести рамы.
Ответ
Напомним, что центр тяжести каждого однородного стержня находится в его середине. Мы можем найти центр тяжести данной системы, считая массу каждого стержня сосредоточенной в его середине. Начнем с определения массы каждого однородного стержня.
Отметим, что плотность и масса однородных стержней в данном примере не указаны. Однако нам известно, что плотность стержня 𝐴𝐷 в два раза больше плотности остальных трех стержней. Поскольку центр тяжести в системе частиц определяется относительным положением каждой частицы по отношению к ее массам, мы знаем, что точное значение плотности не влияет на центр тяжести. Следовательно, определим линейную плотность трех стержней 𝐴𝐵, 𝐵𝐶 и 𝐶𝐷 равной 1 кг/см, что означает, что плотность стержня 𝐴𝐷 равна 2 кг/см.
Это означает, что масса стержня 𝐴𝐷 вдвое больше его длины, а массы остальных трех стержней равны их длинам:
массакгмассакгмассакг𝐴𝐷=2×22=44,𝐵𝐶=66,𝐶𝐷=33.
Чтобы найти массу стержня 𝐴𝐵, нам нужно вычислить его длину. Рисуем прямоугольный треугольник с гипотенузой 𝐴𝐵.
Применяя теорему Пифагора к этому прямоугольному треугольнику, мы получаем длину 𝐴𝐵: 𝐴𝐵=√44+33=55.см
Следовательно, масса стержня 𝐴𝐵 равна 55 кг.
Используя сантиметры в качестве единицы длины, мы можем определить координаты каждой вершины на диаграмме: 𝐴=(0,0),𝐵=(−44,33),𝐶=(22,33),𝐷=(22,0).
Мы можем вычислить координаты середины каждого стержня, взяв среднее значение координат концов: середина середины середины середины середины 𝐴𝐵=0−442,0+332=−22,332,𝐵𝐶=−44+222,33=(−11,33),𝐶𝐷=22,33+02=22,332,𝐝 =22+02,0=(11,0).
Используя то, что мы уже получили, давайте составим таблицу координат и масс.
| Rods | 𝐴𝐵 | 𝐵𝐶 | 𝐶𝐷 | 𝐷𝐴 |
|---|---|---|---|---|
| 𝑥-Coordinate | −22 | −11 | 22 | 11 |
| 𝑦-Coordinate | 332 | 33 | 332 | 0 |
| Масса | 55 кг | 66 кг | 33 кг | 44 кг |
Напомним, что если система частиц имеет массу 𝑚 в положении (𝑥,𝑦), то 𝑥- и 𝑦-координаты ее центра тяжести, обозначаемые COG и COG , соответственно,
COGCOG=∑𝑚𝑥∑𝑚,=∑𝑚𝑦∑𝑚.
Другими словами, каждая координата центра тяжести является средним значением координаты каждой частицы, взвешенной с ее массой. Используя нашу таблицу выше, мы можем умножить каждую координату на массу в том же столбце и просуммировать произведения, чтобы получить 𝑚𝑥=(−22)×55+(−11)×66+22×33+11×44=−726⋅,𝑚𝑦=332×55+33×66+332×33+0×44=3630⋅ .kgcmkgcm
Знаменатель 𝑚 как в 𝑥-, так и в 𝑦-координатах представляет собой общую массу системы, которая получается путем суммирования по последней строке нашей таблицы. Следовательно, мы получаем 𝑚=55+66+33+44=198,кг
Подставляя эти значения в формулу для COG, COGCOG=∑𝑚𝑥∑𝑚=−726198=−113,=∑𝑚𝑦∑𝑚=3630198=553.
Следовательно, координаты центра тяжести равны −113 553.
В предыдущих двух примерах мы нашли координаты центра тяжести системы однородных стержней, или каркаса. Напомним, что в однородном гравитационном поле вес твердого тела представляет собой единую силу, действующую в его центре тяжести.
Поскольку каркас представляет собой твердое тело, его вес представляет собой направленную вниз силу, действующую на его центр тяжести.
Теперь предположим, что мы подвешиваем каркас к одной из его вершин. Когда эта система придет в равновесие, каркас не будет вращаться вокруг подвешенной вершины. Поскольку вес каркаса представляет собой единую силу, действующую на его центр тяжести, равновесие возможно только тогда, когда центр тяжести находится вертикально под точкой подвеса.
Теорема: вертикальная линия в каркасе, подвешенном в вершине
Когда каркас подвешен в вершине, положение равновесия возникает, когда центр тяжести находится непосредственно под подвесной вершиной.
Другими словами, мы можем получить вертикальную линию системы в состоянии равновесия, соединив подвешенную вершину и центр тяжести. Мы всегда можем определить вертикаль, используя этот подход, пока центр тяжести не находится в подвешенной вершине. Мы не можем использовать этот метод, когда центр тяжести совпадает с подвешенной вершиной, так как твердое тело, подвешенное в своем центре тяжести, находится в равновесии в любом заданном положении.
Другими словами, если подвешенная вершина находится в центре тяжести, то вертикальное направление не определено четко, поскольку любое направление является возможным вертикальным направлением в состоянии равновесия.
В нашем следующем примере мы найдем центр тяжести U-образного каркаса и с его помощью найдем угол между вертикалью и одним из стержней, угол наклона, в его положении равновесия.
Пример 4. Нахождение угла между однородным U-образным проводом и вертикалью, когда он свободно подвешен
На рисунке показан однородный провод 𝐴𝐷. Он был согнут в 𝐵 и 𝐶, чтобы образовать прямые углы. Провод был свободно подвешен к 𝐴. Найдите угол наклона от 𝐴𝐵 к вертикали, когда тело висит в положении равновесия. Округлите ответ до ближайшей минуты.
Ответ
Напомним, что в твердом теле под действием однородного гравитационного поля
вес – это сила, действующая в центре тяжести твердого тела. Если твердое тело подвешено в точке, то положение равновесия
возможно, когда центр тяжести находится непосредственно под точкой подвеса.
Следовательно, мы можем идентифицировать вертикаль в равновесии, соединив
точка подвеса и центр тяжести твердого тела.
Поскольку данный провод является твердым телом, начнем с определения его центра тяжести. Эту проволоку можно рассматривать как систему из трех однородных стержней 𝐴𝐵, 𝐵𝐶 и 𝐶𝐷. Чтобы определить центр тяжести, мы предполагаем, что масса каждого стержня сосредоточена в его центре тяжести, который находится в его средней точке. Затем мы можем найти центр тяжести получившейся трехчастичной системы.
Напомним, что если система однородных стержней имеет постоянную плотность, то значение плотности не влияет на центр тяжести. Определив линейную плотность проволоки равной 1 кг/см, можно считать, что масса каждого стержня равна его длине в килограммах. Поместим проволоку в систему координат и обозначим массы и центры тяжести однородных стержней.
Используя сантиметры в качестве единицы длины, мы можем определить координаты каждой точки:
𝐴=(0,49),𝐵=(0,0),𝐶=(36,0),𝐷=(36,21).
Тогда координаты середины каждого стержня являются средним значением координат его концов: середина середины средней точки
Давайте организуем эту информацию в таблицу координат и масс.
| Стержни | 𝐴𝐵 | 𝐵𝐶 | 𝐶𝐷 |
|---|---|---|---|
| 𝑥-координат | 0 | 18 | 36 |
| 492 | 0 | 212 | |
| МАСС | 49 кг | 36 кг | 21 кг |
, мы запоминаем, что в том, что в Систей , то 𝑥- и 𝑦-координаты его центра тяжести, обозначаемые COG и COG соответственно, определяются как COGCOG=∑𝑚𝑥∑𝑚,=∑𝑚𝑦∑𝑚.
Используя нашу таблицу выше, мы можем умножить каждую координату на массу в том же столбце и просуммировать произведения, чтобы получить 𝑚𝑥=0×49+18×36+36×21=1404⋅,𝑚𝑦=492×49+0×36+212×21=1421⋅.kgcmkgcm
Знаменатель 𝑚 как в 𝑥-, так и в 𝑦-координатах — полная масса системы, которая получается суммированием по последней строке нашей таблицы.
Следовательно, мы получаем
𝑚=49+36+21=106.кг
Подставляя эти значения в формулу для COG, COGCOG=∑𝑚𝑥∑𝑚=1404106,=∑𝑚𝑦∑𝑚=1421106.
Следовательно, координаты центра тяжести 1404106,1421106. Линия, соединяющая висячую вершину 𝐴(0,49) и 1404106,1421106 образует вертикаль в положении равновесия. Теперь мы готовы найти угол наклона между вертикалью и 𝐴𝐵.
Чтобы найти угол наклона, обозначенный 𝜃, мы рисуем прямоугольный треугольник, добавляя перпендикулярный фут из центра тяжести к оси 𝑦.
Длины обеих сторон 𝑎 и 𝑏 можно получить из координат точки 𝐴 и центра тяжести: 𝑎=49−1421106=35,745…, 𝑏=1404106=13,245….
Применяя тригонометрию прямоугольного треугольника, мы получаем угол наклона 𝜃=13,245…35,753…=20,4111….tan∘
Поскольку 1=60′∘, мы можем преобразовать десятичную часть градуса в ближайшую минуту с помощью
0,4111…×60=24,667…′,
что составляет 25′ с точностью до минуты. Следовательно, мера угла наклона от 𝐴𝐵 к вертикали, когда тело находится в равновесии, составляет 2025′∘.
В нашем последнем примере. мы найдем центр тяжести каркаса, когда нам дадут информацию о положении в равновесии.
Пример 5. Нахождение центра тяжести свободно подвешенного изогнутого стержня в состоянии равновесия
Однородный стержень 𝐴𝐵𝐶 длиной 46 см был согнут в середине 𝐵, а затем свободно подвешен к 𝐴. Учитывая, что 𝐵𝐶 горизонтально, когда стержень висит в положении равновесия, определите расстояние между центром тяжести стержня и 𝐴.
Ответ
Напомним, что в однородном гравитационном поле центром тяжести является точка, на которую действует вес твердого тела. Поскольку изогнутый стержень является твердым телом, центр тяжести должен находиться непосредственно под точкой подвеса 𝐴 в состоянии равновесия.
Изогнутый стержень можно рассматривать как систему двух однородных стержней, соединенных в точке 𝐵. Каждый однородный стержень 𝐴𝐵 и 𝐵𝐶 имеет длину 462=23см. Так как длины обоих однородных стержней одинаковы, то должны быть одинаковы и их массы.
Поскольку плотность однородного стержня постоянна, центр тяжести однородного стержня находится в его середине. Таким образом, мы можем считать, что массы двух стержней сосредоточены в их средних точках.
Это приводит к системе из двух частиц. Поскольку оба стержня имеют одинаковую массу, две частицы имеют одинаковую массу. Мы хотим найти центр тяжести этой системы. Предположим, что масса каждого стержня равна 𝑀 кг, а расстояние между двумя центрами тяжести равно 𝐿 см. Мы можем провести координатную линию через эти две точки с одной из них в начале координат.
Напомним, что если система частиц имеет массу 𝑚 в позиции 𝑥, то позиция его центра тяжести, обозначаемого COG, определяется выражением COG=∑𝑚𝑥∑𝑚.
В этой системе массы обеих частиц равны 𝑀 кг, а координаты масс равны 0 и 𝐿. Следовательно, COG=∑𝑚𝑥∑𝑚=𝑀×0+𝑀×𝐿𝑀+𝑀=𝑀𝐿2𝑀=𝐿2.
Координата центра тяжести 𝐿2,
которая является серединой отрезка, соединяющего два центра тяжести. Добавим центр тяжести системы на нашу диаграмму.
Поскольку зеленая точка на приведенной выше диаграмме является центром тяжести изогнутого стержня, а стержень подвешен к точке 𝐴, линия, соединяющая точку 𝐴 и центр тяжести, должна быть вертикалью в положении равновесия. Поскольку известно, что 𝐵𝐶 в состоянии равновесия горизонтальна, эти две прямые должны пересекаться перпендикулярно. Добавим на диаграмму вертикаль и обозначим все точки пересечения.
На приведенной выше диаграмме расстояние между 𝐴 и центром тяжести определяется длиной 𝐴𝐸. Чтобы найти эту длину, мы будем использовать подобные и конгруэнтные треугольники. Для этого мы сначала добавляем перпендикулярные футы из точки 𝐷 к вертикали 𝐴𝐹 и горизонтали 𝐵𝐶 и обозначаем новые точки пересечения.
Ищем длину 𝐴𝐸, которая является суммой длин 𝐴𝐻 и 𝐻𝐸.
Начнем с того, что заметим, что прямоугольные треугольники 𝐴𝐻𝐷 и 𝐴𝐹𝐵 подобны, а это означает, что отношение их сторон постоянно. Поскольку 𝐴𝐵 двойное 𝐴𝐷, мы должны иметь это 𝐴𝐻=12𝐴𝐹.
Длину 𝐴𝐹 можно получить, применив теорему Пифагора к прямоугольному треугольнику 𝐴𝐹𝐵.
Мы знаем, что гипотенуза этого прямоугольного треугольника равна 23 см, поэтому нам нужно найти длину его основания 𝐵𝐹.
Чтобы найти длину 𝐵𝐹, нам нужно заметить, что точки 𝐼 и 𝐹 пересекают линию 𝐵𝐺 пополам. Мы можем убедиться в этом, заметив, что треугольники 𝐴𝐻𝐷 и 𝐷𝐼𝐵 равны, что дает 𝐷𝐻=𝐵𝐼. Кроме того, поскольку 𝐷𝐻 и 𝐼𝐹 являются противоположными сторонами прямоугольника 𝐷𝐻𝐹𝐼, 𝐷𝐻=𝐼𝐹. Наконец, поскольку треугольники 𝐷𝐻𝐸 и 𝐺𝐹𝐸 равны, длины 𝐷𝐻 и 𝐹𝐺 равны. Следовательно, мы получили 𝐷𝐻=𝐵𝐼,𝐷𝐻=𝐼𝐹,𝐷𝐻=𝐹𝐺.
Это приводит к тому, что 𝐵𝐼=𝐼𝐹=𝐹𝐺, а значит, 𝐼 и 𝐹 пересекают линию 𝐵𝐺 пополам. Поскольку 𝐺 является серединой линии 𝐵𝐶 и 𝐵𝐶=23 см, мы знаем, что 𝐵𝐺=232: 𝐵𝐹=𝐵𝐼+𝐼𝐹=13𝐵𝐺+13𝐵𝐺=23𝐵𝐺=23×232=233.
Тогда, применяя теорему Пифагора, получаем 𝐴𝐹=√𝐴𝐵−𝐵𝐹=23−233=46√23.
Это приводит к 𝐴𝐻=12𝐴𝐹=23√23.
Далее найдем длину 𝐻𝐸. По конгруэнтности треугольников 𝐷𝐻𝐸 и 𝐺𝐹𝐸 длина 𝐻𝐸 равна длине 𝐸𝐹. С другой стороны, треугольник 𝐺𝐸𝐹 подобен треугольнику 𝐺𝐷𝐼, поэтому отношения соответствующих сторон должны быть постоянными.
Поскольку длина стороны 𝐺𝐷 в два раза больше длины 𝐺𝐸, длина 𝐷𝐼 должна быть в два раза больше 𝐸𝐹. Следовательно,
𝐻𝐸=12𝐷𝐼.
Мы можем найти длину 𝐷𝐼, применив теорему Пифагора к треугольнику 𝐷𝐼𝐵. Гипотенуза 𝐷𝐵 составляет половину длины 𝐴𝐵. Тогда 𝐷𝐵=232см. Также мы знаем, что длина основания 𝐵𝐼 составляет треть длины 𝐵𝐺. Итак, 𝐵𝐼=236. Применяя теорему Пифагора, 𝐷𝐼=√𝐷𝐵−𝐵𝐼=232−236=23√23.
Подставляя это выше, мы получаем 𝐻𝐸=12𝐷𝐼=23√26.
Наконец, сложив две длины, мы получим длину 𝐴𝐸: 𝐴𝐸=𝐴𝐻+𝐻𝐸=23√23+23√26=23√22.
Следовательно, расстояние от точки 𝐴 до центра тяжести 𝐸 равно 23√22 см.
Давайте закончим повторением нескольких важных понятий из этого объяснения.
Ключевые точки
- Центр тяжести однородного стержня находится в его средней точке.
- Чтобы найти центр тяжести системы масс, состоящей из однородных стержней и частиц, можно считать, что масса каждого однородного стержня сосредоточена в его средней точке.
- Твердое тело, состоящее из нескольких однородных стержней, называется каркасом.
Leave A Comment