Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Привет!
Сейчас я расскажу тебе ВСЕ о призме. Без воды. Только то, что нужно.
Помни о своей цели! Тебе нужно подготовиться к ЕГЭ по математике так чтобы поступить в ВУЗ мечты!
Это самый лучший материал в инете.
Не веришь?
Посмотри отзывы внизу статьи и ты все поймешь… И, кстати, можешь оставить свои.
Ладно, хватит болтать — к делу!
СОДЕРЖАНИЕ СТАТЬИ
Определение призмы
 |
|
Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.
Виды призм
 |
|
 |
|
 |
|
Объем и площадь призмы
Главная формула объема призмы:
,
где — площадь основания,
— высота.
Необычная формула объема призмы:
,
где — площадь сечения, перпендикулярного боковому ребру,
— длина бокового ребра.
Площадь полной поверхности призмы – сумма площадей всех граней.
А теперь подробнее….
Что такое призма
Давай ответим сперва картинками:

Смотри: у призмы сверху и снизу два одинаковых многоугольника – они называются основаниями. Остальные грани называются боковыми.
Плоскости оснований параллельный. Боковые грани – параллелограммы.
Рисуем ещё раз:

А теперь: рёбра.
Смотри: бывают рёбра основания и боковые рёбра.

Важно знать, что:
| Все боковые рёбра призмы равны и параллельны. |
- Если в основании призмы лежит треугольник, то призма называется треугольной, если четырёхугольник, то – четырёхугольной и так далее.
- Бывают и десятиугольные, и двадцатиугольные призмы, но , к счастью, не в твоих задачах.
- А у тебя будут встречаться чаще всего треугольные, четырёхугольные и шестиугольные призмы.
Высота призмы
| Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания. |

И ясно, что та же самая высота получится, если опустить перпендикуляр из любой точки на верхней плоскости.
Согласен?
Прямая призма
Если боковые рёбра призмы перпендикулярны основанию, то призма называется прямой.
 |
У прямой призмы:
|
|
У прямой призмы высота совпадает с боковым ребром. |
Правильная призма
Если боковые рёбра призмы перпендикулярны основанию, а в основании лежит правильный многоугольник, то призма называется правильной.
То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Тебе, скорее всего, может встретиться:
1) Правильная треугольная призма – в основании правильный треугольник, боковые грани – прямоугольники.

2) Правильная четырёхугольная призма – это ещё и разновидность прямоугольного параллелепипеда – в основании квадрат, боковые грани – прямоугольники.

3) Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.

Главная формула объема призмы
–площадь основания
– высота

Эта формула верна для любой призмы, но если призма прямая, то «превращается» в боковое ребро. И тогда
– то же самое, что

Необычная формула объёма призмы
Представь себе, есть ещё одна, «перевёрнутая» формула для объёма призмы .
— площадь сечения, перпендикулярного боковому ребру,
— длина бокового ребра.

Используется ли эта формула в задачах? Честно говоря, довольно редко, так что можешь ограничиться знанием основной формулы объёма.
Давай теперь для упражнения посчитаем объём самых популярных призм.
Объем правильной треугольной призмы
Пусть дано, что сторона основания равна , а боковое ребро равно .

Найдём объём:
Вспомним, как находить площадь правильного треугольника

Подставляем в формулу объёма:
.
Объем правильной четырёхугольной призмы
Опять дано: сторона основания равна , боковое ребро равно .

Ну, площадь квадрата долго искать не надо:
Значит, .
Объем правильной шестиугольной призмы

Что же такое ? Как найти?
Смотри: шестиугольник состоит из шести одинаковых правильных треугольников.

Значит:
Ну и теперь .
Площадь поверхности призмы
| Площадь боковой поверхности призмы – сумма площадей всех боковых граней. |
Есть ли общая формула?
Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.

|
Площадь полной поверхности призмы – сумма площадей всех граней.
|

Формулу можно написать для прямой призмы:
Но всё-таки гораздо проще в каждом конкретном случае сложить все площади, чем запоминать дополнительные формулы.
, где — периметр основания.

.
Для примера посчитаем полную поверхность правильной шестиугольной призмы.
Пусть сторона основания равна , а боковое ребро равно .

Все боковые грани – прямоугольники. Значит .
— это уже выводили при подсчёте объёма.
Итак, получаем:
.
ПРИЗМА. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
1. Определение
 |
|
Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.
2. Виды призм:
 |
|
 |
|
 |
|
3. Объем и площадь призмы:
- Главная формула объема призмы:
,
где — площадь основания,
— высота. - Необычная формула объема призмы:
,
где — площадь сечения, перпендикулярного боковому ребру,
— длина бокового ребра. - Площадь полной поверхности призмы – сумма площадей всех граней.
.
Теперь я хочу услышать тебя!
Я постаралась сжато, без воды рассказать о том, что такое призма.
Что тебе понравилось? Что не понравилось?
Может быть ты нашел ошибку?
Или знаешь другой хороший материал на эту тему?
Напиши внизу, в комментариях.
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
можно кликнув по этой ссылке.
Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.
Мы же поведем подробный разговор.
Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников  и
и  , лежащих в параллельных плоскостях, и
, лежащих в параллельных плоскостях, и  параллелограммов
параллелограммов  .
.

Указанные в определении равные многоугольники – основания призмы.
Боковые грани – все грани, кроме оснований (являются параллелограммами).
Боковые ребра – общие стороны боковых граней (параллельны между собой и равны).
Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.
Диагональное сечение –пересечение призмы и диагональной плоскости.

Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

Среди прямых призм выделяют правильные.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).

Частным случаем призмы является параллелепипед.
Параллелепипед – это призма, основаниями которой являются параллелограммы.
Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Частный случай прямоугольного параллелепипеда – куб.
Куб – прямоугольный параллелепипед, все грани которого – квадраты.

Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике.
Нажмите сюда чтобы увеличить

 Смотрите также «Объем призмы. Площадь поверхности призмы».
Смотрите также «Объем призмы. Площадь поверхности призмы».
Призма. Формулы и свойства призмы
Определение.
Призма — это многогранная объемная фигура, которая состоит из двух одинаковых плоских многоугольников (основ), находящихся в двух параллельных плоскостях, а другие грани (боковые грани) — параллелограммы, что имеют общие стороны с этими многоугольниками.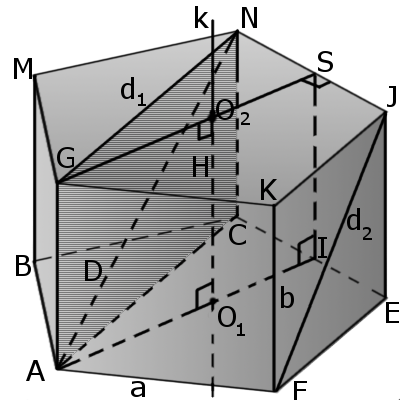 |
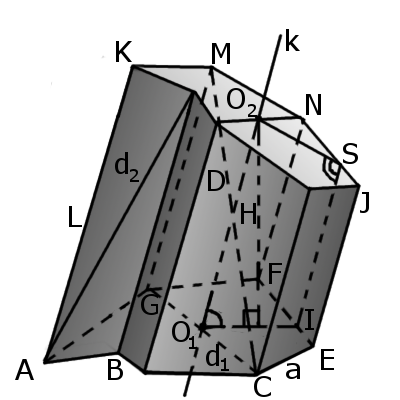 |
|
| Рис.1 | Рис.2 |
Определение. Основы призмы — две грани, которые являются равными параллельными плоскими многоугольниками (ABCEF, GMNJK).
Определение. Боковые грани призмы — все остальные грани за исключением основ.
Определение. Боковая поверхность призмы — совокупность всех боковых граней призмы.
Определение. Поверхность призмы — это совокупность поверхностей двух оснований и боковой поверхности.
Определение. Боковое ребро призмы — общая сторона двух боковых граней.
Определение. Высота — это перпендикуляр, который соединяет две основы призмы под прямым углом.
Определение. Диагональ основания призмы — это отрезок, соединяющий две не соседние вершины, принадлежащие этой же основе.
Определение. Диагональ боковой грани призмы — это отрезок, соединяющий две противоположные вершины, лежащие на одной боковой грани однако принадлежат различным основам.
Определение. Диагональ призмы (AN) — это отрезок, соединяющий две вершины, лежащие на разных основаниях, но не лежат на одной боковой стороне.
Определение. Диагональное сечение — это пересечение призмы плоскостью, проходящей через диагональ основания призмы и боковое ребро. Треугольная призма (в основе призмы треугольники) не имеет диагональных сечений.
Определение. Перпендикулярное сечение — это пересечение призмы плоскостью, пересекающей боковые ребра призмы под прямым углом.
Определение. Прямая призма — это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра.
Определение. Наклонная призма — это призма, в которой боковые грани не перпендикулярны к основанию.
Определение. Правильная призма — это призма, в которой основы являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной.
Определение. Усечённая призма — это призма, в которой две основы не параллельны (рис. 2). Усечённая призма может быть, как прямой, так наклонной.
Объём призмы
Формула. Объём призмы через площадь основания и высоту:V = SоснH
Формула. Объём наклонной призмы через площадь перпендикулярного сечения и длину бокового ребра:V = SпL
Формула. Объём правильной прямой призмы через высоту (h), длину стороны (a) и количество сторон (n):Площадь поверхности призмы
Формула. Площадь боковой поверхности призмы через периметр основания и высоту:Sb = P·h
Формула. Площадь поверхности призмы через площадь основания, периметр основания и высоту:S = 2Soсн + P·h
Формула. Площадь поверхности правильной призмы через высоту (h), длину стороны (a) и количество сторон (n):Основные свойства призмы
Основы призмы — равные многоугольники.
Боковые грани призмы — параллелограммы.
Боковые ребра призмы параллельны и равны между собой.
Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
Высота прямой призмы равна длине бокового ребра.
Высота наклонной призмы всегда меньше длины ребра.
В прямой призме гранями могут быть прямоугольниками или квадратами.
Призма является достаточно простой геометрической объемной фигурой. Тем не менее у некоторых школьников при определении ее основных свойств возникают проблемы, причина которых, как правило, связана с неправильно используемой терминологией. В данной статье рассмотрим, какие призмы бывают, как они называются, а также подробно охарактеризуем правильную четырехугольную призму.
Призма в геометрии
Изучение объемных фигур является задачей стереометрии — важной части пространственной геометрии. В стереометрии под призмой понимают такую фигуру, которая образована параллельным переносом произвольного плоского многоугольника на определенное расстояние в пространстве. Параллельный перенос предполагает такое перемещение, при котором поворот вокруг оси, перпендикулярной плоскости многоугольника, полностью исключен.
Вам будет интересно:Холю и лелею. Что значит лелеять и холить?
В результате описанного способа получения призмы образуется фигура, ограниченная двумя многоугольниками, имеющими одинаковые размеры, лежащими в параллельных плоскостях, и некоторым числом параллелограммов. Их количество совпадает с числом сторон (вершин) многоугольника. Одинаковые многоугольники называются основаниями призмы, а площадь их поверхности — это площадь оснований. Параллелограммы, соединяющие два основания, образуют боковую поверхность.
Элементы призмы и теорема Эйлера
Поскольку рассматриваемая объемная фигура представляет собой полиэдр, то есть образована набором пересекающихся плоскостей, то она характеризуется некоторым количеством вершин, ребер и граней. Все они являются элементами призмы.
В середине XVIII века швейцарский математик Леонард Эйлер установил связь между количеством основных элементов полиэдра. Эта связь записывается следующей простой формулой:
Число ребер = число вершин + число граней — 2
Для любой призмы справедливо это равенство. Приведем пример его использования. Предположим, имеется правильная четырехугольная призма. Она изображена на рисунке ниже.
Видно, что число вершин для нее равно 8 (по 4 для каждого четырехугольного основания). Число сторон, или граней составляет 6 (2 основания и 4 боковых прямоугольника). Тогда количество ребер для нее будет равно:
Число ребер = 8 + 6 — 2 = 12
Все их можно посчитать, если обратится к тому же рисунку. Восемь ребер лежат в основаниях, а четыре ребра перпендикулярны этим основаниям.
Полная классификация призм
С этой классификацией важно разобраться, чтобы впоследствии не путаться в терминологии и использовать правильные формулы для вычисления, например, площади поверхности или объема фигур.
Для любой призмы произвольной формы можно выделить 4 признака, которые ее будут характеризовать. Перечислим их:
- По количеству углов многоугольника в основании: треугольная, пятиугольная, восьмиугольная и так далее.
- По типу многоугольника. Он может быть правильным или неправильным. Например, прямоугольный треугольник является неправильным, а равносторонний — правильным.
- По типу выпуклости многоугольника. Он может быть вогнутым или выпуклым. Чаще всего встречаются выпуклые призмы.
- По углам между основаниями и боковыми параллелограммами. Если все эти углы равны 90o, то говорят о прямой призме, если не все из них являются прямыми, то такую фигуру называют косоугольной.
Из всех этих пунктов хотелось бы остановиться подробнее на последнем. Прямая призма также называется прямоугольной. Связано это с тем, что для нее параллелограммы являются прямоугольниками в общем случае (в некоторых случаях они могут быть квадратами).
Для примера на рисунке выше изображена пятиугольная вогнутая прямоугольная, или прямая фигура.
Правильная четырехугольная призма
Основание этой призмы представляет собой правильный четырехугольник, то есть квадрат. Выше на рисунке уже было показано, как выглядит эта призма. Помимо двух квадратов, которые ее ограничивают сверху и снизу, она также включает 4 прямоугольника.
Обозначим сторону основания правильной четырехугольной призмы буквой a, длину ее бокового ребра обозначим буквой c. Эта длина также является высотой фигуры. Тогда площадь всей поверхности этой призмы выразится формулой:
S = 2*a2 + 4*a*c = 2*a*(a + 2*c)
Здесь первое слагаемое отражает вклад оснований в общую площадь, второе слагаемое — это площадь боковой поверхности.
Учитывая введенные обозначения для длин сторон, запишем формулу для объема рассматриваемой фигуры:
V = a2*c
То есть объем вычисляется как произведение площади квадратного основания на длину бокового ребра.
Фигура куб
Все знают эту идеальную объемную фигуру, но мало кто задумывался, что она представляет собой правильную четырехугольную призму, сторона которой равна длине стороны квадратного основания, то есть c = a.
Для куба формулы полной площади поверхности и объема примут вид:
S = 6*a2
V = a3
Поскольку куб — это призма, состоящая из 6 одинаковых квадратов, то любую параллельную пару из них можно считать основанием.
Куб — это высокосимметричная фигура, которая в природе реализуется в виде кристаллических решеток многих металлических материалов и ионных кристаллов. Например, решетки золота, серебра, меди и поваренной соли являются кубическими.
Источник
- Призма (математика)
Призма (математика)

Призма — многогранник, две грани которого являются конгруэнтными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.
Элементы призмы
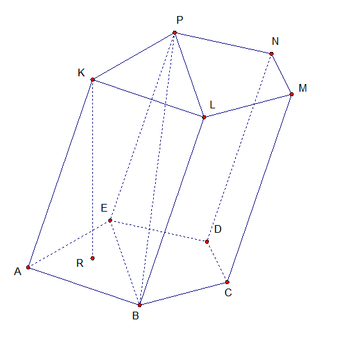
Название Определение Обозначения на чертеже Чертеж Основания Две грани, являющиеся конгруэнтными многоугольниками, лежащими в параллельных плоскостях. ABCDE, KLMNP 
Боковые грани Все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. ABLK, BCML, CDNM, DEPN, EAKP Боковая поверхность Объединение боковых граней. Полная поверхность Объединение оснований и боковой поверхности. Боковые ребра Общие стороны боковых граней. AK, BL, CM, DN, EP Высота Отрезок, соединяющий основания призмы и перпендикулярный им. KR Диагональ Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. BP Диагональная плоскость Плоскость, проходящая через боковое ребро призмы и диагональ основания. Диагональное сечение Пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе его частные случаи — ромб, прямоугольник, квадрат. EBLP Перпендикулярное сечение Пересечение призмы и плоскости, перпендикулярной ее боковому ребру. Свойства призмы
- 1. Основания призмы являются равными многоугольниками.
- 2. Боковые грани призмы являются параллелограммами.
- 3. Боковые ребра призмы параллельны и равны.
- 4. Объём призмы равен произведению её высоты на площадь основания:
- 5. Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Виды призм
Призмы бывают прямые и наклонные.
Прямая призма — призма, у которой все боковые ребра перпендикулярны основанию.
- Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту.
Наклонная призма — призма, у которой хотя бы одно боковое ребро не перпендикулярно основанию.
- Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.
- Объем наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.
Правильная призма — прямая призма, основание которой является правильным многоугольником.
Свойства правильной призмы
- 1. Основания правильной призмы являются правильными многоугольниками.
- 2. Боковые грани правильной призмы являются равными прямоугольниками.
- 3. Боковые ребра правильной призмы равны.
См. также
Ссылки
Многогранники Правильные
(Платоновы тела)Правильные невыпуклые Звёздчатый многогранник (Звёздчатый октаэдр, Звёздчатый додекаэдр, Звёздчатый икосаэдр, Звёздчатый икосододекаэдр) Выпуклые Полуправильные многогранники или Архимедовы тела/двойственные многогранники или Каталановы тела
(Кубооктаэдр/Ромбододекаэдр, Икосододекаэдр/Ромботриаконтаэдр, Усечённый тетраэдр/Triakis tetrahedron,
Усечённый куб/Triakis octahedron, Усечённый октаэдр/Tetrakis hexahedron, Усечённый додекаэдр/Triakis icosahedron,
Усечённый икосаэдр/Pentakis dodecahedron, Ромбокубоктаэдр/Дельтоидальный икоситетраэдр,
Ромбоусечённый кубоктаэдр/Disdyakis dodecahedron, Ромбоикосододекаэдр/Дельтоидальный гексеконтаэдр,
Ромбоусечённый икосододекаэдр/Disdyakis triacontahedron,
Курносый куб/Пентагональный икоситетраэдр, Курносый додекаэдр/Пентагональный гексеконтаэдр,
Звёздчатый кубооктаэдр, правильные призма и антипризма)Формулы, теоремы, теории Прочее Wikimedia Foundation. 2010.
- Эхнатон
- Fiat (компания)
Смотреть что такое «Призма (математика)» в других словарях:
Математика в девяти книгах — (начало) «Математика в девяти книгах» (кит. трад. 九章算術 … Википедия
ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Земляков — Земляков, Александр Николаевич Файл:Zemlyakov.jpg Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик,выдающийся советский и российский педагог, автор учебно педагогической… … Википедия
Земляков, Александр Николаевич — Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик, выдающийся советский и российский педагог, автор учебно педагогической литературы. Биография Закончил в 1967 году с золотой… … Википедия
Правильный многогранник — Додекаэдр Правильный многогранник или платоново тело это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией … Википедия
Пирамида (геометрия) — У этого термина существуют и другие значения, см. Пирамидацу (значения). Достоверность этого раздела статьи поставлена под сомнение. Необходимо проверить точность фактов, изложенных в этом разделе. На странице обcуждения могут быть пояснения … Википедия
Бипирамида — или дипирамида является трёхмерным многогранником, сформированным из двух пирамид, одна из которых является зеркальным отражением другой. Место соединения пирамид образует общую фигуру в виде многоугольника. Простая бипирамида формируется при… … Википедия
Изгибаемый многогранник — Многогранник (точнее многогранная поверхность) называется изгибаемым, если его пространственную форму можно изменить такой непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров (то есть движется как твёрдое тело) … Википедия
Норма (философия) — «Мыслитель», Огюст Роден Философия (др. греч. φιλοσοφία «любовь к мудрости», «любомудрие», от φιλέω люблю и σοφία мудрость) наиболее общая теория … Википедия
Определение философии — «Мыслитель», Огюст Роден Философия (др. греч. φιλοσοφία «любовь к мудрости», «любомудрие», от φιλέω люблю и σοφία мудрость) наиболее общая теория … Википедия
Урок 14. призма — Геометрия — 10 класс
Геометрия, 10 класс
Урок № 14. Призма
Перечень вопросов, рассматриваемых в теме:
- Понятие призмы и виды призм;
- Элементы призмы: вершины, ребра, грани;
- Понятие площади боковой поверхности и площади полной поверхности призмы, формулы для вычисления;
- Призма как модель реальных объектов;
- Пространственная теорема Пифагора.
Глоссарий по теме
Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
Боковые грани – все грани, кроме оснований.
Боковые ребра – общие стороны боковых граней.
Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.
Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.
Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.
Площадь полной поверхности призмы – сумма площадей всех ее граней.
Площадь боковой поверхности призмы – сумма площадей ее боковых граней.
Параллелепипед – призма, все грани которой – параллелограммы.
Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,
геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.
Открытые электронные ресурсы:
Открытый банк заданий ФИПИ http://ege.fipi.ru/
Теоретический материал для самостоятельного изучения
Определение призмы. Элементы призмы.
Рассмотрим два равных многоугольника А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А1В1, А2В2…АnВn, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).

Рисунок 1 – Призма
Заметим, что каждый из n четырехугольников (A1A2B1B2, …AnA1B1Bn) является параллелограммом. Убедимся в этом на примере четырехугольника A1A2B1B2. A1A2 и B1B2 параллельны по свойству параллельных плоскостей, пересеченных третьей плоскостью. А1В1 и А2В2 по условию. Таким образом, в четырехугольнике A1A2B1B2 противоположные стороны попарно параллельны, значит этот четырехугольник — параллелограмм по определению.
Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.
На рисунке 1 основаниями призмы являются многоугольники А1А2…Аn и В1В2…Вn. Боковые грани – параллелограммы A1A2B1B2, …, AnA1B1Bn, а боковые ребра — отрезки А1В1, А2В2, …, АnВn.
Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).
Призму с основаниями А1А2…Аn и В1В2…Вn обозначают А1А2…АnВ1В2…Вn и называют n-угольной призмой.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).

Рисунок 2 – Наклонная призма
Виды призм
Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.
Высота прямой призмы равна ее боковому ребру.
На рисунке 3 приведены примеры прямых призм



Рисунок 3 – Виды призм.
Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.
Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.
Площадь полной поверхности призмы. Площадь боковой поверхности призмы.
Площадью полной поверхности призмы (Sполн) называется сумма площадей всех ее граней, а площадью боковой поверхности (Sбок) призмы – сумма площадей ее боковых граней.
Таким образом, верно следующее равенство: Sполн= Sбок+2Sосн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.
Чему равна площадь боковой поверхности прямой призмы?
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Доказательство
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом Sбок=Pоснh.
Пространственная теорема Пифагора
Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.
Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.

Рисунок 4 – Прямоугольный параллелепипед
Доказательство
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 и найдем квадрат длины его диагонали А1С.
Для этого рассмотрим треугольник А1АС:
Ребро АА1 перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА1 перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА1АС – прямоугольный.
По теореме Пифагора получаем: А1С2=АА12+АС2 (1).
Выразим теперь АС. По условию в основании лежит прямоугольник, значит ΔАВС – прямоугольный. По тереме Пифагора получаем: АС2=ВС2+АВ2.
Подставив результат в (1), получим: А1С2=АА12+ВС2+АВ2.
Так как в основании прямоугольник, то ВС=АD.
Таким образом, А1С2=АА12+АD2+АВ2.
Что и требовалось доказать
Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.
Примеры и разбор решения заданий тренировочного модуля
Задание 1.
Найдите для каждой картинки пару
1) 2)
2)  3)
3) 
4) 5)
5) 
6) 
Решение
Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.
Задание 2
Какие из перечисленных объектов могут быть элементами призмы?
1) параллельные плоскости
2) отрезок
3) точка
4) четырехугольник
Решение:
Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.
Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.
Ответ: 2,3,4
Прямая призма
Прямая призма
Прямая призма — призма, у которой боковые ребра перпендикулярны плоскости основания.
При этом в основании прямой призмы может быть любая геометрическая фигура.
Правильная прямая призма — это призма, в основаниях которой лежит правильный многоугольник.
Например, правильная прямая четырехугольная призма — это параллелепипед.
Частным случаям параллелепипеда является правильная призма — это призма, у которой все грани равны — куб.
Свойства прямой призмы
- Основания призмы равны
- Каждая из боковых граней обязательно является прямоугольником
- Боковые ребра призмы параллельны и равны между собой
- Боковые грани правильной призмы представляют собой равные прямоугольники
- При пересечении призмы и диагональной плоскости сечение представляет собой параллелограмм
- Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы
- Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах
- Перпендикулярное сечение перпендикулярно ко всем боковым граням
- Длина ребра прямой призмы равна ее высоте
Формулы прямой призмы
Где:
Ss — площадь боковой поверхности прямой призмы
Sb — площадь основания
V — объем прямой призмы
Vn — объем прямой призмы с правильным многоугольником в основании
Ssn — площадь боковой поверхности прямой призмы с правильным многоугольником в основании
P — периметр основания
h — высота призмы, она же — длина бокового ребра прямой призмы
n — для прямой призмы, в основании которой лежит правильный многоугольник, количество сторон правильного многоугольника
a — для прямой призмы с правильным многоугольником в основании — длина стороны правильного многоугольника
Руководство по статистике GraphPad Prism 8
На вкладке «Параметры» для одностороннего диалога ANOVA имеется два экрана справки:
• На этой странице описаны варианты множественного сравнения.
• Другая страница объясняет параметры графика и вывода.
Список доступных тестов зависит от цели, которую вы указали на вкладке «Многократные сравнения» (вторая), и от выбора равных SD на вкладке «Экспериментальный дизайн» (первая).
Исправить для множественных сравнений с использованием статистической проверки гипотез
Сравните каждое среднее с любым другим средним
Доступные варианты выбора зависят от того, предполагаете ли вы, что на первой вкладке диалога ANOVA вы принимаете гомоскедастичность (одинаковые значения SD, то есть равные отклонения).
Если вы предполагаете гомоскедастичность (равные SD), вы можете выбрать:
• тест Тьюки (рекомендуется)
• Bonferroni
• Sidak
• Holm-Sidak. Этот тест более мощный, чем метод Тьюки (3), что означает, что иногда он может найти статистически значимое различие, когда метод Тьюки не может. Этот тест не может вычислить доверительные интервалы, и по этой причине мы предпочитаем тест Тьюки.
• Ньюман-Кеулс. Мы предлагаем этот тест только для совместимости со старыми версиями Prism, но мы рекомендуем вам избегать его.Проблема заключается в том, что он не поддерживает частоту ошибок по семейному признаку на указанном уровне (1). В некоторых случаях вероятность ошибки типа I может быть больше указанного вами альфа-уровня.
Если вы не предполагаете гомоскедастичность (равные SD), ваш выбор:
• Games-Howell (рекомендуется для больших выборок)
• Dunnett T3 (рекомендуется, когда размер выборки на группу меньше 50)
• Tamhane T2
Все три метода позволяют вычислить доверительные интервалы и скорректированные по множественности значения P.
Сравнить контрольное среднее с другими средствами
Если вы предполагаете гомоскедастичность (равные SD), ваш выбор:
• Dunnett’s (рекомендуется)
• Bonferroni
• Sidak
• Holm-Sidak. Гланц говорит, что тест Холма должен иметь больше силы, чем тест Даннетта, но это (насколько ему известно) не было подробно изучено (2). Этот тест не может вычислить доверительные интервалы или значения P с поправкой на множественность, и по этой причине мы предпочитаем тест Даннетта.
Если вы не предполагаете гомоскедастичность (равные SD), ваш выбор:
• T3 Даннетта (рекомендуется)
• Tamhane T2
Сравните средства заранее заданных пар столбцов
Если вы предполагаете гомоскедастичность (равные SD), ваш выбор:
• Bonferroni (наиболее часто используемый)
• Sidak (больше мощности, поэтому рекомендуется)
• Holm-Sidak (не может вычислить доверительные интервалы)
Если вы не предполагаете гомоскедастичность (равные SD), ваш выбор:
• Games-Howell (рекомендуется)
• Dunnett T3
• Tamhane T2
Исправьте множественные сравнения, контролируя уровень ложных открытий
Prism предлагает три метода контроля частоты ложных обнаружений.Все решают, какие (если таковые имеются) сравнения помечать как «открытия», и делают это таким образом, чтобы уровень ложных обнаружений был меньше значения Q, которое вы вводите.
Подход FDR не часто используется в качестве контрольного теста для ANOVA, но для этого нет веских причин.
Не исправить для множественных сравнений. Каждое сравнение стоит отдельно.
Если вы выберете этот подход, Prism выполнит тест Фишера наименьшей значимой разницы (LSD).
Этот подход (ЛСД Фишера) имеет гораздо больше возможностей для обнаружения различий.Но более вероятно ошибочно сделать вывод, что разница статистически значима. Когда вы корректируете множественные сравнения (чего не делает ЛСД Фишера), порог значимости (обычно 5% или 0,05) применяется ко всему семейству сравнений. С ЛСД Фишера этот порог применяется отдельно для каждого сравнения.
Используйте ЛСД-подход Фишера только в том случае, если у вас есть веская причина, и внимательно объясните, что вы делали, когда сообщали о результатах.
Поменять направление сравнений
Единственный эффект этой опции — изменение знака всех зарегистрированных различий между средними.Разница в 2,3 будет -2,3, если опция включена. Разница -3,4 будет 3,4, если вы отметите эту опцию. Это чисто личное предпочтение, которое зависит от того, как вы относитесь к данным.
Отчет P скорректированное значение множественности для каждого сравнения
Если вы выберете тест множественных сравнений Бонферрони, Тьюки или Даннетта, Prism также может сообщать значения P, скорректированные с учетом множественности. Если вы отметите эту опцию, Prism сообщит скорректированное значение P для каждого сравнения. Эти расчеты учитывают не только две сравниваемые группы, но и общее количество групп (столбцы набора данных) в ANOVA, а также данные во всех группах.С помощью теста Даннетта Prism может сообщать значение P с поправкой на кратность только тогда, когда оно будет больше 0,0001. В противном случае он сообщает «<0,0001» (до Prism 8 Prism сообщал 0,0001 без символа «меньше»).
Значение P с поправкой на кратность — это наименьший порог значимости (альфа) для всего семейства сравнений, при котором конкретное сравнение (едва ли) будет объявлено «статистически значимым».
До недавнего времени значения P с поправкой на множественность обычно не сообщались.Если вы решите попросить Prism вычислить эти значения, найдите время, чтобы убедиться, что вы понимаете, что они означают. Если вы включите эти значения в публикации или презентации, обязательно объясните, что они собой представляют.
Уровень доверия и значимости (или желаемый FDR)
Традиционно доверительные интервалы рассчитываются для достоверности 95%, а статистическая значимость определяется с использованием альфа 0,05. Prism позволяет выбирать другие значения. Если вы решите контролировать FDR, выберите значение Q (в процентах).Если вы установите Q на 5%, вы ожидаете, что до 5% «открытий» будут ложноположительными.
Рекомендации
1.SA Glantz, Primer of Biostatistics, шестое издание, ISBN = 978-0071435093.
2. М.А.Симэн, Дж.Р. Левин и Р.К. Серлин, Психологический бюллетень 110: 577-586, 1991.
,Определение призмы — Math Open Reference
Определение призмы — Math Open ReferenceТвердое тело с двумя параллельными параллельными гранями, где любое поперечное сечение, параллельное этим граням, совпадает с ними.
Попробуй это Отрегулируйте высоту призмы ниже. Выберите примеры различных типов призмы.
Призма — это твердое тело с двумя гранями, которые параллельно и конгруэнтны. Они называются основаниями призмы.Если вы берете любое поперечное сечение призмы параллельно этим основаниям, делая разрез через нее параллельно основаниям, поперечное сечение будет выглядеть так же, как основания.
На рисунке выше, нажмите «Показать сечение» и перетащите сечение вверх и вниз. Обратите внимание, что оно всегда соответствует базисам; то есть он всегда имеет одинаковую форму и размер. Это верно для правильных и наклонных призм.
Наименование
Призмы названы в честь формы основания. На рисунке выше выберите различные примеры призмы в раскрывающемся меню.Обратите внимание То, как имя призмы зависит от формы основания.
Регулярные и неправильные призмы
Это также соответствует форме оснований. Если основания являются правильными многоугольниками, то призма также называется правильной призмой. Аналогично, неправильные призмы имеют основания, которые являются неправильными многоугольниками.
Право против наклонных призм

Правая призма — это та, где основания находятся точно одна над другой, как на левом изображении. Это означает, что линии, соединяющие соответствующие точки на каждом основании, перпендикулярны основаниям.
На рисунке выше выберите «Разрешить наклон» в меню параметров. Фигура — это правильная призма. Если вы перетащите верхнюю оранжевую точку в сторону, вы можете сделать призму наклонной (или «наклонной»). Поперечные сечения, параллельные основаниям, все еще совпадают с основаниями.
- Для правых призм боковые грани являются прямоугольниками
- Для наклонных призм они являются параллелограммами.
«Толстые» полигоны
Другой способ думать о призмах, если они были многоугольниками, которые имеют добавленное 3-е измерение «толщины».На рисунке выше нажмите «сброс» и потяните верхнюю часть вниз, чтобы длина была равна нулю. Теперь у вас есть многоугольник. При перемещении вверх вы можете видеть, что с увеличением высоты многоугольник становится «толще».Объем призмы
Дается площадь основания, умноженная на высоту. Это верно для правильных и наклонных призм. См. Объем призмы.Площадь поверхности
Площадь поверхности призмы является суммой площадей оснований и сторон. Для получения дополнительной информации см. Площадь поверхности призмы.Цилиндры как призмы
Технически цилиндр не призма, потому что его стороны изогнуты.Но когда основания — это правильные многоугольники с очень большим числом сторон, они выглядят как цилиндры, и все свойства цилиндров применимы к ним. Расчет объема аналогичен. Это изучено далее в Цилиндрическое определение.Призмы и радуги

Если вы светите лучом белого света через треугольную стеклянную призму, он разбивает свет на различные длины волн, создавая характерную «радугу». В учебниках по физике призма обычно рисуется на боку, как на рисунке выше.
В математике призма может быть больше, чем просто треугольная форма, как описано выше.
Что попробовать
- В апплете вверху страницы выберите различные примеры и поймите, что основания призмы могут быть буквально любым многоугольником.
- Для каждого примера установите флажок «Показать поперечное сечение» и сдвиньте сечение вверх и вниз, показывая, что поперечное сечение везде одинаково.
- Для каждого примера отметьте «Разрешить наклонную» и перетащите верхнюю часть вправо, демонстрируя разницу между правой и наклонной призмой.Отрегулируйте поперечное сечение, чтобы оно было постоянным и для наклонных призм.
- Нажмите на кнопку «Скрыть детали». Выполните все вышеперечисленное и угадайте полное правильное название призмы. Затем нажмите «показать детали», чтобы проверить свой ответ.
Похожие темы
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
Загрузка…
- Авторизоваться зарегистрироваться
определение призмы Медицинским словарем
Прозрачное тело (например, пластик, стекло), ограниченное двумя наклонными плоскими поверхностями, которые пересекаются по прямой линии, называемой вершиной, и образуют угол, называемый углом призмы . Лицо напротив вершины называется базой . Это оптический элемент, используемый для отклонения света (к основанию призмы). Угол отклонения d призмы в воздухе задается следующей формулойd = i + i ′ —
, где i — угол падения, i ′ — угол и угол призмы (рис.P15). См. Адаптация к грани ; базовая настройка; призменный диоптрий; сила призмы ; минимальное отклонение призмы ; Глазная призма ; лежачих очков ; спектроскопа.Ахроматическая призма Призма, рассеивающая свет без рассеивания. Он состоит из двух призм, обычно одной из кроненого стекла, а другой из кремня, с одинаковыми угловыми дисперсиями и установлен так, что вершина одной находится напротив основания другой.
адаптация призмы См. адаптация вергенции ; тест адаптации к призме .
выравнивающая призма См. связанная гетерофория .
призматическая балластная линза См. балласт.
Призматическая планка Клиническое устройство, состоящее из серии призм повышенной прочности, расположенных в удобном креплении для быстрого позиционирования перед глазом. Он может использоваться с тестом покрытия или даже для измерения фузионных реакций при определении зоны четкого одиночного бинокулярного зрения, если поворотные призмы недоступны.
базовая призма; базовая призма См. базовую настройку .
би-призма См. би-призма Френеля.
призматический бинокль См. бинокль.
компенсационная призма См. связанная гетерофория ; Разгрузочная призма .
призма
тест крышки См. Тест крышки .
Crete’s p . См. Поворотная призма .
Prism Dioptre См. Prism Dioptre.
диссоциирующая призма Призма, которая, будучи помещена перед глазом, производит диссоциацию.
двойная призма См. Би-призма Френеля.
испытание с двойной призмой См. испытание с двойной призмой .
Dove Prism Равнодушная отражающая призма, используемая для инвертирования изображения в оптической системе. Свет входит в одну сторону, затем преломляется на поверхность основания, где он отражается и снова преломляется через другую сторону.
монтажная призма Призма, предназначенная для инвертирования изображения в оптической системе без изменения размера или формы. Примеры : Призма Дава, Призма Порро. Syn . инвертирующая призма. См. монтажник.
Призма Fresnel Press-On Торговое наименование тонкого диска из прозрачного пластика, состоящего из одной плоской поверхности, которая может прилипать к чистой поверхности линзы при нажатии на место, и другой поверхности, на которой встроены небольшие призматические элементы, уложенные параллельно одной другой.Таким образом, большие оптические эффекты могут быть обеспечены в гораздо более тонкой и легкой форме. Эти прижимные прижимы Френеля могут быть обрезаны до любой желаемой формы и широко используются в ортопедии. См. Линза Френеля; Ортоптика.
Призма Гершеля См. Поворотная призма .
-индуцированная призма Призматический эффект, возникающий, когда зрительная ось пациента не проходит через оптический центр офтальмологической линзы. Количество силы призмы определяется законом Прентиса. См. сходимость, вызванная коррекцией ; Закон Прентиса.
инвертирующий р . Смотри призму , монтаж.
слезная призма См. слезный мениск.
минимальное отклонение призмы Отклонение световых лучей от их первоначального пути является минимальным, когда свет проходит симметрично через призму, так что углы падения и падения равны (рис. P15). См. угол отклонения; призмы.
Nicol prism Оптическое устройство для генерации луча плоско поляризованного света. Он сделан из куска кристалла кальцита, разрезанного по диагонали пополам с двумя половинами, сцементированными вместе. Падающий свет в призме разделяется на обычные и необычные линейно поляризованные лучи: обычный луч достигает границы раздела и полностью отражается, а необычный луч проходит (Рис. P16). См. Анализатор ; Двойное лучепреломление; поляризатор.
офтальмологическая призма Призма, используемая для коррекции или измерения отклонения глаз.Сила такой призмы обычно составляет всего несколько призменных диоптрий. Сила тонкой призмы в воздухе, представленная углом отклонения d , определяется приближенной формулой
d = ( n — 1) a
, где n — показатель преломления призмы и a угол призмы. Пример : если угол призмы равен 10º, а показатель преломления призмы равен 1,523, отклонение будет равно 5,23º или 9.12 Χ. (Рис. P17). См. Prism Dioptre; Призма .Penta Prism См. Рис. P18 .
Поляризационная призма Призма, изготовленная из дважды преломляющего материала. Пример : кварц. См. Анализатор ; поляризованный свет; поляризатор.
Porro prism Комбинированная призма, состоящая из двух полностью отражающих призм 90 °, расположенных под прямым углом друг к другу. Он используется в оптических системах, таких как бинокль, чтобы инвертировать изображение и обеспечить более короткое смещение.Это самая распространенная монтажная призма.
Призма См. Призма .
отражающая призма Призма, в которой свет внутренне отражается на одной или нескольких плоских поверхностях до его появления. Это происходит, когда угол падения у поверхности больше критического угла (рис. P18). Син. отражающей призмы. См. полное отражение .
призматический рефлекторный тест См. Метод Крымского .
облегчающая призма Офтальмологическая призма, предназначенная для облегчения симптомов, вызванных некомпенсированной гетерофорией. Син. компенсационная призма.
Призма Рисли См. Поворотная призма .
Поворотная призма Пара одинаковых тонких призм, установленных одна перед другой, чтобы их можно было вращать на равные количества в противоположных направлениях, чтобы получить результирующую мощность в одном меридиане. Мощность может варьироваться от нуля, когда вершина одной призмы совпадает с основанием другой, до суммы степеней двух призм, когда вершины совпадают.Призма Рисли — это очень распространенный тип вращающейся призмы. Он используется для определения границ зоны четкого, одиночного, бинокулярного зрения, а также в некоторых стереоскопах (например, стереоскопическая система с изменяемой призмой). Другие типы вращающихся призм — это Крита и Гершеля. Син. переменная призма. См. Базовую настройку ; переменная призма стереоскоп .
слезная призма См. слезный мениск.
всего отражающей призмы См. отражающей призмы.
версия призмы См. Призма ярма .
Призма Волластона Две прямоугольные призмы с одинаковым углом, изготовленные из двойного преломляющего кристалла, такого как кварц или кальцит, склеенные между собой гранями гипотенузы для образования прямоугольной единицы. Оптическая ось кристалла в одной призме перпендикулярна оптической оси другой призмы, и обе оси также перпендикулярны направлению падающего света. Луч неполяризованного света, падающий на призму Волластона, появится в виде двух расходящихся лучей, которые поляризованы противоположно и почти не рассеивают.Эта призма используется в некоторых типах кератометров (например, Javal-Schiotz). Син. Волластон поляризатор.
Призма ярма Две призмы, по одной перед каждым глазом, одинакового отклонения и направления (например, 2 BU, OU). Видимый вид движется к вершине призм. Иногда их назначают при лечении нистагма, при визуальных тренировках, прикованном к постели (призмы BD) и в некоторых случаях инвалидности. (Рис. P19) Примечание : также пишется изогнутые призмы. Син. версия призмы.
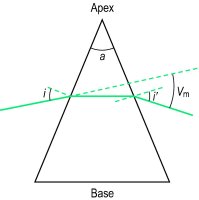
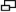
Рис. P15 Призма ( a , угол призмы; i , угол падения = i ′, угол выхода; V м , угол минимального отклонения)
Рис. P16 Призма Никола (О, обыкновенный луч; Е, необыкновенный луч)

Рис. P17 Линия звезд, просматриваемая сквозь призму
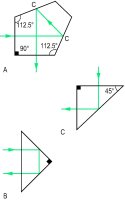
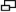
Рис. ,P18 Примеры отражающих призм (A, пятиугольная призма, с поверхностями C, покрытыми серебром или алюминием; B и C, в которых поверхности отражают свет посредством полного внутреннего отражения)
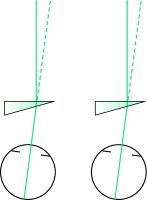
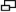
Рис. P19 Призмы хомута

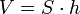
Leave A Comment