Постройте график функции y x2 4x 3. Квадратичная и кубическая функции. Основные свойства квадратичной функции
Словари. Энциклопедии. История. Литература. Русский язык » Русский язык » Постройте график функции y x2 4x 3. Квадратичная и кубическая функции. Основные свойства квадратичной функции
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
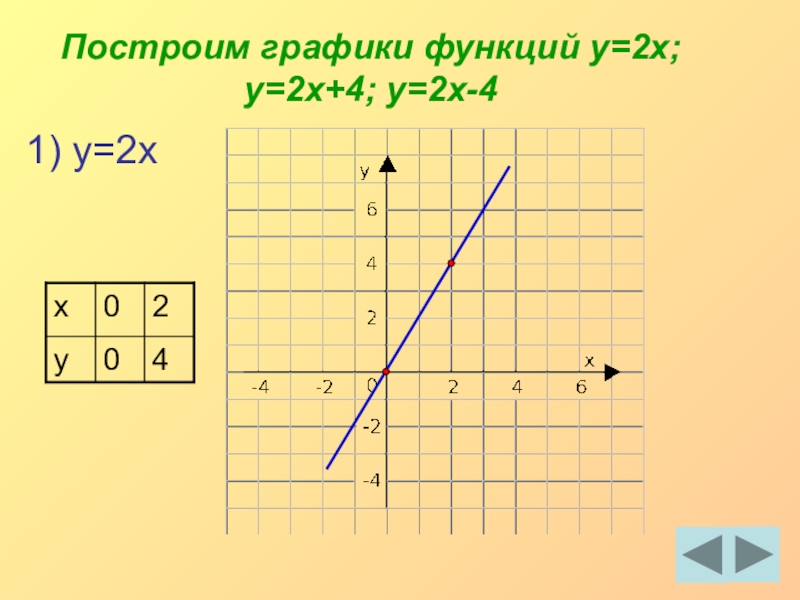
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|.
Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U; график f(х) = х + 2 – это прямая, параллельная прямой f(х) = х, но сдвинутая на две единицы вверх и поэтому проходящая через точку с координатами (0,2) (потому что постоянная равна 2).
Построение графика сложной функции
Найдите нули функции. Нули функции – это значения переменной «х», при которых у = 0, то есть это точки пересечения графика с осью Х.
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.
у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх.
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.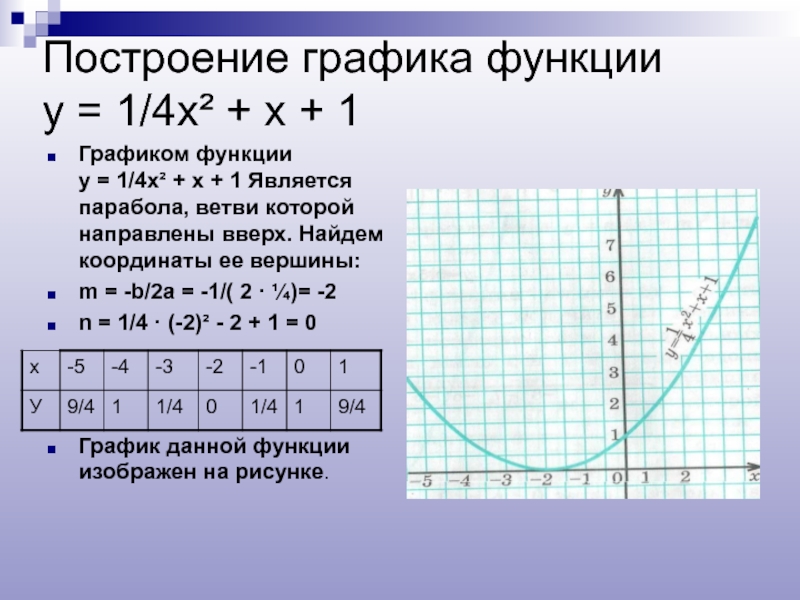
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.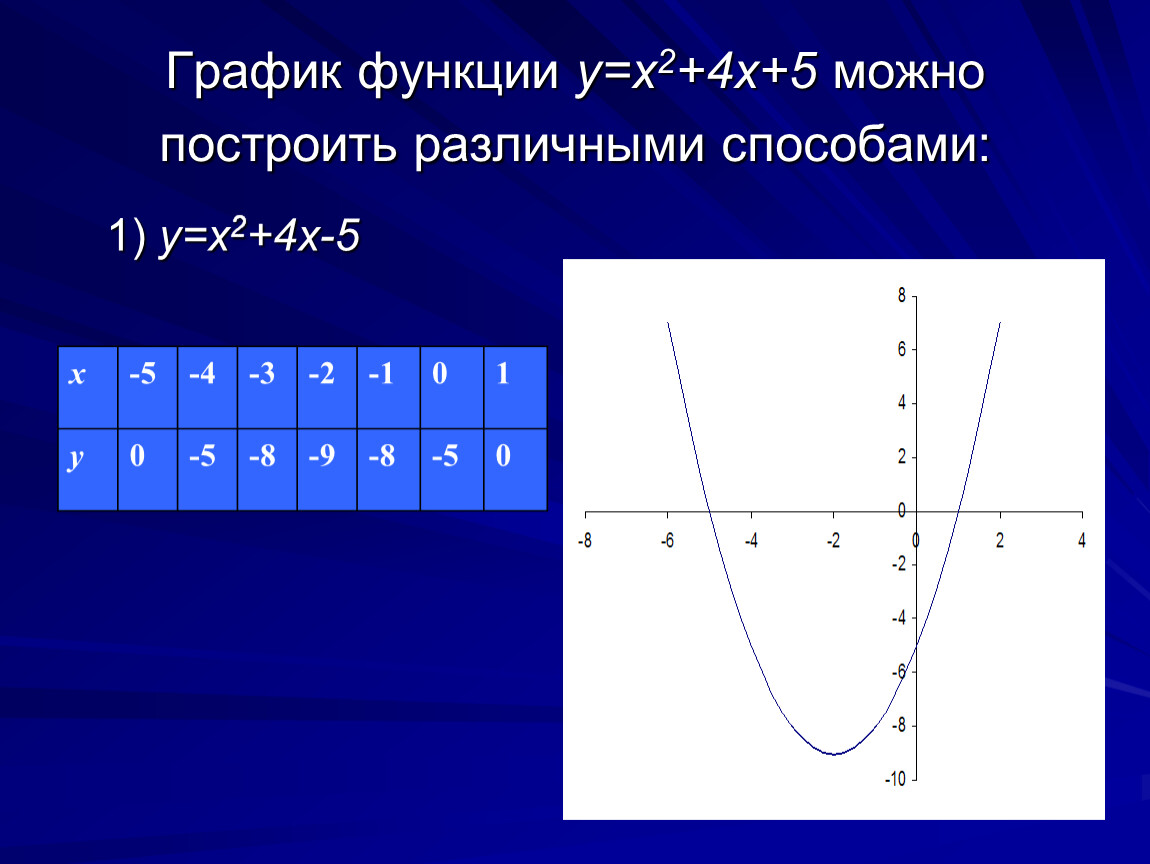
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |Функция y=x^2 называется квадратичной функцией.
Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
3-8Графики квадратных уравнений с использованием оси симметрии
Горячая математика Квадратное уравнение это
многочлен
уравнение
степень
2
.
Стандартная форма квадратного уравнения:
0 «=» а Икс 2 + б Икс + с
где а , б и с все действительные числа и а ≠ 0 .
Если мы заменим 0 с у , то мы получаем квадратичная функция
у «=» а Икс 2 + б Икс + с
график которого будет парабола .
Осью симметрии этой параболы будет линия
Икс
«=»
−
б
2
а
.
Ось симметрии проходит через вершину, поэтому
Икс
-координата вершины
−
б
2
а
.
Заменять
Икс
«=»
−
б
2
а
в уравнении найти
у
-координата вершины.
Замените еще несколько
Икс
-значения в уравнении, чтобы получить соответствующие
у
-значения и построить точки. Соедините их и удлините параболу.
Пример 1:
График параболы у «=» Икс 2 − 7 Икс + 2 .
Сравните уравнение с у «=» а Икс 2 + б Икс + с чтобы найти значения а , б , и с .
Здесь, а «=» 1 , б «=» − 7 и с «=» 2 .
Используя значения коэффициентов, напишите уравнение ось симметрии .
График квадратного уравнения в виде
у
«=»
а
Икс
2
+
б
Икс
+
с
имеет своей осью симметрии линию
Икс
«=»
−
б
2
а
.
Итак, уравнение оси симметрии данной параболы имеет вид
Икс
«=»
−
(
−
7
)
2
(
1
)
или
Икс
«=»
7
2
.
Заменять Икс «=» 7 2 в уравнении найти у -координата вершины.
у «=» ( 7 2 ) 2 − 7 ( 7 2 ) + 2 «=» 494 − 49 2 + 2 «=» 49 − 98 + 8 4 «=» − 41 4
Следовательно, координаты вершины
(
7
2
,
−
41
4
)
.
Теперь замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -ценности.
| Икс | у «=» Икс 2 − 7 Икс + 2 |
| 0 | 2 |
| 1 | − 4 |
| 2 | − 8 |
| 3 | − 10 |
| 5 | − 8 |
| 7 | 2 |
Нанесите точки и соедините их, чтобы получить параболу.
Пример 2:
График параболы у «=» − 2 Икс 2 + 5 Икс − 1 .
Сравните уравнение с у «=» а Икс 2 + б Икс + с чтобы найти значения а , б , и с .
Здесь, а «=» − 2 , б «=» 5 и с «=» − 1 .
Используя значения коэффициентов, напишите уравнение оси симметрии.
График квадратного уравнения в виде
у
«=»
а
Икс
2
+
б
Икс
+
с
имеет своей осью симметрии линию
Икс
«=»
−
б
2
а
.
Итак, уравнение оси симметрии данной параболы имеет вид
Икс
«=»
−
(
5
)
2
(
−
2
)
или
Икс
«=»
5
4
.
Заменять Икс «=» 5 4 в уравнении найти у -координата вершины.
у «=» − 2 ( 5 4 ) 2 + 5 ( 5 4 ) − 1 «=» − 50 16 + 25 4 − 1 «=» − 50 + 100 − 16 16 «=» 34 16 «=» 17 8
Следовательно, координаты вершины
(
5
4
,
17
8
)
.
Теперь замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -ценности.
| Икс | у «=» − 2 Икс 2 + 5 Икс − 1 |
| − 1 | − 8 |
| 0 | − 1 |
| 1 | 2 |
| 2 | 1 |
| 3 | − 4 |
Нанесите точки и соедините их, чтобы получить параболу.
Пример 3:
График параболы Икс «=» у 2 + 4 у + 2 .
Здесь, Икс является функцией у . Парабола открывается «вбок» и ось симметрии параболы горизонтальна. Стандартная форма уравнения горизонтальной параболы: Икс «=» а у 2 + б у + с где а , б , и с все действительные числа и а ≠ 0 а уравнение оси симметрии имеет вид у «=» − б 2 а .
Сравните уравнение с
Икс
«=»
а
у
2
+
б
у
+
с
чтобы найти значения
а
,
б
, и
с
.
Здесь, а «=» 1 , б «=» 4 и с «=» 2 .
Используя значения коэффициентов, напишите уравнение оси симметрии.
График квадратного уравнения в виде Икс «=» а у 2 + б у + с имеет своей осью симметрии линию у «=» − б 2 а . Итак, уравнение оси симметрии данной параболы имеет вид у «=» − 4 2 ( 1 ) или у «=» − 2 .
Заменять у «=» − 2 в уравнении найти Икс -координата вершины.
Икс «=» ( − 2 ) 2 + 4 ( − 2 ) + 2 «=» 4 − 8 + 2 «=» − 2
Следовательно, координаты вершины
(
−
2
,
−
2
)
.
Leave A Comment