СРРООООЧНО!!!!!ПЛИИИЗ ДО ЗАВТРА!!!!НЕ КОПИРОВАТЬ С ЧУЖИХ САЙТОВ!!!!!Пользуясь графиками 2 и 4

Таблица давления твердого тела и газа.Если будете писать фигню кину нарушение.​

Сколько баллов даёт одна 5 в электроном дневнике? И сколько и какие оценки надо получить, чтобы с 4,3 выйти на 4,5 (если что электроный дневник Elscho … ll) дам 100 баллов срочно!!! Оценки: 4,5,5,3,5,4,5,4,4,4,5,4,4,5,3,4,5,5,4,4

ЛАБОРАТОРНА РОБОТА № 9 Тема. Визначення коефіцієнта тертя Ковзання.

1.Согласно рецепту приготовления молочного коктейля лучше всегоиспользовать молоко, имеющее температуру +16°C. На рисункеизображены три термометра. Ук … ажите цену деления того термометра,который подойдёт для измерения температуры молока приприготовлении коктейля.​

ПОМОГИТЕ ПЛИЗ ДАЮ 30 БАЛЛОВ При взвешивании тела в воздухе динамометр показывает 1,4 Н, а в воде 0,6 Н. Определите объем тела. Ответ дайте в см3

Нужно решить задачу. Очень срочно на кану либо 4 либо 3

За графіком залежності сили струму від часу (мал.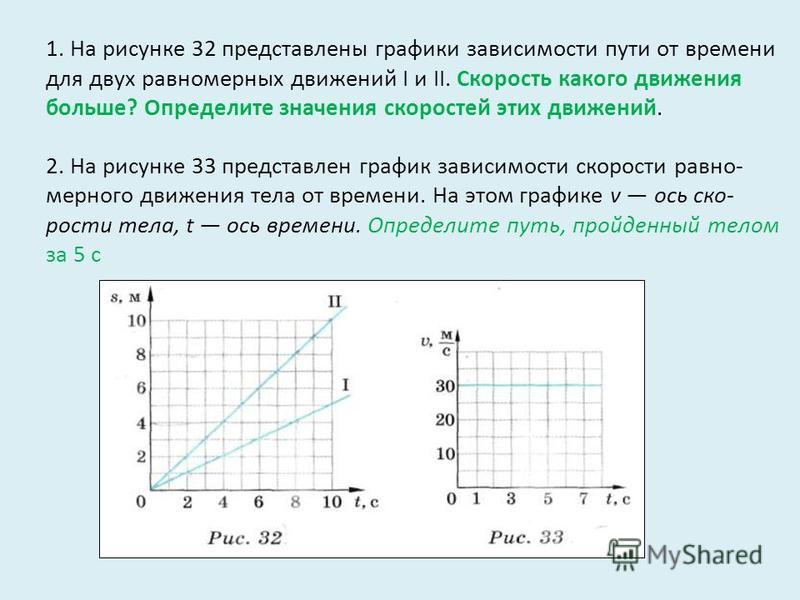

133) визначте заряд, що проходить через поперечний переріз провідника за 3 секунди. Яку фізичну вели … чинуможна визначити, обчисливши площу прямокутникаODBC?​

ПОМОГИТЕ ПОЖАЛУЙСТА!!!СРОЧНО!!!ПЖ!!! Задание 1. Укажи, с какой силой давит воздух на поверхность крышки ящика площадью 0,36 м2. (Принять атмосферное д … авление за 1013 гПа). Ответ (округли до десятых): воздух давит на поверхность крышки ящика с силой F≈___кН. Задание 2. Вес пластины равен 73 Н. Её площадь равна 50 м2. Какое давление оказывает пластина на соответствующую поверхность? Ответ (округли до десятых): давление пластины равно ___Па. Задание 3. Какой должна быть площадь, чтобы силой в 9 кН оказать давление в 2 кПа? Ответ (округли до сотых, если необходимо): площадь должна быть ___м².

Площадь дна ёмкости равна 960 см2. Найди, на сколько увеличится давление ёмкости на стол, если в неё налить воду объёмом 5 л. Принять g=9,8 Н/кг. Отве … т (округли до целого числа): давление ёмкости на стол увеличится на ? Па.

Помогите сделать 7 номер который на фото,отдам свои 100 баллов пж

Open Library — открытая библиотека учебной информации

Механика На рисунке 31 показаны графики движении автомобиля 1 и велосипедиста 2. Пользуись графиками, найдите время и место их встречи

просмотров — 595

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ

График скорости.

Наряду с графиками движения часто пользуются

графиками скорости. Их получают, откладывая по оси абсцисс время, а по оси ординат — проекции скорости тела. Такие графики показывают, как изменяется скорость с течением времени.

В случае прямолинœейного равномерного движения «зависимость» скорости от времени состоит в том, что скорость со временем не изменяется. По этой причине график скорости представляет собой прямую, параллельную оси времени . График 1 на этом рисунке относится к случаю, когда тело движется в сторону положительного направления оси X. График 2 — к случаю, когда тело движется в противоположном оси X направлении (проекция скорости отрицательна).

По графику скорости тоже можно определить перемещение тела за данный промежуток времени. Оно численно равно площади заштрихованного прямоугольника (рис. 30).

Действительно, площадь прямоугольника равна произведению двух смежных его сторон. Но в нашем случае одна из сторон в выбранном масштабе равна времени t, а другая — проекции скорости vx вектора v. А их произведение v{xt как раз и равно проекции вектора перемещения тела.

Решение. График / показывает, что автомобиль движется равномерно вдоль оси X со скоростью 20 м/с. Из графика

2 видно, что велосипедист движется ему навстречу со скоростью 5 м/с. В начальный момент времени (f=0) автомобилист и велосипедист находились на расстоянии 250 м один от другого. Графики пересекаются в точке М. В этой точке и встретились автомобиль и велосипедист. Встреча произошла через 10 с от начала отсчета времени на расстоянии 200 м от начального положения автомобиля и 50 м от начального положения велосипедиста.

Упражнение 3

1. Пользуясь графиками 2 и 4 (см. рис. 28), найдите расстояние между движущимися телами в момент времени ( = 3 с,

2. По графику, изображенному на рисунке 27, определите, как направлена скорость тела. Чему равен модуль скорости?

Задание

По графикам 1 и 2 (см. рис. 29), выражающим зависимость проекций скорости от времени, постройте график модулей скоростей.

Упражнение 3 1. Пользуясь графиками 2 и 4 (см.рис. 28), найдите расстояние между движу-щимися телами в момент времени t = 3 с.​

Физика, 18.03.2019 06:18

Контрольная работа 7 класс «давление твердых тел, жидкостей и газов» вариант № 1 № 1 (в каждом вопросе есть только один правильный ответ) выберите правильную формулировку закона паскаля: а) на тело, погруженное в газ или жидкость, действует выталкивающая сила. б) давление в жидкости и газе передается во все точки не равномерно. в) давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях. г) давление прямо пропорционально зависит от силы и обратно пропорционально от площади поверхности, на которую эта сила действует. давление жидкости на помещенное в неё тело зависит от: а) объема тела б) силы тяжести в) площади основания тела г) высоты жидкостного столба если сила архимеда, действующая на помещенное в жидкость тело, больше чем сила тяжести, действующая на это тело, то… а) плавает внутри жидкости б) тонет в) всплывает г) может плавать, а может и всплыть нормальное атмосферное давление равно… а) 133 па б) 760 мм. рт. ст. в) 10 000 па г) 540 мм. рт. ст выталкивающая сила, действующая на тело со стороны жидкости, в которую это тело поместили, зависит от: а) высоты жидкостного столба б) плотности жидкости и объема тела в) объема жидкости г) плотности тела и объема жидкости тело поместили в жидкость. при этом вес вытесненной этим телом жидкости равен 20 н. сила, архимеда, действующая со стороны жидкости на это тело равно… а) 10 н б) 0н в) 20 н г) 40 н прибор для измерения атмосферного давления называется… а) манометр б) психометр в) тахометр г) барометр тонометр служит для измерения… а) атмосферного давления б) артериального давления в) давления газа г) плотности атмосферное давление впервые рассчитал… а) ньютон б) паскаль в) торричелли г) архимед сосуды, соединенные между собой по нижней части, называются… а) последовательными б) сообщающимися в) параллельными г) соединенными № 2 (соотнесите формулы в левом столбце с их названием в правом столбике) hello_html_m67f6d9c9. gif а. давление жидкости или газа hello_html_220b91ea. gif б) уравнение для гидравлического пресса hello_html_m1810c3d6.gif в) закон архимеда hello_html_m5f583c74.gif г)условия, при которых тело всплывает hello_html_126a2799.gif д) давление № 3 (решите ) рассчитайте давление, которое производит вагон весом 200 кн на рельсы, если площадь соприкосновения всех колес вагона с рельсами равна 0,002 м. определите давление воды на самой большой глубине тихого океана равной 11 035 м. рассчитайте архимедову силу, действующую на железобетонную плиту размером 3,5×1,5×0,2 м, при ее полном погружении в воду? вес тела в воздухе равен 3,5 н, а его объем — 400 см3. потонет ли тело в воде?

Ответов: 3

Вариант 254 Ларина, решение ОГЭ математика 2020

На рисунке изображён план сельской местности (см. выше). Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово.

Из Антоновки в Богданово можно проехать по просёлочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово. Шоссе и просёлочные дороги образуют прямоугольные треугольники. По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км

Задание 1.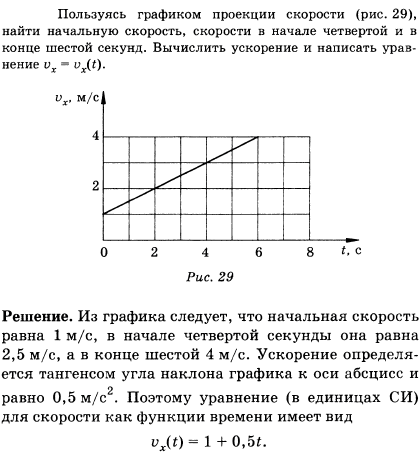

Для деревень, указанных в таблице, определите, какими числами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх чисел без пробелов и других разделительных символов.

ДеревниВанютиноГорюновоЕгоркаЖилино
Числа    

Задание 2.

Найдите расстояние от Горюново до Жилино по шоссе. Ответ дайте в километрах.

Задание 3.

Найдите расстояние от Доломино до Горюново по прямой. Ответ дайте в километрах.

Задание 4.

За какое наименьшее количество минут Таня с дедушкой могут добраться из Антоновки в Горюново?

Задание 5.

На просёлочных дорогах машина дедушки расходует 9,1 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Горюново мимо пруда ей необходим один и тот же объём бензина.

Сколько литров бензина на 100 км машина дедушки расходует на шоссе?

Расстояние между 2 точками

Краткое объяснение

Когда мы знаем расстояния по горизонтали и по вертикали между двумя точками, мы можем вычислить расстояние по прямой следующим образом:

расстояние = √ a 2 + b 2

Представьте, что вы знаете расположение двух точек (A и B), как здесь.

Какое расстояние между ними?

Мы можем провести линии вниз от A и вдоль от B, чтобы получился прямоугольный треугольник.

И с небольшой помощью Пифагора мы знаем, что:

a 2 + b 2 = c 2

Теперь отметьте координаты точек A и B.

x A означает координату x точки A
y A означает координату y точки A

Горизонтальное расстояние a равно (x A — x B )

Расстояние по вертикали b равно (y A — y B )

Теперь мы можем найти c (расстояние между точками):

Начнем с: c 2 = a 2 + b 2

Поместите в вычисления для a и b: c 2 = (x A — x B ) 2 + (y A — y B ) 2

Квадратный корень из обеих сторон: Выполнено!

Примеры

Пример 1

Введите значения:

Пример 2

Неважно, в каком порядке расположены точки, потому что возведение в квадрат удаляет любые негативы:

Введите значения:

Пример 3

А вот еще пример с некоторыми отрицательными координатами. .. все еще работает:

Введите значения:

(Примечание √136 может быть дополнительно упрощено до 2√34, если хотите)

Попробуйте сами

Перетащите точки:

Три или более измерения

Отлично работает в 3 (и более!) Измерениях.

Возвести в квадрат разность для каждой оси, затем просуммировать их и извлечь квадратный корень:

Расстояние = √ [(x A — x B ) 2 + (y A — y B ) 2 + (z A — z B ) 2 ]

Пример: расстояние между двумя точками (8,2,6) и (3,5,7) составляет:

= √ [(8−3) 2 + (2−5) 2 + (6−7) 2 ]
= √ [5 2 + (−3) 2 + (−1) 2 ]
= √ (25 + 9 + 1)
= √35
Что примерно равно 5. 9

Какова формула определения расстояния?

Расстояние между двумя точками

Если вы вспомните теорему Пифагора, формула расстояния на самом деле является вариацией этой теоремы.

Две точки на плоскости

Давайте углубимся в это с помощью точек на графике выше. У нас есть две точки: одна в x1, y1 и другая в x2, y2. Чтобы вычислить расстояние между ними, соедините точки вместе и сформируйте прямоугольный треугольник, который использует две точки в качестве углов.2

Следовательно, если бы мы подставили точки (x1, y1) и (x2, y2), а затем переместили квадрат на другую сторону уравнения, чтобы он стал квадратным корнем, мы получим формулу за расстояние.

Какова формула расстояния?

d используется для обозначения расстояния в этом случае. Эта формула всегда верна и полезна, когда у вас есть два очка. Если вы знаете, где они находятся на графике, вы можете построить их, а затем нарисовать прямоугольный треугольник, который поможет вам найти длину его гипотенузы. Это использует теорему Пифагора, которую мы узнали еще при изучении геометрии. Гипотенуза — это расстояние, которое вы ищете между двумя точками! Теперь вы узнали, как работает формула расстояния.

При расчете расстояния следует помнить следующее: 1) Следите за тем, чтобы ваши значения x и y не совпадали. Убедитесь, что вы правильно сопоставили их в правильном порядке, так что если вы используете значение x в точке A, сопоставьте его со значением x в точке B при вычитании.Затем для второй части формулы убедитесь, что вы снова используете значение y из точки A, а затем вычитаете значение y из точки B. 2) Упростите то, что указано в круглых скобках, прежде чем выполнять возведение в квадрат. Это правильный порядок при решении математических задач, и он верен в формуле расстояния. 3) Не забудьте записать символ квадратного корня. Это хорошая привычка, и если вы оставите ее до конца, вы можете забыть вернуть ее и получить неправильный ответ.

Примеры определения расстояния

Давайте воспользуемся формулой для расчета расстояния с примером вопроса.

Вопрос: какое расстояние между точками A (4,2) и B (6,8)?

Мы знаем, что будем использовать как значения x, так и значения y. Просто подставьте числа в формулу расстояния. Это будет выглядеть примерно так:

Этапы использования формулы расстояния

Выше мы рассматриваем B как точку 2 и последовательно используем координаты точки 2 перед A в формуле. Не забудьте возвести в квадрат разницу между X и Y, и вы получите число под квадратным корнем.Обязательно упростите ответ, чтобы некоторые числа можно было вынести из радикального символа.

Как насчет того, чтобы делать горизонтальные или вертикальные линии? Подойдет ли формула расстояния? Короткий ответ — будет. Однако есть более простой способ сделать это. При работе с горизонтальными линиями длина линии — это просто разница между x-координатами двух точек. Аналогичным образом длину вертикальной линии можно найти, вычитая одну из координат y с другой.Вы можете свободно попробовать это самостоятельно с координатами по вертикальной или горизонтальной линии, и вы обнаружите, что получите тот же ответ, просто вычтя координаты и используя формулу расстояния.

Чтобы подытожить концепцию, вот хороший ресурс, который вы можете изучить. Если вы хотите поиграть с разными координатами и посмотреть, как работает формула расстояния, попробуйте ее на этой интерактивной диаграмме!

Расстояние, середина и парабола

Конические секции

Коническое сечение Кривая, полученная на пересечении прямого кругового конуса и плоскости.кривая, полученная из пересечения прямого кругового конуса и плоскости. Конические сечения — это парабола, круг, эллипс и гипербола.

Цель состоит в том, чтобы нарисовать эти графики на прямоугольной координатной плоскости.

Формулы расстояния и средней точки

Начнем с обзора формулы расстояния. Для двух точек (x1, y1) и (x2, y2) расстояние d между ними определяется как d = (x2 − x1) 2+ (y2 − y1) 2.. Для двух точек (x1, y1) и (x2, y2) в прямоугольной координатной плоскости расстояние d между ними определяется формулой расстояния

д = (х2-х1) 2+ (у2-у1) 2

Кроме того, точка, которая делит пополам отрезок прямой, образованный этими двумя точками, называется средней точкой.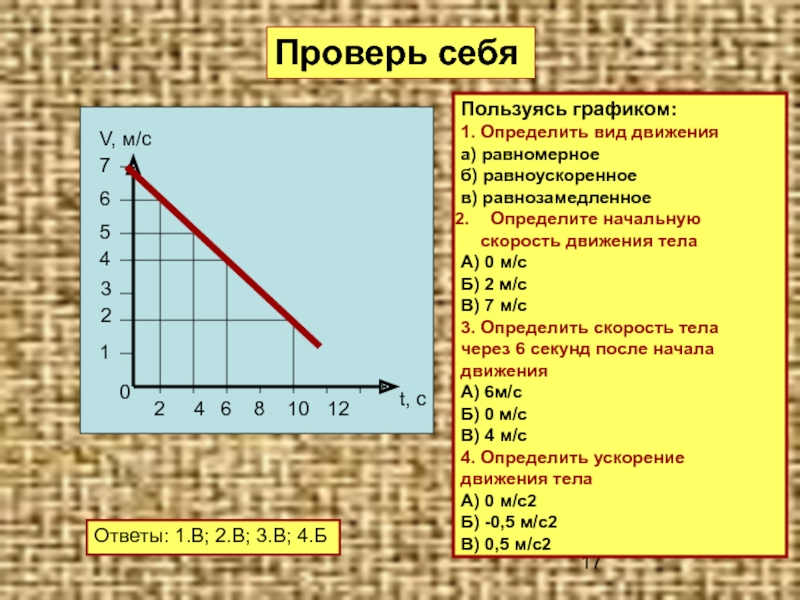 Учитывая две точки (x1, y1) и (x2, y2), средняя точка представляет собой упорядоченную пару, заданную формулой (x1 + x22, y1 + y22). . и определяется формулой

(x1 + x22, y1 + y22)

Средняя точка — это упорядоченная пара, образованная средним значением x и средним значением y .

Пример 1

Учитывая (−2, −5) и (−4, −3), вычислите расстояние и среднюю точку между ними.

Решение:

В этом случае мы будем использовать формулы со следующими точками:

(x1, y1) (x2, y2) (- 2, −5) (- 4, −3)

Рекомендуется включать формулу в ее общем виде перед заменой значений переменных; это улучшает читаемость и снижает вероятность ошибок.

d = (x2 − x1) 2+ (y2 − y1) 2 = [- 4 — (- 2)] 2 + [- 3 — (- 5)] 2 = (- 4 + 2) 2 + (- 3 +5) 2 = (- 2) 2+ (2) 2 = 4 + 4 = 8 = 22

Затем определите среднюю точку.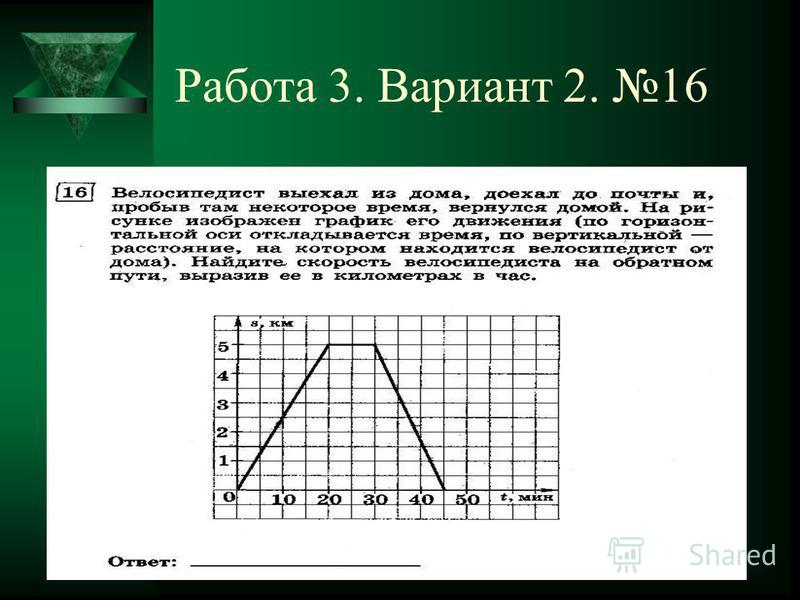

(x1 + x22, y1 + y22) = (- 2 + (- 4) 2, −5 + (- 3) 2) = (- 62, −82) = (- 3, −4)

Нанося эти точки на имеющийся график,

Ответ: Дистанция: 22 единицы; средняя точка: (−3, −4)

Пример 2

Диаметр круга определяется двумя точками (−1,2) и (1, −2).Определите радиус круга и используйте его для вычисления его площади.

Решение:

Найдите диаметр по формуле расстояния.

d = (x2 − x1) 2+ (y2 − y1) 2 = [1 — (- 1)] 2 + (- 2−2) 2 = (2) 2 + (- 4) 2 = 4 + 16 = 20 = 25

Напомним, что радиус круга равен половине диаметра круга. Следовательно, если d = 25 единиц, то

г = d2 = 252 = 5

Площадь круга определяется формулой A = πr2, и мы имеем

А = π (5) 2 = π⋅5 = 5π

Площадь измеряется в квадратных единицах.

Ответ: Радиус: 5 единиц; площадь: 5π квадратных единиц

Попробуй! Учитывая (0,0) и (9, −3), вычислите расстояние и среднюю точку между ними.

Ответ: Дистанция: 310 единиц; середина: (92, −32)

Парабола

Парабола Множество точек на плоскости, равноудаленных от заданной линии, называемой директрисой, и точки, не лежащей на линии, называемой фокусом.- это набор точек на плоскости, равноотстоящих от заданной линии, называемый директрисой, и точка, не лежащая на прямой, называемая фокусом. Другими словами, если задана линия L директрисой, а точка F — фокус, то (x, y) является точкой на параболе, если кратчайшее расстояние от нее до фокуса и от нее до линии равно как на картинке ниже:

Вершина параболы — это точка, в которой кратчайшее расстояние до директрисы минимально. Кроме того, парабола образуется пересечением конуса с наклонной плоскостью, параллельной стороне конуса:

Напомним, что график квадратичной функции, полиномиальной функции степени 2, является параболическим. Мы можем записать уравнение параболы в общем виде Уравнение параболы, записанное в виде y = ax2 + bx + c или x = ay2 + by + c, где a , b и c являются действительными числа и a 0. или мы можем записать уравнение параболы в стандартной форме Уравнение параболы, записанное в виде y = a (x − h) 2 + k или x = a (y − k) 2 + h.:

Стандарт общего вида Formy = ax2 + bx + c y = a (x − h) 2 + k

Здесь a , b и c — действительные числа, a 0. Обе формы полезны для определения общей формы графика. Однако в этом разделе мы сосредоточимся на получении стандартной формы, которую часто называют вершинной формой. Уравнение параболы, записанное в стандартной форме, часто называют вершинной формой. В этой форме вершина очевидна: (h, k) .. Для квадратичной функции в стандартной форме вершиной является (h, k).Чтобы убедиться в этом, рассмотрим построение графика y = (x + 3) 2 + 2 с использованием преобразований.

y = x2 Базовая функция возведения в квадрат. Y = (x + 3) 2 Горизонтальный сдвиг влево на 3 единицы. Y = (x + 3) 2 + 2 Вертикальный сдвиг вверх на 2 единицы.

Используйте эти переводы, чтобы нарисовать график,

Здесь мы видим, что вершина равна (−3,2). Это можно определить непосредственно из уравнения в стандартной форме

y = a (x − h) 2 + k ↓ ↓ y = [x — (- 3)] 2 + 2

В таком виде мы видим, что вершина равна (−3,2).Однако это уравнение обычно не приводится в стандартной форме. Преобразование общей формы в стандартную путем завершения квадрата — это основной процесс, с помощью которого мы нарисуем все конические сечения.

Пример 3

Перепишем уравнение в стандартной форме и определим вершину его графика: y = x2−8x + 15.

Решение:

Начните с того, что освободите место для постоянного члена, завершающего квадрат.

y = x2−8x + 15 = x2−8x + ___ + 15 −___

Идея состоит в том, чтобы сложить и вычесть значение, завершающее квадрат, (b2) 2, а затем разложить на множители.В этом случае сложите и вычтите (b2) 2 = (- 82) 2 = (- 4) 2 = 16.

y = x2−8x + 15 Сложить и вычесть 16. = (x2−8x +16) +15 −16Factor. = (X − 4) (x − 4) −1 = (x − 4) 2−1

Добавление и вычитание одного и того же значения в выражении не меняют его. Это эквивалентно добавлению 0. Когда уравнение имеет такую ​​форму, мы можем легко определить вершину.

y = a (x — h) 2 + k ↓ ↓ y = (x − 4) 2 + (- 1)

Здесь у нас есть перевод вправо на 4 единицы и вниз на 1 единицу.Следовательно, h = 4 и k = −1.

Ответ: y = (x − 4) 2−1; вершина: (4, −1)

Если есть ведущий коэффициент, отличный от 1, то начните с вынесения этого ведущего коэффициента из первых двух членов трехчлена.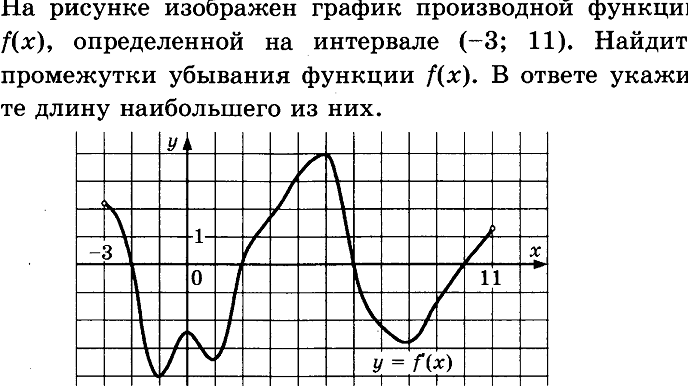

Пример 4

Перепишем уравнение в стандартной форме и определим вершину графика: y = −2×2 + 12x − 16.

Решение:

Поскольку a = −2, вычтите это из первых двух членов, чтобы завершить квадрат.Оставьте место в круглых скобках для добавления и вычитания значения, завершающего квадрат.

y = −2×2 + 12x − 16 = −2 (x2−6x + ___ − ___) — 16

Теперь используйте −6, чтобы определить значение, завершающее квадрат. В этом случае (b2) 2 = (- 62) 2 = (- 3) 2 = 9. Сложите и вычтите 9 и разложите множители следующим образом:

y = −2×2 + 12x − 16 = −2 (x2−6x + ___ −___) −16 Сложить и вычесть 9. = — 2 (x2−6x + 9−9) −16 Фактор. = — 2 [(x− 3) (x − 3) −9] −16 = −2 [(x − 3) 2−9] −16 Распределите −2. = — 2 (x − 3) 2 + 18−16 = −2 (x −3) 2 + 2

В таком виде мы можем легко определить вершину.

y = a (x − h) 2 + k ↓↓ y = −2 (x − 3) 2 + 2

Здесь h = 3 и k = 2.

Ответ: y = −2 (x − 3) 2 + 2; вершина: (3,2)

Используйте как общую, так и стандартную форму при построении графика параболы.

Пример 5

График: y = −2×2 + 12x − 16.

Решение:

Из предыдущего примера у нас есть две эквивалентные формы этого уравнения:

Общая форма Стандартная форма: y = −2×2 + 12x − 16 y = −2 (x − 3) 2 + 2

Напомним, что если старший коэффициент a> 0, парабола открывается вверх, а если a <0, парабола открывается вниз.В этом случае a = −2, и мы заключаем, что парабола открывается вниз. Используйте общую форму для определения точки перехвата y . Когда x = 0, мы видим, что интервал y равен (0, -16). Из уравнения в стандартной форме видно, что вершиной является (3,2). Чтобы найти перехват x , мы могли бы использовать любую форму. В этом случае мы будем использовать стандартную форму для определения значений x , где y = 0,

y = −2 (x − 3) 2 + 2 Положим y = 0 и решим: 0 = −2 (x − 3) 2 + 2 −2 = −2 (x − 3) 21 = (x − 3) 2 Примените свойство квадратного корня.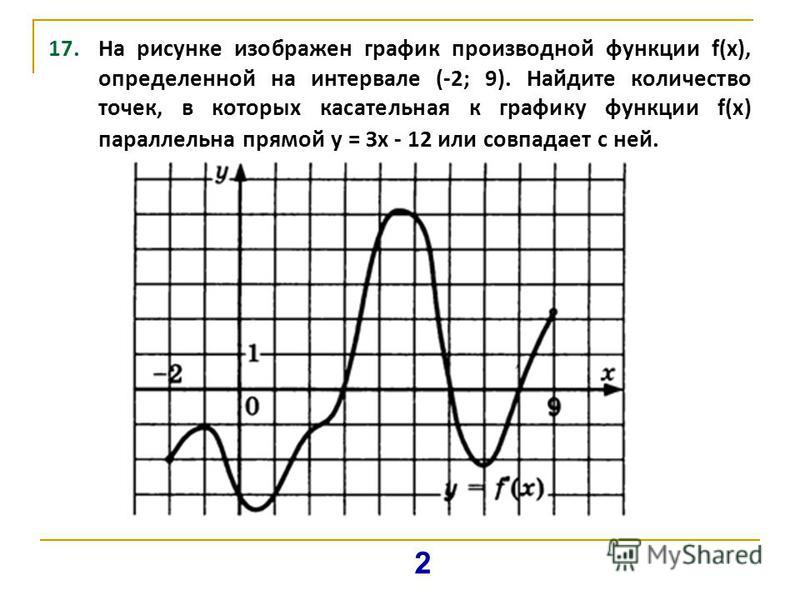 ± 1 = х-33 ± 1 = х

Здесь x = 3−1 = 2 или x = 3 + 1 = 4, и поэтому x -перехватывания равны (2,0) и (4,0). Используйте эту информацию, чтобы нарисовать график.

Ответ:

До сих пор мы рисовали параболы, которые открываются вверх или вниз, потому что эти графики представляют функции. На этом этапе мы расширяем наше исследование, включив параболы, которые открываются вправо или влево. Если мы возьмем уравнение, определяющее параболу в предыдущем примере,

у = −2 (х − 3) 2 + 2

и переключая значения x и y , получаем

х = -2 (у-3) 2 + 2

Это создает новый график с симметрией относительно прямой y = x.

Обратите внимание, что полученный график не является функцией. Однако он имеет ту же общую параболическую форму, которая открывается влево. Мы можем распознать уравнения парабол, которые открываются влево или вправо, заметив, что они квадратичны относительно y вместо x . Графическое изображение парабол, открывающихся влево или вправо, аналогично графическому изображению парабол, открывающихся вверх и вниз. В целом у нас

Во всех случаях вершина равна (h, k).Обратите внимание на размещение h и k в каждом уравнении.

Пример 6

График: x = y2 + 10y + 13.

Решение:

Поскольку коэффициент при y2 положительный, a = 1, мы заключаем, что график представляет собой параболу, которая открывается вправо. Кроме того, когда y = 0, ясно, что x = 13 и, следовательно, пересечение x равно (13,0). Заполните квадрат, чтобы получить стандартную форму. Здесь мы будем складывать и вычитать (b2) 2 = (102) 2 = (5) 2 = 25.

x = y2 + 10y + 13 = y2 + 10y + 25−25 + 13 = (y + 5) (y + 5) −12 = (y + 5) 2−12

Следовательно,

x = a (y − k) 2 + h ↓↓ x = (y — (- 5)) 2 + (- 12)

Отсюда видно, что вершина (h, k) = (- 12, −5). Затем используйте стандартную форму, чтобы найти y -перехватывания, установив x = 0.

x = (y + 5) 2−120 = (y + 5) 2−1212 = (y + 5) 2 ± 12 = y + 5 ± 23 = y + 5−5 ± 23 = y

Интерпретациями y являются (0, −5−23) и (0, −5 + 23). Используйте эту информацию, чтобы нарисовать график.

Ответ:

Пример 7

График: x = −2y2 + 4y − 5.

Решение:

Поскольку коэффициент при y2 равен a = −2, мы заключаем, что график представляет собой параболу, которая открывается влево. Кроме того, когда y = 0, ясно, что x = −5 и, следовательно, пересечение x равно (−5,0). Начните с вычитания ведущего коэффициента следующим образом:

x = −2y2 + 4y − 5 = −2 (y2−2y + ___ − ___) — 5

Здесь мы будем складывать и вычитать (b2) 2 = (- 22) 2 = (- 1) 2 = 1.

x = −2y2 + 4y − 5 = −2 (y2−2y + 1−1) −5 = −2 [(y − 1) 2−1] −5 = −2 (y − 1) 2 + 2− 5 = −2 (y − 1) 2−3

Следовательно, из формы вершины x = −2 (y − 1) 2−3, мы видим, что вершина равна (h, k) = (- 3,1). Поскольку вершина находится в точке (−3,1), а парабола открывается слева, мы можем заключить, что нет пересечений y . Поскольку у нас есть только две точки, выберите несколько значений y и найдите соответствующие значения x .

xyx = −2 (y − 1) 2−3−11−1x = −2 (−1−1) 2−3 = −2 (−2) 2−3 = −11−52x = −2 (2− 1) 2−3 = −2 (1) 2−3 = −5−113x = −2 (3−1) 2−3 = −2 (2) 2−3 = −11

Ответ:

Попробуй! График: x = y2 − y − 6.

Ответ:

Ключевые выводы

  • Используйте формулу расстояния, чтобы определить расстояние между любыми двумя заданными точками. Используйте формулу средней точки, чтобы определить среднюю точку между любыми двумя заданными точками.
  • Парабола может открываться вверх или вниз, в этом случае это функция. В этом разделе мы расширяем наше исследование парабол, чтобы включить те, которые открываются влево или вправо.Такие графики не представляют функций.
  • Уравнение параболы, которая открывается вверх или вниз, квадратично относительно x , y = ax2 + bx + c. Если a> 0, то парабола открывается вверх, а если a <0, то парабола открывается вниз.
  • Уравнение параболы, которая открывается влево или вправо, квадратично относительно y , x = ay2 + by + c. Если a> 0, то парабола открывается вправо, а если a <0, то парабола открывается влево.
  • Уравнение параболы в общем виде y = ax2 + bx + c или x = ay2 + by + c может быть преобразовано к стандартной форме y = a (x − h) 2 + k или x = a (y − k) 2 + ч, завершив пл.
  • При заполнении квадрата убедитесь, что ведущий коэффициент группировки переменных равен 1, прежде чем добавлять и вычитать значение, завершающее квадрат.
  • Как общие, так и стандартные формы полезны при построении парабол. В стандартной форме вершина очевидна (h, k). Чтобы найти точку пересечения x , установите y = 0 и решите относительно x , а чтобы найти точку пересечения y , установите x = 0 и решите относительно y .

Тематические упражнения

    Часть A: Формулы расстояния и средней точки

      Вычислить расстояние и среднюю точку между заданными двумя точками.

    1. (−1, −3) и (5, −11)

    4. (−5, −6) и (−3, −4)

    6. (−6, −4) и (−12,1)

    12. (-43,2) и (-13, -12)

    13. (15, -95) и (310, -52)

    14. (-12,43) и (-23,56)

      Определите площадь круга, диаметр которого определяется двумя заданными точками.

      Определите периметр треугольника по координатам вершин.

    1. (5,3), (2, −3) и (8, −3)

    2. (−3,2), (−4, −1) и (−1,0)

    3. (3,3), (5,3−23) и (7,3)

      Найдите a так, чтобы расстояние d между точками было равно заданной величине.

    1. (1,2) и (4, а); d = 5 шт.

    2. (−3, а) и (5,6); d = 10 шт.

    3. (3,1) и (а, 0); d = 2 шт.

    4. (а, 1) и (5,3); d = 13 шт.

    Часть B: Парабола

      График.Обязательно найдите вершину и все пересечения.

      Перепишите в стандартном виде и дайте вершину.

      Перепишите в стандартной форме и графике.Обязательно найдите вершину и все пересечения.

    Часть C: Обсуждение

    1. Исследуйте и обсуждайте реальные приложения, использующие параболу.

    2. Все ли параболы имеют точки пересечения x ? Объяснять.

    3. Все ли параболы имеют точки пересечения и ? Объяснять.

    4. Составьте свою собственную параболу, которая открывается влево или вправо, запишите ее в общем виде и нанесите на график.

ответов

  1. Дальность: 10 единиц; середина: (2, −7)

  3. Дистанция: 213 единиц; средняя точка: (1, −4)

  5. Дальность: 52 единицы; середина: (192,52)

  7. Дальность: 5 единиц; середина: (22,32)

  9. Дальность: 5 единиц; середина: (352, −3)

  11. Дистанция: 522 единицы; средняя точка: (-34,14)

  13. Дальность: 22 единицы; середина: (14, −4320)

  15. Дистанция: юниты a2 + b2; середина: (a2, b2)

  15. у = (х — 3) 2 + 9; вершина: (3,9)

  17. х = (у + 10) 2−13; вершина: (−13, −10)

  19. у = (х − 7) 2; вершина: (7,0)

  21. х = 2 (у — 1) 2 + 3; вершина: (3,1)

  23. у = 6 (х + 3) 2; вершина: (−3,0)

  25. y = 2 (x − 12) 2−32; вершина: (12, −32)

  27. х = — (у-52) 2 + 54; вершина: (54,52)

  29. y = (x − 2) 2−9;

  31. у = — (х − 6) 2 + 4;

  33. у = 2 (х + 1) 2 + 7;

  35. y = −5 (x − 3) 2;

  37. х = (y − 1) 2−9;

  39. x = (y − 1) 2−4;

  41. х = — (у + 5) 2 + 1;

  43. х = 3 (у + 2) 2;

  45. x = (y − 2) 2−7;

  47. х = — (у − 1) 2 + 6;

  49. y = −3 (x − 13) 2 + 43;

  51. х = -4 (у + 12) 2-4;

  53. y = (x + 52) 2−294;

  55. х = 2 (у + 52) 2−12;

Как найти длину отрезка по формуле расстояния

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Найдите расстояние между точкой и линией

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Графические уравнения с программой «Пошаговое решение математических задач»

Язык математики особенно эффективен для представления отношений между двумя или более переменными.В качестве примера рассмотрим пройденное расстояние через определенный промежуток времени автомобилем, движущимся с постоянной скоростью 40 миль в час. Мы можем представить эту взаимосвязь как

  1. 1. Словесное предложение:
    Пройденное расстояние в милях равно сороккратному количеству пройденных часов.
  2. 2. Уравнение:
    d = 40r.
  3. 3. Таблица значений.
  4. 4. График, показывающий зависимость между временем и расстоянием.

Мы уже использовали словесные предложения и уравнения для описания таких отношений; В этой главе мы будем иметь дело с табличным и графическим представлениями.

7.1 РЕШЕНИЕ УРАВНЕНИЙ ОТ ДВУХ ПЕРЕМЕННЫХ

ЗАКАЗАННЫЕ ПАРЫ

Уравнение d = 40f объединяет расстояние d для каждого момента времени t. Например,


если t = 1, то d = 40
, если t = 2, то d = 80
, если t = 3, то d = 120

и так далее.

Пара чисел 1 и 40, рассматриваемая вместе, называется решением уравнение d = 40r, потому что, когда мы подставляем 1 вместо t и 40 вместо d в уравнении, мы получаем верное утверждение. Если мы согласны ссылаться на парные номера в указанном порядок, в котором первое число относится ко времени, а второе число относится к расстояния, мы можем сократить приведенные выше решения как (1, 40), (2, 80), (3, 120) и скоро.Мы называем такие пары чисел упорядоченными парами и ссылаемся на первую и вторые числа в парах как компоненты. В соответствии с этим соглашением решения Уравнение d — 40t — это упорядоченные пары (t, d), компоненты которых удовлетворяют уравнению. Некоторые упорядоченные пары для t, равного 0, 1, 2, 3, 4 и 5, равны

(0,0), (1,40), (2,80), (3,120), (4,160) и (5,200)

Такие пары иногда показаны в одной из следующих табличных форм.

В любом конкретном уравнении, включающем две переменные, когда мы присваиваем значение одной переменных определяется значение другой переменной и, следовательно, зависит от первого.Удобно говорить о переменной, связанной с первый компонент упорядоченной пары как независимая переменная и переменная связанный со вторым компонентом упорядоченной пары в качестве зависимой переменной. Если в уравнении используются переменные x и y, подразумевается, что заменить — элементы для x являются первыми компонентами и, следовательно, x — независимая переменная и замены y являются вторыми компонентами и, следовательно, y является зависимой переменной. Например, мы можем получить пары для уравнения

, подставив конкретное значение одной переменной в уравнение (1) и решив для другая переменная.

Пример 1

Найдите недостающий компонент, чтобы заказанная пара была решением для

2x + y = 4

а. (0 ,?)

г. (1 ,?)

г. (2 ,?)

Решение

если x = 0, то 2 (0) + y = 4
y = 4

если x = 1, то 2 (1) + y = 4
y = 2

если x = 2, то 2 (2) + y = 4
y = 0

Три пары теперь могут отображаться как три упорядоченные пары

(0,4), (1,2) и (2,0)

или в табличной форме

ЯВНО ВЫРАЖАЮЩИЙ ПЕРЕМЕННУЮ

Мы можем прибавить -2x к обоим членам 2x + y = 4, чтобы получить

-2x + 2x + y = -2x + 4
y = -2x + 4

В уравнении (2), где y есть само по себе, мы говорим, что y явно выражается через из х.Часто бывает проще получить решения, если сначала выразить уравнения в такой форме потому что зависимая переменная явно выражается через независимые Переменная.

Например, в уравнении (2) выше

, если x = 0, то y = -2 (0) + 4 = 4
, если x = 1, то y = -2 (1) + 4 = 2
, если x = 2, то y = -2 (2) + 4 = 0

Мы получаем те же пары, которые мы получили с помощью уравнения (1)

(0,4), (1,2) и (2,0)

Мы получили уравнение (2) добавлением одинаковой величины -2x к каждому члену уравнения (1), таким образом получая y само по себе.В общем, мы можем написать эквивалент уравнения с двумя переменными, используя свойства, которые мы ввели в главе 3, где мы решали уравнения первой степени с одной переменной.

Уравнения эквивалентны, если:

  1. Одно и то же количество прибавляется к равным количествам или вычитается из них.
  2. Равные количества умножаются или делятся на одинаковое ненулевое количество.

Пример 2

Решите 2y — 3x = 4 явно для y через x и получите решения для x = 0, х = 1 и х = 2.

Решение
Во-первых, добавив 3x к каждому члену, мы получим

2y — 3x + 3x = 4 + 3x
2y = 4 + 3x (продолжение)

Теперь, разделив каждый член на 2, получим

В этой форме мы получаем значения y для заданных значений x следующим образом:

В этом случае три решения: (0, 2), (1, 7/2) и (2, 5).

ОБОЗНАЧЕНИЕ ФУНКЦИЙ

Иногда мы используем специальные обозначения для наименования второго компонента упорядоченного пара, которая связана с указанным первым компонентом.Символ f (x), который часто бывает используется для обозначения алгебраического выражения в переменной x, также может использоваться для обозначения значение выражения для конкретных значений x. Например, если

f (x) = -2x + 4

, где f (x) играет ту же роль, что и y в уравнении (2) на странице 285, тогда f (1) представляет значение выражения -2x + 4, когда x заменяется на 1

f (l) = -2 (1) + 4 = 2

Аналогично

f (0) = -2 (0) + 4 = 4

и

f (2) = -2 (2) + 4 = 0

Символ f (x) обычно называют обозначением функции.

Пример 3

Если f (x) = -3x + 2, найти f (-2) и f (2).

Решение

Замените x на -2, чтобы получить
f (-2) = -3 (-2) + 2 = 8

Замените x на 2, чтобы получить
f (2) = -3 (2) + 2 = -4

7.2 ГРАФИКИ ЗАКАЗАННЫХ ПАР

В разделе 1.1 мы видели, что каждое число соответствует точке в строке. Simi- Как правило, каждая упорядоченная пара чисел (x, y) соответствует точке на плоскости. К граф упорядоченной пары чисел, мы начинаем с построения пары перпендикулярных числовые линии, называемые осями.Горизонтальная ось называется осью x, вертикальная ось называется осью Y, а точка их пересечения называется началом координат. Эти топоры разделите плоскость на четыре квадранта, как показано на рисунке 7.1.

Теперь мы можем присвоить упорядоченную пару чисел точке на плоскости, указав на перпендикулярное расстояние точки от каждой из осей. Если первый составляющая положительная, точка лежит правее вертикальной оси; если отрицательный, это лежит слева.Если второй компонент положительный, точка находится выше Горизонтальная ось; если отрицательный, он находится внизу.

Пример 1

График (3, 2), (-3, 2), (-3, -2) и (3, -2) в прямоугольной системе координат.

Решение
График (3, 2) находится на 3 единицы правее ось y и на 2 единицы выше оси x; график (-3,2) лежит на 3 единицы слева от ось y и на 2 единицы выше оси x; график (-3, -2) лежит на 3 единицы слева от ось y и на 2 единицы ниже оси x; график (3, -2) лежит на 3 единицы правее ось y и на 2 единицы ниже оси x.

Расстояние y, на котором точка расположена от оси x, называется ординатой. точки, а расстояние x, на котором точка расположена от оси y, называется абсцисса точки. Абсцисса и ордината вместе называются прямоугольником. Гулярные или декартовы координаты точки (см. рисунок 7.2).

7.3 ИЗОБРАЖЕНИЕ УРАВНЕНИЙ ПЕРВОГО УРОВНЯ

В разделе 7.1 мы увидели, что решение уравнения с двумя переменными является упорядоченным пара.В разделе 7.2 мы видели, что компонентами упорядоченной пары являются координаты точки на плоскости. Таким образом, чтобы построить график уравнения с двумя переменными, мы Изобразите набор упорядоченных пар, которые являются решениями уравнения. Например, мы может найти некоторые решения уравнения первой степени

у = х + 2

, положив x равным 0, -3, -2 и 3. Затем

для x = 0, y = 0 + 2 = 2
для x = 0, y = -3 + 2 = -1
для x = -2, y = -2 + 2-0
для x = 3, y = 3 + 2 = 5

и получаем решения

(0,2), (-3, -1), (-2,0) и (3,5)

, который может отображаться в табличной форме, как показано ниже.

Если мы изобразим точки, определенные этими упорядоченные пары и проведите прямую через их, мы получаем график всех решений y = x + 2, как показано на рисунке 7.3. То есть, каждое решение y = x + 2 лежит на прямой, и каждая точка на линии является решением у = х + 2.

Графики уравнений первой степени в двух переменные всегда прямые; следовательно, такие уравнения также называются линейными уравнения.

В приведенном выше примере значения, которые мы использовали для x были выбраны случайным образом; мы могли бы использовать любые значения x, чтобы найти решения уравнения.Графики любых других упорядоченных пар, которые являются решениями уравнения, также будут быть на линии, показанной на рисунке 7.3. Фактически каждое линейное уравнение с двумя переменными имеет бесконечное количество решений, график которых лежит на прямой. Однако мы только нужно найти два решения, потому что для определения прямая линия. Третий балл можно получить как проверку.

Чтобы изобразить уравнение первой степени:

  1. Постройте набор прямоугольных осей, показывающих масштаб и переменную, представляющую отправляется каждой осью.
  2. Найдите две упорядоченные пары, которые являются решениями уравнения, которое нужно построить на графике. присвоение любого удобного значения одной переменной и определение соответствующего значение другой переменной.
  3. Изобразите эти заказанные пары.
  4. Проведите прямую линию через точки.
  5. Проверьте, построив график третьей упорядоченной пары, которая является решением уравнения и убедитесь, что он лежит на линии.

Пример 1

Изобразите уравнение y = 2x — 6.

Решение
Сначала мы выбираем любые два значения x, чтобы найти соответствующие значения y.
Мы будем использовать 1 и 4 для x.
Если x = 1, y = 2 (1) — 6 = -4
, если x = 4, y = 2 (4) — 6 = 2
Таким образом, два решения уравнения:
(1, -4) и (4, 2).
Затем мы строим график этих упорядоченных пар и проводим прямую линию через точки, как показано на рисунке. Мы используем стрелки, чтобы показать, что линия тянется бесконечно далеко в обоих направлениях. Любая третья упорядоченная пара, удовлетворяющая Уравнение можно использовать в качестве проверки:
, если x = 5, y = 2 (5) -6 = 4
Затем отметим, что график (5, 4) также лежит на линии
. Чтобы найти решения уравнения, как мы уже отмечали, часто проще всего сначала решить явно для y через x.

Пример 2

График x + 2y = 4.

Решение
Сначала решаем y через x, чтобы получить

Теперь мы выбираем любые два значения x, чтобы найти соответствующие значения y. Мы будем использовать 2 и 0 для x.

Таким образом, двумя решениями уравнения являются (2, 1) и (0, 2).

Затем мы графически отображаем эти упорядоченные пары и проведите через точки прямую, как показано на рисунке.

Любая третья упорядоченная пара, удовлетворяющая уравнение можно использовать как проверку:

Затем отметим, что график (-2, 3) также лежит на линии.

ОСОБЫЕ СЛУЧАИ ЛИНЕЙНЫХ УРАВНЕНИЙ

Уравнение y = 2 можно записать как

0x + y = 2

и может рассматриваться как линейное уравнение в двух переменные, у которых коэффициент при x равен 0. Некоторые решения 0x + y = 2 равны

(1,2), (-1,2) и (4,2)

Фактически, любая упорядоченная пара вида (x, 2) является решение (1). Графическое изображение решений дает горизонтальную линию, как показано на рисунке 7.4.

Аналогично, уравнение, такое как x = -3, может можно записать как

х + 0у = -3

и может рассматриваться как линейное уравнение в двух переменные, у которых коэффициент при y равен 0.

Некоторые решения x + 0y = -3 являются (-3, 5), (-3, 1) и (-3, -2). Фактически любой упорядоченная пара вида (-3, y) является решением из (2). Построение графика решений дает вертикальную линии, как показано на рисунке 7.5.

Пример 3

График

а. у = 3
б. х = 2

Решение
а. Мы можем записать y = 3 как Ox + y = 3.
Некоторые решения: (1, 3), (2,3) и (5, 3).

б. Мы можем записать x = 2 как x + Oy = 2.
Некоторые решения: (2, 4), (2, 1) и (2, -2).

7.4 МЕТОД ПЕРЕСЕЧЕНИЯ ГРАФИКА

В разделе 7.3 мы присвоили значения x в уравнениях с двумя переменными, чтобы найти соответствующие значения y. Решения уравнения с двумя переменными, равные как правило, легче всего найти те, в которых первый или второй компонент 0. Например, если мы заменим 0 на x в уравнении

3x + 4y = 12

у нас

3 (0) + 4y = 12
y = 3

Таким образом, решением уравнения (1) является (0, 3).Мы также можем найти упорядоченные пары, которые решения уравнений с двумя переменными путем присвоения значений y и определения соответствующие значения x. В частности, если мы подставим 0 вместо y в уравнение (1), мы получить

3x + 4 (0) = 12
x = 4

и второе решение уравнения (4, 0). Теперь мы можем использовать упорядоченные пары (0, 3) и (4, 0) для построения графика уравнения (1). График представлен на рисунке 7.6. Уведомление что линия пересекает ось x в точке 4 и ось y в точке 3. По этой причине число 4 называется пересечением по оси x графа, а число 3 — точкой пересечения по оси y.

Этот метод построения графика линейного уравнения называется пересечением. метод построения графиков. Обратите внимание, что когда мы используем этот метод построения графиков линейного уравнение, нет никакого преимущества в том, чтобы сначала явно выразить y через x.

Пример 1

График 2x — y = 6 методом пересечения.

Решение
Мы находим точку пересечения с x, подставляя 0 вместо y в уравнение, чтобы получить

2x — (0) = 6
2x = 6
x = 3

Теперь мы находим точку пересечения по оси Y, подставляя для x в уравнении, чтобы получить

2 (0) — y = 6
-y = 6
y = -6

Упорядоченные пары (3, 0) и (0, -6) являются решениями 2x — y = 6.Графическое изображение этих точки и соединив их прямой линией, получим график 2x — y = 6. Если график пересекает оси в или около начала координат, метод перехвата не работает. удовлетворительно. Затем мы должны построить график упорядоченной пары, которая является решением уравнения и чей график не является началом координат или не слишком близок к началу координат.

Пример 2

График y = 3x.

Решение
Мы можем заменить 0 на x и найти
y = 3 (0) = 0
Аналогичным образом, заменив 0 на y, мы получим
0 = 3.x, x = 0
Таким образом, 0 является пересечением по оси x и точкой пересечения по оси y.

Так как одной точки недостаточно, чтобы получить = 3x, мы прибегаем к методам, описанным в Раздел 7.3. Выбирая любое другое значение для x, скажем 2, мы получаем

у = 3 (2) = 6

Таким образом, (0, 0) и (2, 6) являются решениями уравнение. График y = 3x показан на верно.

7,5 НАКЛОН ЛИНИИ

ФОРМУЛА НАКЛОНА

В этом разделе мы изучим важное свойство линии.Мы назначим число к линии, которую мы называем уклоном, что даст нам меру «крутизны» или «направление» линии.

Часто бывает удобно использовать специальные обозначения для различения прямоугольников. Гулярные координаты двух разных точек. Мы можем обозначить одну пару координат на (x 1 , y 1 (читается «x sub one, y sub one»), связанный с точкой P 1 , и второй пара координат по (x 2 , y 2 ), связанная со второй точкой P 2 , как показано на рисунке 7.7. Обратите внимание на рисунок 7.7, что при переходе от P 1 к P 2 вертикальное изменение (или расстояние по вертикали) между двумя точками составляет y 2 — y 1 , а изменение по горизонтали (или расстояние по горизонтали) составляет x 2 — x 1 .

Отношение вертикального изменения к горизонтальному называется крутизной линия, содержащая точки P 1 и P 2 . Это соотношение обычно обозначают m. Таким образом,

Пример 1

Найдите наклон прямой, содержащей два точки с координатами (-4, 2) и (3, 5) как показано на рисунке справа.

Решение
Обозначим (3, 5) как (x 2 , y 2 ) и (-4, 2) как (x 1 , y 1 ). Подставляя в уравнение (1) дает

Обратите внимание, что мы получим тот же результат, если подставим -4 и 2 вместо x 2 и y 2 и 3 и 5 для x 1 и y 1

Линии с различным уклоном показаны на Рисунке 7.8 ниже. Наклоны линий, которые вверх вправо положительны (рисунок 7.8а) и наклоны спускающихся вниз справа отрицательны (рис. 7.8b). Обратите внимание (рис. 7.8c), что, поскольку все точки на горизонтальной линии имеют одинаковое значение y, y 2 — y 1 равняется нулю для любых двух точек, а наклон линии просто

Также обратите внимание (рисунок 7.8c), что, поскольку все точки на вертикали имеют одинаковое значение x, x 2 — x 1 равняется нулю для любых двух точек. Однако

не определено, поэтому вертикальная линия не имеет наклона.

ПАРАЛЛЕЛЬНЫЕ И ПЕРПЕНДИКУЛЯРНЫЕ ЛИНИИ

Рассмотрим линии, показанные на рисунке 7.9. Линия l 1 имеет наклон m 1 = 3, а линия l 2 имеет уклон уклон м 2 = 3. В данном случае

Эти линии никогда не пересекаются и называются параллельными линиями. Теперь рассмотрим строки показано на рисунке 7.10. Линия l 1 имеет наклон m 1 = 1/2, а линия l 2 имеет наклон m 2 = -2. В данном случае

Эти линии пересекаются, образуя прямой угол, и называются перпендикулярными линиями.

Как правило, если две линии имеют уклон и м2:

    а. Линии параллельны, если они имеют одинаковый наклон, т. Е. если m 1 = m 2 .
    г. Линии перпендикулярны, если произведение их уклонов равно -1, то есть если m 1 * m 2 = -1.

7.6 УРАВНЕНИЯ ПРЯМЫХ ЛИНИЙ

ФОРМА POINT-SLOPE

В разделе 7.5 мы нашли наклон прямой по формуле

Допустим, мы знаем, что линия проходит через точку (2, 3) и имеет наклон 2.Если обозначить любую другую точку на прямой как P (x, y) (см. Рис. 7.1а), наклоном формула

Таким образом, уравнение (1) — это уравнение прямой, проходящей через точку (2, 3), и имеет уклон 2.

В общем, допустим, мы знаем, что линия проходит через точку P 1 (x 1 , y 1 и имеет уклон м. Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рис. 7.11 b), то через формула наклона

Уравнение (2) называется формой точечного уклона для линейного уравнения.В уравнении (2), m, x 1 и y 1 известны, а x и y — переменные, которые представляют координаты любая точка на линии. Таким образом, всякий раз, когда мы знаем наклон линии и точки на линии, мы можем найти уравнение линии, используя уравнение (2).

Пример 1

Прямая имеет наклон -2 и проходит через точку (2, 4). Найдите уравнение прямой.

Решение
Замените -2 вместо m и (2, 4) вместо (x 1 , y 1 ) в уравнении (2)

Таким образом, прямая с наклоном -2, проходящая через точку (2, 4), имеет уравнение у = -2х + 8.Мы могли бы также записать уравнение в эквивалентной форме y + 2x = 8, 2x + y = 8 или 2x + y — 8 = 0.

ФОРМА НАКЛОНА

Теперь рассмотрим уравнение прямой с наклоном m и точкой пересечения оси y b, как показано на Рисунок 7.12. Подставив 0 вместо x 1 и b вместо y 1 в форме точечного наклона линейного уравнение, имеем

y — b = m (x — 0)
y — b = mx

или

y = mx + b

Уравнение (3) называется формой пересечения наклона для линейного уравнения.Наклон и пересечение по оси Y можно получить непосредственно из уравнения в эта форма.

Пример 2 Если линия имеет уравнение

, то наклон линии должен быть -2, а точка пересечения оси Y должна быть 8. Аналогично, график

г = -3x + 4

имеет наклон -3 и точку пересечения по оси Y 4; и график

имеет наклон 1/4 и точку пересечения по оси Y -2.

Если уравнение не записано в форме x = mx + b, и мы хотим знать наклон и / или точку пересечения с y, мы переписываем уравнение, решая относительно y через x.

Пример 3

Найдите наклон и точку пересечения оси Y 2x — 3y = 6.

Решение
Сначала мы решаем y через x, добавляя -2x к каждому члену.

2x — 3y — 2x = 6 — 2x
— 3y = 6 — 2x

Теперь, разделив каждого члена на -3, мы получим

Сравнивая это уравнение с формой y = mx + b, отметим, что наклон m (величина коэффициент при x) равен 2/3, а точка пересечения оси y равна -2.

7.7 ПРЯМОЕ ИЗМЕНЕНИЕ

Частный случай уравнения первой степени с двумя переменными дается

y = kx (k — постоянная)

Такая связь называется прямой вариацией.Мы говорим, что переменная y изменяется непосредственно как x.

Пример 1

Мы знаем, что давление P в жидкости прямо пропорционально глубине d ниже поверхность жидкости. Мы можем обозначить это соотношение в символах как

P =

кД

В прямом варианте, если мы знаем набор условий для двух переменных, и если мы также знаем другое значение для одной из переменных, мы можем найти значение вторая переменная для этого нового набора условий.

В приведенном выше примере мы можем решить для константы k, чтобы получить

Поскольку отношение P / d постоянно для каждого набора условий, мы можем использовать соотношение для решения задач, связанных с прямым изменением.

Пример 2

Если давление P напрямую зависит от глубины d и P = 40, когда d = 10, найдите P, когда d = 15.

Решение
Поскольку отношение P / d является постоянным, мы можем подставить значения для P и d и получить пропорция

Таким образом, P = 60 при d = 15.

7.8 НЕРАВЕНСТВА В ДВУХ ПЕРЕМЕННЫХ

В разделах 7.3 и 7.4 мы построили уравнения с двумя переменными. В этом разделе мы построит график неравенств по двум переменным. Например, рассмотрим неравенство

у ≤ -x + 6

Решения — это упорядоченные пары чисел, которые «удовлетворяют» неравенству.То есть, (a, b) является решением неравенства, если неравенство является истинным утверждением после того, как мы заменим a на x и b на y.

Пример 1

Определите, является ли данная упорядоченная пара решением y = -x + 6.

а. (1, 1)
б. (2, 5)

Решение
Упорядоченная пара (1, 1) является решением, потому что, когда 1 заменяется на x, а 1 подставляем вместо y, получаем

(1) = — (1) + 6, или 1 = 5

, что является правдой. С другой стороны, (2, 5) не является решением, потому что когда 2 заменяется на x и 5 заменяется на y, мы получаем

(5) = — (2) + 6, или 5 = 4

, что является ложным заявлением.

Чтобы изобразить неравенство y = -x + 6, сначала построим уравнение y = -x + 6 показано на рисунке 7.13. Обратите внимание, что (3, 3), (3, 2), (3, 1), (3, 0) и т. Д., Связанные с точками, находящимися на линии или под ней, являются решениями неравенства y = -x + 6, тогда как (3,4), (3, 5) и (3,6), связанные с точками над линии не являются решениями неравенства. Фактически, все упорядоченные пары, связанные с точки на линии или ниже являются решениями y = — x + 6. Таким образом, каждая точка на или под чертой находится на графике.Мы представляем это, закрашивая область под линия (см. рисунок 7.14).

В общем, чтобы построить график неравенства первой степени с двумя переменными в виде Ax + By = C или Ax + By = C, сначала строим график уравнения Ax + By = C и затем определите, какая полуплоскость (область выше или ниже линии) содержит решения. Затем закрашиваем эту полуплоскость. Мы всегда можем определить, какая половина плоскость заштриховать, выбрав точку (не на линии уравнения Ax + By = C) и тестирование, чтобы увидеть, является ли упорядоченная пара, связанная с точкой, решением учитывая неравенство.Если да, то закрашиваем полуплоскость, содержащую контрольную точку; иначе, закрашиваем другую полуплоскость. Часто (0, 0) — удобная контрольная точка.

Пример 2

График 2x + 3y = 6

Решение
Сначала построим линию 2x + 3y = 6 (см. График a). Используя начало координат как контрольную точку, мы определяем, является ли (0, 0) решением 2x + 3y ≥ 6. Поскольку утверждение

2 (0) + 3 (0) = 6

ложно, (0, 0) не является решением и мы закрашиваем полуплоскость, не содержащую начало координат (см. график b).

Когда линия Ax + By = C проходит через начало координат, (0, 0) не является допустимым тестом точка, так как она находится на линии.

Пример 3

График y = 2x.

Решение
Начнем с построения линии y = 2x (см. График a). Поскольку линия проходит через начало координат, мы должны выбрать другую точку не на линии в качестве нашей тестовой точки. Мы будем используйте (0, 1). Поскольку выписка

(1) = 2 (0)

верно, (0, 1) — решение, и мы закрашиваем полуплоскость, содержащую (0, 1) (см. график б).

Если символ неравенства — ‘, точки на графике Ax + By = C не являются решениями неравенства. Затем мы используем пунктирную линию для графика Ax + By = C.

РЕЗЮМЕ ГЛАВЫ

  1. Решение уравнения с двумя переменными — это упорядоченная пара чисел. в упорядоченная пара (x, y), x называется первым компонентом, а y называется вторым компонент. Для уравнения с двумя переменными переменная, связанная с первой компонент решения называется независимой переменной, а переменная связанный со вторым компонентом, называется зависимой переменной.Обозначение функции f (x) используется для обозначения алгебраического выражения в x. Когда х в символ f (x) заменяется определенным значением, символ представляет значение выражения для этого значения x.

  2. Пересечение двух перпендикулярных осей в системе координат называется происхождение системы, и каждая из четырех областей, на которые делится плоскость называется квадрантом. Компоненты упорядоченной пары (x, y), связанной с точки на плоскости называются координатами точки; x называется абсциссой точки, а y называется ординатой точки.

  3. График уравнения первой степени с двумя переменными представляет собой прямую линию. То есть каждый упорядоченная пара, которая является решением уравнения, имеет график, лежащий на линии, и каждая точка в строке связана с упорядоченной парой, которая является решением уравнение.

    Графики любых двух решений уравнения с двумя переменными могут быть использованы для получить график уравнения. Однако два решения уравнения в двух переменные, которые обычно легче всего найти, — это те, в которых либо первая, либо второй компонент равен 0.Координата x точки, в которой линия пересекает ось x. называется пересечением по оси x линии, а координата y точки, в которой линия пересекает ось ординат и называется пересечением линии. Использование точек пересечения для построения графика уравнение называется методом построения графика с пересечением.

  4. Наклон линии, содержащей точки P 1 (x 1 , y 1 ) и P 2 (x 2 , y 2 ), определяется как

    Две прямые параллельны, если они имеют одинаковый наклон (м 1 = м 2 ).

    Две линии перпендикулярны, если произведение их уклонов равно — l (m 1 * m 2 = -1).

  5. Угол наклона линии с наклоном m, проходящей через точку (x 1 , y 1 ) это

    г — г 1 — м (х — х 1 )

    Форма точки пересечения наклона линии с наклоном m и точкой пересечения оси y b равна

    y = mx + b

  6. Взаимосвязь, определяемая уравнением вида

    y = kx (k постоянная)

    называется прямой вариацией.

  7. Решением неравенства с двумя переменными является упорядоченная пара чисел, которая, при подстановке в неравенство делает неравенство истинным утверждением. В График линейного неравенства от двух переменных представляет собой полуплоскость. Символы, представленные в этой главе, появляются на внутренней стороне передней обложки.

Как рассчитать расстояние между двумя координатами

Обновлено 15 декабря 2020 г.

Автор Nucreisha Langdon

Знание того, как рассчитать расстояние между двумя координатами, имеет множество практических применений в науке и строительстве.Чтобы найти расстояние между двумя точками на двумерной сетке, вам необходимо знать координаты x и y каждой точки. Чтобы найти расстояние между двумя точками в трехмерном пространстве, вам также необходимо знать z-координаты этих точек.

Формула расстояния используется для выполнения этой работы и проста: возьмите разницу между значениями X и разницу между значениями Y, сложите их квадраты и извлеките квадратный корень из суммы, чтобы найти прямую -линейное расстояние, то есть расстояние между двумя точками на картах Google над землей, а не на извилистой дороге или водном пути.

Расстояние в двух измерениях

    Вычислите положительную разницу между координатами x и назовите это число X. Координаты x — это первые числа в каждом наборе координат. Например, если две точки имеют координаты (-3, 7) и (1, 2), то разница между -3 и 1 равна 4, и поэтому X = 4.

    Вычислите положительную разницу между координатами y. и назовем это число Y. Координаты Y — вторые числа в каждом наборе координат.2 = 41

    Таким образом, квадрат расстояния между координатами равен 41.

    Извлеките квадратный корень из D 2 , чтобы найти D, фактическое расстояние между двумя точками. Например, если D 2 = 41, то D = 6,403, и поэтому расстояние между (-3, 7) и (1, 2) равно 6,403.

Расстояние в трех измерениях

    Вычислите положительную разницу между координатами z и назовите это число Z. Координаты z — это третьи числа в каждом наборе координат.