По ребру a тетраэдра определите радиус вписанной сферы: 49. Найдите радиус шара, описанного около правильного тетраэдра с ребром а.

Как найти радиус вписанного в правильную пирамиду шара (сферы): формулы

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение радиуса шара (сферы), вписанного в правильную пирамиду

В данной публикации представлены формулы, с помощью которых можно найти радиус шара (сферы), вписанного в правильную пирамиду: треугольную, четырехугольную, шестиугольную и тетраэдр.

• Формулы расчета радиуса шара (сферы)
  • Правильная треугольная пирамида
  • Правильная четырехугольная пирамида
  • Правильная шестиугольная пирамида

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На рисунке:

• a – ребро основания пирамиды, т.е. это равные отрезки AB, AC и BC;
• DE – высота пирамиды (h).

Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:

Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:

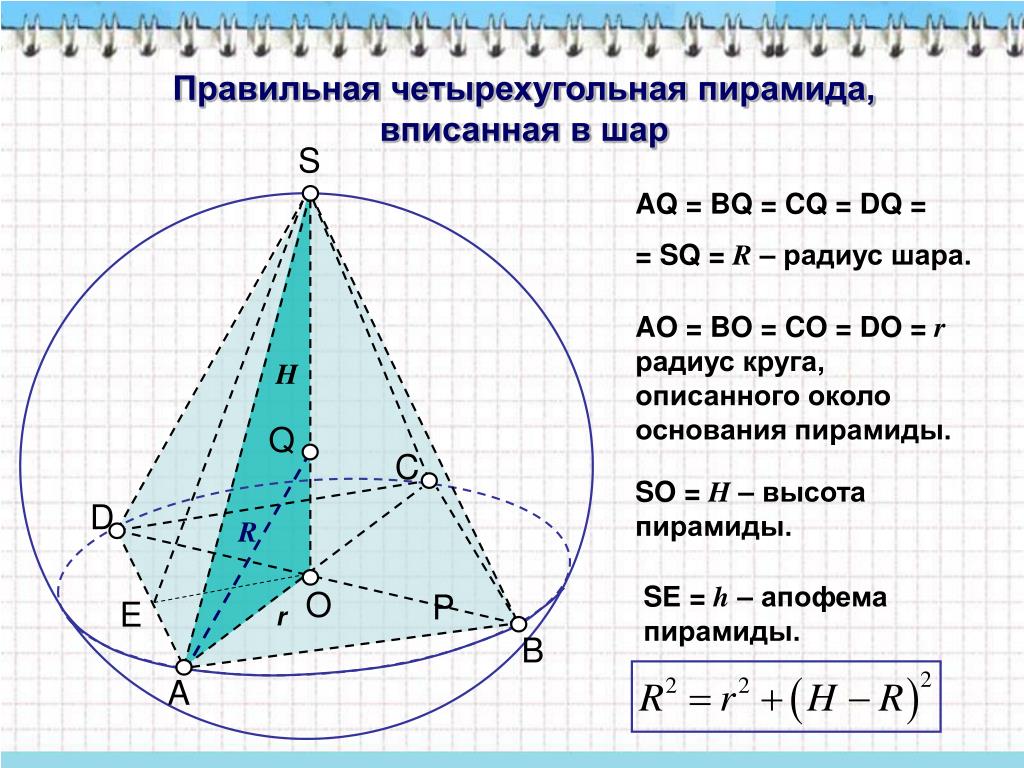
Правильная четырехугольная пирамида

На рисунке:

• a – ребро основания пирамиды, т.е. AB, BC, CD и AD;
• EF – высота пирамиды (h).

Радиус (r) вписанного шара/сферы рассчитывается так:

Правильная шестиугольная пирамида

На рисунке:

• a – ребро основания пирамиды, т. е. AB, BC, CD, DE, EF, AF;
• GL – высота пирамиды (h).

Радиус (r) вписанного шара/сферы вычисляется по формуле:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия

Справочник по математике

Геометрия (Стереометрия)

Вписанные и описанные фигуры

Биссекторная плоскость. Основное свойство биссекторной плоскости

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

Радиус сферы, вписанной в правильную n — угольную пирамиду

Сфера, вписанная в треугольную пирамиду. Формула для радиуса вписанной сферы

Биссекторная плоскость. Основное свойство биссекторной плоскости

      Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).

Рис.1

      Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.

      Доказательство. Рассмотрим произвольную точку   O,  расположенную внутри двугранного угла, и проведем через эту точку плоскость   δ,  перпендикулярную к ребру   AB  двугранного угла (рис. 2).

Рис.2

      Плоскость   δ   пересекает ребро   AB   двугранного угла в точке   C,   а грани двугранного угла   α   и   β   по лучам   CD   и   CE   соответственно. Угол   DCE  является линейным углом двугранного угла. Биссекторная плоскость   γ  пересекает плоскость   δ  по биссектрисе   CF   линейного угла   DCE .

      Поскольку плоскости   α   и   β   проходят через перпендикуляр   AB   к плоскости   δ,   то плоскости   α  и β  перпендикулярны к плоскости   δ. Поскольку плоскости   α   и   β   проходят через перпендикуляр   AB   к плоскости   δ,   то плоскости   α  и β  перпендикулярны к плоскости   δ.   Из свойств прямой, перпендикулярной к плоскости, свойств прямой, перпендикулярной к плоскости, следует, что и перпендикуляры, опущенные из точки   O  на грани двугранного угла   α  и β,  лежат в плоскости   δ.

      Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла.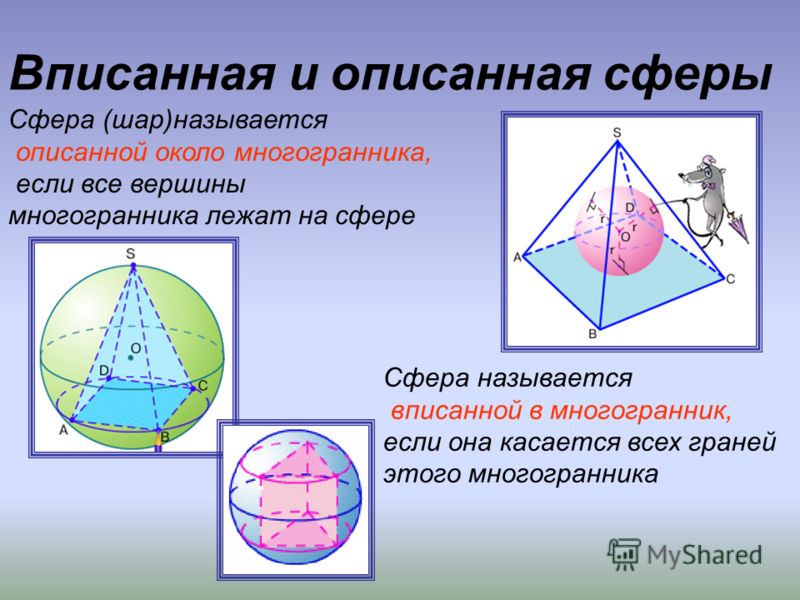 Доказано.

      Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис. 3).

Рис.3

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

      Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).

Рис.4

      Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.

      Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.

      Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.

      Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.

      Рассмотрим несколько типов пирамид, в которые можно вписать сферу.

      Утверждение 2. Если у пирамиды   SA₁A₂ … A_n   основание   O  перпендикуляра, опущенного из вершины   S   на плоскость основания пирамиды, лежит внутри многоугольника   A₁A₂ . .. A_n ,   а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.

     Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом   φ ,  а высота пирамиды равна   h.   Рассмотрим, например, боковую грань   SA₁A₂   и проведем в ней высоту   SB   (рис. 5).

Рис.5

      По теореме о трех перпендикулярах отрезок   OB   перпендикулярен ребру   A₁A₂.   Следовательно, угол   SBO   является линейным углом двугранного угла между боковой гранью   SA₁A₂   и плоскостью основания пирамиды и равен   φ.   Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке   O’   (рис. 6).

Рис.6

      Катет   OB   прямоугольного треугольника   SOB   выражается через высоту пирамиды   h   и угол   φ   по формуле

OB = h ctg φ .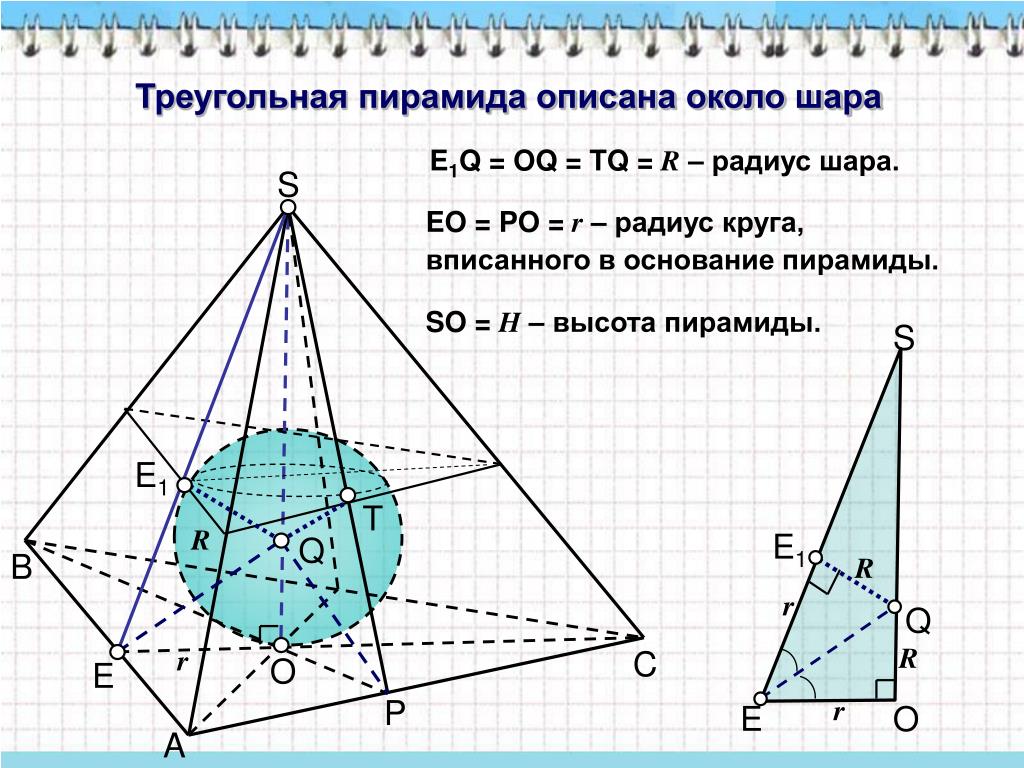

      Катет   OO’   прямоугольного треугольника   OO’B   выражается через высоту пирамиды   h   и угол   φ   по формуле

      Поскольку длина отрезка   OO’   не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке   O’,   которая и является центром вписанной в пирамиду сферы.

      Доказательство утверждения 2 завершено.

      Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо

      Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус   R  выражается через высоту пирамиды   h   и внутренний двугранный угол при основании пирамиды   φ   по формуле

(1)

Радиус сферы, вписанной в правильную n — угольную пирамиду

      Задача. Высота правильной n — угольной пирамиды равна   h ,   а длина ребра основания равна   a .   Найти радиус сферы, вписанной в пирамиду.

      Решение. Рассмотрим правильную n — угольную пирамиду   SA₁A₂ … A_n   и обозначим символом   O’   центр вписанной в пирамиду сферы, а буквой   O  – центр основания пирамиды. Проведем плоскость через высоту пирамиды   SO   и апофему   SB   какой-либо боковой грани (рис. 7).

Рис.7

      Буквой   R   на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой   r   – радиус вписанной в основание пирамиды окружности, а буквой   φ   – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника   OSB   получаем

(2)

      В силу следствия 2 из формул (1) и (2) получаем

(3)

      Поскольку радиус вписанной в правильный n — угольник окружности выражается через сторону этого многоугольника по формуле радиус вписанной в правильный n — угольник окружности выражается через сторону этого многоугольника по формуле

из формулы (3) получаем соотношение

      Ответ.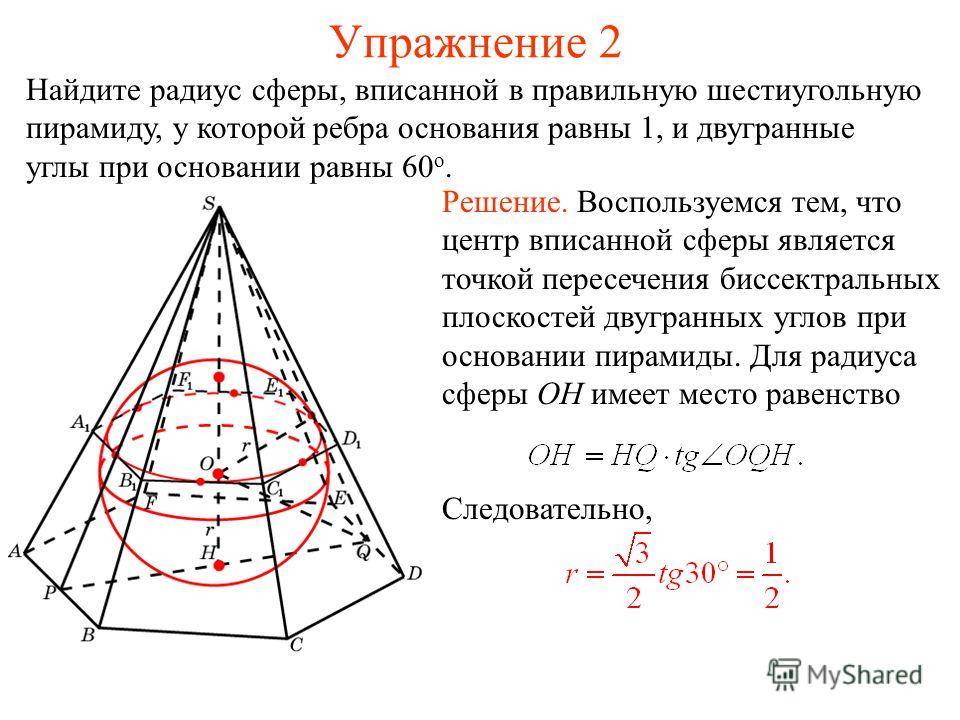

      Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой   h   и ребром основания  a,   равен

      Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром  a,   равен

      Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой   h   и ребром основания   a,   равен

      Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой   h   и ребром основания  a,   равен

Сфера, вписанная в треугольную пирамиду.

Формула для радиуса вписанной сферы

      Утверждение 3. В любую треугольную пирамиду можно вписать сферу.

      Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.

      Действительно, пусть   SABC   – произвольный тетраэдр. Биссекторная плоскость внутреннего двугранного угла с ребром   AC   и биссекторная плоскость внутреннего двугранного угла с ребром   AB   пересекаются по некоторой прямой, проходящей через вершину   A.   Биссекторная плоскость внутреннего двугранного угла в ребром   BC   пересекает эту прямую в единственной точке   O  , которая и является центром вписанной сферы (рис. 8).

Рис.8

        Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр   SABC   сферы. Для этого заметим, что объем пирамиды   SABC   равен сумме объемов пирамид   OABC, OSCA, OSAB, OSCB,   причем высота каждой из пирамид   OABC, OSCA, OSAB, OSCB   равна радиусу   R   вписанной в пирамиду   SABC   сферы. Если обозначить площади граней тетраэдра   SABC   символами

S_ABC , S_ASC , S_ASB , S_BSC ,

а объемы пирамид   SABC, OABC, OSCA, OSAB, OSCB   – символами

V_ABC , V _ASC , V _ASB , V _BSC ,

то справедливы следующие равенства:

где символом   S_полн   обозначена площадь полной поверхности пирамиды   SABC.

      Следовательно,

      Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы

где символами   V_пир   и   S_полн   обозначены объем и площадь полной поверхности пирамиды соответственно.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

геометрия — Радиус вписанной сферы в правильный тетраэдр

спросил 11 лет, 6 месяцев назад

Изменено 10 лет, 9 месяцев назад

Просмотрено 22к раз

$\begingroup$

Ответ на вопрос:

Сфера вписана в правильный тетраэдр. Если длина высоты тетраэдра равна 36, какова длина радиуса сферы?

Не знаю, с чего начать.

Вот что я думаю пока:

• Я думаю, что сфера касается «центра» каждой стороны тетраэдра.
• На полпути вниз по одной из сторон тетраэдра, там, где он пересекается с «высотной линией» перпендикулярно, находится радиус сферы.

Судя по всему, ответ 9.

• геометрия

$\endgroup$

$\begingroup$

Центр тетраэдра делит каждую из четырех высот (или медиан) в отношении $1:3$ (в равностороннем треугольнике соответствующее отношение равно $1:2$). Меньшая часть также является радиусом вписанной сферы. Следовательно, радиус этой сферы составляет четверть высоты или $9$ в вашем случае.

$\endgroup$

$\begingroup$

Интуитивный способ думать об этом состоит в том, чтобы понять, что центр тяжести тетраэдра (и, следовательно, сферы) является средним значением положений четырех углов.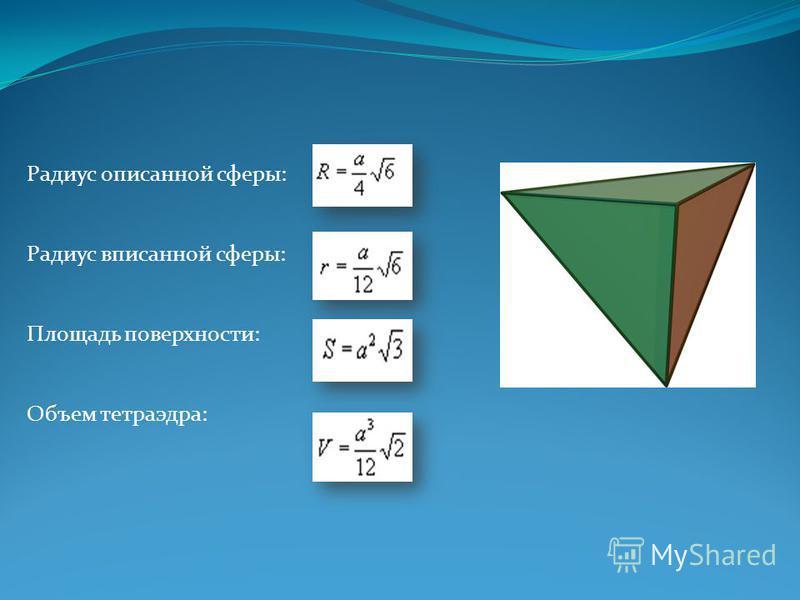 Если три из четырех углов находятся на земле (то есть высота равна 0), а четвертый угол имеет высоту 36, то довольно просто вычислить, как высоко над землей находится центр тяжести. Вам нужен радиус сферы, вписанной в тетраэдр? Это расстояние от центра тяжести до земли. Хотите радиус сферы, вписанной в тетраэдр? Это расстояние от центра тяжести до верхнего угла.

$\endgroup$

$\begingroup$

Тетраэдр с площадью грани $F$ и высотой (до этой грани) $a$ имеет объем $\frac{1}{3}a F$.

Теперь рассмотрим подтетраэдр, определяемый данной гранью, с четвертой вершиной в центре вписанной сферы. Поскольку сфера касается грани, высота этой грани равна радиусу, скажем, длиной $r$. Если большой тетраэдр правильный (с площадью грани $F$ и высотой $a$), то четыре субтетраэдра конгруэнтны с объемом $\frac{1}{3}r F$.

Вместе подтетраэдры заполняют большой тетраэдр, поэтому четыре подобъема в сумме составляют большой объем:

$$4 \cdot \frac{1}{3} r F = \frac{1}{3 } a F$$

, так что $4 r = a$.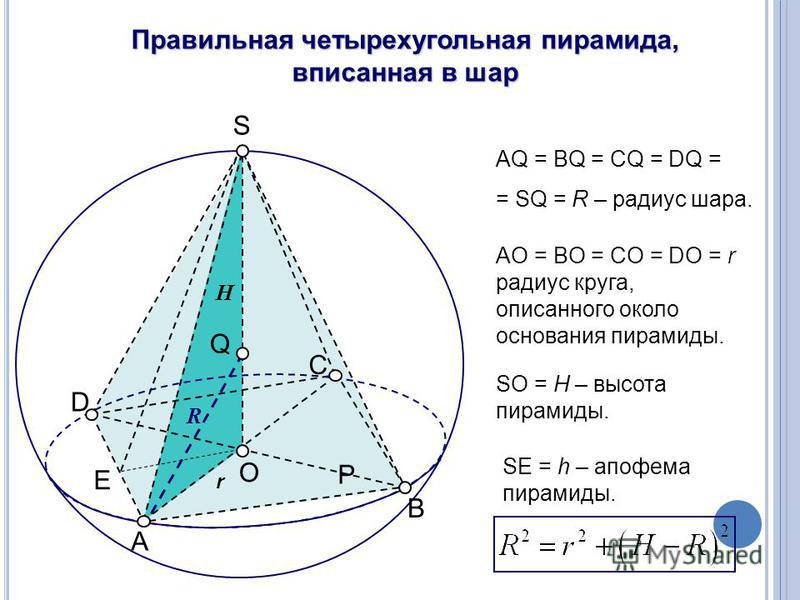 Вам дано, что $a=36$; следовательно, $r = 36/4 = 9$.

---

Примечание. Правильный или нет, основной аргумент показывает, что объем ($V$) тетраэдра определяется его внутренним радиусом ($r$) и общей площадью поверхности ($S$):

$$V = \frac{ 1}{3} r S$$

Это аналогично тому факту, что площадь ($A$) треугольника определяется внутренней стороной ($r$) и его периметром ($p$):

$$A = \frac{1}{2}r p$$

Паттерн продолжается в $d$-мерное пространство с умноженной константой, равной $\frac{1}{d}$.

$\endgroup$

$\begingroup$

Чтобы вывести результаты из первых принципов, я бы назвал длину стороны тетраэдра $s$ и работал с числами, кратными $s$, пока не получил выражения для высоты и радиуса вписанной сферы.

Первый шаг — найти некоторые длины в каждом из равносторонних треугольников, образующих стороны тетраэдра, в частности, расстояние между средней точкой и углом и расстояние по перпендикуляру от середины до одного из ребер.

Оба легко найти, разделив треугольник на соответствующие 30-60-90 треугольников.

На втором этапе мы переходим к 3D. По симметрии центр вписанной сферы должен лежать на всех четырех высотах (по одной из каждого угла), поэтому мы можем найти его точно, пересекая две высоты. Итак, мы работаем в плоскости, содержащей две высоты. Эта плоскость содержит два угла А и В, а также середины противоположных сторон, а также середину ребра между двумя противоположными сторонами. Таким образом, сечение тетраэдра этой плоскостью содержит несколько

длины , которые мы уже знаем с первых шагов. В поперечном сечении нет хорошо известных углов , но длин достаточно, чтобы применить треугольники Пифагора и подобные треугольники, чтобы найти две длины, которые вас в конечном итоге интересуют.

$\endgroup$

$\begingroup$

Другой способ взглянуть на это, очень похожий на ответ IV, заключается в следующем. 3$. Здесь симметрия положения диктует, что центр вписанной сферы находится в центре куба, то есть в точке $(a/2,a/2,a/2)$.

Давайте посмотрим на высоту, начиная с начала координат. Остальные три вершины лежат в плоскости $x+y+z=2a$, поэтому высота параллельна вектору $\vec{n}=(1,1,1)$. Центроид находится в плоскости $x+y+z=3a/2$, также нормальной к $\vec{n}$. Следовательно, центроид делит высоту в соотношении $3:1$. Претензия следует.

$\endgroup$

Обладают ли кубы и квадраты теми же свойствами, что и сферы и круги? – AP Central

Студенты, изучающие математику, часто бывают заинтригованы, когда понимают, что производная формулы объема сферы по отношению к радиусу сферы является формулой поверхности сферы: . Их также восхищает тот факт, что производная формулы площади круга есть формула его длины окружности: . Эти результаты, по-видимому, неприменимы к кубам и квадратам, потому что , площадь поверхности куба и , периметр квадрата. Почему сферы и круги ведут себя так, а кубы и квадраты иначе?

Рассмотрим производную площади круга. По определению производной:

Геометрически этот результат легко увидеть, поскольку область между двумя концентрическими окружностями, одна с радиусом r, а другая с радиусом r + h, по существу представляет собой полосу шириной h и длиной 2πr, как показано на рисунке 1.

Аналогичное вычисление верно для производной объема сферы. По определению производной:

Геометрически этот результат легко понять, поскольку область между двумя концентрическими сферами, одна с радиусом r, а другая с радиусом r + h, по существу представляет собой полый шар толщиной h и площадью поверхности 4πr ² .

Подобные результаты неверны для стандартной формулы объема куба и площади квадрата, как показано в первом абзаце. Рассмотрим разные формулы: Пусть s — расстояние от центра квадрата перпендикулярно противоположной стороне, как показано на рис. 2. Тогда, поскольку s — половина длины ребра квадрата, имеем формулу A = (2с) ² = 4s ² и P = 8s для площади квадрата и периметра квадрата соответственно.

Рассмотрим производные от этой новой формулы площади квадрата. Так как A = 4s ² , что является нашей формулой для периметра квадрата. Точно так же пусть s будет расстоянием от центра куба перпендикулярно противоположной стороне. Тогда, поскольку s — половина длины ребра куба, имеем формулу V = (2s) ³ = 8s ³ для объема куба и (2s) ² = 4s ² для площади каждой грани. Поскольку V = 8s ³ , то , что в 6 раз больше площади грани куба, и, таким образом, это выражение равно площади поверхности куба. Записав формулы в терминах s, равной половине длины ребра, мы получим формулы, свойства которых согласуются со свойствами сфер и кругов.

Мы можем распространить этот результат на равносторонние треугольники. Пусть e будет длиной ребра треугольника, как показано на рис. 3.

Площадь треугольника , а его периметр 3e. Производная площади равна , что и отдаленно не похоже на периметр треугольника. Давайте теперь изменим переменную и пусть s представляет собой расстояние по перпендикуляру от центра треугольника до одной из сторон, как показано на рисунке 4.

Используя соотношение Пифагора, или . В терминах s площадь треугольника равна , а периметр равен . Так как , производная площади равностороннего треугольника является периметром треугольника. На рис. 5 видно, что разность между треугольными областями при использовании s и s + h представляет собой по существу трехстороннюю полосу шириной h и длиной, равной периметру треугольника, что геометрически подтверждает наш результат.

Случай равностороннего треугольника предлагает способ обобщить этот результат на другие правильные многоугольники. Отрезок s, проходящий от центра многоугольника перпендикулярно стороне, называется апофемой многоугольника. Тогда длина стороны многоугольника равна , где n — количество сторон, поэтому периметр многоугольника равен . Площадь многоугольника равна длине апофемы, умноженной на половину длины периметра. В символах:

Теперь мы можем проверить периметр правильного многоугольника.

Предложите своим ученикам применить этот метод к правильному шестиугольнику. Они должны найти формулы площади и периметра шестиугольника через его апофему. Затем они должны показать, что одно является производным от другого.

Мы также можем распространить наши результаты на трехмерные фигуры. Для правильных многогранников апофемой является радиус вписанной сферы. Рассмотрим тетраэдр.

Стандартные формулы для объема и площади поверхности тетраэдра обычно основаны на длине ребра а тетраэдра. Однако их нетрудно переписать в терминах длины r апофемы — радиуса вписанной сферы.

r = радиус вписанной сферы = апофема многогранника
R = радиус описанной сферы
a = длина ребра тетраэдра
S = площадь поверхности тетраэдра
V = объем тетраэдра

В терминах r вписанный радиус:

Таким образом, мы легко можем видеть, что в терминах апофемы производная формулы объема тетраэдра есть формула площади его поверхности.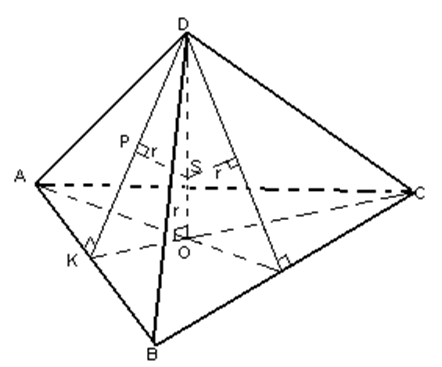

Аналогичным образом, используя стандартные формулы для объема и площади поверхности октаэдра, исходя из длины ребра а октаэдра. Мы можем переписать их через длину r апофемы.

Опять же, ясно, что производная формулы объема по r является формулой площади поверхности.

Вот формулы для объема и площади поверхности двух других правильных многогранников через длину вписанного радиуса r.

Додекаэдр:

Икосаэдр:

Вы можете поручить учащимся сложную задачу проверки того, что производная приведенной выше формулы для объема додекаэдра на самом деле является заданной формулой для площади его поверхности.

Каково значение этого результата? Это просто академическое упражнение? На самом деле, эти формулы позволяют легко найти формулу площади поверхности правильного твердого тела, если вы знаете формулу его объема, или наоборот. Просто запишите формулу в терминах апофемы твердого тела и продифференцируйте или антидифференцируйте соответственно, чтобы найти другую формулу.

Ссылки

http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html#октаэдр

http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html

Джон Ф. Махони представил статистику AP в средней школе Баннекера в 2002-03 годах и в том году обучил 59 учащихся. Каждый из студентов сдал экзамен AP, и Махони считает, что у них, возможно, был самый высокий процент пожилых людей, сдающих статистику AP в стране. В этом году он также преподает исчисление AP уровня AB и BC. Он консультант AP и давний участник программы AP Calculus Reading. В настоящее время он является одним из руководителей экзамена. Он также возглавляет редакционную коллегию ON-Math NCTM: www.nctm.org/onmath. В старшей школе Баннекера он является одним из наставников группы робототехники и помогает учащимся проектировать зубчатые приводы — так же, как это делал сам Баннекер более 200 лет назад. Им помогают многие инженеры, в том числе из Университета Говарда, расположенного через Джорджию-авеню от средней школы.