Плоскость параллельная стороне ас треугольника авс пересекает сторону ав: 1 задача. Плоскость, параллельная стороне АВ треугольника АВС, пересекает его стороны АС и ВС в...

Плоскость β пересекает стороны AB и AC треугольника ABC в точках N и D соответственно и параллельна стороне BC, AD = 6 см, DN : CB = 3 : 4. Найдите сторону AC треугольника. — вопрос №4120299





Ответы

22.

12.20

Михаил Александров

Читать ответы

Андрей Андреевич

Читать ответы

Eleonora Gabrielyan

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

Сколькими нулями оканчивается произведение всех натуральных чисел от 41 до 64 включительно

сокращенное ионное уравнение реакции Ba(2+) + SO4(2-) = BaSO4 соответствует взаимодействию

Две стороны треугольника равны 7 и 8 см, а угол между ними равен 120 градусам.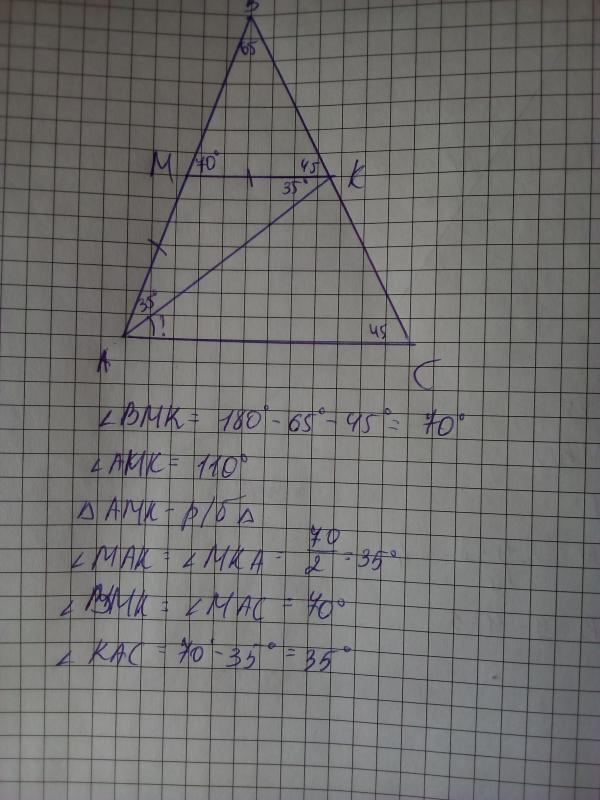 2. Найдите площадь полной поверхности цилиндра

Пользуйтесь нашим приложением

Решение задач по теме «Параллельность прямой и плоскости»

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Определение

Две прямые в пространстве называются
параллельными, если
1) они лежат в одной плоскости и
2) не пересекаются
b
a
2
Теорема (Признак параллельности прямой и плоскости)
Если прямая не лежащая в данной плоскости, параллельна
какой-нибудь прямой, лежащей в этой плоскости, то она
параллельна этой плоскости.

a
b
Если плоскость проходит через данную прямую,
параллельную другой плоскости, и пересекает эту
плоскость, то линия пересечения плоскостей параллельна
данной прямой.
a II
Следствие 10
a
b
b II a
4
Если одна из двух параллельных прямых параллельна данной
плоскости, то другая прямая либо также параллельна данной
плоскости, либо лежит в этой плоскости.
Следствие 20
а
b
a II b
a II
b II
b
5
О.
Пр.
а
а
в
a¢α
а ||
а ||
а || в
в
У1
β
у2
а
а
а
в
в
а ||
а β
а ‫ ׀׀‬в
β = в
в
а ||
а || в
в ||
или
в
№ 26 (учебник)
Сторона АС треугольника АВС параллельна плоскости a , а
стороны АВ и ВС пересекаются с этой плоскостью в точках М
и N. Докажите, что треугольники АВС и МВN подобны.
Доказательство
1. По утверждению 1° : МN || АC. Тогда угол А = углу
ВМN (как односторонние при параллельных прямых).

2. угол В — общий.
З. Таким образом, по двум углам треугольник АВС
подобен треугольнику МВN.
№ 28
На сторонах АВ и АС треугольника АВС взяты соответственно точки D
и E так, что ОE = 5 см и ВD = 2/3. Плоскость a проходит через точки B и
С и параллельна отрезку ОE. Найдите длину отрезка ВС.
Решение:
Из условия задачи № 26: треугольник АВС подобен
треугольнику АDЕ.
Тогда АВ/АD = ВС/DЕ, 5/3 = х/5, х = 25/3, х = 81/3.
Ответ: 81/3.
В треугольнике АВС на стороне АВ выбрана точка D, такая, что BD : BA = 1 : 3.
Плоскость, параллельная прямой АС и проходящая через точку D, пересекает
отрезок ВС в точке D1.
а) Докажите, что треугольник DBD1 подобен треугольнику АВС
б) Найдите АС, если DD1 = 4 см.
На стороне AD параллелограмма ABCD выбрана точка А1, так, что DA1 = 4 см. Плоскость,
параллельная диагонали АС, проходит через точку А1 и пересекает сторону CD в точке С1.
а) Докажите, что треугольник C1DA1 подобен треугольнику АВС
б) Найдите АС, если BC = 10 см, A1C1 = 6 см
1.

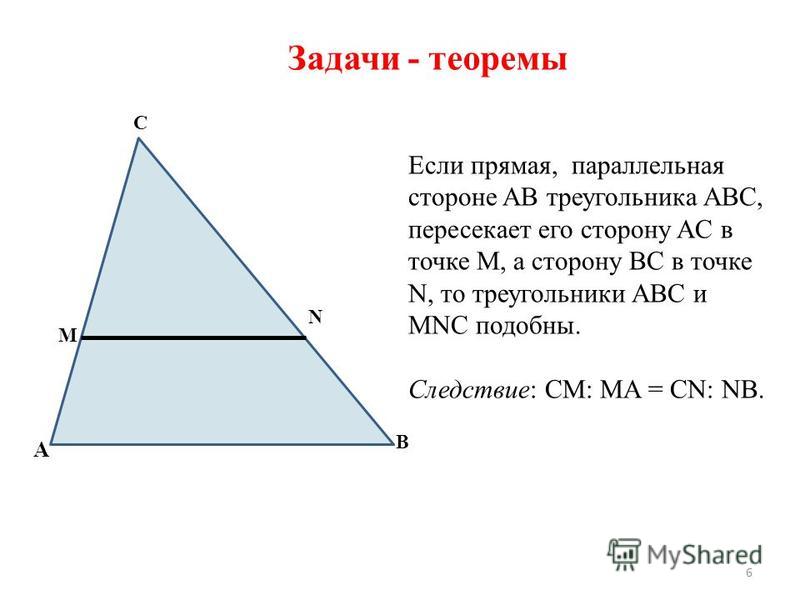Точка D лежит на отрезке АВ, причем BD : BA = 1 : 4.
Через точку А проведена плоскость α, через точку D –
отрезок DD1, параллельный α. Прямая BD1, пересекает

плоскость α в точке С.
а) Докажите, что треугольник DBD1 подобен
треугольнику АВС
б) Найдите DD1, если АС =12 см.
2. На стороне ВС параллелограмма ABCD выбрана точка
С1, так, что ВС1 = 3 см. Плоскость, параллельная диагонали
АС, проходит через точку С1 и пересекает сторону АВ в
точке А1.
а) Докажите, что треугольник C1ВA1
подобен
треугольнику АDС
б) Найдите АD, если AC = 12 см, A1C1 = 4 см

English Русский Правила

Обдумайте эту геометрию

Ваш Javascript отключен. Некоторая навигация на этом сайте не будет работать без Javascript. Пожалуйста, включите Javascript в вашем браузере, чтобы пользоваться всеми функциями этого сайта.

Дом О нас Преподаваемые предметы Часто задаваемые вопросы Отзывы Подумайте об этом Свяжитесь с нами

Вызов алгебры Задача по геометрии Вызов исчисления Физика I Challenge

Все нужно сделать как можно проще, но не проще.
Альберт Эйнштейн

1. Сложность: Новичок

Углы A и B дополняют друг друга, а угол A в четыре раза больше угла B . Найдите величину угла A .

72 градуса

2. Сложность: Новичок

В треугольнике ABC угол A равен 2 градусам, угол B равен 3 градусам, а угол C равен 4x-9 градусам. Найдите величину угла C .

75 градусов

3. Сложность: Новичок

В треугольнике ABC угол A равен 30 градусам. Размеры сторон BC и AC 2см и 3см соответственно. Найдите величину угла B .

48,6 градусов

4. Сложность: Новичок

Длина стороны AC в треугольнике ABC равна 6 см. Точки D и E лежат на сторонах AB и BC соответственно. Отрезок DE параллелен AC , а длина сегмента AD вдвое больше длины сегмента 9.0016 БД . Найдите длину отрезка DE .

2см

5. Сложность: Новичок

Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой 4см.

8 квадратных сантиметров

6. Сложность: Easy

Даны три точки на плоскости, не все на одной прямой. Сколько прямых можно провести на равном расстоянии от этих точек?

7. Сложность: Легко

Даны три точки на плоскости: A(-1,6), B(3,5) и C(7,13) . Найдите уравнение прямой, проходящей через точку A , равноудаленной от точек B и C .

Y = 0,5X + 13/2

8. Сложность: Легко

В треугольнике ABC длина стороны AB составляет 4 см, а длина стороны AC составляет 6 см. Угол A равен 60 градусам. Найдите длину отрезка, соединяющего середины сторон АВ и АС .

9. Трудность: Easy

По кругу O перпендикулярные хорды AB и CD пересекаются в точке E так, что AE = 2 см, EB = 12 см, и CE = 4 см . Найдите меру отрезка ED .

6см

10. Сложность: Средняя

в круге O , перпендикулярные аккорды AB и CD пересекаются в точке E , так что AE = 2CM, EB = 12CM и . предыдущую задачу). Найдите меру радиуса окружности O .

11. Сложность: Среда

В треугольнике ABC точка D лежит на стороне BC так, что AB=BD . Угол BAC на 50 градусов больше, чем угол BCA . Найдите величину угла CAD .

25 градусов.

12. Сложность: Средняя
Длина большего основания трапеции 54см. Длина отрезка, соединяющего середины диагоналей, равна 5 см. Найдите длину меньшего основания трапеции.
44см
13. Сложность: Средняя
Два телефонных столба высотой 30 футов и 20 футов соответственно расположены рядом друг с другом. В качестве частичной поддержки линия проходит от верха каждого столба к основанию другого. На какой высоте над землей находится точка пересечения двух опорных линий?
12 футов

14. Сложность: Средняя
Длины сторон прямоугольного треугольника равны 60см, 80см и 100см. Найдите длину отрезка, проведенного из вершины прямого угла к гипотенузе, которая делит треугольник на два треугольника с равными периметрами.
15. Сложность: Средняя
Высота AD равностороннего треугольника ABC диаметр круга O . Если окружность пересекает стороны AB и AC в точках E и F соответственно, найдите отношение EF:BC .
3 : 4
16. Сложность: Средняя
Окружность радиусом R=3см вписана в квадрат. Найдите радиус r окружности, вписанной между двумя сторонами квадрата и исходной окружностью.
17. Сложность: Средняя
Найдите отношение площади квадрата, вписанного в окружность, к площади равностороннего треугольника, описанного около этой окружности.
18. Сложность: Средняя
В треугольнике ABC, AB=8см, AC=9см и BC=12см . Точки D и E взяты на отрезках AB и AC соответственно, так что AD=AE . Если площадь треугольника ADE равна ½ площади треугольника ABC , найдите длину AD .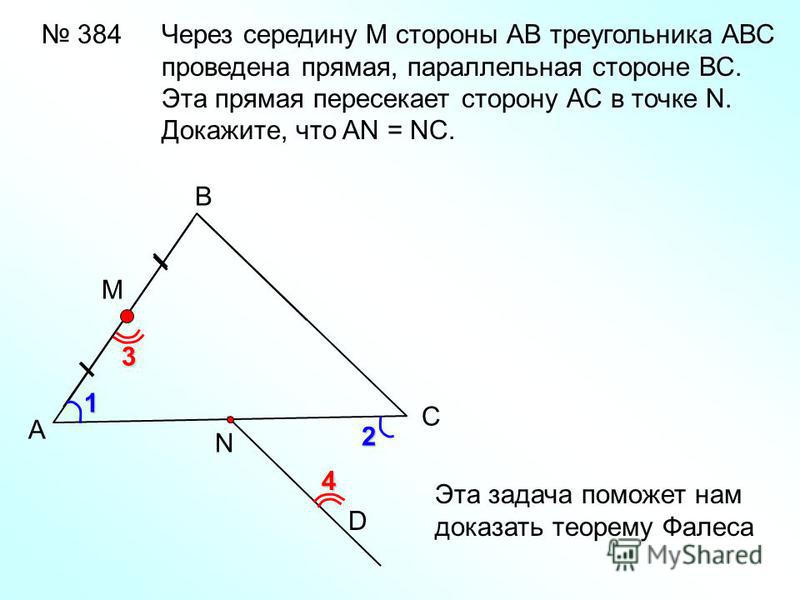
6см

19. Трудность: Тяжелая
В треугольнике ABC мера угла BAC составляет 120 градусов. Отрезок AD является внутренней биссектрисой угла BAC (точка D лежит на стороне BC ). Выразите длину отрезка AD через длины смежных сторон AB и AC .
20. Сложность: Hard
Отрезки AB и CD являются основаниями трапеции ABCD и имеют длину 24 см и 12 см соответственно. Диагонали AC и DB пересекаются в точке P. Найдите длину отрезка EF , проходящего через точку P и параллельного основаниям с концами на катетах трапеции.
16см

21. Трудность: Трудно
Докажите, что сумма квадратов мер отрезков, образованных двумя перпендикулярными хордами, равна квадрату меры диаметра данной окружности.
22. Трудность: Тяжелая
Две окружности вписаны в большую окружность так, что их общая внутренняя касательная пересекает большую окружность в точках А и В (см. рисунок). Размер хорды AB равен 6 см. Найдите площадь заштрихованной области.

23. Сложность: Трудно
Найдите площадь треугольника, медианы которого равны 21 см, 45 см и 60 см.
24. Сложность: Трудно
В треугольник со сторонами 10 см, 10 см и 12 см вписана окружность. Второй, меньший круг вписан по касательной к первому кругу и к равным сторонам треугольника. Найдите меру радиуса второй (меньшей) окружности.
0,75 см
25. Сложность: Трудно
Докажите, что от любой точки внутри равностороннего треугольника сумма мер расстояний до сторон треугольника постоянна. Найдите эту сумму для равностороннего треугольника со стороной 8 см.
26. Сложность: Эксперт
Отрезки PA и PC касаются окружности, а прямая PBD является секущей (см. рисунок). Проведены хорды AB, BC, CD и DA . Если AB = 5 см, CD = 4 см, и DA = 8 см , найдите BC .
2,5 см

27. Трудность: Эксперт
В треугольнике ABC меры сторон AB, BC, и AC 13 см, 4 см и 15 см соответственно. В этот треугольник вписана полуокружность так, что ее диаметр лежит на стороне АС (см. рисунок). Найдите радиус вписанной полуокружности.
48/17 см

28. Сложность: Эксперт
Найдите площадь квадрата ABCD , содержащего точку P , такую, что PA=3, PB=7, и PD=5 .
58
29. Сложность: Эксперт
Две окружности, каждая из которых проходит через центр другой, пересекаются в точках M и N . Прямая из точки M пересекает окружности в точках K и L . Если размер KL равен 5 см, найдите размеры LN и KN .
ЛН = КН = 5см

30. Сложность: Эксперт
Найдите площадь треугольника, образованного соединением середины сторон треугольника, медианы которого имеют меры 15, 15 и 18.
36
31. Сложность: Эксперт
Расстояние между центрами двух пересекающихся окружностей радиусов R и r равно d ( d < R + r ). Найдите площадь перекрытия (по R, r, и d ).
32. Сложность: Эксперт
Стороны треугольника имеют размеры 13, 14 и 15. Линия, перпендикулярная стороне измерения 14, делит внутреннюю часть треугольника на две области равной площади. Найдите меру отрезка этой перпендикулярной прямой, лежащей внутри треугольника.
33. Трудность: Эксперт
Равносторонний треугольник ABC вписан в окружность с центром O и радиусом Р . Другая окружность с центром O’ касается сторон AB и BC треугольника и окружности O .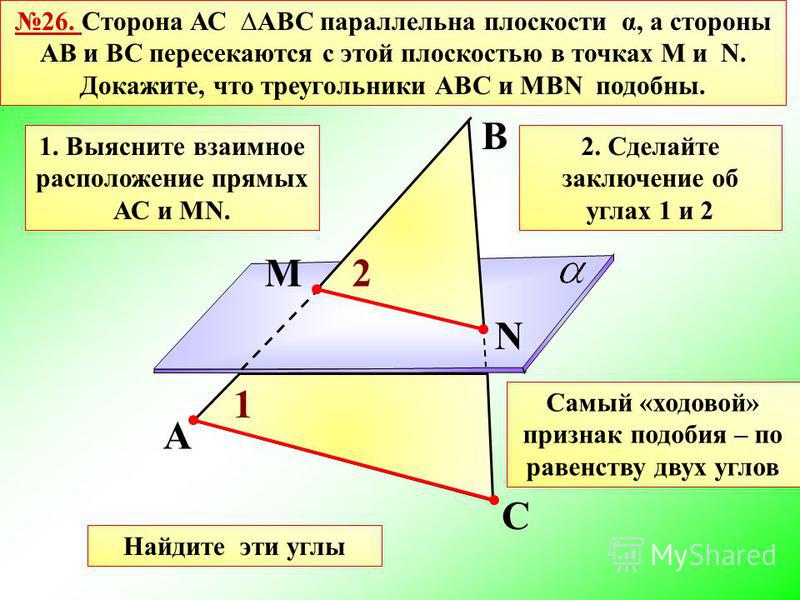 Найдите меру отрезка AO’ (в пересчете на радиус R ).

34. Трудность: Эксперт
Докажите, что в равнобедренном треугольнике сумма расстояний от любой точки основания до двух других сторон фиксирована (постоянна).
35. Сложность: Expert
Окружность радиусом r касается 3 больших конгруэнтных окружностей, причем каждая из этих больших окружностей также касается двух других (см. рисунок). Найдите площадь заштрихованной области ABC (в пересчете на r ).

36. Сложность: Эксперт
На плоскости даны две пересекающиеся линии. Найдите геометрическое место точек A такое, что сумма расстояний от A в каждой строке равно заданному значению ч .
37. Сложность: Эксперт
Точка O расположена внутри равностороннего треугольника ABC . Меры углов BOC и AOC равны x и y градусов соответственно. Найдите через x и y углы треугольника со сторонами, равными AO , BO и СО .
y-60 градусов
х-60 градусов
300 – х – у градусов

38. Сложность: Эксперт
Вам даны два параллельных отрезка AB и DC . Используя только линейку, разделите отрезок AB на две равные части .
Выбрать любые две точки E и G на отрезке DC (могут быть точки D и C или любые другие точки на сегменте). Нарисуйте линии AE и BG . Назовем пересечение линий AE и BG точкой P . Проведите диагонали в трапеции ABGE . Диагонали пересекаются в точке O . Нарисуйте линию PO . Пересечение линии PO и отрезка AB является серединой отрезка AB .
39. Сложность: Эксперт
Вам даны два параллельных отрезка AB и DC (см. предыдущую задачу). Используя только линейку, разделите отрезок AB на шесть равных частей.
Используя метод, описанный в предыдущей задаче, разделите сегмент DC на 8 равных частей — сначала разделите его на 2 равные части, затем снова разделите каждую часть и т. д. Выберите последовательно 6 равных частей, скажем, DE, EF, FG, GH, HJ, JK . Затем выполнить гомотетическое отображение их объединения на другой отрезок — т.е. провести линии AD и BK , найти их пересечение (точка P ) и провести еще 5 линий: PE, PF, PG, PH, и PJ . Пересечения этих прямых с отрезком AB делят этот отрезок на 6 равных частей.

40. Сложность: Эксперт
На плоскости нарисован круг с нарисованным диаметром. Учитывая точку M вне круга, проведите из точки M перпендикуляр к диаметру, используя только линейку.
Высота проходит через точку P — ортоцентр треугольника ABM , см. рисунок.

© Copyright Angas Tutoring. Все права защищены.
Теорема о биссектрисе перпендикуляра. Доказательства, примеры решений
Когда прямая делит другой отрезок на две равные половины через его середину в точке0º, он называется , перпендикулярным этого отрезка. Теорема о серединном перпендикуляре утверждает, что любая точка на биссектрисе равноудалена от обоих концов отрезка, на котором она проведена. Если столб стоит в центре моста под углом, все точки на столбе будут равноудалены от конечных точек моста.
1. Что такое биссектриса?
2. Что такое теорема о биссектрисе?
3. Что такое теорема, обратная теореме о биссектрисе перпендикуляра?
4. Доказательство теоремы о перпендикулярной биссектрисе
5. Решенные примеры теоремы о перпендикулярной биссектрисе
6. Практические вопросы по теореме о биссектрисе перпендикуляра
7. FAQ по теореме 9 о биссектрисе перпендикуляра0734

Что такое теорема о биссектрисе?
Теорема о серединном перпендикуляре утверждает, что любая точка на биссектрисе равноудалена от обоих концов отрезка, на котором она проведена.
На приведенном выше рисунке
MT = NT
MS = NS
MR = NR
MQ = NQ
Что такое обратная теорема о перпендикулярной биссектрисе?
Теорема, обратная теореме о биссектрисе, утверждает, что если точка равноудалена от обеих концов отрезка прямой в одной плоскости, то эта точка находится на биссектрисе отрезка.
На изображении выше XZ=YZ
Это означает, что ZO – это серединный перпендикуляр к отрезку XY.
Доказательство теоремы о перпендикулярной биссектрисе
Давайте посмотрим на доказательство двух вышеупомянутых теорем о перпендикулярной биссектрисе.
Доказательство теоремы о биссектрисе
Рассмотрим следующий рисунок, на котором C — произвольная точка серединного перпендикуляра к AB (которая пересекает AB в точке D):

Сравните \(\Delta ACD\) и (\Дельта BCD\). Имеем:
AD = BD
CD = CD (общий)
∠ADC =∠BDC = 90°
Мы видим, что \(\Delta ACD \cong \Delta BCD\) по критерию соответствия SAS. CA = CB, что означает, что C равноудален от A и B.
Примечание. Обратитесь к критерию соответствия SAS, чтобы понять, почему \(\Delta ACD\) и \(\Delta BCD\) совпадают.
Теорема о перпендикулярной биссектрисе Обратное доказательство
Рассмотрим CA = CB на приведенном выше рисунке.
Чтобы доказать, что AD = BD.
Из точки C проведите перпендикуляр, пересекающий отрезок AB в точке D.
Теперь сравните \(\Delta ACD\) и \(\Delta BCD\). У нас есть:
AC= BC
CD = CD (общий)
∠ADC = ∠BDC = 90°
Мы видим, что \(\Delta ACD \cong \Delta BCD\) по критерию соответствия SAS. Таким образом, AD = BD, что означает, что C равноудален от A и B .
Важные примечания
Теорема о перпендикулярной биссектрисе и ее обращение могут быть доказаны критерием конгруэнтности SAS.
Теорема о перпендикулярном биссектрисе используется при строительстве зданий, мостов и т. д., а также при создании проектов, где нам нужно построить что-то в центре и на равном расстоянии от концов.
Связанные темы по теореме о биссектрисе перпендикуляра
Биссектриса угла
Построение угла 90 градусов
Конгруэнтные треугольники
Как узнать, являются ли два отрезка перпендикулярными?

Пример 1. В пирамиде отрезок AD — это серединный перпендикуляр к треугольнику ABC на отрезке BC. Если AB = 20 футов и BD = 7 футов, найдите длину стороны AC.
Решение
Дана биссектриса AD на отрезке BC.
Итак, по теореме о биссектрисе перпендикуляра любая точка на отрезке AD находится на одинаковом расстоянии от точек B и C. Отсюда следует, что AB = AC
AC = 20 футов.
Пример 2. Можем ли мы сказать, что в любом равностороннем или равнобедренном треугольнике вершина между равными сторонами лежит на серединном перпендикуляре к основанию?

Раствор
Из вершины X проведите перпендикуляр, который пересекает отрезок YZ в точке \(O\).
Если XY = XZ,
Затем с помощью обратной теоремы о серединном перпендикуляре доказывается, что OY=OZ .
\(\следовательно\) Вершина X лежит на серединном перпендикуляре к основанию YZ треугольника.

перейти к слайдуперейти к слайду

Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу с Cuemath.
БЕСПЛАТНАЯ ИСПОЛЬЗОВАНИЯ КЛАСС
С. С. С. С. Слдего, чтобы скользить, чтобы скользить
Часто задаваемые вопросы (FAQS)
81 What The PERPEREMCEREEM -BEREMICER?
Теорема о серединном перпендикуляре утверждает, что любая точка на биссектрисе равноудалена от обоих концов отрезка, на котором она проведена.
Что такое теорема о биссектрисе угла?
Теорема о биссектрисе угла гласит, что в треугольнике биссектриса любого угла будет делить противоположную сторону в отношении сторон, содержащих этот угол.