Геометрия ОГЭ-2022
Курсы для аттестации учителей от 800 ₽ (72 часа). Документы об окончании по почте БЕСПЛАТНО…
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Выбрать материалы
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
10 задач по геометрии тестовой части
Вопрос 1
В треугольнике ABC известно, что , . Найдите угол BCA. Ответ дайте в градусах.
Найдите угол BCA. Ответ дайте в градусах.
Варианты ответов
- 36
- 46
Вопрос 2
Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
Варианты ответов
- 4,5
- 4
- 3
Вопрос 3
Найдите площадь квадрата, описанного вокруг окружности радиуса 39.
Варианты ответов
- 6084
- 5860
- 5480
Вопрос 4
Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Варианты ответов
- 12
- 10
- 8
Вопрос 5
Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба, делённую на .
Варианты ответов
- 50
- 30
- 60
Вопрос 6
В трапеции ABCD известно, что AD = 4, BC = 3, а её площадь равна 84. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Варианты ответов
- 42
- 39
Вопрос 7
Найдите тангенс угла AOB
Варианты ответов
- 6
- 8
- 2
Вопрос 8
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
Варианты ответов
- 5
- 3
- 4
Вопрос 9
Какие из следующих утверждений верны?
1) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
2) Все диаметры окружности равны между собой.
3) Один из углов треугольника всегда не превышает 60 градусов.
Если вариантов ответов несколько, укажите их в порядке возрастания без пробелов и знаков препинания
Варианты ответов
- 3
- 23
Вопрос 10
Какие из следующих утверждений верны?
1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.
2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
3) Площадь трапеции меньше произведения суммы оснований на высоту.
4) Площадь прямоугольного треугольника меньше произведения его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
Варианты ответов
- 234
- 13
- 24
Пройти тест
Сохранить у себя:
© 2022, Афян Асмик Шамировна 941
Задача 19 ОГЭ математика
Задача 19
Сложность у всех задач примерно одинаковая
-
Какое из следующих утверждений верно?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны.
2) Сумма углов прямоугольного треугольника равна 180°.
3) Любая медиана равнобедренного треугольника является его высотой.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) В любом параллелограмме есть два равных угла.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) Дана окружность. Через любую точку плоскости можно провести к ней касательную прямую.
2) Если в параллелограмме некоторый угол равен 90°, то это квадрат.
В ответе запишите номер выбранного утверждения.
-
Какое из следующих утверждений верно?
1) Внутренние односторонние углы при пересечении параллельных прямых секущей равны.
2) Площадь трапеции равна произведению высоты на сумму оснований.
3) В любом квадрате все углы равны.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Сумма катетов длиннее гипотенузы.
2) Длина суммы векторов длиннее суммы длин самих векторов.
3) В любом треугольнике найдется острый угол.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) Сумма длин трех сторон четырехугольника всегда длиннее четвертой стороны.
2) В любой выпуклый четырехугольник можно вписать окружность.
3) Диагонали ромба равны.В ответе запишите номер выбранного утверждения.
-
Какое из следующих утверждений верно?
1) Площадь треугольника равна произведению стороны на высоту, проведенную к этой стороне.
2) Треугольники равны, если их соответствующие стороны равны.
3) У подобных треугольников площади равны.В ответе запишите номер выбранного утверждения.
-
Какое из следующих утверждений верно?
1) Сумма вертикальных углов равна 180°.
2) Корень квадратный из площади квадрата равен длине его стороны.
3) Периметр прямоугольника всегда больше его площади.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) У подобных треугольников соответствующие углы равны.
2) В правильном пятиугольнике все углы равны.
3) Площадь прямоугольника равна квадрату любой его стороны. -
Какое из следующих утверждений верно?
1) В правильном шестиугольнике все углы по 160°.
2) Не существует треугольника со сторонами 10,12 и 16.
3) Диагонали прямоугольника равны.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) В любой прямоугольник можно вписать окружность.
2) Вписанные углы, опирающиеся на одну дугу окружности, равны.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

-
Какое из следующих утверждений верно?
1) Косинус угла в прямоугольном треугольнике это отношение прилежащего катета к противолежащему катету.
2) Катет лежащий против угла в 60° в два раза короче гипотенузы.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Центр окружности вписанной в треугольник находится на пересечении биссектрис.
2) В правильном шестиугольнике все стороны равны.
3) Сумма двух соседних углов параллелограмма равна 180°.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) Дана прямая. Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.
Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.
2) Высоты треугольника пересекаются в одной точке.
3) Высота треугольника всегда лежит внутри треугольника.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) Диагонали ромба пересекаются и точкой пересечения делятся пополам.
2) Площадь прямоугольника равна произведению двух противоположных сторон.
3) Длина вектора равна сумме квадратов его координат.В ответе запишите номер выбранного утверждения.
-
Какое из следующих утверждений верно?
1) Сумма смежных углов равна 180°.
2) Если скалярное произведение векторов равно нулю, то векторы параллельны.
3) В любой трапеции есть, по крайней мере, два острых угла.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Площадь любого треугольника равна половине произведения сторон на синус угла между ними.
2) Все точки лежащие на биссектрисе некоторого угла равноудалены от сторон этого угла.
3) Площадь ромба равна половине произведения сторон.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) Если две окружности касаются, то у них радиусы равны.
2) Периметр прямоугольника равен произведению двух соседних сторон.
3) Сумма углов пятиугольника равна 540°.
В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Вокруг любого четырехугольника можно описать окружность.
2) Если некоторая окружность касается прямой, то расстояние от центра окружности до этой прямой равно радиусу окружности.
3) Если соответственные углы при пересечении двух прямых секущей равны, то прямые параллельны.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) Через точку, лежащую на окружности, всегда можно провести касательную к этой окружности.
2) Длина окружности всегда больше ее радиуса.
3) Если в треугольнике одна сторона равна половине второй, то в треугольнике есть угол в 30°.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) Если в параллелограмме все углы равны, то это квадрат.
2) Длина самой длинной стороны в треугольнике меньше суммы длин двух других сторон.
3) Вокруг любого четырехугольника можно описать окружность.В ответе запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Диагональ параллелограмма делит его на два равных треугольника.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

-
Какие из следующих утверждений верны?
1) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) Любой квадрат является прямоугольником.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
2) Каждая из биссектрис равнобедренного треугольника является его медианой.
3) В любой ромб можно вписать окружность.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

-
Какие из следующих утверждений верны?
1) Любые два прямоугольных треугольника подобны.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Стороны треугольника пропорциональны синусам противолежащих углов.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) Треугольник со сторонами, длины которых равны 3,4 и 5, является тупоугольным.
2) Прямоугольник обладает центром симметрии.
3) Любой прямоугольный треугольник не обладает центром симметрии.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) У квадрата ровно две оси симметрии.
2) Центром симметрии ромба является точка пересечения его диагоналей.
3) Площадь прямоугольного треугольника меньше произведения его катетов.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) В правильный шестиугольник всегда можно вписать окружность.
2) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
3) Сумма вертикальных углов равна 180°.В ответ запишите номер выбранного утверждения.
-
Какое из следующих утверждений верно?
1) Через любые две точки на плоскости можно провести окружность, причем только одну.
2) У прямоугольного треугольника не может быть оси симметрии.
3) Диагонали трапеции всегда пересекаются.В ответ запишите номер выбранного утверждения.
-
Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат.
2) В параллелограмме есть два равных угла.
3) Площадь параллелограмма меньше или равна произведению двух его соседних сторон.В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какие из следующих утверждений верны?
1) Косинус острого угла прямоугольного треугольника равен отношению катета, прилежащего к этому углу, к гипотенузе.
2) Если в параллелограмме все углы равны, то это прямоугольник.
3) Все высоты равнобедренного треугольника лежать внутри этого треугольника.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
-
Какое из следующих утверждений верно?
1) К двум окружностям всегда можно провести две общие касательные.
2) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник – параллелограмм.
3) Точка пересечения биссектрис любого треугольника всегда лежит внутри этого треугольника.В ответ запишите номер выбранного утверждения.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Как найти площадь прямоугольного треугольника
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Learn by Concept
PSAT Math Help » Геометрия » Плоская геометрия » Треугольники » Прямоугольные треугольники » Как найти площадь прямоугольного треугольника
Периметр прямоугольного треугольника равен 40 единицам.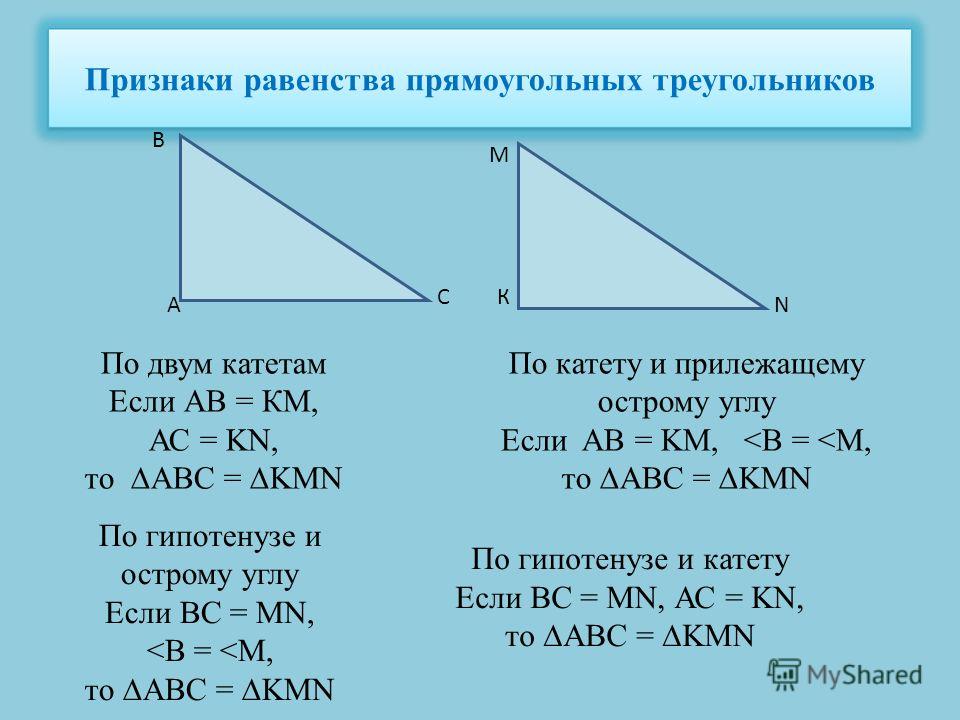 Если длины сторон равны , и единицам, то какова площадь треугольника?
Если длины сторон равны , и единицам, то какова площадь треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку периметр равен сумме длин трех сторон треугольника, мы можем сложить три выражения для длин и установить их равными 40.
Периметр:
Упростить x условия.
Упростите константы.
Вычтите 8 с обеих сторон.
Разделить на 4
Одна сторона равна 8.
Вторая сторона равна
.
Третья сторона
.
Таким образом, стороны треугольника равны 8, 15 и 17.
Вопрос касается площади треугольника, которая определяется формулой (1/2)bh. Нам говорят, что это прямоугольный треугольник, поэтому мы можем использовать одну из сторон в качестве основания, а другую сторону в качестве высоты, так как стороны будут пересекаться под прямым углом. Катетами прямоугольного треугольника должны быть наименьшие стороны (самая длинная должна быть гипотенуза), которые в данном случае равны 8 и 15. Итак, предположим, что 8 — это основание, а 15 — это высота.
Катетами прямоугольного треугольника должны быть наименьшие стороны (самая длинная должна быть гипотенуза), которые в данном случае равны 8 и 15. Итак, предположим, что 8 — это основание, а 15 — это высота.
Площадь треугольника равна (1/2)bh. Мы можем заменить 8 и 15 на b и h.
.
Ответ: 60 единиц в квадрате.
Сообщить об ошибке
Рисунок выполнен не в масштабе.
На рисунке выше лучи PA и PB касаются окружности O в точках A и B соответственно. Если диаметр окружности O равен 16 единицам, а длина отрезка PO равна 17 единицам, какова площадь четырехугольника PAOB в квадратных единицах?
Возможные ответы:
60
120
136
240
68
Правильный ответ:
150 100 Объяснение:
Поскольку PA и PB касаются окружности O, углы PAO и PBO должны быть прямыми; следовательно, треугольники PAO и PBO прямоугольные.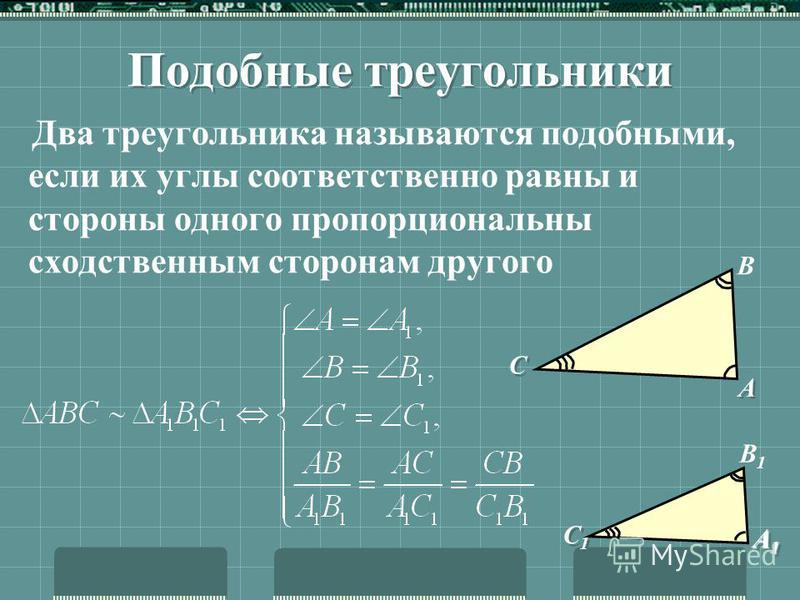
Так как AO и OB являются радиусами окружности O, они конгруэнтны. Кроме того, поскольку PA и PB являются внешними касательными, исходящими из одной и той же точки, они также должны быть конгруэнтны.
Итак, в треугольниках PAO и PBO две стороны равны, и между ними есть конгруэнтный угол (все прямые углы конгруэнтны). Следовательно, по теореме о конгруэнтности сторона-угол-сторона (SAS) треугольники PAO и PBO конгруэнтны.
Обратите внимание, что четырехугольник PAOB можно разбить на треугольники PAO и PBO. Поскольку эти треугольники конгруэнтны, каждый из них должен составлять половину площади четырехугольника PAOB. В результате, если мы найдем площадь одного из треугольников, мы можем удвоить ее, чтобы найти площадь четырехугольника.
Определим площадь треугольника PAO. Мы уже установили, что это прямоугольный треугольник. Нам говорят, что PO, гипотенуза треугольника, равна 17. Нам также говорят, что диаметр окружности O равен 16, а это означает, что каждый радиус окружности равен 8, потому что радиус равен половине размера диаметра.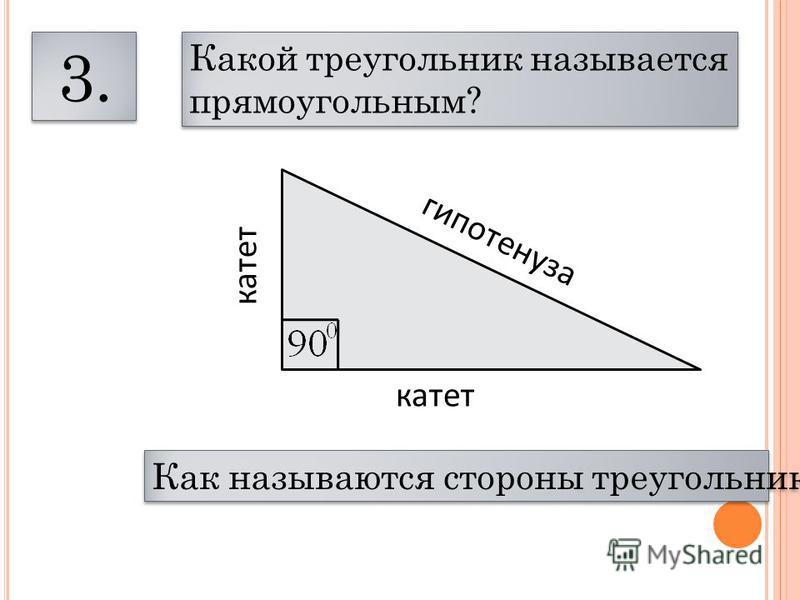 Поскольку отрезок AO является радиусом, его длина должна быть равна 8.
Поскольку отрезок AO является радиусом, его длина должна быть равна 8.
Итак, треугольник PAO — прямоугольный с гипотенузой 17 и катетом 8. Мы можем использовать теорему Пифагора, чтобы найти другой катет. Согласно теореме Пифагора, если а и b — длины катетов прямоугольного треугольника, а с — длина гипотенузы, то:
a 2 + b 2 = c 2
Пусть b обозначает длину PA.
8 2 + b 2 = 17 2
64 + b 2 = 289
Вычесть 64 с обеих сторон.
b 2 = 225
Извлеките квадратный корень из обеих частей.
b = 15
Это означает, что длина PA равна 15.
Теперь применим формулу площади прямоугольного треугольника. Поскольку катеты прямоугольного треугольника перпендикулярны, один из них можно считать основанием, а другой — высотой треугольника.
площадь треугольника PAO = ( 1 / 2 )bh
= ( 1 / 2 )(8)(15) = 60
В конечном счете, мы должны найти площадь четырехугольника OB; однако ранее мы определили, что треугольники PAO и PBO составляют половину четырехугольника каждый. Таким образом, если мы удвоим площадь PAO, мы получим площадь четырехугольника PAOB.
Таким образом, если мы удвоим площадь PAO, мы получим площадь четырехугольника PAOB.
Площадь PAOB = 2(площадь PAO)
= 2(60) = 120 квадратных единиц
Ответ: 120.
Сообщить об ошибке
Если гипотенуза треугольника равна 5 метрам, какое из следующих значений является ближайшим значением к площади треугольника?
Возможные ответы:
5
45
54
26
12
Правильный ответ:
12
Пояснение:
Ответ: 12. В этом случае площадь треугольника не может быть меньше длины его гипотенузы и не может быть больше квадрата гипотенузы (это будет площадь квадрата).
Сообщить об ошибке
Треугольник ABC построен между точками A(4, 3), B(4, 8) и C(7, 3). Чему равна площадь АВС?
Возможные ответы:
Правильный ответ:
Пояснение:
Быстрый набросок этого треугольника покажет, что это прямоугольный треугольник. Линии AB и AC образуют высоту и основание этого треугольника взаимозаменяемо, в зависимости от того, как вы на него смотрите.
Линии AB и AC образуют высоту и основание этого треугольника взаимозаменяемо, в зависимости от того, как вы на него смотрите.
В любом случае формула площади треугольника представляет собой расстояние от А до В, умноженное на расстояние от А до С, деленное на 2.
Это
Сообщить об ошибке
Прямоугольный треугольник имеет общий периметр 12, а длина его гипотенузы 5. Какова площадь этого треугольника?
Возможные ответы:
6
10
15
12
3
Правильный ответ:
6
Пояснение:
Площадь треугольника определяется уравнением 1/2b x h.
b обозначает длину основания, а h обозначает высоту.
Здесь нам говорят, что периметр (суммарная длина всех трех сторон) равен 12, а гипотенуза (сторона, которая не является ни высотой, ни основанием) равна 5 единицам длины.
Итак, 12-5 = 7 для суммы периметра основания и высоты.
7 не делится на два точно, но распадается на 3 и 4,
и 1/2 (3×4) дает 6.
Еще один способ решить эту проблему: если вы вспомните свои правила для прямоугольных треугольников, одним из самых основных является треугольник 3,4,5, который у нас есть именно здесь
Сообщить об ошибке
Отношение для длина стороны прямоугольного треугольника равна 3:4:5. Если периметр равен 48, какова площадь треугольника?
Возможные ответы:
108
48
240
96
50
5 9 Правильный ответ:0012
96
Пояснение:
Длины сторон треугольника можно смоделировать как 3x, 4x и 5x. Мы знаем, что периметр равен 3x+4x+5x=48, значит, x=4. Это говорит нам о том, что катеты прямоугольного треугольника 3x=12 и 4x=16, поэтому площадь A=1/2 bh=(1/2)(12)(16)=96.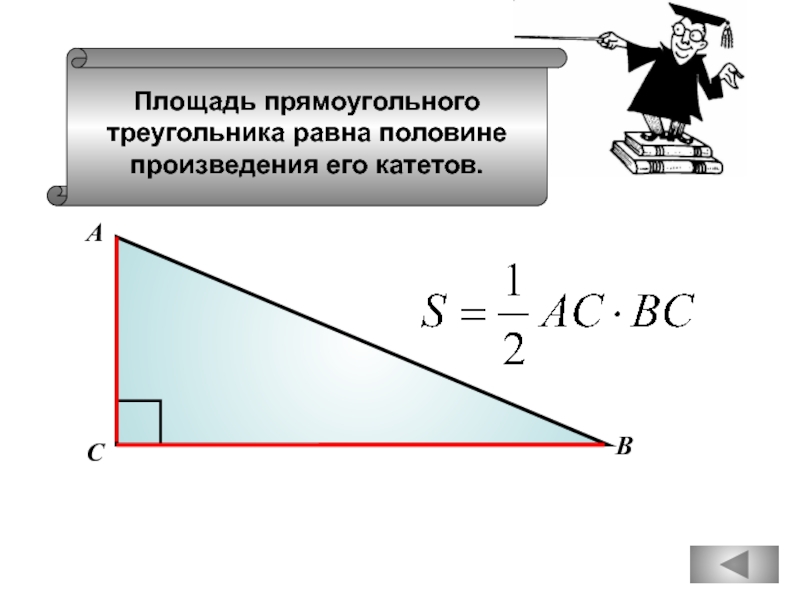
Сообщить об ошибке
Длина катета равностороннего треугольника равна 6. Чему равна площадь треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Основание равно 6.
Высота равностороннего треугольника равна , где длина основания.
Сообщить об ошибке
Примечание. Рисунок выполнен НЕ в масштабе.
См. схему выше. С точки зрения площади, какова доля ?
Возможные ответы:
Недостаточно информации для ответа на вопрос.
Правильный ответ:
Пояснение:
Площадь треугольника равна половине произведения его основания на высоту.
Площадь равна
Площадь равна
Следовательно, это из .
Обратите внимание, что на самом деле находить меру не обязательно.
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы PSAT
10 Диагностические тесты 421 практический тест Вопрос дня Карточки Learn by Concept
Прямоугольный треугольник | Энциклопедия MDPI
Прямоугольный треугольник (американский вариант английского языка) или прямоугольный треугольник (британский вариант английского языка) — это треугольник, в котором один угол является прямым (то есть угол равен 90 градусов). Соотношение между сторонами и углами прямоугольного треугольника является основой тригонометрии. Сторона, противолежащая прямому углу, называется гипотенузой (сторона с на рисунке). Стороны, прилегающие к прямому углу, называются катетами (или катетами, в единственном числе: катетами). Сторона а может быть идентифицирована как сторона, примыкающая к углу В и противоположная (или противоположная) углу А, а сторона b — это сторона, примыкающая к углу А и противолежащая углу В. Если длины всех трех сторон прямоугольного треугольника равны целые числа, треугольник называется пифагорейским треугольником, а длины его сторон в совокупности известны как пифагорейская тройка.
Сторона а может быть идентифицирована как сторона, примыкающая к углу В и противоположная (или противоположная) углу А, а сторона b — это сторона, примыкающая к углу А и противолежащая углу В. Если длины всех трех сторон прямоугольного треугольника равны целые числа, треугольник называется пифагорейским треугольником, а длины его сторон в совокупности известны как пифагорейская тройка.
1. Основные свойства
1.1. Площадь
Как и у любого треугольника, площадь равна половине основания, умноженной на соответствующую высоту. В прямоугольном треугольнике, если один катет принять за основание, то другой является высотой, поэтому площадь прямоугольного треугольника равна половине произведения двух катетов. По формуле площадь T равна
- [math]\displaystyle{ T=\tfrac{1}{2}ab}[/math]
, где a и b — стороны треугольника.
Если вписанная окружность касается гипотенузы AB в точке P, то обозначив полупериметр ( a + b + c ) / 2 как s , получим PA = s − a и PB = s − b , а площадь определяется как
- [math]\displaystyle{ T=\text{PA} \cdot \text{PB} = (s-a)(s-b).
 }[/математика]
}[/математика]
Эта формула применима только к прямоугольным треугольникам. [1]
1.2. Высоты
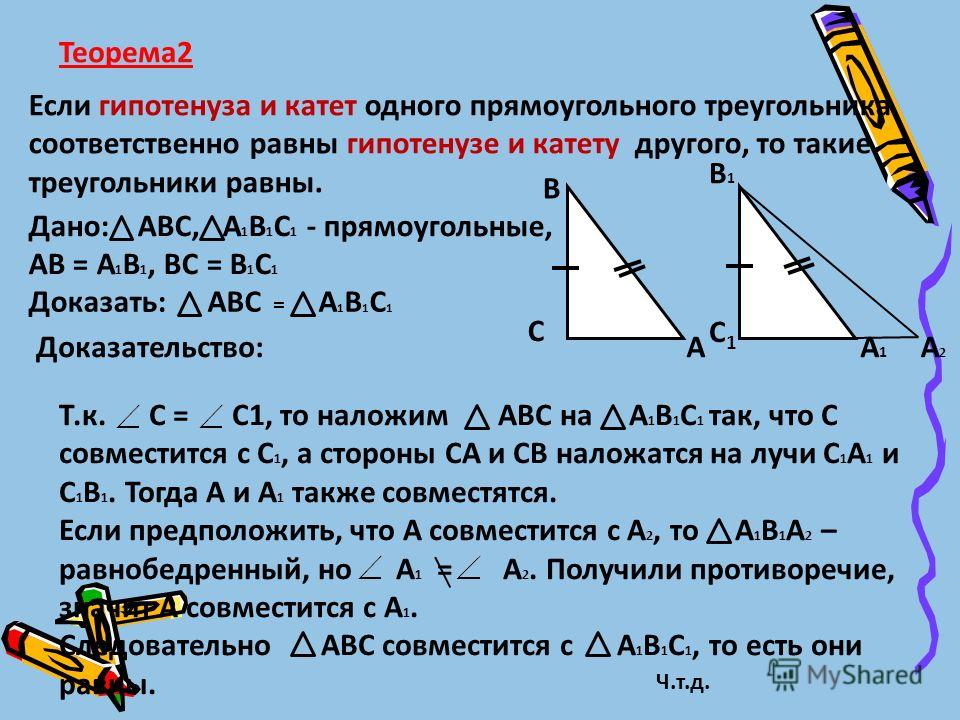
Высота прямоугольного треугольника. https://handwiki.org/wiki/index.php?curid=1399518
Если из вершины с прямым углом к гипотенузе провести высоту, то треугольник делится на два меньших треугольника, которые оба подобны исходному и поэтому похожи друг на друга. Отсюда:
- Высота до гипотенузы — это среднее геометрическое (среднее пропорциональное) двух отрезков гипотенузы. [2] :243 92}. }[/математика]
Решения этого уравнения в целых числах a, b, f и c см. здесь.
Высота одной ноги совпадает с высотой другой ноги. Поскольку они пересекаются в прямоугольной вершине, ортоцентр прямоугольного треугольника — пересечение трех его высот — совпадает с прямоугольной вершиной.
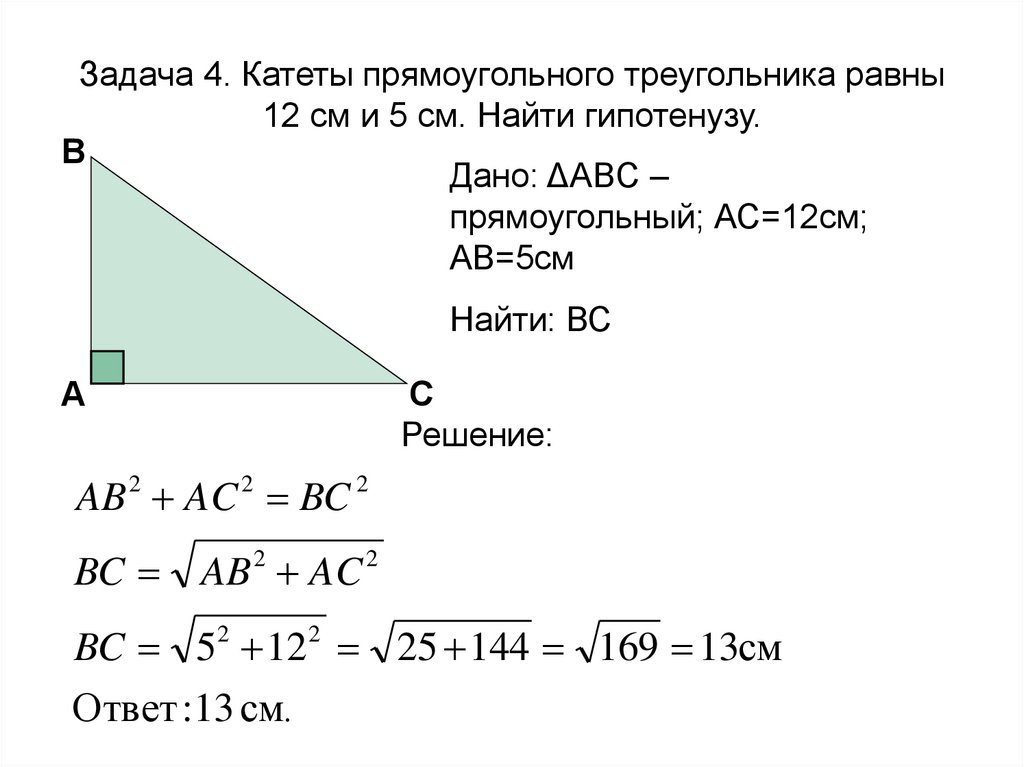
1.3. Теорема Пифагора
Теорема Пифагора утверждает, что:
В любом прямоугольном треугольнике площадь квадрата, стороной которого является гипотенуза (сторона, противоположная прямому углу), равна сумме площадей квадратов, сторонами которых являются два катета (две стороны, пересекающиеся под прямым углом).
 угол). 92 }[/математика]
угол). 92 }[/математика], где c — длина гипотенузы, а a и b — длины двух оставшихся сторон.
Тройки Пифагора — это целые числа a, b, c , удовлетворяющие этому уравнению.
1.4. Внутренний и окружной радиус
Иллюстрация теоремы Пифагора . https://handwiki.org/wiki/index.php?curid=1201314
Радиус вписанной окружности прямоугольного треугольника с катетами a и b и гипотенуза c равно
- [math]\displaystyle{ r = \frac{a+b-c}{2} = \frac{ab}{a+b+c}. }[/математика]
Радиус описанной окружности равен половине длины гипотенузы,
- [math]\displaystyle{ R = \frac{c}{2}. }[/математика]
Таким образом, сумма радиуса описанной окружности и внутреннего радиуса составляет половину суммы катетов: [6]
- [math]\displaystyle{ R+r = \frac{a+b}{2}. }[/математика]
Один из катетов можно выразить через внутренний радиус, а другой как
- [math]\displaystyle{ \displaystyle a=\frac{2r(b-r)}{b-2r}.
 }[/математика]
}[/математика]
2. Характеристики
Треугольник ABC со сторонами [math]\displaystyle{ a \le b \lt c }[/math], полупериметр s , площадь T , высота h напротив наибольшей сторона, радиус описанной окружности R , внутренний радиус r , внешний радиус R A , R B , R C (Tangent до A , B , C, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ). , m c является прямоугольным треугольником тогда и только тогда, когда верно любое из утверждений в следующих шести категориях. Все они, конечно, также являются свойствами прямоугольного треугольника, поскольку характеристики являются эквивалентностями.
2.1. Стороны и полупериметр 92{С}=1.
 }[/математика] [10]
}[/математика] [10] - [математика]\displaystyle{ \displaystyle \sin{2A}=\sin{2B}=2\sin{A}\sin{B}. }[/математика]
2.3. Площадь
- [математика]\displaystyle{ \displaystyle T=\frac{ab}{2} }[/math]
- [математика]\displaystyle{ \displaystyle T=r_ar_b=rr_c}[/math]
- [математика] \ displaystyle { \ displaystyle T = r (2R + r)} [/ math]
- [math]\displaystyle{ T=PA\cdot PB, }[/math] где P — точка касания вписанной окружности на самой длинной стороне АБ . [11]
2.4. Inradius и Exradii
- [математика] \ displaystyle { \ displaystyle r = s-c = (a + b-c) / 2 } [/ math]
- [математика]\displaystyle{ \displaystyle r_a=s-b=(a-b+c)/2}[/math]
- [математика]\displaystyle{ \displaystyle r_b=s-a=(-a+b+c)/2}[/math]
- [математика]\displaystyle{ \displaystyle r_c=s=(a+b+c)/2}[/math]
- [математика]\displaystyle{ \displaystyle r_a+r_b+r_c+r=a+b+c}[/math] 92 }[/математика]
- [математика]\displaystyle{ \displaystyle r=\frac{r_ar_b}{r_c}.
 2. }[/математика] [6] :Вероятность. 954, с. 26
2. }[/математика] [6] :Вероятность. 954, с. 26 - Длина одной медианы равна радиусу описанной окружности.
- Кратчайшая высота (из вершины с наибольшим углом) равна среднему геометрическому отрезков, на которые она делит противоположную (самую длинную) сторону. Это теорема о высоте прямоугольного треугольника.
2.6. Окружность и вписанная окружность
- Треугольник можно вписать в полуокружность так, чтобы одна сторона совпадала со всем диаметром (теорема Фалеса).
- Центр описанной окружности — это середина самой длинной стороны.
- Самая длинная сторона равна диаметру описанной окружности [math]\displaystyle{ \displaystyle (c=2R). }[/математика]
- Описанная окружность касается окружности с девятью точками. [8]
- Ортоцентр лежит на описанной окружности. [6]
- Расстояние между вписанным центром и ортоцентром равно [math]\displaystyle{ \sqrt{2}r }[/math].
 [6]
[6]
3. Тригонометрические отношения
Тригонометрические функции для острых углов можно определить как отношения сторон прямоугольного треугольника. Для заданного угла можно построить прямоугольный треугольник с этим углом, а стороны помечены как противоположные, смежные и гипотенуза относительно этого угла в соответствии с приведенными выше определениями. Эти отношения сторон зависят не от конкретного выбранного прямоугольного треугольника, а только от данного угла, так как все треугольники, построенные таким образом, подобны. Если для заданного угла α противолежащая сторона, прилежащая сторона и гипотенуза обозначены O , A и H соответственно, тогда тригонометрические функции равны
- [math]\displaystyle{ \sin\alpha =\frac {O}{H},\,\cos\alpha =\frac {A}{H},\,\tan\alpha =\frac {O}{A},\,\sec\alpha =\frac {H}{A},\,\cot\alpha =\frac {A {O},\,\csc\alpha =\frac {H}{O}. }[/математика]
О выражении гиперболических функций в виде отношения сторон прямоугольного треугольника см. Гиперболический треугольник гиперболического сектора.
Гиперболический треугольник гиперболического сектора.
4. Особые прямоугольные треугольники
Значения тригонометрических функций можно вычислить точно для определенных углов, используя прямоугольные треугольники со специальными углами. К ним относятся треугольник 30-60-90 , который можно использовать для вычисления тригонометрических функций для любого числа, кратного π/6, и треугольник 45-45-90 , который можно использовать для вычисления тригонометрических функций для любого числа, кратного π/6. π/4.
4.1. Треугольник Кеплера
Пусть H , G и A будут средним гармоническим, средним геометрическим и средним арифметическим двух положительных чисел 9{3}, \, }[/math]
где [math]\displaystyle{ \phi }[/math] — это золотое сечение [math]\displaystyle{ \tfrac{1+ \sqrt{5}}{2}. \, }[/math] Поскольку стороны этого прямоугольного треугольника находятся в геометрической прогрессии, это треугольник Кеплера.
5. Теорема Фалеса
Медиана прямого угла треугольника. https://handwiki.org/wiki/index.php?curid=2027876
Теорема Фалеса утверждает, что если A является любой точкой окружности с диаметром BC (за исключением самих B или C ) ABC — прямоугольный треугольник, где A — прямой угол. Обратное утверждение гласит, что если прямоугольный треугольник вписан в окружность, то гипотенуза будет диаметром окружности. Следствием этого является то, что длина гипотенузы в два раза больше расстояния от вершины прямого угла до середины гипотенузы. Кроме того, центр окружности, описанной вокруг прямоугольного треугольника, является серединой гипотенузы, а его радиус равен половине длины гипотенузы. 92. }[/математика]
7. Прямая Эйлера
В прямоугольном треугольнике прямая Эйлера содержит медиану на гипотенузе, то есть она проходит как через прямоугольную вершину, так и через середину стороны, противоположной этой вершине.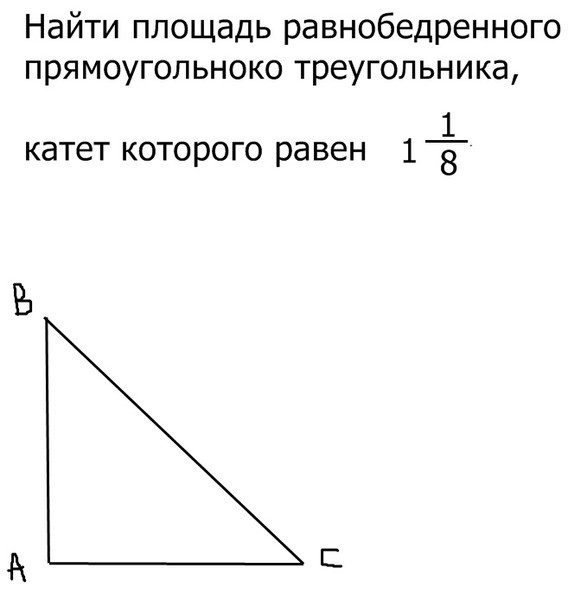 Это связано с тем, что ортоцентр прямоугольного треугольника, точка пересечения его высот, приходится на прямоугольную вершину, а его центр описанной окружности, точка пересечения серединных перпендикуляров сторон, приходится на середину гипотенузы.
Это связано с тем, что ортоцентр прямоугольного треугольника, точка пересечения его высот, приходится на прямоугольную вершину, а его центр описанной окружности, точка пересечения серединных перпендикуляров сторон, приходится на середину гипотенузы.
8. Неравенства
В любом прямоугольном треугольнике диаметр вписанной окружности меньше половины гипотенузы и, что более важно, меньше или равен гипотенузе, умноженной на [math]\displaystyle{ (\sqrt{2}-1). }[/math] [14] :p.281
В прямоугольном треугольнике с катетами a , b и гипотенузой c ,
- {c]\gedisplay [math \gedisplay frac{\sqrt{2}}{2}(a+b)}[/math]
с равенством только в равнобедренном случае. [14] :стр.282,стр.358
Если высоту от гипотенузы обозначить h c , то
\fracc_stylehdisplay{math} \sqrt {2}}{4}(a+b)}[/math] с равенством только в равнобедренном случае.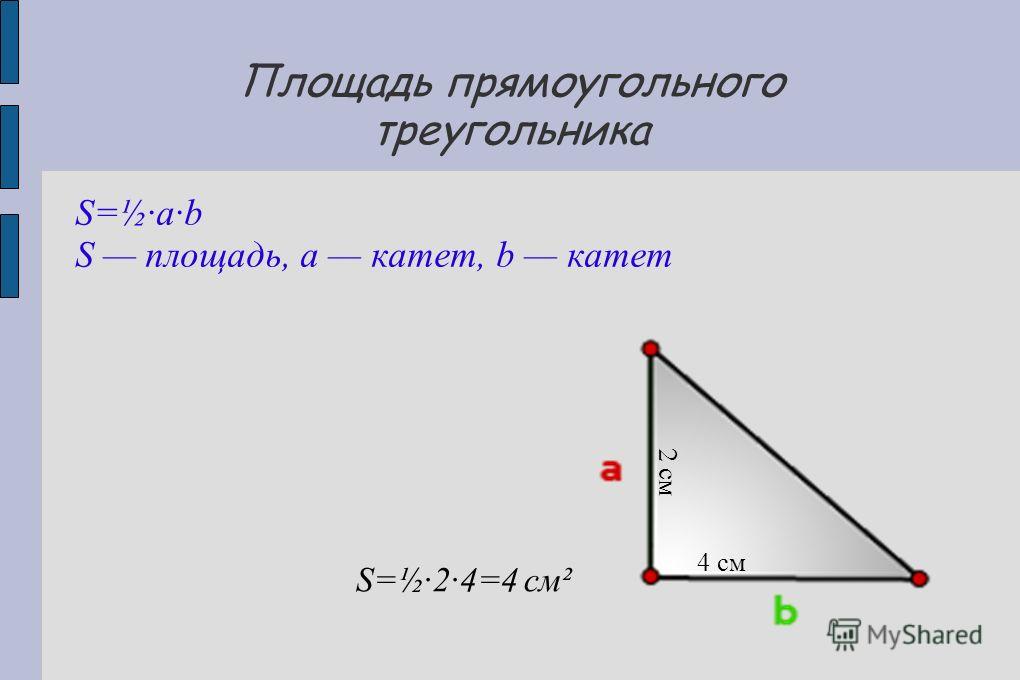





 Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.
Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной. 






 }[/математика]
}[/математика]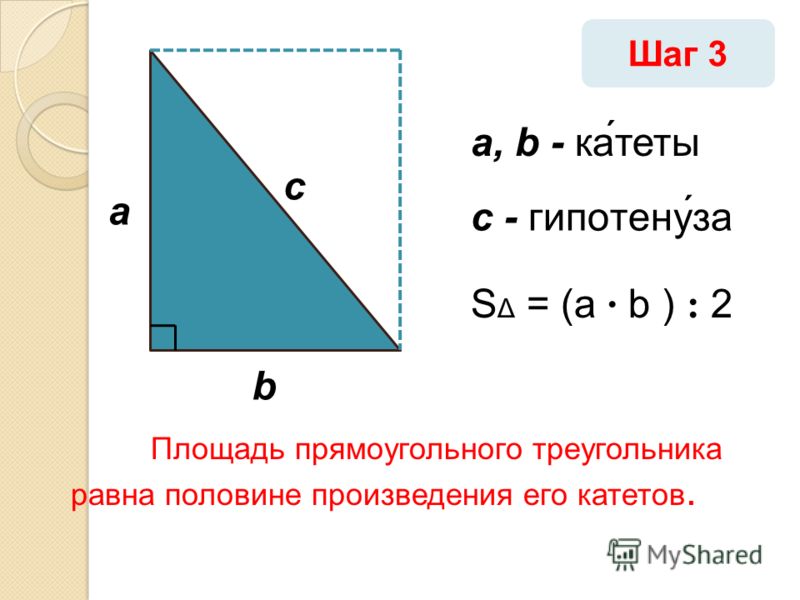 угол). 92 }[/математика]
угол). 92 }[/математика] }[/математика]
}[/математика] }[/математика] [10]
}[/математика] [10]  2. }[/математика] [6] :Вероятность. 954, с. 26
2. }[/математика] [6] :Вероятность. 954, с. 26  [6]
[6]
Leave A Comment