7 способов найти площадь прямоугольника
10 марта 2020 Ликбез Образование
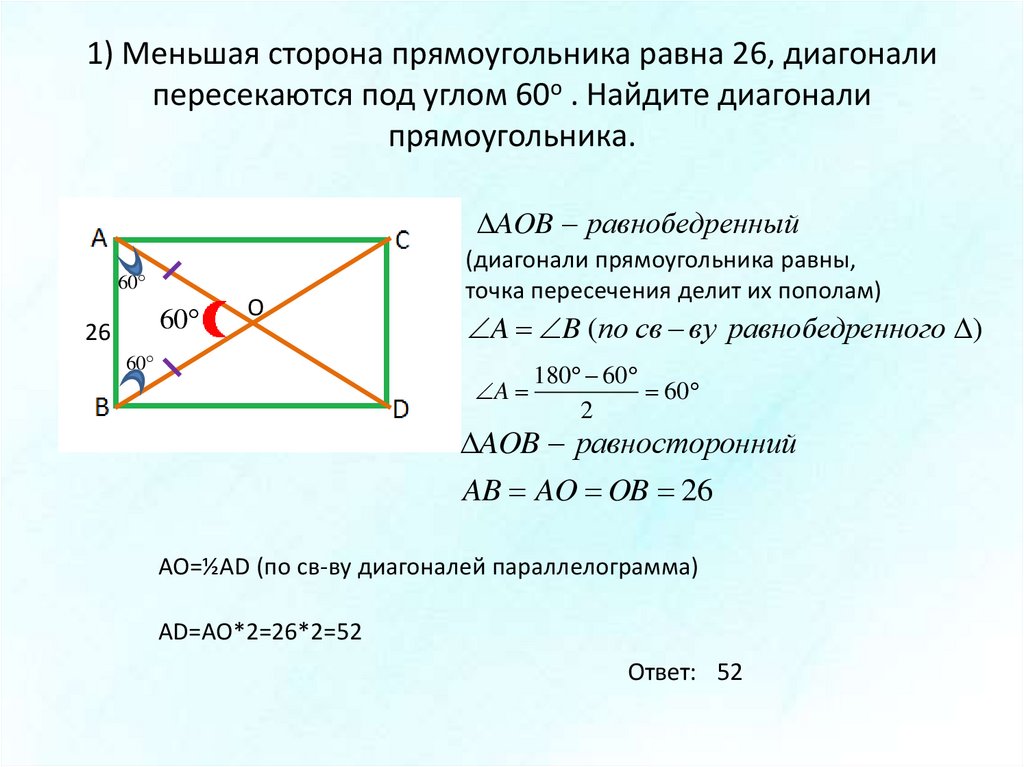
Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6.
 Если известны диагональ и угол между диагоналями
Если известны диагональ и угол между диагоналямиНайдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Площадь прямоугольника формулы и калькулятор
{S = a \cdot b}
Найти площадь прямоугольника
через сторонычерез сторону и диагональдиагонали и угол между нимичерез сторону и периметрчерез сторону и радиус описанной окружностичерез радиус описанной окружности и угол между диагоналями
Сторона a
ммсмдммкмдюймы (in)футы (ft)
Сторона b
ммсмдммкмдюймы (in)футы (ft)
Результат в
мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)
дюймы (in²)кв. футы (ft²)
Виджет
Ссылка на расчет
Сохранить расчет
Печатать
Найти площадь прямоугольника вы сможете с помощью калькуляторов или по формулам вручную. Для этого мы подготовили 6 формул и калькулятор, который позволяет произвести расчет по любой из них.
Прямоугольник — четырехугольник, у которого все углы равны 90° (прямые).
Содержание:
- калькулятор площади прямоугольника
- формула площади прямоугольника через стороны
- формула площади прямоугольника через сторону и диагональ
- формула площади прямоугольника через диагонали и угол
- формула площади прямоугольника через сторону и периметр
- формула площади прямоугольника через радиус описанной окружности и угол между диагоналями
- примеры задач
Формула площади прямоугольника через стороны
S = a \cdot b
a, b — стороны прямоугольника (длина и ширина)
Формула площади прямоугольника через сторону и диагональ
S=a \cdot \sqrt{d^2 — a^2}
d — диагональ прямоугольника
a — сторона прямоугольника
Формула площади прямоугольника через диагонали и угол
S = \dfrac{1}{2} \cdot d^2 \cdot \sin(\alpha)
d — диагональ прямоугольника
α — угол между диагоналями
Формула площади прямоугольника через сторону и периметр
S = \dfrac{a \cdot P — 2a^2}{2}
a — сторона прямоугольника
P — периметр прямоугольника
Формула площади прямоугольника через сторону и радиус описанной окружности
S = a \cdot \sqrt{4R^2 — a^2}
R — радиус описанной окружности
a — сторона прямоугольника
Формула площади прямоугольника через радиус описанной окружности и угол между диагоналями
S = 2R^2 \cdot \sin{\alpha}
R — радиус описанной окружности
α — угол между диагоналями
Примеры задач на нахождение площади сектора круга
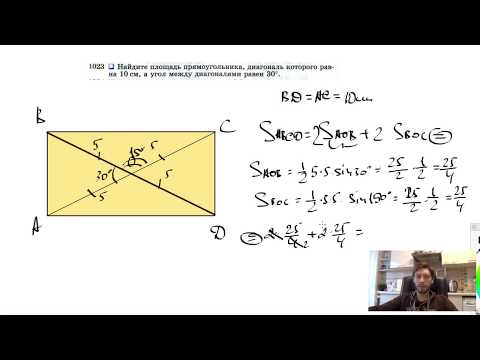
Задача 1
Найдите площадь прямоугольника диагональ которого равна 10 см, а угол между диагоналями равен 30°. 2
2
Ответ: 28 см²
Проверка .
\circ$.Диагональ — это отрезок, соединяющий две несмежные вершины многоугольника. Слово «диагональ» происходит от древнегреческого слова « diagonios », (латинское диагональ) , что означает «от угла к углу».
И Евклид, и Страбон использовали его для описания линии, соединяющей две вершины прямоугольного параллелепипеда или ромба; позже она стала известна на латыни как diagonus (наклонная линия).
Диагонали прямоугольника Определение
Отрезок, соединяющий любые две противоположные вершины прямоугольника, называется диагональю прямоугольника.
Рассмотрим ▭ABCD. Прямоугольник с диагоналями AC и BD, как показано ниже.
Здесь $AC = BD$.
Родственные игры
Свойства диагоналей прямоугольника
- Диагонали прямоугольника равны.
$\left[AC = BD\right]$
- Каждая диагональ делит прямоугольник на два конгруэнтных прямоугольных треугольника.
 9\circ$, это называется квадратом.
9\circ$, это называется квадратом.
- При пересечении двух диагоналей они образуют один тупой угол и один острый угол. Противоположные центральные углы равны.
- Смежные углы, образованные диагоналями, являются дополнительными.
- Диагонали прямоугольника образуют гипотенузу прямоугольного треугольника.
Связанные рабочие листы
Формула диагонали прямоугольника
Формула диагонали прямоугольника помогает найти длину диагонали, когда известны длина и ширина прямоугольника. 92)}$
где $d = диагональ$
$l = длина$
$w = ширина$
Эту формулу можно использовать для определения длины диагонали прямоугольника.
Вывод формулы диагонали прямоугольника
Формула диагонали прямоугольника выводится с помощью теоремы Пифагора. Разделите прямоугольник на два прямоугольных треугольника, образованных диагональю.
Применяя теорему Пифагора к прямоугольному треугольнику PSR, имеем 92} = \sqrt{9 + 16} = \sqrt{25} = 5$ единиц
Углы, образованные диагоналями прямоугольника
Как обсуждалось выше, если диагонали многоугольника пересекаются пополам, он называется квадратом .
Диагонали прямоугольника равны по длине, делят друг друга пополам. Они не сходятся под прямым углом в центре. Диагонали прямоугольника не делят внутренние углы прямоугольника пополам.
Пример: Взгляните на изображение ниже.
На приведенном выше изображении AC и BD являются диагоналями. 9\circ$
Факты о диагоналях прямоугольника
- Две диагонали прямоугольника делят его на четыре треугольника.
- Каждая диагональ прямоугольника делит его на два конгруэнтных прямоугольных треугольника.
- Пересечение диагоналей является центром описанной окружности. То есть вы можете нарисовать круг с этим в центре, чтобы пройти через четыре угла.

Таким образом, диагональ $= 2r$ …где r — радиус описанной окружности 92)}$
- Прямоугольник называется квадратом, если его диагонали делятся пополам под прямым углом.
- Поскольку диагонали обычно имеют наклон, для обозначения диагоналей используется наклонный символ «/».
Заключение
В этой статье мы узнали о диагоналях прямоугольника, его свойствах, формулах и фактах. Теперь давайте решим несколько примеров на основе изученных выше формул.
Решенные примеры для диагоналей прямоугольника
1. Определите длину, ширину и диагональ данного прямоугольника.
Решение:
Длина $\rightarrow$ AD и BC
Ширина $\rightarrow$ AB и CD
Диагонали $\rightarrow$ AC и BD
2. Найдите длину каждой диагонали прямоугольник длиной 15 единиц и шириной 8 единиц.
Решение:
Длина прямоугольника $l = 15$ единиц.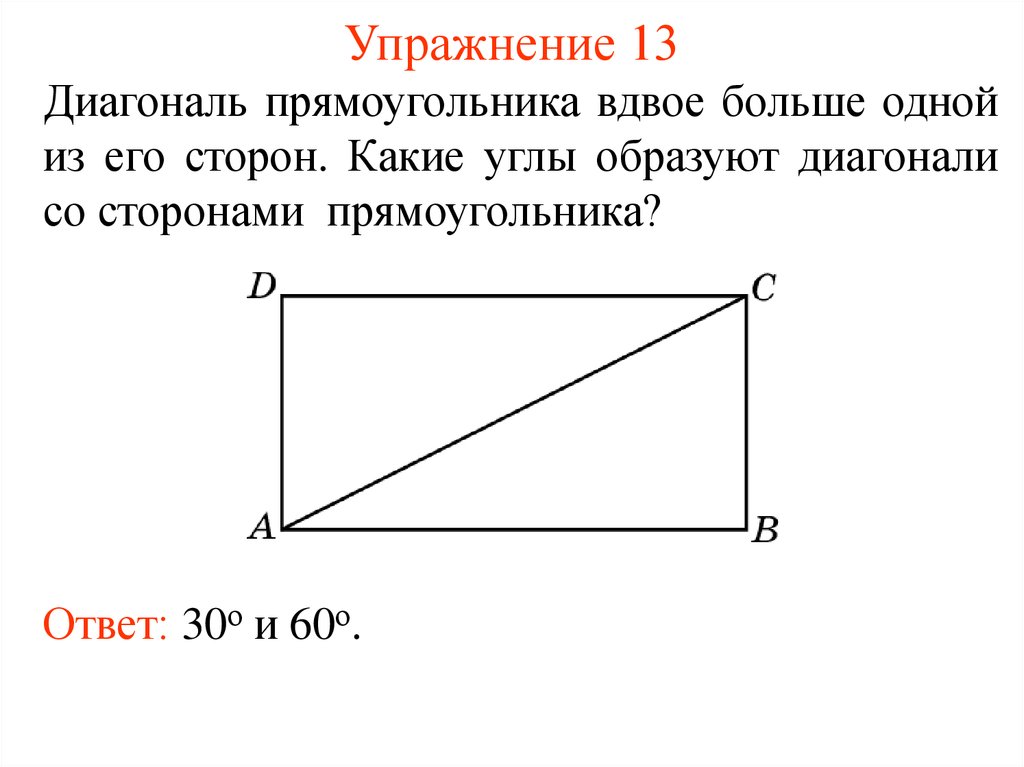
Ширина прямоугольника, $b = 8$ единиц. 92)}$
$d = \sqrt{(64 + 225)}$
$d = 0004 $d = 17$ единиц.
Длина диагонали 17 единиц.
3. Прямоугольный парк имеет длину 30 футов и ширину 16 футов. Определить диагональ прямоугольного парка.
Решение:
Длина прямоугольного парка $= 30$ футов
Ширина прямоугольного парка $= 15$ футов 92)}$
$= \sqrt{(256+ 900)}$
$= 34 $ ft
Диагональ прямоугольного парка составляет 34 фута.
4. Найдите длину диагонали данного прямоугольника.
Решение:
Длина $= 12$ в
Ширина $= 5$ в
Диагональ $= ?$
Используя теорему Пифагора, получаем: 92 = 25 \;-\; 9$
$l = \sqrt{16}$
$l = 4$ в
Длина прямоугольника 4 дюйма.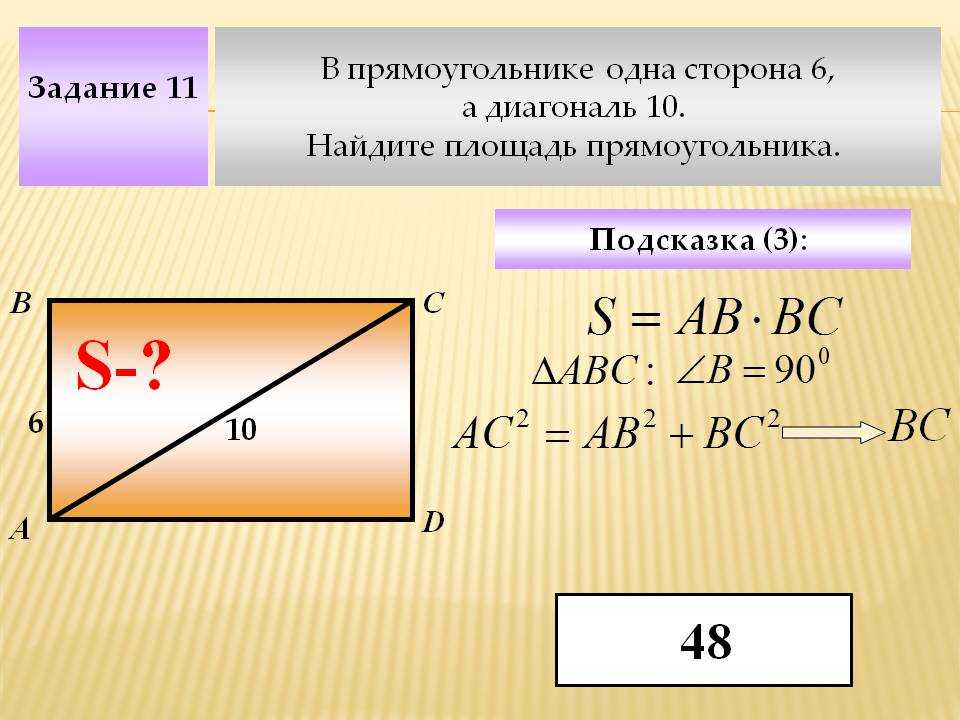
Практические задачи на диагонали прямоугольника
1
Отрезок, соединяющий любые две противоположные вершины прямоугольника, называется его _________.
диагональ
длина
ширина
Ничего из вышеперечисленного
Правильный ответ: диагональ
Отрезок, соединяющий любые две противоположные вершины прямоугольника, называется его диагональю.
2
Диагонали прямоугольника ______.
перпендикулярно
равно
не равно
Ничего из вышеперечисленного.
Правильный ответ: равны
Диагонали прямоугольника равны по длине.
3
Что из перечисленного НЕ ВЕРНО?
Каждая диагональ делит прямоугольник на 2 равных прямоугольных треугольника.
Диагонали прямоугольника делят друг друга пополам.
Длины диагоналей прямоугольника равны. 92)}$
где, $d =$ диагональ прямоугольника
$l =$ длина прямоугольника
$b =$ ширина прямоугольника
5
Смежные углы, образованные диагоналями прямоугольника, равны ________.

дополнительный
конгруэнтный
дополнительный
прямой
Правильный ответ: дополнительный
Смежные углы, образованные диагоналями, являются дополнительными.
Часто задаваемые вопросы о диагоналях прямоугольника
Почему диагонали прямоугольника равны по длине?
Прямоугольник – это четырехугольник, у которого все углы прямые. Прямоугольник также является параллелограммом, у которого противоположные стороны равны.
Рассмотрим этот прямоугольник ABCD.
В приведенном выше прямоугольнике рассмотрим треугольники ABC и DCB.
$\угол ABC = \угол DCB = 90$ [Углы прямоугольника]
$BC = BC$ (общая сторона)
$AB = DC$ (противоположные стороны параллелограмма равны)
Следовательно, $ABC\congDCB$
$AC = DB$ [CPCTC]
Следовательно, диагонали прямоугольника равны.
Всегда ли диагонали прямоугольника делят друг друга пополам?
Диагонали прямоугольника всегда делят друг друга пополам.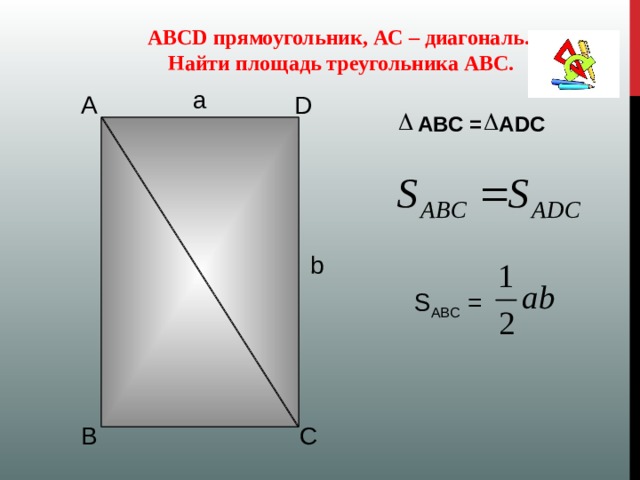 Однако они не пересекаются под углом 90 градусов, за исключением случаев, когда прямоугольник является квадратом.
Однако они не пересекаются под углом 90 градусов, за исключением случаев, когда прямоугольник является квадратом.
По какой формуле находится площадь прямоугольника?
Площадь прямоугольника равна произведению длины на ширину. Площадь прямоугольника $= l\timesb$
Почему площадь прямоугольника равна произведению длины и ширины?
Давайте разберемся, почему площадь прямоугольника равна $длине \ширине$.
Рассмотрим ▭ ABCD. Мы видим, что диагональ AC делит прямоугольник на два равных треугольника, $\Delta ABC$ и $\Delta ADC$.
Площадь прямоугольника $ABCD =$ Площадь треугольника $ABC +$ Площадь треугольника ADC
$= 2\times$ Площадь треугольника ABC
$= 2 \times (\frac{1}{2} \times Основание\умножить на высоту)$
$= AB \times BC$
$= Длина \times Ширина$
Площадь прямоугольника равна произведению длины и ширины.
Сколько диагоналей в прямоугольнике? Всегда ли диагонали прямоугольника равны?
Прямоугольник имеет две диагонали. Каждая диагональ делит прямоугольник на два прямоугольных треугольника. Две диагонали прямоугольника всегда равны.
Каждая диагональ делит прямоугольник на два прямоугольных треугольника. Две диагонали прямоугольника всегда равны.
В прямоугольнике диагонали перпендикулярны?
Нет! Две диагонали прямоугольника не пересекаются под прямым углом.
Площадь прямоугольника — формула
Площадь прямоугольника — это область, занимаемая границами прямоугольника. Другими словами, количество поверхности, заключенной в прямоугольник, называется площадью прямоугольника. Это можно рассчитать, используя формулу площади прямоугольника и используя различные методы в зависимости от заданных размеров. На этом уроке мы научимся находить площадь прямоугольника.
| 1. | Что такое площадь прямоугольника? |
| 2. | Формула площади прямоугольника |
| 3. | Как найти площадь прямоугольника? |
| 4. | Площадь прямоугольника по диагонали |
5. | Часто задаваемые вопросы о площади прямоугольника |
Что такое площадь прямоугольника?
Площадь прямоугольника — это количество единичных квадратов, которые могут поместиться в прямоугольник. Площадь определяется как количество пространства, занимаемого плоской поверхностью определенной формы. Площадь любой формы — это количество единичных квадратов, которые могут в нее поместиться, и она измеряется с точки зрения «количества» квадратных единиц (квадратных сантиметров, квадратных дюймов, квадратных футов и т. д.). Некоторыми примерами прямоугольных форм являются плоские поверхности мониторов ноутбуков, школьных досок, холста для рисования и т. Д. Площадь прямоугольника можно рассчитать, используя формулу площади прямоугольника, чтобы найти пространство, занимаемое этими объектами.
Площадь прямоугольника Определение
Область, занимаемая прямоугольником внутри его границ, определяется как площадь прямоугольника.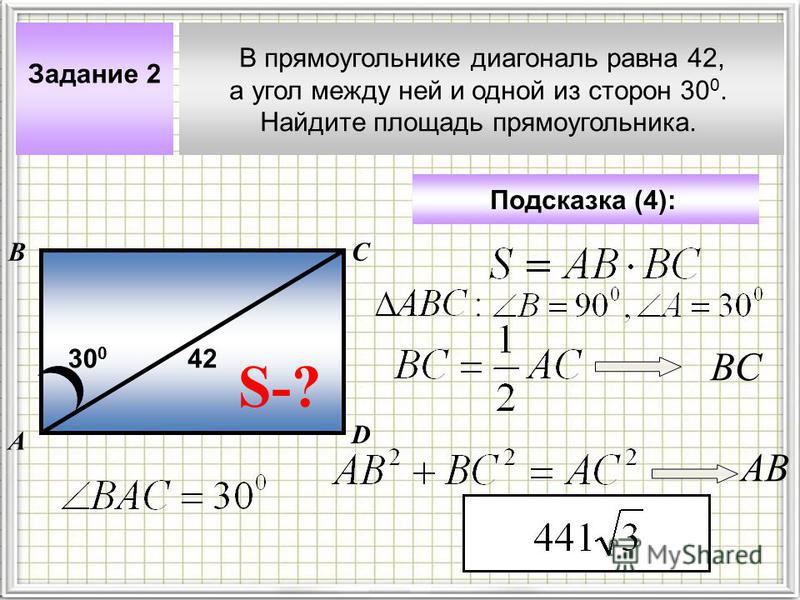
Формула площади прямоугольника
Формула площади прямоугольника используется для нахождения площади, занимаемой прямоугольником внутри его границы. Площадь прямоугольника получается путем умножения его длины на ширину (ширину). Таким образом, формула площади прямоугольника, длина и ширина которого равны «l» и «w» соответственно, выражается следующим образом. Площадь прямоугольника = l × w. Другими словами,
Как найти площадь прямоугольника?
Площадь прямоугольника равна произведению его длины на ширину (ширину). Площадь прямоугольника можно рассчитать, используя следующие шаги:
- Шаг 1: Обратите внимание на размеры длины и ширины (ширины) по заданным данным.
- Шаг 2: Найдите произведение значений длины и ширины.
- Шаг 3: Дайте ответ в квадратных единицах.
Давайте рассмотрим пример, чтобы понять вычисление площади прямоугольника.
Пример: Найдите площадь прямоугольника, длина которого 15 единиц, а ширина 4 единицы.
Решение: Дано, длина = 15 единиц, а ширина = 4 единицы.
Формула для нахождения площади прямоугольника: A = l × w. Подставьте 15 вместо «l» и 4 вместо «w» в этой формуле. Следовательно, площадь прямоугольника = 15 × 4 = 60
Следовательно, площадь прямоугольника = 60 квадратных единиц.
Единица площади прямоугольника
Единица площади прямоугольника выражается в квадратных единицах. Мы знаем, что длина всегда измеряется и выражается в таких единицах, как сантиметры, дюймы и т. д. Теперь давайте разберемся, почему площадь прямоугольника выражается в квадратных единицах, используя следующий пример.
Пример: Длина прямоугольника 4 дюйма, а ширина 3 дюйма. Обратите внимание на рисунок, приведенный ниже, на котором мы можем разделить фигуру на 12 маленьких квадратов, каждый из которых является квадратом, то есть по 1 дюйму с каждой стороны, то есть по 1 квадратному дюйму. Поскольку в этом прямоугольнике может поместиться 12 квадратов одинакового размера, они также показывают пространство, занимаемое всем прямоугольником. Итак, прямоугольник со сторонами 4 дюйма и 3 дюйма имеет площадь 12 квадратных дюймов или 12 дюймов 9.0546 2
Поскольку в этом прямоугольнике может поместиться 12 квадратов одинакового размера, они также показывают пространство, занимаемое всем прямоугольником. Итак, прямоугольник со сторонами 4 дюйма и 3 дюйма имеет площадь 12 квадратных дюймов или 12 дюймов 9.0546 2
В этом случае, поскольку длина и ширина этого прямоугольника даны в дюймах, площадь измеряется и записывается в квадратных дюймах (в 2 ). Точно так же, если длина и ширина любого прямоугольника даны в см, то площадь будет выражена в квадратных сантиметрах (см 2 ).
Площадь прямоугольника по диагонали
Площадь прямоугольника можно вычислить, если известны диагональ и одна сторона. Диагональ прямоугольника — это прямая линия внутри прямоугольника, соединяющая его противоположные вершины.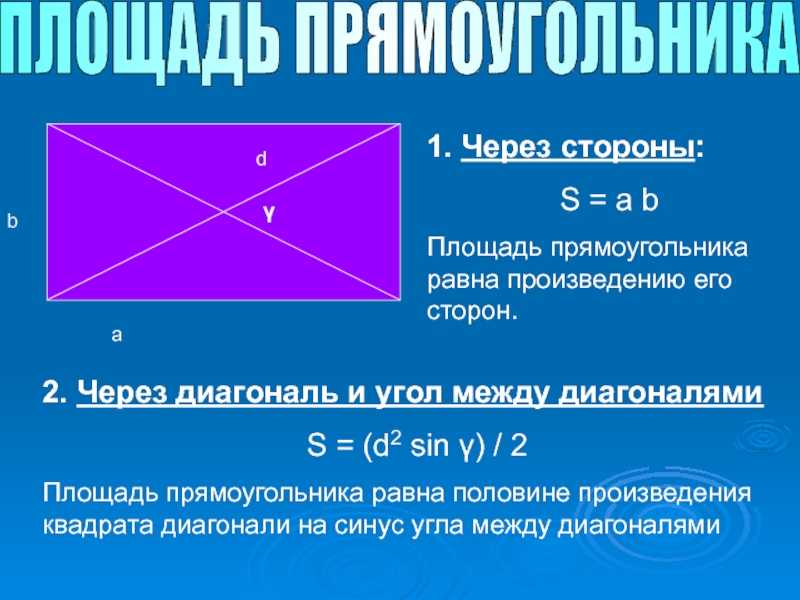
Метод 1:
Мы можем найти значение недостающей стороны, используя теорему Пифагора, а затем найти площадь. Давайте разберемся в этом на примере.
Пример: Найдите площадь прямоугольника, длина которого 4 см, а диагональ 5 см.
Решение:
Ширина прямоугольника отсутствует, и ее можно рассчитать по теореме Пифагора, поскольку диагонали прямоугольника образуют 2 прямоугольных треугольника.
В этом случае ширину можно рассчитать по формуле ширина = ⎷[(Диагональ) 2 — (длина) 2 ]
После подстановки данных значений получаем, ширина = ⎷[(Диагональ ) 2 — (длина) 2 ]
ширина = ⎷[(5) 2 — (4) 2 ]
ширина = ⎷(25 — 16) 3
ширина = ⎷(25 — 16) 39007
Теперь мы знаем, что длина = 4 см, ширина = 3 см. Итак, площадь прямоугольника = l × w. В этом случае
Итак, площадь прямоугольника = l × w. В этом случае
A = l × w
Площадь = 4 × 3 = 12 см 2
Этот метод также использует ту же логику, но мы используем прямую формулу для нахождения площади прямоугольника.
- Например, если длина прямоугольника отсутствует, а нам известны диагональ и ширина, то мы можем выразить длину через ширину и диагональ и затем использовать это в формуле площади прямоугольника .
- Мы знаем, что (Диагональ) 2 = (Длина) 2 + (Ширина) 2 . Таким образом, это также можно записать как (Длина) 2 = (Диагональ) 2 — (Ширина) 2 . Кроме того, это можно выразить как Длина = ⎷[(Диагональ) 2 — (Ширина) 2 ]. Здесь длина выражается через диагональ и ширину. Эту формулу можно использовать вместо длины.
- Мы знаем, что формула для вычисления площади прямоугольника: Площадь прямоугольника = Длина × Ширина.
 Теперь, если мы заменим приведенную выше формулу длины формулой площади прямоугольника, то формула площади прямоугольника может быть выражена следующим образом: Площадь прямоугольника = ⎷[(Диагональ) 2 — (Ширина) 2 ] × Ширина
Теперь, если мы заменим приведенную выше формулу длины формулой площади прямоугольника, то формула площади прямоугольника может быть выражена следующим образом: Площадь прямоугольника = ⎷[(Диагональ) 2 — (Ширина) 2 ] × Ширина - Итак, площадь прямоугольника = ширина ⎷[(диагональ) 2 — (ширина) 2 ]
- Мы можем использовать ту же формулу, если мы знаем длину и если ширина отсутствует.
Давайте рассмотрим это на примере.
Пример: Найдите площадь прямоугольника, у которого ширина 6 единиц, а диагональ 10 единиц.
Решение: Нам известны диагональ и ширина прямоугольника. Итак, применим прямую формулу Площадь прямоугольника = Ширина ⎷[(Диагональ) 2 — (Ширина) 2 ]
После подстановки значений диагонали = 10 единиц и ширины = 6 единиц, мы получаем Площадь прямоугольника = Ширина ⎷ [(Диагональ) 2 — (Ширина) 2 ]
Площадь = 6 ⎷[(10) 2 — (6) 2 ]
Площадь = 6 ⎷(100 — 36)
Площадь = 6 ×
4 прямоугольника = 48 квадратных единицПлощадь прямоугольника с использованием периметра
Площадь прямоугольника можно вычислить, если известны периметр и одна из его сторон.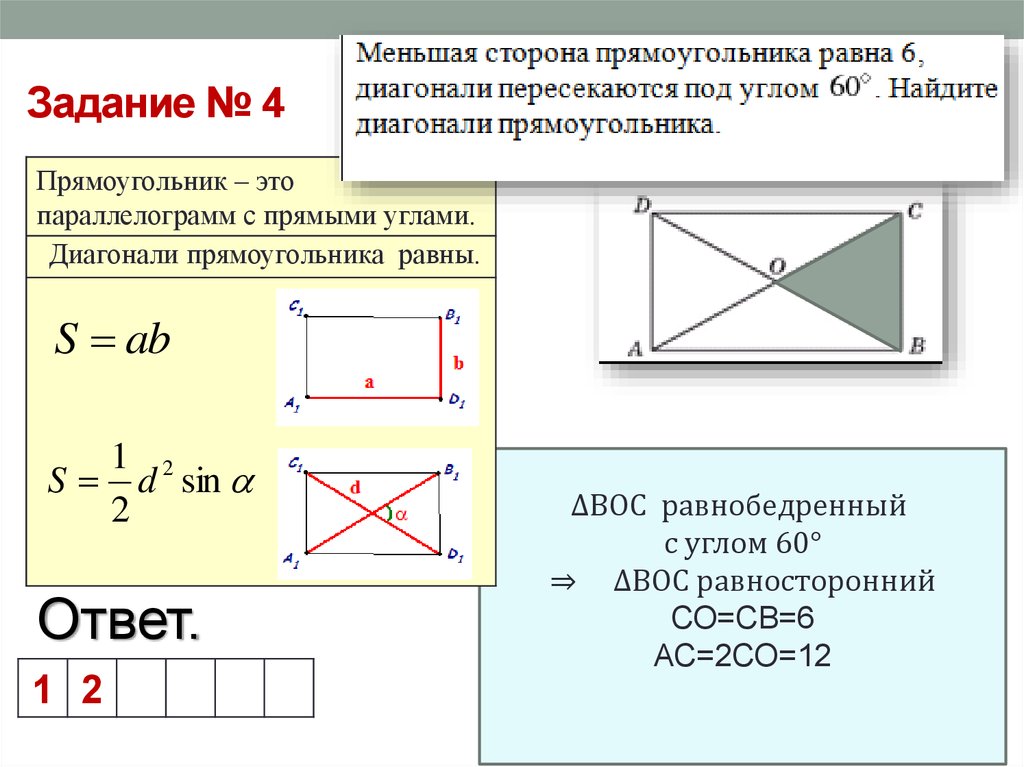 С помощью периметра мы можем найти неизвестную сторону, а затем вычислить площадь по той же формуле: площадь прямоугольника = длина × ширина. Давайте разберемся в этом с помощью примера.
С помощью периметра мы можем найти неизвестную сторону, а затем вычислить площадь по той же формуле: площадь прямоугольника = длина × ширина. Давайте разберемся в этом с помощью примера.
Пример: Найдите площадь прямоугольника, если периметр равен 24 единицам, а длина 7 единицам.
Решение: Периметр прямоугольника = 24 единицы, длина = 7 единиц. Мы можем найти ширину, используя формулу:
Периметр прямоугольника = 2 (l + w)
24 = 2 (7 + w)
12 = 7 + w
w = 5 единиц
Теперь, когда мы знаем ширина = 5 единиц и длина = 7 единиц, мы можем найти площадь.
Площадь прямоугольника = l × w
Площадь = 7 × 5 = 35 квадратных единиц
Вывод формулы площади прямоугольника
Формула обратной стороны прямоугольника может быть получена с использованием следующего объяснения. Прямоугольник ABCD имеет диагональ. Мы видим, что диагональ AC делит прямоугольник ABCD на два равных треугольника.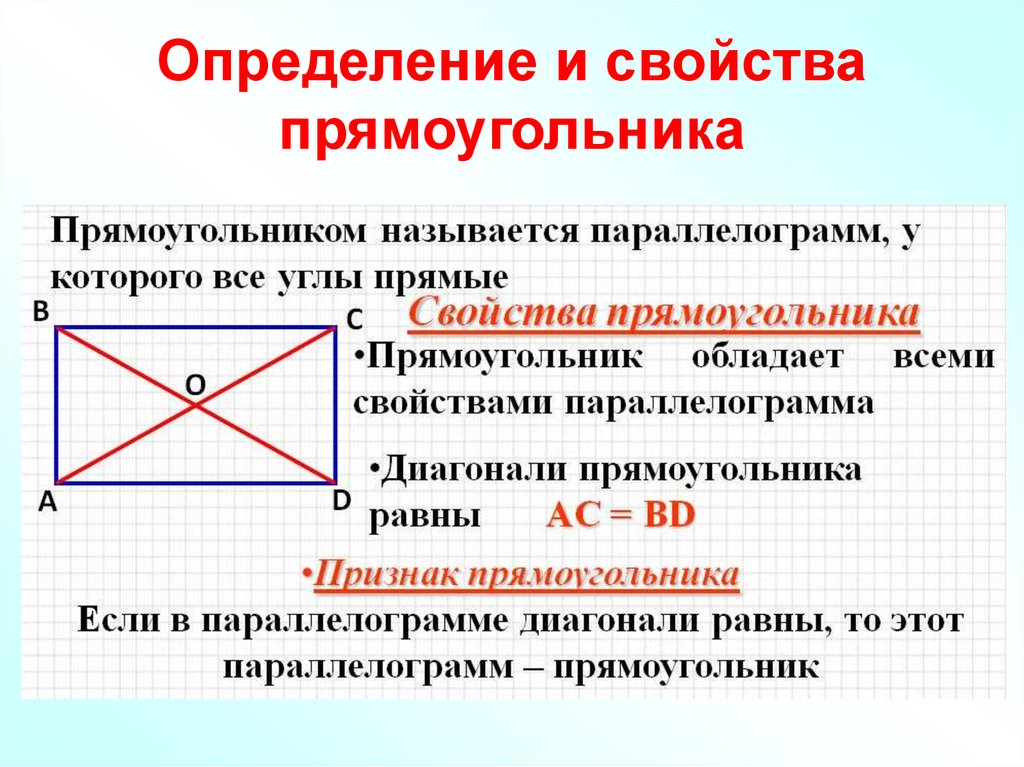 Площадь прямоугольника равна сумме площадей этих двух треугольников.
Площадь прямоугольника равна сумме площадей этих двух треугольников.
Площадь прямоугольника ABCD = площадь треугольника ABC + площадь треугольника ADC
Поскольку оба треугольника (ABC и ADC) равны, мы можем выразить это следующим образом.
Площадь прямоугольника ABCD = 2 × площадь треугольника ABC
Площадь прямоугольника ABCD = 2 × (1/2 × основание × высота)
Площадь прямоугольника ABCD = 2 × 1/2 × AB × BC
Площадь прямоугольника ABCD = AB × BC
Следовательно, площадь прямоугольника = длина × ширина
☛ Похожие статьи
- Площадь треугольника
- Площадь квадрата
- Площадь круга
- Периметр прямоугольника
- Разница между площадью и периметром
Cuemath — одна из ведущих в мире платформ для обучения математике, предлагающая онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах.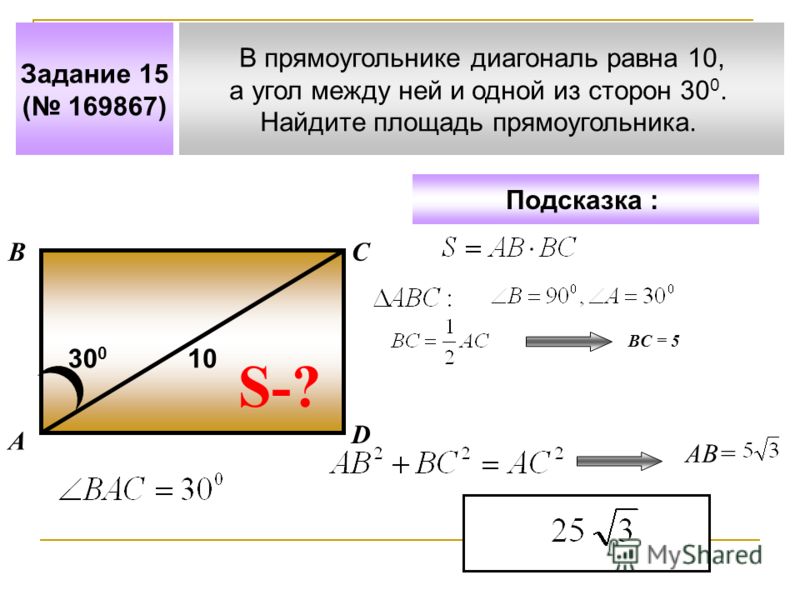 Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Площадь прямоугольника Примеры
Пример 1: Длина и ширина прямоугольной фермы равны 80 ярдам и 60 ярдам. Найдите площадь фермы.
Решение:
Длина фермы l = 80 ярдов и ширина фермы w = 60 ярдов
Мы знаем, что формула площади прямоугольника равна
Площадь прямоугольника = длина × ширина Итак, площадь фермы равна: A = l × w
= 80 × 60
= 4800 квадратных метров
Следовательно, площадь фермы составляет 4800 квадратных метров.
Пример 2:
Найдите площадь прямоугольника, длина и ширина которого равны 25 см и 16 см соответственно.
Solution
Длина прямоугольника = 25 см
Ширина (ширина) прямоугольника = 16 см
Площадь прямоугольника = l × w
Площадь прямоугольника = 25 × 16
Площадь прямоугольника = 400 см 2
Пример 3:
Найдите площадь прямоугольника, длина которого = 4,5 см, а ширина = 2 см.

Решение
Длина прямоугольника = 4,5 см
Ширина прямоугольника = 2 см
Площадь прямоугольника = 4,5 × 2
Площадь прямоугольника = 9 см
6 7 2
перейти к слайдуперейти к слайдуперейти к слайду
У вас есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы о площади прямоугольника
Какова площадь прямоугольника в геометрии?
Площадь прямоугольника — это пространство, занимаемое в границах прямоугольника. Он рассчитывается путем нахождения произведения длины и ширины (ширины) прямоугольника и выражается в квадратных единицах.
Что такое периметр и площадь прямоугольника?
Периметр прямоугольника равен сумме его четырех сторон. Он рассчитывается по формуле Периметр прямоугольника = 2 (длина + ширина). Площадь прямоугольника — это область, охватываемая его границами, и ее можно рассчитать по формуле площадь прямоугольника = длина × ширина.
Площадь прямоугольника — это область, охватываемая его границами, и ее можно рассчитать по формуле площадь прямоугольника = длина × ширина.
Какая формула площади прямоугольника?
Формула площади прямоугольника представляет собой произведение его длины на ширину (ширину). Это выражается как Площадь прямоугольника = длина × ширина
Какова единица площади прямоугольника?
Площадь прямоугольника выражается в квадратных единицах. Например, если размеры прямоугольника указаны в дюймах, то площадь выражается в квадратных дюймах ( 2 ). Точно так же, если размеры даны в см, то площадь выражается в квадратных см (см 2 ). Например, если длина прямоугольника 4 см, а ширина 3 см, то его площадь = 4 × 3 = 12 см 2
Как найти площадь прямоугольника по диагонали?
Площадь прямоугольника можно вычислить, если известны диагональ и одна из его сторон. Мы можем найти значение недостающей стороны, используя теорему Пифагора, а затем найти площадь.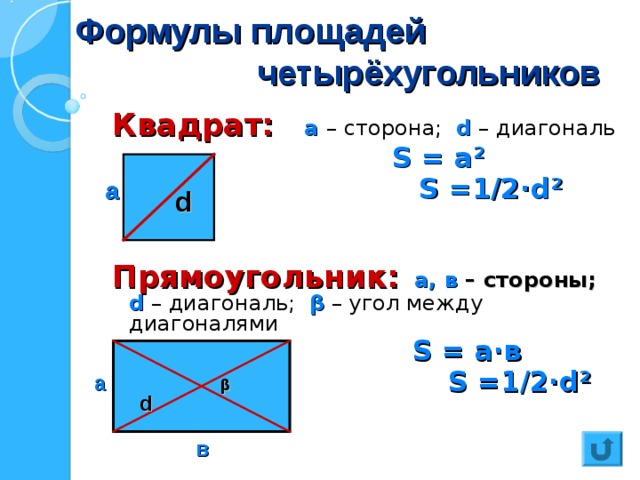 Например, давайте найдем площадь прямоугольника, диагональ которого равна 10 единицам, а длина — 8 единицам, используя следующие шаги.
Например, давайте найдем площадь прямоугольника, диагональ которого равна 10 единицам, а длина — 8 единицам, используя следующие шаги.
- Шаг 1: В этом случае мы можем найти ширину по формуле Ширина = ⎷[(Диагональ) 2 — (Длина) 2 ]
- Шаг 2: После подстановки заданных значений получаем ширину = ⎷[(10) 2 — (8) 2 ] = ⎷36 = 6 единиц
- Шаг 3: Теперь мы знаем, что длина = 8 единиц, ширина = 6 см. Итак, площадь прямоугольника = l × w. В этом случае Площадь = 8 × 6 = 48 единиц 2
Что такое прямоугольник?
Прямоугольник – это замкнутая двумерная фигура с четырьмя сторонами, причем противоположные стороны равны и параллельны друг другу. У прямоугольника все углы равны 90°.
Как найти площадь прямоугольника с дробями?
Площадь прямоугольника с дробями можно вычислить так же, как и с другими целыми числами. Нам просто нужно упростить дроби, используя их правила упрощения. Если у нас есть правильные дроби, мы можем просто использовать формулу площади прямоугольника и умножить длину и ширину. Однако, если у нас есть размеры, данные в смешанных дробях, нам нужно преобразовать их в неправильные дроби, а затем упростить, используя та же формула. Например, давайте найдем площадь прямоугольника, в котором длина задана как \(2\dfrac{1}{3}\) единиц, а ширина задана как \(1\dfrac{1}{3}\) единиц, теперь мы преобразуем смешанные дроби в неправильные дроби, и мы получим длину как 7/3, а ширину как 4/3. Теперь мы можем найти площадь, Площадь прямоугольника = 7/3 × 4/3 = 28/9= \(3\dfrac{1}{9}\) квадратных единиц.
Если у нас есть правильные дроби, мы можем просто использовать формулу площади прямоугольника и умножить длину и ширину. Однако, если у нас есть размеры, данные в смешанных дробях, нам нужно преобразовать их в неправильные дроби, а затем упростить, используя та же формула. Например, давайте найдем площадь прямоугольника, в котором длина задана как \(2\dfrac{1}{3}\) единиц, а ширина задана как \(1\dfrac{1}{3}\) единиц, теперь мы преобразуем смешанные дроби в неправильные дроби, и мы получим длину как 7/3, а ширину как 4/3. Теперь мы можем найти площадь, Площадь прямоугольника = 7/3 × 4/3 = 28/9= \(3\dfrac{1}{9}\) квадратных единиц.
Как найти площадь прямоугольника, зная периметр?
Площадь прямоугольника можно вычислить, если известны периметр и одна из его сторон. С помощью периметра мы можем найти недостающую сторону, а затем вычислить площадь прямоугольника по той же формуле: площадь прямоугольника = длина × ширина. Давайте разберемся в этом с помощью примера. Например, найдем площадь прямоугольника, периметр которого равен 30 единицам, а ширина — 4 единицам.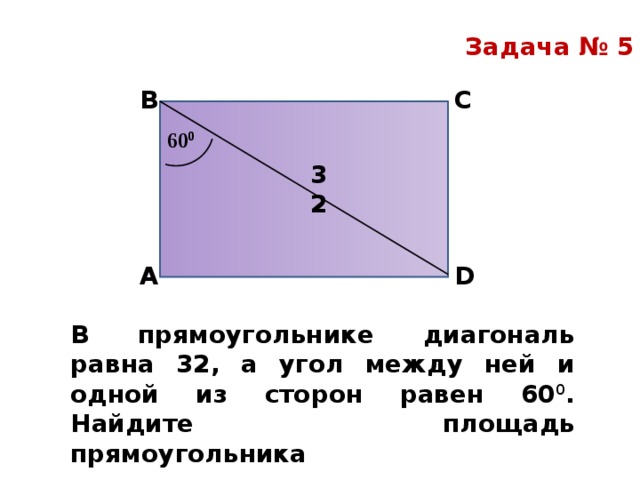

 9\circ$, это называется квадратом.
9\circ$, это называется квадратом.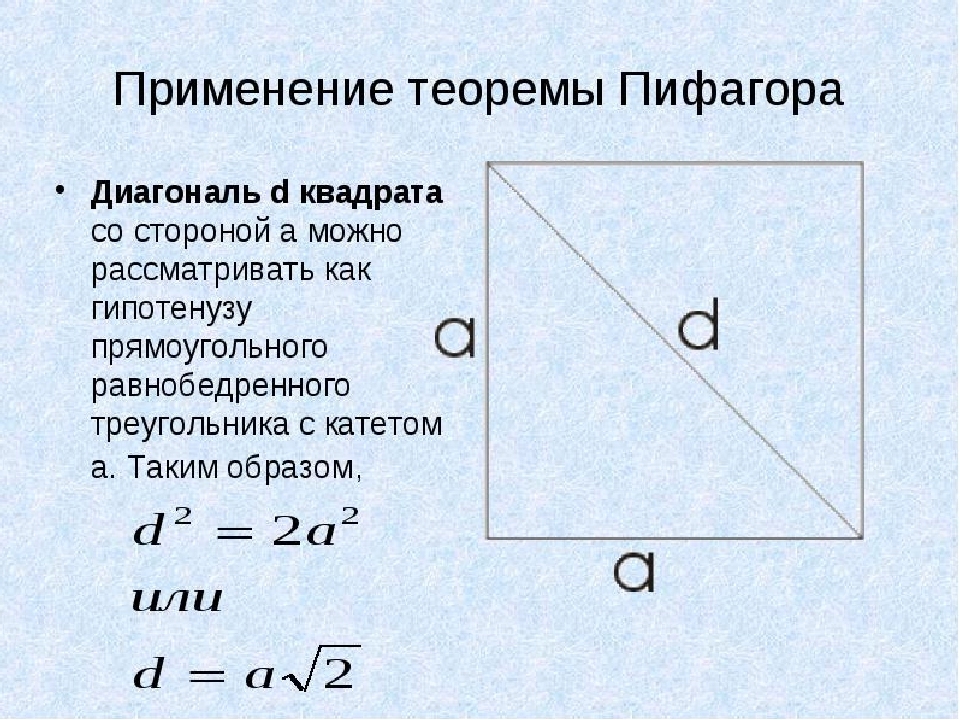
 Теперь, если мы заменим приведенную выше формулу длины формулой площади прямоугольника, то формула площади прямоугольника может быть выражена следующим образом: Площадь прямоугольника = ⎷[(Диагональ) 2 — (Ширина) 2 ] × Ширина
Теперь, если мы заменим приведенную выше формулу длины формулой площади прямоугольника, то формула площади прямоугольника может быть выражена следующим образом: Площадь прямоугольника = ⎷[(Диагональ) 2 — (Ширина) 2 ] × Ширина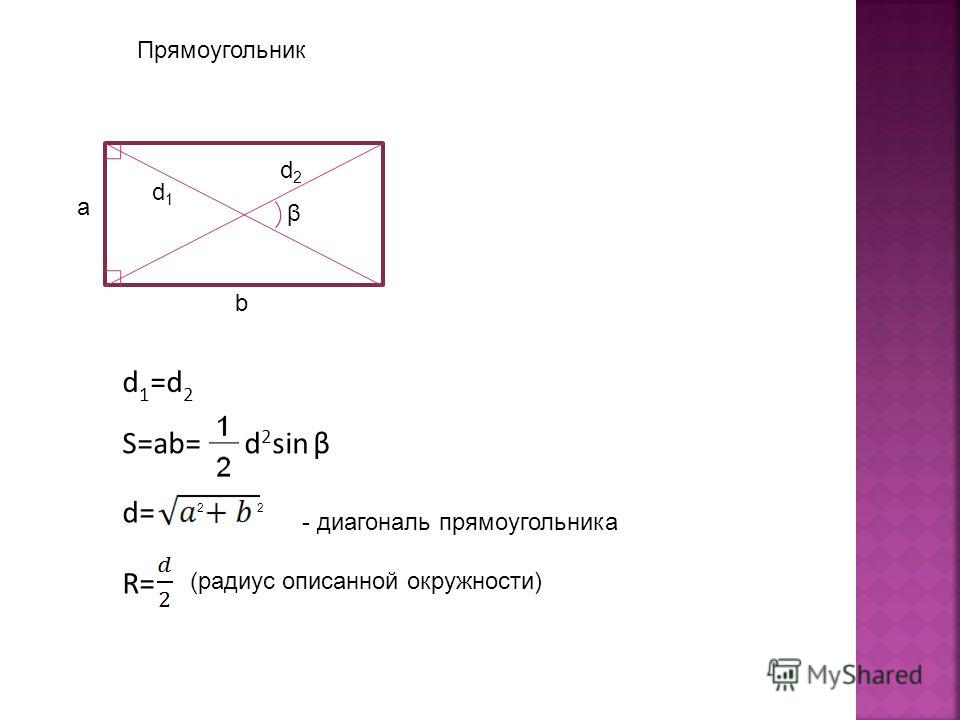
Leave A Comment