Задачи 8 ЕГЭ профильная математика, сортировка по темам
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 Найдите площадь сечения, проходящего через вершины A, C и C1.
Найдите площадь сечения, проходящего через вершины A, C и C1.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ

посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 Уровень воды достигает 8 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд такой же формы, у которого сторона основания в 2 раза больше, чем у первого? Ответ выразите в сантиметрах.
Уровень воды достигает 8 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд такой же формы, у которого сторона основания в 2 раза больше, чем у первого? Ответ выразите в сантиметрах.
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ

посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
 Найдите тангенс угла BE1E.
Найдите тангенс угла BE1E.
посмотреть ответ
посмотреть ответ
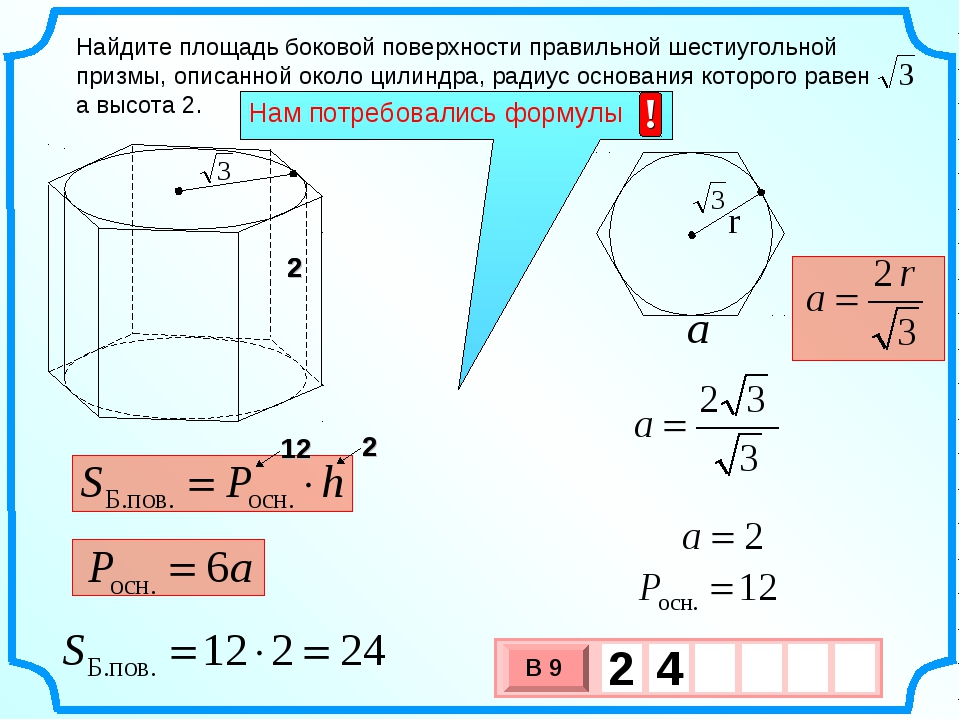
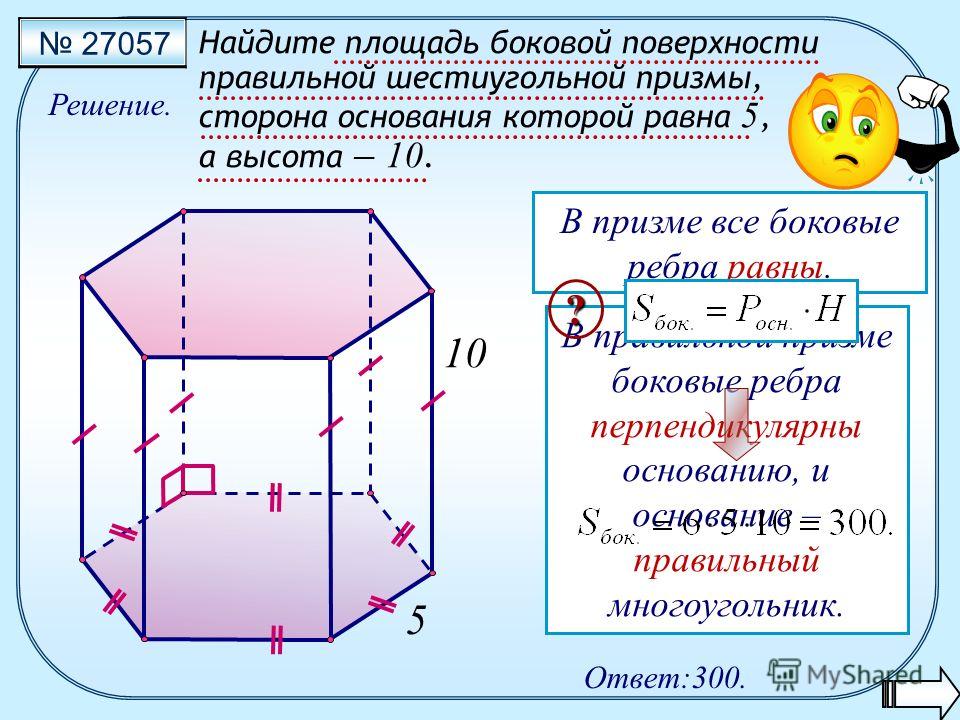
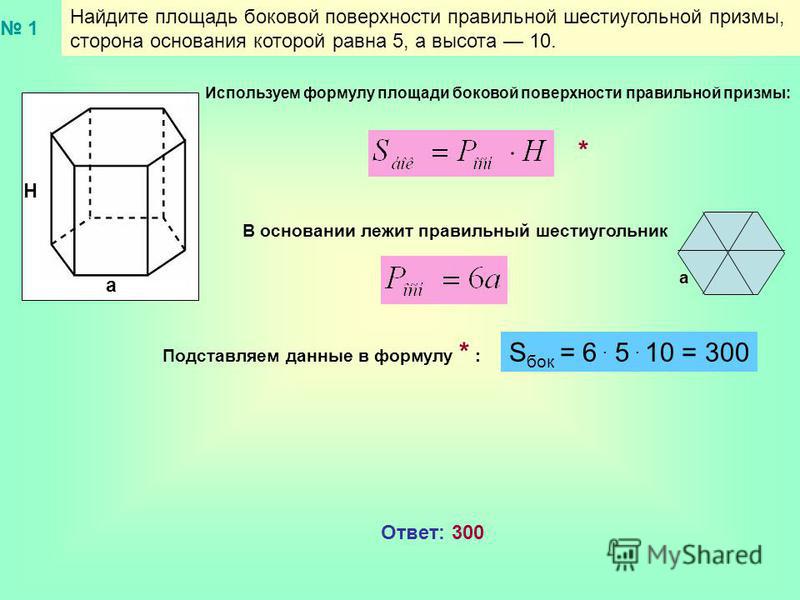
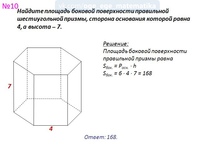
/9. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10.
Все прототипы заданий В года
1. Прототип задания B13 ( 27054) выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. Все прототипы заданий В13
ПодробнееВсе прототипы заданий года
1. Прототип задания 12 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий 12
ПодробнееВсе прототипы заданий В года
1. Прототип задания B13 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий
ПодробнееСтереометрия: призма.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: призма. 27047. В сосуд, имеющий форму
http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: призма. 27047. В сосуд, имеющий форму
Куб. Прямоугольный параллелепипед
Куб 1. Задание 16 27098. Диагональ куба равна. Найдите его объем. О т в е т : 8 2. Задание 16 500957. Во сколько раз увеличится объем куба, если все его рѐбра увеличить в 5 раз? О т в е т : 1 2 5 3. Задание
ПодробнееЗадание 8 Стереометрия.
Задание 8 Стереометрия. Куб 1. Площадь поверхности куба равна 18. Найдите его диагональ. 2. Объем куба равен 8. Найдите площадь его поверхности. 3. Если каждое ребро куба увеличить на 1, то его площадь
ПодробнееЗадание 16 Задачи по стереометрии
Задание 16 Задачи по стереометрии Куб 1.Диагональ куба равна 12. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30
ПодробнееКуб. 3. Найдите объем многогранника, вершинами которого являются точки,,,,, прямоугольного параллелепипеда, у которого,,.
Куб. 1. Диагональ куба равна. Найдите его объем. 2.Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30 см без одной грани, нужно покрасить
ПодробнееПрямоугольный параллелепипед
ЗАДАНИЕ 10 Стереометрия Куб 1.Площадь поверхности куба равна 18. Найдите его диагональ. 2. Диагональ грани куба равна 2 6. Найдите диагональ куба. 3. Диагональ грани куба равна 6. Найдите диагональ куба.
ПодробнееВсе прототипы задания В11 (2013)
Все прототипы задания В11 (2013) ( 25541) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).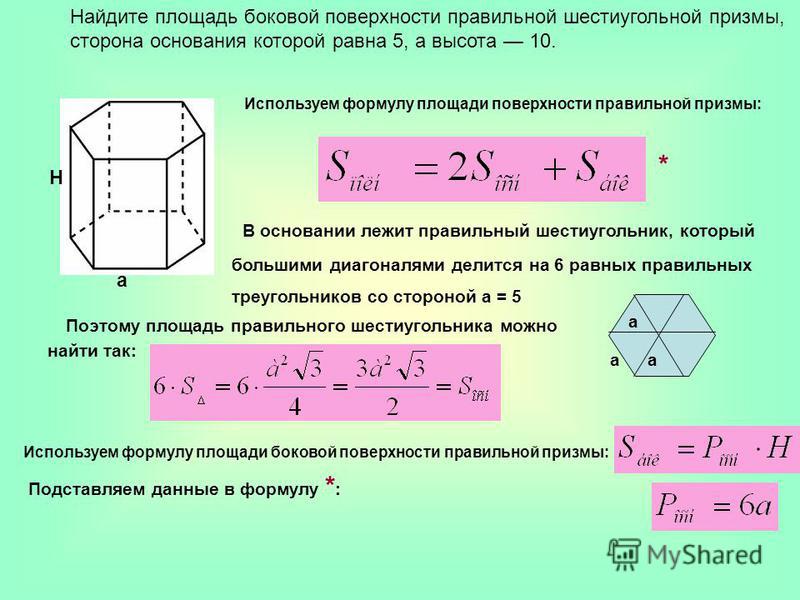 ( 25561) Найдите площадь поверхности многогранника, изображенного
( 25561) Найдите площадь поверхности многогранника, изображенного
Задание 13. Задачи по стереометрии
Задание 13 Задачи по стереометрии 1.Диагональ куба равна Куб. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30 см
ПодробнееТригонометрические уравнения
Тригонометрические уравнения С б) Укажите корни, принадлежащие отрезку. а) Решите уравнение б) Укажите корни уравнения, принадлежащие отрезку а) Решbте уравнение. б) Укажите корни этого уравнения, принадлежащие
ПодробнееВсе прототипы задания В9 (2013)
Все прототипы задания В9 (2013) ( 245359) Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. ( 245360) Найдите расстояние между вершинами и прямоугольного параллелепипеда,
ПодробнееСтартовая контрольная работа
Стартовая контрольная работа Контрольная работа 1(на 20 мин) 1. Найдите координаты вектора АВ, если А (5; 1; 3), В (2; 2; 4). 2. Даны векторы b (3; 1; 2) и c 2b c (1; 4; 3). Найдите. 3. Изобразите систему
ПодробнееВсе прототипы В года
1. Прототип задания B9 ( 245359) Все прототипы В5 2013 года Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. 2. Прототип задания B9 ( 245360) Найдите расстояние
Подробнееc c
Тема: Многогранники Призмы Демонстрационный вариант Решение Задание Стереометрия Задачи 9 и (ЕГЭ профиль) Задача 6 (ЕГЭ база) Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны
ПодробнееТест по теме 60 «Параллелепипед и куб»
Тест по теме 60 «Параллелепипед и куб» 1. Существует ли параллелепипед, у которого только одна боковая грань перпендикулярна основанию?, если в основании квадрат 2. Существует ли параллелепипед, у которого
Существует ли параллелепипед, у которого только одна боковая грань перпендикулярна основанию?, если в основании квадрат 2. Существует ли параллелепипед, у которого
1 Расстояние от точки до прямой
1 Расстояние от точки до прямой 1 1 1 1 1.1. В единичном кубе 1 1 1 1 найдите расстояние от точки до прямой 1. 1 1.2. В правильной треугольной призме 1 1 1, все ребра которой равны 1, найдите расстояние
ПодробнееЗадачи по с т е р е о м е т р и и
Задачи по с т е р е о м е т р и и Ермак Елена Анатольевна, доктор педагогических наук, профессор кафедры математического анализа и методики обучения математике Псковского государственного университета
ПодробнееПодготовка к ЕГЭ по математике
2015 2016 Подготовка к ЕГЭ по математике Прототипы задач из открытого банка заданий ЕГЭ по математике (профильный уровень) http://mathege.ru Стереометрия. Параллелепипед. Куб. Александр и Наталья Крутицких
ПодробнееЧАСТЬ I. Координаты и векторы
ЭКЗАМЕН ПО ГЕОМЕТРИИ КЛАСС ЧАСТЬ I Координаты и векторы Составьте уравнение плоскости, проходящей через точку M (;3;5 ) параллельно векторам a = ( ; ;5) и b = ( 4;3;0 ) Составьте уравнение плоскости, проходящей
ПодробнееСборник заданий С2. Пирамида Ответ
Сборник заданий С Пирамида Ответ Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 08, а площадь полной поверхности этой пирамиды равна. Найдите площадь сечения, проходящего через
ПодробнееСтереометрия: пирамиды.
А.С. Крутицких и Н.С. Крутицких.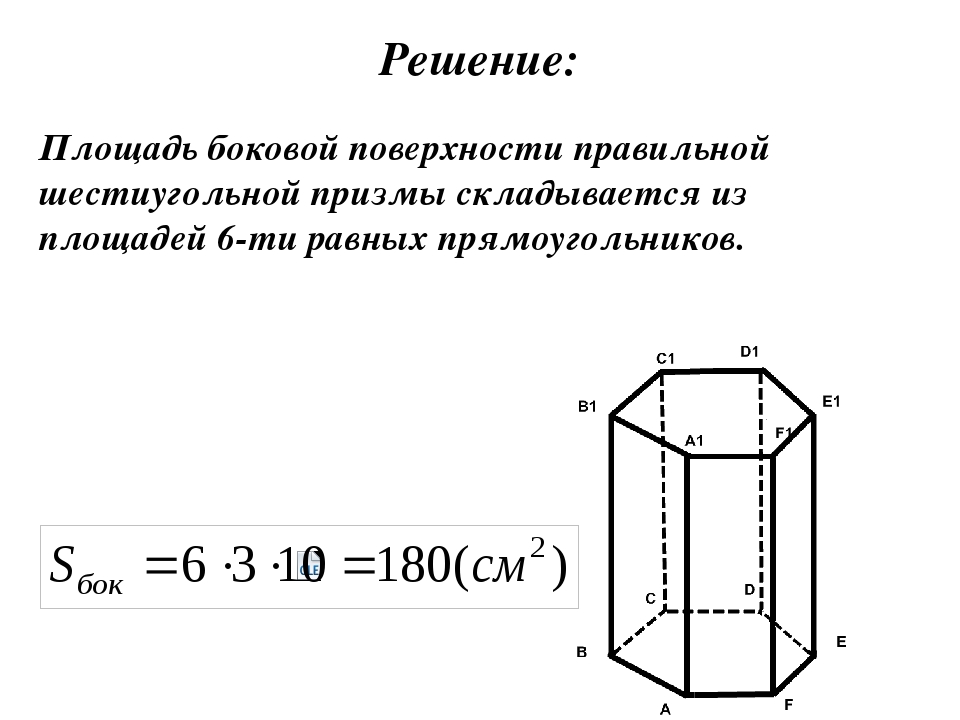 Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: пирамиды. 27069. Стороны основания правильной
Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: пирамиды. 27069. Стороны основания правильной
ID_7154 1/10 neznaika.pro
1 Задачи по стереометрии Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. Найдите объём
Подробнее12+ УДК 373:51 ББК 22.1я72 Г68
УДК 373:51 ББК 22.1я72 Г68 Г68 Гордин Р. К. ЕГЭ 2018. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень) / Под ред. И. В. Ященко. М.: МЦНМО, 2018. 128 с. ISBN 978-5-4439-1214-1 Пособия
Подробнее7. Задачи по стереометрии
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ 7 Задачи по стереометрии методические указания для абитуриентов физического факультета Ростов-на-Дону 00 Печатается по решению учебнофакультета РГУ методической комиссии
ПодробнееСтереометрия: комбинации тел.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: комбинации тел. 27041. Прямоугольный параллелепипед
Подробнее
| С4Дан параллелограмм $ABCD$, сторона которого $AB=13$. Из углов $А$ и $В$ проведены биссектрисы, которые пересекаются в точке $O$. Расстояние от точки $O$ до отрезка АВ равно $\frac{60}{13}$. Определите отрезки $BO$ и $OA$. [посмотреть решение] C3Решите неравенство [посмотреть решение] $$ \log_4y\cdot\log_{y-2}2\leq1 $$ В6Найдите центральный угол AOB, если он на $33^{\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. В7Найдите, если $\operatorname{tg}\alpha=-4$ [посмотреть решение] |
Задание 3. Объём правильной призмы
Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
1. Диагональное сечение правильной четырёхугольной призмы – квадрат, площадь которого равна Q. Найдите объём призмы. а) 0,5Q√͞͞͞͞͞Q;б) 0,2Q√͞͞͞͞͞Q; в) 1,5Q√͞͞͞͞͞Q;
г) 1,2Q√͞͞͞͞͞Q. 2. Сторона основания правильной треугольной призмы
АВСА1В1С1
равна 8 дм, угол между плоскостью основания и сечением АВ1С равен 45°. Найдите объём призмы. а) 196 дм3;
б) 194 дм3; в) 190 дм3;
г) 192 дм3. 3. Найдите объём правильной шестиугольной призмы, длины диагоналей которой соответственно равны 35 дм и 31 дм. а) 5144√͞͞͞͞͞3 дм3; б) 5148√͞͞͞͞͞3 дм3; в) 5142√͞͞͞͞͞3 дм3; г) 5158√͞͞͞͞͞3 дм3. 4. Наименьшее диагональное сечение правильной шестиугольной призмы – квадрат. Большая диагональ призмы 14 дм. Найдите объём призмы. а) 256 дм3;
б) 250 дм3; в) 252 дм3;
г) 258 дм3.
5. Площадь основания и площадь боковой поверхности
правильной шестиугольной призмы соответственно равны S и Q. Найдите
объём призмы.
Площадь основания и площадь боковой поверхности
правильной шестиугольной призмы соответственно равны S и Q. Найдите
объём призмы.
а) 0,5Q;
б) 1,75Q;
г) 1,25Q. 7. Диагональ боковой грани правильной четырёхугольной призмы равна 8 см и образует с плоскостью основания 30°. Найдите объём призмы. а) 192 см3;
б) 198 см3; в) 190 см3;
г) 194 см3. 8. Объём правильной треугольный призмы равен 18√͞͞͞͞͞3, а её высота – 8. Найдите сторону основания. а) 4;
б) 5; в) 3;
г) 2. 9. Диагональ правильной четырёхугольной призмы равна 4√͞͞͞͞͞2 и составляет с плоскостью боковой грани угол 30°. Найдите объём призмы. а) 38;
б) 32; в) 34;
г) 30. 10. Высота правильной треугольной призмы равна h. Найдите объём призмы, если диагонали боковых граней, не исходящие из одной точки, перпендикулярны. а) 0,25h3√͞͞͞͞͞3; б) 0,5h3√͞͞͞͞͞3; в) 1,25h3√͞͞͞͞͞3; г) 1,5h3√͞͞͞͞͞3. 11. Сторона основания правильной треугольной призмы равна а. Боковая поверхность равновелика сумме оснований. Найдите объём призмы. а) 0,15а3;
б) 0,5а3; в) 0,25а3;
г) 0,125а3. 12. Диагональным сечением правильной четырёхугольной призмы является квадрат, площадь которого равна 144 см2.
 Найдите
объём призмы. а) 868 см3;
Найдите
объём призмы. а) 868 см3; б) 864 см3; в) 862 см3;
г) 866 см3.
Задания к уроку 4
Площадь боковой поверхности шестиугольной призмы. Площадь боковой поверхности призмы
Это самые распространенные объемные фигуры среди остальных подобных, которые встречаются в быту и природе. Изучением их свойств занимается стереометрия, или пространственная геометрия. В данной статье раскроем вопрос о том, как можно найти площадь боковой поверхности правильной треугольной призмы, а также четырехугольной и шестиугольной.
Что собой представляет призма?
Перед тем как рассчитывать площадь боковой поверхности правильной треугольной призмы и других видов этой фигуры, следует разобраться, что они собой представляют. Затем научимся определять интересующие величины.
Призмой, с точки зрения геометрии, называется объемное тело, которое ограничено двумя произвольными одинаковыми многоугольниками и n параллелограммами, где n — это число сторон одного многоугольника. Нарисовать такую фигуру легко, для этого следует изобразить какой-нибудь многоугольник. Потом провести из каждой его вершины отрезок, который будет равен по длине и параллелен всем остальным. Затем требуется соединить концы этих линий между собой так, чтобы получился еще один многоугольник, равный исходному.
Выше видно, что фигура ограничена двумя пятиугольниками (они называются нижним и верхним основаниями фигуры) и пятью параллелограммами, которые на рисунке соответствуют прямоугольникам.
Все призмы отличаются друг от друга двумя главными параметрами:
- типом многоугольника, лежащего в основании фигуры;
- углами между параллелограммами и основаниями.
Количество сторон прямоугольника дает название призме. Отсюда получаем выше упомянутые треугольную, шестиугольную и четырехугольную фигуры.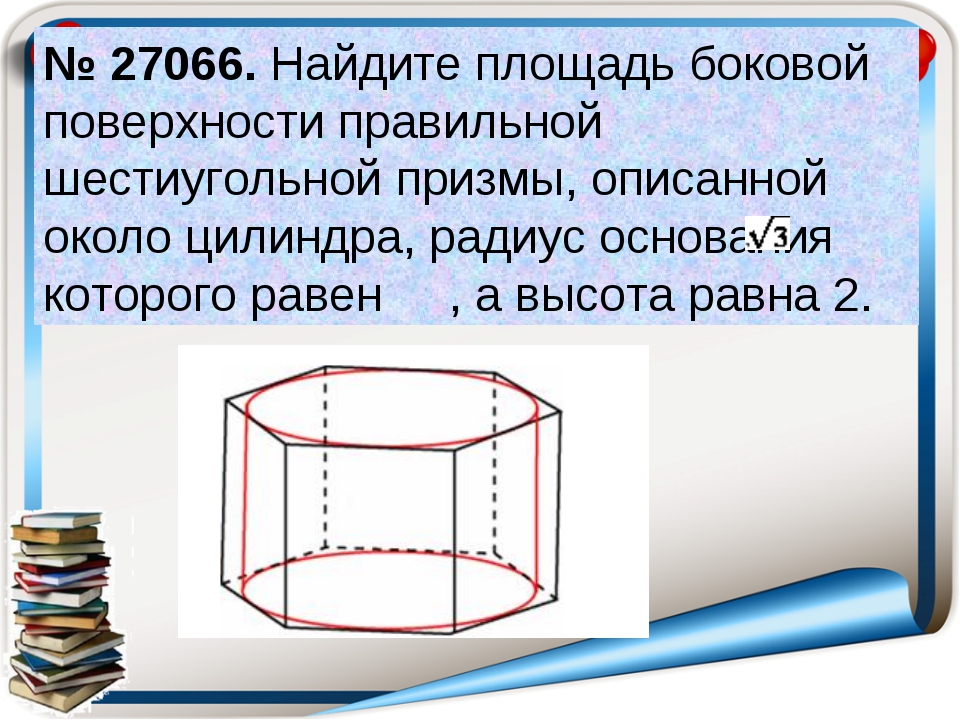
Также они различаются по величине наклона. Что касается отмеченных углов, то если они равны 90 o , тогда такую призму называют прямой, или прямоугольной (угол наклона равен нулю). Если некоторые из углов прямыми не являются, то фигура зовется косоугольной. Различие между ними видно с первого взгляда. Рисунок ниже демонстрирует эти разновидности.
Как видно, высота h совпадает с длиной ее бокового ребра. В случае косоугольной этот параметр всегда меньше.
Какая призма называется правильной?
Поскольку мы должны ответить на вопрос о том, как найти площадь боковой поверхности правильной призмы (треугольной, четырехугольной и так далее), то нужно дать определение этому типу объемной фигуры. Разберем материал подробнее.
Правильная призма — это прямоугольная фигура, у которой правильный многоугольник образует идентичные основания. Этой фигурой может быть треугольник равносторонний, квадрат и другие. Любой n-угольник, все длины сторон и углы которого одинаковые, будет правильным.
Ряд таких призм показан схематически на рисунке ниже.
Боковая поверхность призмы
Как было сказано в эта фигура состоит из n + 2 плоскостей, которые, пересекаясь, образуют n + 2 грани. Две из них принадлежат основаниям, остальные образованы параллелограммами. Площадь всей поверхности состоит из суммы площадей указанных граней. Если в нее не включать значения двух оснований, тогда мы получаем ответ на вопрос о том, как найти площадь боковой поверхности призмы. Так, можно определить ее значение и оснований отдельно друг от друга.
Ниже приводится для которой боковая поверхность образована тремя четырехугольниками.
Рассмотрим процесс вычислений далее. Очевидно, что площадь боковой поверхности призмы равна сумме n площадей соответствующих параллелограммов. Здесь n — это число сторон многоугольника, образующего основание фигуры. Площадь каждого параллелограмма можно найти, если умножить длину его стороны на опущенную на нее высоту.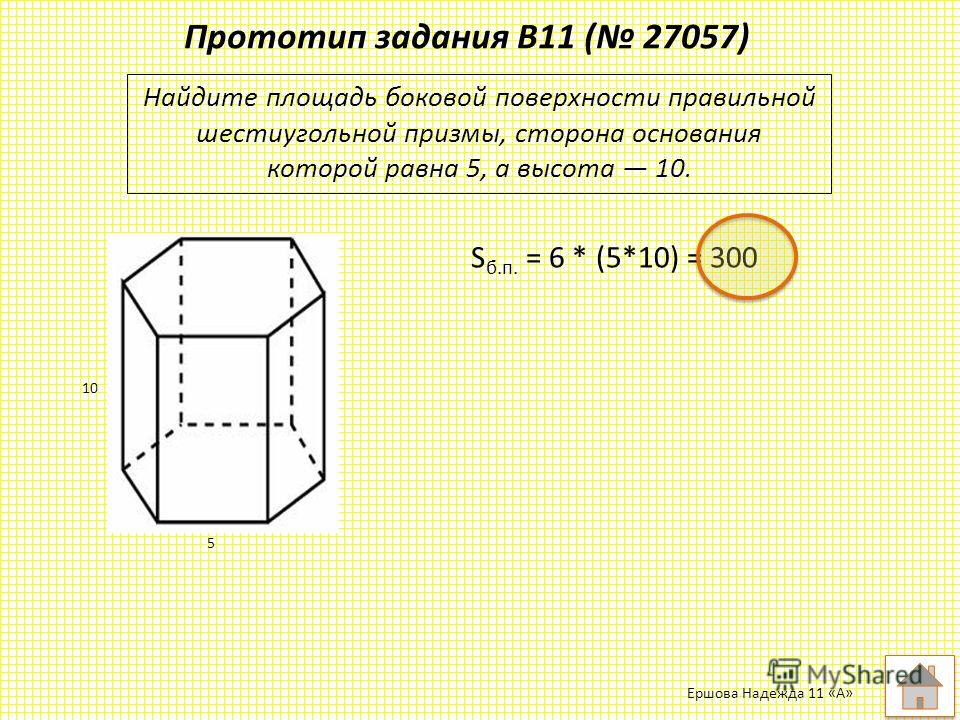 Это касаемо общего случая.
Это касаемо общего случая.
Если изучаемая призма является прямой, тогда процедура определения площади ее боковой поверхности S b значительно облегчается, поскольку такая поверхность состоит из прямоугольников. В этом случае можно воспользоваться следующей формулой:
Где h — высоты фигуры, P o — периметр ее основания
Правильная призма и ее боковая поверхность
Приведенная в пункте выше формула в случае такой фигуры принимает вполне конкретный вид. Поскольку периметр n-угольника равен произведению числа его сторон на длину одной, то получается следующая формула:
Где a — длина стороны соответствующего n-угольника.
Площадь боковой поверхности четырехугольной и шестиугольной
Воспользуемся формулой выше, чтобы определить необходимые значения для отмеченных трех типов фигур. Расчеты будут выглядеть следующим образом.
Для треугольной формула примет вид:
Например, сторона треугольника равна 10 см, а высота фигуры — 7 см, тогда:
S 3 b = 3*10*7 = 210 см 2
В случае четырехугольной призмы искомое выражение принимает форму:
Если взять те же значения длин, что и в предыдущем примере, тогда получаем:
S 4 b = 4*10*7 = 280 см 2
Площадь боковой поверхности шестиугольной призмы рассчитывается по формуле:
Подставляя те же числа, что и в предыдущих случаях, имеем:
S 6 b = 6*10*7 = 420 см 2
Заметим, что в случае правильной призмы любого типа ее боковая поверхность образована одинаковыми прямоугольниками. В примерах выше площадь каждого из них составляла a*h = 70 см 2 .
Расчет для косоугольной призмы
Определение значения площади боковой поверхности для данной фигуры выполнить несколько сложнее, чем для прямоугольной. Тем не менее приведенная выше формула остается той же самой, только вместо периметра основания следует взять периметр перпендикулярного среза, а вместо высоты — длину бокового ребра.
Рисунок выше демонстрирует четырехугольную косоугольную призму. Заштрихованный параллелограмм — это и есть тот перпендикулярный срез, периметр которого P sr необходимо рассчитать. Длина бокового ребра на рисунке обозначена буквой C. Тогда получаем формулу:
Периметр среза можно найти, если известны углы параллелограммов, образующих боковую поверхность.
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10. a Н Используем формулу площади поверхности правильной призмы: В основании лежит правильный шестиугольник, который большими диагоналями делится на 6 равных правильных треугольников со стороной а = 5 Поэтому площадь правильного шестиугольника можно найти так: Используем формулу площади боковой поверхности правильной призмы: а а Подставляем данные в формулу * : *
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10. a Н В основании лежит правильный шестиугольник Используем формулу площади боковой поверхности правильной призмы: а Подставляем данные в формулу * : * S бок = = Ответ: 300
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна Используем формулу площади поверхности правильной призмы: В основании лежит квадрат со стороной а = 20 Используем формулу площади боковой поверхности правильной призмы: Подставляем данные в формулу * : * 1760 = Н 1760 = Н 80Н = Н = 12 Ответ: 12
Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны. 3 Н а Используем формулу объёма правильной призмы: В основании лежит правильный шестиугольник, который большими диагоналями делится на 6 равных правильных треугольников со стороной а = 1 а Поэтому площадь правильного шестиугольника можно найти так: Н – высота (боковое ребро) правильной призмы Подставляем данные в формулу * : *
Гранью параллелепипеда является ромб со стороной 1 и острым углом Одно из ребер параллелепипеда составляет с этой гранью угол в 60 0 и равно 2. Найдите объем параллелепипеда.
Найдите объем параллелепипеда.
Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Площадь боковой поверхности призмы. Здравствуйте! В этой публикации мы с вами разберём группу задач по стереометрии. Рассмотрим комбинацию тел – призмы и цилиндра. На данный момент эта статья завершает всю серию статей связанных с рассмотрением типов заданий по стереометрии.
Если в банке заданий будут появляться новые, то, конечно же, будут и дополнения на блоге в будущем. Но и того что уже есть вполне достаточно, чтобы вы могли научиться решать все задачи с кратким ответом в составе экзамена.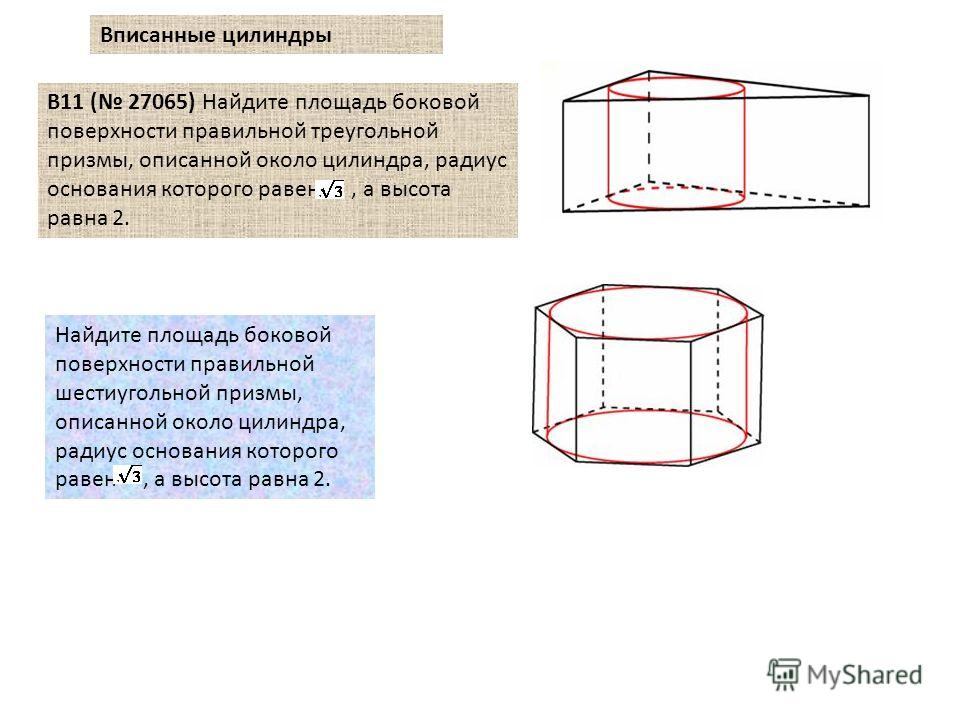 Материала хватит на годы вперёд (программа по математике статична).
Материала хватит на годы вперёд (программа по математике статична).
Представленные задания связаны с вычислением площади призмы. Отмечу, что ниже рассматривается прямая призма (и соответственно прямой цилиндр).
Без знания всяких формул, мы понимаем, что боковая поверхность призмы это все её боковые грани. У прямой призмы боковые грани это прямоугольники.
Площадь боковой поверхности такой призмы равна сумме площадей всех её боковых граней (то есть прямоугольников). Если речь идёт о правильной призме, в которую вписан цилиндр, то понятно, что все грани этой призмы являются РАВНЫМИ прямоугольниками.
Формально площадь боковой поверхности правильной призмы можно отразить так:
27064. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Боковая поверхность данной призмы состоит из четырёх равных по площади прямоугольников. Высота грани равна 1, ребро основания призмы равно 2 (это два радиуса цилиндра), следовательно площадь боковой грани равна:
Площадь боковой поверхности:
73023. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √0,12, а высота равна 3.
Площадь боковой поверхности данной призмы равна сумме площадей трёх боковых граней (прямоугольников). Для нахождения площади боковой грани необходимо знать её высоту и длину ребра основания. Высота равна трём. Найдём длину ребра основания. Рассмотрим проекцию (вид сверху):
Имеем правильный треугольник в который вписана окружность с радиусом √0,12. Из прямоугольного треугольника АОС можем найти АС. А затем и AD (AD=2АС). По определению тангенса:
Значит AD=2АС=1,2.Таким образом, площадь боковой поверхности равна:
27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √75, а высота равна 1.
Искомая площадь равна сумме площадей всех боковых граней. У правильной шестиугольной призмы боковые грани это равные прямоугольники.
Для нахождения площади грани необходимо знать её высоту и длину ребра основания. Высота известна, она равна 1.
Найдём длину ребра основания. Рассмотрим проекцию (вид сверху):
Имеем правильный шестиугольник, в который вписана окружность радиуса √75.
Рассмотрим прямоугольный треугольник АВО. Нам известен катет ОВ (это радиус цилиндра). ещё можем определить угол АОВ, он равен 300 (треугольник АОС равносторонний, ОВ –биссектриса).
Воспользуемся определением тангенса в прямоугольном треугольнике:
АС=2АВ, так как ОВ является медианой, то есть делит АС пополам, значит АС=10.
Таким образом, площадь боковой грани равна 1∙10=10 и площадь боковой поверхности:
76485. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 8√3, а высота равна 6.
Площадь боковой поверхности указанной призмы из трёх равных по площади граней (прямоугольников). Чтобы найти площадь требуется знать длину ребра основания призмы (высота нам известна). Если рассматривать проекцию (вид сверху), то имеем правильный треугольник вписанный в окружность. Сторона этого треугольника выражается через радиус как:
Подробности этой взаимосвязи . Значит она будет равна
Тогда площадь боковой грани равна: 24∙6=144. А искомая площадь:
245354. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Предыдущая статья: «Табель о рангах всех чинов воинских, статских и придворных… Следующая статья: Ребенок едет учиться за рубеж
Площадь боковой поверхности призмы
Площадь боковой поверхности призмы. Здравствуйте! В этой публикации мы с вами разберём группу задач по стереометрии. Рассмотрим комбинацию тел – призмы и цилиндра. На данный момент эта статья завершает всю серию статей связанных с рассмотрением типов заданий по стереометрии.
Рассмотрим комбинацию тел – призмы и цилиндра. На данный момент эта статья завершает всю серию статей связанных с рассмотрением типов заданий по стереометрии.
Если в банке заданий будут появляться новые, то, конечно же, будут и дополнения на блоге в будущем. Но и того что уже есть вполне достаточно, чтобы вы могли научиться решать все задачи с кратким ответом в составе экзамена. Материала хватит на годы вперёд (программа по математике статична).
Представленные задания связаны с вычислением площади боковой поверхности призмы. Отмечу, что ниже рассматривается прямая призма (и соответственно прямой цилиндр).
Без знания всяких формул, мы понимаем, что боковая поверхность призмы это все её боковые грани. У прямой призмы боковые грани это прямоугольники.
Площадь боковой поверхности такой призмы равна сумме площадей всех её боковых граней (то есть прямоугольников). Если речь идёт о правильной призме, в которую вписан цилиндр, то понятно, что все грани этой призмы являются РАВНЫМИ прямоугольниками.
Формально площадь боковой поверхности правильной призмы можно отразить так:
27064. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Боковая поверхность данной призмы состоит из четырёх равных по площади прямоугольников. Высота грани равна 1, ребро основания призмы равно 2 (это два радиуса цилиндра), следовательно площадь боковой грани равна:
Площадь боковой поверхности:
Ответ: 8
73023. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √0,12, а высота равна 3.
Площадь боковой поверхности данной призмы равна сумме площадей трёх боковых граней (прямоугольников). Для нахождения площади боковой грани необходимо знать её высоту и длину ребра основания. Высота равна трём. Найдём длину ребра основания. Рассмотрим проекцию (вид сверху):
Имеем правильный треугольник в который вписана окружность с радиусом √0,12. Из прямоугольного треугольника АОС можем найти АС. А затем и AD (AD=2АС). По определению тангенса:
Из прямоугольного треугольника АОС можем найти АС. А затем и AD (AD=2АС). По определению тангенса:
Значит AD=2АС=1,2.Таким образом, площадь боковой поверхности равна:
Ответ: 3,6
27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √75, а высота равна 1.
Искомая площадь равна сумме площадей всех боковых граней. У правильной шестиугольной призмы боковые грани это равные прямоугольники.
Для нахождения площади грани необходимо знать её высоту и длину ребра основания. Высота известна, она равна 1.
Найдём длину ребра основания. Рассмотрим проекцию (вид сверху):
Имеем правильный шестиугольник, в который вписана окружность радиуса √75.
Рассмотрим прямоугольный треугольник АВО. Нам известен катет ОВ (это радиус цилиндра). ещё можем определить угол АОВ, он равен 300 (треугольник АОС равносторонний, ОВ –биссектриса).
Воспользуемся определением тангенса в прямоугольном треугольнике:
АС=2АВ, так как ОВ является медианой, то есть делит АС пополам, значит АС=10.
Таким образом, площадь боковой грани равна 1∙10=10 и площадь боковой поверхности:
Ответ: 60
76485. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 8√3, а высота равна 6.
Площадь боковой поверхности указанной призмы из трёх равных по площади граней (прямоугольников). Чтобы найти площадь требуется знать длину ребра основания призмы (высота нам известна). Если рассматривать проекцию (вид сверху), то имеем правильный треугольник вписанный в окружность. Сторона этого треугольника выражается через радиус как:
Подробности этой взаимосвязи изложены здесь. Значит она будет равна
Тогда площадь боковой грани равна: 24∙6=144. А искомая площадь:
Ответ: 432
245354. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2.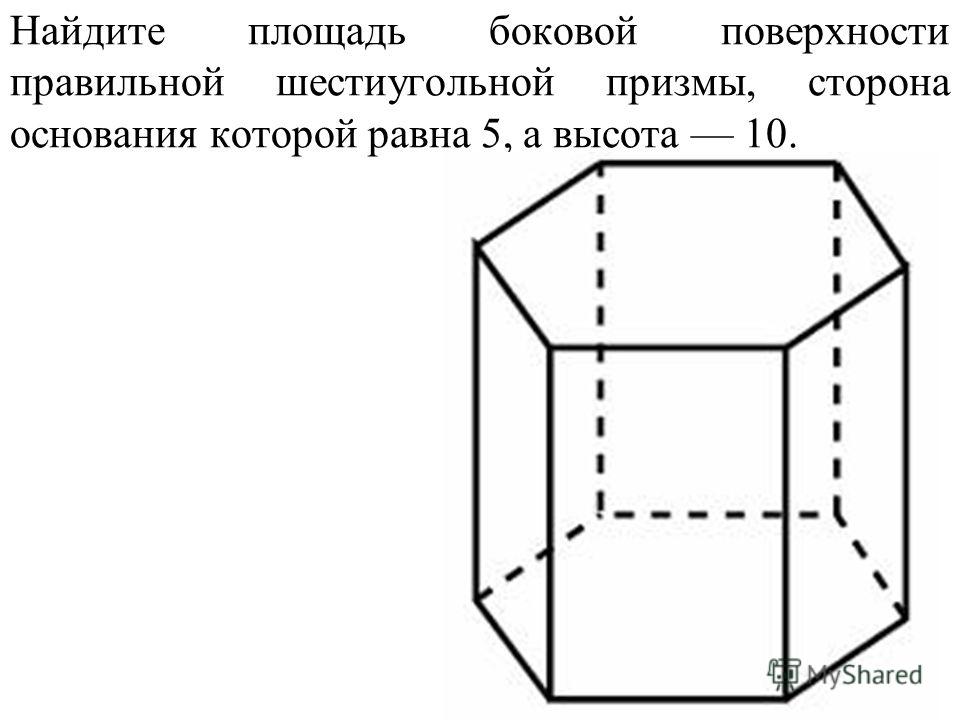 Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Всё просто. Имеем четыре равных по площади боковые грани, следовательно площадь одной грани равна 48:4=12. Так как радиус основания цилиндра равен 2, то ребро основания призмы будет рано 4 – оно равно диаметру цилиндра (это два радиуса). Нам известна площадь грани и одно ребро, второе являющееся высотой будет равно 12:4=3.
Ответ: 3
27065. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Посмотреть решение
27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Посмотреть решение
27170. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.
Посмотреть решение
Как видите задачки на раз-два. На этом всё! Успеха вам!
С уважением, Александр.
Делитесь информацией в социальных сетях.
Тест по геометрии «Призма» с ответами
1. Не существует призмы, у которой все грани:
а) треугольники +
б) квадраты
в) прямоугольники
2. Найдите боковое ребро правильной четырёхугольной призмы, если сторона её основания равна 20, а площадь поверхности 1760:
а) 11
б) 22 +
в) 44
3. Если основаниями прямой призмы являются правильные многоугольники, то она:
а) наклонная
б) пятиугольная
в) правильная +
4. Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все её ребра увеличить в три раза:
а) 54 +
б) 27
в) 108
5. Многоугольники призмы, лежащие в разных плоскостях и совмещенные параллельным переносом являются ее основаниями, так ли это:
а) нет
б) отчасти
в) да +
6. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 16 и отстоит от других боковых ребер на 9 и 12. Найдите площадь боковой поверхности этой призмы:
Их общее ребро равно 16 и отстоит от других боковых ребер на 9 и 12. Найдите площадь боковой поверхности этой призмы:
а) 678
б) 576 +
в) 288 +
7. В какой призме боковые ребра параллельны ее высоте:
а) у наклонной
б) у четырехугольной
в) у прямой +
8. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 8, а боковые ребра равны 4√3 и наклонены к плоскости основания под углом 30°:
а) 576 +
б) 288
в) 432
9. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, так ли это:
а) нет
б) отчасти
в) да +
10. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объём отсеченной треугольной призмы равен 19,5. Найдите объем исходной призмы:
а) 39
б) 78 +
в) 156
11. Основания призмы:
а) параллельны и равны +
б) скрещиваются
в) пересекаются и равны
12. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 26, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы:
а) 26
б) 13 +
в) 52
13. Грани многогранника параллельны и равны, так ли это:
а) нет +
б) да
в) отчасти
14. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы:
а) 32
б) 16
в) 8 +
15. Расстояние между плоскостями оснований призмы называется:
а) высотой +
б) диагональю
в) ребром
16. В сосуд, имеющий формулу правильной треугольной призмы, налили 1300 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 28 см. Найдите объем детали:
а) 132 см3
б) 156 см3 +
в) 188 см3
17. Могут ли диагонали призмы быть не равными:
а) нет
б) зависит от задачи
в) да +
18. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 6, боковое ребро равно 5. Найдите объем призмы:
Найдите объем призмы:
а) 30
б) 60 +
в) 120
19. Найдите площадь боковой поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 5:
а) 10
б) 50
в) 100 +
20. Найдите боковое ребро правильной четырехугольной призмы, если сторона её основания равна 15, а площадь поверхности равна 930:
а) 16
б) 8 +
в) 32
21. Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани 10 см. Найдите площадь боковой поверхности призмы:
а) 180 +
б) 90
в) 45
22. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота – 10:
а) 160
б) 180 +
в) 220
23. Боковая поверхность призмы состоит из:
а) треугольников
б) ромбов
в) параллелограммов +
24. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 25 и 60, и боковым ребром, равным 25:
а) 4550
б) 4750 +
в) 750
25. Если в основании призмы лежит параллелограмм, то она является:
а) правильной призмой
б) правильным многоугольником
в) параллелепипедом +
26. Площадь боковой поверхности правильной шестиугольной призмы равна 324 см2, а большая из диагоналей призмы – 15 см. Найди периметр прямоугольника, который является большим из диагональных сечений призмы:
а) 84
б) 42 +
в) 21
27. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь её боковой поверхности:
а) 240 +
б) 120
в) 480
28. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота – 8:
а) 576
б) 144
в) 288 +
29. Боковые грани правильной треугольной призмы являются квадратами. Выбери правильное утверждение для данной призмы:
а) Косинус угла между боковыми диагоналями призмы равна 0,75. 2 \; h} \)
2 \; h} \)
Где:
\ (\ large {V} \) = объем
\ (\ large {a} \) = край
\ (\ large {h} \) = высота
Площадь призмы
В площадь боковой поверхности призма — сумма площадей его боковых граней.
В общее площадь поверхности призмы представляет собой сумму площадей его боковых граней и двух его оснований.
Обычно, если «правая» или «наклонная» не упоминаются, можно предположить, что призма — это правая призма.
Общая формула для площади боковой поверхности правой призмы:
L
.
S
.А
.
знак равно
п
час
где
п
представляет периметр основания и
час
представляет высоту призмы.
Пример 1:
Найдите площадь боковой поверхности треугольной призмы с краями основания. 3 дюймы, 4 дюймов и 5 дюймы и высота 8 дюймы.
Периметр — это сумма оснований.
п знак равно 3 + 4 + 5 знак равно 12 дюймы
Боковая поверхность знак равно 12 ( 8 ) знак равно 96 дюймы 2
Общая формула для общая площадь поверхности правой призмы
Т
. S
.
А
.
знак равно
п
час
+
2
B
где
п
представляет периметр основания,
час
высота призмы и
B
площадь основания.
S
.
А
.
знак равно
п
час
+
2
B
где
п
представляет периметр основания,
час
высота призмы и
B
площадь основания.
В целом нет простого способа рассчитать площадь поверхности наклонной призмы. Лучше всего найти отдельно площади оснований и боковых граней и сложить их.
Пример 2:
Найдите общую площадь поверхности равнобедренной трапециевидной призмы с параллельными краями основания. 6 см и 12 см, ножки основания 5 см каждый, высота основания 4 см и высота призмы 10 см.
Периметр основания складывается из длин сторон.
п знак равно 6 + 5 + 12 + 5 знак равно 28 год см
Поскольку основание представляет собой равнобедренную трапецию, его площадь равна
1
2
час
(
б
1
+
б
2
)
.
B знак равно 1 2 ( 4 ) ( 6 + 12 ) знак равно 36 см 2
Т .S . А . знак равно п час + 2 B знак равно 28 год ( 10 ) + 2 ( 36 ) знак равно 280 + 72 знак равно 352 см 2
Боковая площадь
Боковая площадь
В геометрии трехмерная фигура — это объект, который имеет трехмерные измерения длины, ширины и высоты. Используя эти 3 измерения, анализируются различные расчеты объема, площади поверхности. Такие фигуры, как многогранники, цилиндры, конусы и сферы, представляют собой трехмерные фигуры. Многогранники — это формы, которые имеют плоские поверхности, известные как грани, и эти грани состоят из многоугольников. Примеры многогранников — пирамиды и призмы. Цилиндры, конусы, сферы трехмерны, но не являются многогранниками, поскольку не имеют плоских поверхностей. У них изогнутые поверхности. Цилиндры имеют 2 конгруэнтных базовых круга, соединенных изогнутой поверхностью.Конус — это фигура, у которой базовая окружность соединена с вершиной наверху изогнутой поверхностью. Сфера также является одной из таких пространственных фигур, все точки которой находятся на одинаковом расстоянии от центральной точки.
Используя эти 3 измерения, анализируются различные расчеты объема, площади поверхности. Такие фигуры, как многогранники, цилиндры, конусы и сферы, представляют собой трехмерные фигуры. Многогранники — это формы, которые имеют плоские поверхности, известные как грани, и эти грани состоят из многоугольников. Примеры многогранников — пирамиды и призмы. Цилиндры, конусы, сферы трехмерны, но не являются многогранниками, поскольку не имеют плоских поверхностей. У них изогнутые поверхности. Цилиндры имеют 2 конгруэнтных базовых круга, соединенных изогнутой поверхностью.Конус — это фигура, у которой базовая окружность соединена с вершиной наверху изогнутой поверхностью. Сфера также является одной из таких пространственных фигур, все точки которой находятся на одинаковом расстоянии от центральной точки.
Что такое боковая область?
Боковая площадь — это сумма площадей всех поверхностей фигуры, кроме основной и верхней. Это означает, что боковая площадь — это сумма площадей только всех граней или боковых поверхностей. Исходя из формы фигуры, можно соответственно рассчитать боковую площадь.Боковая площадь измеряется в квадратных единицах. Например, если размеры указаны в «метрах», то единицей боковой площади будут квадратные метры.
Боковая площадь геометрических фигур:
Боковая площадь различных геометрических фигур может быть рассчитана с использованием размеров этой конкретной формы. Для вычисления боковой поверхности мы не складываем площади верхней и нижней поверхности фигуры. При вычислении общей площади фигуры мы складываем площади всех поверхностей (включая верхнюю и нижнюю), но для боковой площади нужно складывать только площади боковых граней.
Теперь давайте посчитаем боковую площадь различных геометрических фигур с разными размерами:
1) Боковая площадь призмы:
Призма — очень популярная трехмерная фигура, состоящая из плоских граней и одинаковых оснований. Основания совпадают и параллельны друг другу. По всей длине призмы имеют одинаковое поперечное сечение. Призма представляет собой многогранник, поэтому у нее нет изогнутых сторон. Его грани плоские, а края (или стороны) выполнены в виде прямых линий.Мы можем классифицировать различные типы призм на основе поперечного сечения или основания призмы. Если основание или поперечное сечение призмы представляет собой квадрат, то это называется квадратной призмой. Если поперечное сечение по длине представляет собой треугольник, то это называется треугольной призмой.
По всей длине призмы имеют одинаковое поперечное сечение. Призма представляет собой многогранник, поэтому у нее нет изогнутых сторон. Его грани плоские, а края (или стороны) выполнены в виде прямых линий.Мы можем классифицировать различные типы призм на основе поперечного сечения или основания призмы. Если основание или поперечное сечение призмы представляет собой квадрат, то это называется квадратной призмой. Если поперечное сечение по длине представляет собой треугольник, то это называется треугольной призмой.
Боковую площадь любой призмы можно рассчитать по формуле, показанной ниже:
Боковая площадь призмы = (периметр основания) * (высота призмы) ==> L = P * ha) Боковая площадь прямоугольной призмы: Прямоугольная призма имеет 6 прямоугольных граней, включая верхнюю и нижнюю поверхности.Поскольку основание поперечного сечения призмы представляет собой прямоугольник, она известна как прямоугольная призма. Чтобы рассчитать боковую площадь прямоугольной призмы, мы учитываем только площадь четырех боковых граней и не рассчитываем площадь двух оснований призмы. Периметр основания прямоугольной призмы есть не что иное, как периметр прямоугольника основания. Периметр прямоугольника — это сумма длин всех его сторон. Это подразумевает периметр прямоугольника, P = 2l + 2w (где l = длина и w = ширина прямоугольника).
Следовательно, боковая площадь прямоугольной призмы теперь также может быть записана как:
Боковая площадь прямоугольной призмы = периметр основания * высота призмы
L = P * h
L = (2l + 2w) * h
или L = 2lh + 2wh (где l = длина, w = ширина, h = высота)
Пример: Рассчитайте поперечную площадь прямоугольной призмы, если учесть, что длина 6 м, ширина 5 м и высота 8 м.
Учитывая, что длина l = 6 м, ширина w = 5 м и высота h = 8 м.
Боковая площадь прямоугольной призмы, L = периметр основания * высота
L = 2lh + 2wh
==> L = (2 * 6 * 8) + (2 * 5 * 8)
==> L = 96 + 80 = 176м
Следовательно, боковая площадь L = 176 квадратных метров.
b) Боковая площадь треугольной призмы: Треугольная призма — это призма, основание которой (или поперечное сечение по длине) представляет собой треугольник. Если стороны базового треугольника равны «a», «b» и «c», то периметр треугольника равен сумме всех его сторон = (a + b + c).
Боковая площадь треугольной призмы = (периметр базового треугольника) * (высота призмы) L = (a + b + c) * h
Пример: Какова поперечная площадь треугольной призмы высотой 12 см, имеющей треугольник в основании со стороной 6 см, 4 см и 5 см?
Учитывая высоту призмы, h = 12 см
Стороны треугольника с основанием имеют длину a = 6 см, b = 4 см и c = 5 см.
Боковая площадь треугольной призмы = (периметр базового треугольника) * (высота призмы)
L = (a + b + c) * h
Следовательно, L = (6 см + 4 см + 5 см) * 12 см == > L = 180 квадратных сантиметров.
c) Боковая площадь правильной шестиугольной призмы: Шестиугольная призма — это призма, основание которой (или поперечное сечение по длине) представляет собой шестиугольник. Шестиугольник — это многоугольник с 6 сторонами. Шестиугольная призма состоит из двух одинаковых шестиугольных оснований и четырех прямоугольных граней. Правильный шестиугольник — это многоугольник, у которого 6 равных сторон.
Если длина стороны основного правильного шестиугольника равна ‘s’, тогда периметр основного шестиугольника равен сумме всех его сторон = s + s + s + s + s + s = 6s.
Боковая площадь шестиугольной призмы, L = (Периметр основного правильного шестиугольника) * (Высота призмы) L = (6 * s) * h
Пример: Если высота призмы 10 см, а основание — правильный шестиугольник со стороной 4 см, то каков периметр этой шестиугольной призмы?
Заданная высота призмы, h = 10 см
Длина стороны основного правильного шестиугольника, s = 4 см
Боковая площадь шестиугольной призмы, L = (Периметр основного шестиугольника) * (Высота призмы)
L = (6 * s) * h
Следовательно, L = (6 * 4 см) * 10 см ==> L = 240 квадратных сантиметров.
2) Боковая площадь пирамиды:
Пирамида — это трехмерная фигура, основание которой представляет собой многоугольник и треугольные грани пересекаются в верхней вершине (также известной как «вершина»). Боковая площадь пирамиды — это сумма площадей боковых граней пирамидальной конструкции без учета площади основания. Как и призма, существуют разные типы пирамид в зависимости от формы ее основания. Если основание пирамиды — треугольник, то она известна как треугольная пирамида.Если основание пирамиды представляет собой прямоугольник, то она известна как прямоугольная пирамида.
Если базовый многоугольник — правильный многоугольник, то мы получаем правильную пирамиду. Если базовый многоугольник является неправильным многоугольником, то образованная пирамида является неправильной пирамидой.
Боковая площадь правильной пирамиды = 1/2 * (периметр основания) * (наклонная высота пирамиды)
(Примечание: наклонная высота — это высота перпендикуляра, проведенная от вершины (вершины) к основанию бокового треугольника, как показано на рисунке выше).
Боковая площадь неправильной пирамиды = Сумма площадей каждой боковой треугольной грани
a) Боковая площадь квадратной пирамиды:
Квадратная пирамида — это пирамида с квадратным основанием.
Если длина стороны квадратного основания равна ‘a, тогда периметр квадратного основания = 4 * a
Пусть наклонная высота, которая представляет собой перпендикулярное расстояние, проведенное от вершины до основания бокового треугольника, будет = s
Боковая площадь квадратной пирамиды = 1/2 * (периметр квадратного основания) * (наклонная высота пирамиды ) = 1/2 * 4a * s = 2 * a * s
Следовательно, поперечная площадь квадратной пирамиды = 2 * a * s
Пример: Найдите боковую площадь квадратной пирамиды, квадратное основание которой имеет длину стороны 5 м и наклонную высоту 9 м.

Учитывая длину стороны квадратного основания пирамиды, a = 5 м
Наклонная высота пирамиды, s = 9м
Боковая площадь квадратной пирамиды = 2 * a * s = 2 * 5 м * 9 м = 90 м 2
б) Боковая площадь треугольной пирамиды:
Пирамида, состоящая из треугольного основания, известна как Треугольная пирамида. В общих случаях, базовый треугольник является равносторонним треугольником и, следовательно, представляет собой равностороннюю треугольную пирамиду, также известную как правильная треугольная пирамида.Но в случае, если у базового треугольника нет равных сторон, пирамида известна как неправильная пирамида.
Если длины сторон треугольника основания равны «a», «b» и «c», тогда периметр треугольника = (a + b + c)
Пусть наклонная высота пирамиды = s
Тогда боковая площадь треугольной пирамиды = 1/2 * (a + b + c) * s
Пример: Рассчитайте поперечную площадь равносторонней треугольной пирамиды со стороной основания 6 м и высотой наклона 10 м.
Учитывая сторону основного равностороннего треугольника, a = 6 м (равносторонние треугольники имеют равные стороны)
Отсюда a = b = c = 6m
Наклонная высота пирамиды, s = 10м
Боковая площадь треугольной пирамиды = 1/2 * (a + b + c) * s ==> L = 1/2 * (6+ 6+ 6) * 10 = 90 м 2
c) Боковая площадь пятиугольной пирамиды:
Пирамида, состоящая из пятиугольного основания, известна как пятиугольная пирамида. Пятиугольник — это многоугольник, состоящий из 5 сторон.
Если основной пятиугольник имеет длину сторон ‘a’, ‘b’, ‘c’, ‘d’ и ‘e’, тогда периметр пятиугольника = сумма всех его сторон = (a + b + c + d + e )
Пусть наклонная высота пирамиды =
с. Боковая площадь пятиугольной пирамиды = 1/2 * (периметр основного пятиугольника) * (наклонная высота)
Итак, Боковая площадь пятиугольной пирамиды = 1/2 * (a + b + c + d + e) * s
Пример: Даны длины сторон правильной пятиугольной пирамиды, равные 5 см, и наклонная высота пирамиды, равная 12 см.
 Какова боковая площадь этой правильной пятиугольной пирамиды?
Какова боковая площадь этой правильной пятиугольной пирамиды? У правильного пятиугольника 5 равных сторон.
Учитывая длины сторон пятиугольника основания как a = b = c = d = e = 5 см
Наклонная высота пятиугольной пирамиды, s = 12см
Боковая площадь пятиугольной пирамиды = 1/2 * (5+ 5+ 5+ 5+ 5) * 12 = 150 см 2
2) Боковая площадь цилиндра:
Цилиндры обычно встречаются в нашей повседневной жизни. Цилиндр — это трехмерная сплошная замкнутая фигура, состоящая из 2 конгруэнтных круглых оснований, соединенных изогнутой поверхностью.Цилиндр имеет 2 конгруэнтных круглых основания, параллельных друг другу. Длина перпендикуляра между двумя круглыми основаниями известна как «высота цилиндра» или «высота».
Для данного цилиндра пусть радиус круглого основания = ‘r’
Пусть высота (или высота), которая представляет собой перпендикулярное расстояние между двумя круглыми основаниями, равна ‘h’
. Тогда поперечная площадь цилиндра определяется следующим уравнением:
Боковая площадь цилиндра = (Окружность круглого основания) * (Высота цилиндра)
Следовательно, Боковая площадь цилиндра = 2 * ???? * г * ч
Пример: Рассчитайте поперечную площадь цилиндра, радиус круглого основания которого равен 6 м, а высота цилиндра — 8 м.
Учитывая радиус круглого основания, r = 6 м
Высота цилиндра, h = 8м
Боковая площадь цилиндра = 2 * ???? * r * h ==> L = 2 * 3,14 * 6 м * 8 м = 301,44 м 2
3) Боковая площадь конуса:
Конус — это трехмерная фигура, имеющая круглое основание, соединенное с единственной вершиной наверху (также известной как «вершина») изогнутой поверхностью. Высота конуса — это расстояние по перпендикуляру от вершины до центра круглого основания.Высота наклона — это расстояние по поверхности конуса от вершины до окружности, как показано на рисунке справа.
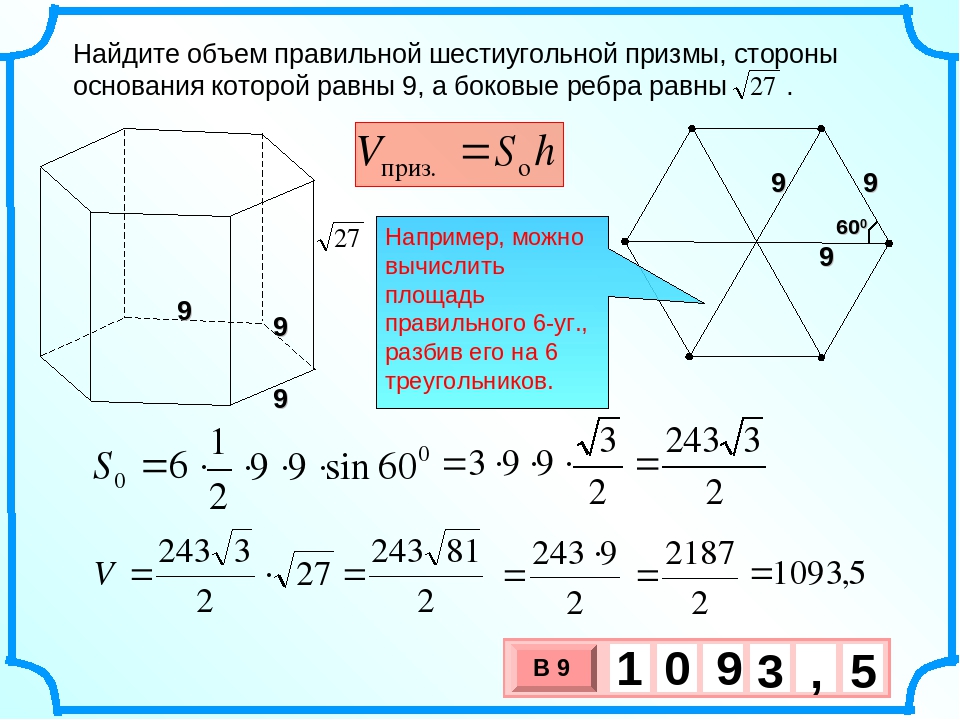
Для данного конуса пусть радиус круглого основания = r
Пусть высота конуса = h, а наклонная высота конуса = s
. Из рисунка видно, что наклонная высота s = √ (h 2 + r 2 ) (Используя теорему Пифагора)
Тогда боковая площадь конуса может быть рассчитана следующим образом:
Боковая площадь конуса = ???? * r * s
Следовательно, боковая площадь конуса = ???? * r * √ (h 2 + r 2 )
Пример: Рассчитайте наклонную высоту и поперечную площадь конуса, если радиус конуса равен 6 см, а высота конуса равна 8 см.
Учитывая радиус конуса, r = 6см
Высота конуса, h = 8см
Наклонная высота, s = √ (h 2 + r 2 ) = √ (6 2 + 8 2 ) = 10 см
Боковая площадь конуса = ???? * r * √ (h 2 + r 2 ) = 3,14 * 6 * √ (6 2 + 8 2 ) = 188,4 см 2
4) Боковая область сферы и полушария:
Сфера — это трехмерная геометрическая фигура, идеально симметричная по форме.Это замкнутая фигура, образованная точками, равноудаленными от центра. У сферы нет ребер (сторон) или вершин (углов).
Если радиус сферы равен «r», то мы можем рассчитать боковую площадь, как показано ниже:
Боковая площадь сферы = 4 * ???? * r 2
Когда сфера разрезается на равные половины, мы получаем полусферу. Следовательно, боковая площадь полушария составляет половину боковой площади сферы.
Боковая площадь полушария = 2 * ???? * r 2
Пример: Если радиус сферы составляет 5 см, то какова поперечная площадь сферы и полусферы?
Учитывая радиус сферы, r = 5 см
Боковая площадь сферы = 4 * ???? * r 2 ==> L = 4 * 3.
 14 * (5 см) 2 = 314 см 2
14 * (5 см) 2 = 314 см 2 Боковая площадь полушария = 2 * ???? * r 2 ==> L = 2 * 3,14 * (5 см) 2 = 157 см 2
Калькулятор треугольной призмы
Форма треугольной призмы
a = длина стороны a
b = длина стороны b = основание нижнего треугольника b
c = длина стороны c
h = высота призмы
H = высота нижнего треугольника
V = объем
A tot = общая площадь = со всех сторон
A lat = площадь боковой поверхности = все прямоугольные стороны
A верх = площадь верхней поверхности = верхний треугольник
A bot = площадь нижней поверхности = нижний треугольник
Треугольная призма — это твердое геометрическое тело с треугольником в качестве основания.Это трехсторонняя призма, в которой основание и вершина — равные треугольники, а остальные 3 стороны — прямоугольники.
Использование калькулятора
Калькулятор позволяет найти объем, площадь поверхности и высоту треугольной призмы. Расчет площади поверхности включает верхнюю, нижнюю, боковые стороны и общую площадь поверхности. Высота рассчитывается на основе известного объема или площади боковой поверхности.
Единицы: Единицы показаны для удобства, но не влияют на вычисления.Ответы будут одинаковыми, будь то футы, футы 2 , футы 3 , или метры, 2 , м 3 , или любая другая единица измерения.
Значащие цифры: Выберите количество значащих цифр или оставьте значение «Авто», чтобы калькулятор определял точность чисел.
Формулы треугольной призмы по высоте и длинам сторон треугольника a, b и c:
Формула объема треугольной призмы
Находит трехмерное пространство, занятое треугольной призмой.
\ [V = \ dfrac {1} {4} h \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]
\ [V = \ dfrac {1} {4} h \ sqrt {(c + ab) (a + bc)} \\\ times \ sqrt {(a + b + c) (b + ca)} \]
Площадь верхней поверхности треугольной призмы по формуле
Находит площадь треугольной поверхности наверху призмы. Это та же область, что и нижняя поверхность.
\ [A_ {top} = \ dfrac {1} {4} \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]
\ [A_ {top} = \ dfrac {1} {4} \ sqrt {(c + ab) (a + bc)} \\\ times \ sqrt {(a + b + c) (b + ca)} \]
Площадь нижней поверхности треугольной призмы по формуле
Находит площадь треугольной поверхности в нижней части призмы.Это та же область, что и верхняя поверхность.
\ [A_ {bot} = \ dfrac {1} {4} \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]
\ [A_ {bot} = \ dfrac {1} {4} \ sqrt {(c + ab) (a + bc)} \\\ times \ sqrt {(a + b + c) (b + ca)} \]
Площадь боковой поверхности треугольной призмы по формуле
Находит общую площадь трех прямоугольных сторон призмы. Вы можете представить себе площадь боковой поверхности как общую площадь поверхности призмы за вычетом двух треугольных областей вверху и внизу призмы.
\ [A_ {lat} = h (a + b + c) \]Общая площадь поверхности треугольной призмы по формуле
Находит общую площадь всех сторон треугольной призмы. Общая площадь поверхности призмы включает площадь верхней и нижней сторон треугольника призмы, а также площадь всех трех сторон прямоугольника.
Общая площадь поверхности призмы включает площадь верхней и нижней сторон треугольника призмы, а также площадь всех трех сторон прямоугольника.
Формула высоты треугольной призмы в единицах объема
Находит высоту треугольной призмы, решая формулу объема для высоты.Высота h рассчитывается из объема V и длин сторон a, b и c.
\ [h = \ dfrac {4V} {\ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)}} \]
\ [h = 4V \ div \ left [\, \ sqrt {(c + ab) (a + bc)} \\\ times \ sqrt {(a + b + c) (b + ca)} \, \ справа] \]
Формула высоты треугольной призмы через площадь боковой поверхности
Находит высоту треугольной призмы, решая формулу площади боковой поверхности для высоты.Высота h рассчитывается из площади боковой поверхности A lat и длин сторон a, b и c.
\ [h = \ dfrac {A_ {lat}} {(a + b + c)} \]Артикул
Weisstein, Eric W. «Площадь треугольника». Из MathWorld — веб-ресурс Wolfram, Площадь треугольника.
Объяснитель урока: Площадь поверхности призм
Пример 2: Определение общей площади поверхности призмы
Определите площадь поверхности призмы.
Ответ
Чтобы решить этот тип вопросов, полезно нарисовать сеть призмы, чтобы визуализировать все ее
лица. Во-первых, нам нужно определить основание призмы.
Помните, что призма имеет два основания, которые представляют собой две параллельные конгруэнтные грани.
Мы видим, что призма здесь имеет пару L-образных оснований.
Все грани между основаниями — прямоугольники.
Используя информацию, представленную на диаграмме, мы можем нарисовать сетку призмы.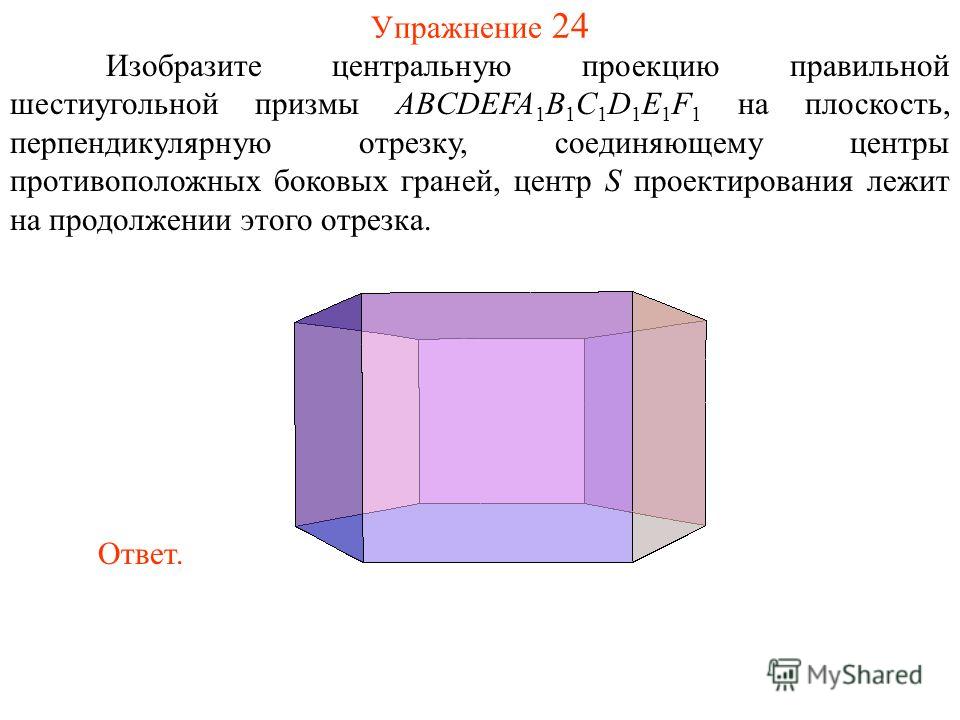
В сети отчетливо видны прямоугольные грани между двумя основаниями.Мы видим, что все прямоугольники имеют одинаковую длину: это высота призмы, здесь 3 шт. Они образуют большой прямоугольник длиной 3 и шириной 𝑎 + 2 + 4 + 5 + 1 + 𝑏, где 𝑎 и 𝑏 — две недостающие стороны основания призмы. Ширина прямоугольника, образованного всеми боковыми гранями, фактически является периметром основания.
Недостающие длины можно легко найти, учитывая, что все углы в основаниях прямые. Следовательно, мы имеем 𝑎 + 1 = 4𝑏 + 2 = 5.и
Мы находим, что 𝑎 = 3𝑏 = 3 и
Теперь мы можем определить площадь большого прямоугольника, образованного всеми боковыми гранями призма, которая задается умножением ее длины на ширину: 𝐴 = 3⋅ (3 + 2 + 4 + 5 + 1 + 3) = 3⋅18 = 54. боковая единица
Нам нужно найти площадь двух оснований. Основание можно увидеть как состоящее из двух прямоугольников, или как прямоугольник длиной 5 и шириной 4, из которого прямоугольник длиной 𝑏 и ширина 𝑎 был удален.Вторым методом находим 𝐴 = 5⋅4−3⋅3 = 11.baseunit
Мы, конечно, можем проверить, что мы находим ту же площадь, добавив площадь двух прямоугольников. изготовление основы, например, 𝐴 = 2⋅4 + 3⋅1𝐴 = 2⋅3 + 5⋅1.basebaseor
Мы действительно находим ту же область, однако мы составляем прямоугольники, чтобы сделать основу.
Чтобы найти общую площадь призмы, нам просто нужно добавить в два раза больше площади призмы. база (потому что есть две базы) к боковой области.Мы находим, что 𝐴 = 2⋅𝐴 + 𝐴 = 2⋅11 + 54 = 76. общая базовая боковая единица
Площадь поверхности призмы составляет 76 единиц.
какова площадь боковой поверхности правой шестиугольной призмы, основание которой представляет собой правильный шестиугольник с длиной сторон 8 дюймов и высотой 6 дюймов
Мне нужно найти площадь и объем правильной правильной шестиугольной призмы.

Мне нужно найти площадь и объем правильной правильной шестиугольной призмы. Высота составляет 10 см, а размеры сторон основания 18 см.Вы округлите до ближайшей сотой.
Основание правильной пирамиды — квадрат, стороны которого имеют длину 8 см.
Основание правильной пирамиды — квадрат, длина сторон которого составляет 8 см. Если боковой край этой пирамиды имеет длину 20 см, какова площадь поверхности пирамиды?
площадь основания треугольной призмы А составляет 15 квадратных дюймов, а высота — 8 дюймов.
площадь основания треугольной призмы A составляет 15 квадратных дюймов, а высота — 8 дюймов.Прямоугольная призма B имеет квадратное основание размером 2 дюйма с каждой стороны. Если присим А и приз В имеют одинаковые объемы, какова должна быть высота присима b?
какова боковая площадь правильной пирамиды с основанием 6 и высотой наклона 8
какова боковая площадь правильной пирамиды с основанием 6 и высотой наклона 8 ?????????????
Какова площадь боковой поверхности прямоугольной призмы с периметром основания 40 сантиметров и высотой 12 сантиметров
Какова площадь боковой поверхности прямоугольной призмы с периметром основания 40 сантиметров и высотой 12 сантиметров? Спасибо Джанет
Сплошная правая пирамида имеет правильное шестиугольное основание с площадью из 7.4 шт 2. …
Сплошная правая пирамида имеет правильное шестиугольное основание с площадью 7,4 шт2. Пирамида имеет высоту 6 единиц. Каков объем пирамиды? 11,1 шт3 14,8 шт3 22,2 шт3 44,4 шт3 co
Боковые края правильной шестиугольной пирамиды имеют длину 20 см, а края основания — 16 см.
Боковые края правильной шестиугольной пирамиды имеют длину 20 см, а края основания — 16 см. С точностью до куб. См, каков объем этой пирамиды? Какова суммарная площадь основания и шести боковых сторон с точностью до квадратного сантиметра?
Площадь боковой поверхности правильной пирамиды составляет 160 см2, а периметр основания — 40 см.
Площадь боковой поверхности правильной пирамиды составляет 160 см2, а периметр основания — 40 см.Какая наклонная высота?
Найдите площадь поверхности правой прямоугольной призмы размером 2 на 3 на 4 фута.
Найдите площадь поверхности правой прямоугольной призмы размером 2 на 3 на 4 фута.
Найдите площадь боковой поверхности одной стороны стены, основание которой лежит на …
Найдите площадь боковой поверхности одной стороны стены, основание которой лежит на части круга 2? + y2 = 16 в квадрантах I, II и III, высота которых задается функцией h (x, y) = 5xy.160
| Определение
Площадь конуса
Мы можем разделить поверхность конуса на две части:
-
A = A (боковой) + A (основание), так как у нас только одно основание, в отличие от цилиндра.
Основание — это снова площадь круга A (основание) = π * r² , но происхождение площади боковой поверхности может быть не так очевидно:
-
A (боковой) = π * r * √ (r² + h²)
Давайте посмотрим на этот шаг за шагом вывод:
- Раскатайте боковую поверхность. Это круговой сектор, который является частью круга с радиусом s ( s — наклонная высота конуса).
- Для окружности с радиусом s, , длина окружности равна
2 * π * s. Длина дуги сектора равна2 * π * r. - Площадь сектора , который является нашей боковой поверхностью конуса, определяется по формуле:
-
A (сбоку) = (s * (длина дуги)) / 2 = (s * 2 * π * r) / 2 = π * r * s
Формула может быть получена из пропорции: отношение площадей фигур такое же, как отношение длины дуги к окружности:
(площадь сектора) / (площадь большого круга) = (длина дуги) / (окружность большого круга) так:
(площадь сектора) / (π * s²) = (2 * π * r) / (2 * π * s)
(площадь сектора) = (π * s²) * (2 * π * r) / (2 * π * s)
- Обычно у нас указывается не
s, аh, что составляет высоты конуса.

 Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье.
Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье. Ответ дайте в градусах. [посмотреть решение]
Ответ дайте в градусах. [посмотреть решение]

Leave A Comment