Как найти Объем Параллелепипеда?

Поможем понять и полюбить математику

Начать учиться

В 5 классе ученики знакомятся с объемными фигурами. Оглянитесь вокруг — мир состоит из параллелепипедов. Так что в любой непонятной ситуации просто ищите их объём. Давай научимся это делать. В статье найдете все необходимые формулы и правила.

Понятие объема

Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.

Объём — это количественная характеристика пространства, занимаемого телом или веществом.

Другими словами, это то, сколько места занимает предмет.

Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.

За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).

Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.

Два свойства объёма


  1. У равных тел равные объёмы. Например, у двух одинаковых пакетов сока равные объемы.

  2. Если геометрическое тело состоит из нескольких геометрических тел, то его объём равен сумме объёмов этих тел.

Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Объем прямоугольного параллелепипеда

Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.

Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.



Формула объема прямоугольного параллелепипеда

Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:

V = a × b × h

Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.

a

длина параллелепипеда

b

ширина параллелепипеда

h

высота параллелепипеда

P (осн)

периметр основания

S (осн)

площадь основания

S (бок)

площадь боковой поверхности

S (п. п.)

площадь полной поверхности

V

объем

Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.


a = 9 см

b = 6 см

h = 3 см

V = a × b × h

V = 9 × 6 × 3 = 162 см3.

Ответ: объем прямоугольного параллелепипеда равен 162 см3.

Следствие

Объем параллелепипеда равен произведению площади основания на высоту.

V = Sосн × h

Из этого следствия выведем формулу нахождения площади основания параллелепипеда.

Sосн = V : h

Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.


V = 96 см3

h = 8 см

V = Sосн × h

Sосн = V : h

Sосн = 82 см3 : 8 см = 12 см2.

Ответ: площадь основания параллелепипеда равна 12 см2.

Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!

Вычисление площади

Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.

Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.

Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:

  • Sб. п. = 2 (ac + bc)

Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:

  • Sп. п. = 2 (ab + ac + bc)

Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.


Sп. п. = 2 (ab + ac + bc)

Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.

Ответ: площадь поверхности параллелепипеда — 108 см2.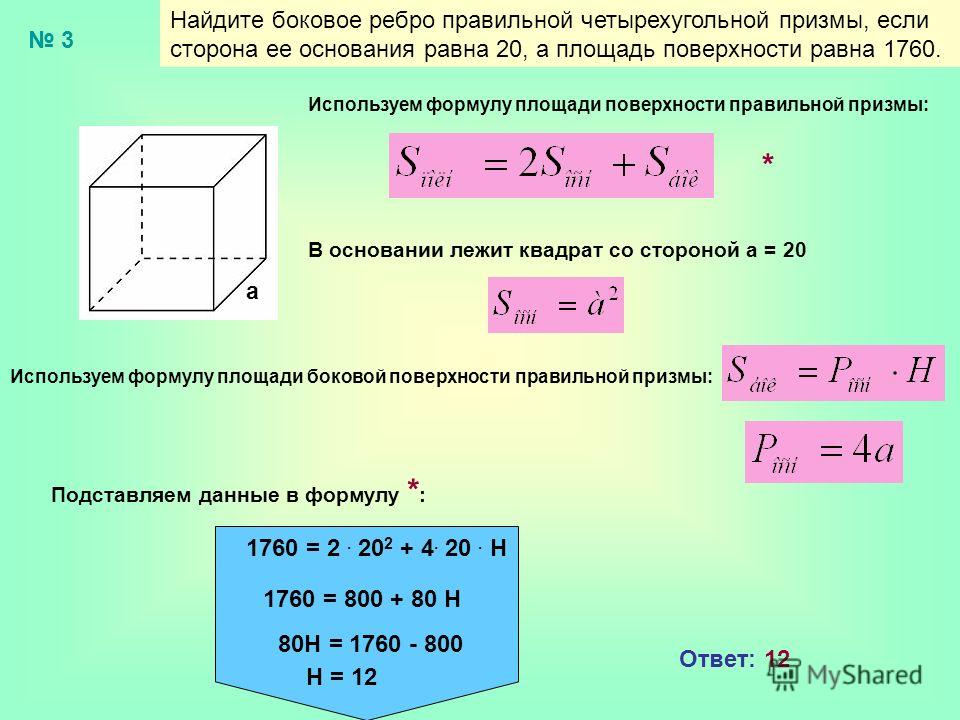

Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.

Задачи на самопроверку

Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.

Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.


Как решаем:

a = 18 см

b = 10 см

h = 7 см

Формула нахождения объема параллелепипеда:

V = a × b × h

Подставляем наши числа:

V = 18 × 10 × 7 = 1260 см3.

Ответ: объём параллелепипеда равен 1260 см3.

Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см3, а высота — 15 см.


Как решаем:

V = 120 см

h = 15 см

V = Sосн × h

Sосн = V : h

Sосн = 120 см3: 15 см = 8 см2.

Ответ: площадь основания параллелепипеда равна 8 см2.

Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.

Как решаем:

Sп. п. = 2 (ab + ac + bc)

Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см

2.

Ответ: площадь полной поверхности параллелепипеда равна 1140 см2.

Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.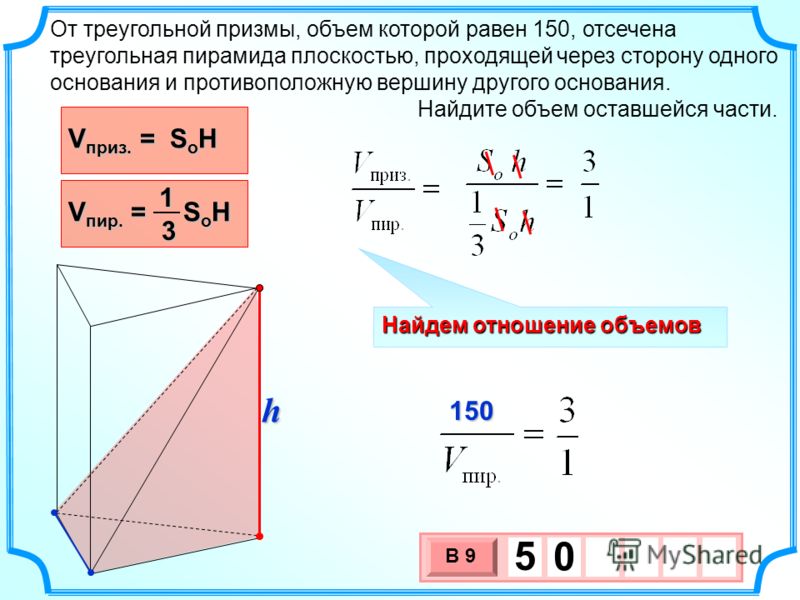

V параллелепипеда

V = a × b × h

 

V = Sосн × h

S боковой поверхности

Sб. п. = 2 (ac + bc)

S полной поверхности

Sп. п. = 2 (ab + ac + bc)

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Анастасия Белова

К предыдущей статье

388.5K

Время, скорость, расстояние

К следующей статье

475. 6K

Порядок действий в математике

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

  1. Выявим пробелы в знаниях и дадим советы по обучению

  2. Расскажем, как проходят занятия

  3. Подберём курс

Формулы объема геометрических фигур

Формулы объема геометрических фигур

Объем геометрической фигуры

— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Навигация по странице: Формулы объема куба Формулы объема призмы Формулы объема параллелепипеда Формулы объема прямоугольного параллелепипеда Формулы объема пирамиды Формулы объема правильного тетраэдра Формулы объема цилиндра Формулы объема конуса Формулы объема шара

Онлайн калькуляторы для вычисления объемов



Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы:

V = So h

где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.

Онлайн калькулятор для расчета объема призмы

Формулы площади геометрических фигур для определения площади основания призмы



Объем прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда:

V = a · b · h

где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.

Смотрите также онлайн калькулятор для расчета объема прямоугольного параллелепипеда


Объем пирамиды

Объем пирамиды равен трети от произведения площади ее основания на высоту.

Формула объема пирамиды:

V = 1 So · h
3

где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.

Онлайн калькулятор для расчета объема пирамиды

Формулы площади геометрических фигур для определения площади основания пирамиды


Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра:

V = π R2 h

V = So h

где V — объем цилиндра,
So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.

Смотрите также онлайн калькулятор для расчета объема цилиндра


Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.

Формулы объема конуса:

V = 1 π R2 h
3

V = 1 So h
3

где V — объем конуса,
So — площадь основания конуса,
R — радиус основания конуса,
h — высота конуса,
π = 3. 141592.

Смотрите также онлайн калькулятор для расчета объема конуса

Все таблицы и формулы

Расчет объема | SkillsYouNeed

На этой странице объясняется, как рассчитать объем твердых предметов, т.е. сколько вы могли бы вместить в предмет, если, например, вы наполнили его жидкостью.

Площадь — это мера того, сколько места находится внутри двухмерного объекта (дополнительную информацию см. на нашей странице: Расчет площади).

Объем — это мера пространства внутри трехмерного объекта. Наша страница о трехмерных фигурах объясняет основы таких фигур.

В реальном мире вычисление объема, вероятно, не будет использоваться так часто, как вычисление площади.

Тем не менее, это может быть важно. Возможность рассчитать объем позволит вам, например, определить, сколько места у вас есть для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете поместить в банку.

Это также может быть полезно для понимания того, что имеют в виду СМИ, когда говорят о мощности плотины или расходе реки.

Примечание по единицам измерения

Площадь выражается в квадратных единицах ( 2 ), поскольку она измеряется в двух измерениях (например, длина × ширина).

Объем выражается в кубических единицах ( 3 ), поскольку он измеряется в трех измерениях (например, длина × ширина × глубина). Кубические единицы включают см3, м3 и кубические футы. Кубические единицы включают 3 см, 3 м и кубические футы.

ВНИМАНИЕ!

Объем также может быть выражен как емкость по жидкости.

Метрическая система

В метрической системе вместимость жидкости измеряется в литрах, что напрямую сравнимо с кубическим измерением, поскольку 1 мл = 1 см 3 . 1 литр = 1000 мл = 1000 см 3 .

Имперская/английская система

В имперской/английской системе эквивалентными единицами измерения являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы.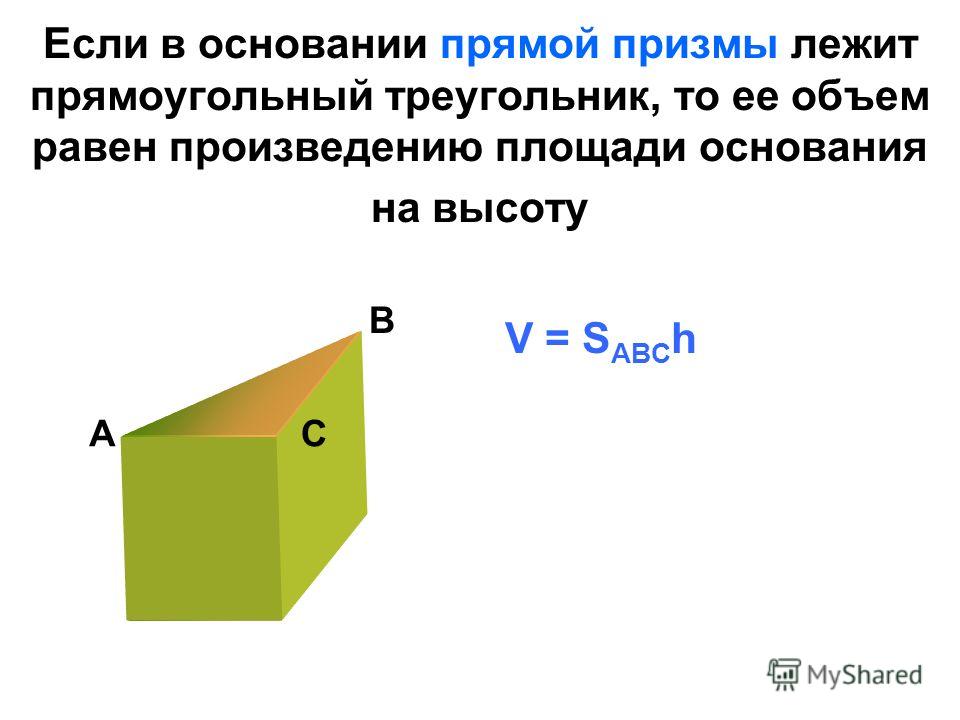 Поэтому лучше всего придерживаться либо жидких, либо твердых единиц объема.

Для получения дополнительной информации см. нашу страницу о системах измерения.

Основные формулы для вычисления объема

Объем тел, основанных на прямоугольниках


В то время как основная формула площади прямоугольной формы — длина × ширина, основная формула объема — длина × ширина × высота.

То, как вы ссылаетесь на различные измерения, не меняет расчет: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются вместе. Вы можете умножать в любом порядке, поскольку это не изменит ответ (см. нашу страницу на умножить на для большего).

Объем коробки шириной 15 см, длиной 25 см и высотой 5 см:
15 × 25 × 5 = 1875 см 3

Объем призм и цилиндров

для покрытия объема цилиндров и призм тоже. Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.

Фактически, для цилиндров и призм объем равен площади одной стороны, умноженной на глубину или высоту формы.

Таким образом, основная формула для объема призм и цилиндров:

Площадь торца × высота/глубина призмы/цилиндра.

Остерегайтесь несовместимых единиц!

Прямой отрезок круглой трубы имеет внутренний диаметр 2 см и длину 1,7 м. Рассчитайте объем воды в трубе.

В этом примере вам нужно рассчитать объем очень длинного тонкого цилиндра, образующего внутреннюю часть трубы. Площадь одного конца можно рассчитать по формуле площади круга πr 2 . Диаметр 2см, значит радиус 1см. Таким образом, площадь равна π × 1 2 , что составляет 3,14 см 2 .

Длина трубы 1,7 м, поэтому вам нужно умножить площадь конца на длину, чтобы найти объем.

Остерегайтесь несовместимых юнитов! Площадь в сантиметрах, а длина в метрах. Сначала преобразуйте длину в см 1,7 × 1000 = 1700 см.

Таким образом, объем равен 3,14 × 1700 = 5338 см 3 . Это эквивалентно 5,338 литра или 0,0053 м 3 .

Объем конусов и пирамид

Тот же принцип, что и выше (ширина × длина × высота), применяется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они сходятся в точке, объем составляет лишь долю сумма, которая была бы, если бы они продолжали иметь ту же форму (поперечное сечение) насквозь.

Объем конуса или пирамиды составляет ровно одну треть объема коробки или цилиндра с таким же основанием.

Таким образом, формула выглядит следующим образом:

Площадь основания или торца × высота конуса/пирамиды × 1 / 3

Вернитесь к нашей странице 05

Расчет площади 900 не может вспомнить, как вычислить площадь круга или треугольника.

Например, чтобы рассчитать объем конуса с радиусом 5 см и высотой 10 см:

Площадь внутри круга = πr 2 (где π (пи) приблизительно равно 3,14, а r – радиус круг).

В этом примере площадь основания (круга) = πr 2 = 3,14 × 5 × 5 = 78,5 см 2 .

78,5 × 10 = 785

785 × 1/3 = 261,6667см 3

Объем сферы

Формула 4/3 × π × радиус 3 .

Вам может быть интересно, как можно вычислить радиус мяча. Если не считать протыкания вязальной спицы (эффективно, но смертельно для мяча!), есть более простой способ.

Расстояние вокруг самой широкой точки сферы можно измерить напрямую, например, рулеткой. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.

Длина окружности рассчитывается как 2 x π x радиус.

Чтобы вычислить радиус по длине окружности:

Разделите длину окружности на (2 x π) .

Примеры работы: Расчет объема


Расчет объема неправильных тел

Точно так же, как вы можете рассчитать площадь неправильных двумерных фигур, разбив их на правильные, вы можете сделать то же самое для расчета объема неправильных тел. Просто разделите тело на более мелкие части, пока не получите только многогранники, с которыми вам будет легко работать.


Дальнейшее чтение из книги «Навыки, которые вам нужны»

Понимание геометрии
Часть руководства «Навыки, которые вам необходимы для счета»

В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства форм, линий и твердых тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.

Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.

В заключение…

Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем почти всего в вашей жизни, будь то упаковочный ящик, комната или водяной цилиндр.

Как найти объем, используя площадь и высоту?

Измерение — это часть математики, которая занимается изучением различных геометрических фигур, их площадей и объемов. Проще говоря, измерение — это все об измерении. Измерение различных размеров тела и расчет площади, площади поверхности и объема изучаются при измерении.

Объем

Объем определяется как трехмерное пространство, которое закрыто или ограничено объектом. Нахождение объема объекта может помочь нам определить количество, необходимое для заполнения объекта, например, количество воды, необходимое для заполнения бутылки, бассейна или резервуара для воды. Объем объекта оценивается в кубических единицах, таких как кубические сантиметры, кубический дюйм, кубический фут, кубический метр и т. д.

Объем большинства объектов можно легко рассчитать, зная площадь основания и высоту, даже сложных. Сложные объекты можно разделить на более простые фигуры, и, таким образом, сложив объемы этих более простых фигур, можно суммировать, чтобы получить объем всего объекта.

Как найти объем, используя площадь и высоту?

Чтобы найти объем данного объекта, это можно сделать следующими способами:

  1. Найти площадь основания
  2. Умножить площадь основания на соответствующую высоту.

Вычисление объема некоторых знакомых фигур,

Куб

Куб — это трехмерный объект, имеющий шесть конгруэнтных квадратных граней. Размеры всех шести квадратных граней куба одинаковы. Кубу редко также приписывают правильный шестигранник или квадратную призму.

Площадь основания куба = сторона × сторона

Высота куба = сторона

Объем куба = площадь основания × высота = сторона 3

Прямоугольник

3 трехмерная твердая фигура, имеющая шесть граней, восемь вершин и 12 ребер. Это одна из распространенных форм вокруг нас, которая имеет три измерения: длину, ширину и высоту.

Площадь основания прямоугольного параллелепипеда = длина × ширина

Высота прямоугольного параллелепипеда = глубина

Объем прямоугольного параллелепипеда = площадь основания × высота = длина × ширина × глубина

Цилиндр

круглые основания, ограниченные изогнутой поверхностью на точном расстоянии от центра.