Шар в заданиях ЕГЭ — презентация онлайн
Шарв заданиях
ЕГЭ
2. Содержание
Задача №1Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
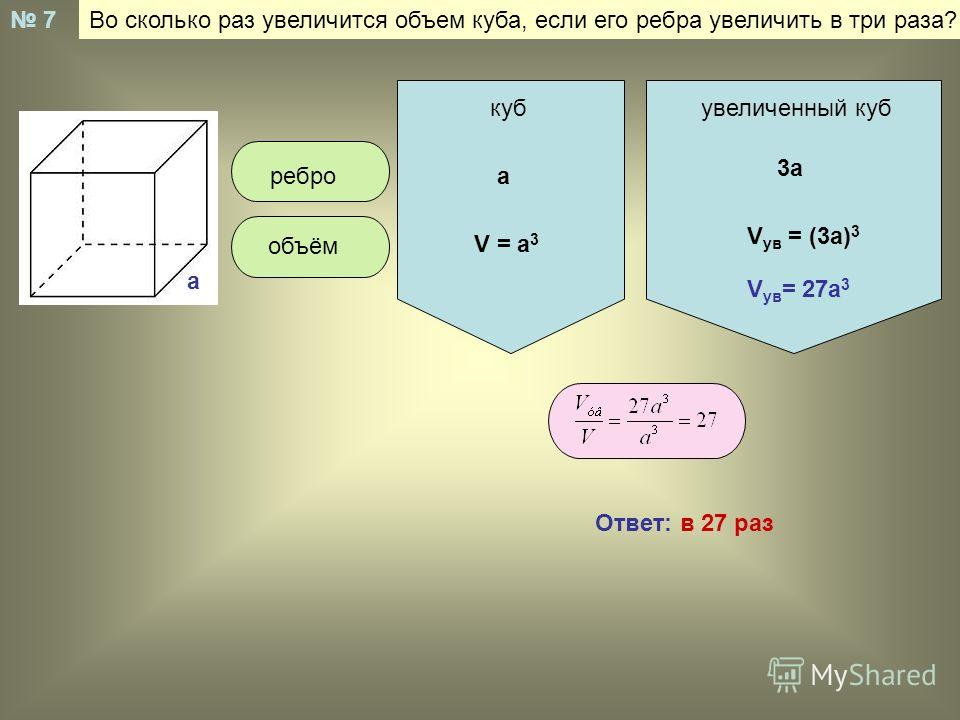
Задача №7
• Задачи
Задача №8
Задача №9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №`4
Задача №15
Задача №16
Задача №17
Задача №18
для самостоятельного решения
3. Задача №1
Площадь большого круга шара равна 3. Найдите площадьповерхности шара
Радиус большого круга является радиусом шара.
Площадь
первого
выражается
через
радиус
как
Skp.=πR², а площадь
поверхности сферы – как Sш.= 4πR². Видно, что
площадь поверхности шара в
4 раза больше
площади поверхности большого круга. Значит
Sш.= 4·3 = 12
4. Задача №2
Во сколько раз увеличится площадь поверхности шара,если радиус шара увеличить в 2 раза?
Площадь
поверхности
шара
выражается
через
его
радиус
формулой Sш.

увеличении радиуса вдвое площадь
увеличится в 22 = 4 раза.
5. Задача №3
Во сколько раз увеличится объем шара, если его радиусувеличить в три раза?
Т.к. объём шара вычисляется по формуле:
V = 4/3·π·r³, то
при увеличении радиуса втрое, объем
шара увеличится в 27 раз.
6. Задача №4
Объем одного шара в 27 раз больше объема второго. Восколько раз площадь поверхности первого шара больше
площади поверхности второго?
Решение. 1) Объемы шаров соотносятся как
V1:V2= R1³: R2³= (R1/R2)³=27 => R1/R2 =3
2) Площади их поверхностей соотносятся как
7. Задача №5
Даны два шара. Диаметр первого шара в 8 раз большедиаметра второго. Во сколько раз площадь поверхности
первого шара больше площади поверхности второго?
S1:S2= R1²: R2²= (R1/R2)²=(d1/d2)²=8²=64
8. Задача №6
Однородный шар диаметром 3 см имеет массу 162 грамма.Чему равна масса шара, изготовленного из того же
материала, с диаметром 2 см? Ответ дайте в граммах.

Масса шара прямо пропорциональна
его объёму. Объёмы шаров относятся
как кубы их радиусов:
V1:V2= R1³: R2³= (R1/R2)³= (d1/d2)²=(2/3)³=8/27
= m1/m2
Следовательно, масса
второго,
меньшего
шара
равна
9. Задача №7
Даны два шара с радиусами 8 и 4. Во сколько раз площадьповерхности первого шара больше площади поверхности
второго?
Решение. Т.к. Площадь поверхности шара вычисляется по
формуле: S = 4π·r², то
1) Найдём площадь поверхности первого шара: 256π
2) Найдём площадь поверхности второго шара: 64π
3) Найдём отношение площадей:
256π : 64π = 4
10. Задача №8
Даны два шара с радиусами 2 и 1. Во сколько раз объёмпервого шара больше объёма второго?
Решение. Т.к. объём шара вычисляется по формуле:
V = 4/3·π·r³, то
1) Найдём объём первого шара: 4/3·8π
3) Найдём отношение объёмов: 4/3·8π : 4/3·π = 8
11.
 Задача №9 Шар, объём которого равен 6π, вписан в куб. Найдите
Задача №9 Шар, объём которого равен 6π, вписан в куб. Найдитеобъём куба.
Ребро куба равно двум радиусам вписанного
в куб шара, поэтому объем куба,
выраженный через радиус вписанного в него
шара, находится по формуле Vk.=(2R)³= 8R³
Объём шара вычисляется по формуле
V= 4/3·πR³ и это равно 6π.
Значит 4/3·πR³= 6π => R³=18π/4π =9/2.
Тогда Vk.= 8R³= 8·(9/2)=36
12. Задача №10
В куб с ребром 3 вписан шар. Найдите объем этого шара,деленный на π .
Радиус вписанного в куб шара равен
половине длины ребра:
R=a:2=3:2=1,5
3
4 27
9
V R 4,5
3
3 2
3 8
2
13. Задача №11
Объем шара равен 288π. Найдите площадь егоповерхности, деленную на π .
Из формулы объёма шара V = 4/3·π·r³
выразим радиус и вычислим его:
3
V
3
288
R 3
3
6
4
4
Тогда площадь поверхности шара будет равна
S = 4π·r² = 4π·36=144π
14.
 Задача №12 Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара,
Задача №12 Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара,объем которого равен сумме их объемов.
Объёма шара V = 4/3·π·r³
Поэтому cумма объёмов трёх шаров равна
4
4
4
4
3
3
3
6 8 10 (6 3 8 3 10 3 )
3
3
3
3
4
4
4
3
3
3
3
3
2 (3 4 5 ) 2 6 12 3
3
3
3
Значит искомый радиус равен 12.
15. Задача №13
Около куба с ребром √3 описан шар. Найдите объемэтого шара, деленный на π .
Пусть длина ребра куба равна а, а его
диагональ равна d. Радиус описанного
шара R равен половине диагонали куба:
1
1
1
3
R d a 3
3 3
2
2
2
2
3
4 3 4 3
9
V R
3
3 2
2
Ответ: 4,5
16. Задача №14
Радиусы двух шаров равны 6, 8. Найдите радиус шара,площадь поверхности которого равна сумме площадей их
поверхностей.
Из условия S3=S1+S2 и S = 4π·r²
найдём
4 R 4 R 4 R
2
3
2
1
2
2
R3 R R 36 64 10
1
2
2
17.
 Задача №15 Вершина А куба ABCDA1B1C1D1 со стороной 1,6 является
Задача №15 Вершина А куба ABCDA1B1C1D1 со стороной 1,6 являетсяцентром сферы, проходящей через точку A1. Найдите
площадь S части сферы, содержащейся внутри куба. В
ответе запишите величину S/π .
Решение. Так как одна из вершин куба является центром
сферы с радиусом, меньшим либо равным стороне куба,
в кубе содержится 1/8 сферы и, соответственно, 1/8 ее
поверхности, равная
1
1
2
2
S 4 R 1,6 1,28
8
8
2
18. Задача №16
Середина ребра куба со стороной 1,9 является центромшара радиуса 0,95. Найдите площадь S части поверхности
шара, лежащей внутри куба. В ответе запишите S/π .
Решение.
диаметр которой равен ребру куба, в кубе содержится 1/4 сферы
и, соответственно, 1/4 ее поверхности.
1
1
2
2
S 4 R 0,95 0,9025
4
4
19. Задача №17
Конус вписан в шар. Радиус основания конуса равен радиусушара.
 Объем конуса равен 6. Найдите объем шара.
Объем конуса равен 6. Найдите объем шара.1
1 2
Vk. Soc. h R R 6
3
3
4 3
Vш. R 24
3
20. Задача №18
Куб вписан в шар радиуса √3 . Найдите объем куба.Диаметр шара, описанного вокруг куба,
совпадает с его диагональю и вдвое
равна 2√3. Если ребро куба равно а, то
диагональ
куба
вычисляется
по
формуле d=a√3. Следовательно, ребро
куба равно 2, а его объем равен 8.
Задачи
для самостоятельного
решения
22. Задача №1 Решите самостоятельно
1) Площадь большого круга шара равна 41. Найдитеплощадь поверхности шара.
Ответ: 164
2) Площадь большого круга шара равна 10. Найдите
площадь поверхности шара
3) Площадь большого круга шара равна 26. Найдите
площадь поверхности шара
23. Задача №2 Решите самостоятельно
1) Во сколько раз увеличится площадь поверхности шара,если радиус шара увеличить в 45 раз?
Ответ: 2025
если радиус шара увеличить в 16 раз?
3) Во сколько раз увеличится площадь поверхности шара,
если радиус шара увеличить в 1,5 раза?
24.
 Задача №3 Решите самостоятельно 1) Во сколько раз увеличится объем шара, если его радиус
Задача №3 Решите самостоятельно 1) Во сколько раз увеличится объем шара, если его радиусувеличить в 10 раз?
2) Во сколько раз увеличится объем шара, если его радиус
увеличить в 4 раза?
3) Во сколько раз увеличится объем шара, если его радиус
увеличить в 15 раз?
25. Задача №4 Решите самостоятельно
Задача №4 Решите1)
самостоятельно
Объем одного шара в 2197 раз больше объема второго. Во
сколько раз площадь поверхности первого шара больше
площади поверхности второго?
Ответ: 169
2) Объем одного шара в 1331 раз больше объема второго. Во
площади поверхности второго?
3) Объем одного шара в 1000 раз больше объема второго. Во
сколько раз площадь поверхности первого шара больше
площади поверхности второго?
26. Задача №6 Решите самостоятельно
1) Однородный шар диаметром 3 см имеет массу 81грамма. Чему равна масса шара, изготовленного из того
же материала, с диаметром 5 см? Ответ дайте в
граммах.

Ответ:375
27. Задача №7 Решите самостоятельно
1) Даны два шара с радиусами 5 и 1. Во сколько разплощадь поверхности первого шара больше площади
поверхности второго?
2) Даны два шара с радиусами 3 и 1. Во сколько раз
площадь поверхности первого шара больше площади
поверхности второго?
Ответ: 9
3) Даны два шара с радиусами 14 и 2. Во сколько раз
площадь поверхности первого шара больше площади
поверхности второго?
Ответ: 49
28. Задача №8 Решите самостоятельно
1) Даны два шара с радиусами 4 и 1. Во сколько раз объёмпервого шара больше объёма второго?
Ответ: 64
29. Задача №10 Решите самостоятельно
1) В куб с ребром 21 вписан шар. Найдите объем этогошара, деленный на π .
2) В куб с ребром 9 вписан шар. Найдите объем этого
шара, деленный на π .
3) В куб с ребром 18 вписан шар. Найдите объем этого
шара, деленный на π .
30. Задача №11 Решите самостоятельно
1) Объем шара равен 18 432 π. Найдите площадь его
Найдите площадь егоповерхности, деленную на π .
2) Объем шара равен 12 348π. Найдите площадь его
поверхности, деленную на π .
3) Объем шара равен 26.244π. Найдите площадь его
поверхности, деленную на π .
4) Объем шара равен 972π. Найдите площадь его
поверхности, деленную на π .
31. Задача №12 Решите самостоятельно
1) Радиусы трех шаров равны 2, 12 и 16. Найдите радиусшара, объем которого равен сумме их объемов.
Ответ:18
2) Радиусы трех шаров равны 1, 6 и 8. Найдите радиус
шара, объем которого равен сумме их объемов.
3) Радиусы трех шаров равны 15, 20 и 25. Найдите радиус
шара, объем которого равен сумме их объемов.
32. Задача №13 Решите самостоятельно
1) Около куба с ребром √243 описан шар. Найдитеобъем этого шара, деленный на π . Ответ:
2) Около куба с ребром √300 описан шар. Найдите
объем этого шара, деленный на π .
3) Около куба с ребром √507 описан шар. Найдите
объем этого шара, деленный на π .

33. Задача №14 Решите самостоятельно
1) Радиусы двух шаров равны 21, 72. Найдите радиусшара, площадь поверхности которого равна сумме
площадей их поверхностей.
Ответ: 75
2) Радиусы двух шаров равны 8, 15. Найдите радиус шара,
площадь поверхности которого равна сумме площадей
их поверхностей.
3) Радиусы двух шаров равны 32, 60. Найдите радиус
шара, площадь поверхности которого равна сумме
площадей их поверхностей.
34. Задача №15 Решите самостоятельно
1) Вершина А куба ABCDA1B1C1D1 со стороной 1,2 являетсяцентром сферы, проходящей через точку A1. Найдите
площадь S части сферы, содержащейся внутри куба. В ответе
запишите величину S/π .
2) Вершина А куба ABCDA1B1C1D1 со стороной 0,7 является
центром сферы, проходящей через точку A1. Найдите
площадь S части сферы, содержащейся внутри куба. В ответе
запишите величину S/π .
3) Вершина А куба ABCDA1B1C1D1 со стороной 0,9 является
центром сферы, проходящей через точку A1.
 Найдите
Найдитеплощадь S части сферы, содержащейся внутри куба. В ответе
запишите величину S/π .
35. Задача №16 Решите самостоятельно
1) Середина ребра куба со стороной 1,8 является центромшара радиуса 0,8. Найдите площадь S части
поверхности шара, лежащей внутри куба. В ответе
запишите S/π .
2) Середина ребра куба со стороной 2,4 является центром
шара радиуса 1,2. Найдите площадь S части
поверхности шара, лежащей внутри куба. В ответе
запишите S/π .
36. Задача №17 Решите самостоятельно
1) Конус вписан в шар. Радиус основания конуса равенрадиусу шара. Объем конуса равен 27. Найдите объем
шара.
2) Конус вписан в шар. Радиус основания конуса равен
радиусу шара. Объем конуса равен 45. Найдите объем
шара.
3) Конус вписан в шар. Радиус основания конуса равен
радиусу шара. Объем конуса равен 12√3. Найдите
объем шара.
37. Задача №18 Решите самостоятельно
Задача №18 Решите1)
2)
3)
4)
самостоятельно
Куб вписан в шар радиуса 0,5√3 .
 Найдите объем
Найдите объемкуба.
Ответ: 1
Куб вписан в шар радиуса 10,5√3 . Найдите объем
куба.
Куб вписан в шар радиуса 8√3 . Найдите объем
куба.
Куб вписан в шар радиуса 15,5√3 . Найдите объем
куба.
38. Используемые ресурсы
• Шаблон подготовилаучитель русского языка и литературы
Тихонова Надежда Андреевна
• «Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ.
Режим доступа: http://mathb.reshuege.ru
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
Автор и источник заимствования неизвестен
http://www.ourcity.ru/images/art/img_big_1274700246.jpg
http://oboi.ucoz.de/_ph/4/980025544.jpg
http://gym1517.narod.ru/awg/d55.jpg
Зачет по теме «Объем шара» Вариант1 1. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза? | Зачет по теме «Объем шара» Вариант2 1. |
2. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов. | 2. Радиусы трех шаров равны 1, 6 и 8. Найдите радиус шара, объем которого равен сумме их объемов. |
3. В куб с ребром 18 вписан шар. Найдите объем этого шара, деленный на π. | 3. В куб с ребром 21 вписан шар. Найдите объем этого шара, деленный на π. |
4. Около куба с ребром описан шар. Найдите объем этого шара, деленный на π. | 4Около куба с ребром описан шар. Найдите объем этого шара, деленный на π. |
5. Объем одного шара в 1331 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго? | 5. |
6. Объем шара равен 288 . Найдите площадь его поверхности, деленную на π. | 6. Объем шара равен 972 . Найдите площадь его поверхности, деленную на π. |
7. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 27. Найдите объем шара. | 7. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 12. Найдите объем шара. |
8.Две параллельные плоскости, расстояние между которыми 2, пересекают шар. Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,84. Найдите объем шара. | 8. Две параллельные плоскости, расстояние между которыми 4, пересекают шар. |
Зачётная работа №6 (геометрия)
1. Задание 8 № . Пожарную лестницу длиной 13 м приставили к окну дома (см. рисунок). Нижний конец лестницы отстоит от стены дома на 5 м. На какой высоте расположено окно? Ответ дайте в метрах.
2. Задание 8 . Диагональ прямоугольного телевизионного экрана равна 100 см, а ширина экрана – 80 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
3. Задание 8 . Прямоугольный участок земли имеет стороны 35 и 45 м. Короткой стороной участок примыкает к стене дома. Найдите длину забора, которым нужно огородить оставшуюся часть границы участка (в метрах).
4. Задание 8 Колесо имеет 25 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
5. Задание 8 № Дачный участок имеет форму прямоугольника со сторонами 25 метров и 15 метров. Хозяин планирует обнести его изгородью и отгородить такой же изгородью квадратный участок со стороной 8 м (см. рис.). Найдите суммарную длину изгороди в метрах.
6. Задание8. Два садовода, имеющие прямоугольные участки размерами 20 м на 30 м с общей границей, договорились и сделали общий круглый пруд площадью 140 квадратных метров (см. чертёж), причём граница участков проходит точно через центр пруда. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
7. Задание 8 Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил относительно земли равна 1,4 м, а наибольшая h2 равна 2,4 м. Ответ дайте в метрах.
Ответ дайте в метрах.
8. Задание 8 Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота перил h1 равна 1,65 м, а наибольшая высота h2 равна 2,65 м. Ответ дайте в метрах.
9. Задание 8 Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил относительно земли равна 2,1 м, а наибольшая h2 равна 3,1 м. Ответ дайте в метрах.
10. Задание 8 . Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 16 : 00 ?
11. Задание 8 Два садовода, имеющие прямоугольные участки размерами 25 м на 30 м с общей границей, договорились и сделали общий прямоугольный пруд размером 10 м на 15 м (см. чертёж), причём граница участков проходит точно через центр. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
чертёж), причём граница участков проходит точно через центр. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
12. Задание 8 Дачный участок имеет форму прямоугольника со сторонами 20 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите общую длину забора в метрах.
13. Задание 8 План местности разбит на клетки. Каждая клетка обозначает квадрат 1м × 1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
14. Задание 8 Колесо имеет 5 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
15. Задание 8 Диагональ прямоугольного телевизионного экрана равна 60 см, а ширина экрана ― 48 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
16. Задание 8 . Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота h горки равна 3,2 м. Ответ дайте в метрах.
17. Задание 8 . Прямоугольный участок земли имеет стороны 28 и 40 м. Короткой стороной участок примыкает к стене дома. Найдите длину забора, которым нужно огородить оставшуюся часть границы участка (в метрах).
18. Задание 8 . Строители огораживают место для проведения работ забором. Забор имеет форму прямоугольника со сторонами 18 м и 16 м. Причём необходимо оставить проёмы в заборе для проезда машин. Проездов четыре, каждый шириной 2 м. Найдите общую длину забора.
19. Задание 8 . Детская горка укреплена вертикальным столбом, расположенным посередине спуска. Найдите высоту l этого столба, если высота h горки равна 2 метрам. Ответ дайте в метрах.
Ответ дайте в метрах.
20. Задание 8 . Квартира состоит из комнаты, кухни, коридора и санузла. Кухня имеет размеры 3 м на 3,5 м, санузел — 1 на 1,5 м, длина коридора — 5,5 м. Найдите площадь комнаты. Ответ запишите в квадратных метрах.
21. Задание 13 . Найдите угол прямоугольного параллелепипеда, для которого , , . Ответ дайте в градусах.
22. Задание 13 . Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна . Найдите радиус сферы.
23. Задание 13 . Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
24. Задание 13 . Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.
25. Задание 13 . Сторона основания правильной треугольной призмы ABCA1B1C1 равна 3, а высота этой призмы равна Найдите объём призмы ABCA1B1C1.
Задание 13 . Сторона основания правильной треугольной призмы ABCA1B1C1 равна 3, а высота этой призмы равна Найдите объём призмы ABCA1B1C1.
26. Задание 13 . Найдите объем многогранника, вершинами которого являются точки , , , , , , , правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2.
27. Задание 13 . Площадь боковой поверхности цилиндра равна 14 , а диаметр основания равен 2. Найдите высоту цилиндра.
28. Задание 13 Найдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
29. Задание 13 . В правильной треугольной призме , все ребра которой равны 3, найдите угол между прямыми и . Ответ дайте в градусах.
Ответ дайте в градусах.
30. Задание 13 Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 3, а боковые ребра равны и наклонены к плоскости основания под углом 30 .
31. Задание 13 Диаметр основания конуса равен 42, а длина образующей равна 75. Найдите высоту конуса.
32. Задание 13 Объем одного шара в 2197 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
33. Задание 13 . Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
34. Задание 13 Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найдите площадь полной поверхности цилиндра.
35. Задание 13 . Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .
Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .
36. Задание 13 Найдите тангенс угла многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
37. Задание 13 № 284355. В правильной треугольной пирамиде медианы основания пересекаются в точке . Площадь треугольника равна , . Найдите объем пирамиды.
38. Задание 13 Плоскость, проходящая через три точки и разбивает правильную треугольную призму на два многогранника. Сколько вершин у многогранника, у которого меньше граней?
39. Задание 13 . Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамидыSABCDEF, равен 23. Найдите объем шестиугольной пирамиды.
40. Задание 13 . Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
41. Задание 15 . В треугольнике угол равен 90°, . Найдите .
42. Задание 15 . Найдите ординату точки пересечения прямых, заданных уравнениями 3x + 2y = 6 и y = −x.
43. Задание 15 . Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен . Найдите меньшее основание.
44. Задание15. Точки O(0; 0), B(8; 2), C(2; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.
45. Задание 15 . Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
46. Задание 15 . Найдите косинус угла . В ответе укажите значение косинуса, умноженное на .
47. Задание 15 В треугольнике угол равен , угол равен . , и – высоты, пересекающиеся в точке . Найдите угол . Ответ дайте в градусах.
48. Задание 15 Какого радиуса должна быть окружность с центром в точке P(8; 6), чтобы она касалась оси абсцисс?
49. Задание15. В треугольнике ABC угол ACBравен 90°, cos A = 0,8, AC = 4. Отрезок CH — высота треугольника ABC (см. рисунок). Найдите длину отрезка AH.
50. Задание 15 На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
51. Задание 15 К окружности, вписанной в треугольникABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
52. Задание 15 . В тупоугольном треугольнике , – высота, . Найдите .
Найдите .
53. Задание 15 . В треугольнике угол равен 90°, . Найдите тангенс внешнего угла при вершине .
54. Задание 15 . На окружности радиуса 3 взята точка С . Отрезок АВ — диаметр окружности, . Найдите ВС.
55. Задание 15 . Меньшая сторона прямоугольника равна 6, диагонали пересекаются под углом . Найдите диагонали прямоугольника.
56. Задание 15 . Стороны четырехугольника , , и стягивают дуги описанной окружности, градусные величины которых равны соответственно , , , . Найдите угол этого четырехугольника. Ответ дайте в градусах.
57. Задание 15 № 55453.
Средняя линия и высота трапеции равны соответственно 28 и 4. Найдите площадь трапеции.
58. Задание 15 . На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.
Найдите длину его высоты, опущенной на сторону AB.
59. Задание 15 . Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
60. Задание 15 . Точки O(0; 0), A(6; 8), B(6; 2) и C являются вершинами параллелограмма. Найдите ординату точки C.
61. Задание 16 . Два ребра прямоугольного параллелепипеда равны 6 и 4, а объём параллелепипеда равен 240. Найдите площадь поверхности этого параллелепипеда.
62. Задание 16 . Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .
63. Задание 16 Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
64. Задание 16 .
Два ребра прямоугольного параллелепипеда равны 8 и 5, а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
65. Задание 16 . Сторона основания правильной четырехугольной пирамиды равна 4, а боковое ребро равно Найдите объем пирамиды.
66. Задание 16 . Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
67. Задание 16
В правильной четырёхугольной пирамиде SABCD высота SO равна 13, диагональ основания BD равна 8. Точки К и М — середины рёбер CD и ВСсоответственно. Найдите тангенс угла между плоскостью SMK и плоскостью основания ABC.
68. Задание 16 . В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 2, а гипотенуза равна Найдите объём призмы, если её высота равна 3.
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 2, а гипотенуза равна Найдите объём призмы, если её высота равна 3.
69. Задание 16 . Объём конуса равен 32. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
70. Задание 16 . Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
71. Задание 16 Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 5 и 7. Найдите его площадь поверхности.
72. Задание 16 . Объем шара равен 288 . Найдите площадь его поверхности, деленную на .
Объем шара равен 288 . Найдите площадь его поверхности, деленную на .
73. Задание 16 № 271811. Найдите угол прямоугольного параллелепипеда, для которого , , . Ответ дайте в градусах.
74. Задание 16 Объем прямоугольного параллелепипеда равен 162. Площадь одной его грани равна 18. Найдите ребро параллелепипеда, перпендикулярное этой грани.
75. Задание 16 . Даны два шара с радиусами 8 и 4. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
76. Задание 16 № 315131. В прямоугольном параллелепипеде ребро , ребро , ребро . Точка — середина ребра Найдите площадь сечения, проходящего через точки и .
77. Задание 16 . Два ребра прямоугольного параллелепипеда равны 8 и 5, а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
78. Задание 16 . Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
79. Задание 16 . Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите .
80. Задание 16 . В правильной четырёхугольной пирамиде все рёбра равны 1. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
Эколого-экономическая оценка необходимости извлечения донных отложений оз. Нюдъявр Мончегорского района Мурманской области
Вестник МГТУ, том 14, №4, 2011 г. стр.884-891
891
очистки вод, сбрасываемых в оз. Имандра. Нерастворимая фаза, конгломерированная в частицы
различных размеров, может находиться в водной толще достаточно длительное время, и для их
осаждения необходимо время и специфические условия. На эффективность осаждения взвесей
отрицательное влияние оказывает турбулентность потока, особенно в зимний период, когда за счет
промерзания резко сокращается толщина и, соответственно, объем водного слоя.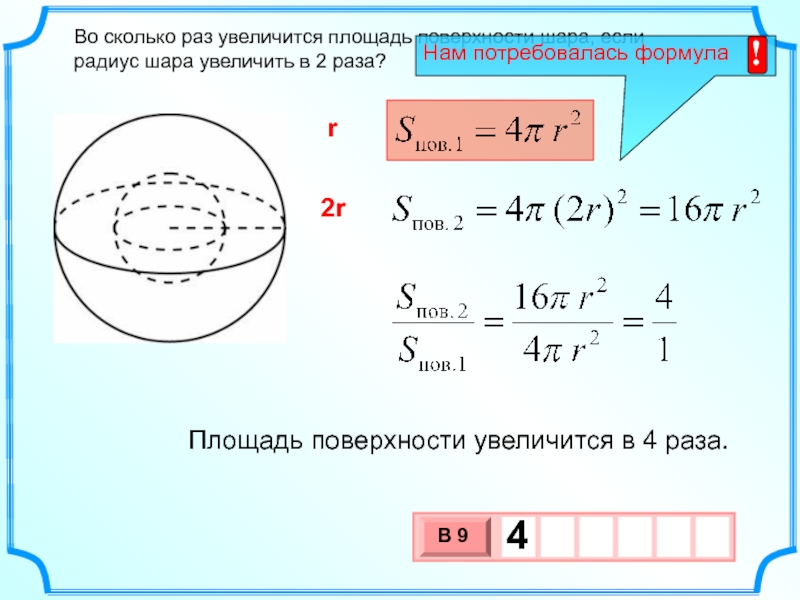 Проведенный анализ
Проведенный анализ
концентраций ряда веществ вдоль поперечного разреза в северной части оз. Нюдъявр в зимний период
показывает наличие четко выраженных русловых явлений. Воды, сбрасываемые через трубы перетока,
напрямую транспортируются к истоку р. Нюдуай и сбрасываются в оз. Имандра. Быстрое прохождение в
оз. Нюдъявр и высокая турбулентность потока не дают возможности отстаиваться нерастворимой фазе.
Препятствием служит и минимальный объем водной массы. Приведенные факторы позволяют
утверждать: любые рекомендуемые сегодня мероприятия по снижению содержания вредных веществ в
воде малорезультативны. Эффекты вторичного загрязнения вод веществами, накопленными в ДО, будут
превышать эффекты по снижению их содержания в воде.
Проведенные исследования показали: на сегодняшний день емкость оз. Нюдъявр по накоплению
техногенных ДО достигла своего предела. Самоочищающие возможности водоема полностью
исчерпаны.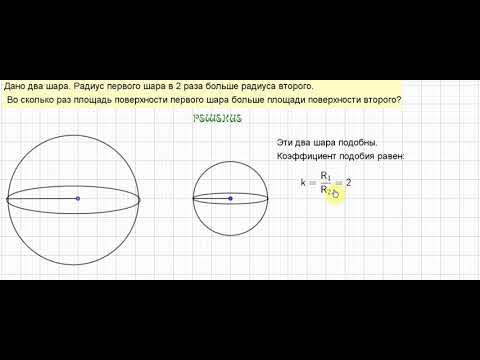
Решение данной проблемы мы видим в проведении ряда мероприятий по извлечению
накопленных ДО, изменению расположения и формы выпуска, структуризации внутриводоемного
пространства фильтрующими дамбами и созданию фильтро-сорбционного каскада в долине р. Нюдуай.
Опасность взмучивания донных отложений во время строительства исключается проведением
первоначального строительства системы выпускных фильтрующих дамб и извлечения ДО. Для их
добычи рекомендуется гидронасосный способ.
Реализация такого комплекса мер позволит очистить дно озера, увеличить объем водной массы,
избавиться от источника вторичного загрязнения, создать условия для эффективного осаждения
нерастворимой фазы. Учитывая значительность запасов металлов, накопленных в ДО, проведение
данных мероприятий даст не только ощутимый экологический эффект, но и существенную
экономическую выгоду.
Литература
Håkanson L.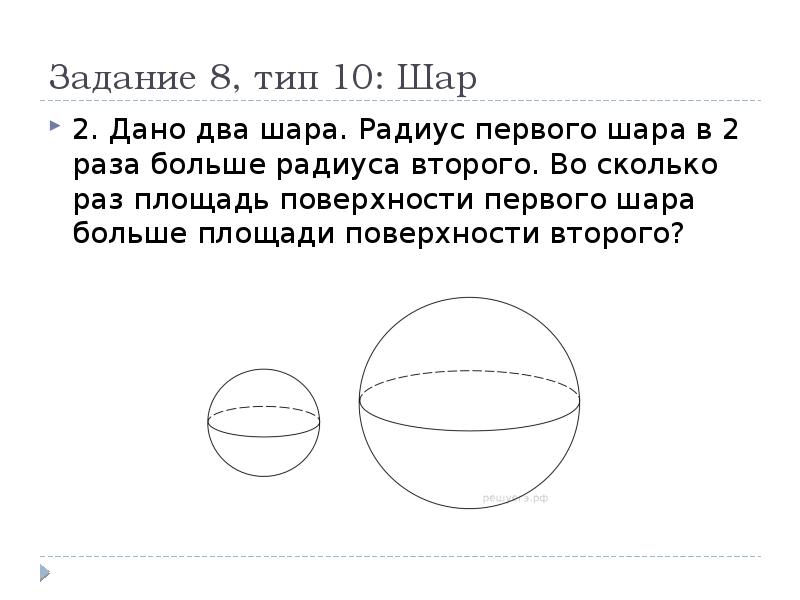 An ecological risk index for aquatic pollution control – a sedimentological approach. Water Res.,
An ecological risk index for aquatic pollution control – a sedimentological approach. Water Res.,
v.14, p.975-1001, 1980.
Pozniakov V.Ya. The «Severonickel» smelter complex: History of development. In: Aerial pollution in Kola
Peninsula. Eds. Kozlov M.V., Haukioja E., Yarmishko V.T. Proceedings of the International Workshop.
April 14-16, 1992, Saint-Petersburg, p.16-19, 1993.
Skogheim O.K. Rapport fra Arungenprosjectet. Oslo, As-NLH, N 2, 7 p., 1979.
Standard method for examination for water and wastewater. 14
th
edition, ALHA-AWWA-WPCF. Washington,
American Public Health Association, 1195 p., 1975.
Алекин О.А. Основы гидрохимии. Л., Гидрометеоиздат, 296 с., 1953.
Даувальтер В.А. Закономерности осадконакопления в водных объектах европейской Субарктики
(природоохранные аспекты проблемы). Дис. … докт. геогр. наук, Апатиты, 398 с., 1999.
Даувальтер В.А., Моисеенко Т.И., Кудрявцева Л.П., Сандимиров С.С. Накопление тяжелых металлов в
Накопление тяжелых металлов в
оз. Имандра в условиях его промышленного загрязнения. Водные ресурсы, т.27, № 3, с.279-287, 2000.
Кашулин Н.А., Даувальтер В.А., Кашулина Т.Г., Сандимиров С.С., Раткин Н.Е., Кудрявцева Л.П.,
Королева И.М., Вандыш О.И., Мокротоварова О.И. Антропогенные изменения лотических
экосистем Мурманской области. Часть 1: Ковдорский район. Апатиты, КНЦ РАН, 234 с., 2005.
Кашулин Н.А., Даувальтер В.А., Сандимиров С.С., Раткин Н.Е., Терентьев П.М., Королева И.М.,
Вандыш О.И., Кудрявцева Л.П. Антропогенные изменения лотических экосистем Мурманской
области. Ч. 2: Озерно-речная система реки Чуна в условиях аэротехногенного загрязнения.
Апатиты, КНЦ РАН, 238 с., 2007.
Моисеенко Т.И., Родюшкин И.В., Даувальтер В.А., Кудрявцева Л.П. Формирование качества вод и
донных отложений в условиях антропогенных нагрузок на водоемы арктического бассейна (на
примере Кольского Севера). Апатиты, КНЦ РАН, 263 с., 1996.
Апатиты, КНЦ РАН, 263 с., 1996.
Моисеенко Т.И., Даувальтер В.А., Лукин А.А., Кудрявцева Л.П., Ильяшук Б.П., Ильяшук Е.А.,
Сандимиров С.С., Каган Л.Я., Вандыш О.И., Шаров А.Н., Шарова Ю.Н., Королева И.М.
Антропогенные модификации экосистемы озера Имандра. М., Наука, 487 с., 2002.
Россолимо Л.Л. Изменение лимнических экосистем под воздействием антропогенного фактора. М.,
Наука, 205 с., 1977.
Руководство по химическому анализу поверхностных вод суши. Л., Гидрометеоиздат, 541 с., 1977.
Разработка модели динамического роста для плантаций тика в Индии | Лесные экосистемы
Данные
Данные, использованные в этом исследовании, были собраны на 27 исследовательских площадках из чистого и одновозрастного тика разного возраста (от 11 до 38 лет) и плотности (от 498 до 2061 деревьев на га −1 ), созданных в 2010 г. в насаждениях, представляющих пять лесных участков в Карнатаке. Годовое количество осадков в этих районах колеблется от 1600 мм до 4500 мм. Среднегодовые минимальные и максимальные температуры колеблются от 11 ° C до 38 ° C.Участки расположены по всей территории штата, где выращивают тик, и были выбраны с учетом существующего диапазона возрастов, плотности насаждений и участков. Участки имеют прямоугольную форму и их размер варьируется от 220 до 436 м 2 , в зависимости от плотности насаждений, чтобы на каждом участке было не менее 30 деревьев. Диаметр на высоте груди (dbh, 1,37 м над уровнем земли) измеряли с точностью до 0,1 см цифровыми штангенциркулями на всех деревьях на делянках. Общая высота измерялась с точностью до нуля.1 м с цифровым гипсометром. Возраст рассчитывали от года посадки. Участки подвергались повторным измерениям ежегодно в течение 2010–2013 гг., И для каждого участка было доступно в общей сложности три годовых измерения.
Среднегодовые минимальные и максимальные температуры колеблются от 11 ° C до 38 ° C.Участки расположены по всей территории штата, где выращивают тик, и были выбраны с учетом существующего диапазона возрастов, плотности насаждений и участков. Участки имеют прямоугольную форму и их размер варьируется от 220 до 436 м 2 , в зависимости от плотности насаждений, чтобы на каждом участке было не менее 30 деревьев. Диаметр на высоте груди (dbh, 1,37 м над уровнем земли) измеряли с точностью до 0,1 см цифровыми штангенциркулями на всех деревьях на делянках. Общая высота измерялась с точностью до нуля.1 м с цифровым гипсометром. Возраст рассчитывали от года посадки. Участки подвергались повторным измерениям ежегодно в течение 2010–2013 гг., И для каждого участка было доступно в общей сложности три годовых измерения.
Данные участка включают: возраст древостоя ( т, , лет), плотность ( N, деревьев га, −1 ), средний квадратичный диаметр ( D, см), среднюю высоту h¯, м, доминанту высота ( H , м), определяемая как средняя высота 100 самых толстых деревьев на гектар, базальная площадь ( B , м 2 га −1 ) и общий объем древостоя ( V , м 3 ). Общий объем древостоя был рассчитан с помощью совместимого уравнения объема деревьев (Tewari et al. , 2013). Сводная статистика этих переменных насаждений представлена в Таблице 1. Хотя механические (систематические) и лесоводственные (выборочные) рубки ухода прописаны в рабочих планах управления лесами, однако рубки ухода проводились только в одном насаждении. Кроме того, было проведено исчерпывающее изучение данных, чтобы отклонить выборочные участки, на которых были обнаружены незаконные рубки, чтобы убедиться, что сокращение количества наблюдаемых деревьев произошло из-за естественной смертности.
Общий объем древостоя был рассчитан с помощью совместимого уравнения объема деревьев (Tewari et al. , 2013). Сводная статистика этих переменных насаждений представлена в Таблице 1. Хотя механические (систематические) и лесоводственные (выборочные) рубки ухода прописаны в рабочих планах управления лесами, однако рубки ухода проводились только в одном насаждении. Кроме того, было проведено исчерпывающее изучение данных, чтобы отклонить выборочные участки, на которых были обнаружены незаконные рубки, чтобы убедиться, что сокращение количества наблюдаемых деревьев произошло из-за естественной смертности.
Структура модели
Из 27 участков 5 участков, на которых были выявлены незаконные рубки, были исключены из анализа. Модель динамического роста, разработанная на основе этих данных, основана на подходе пространства состояний и аналогична моделям García (2011), García et al. (2011) и Гарсия (2013). В этой модели предполагается, что поведение любого насаждения тика, эволюционирующего во времени, можно аппроксимировать, описав его текущее состояние четырьмя переменными состояния: доминирующая высота ( H ), количество деревьев на гектар ( N ), базальная высота. площадь ( B ) и показатель занятости узла (Ω) с использованием функций перехода для оценки изменения состояний как функции текущего состояния переменных.
(2011) и Гарсия (2013). В этой модели предполагается, что поведение любого насаждения тика, эволюционирующего во времени, можно аппроксимировать, описав его текущее состояние четырьмя переменными состояния: доминирующая высота ( H ), количество деревьев на гектар ( N ), базальная высота. площадь ( B ) и показатель занятости узла (Ω) с использованием функций перехода для оценки изменения состояний как функции текущего состояния переменных.
Функции перехода используются для прогнозирования роста путем обновления переменных состояния, обеспечивая два естественных свойства (Гарсия, 1994): (i) согласованность, то есть отсутствие изменений в течение нулевого прошедшего времени; (ii) инвариантность пути, когда результатом проецирования состояния сначала от t 0 до t 1 , а затем от t 1 до t 2 , должно быть То же, что и для одношаговой проекции от t 0 до t 2 . Функции перехода, генерируемые интегрированием дифференциальных уравнений (или суммированием разностных уравнений при использовании дискретного времени), удовлетворяют этим условиям и позволяют вычислить траекторию будущего состояния. Эти свойства также могут быть достигнуты с помощью методов вывода динамических уравнений, известных в лесоводстве как алгебраический разностный подход (ADA; Bailey and Clutter, 1974) или его обобщения (GADA; Cieszewski and Bailey, 2000).
Функции перехода, генерируемые интегрированием дифференциальных уравнений (или суммированием разностных уравнений при использовании дискретного времени), удовлетворяют этим условиям и позволяют вычислить траекторию будущего состояния. Эти свойства также могут быть достигнуты с помощью методов вывода динамических уравнений, известных в лесоводстве как алгебраический разностный подход (ADA; Bailey and Clutter, 1974) или его обобщения (GADA; Cieszewski and Bailey, 2000).
Переходная функция для доминирующей высоты
(Уравнение параметров для двух участков, полученное из базовой модели Корфа и предложенное Тевари et al. 2014), использовалась как переходная функция для доминирующей высоты. Модель GADA допускает одновременный одновременный полиморфизм и множественные асимптоты, две характеристики уравнений сайта, которые иногда желательны (Cieszewski, 2002). Математическое выражение этой модели:
h3 = expX0exp − 13.6964 + 22.3517 / X0t2−1.2229withX0 = 12t1−1.222913.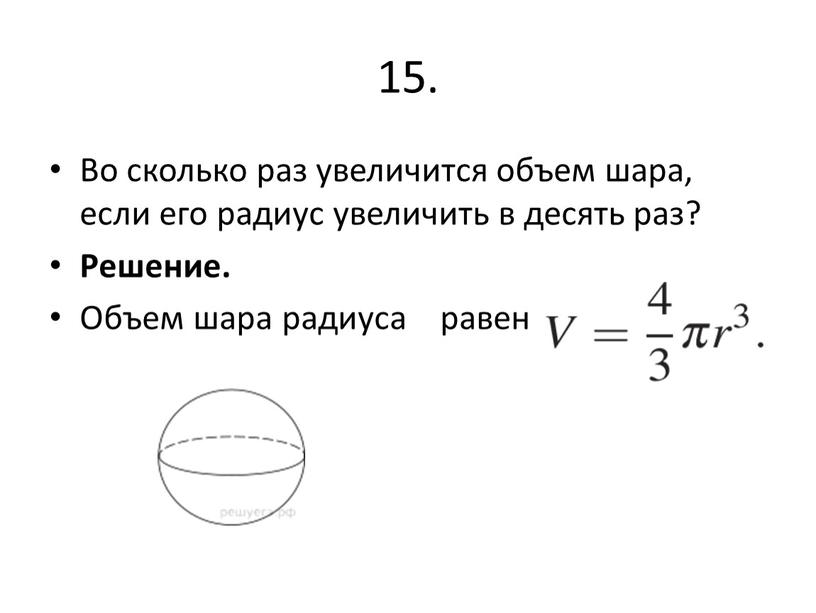 6964 + t11.2229lnh2 ++ 89.4068t11.2229 + 13.6964 + t11.2229ln0004
6964 + t11.2229lnh2 ++ 89.4068t11.2229 + 13.6964 + t11.2229ln0004
, где H 1 и t 1 представляют прогнозируемую высоту (метры) и возраст (годы), а H 2 — прогнозируемую высоту в возрасте t 2 .
Переходная функция для смертности
Естественная смертность или выживаемость чрезвычайно изменчивы и особенно трудно предсказуемы. Функция перехода смертности основана на предположении, что скорость изменения N относительно доминирующего прироста высоты зависит от текущих значений H и N :
, где N — это количество деревьев на га. 1 , H — основная высота, а a i — параметры, которые необходимо оценить.
Группирование членов уравнения (2) и интегрирование обеих частей дает следующий инвариант:
dNNa3 = −a1Ha2dH⇒N1 − a3 − a1a3−1a2 + 1Ha2 + 1 = константа
(3)
Приравнивание инварианта для времен 1 и 2 дает следующую функцию перехода для количества деревьев ha −1 :
N2 = N11 − a3 + a1a3−1a2 + 1h3a2 + 1 − h2a2 + 11/1 − a3
(4)
Это предсказывает N 2 на высоте H 2 при любых начальных значениях ( H 1 ; N 1 ). Уравнение (4) было построено с использованием двух различных подходов. В первом случае не предполагалось никаких ограничений по параметрам, а во втором случае ограничения по параметрам были получены путем принятия предельных значений для наклона самоуонижающихся линий на основе среднего квадрата шага S = 100 / N (Garcia, 2009). Скорость изменения среднего квадрата шага относительно доминирующего прироста высоты зависит от начальных значений тех же переменных:
Уравнение (4) было построено с использованием двух различных подходов. В первом случае не предполагалось никаких ограничений по параметрам, а во втором случае ограничения по параметрам были получены путем принятия предельных значений для наклона самоуонижающихся линий на основе среднего квадрата шага S = 100 / N (Garcia, 2009). Скорость изменения среднего квадрата шага относительно доминирующего прироста высоты зависит от начальных значений тех же переменных:
dSdH = βγHγ − 1Sα − 1
(5)
Интегрируя уравнение (5) и логарифмируя, получается следующий инвариант:
Sα = αγβHγ⇒αlog100 − α2logN = logα / γ + γlogβ + γlogH⇒⇒logN = −2γαlogH + constant
(6)
Любое предельное значение, принятое для 2γ / α в уравнении (6), представляет наклон линии самоудонения, принятый для данного вида.Сравнивая с уравнением (3), получается следующее соотношение:
Это соотношение может быть полезно для оценки параметров переходной функции смертности, когда доступные данные ограничены, чтобы гарантировать биологически согласованное поведение (García, 2009). Значения 2 и 3 были приняты для отношения -2γ / α, т. Е. Для наклона линии самоутончения.
Значения 2 и 3 были приняты для отношения -2γ / α, т. Е. Для наклона линии самоутончения.
Функция перехода для базальной площади
Вместо прямого прогнозирования базальной площади ( B ) мы выбираем моделирование роста продукта W = BH .Скорость изменения W может быть выражена как разница между двумя составляющими: валовой прирост и смертность. В чистых и одновозрастных насаждениях (например, рассматриваемых в этой статье) валовой прирост можно записать как b1ΩHNb2, где Ω — относительный коэффициент занятости, который снижает рост молодых или недавно прореженных насаждений, которые еще не полностью занимают участок. . Смертность выражается как -kWNdNdH = -kWdlogNdH, где k представляют средний размер умирающих деревьев по отношению к среднему размеру выживших, который считается постоянным.Следовательно, общая модель роста W:
dWdH = b1ΩHNb2 + kWdlogNdH
(8)
Простое решение дифференциального уравнения (8) в замкнутой форме может быть получено в частном случае, когда b 2 равно k :
dWdH = b1ΩHNk + kWdlogNdH
(9)
Интуитивно Ω представляет собой перехват ресурсов (например, света, питательных веществ, влаги). Вначале заполняемость молодых насаждений низкая и постепенно увеличивается, приближаясь к 1, когда навес закрывается.Мы предполагаем, что скорость закрытия изначально зависит от H таким же образом, как и общий прирост, и уменьшается до нуля по мере приближения к полному закрытию.
Вначале заполняемость молодых насаждений низкая и постепенно увеличивается, приближаясь к 1, когда навес закрывается.Мы предполагаем, что скорость закрытия изначально зависит от H таким же образом, как и общий прирост, и уменьшается до нуля по мере приближения к полному закрытию.
Интегрирование дает инвариант:
1 − Ωexpc1h3 / 2 = constant
(11)
В этой модели занятости интегрирование уравнения (9) дает уравнение перехода для базовой площади:
B2 = N2kB1h2N1 − k + b1h32 − h22 / 2 − Ω2 − Ω1 / c1 / h3
(12)
с
Ω2 = 1 − exp − c1h32 − h22 / 21 − Ω1
(13)
Чтобы понять методологию и вывод уравнения перехода для базовой площади, интегрирование дифференциального уравнения (9) представлено в Приложении.
Уравнение общего объема древостоя
Объемы на гектар можно оценить с учетом переменных состояния с помощью выходной функции. Были подобраны два различных уравнения общего объема древостоя с использованием в качестве независимых переменных доминирующей высоты и базальной площади.
Были подобраны два различных уравнения общего объема древостоя с использованием в качестве независимых переменных доминирующей высоты и базальной площади.
Эти модели широко используются для оценки общего объема насаждений (см., Например, Husch et al. , 2003; van Laar and Akça, 2007; Weiskittel et al. , 2011).
Модели были подогнаны с использованием обобщенного метода моментов (GMM) в процедуре MODEL SAS / ETS® (SAS Institute Inc., 2008). Этот метод дает эффективные оценки параметров в гетероскедастических условиях без оценки дисперсии гетероскедастической ошибки (Greene, 2012). Главный недостаток этого метода заключается в том, что оценки ошибок для прогнозов не могут быть сгенерированы без указания структуры ошибок (Parresol, 2001).
Оценка параметров и выбор модели
Модель была подобрана на основе прогнозов по парам последовательных измерений. Поскольку функция перехода для доминирующей высоты была подобрана ранее, наблюдаемые доминирующие высоты в базе данных были заменены прогнозируемыми значениями этой модели, чтобы учесть ошибку оценок в модели роста всего древостоя.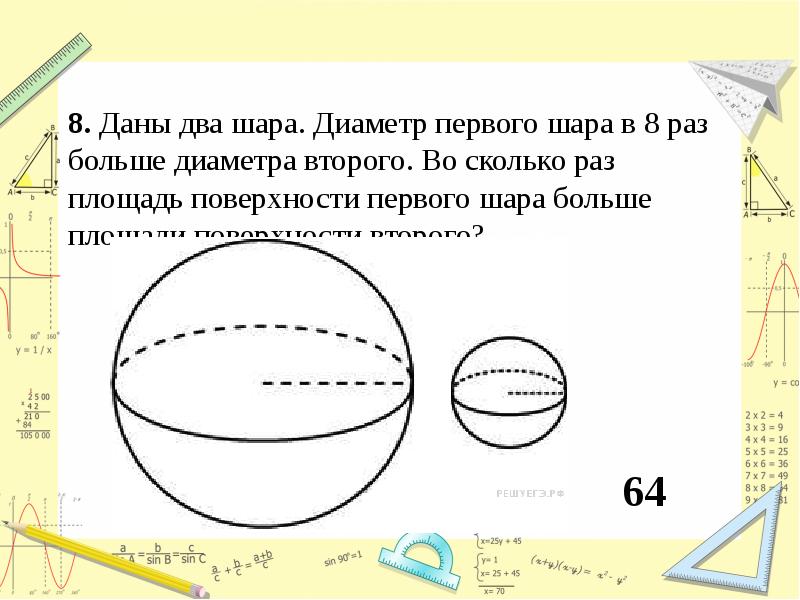 Считалось удобным инициализировать переменные состояния на уровне груди, где известны H, = 1,37 и B = 0. Количество N b деревьев на гектар в это время было оценено путем применения коэффициента выживаемости 82,5% (так как коэффициент выживаемости, наблюдаемый после одного года посадки в этих насаждениях, составлял 80-85%) к плотности от принятого расстояния. на момент посадки — 2 × 2 м, за исключением одного участка, на котором он был 1,5 × 1,5 м. Согласно Гарсия (2011), занятость была инициализирована на уровне груди как:
Считалось удобным инициализировать переменные состояния на уровне груди, где известны H, = 1,37 и B = 0. Количество N b деревьев на гектар в это время было оценено путем применения коэффициента выживаемости 82,5% (так как коэффициент выживаемости, наблюдаемый после одного года посадки в этих насаждениях, составлял 80-85%) к плотности от принятого расстояния. на момент посадки — 2 × 2 м, за исключением одного участка, на котором он был 1,5 × 1,5 м. Согласно Гарсия (2011), занятость была инициализирована на уровне груди как:
Омb = 1−1 − minNb / c2,1c3
(16)
где, c i — параметры, подлежащие оценке; c 2 представляет плотность на высоте груди, при которой стойка будет полностью закрыта.
(García et al. 2011) соответствовал каждой переходной функции отдельно. Здесь функции перехода для смертности и базальной площади были подобраны одновременно с использованием полной информации максимального правдоподобия (FIML), чтобы получить оценки, которые являются согласованными и эффективными и способствуют повышению точности прогнозов модели. Поскольку сходимость с этим подходом очень чувствительна к начальным значениям параметров, обе функции перехода сначала подбирались отдельно, чтобы получить наилучший набор начальных значений.
Поскольку сходимость с этим подходом очень чувствительна к начальным значениям параметров, обе функции перехода сначала подбирались отдельно, чтобы получить наилучший набор начальных значений.
Модели роста и урожайности отдельных лесов обычно используют набор уравнений для описания развития древостоя с течением времени. В литературе по лесному хозяйству нет ничего необычного в том, чтобы рассматривать одну и ту же переменную как зависимую в одном уравнении и независимую в другом. Когда переменная используется как эндогенная (зависимая) переменная в левой части одного уравнения и в правой части другого уравнения, это делает систему уравнений одновременной (Goldberger, 1964). В настоящем исследовании смертность используется как зависимая переменная в уравнении (4) и как независимая переменная в уравнении (12), что делает систему уравнений одновременной.Методы одновременной регрессии приводят к более эффективным оценкам. Повышение эффективности увеличивает точность прогнозов результирующей модели. Повышение эффективности выше, когда ошибки между различными уравнениями сильно коррелированы (Судья и др. , 1988).
Повышение эффективности выше, когда ошибки между различными уравнениями сильно коррелированы (Судья и др. , 1988).
Ошибка была смоделирована с использованием структуры непрерывной авторегрессионной ошибки (CAR (×)), которая учитывала время между измерениями. Возраст на уровне груди оценивался с использованием итеративной процедуры, основанной на функции перехода доминирующего роста, описанной ранее.Для оценки доминирующего роста в возрасте, измеренном на графике, использовали разный возраст при достижении высоты груди, и возраст, который минимизировал сумму квадратов различий между наблюдаемым и прогнозируемым доминирующим ростом, был выбран в качестве возраста достижения высоты груди. Эти возрасты использовались только для получения правильных последовательных оценок параметров и их стандартных ошибок.
Оценка параметров проводилась с помощью процедуры МОДЕЛЬ SAS / ETS® (SAS Institute Inc., 2008). В этой процедуре была запрограммирована структура ошибок CAR (×), которая позволяет динамически обновлять остатки.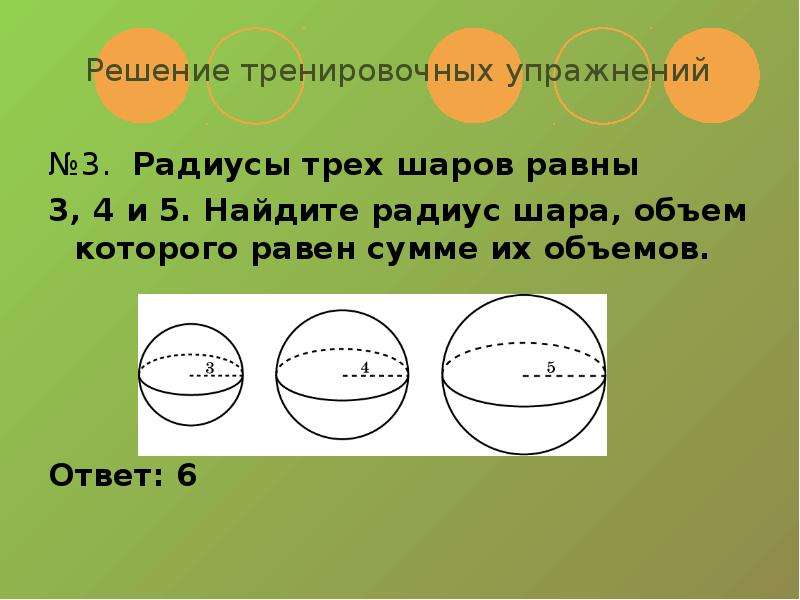 i и y¯ — наблюдаемые, оценочные и средние значения зависимой переменной, n — общее количество наблюдений, используемых для соответствия модели, а p — количество параметров модели.
i и y¯ — наблюдаемые, оценочные и средние значения зависимой переменной, n — общее количество наблюдений, используемых для соответствия модели, а p — количество параметров модели.
В дополнение к проверке отдельных компонентов модели динамического роста была проведена общая проверка всей модели. Были использованы все возможные комбинации инвентаризаций, и наблюдаемые значения H, N и B из первой инвентаризации были использованы для оценки общего объема древостоя на момент последней инвентаризации, включая все компоненты всей модели древостоя.i и y¯ — наблюдаемые, прогнозируемые и средние значения общего объема древостоя, а τ — стандартное нормальное отклонение при заданном уровне вероятности (τ = 1,96 для α = 0,05). χn2 получено для α = 0,05 с n степенями свободы. Помимо использования этой статистики, был также исследован график зависимости наблюдаемых значений от прогнозируемых значений общего объема древостоя.
% PDF-1. 4
%
1 0 obj
>
endobj
2 0 obj
> поток
2014-04-01T16: 45: 22 + 05: 30Adobe InDesign CS6 (Windows) 2014-09-19T16: 19: 09 + 02: 002014-09-19T16: 19: 09 + 02: 00Adobe PDF Library 10.0,1; изменено с помощью iText® 5.3.1 © 2000-2012 1T3XT BVBA (AGPL-версия) application / pdfuuid: d5c17371-fece-4c02-8061-1648039b59d4uuid: a363918f-cffb-421b-8921-7879cae384d7defaultcud8: 426-326cverted a9c5-660dab3318aacconverted to PDF / A-1bpdfToolbox2014-04-01T17: 06: 20 + 05: 30
4
%
1 0 obj
>
endobj
2 0 obj
> поток
2014-04-01T16: 45: 22 + 05: 30Adobe InDesign CS6 (Windows) 2014-09-19T16: 19: 09 + 02: 002014-09-19T16: 19: 09 + 02: 00Adobe PDF Library 10.0,1; изменено с помощью iText® 5.3.1 © 2000-2012 1T3XT BVBA (AGPL-версия) application / pdfuuid: d5c17371-fece-4c02-8061-1648039b59d4uuid: a363918f-cffb-421b-8921-7879cae384d7defaultcud8: 426-326cverted a9c5-660dab3318aacconverted to PDF / A-1bpdfToolbox2014-04-01T17: 06: 20 + 05: 30
 Оригинальный документ IDURI
Оригинальный документ IDURI 0 0,0 439,37 666,14] / Аннотации [9 0 R] / Повернуть 0 >>
endobj
9 0 объект
>>>
endobj
6 0 obj
>
endobj
5 0 obj
> поток
xS (ҏ0Tp
0 0,0 439,37 666,14] / Аннотации [9 0 R] / Повернуть 0 >>
endobj
9 0 объект
>>>
endobj
6 0 obj
>
endobj
5 0 obj
> поток
xS (ҏ0TpПовышение уровня моря и последствия для низкорасположенных островов, побережий и сообществ — Специальный доклад об океане и криосфере в условиях изменяющегося климата
В этой главе оценивается прошлый и будущий вклад в глобальные, региональные и экстремальные изменения уровня моря, связанный с этим риск для низколежащих островов, побережий, городов и поселений, а также варианты ответных мер и пути к устойчивости и устойчивому развитию вдоль побережья.
Глобальный средний уровень моря (GMSL) повышается ( практически наверняка ) и ускоряется ( высокая достоверность ). Сумма вкладов ледников и ледникового щита в настоящее время является доминирующим источником повышения GMSL ( очень высокая степень достоверности ) . GMSL по мареографам и альтиметрическим наблюдениям увеличилась с 1,4 мм / год за период 1901–1990 гг. До 2,1 мм / год за период 1970–2015 гг. До 3.От 2 мм в год за период 1993–2015 гг. До 3,6 мм в год за период 2006–2015 годов ( высокая достоверность ). Доминирующей причиной роста GMSL с 1970 г. является антропогенное воздействие ( высокая достоверность ). {4.2.2.1.1, 4.2.2.2}
До 2,1 мм / год за период 1970–2015 гг. До 3.От 2 мм в год за период 1993–2015 гг. До 3,6 мм в год за период 2006–2015 годов ( высокая достоверность ). Доминирующей причиной роста GMSL с 1970 г. является антропогенное воздействие ( высокая достоверность ). {4.2.2.1.1, 4.2.2.2}
GMSL был значительно выше, чем сегодня, во время прошлых климатических состояний, которые были более теплыми, чем доиндустриальные, включая Последнее межледниковье (LIG; 129–116 тыс. Лет назад), когда глобальная средняя температура поверхности была на 0,5 ° C. — на 1,0 ° C теплее, а средний плиоценовый теплый период (mPWP; ~ 3.3–3,0 миллиона лет назад), на 2ºC — На 4ºC теплее. Несмотря на скромное глобальное потепление последнего межледниковья, GMSL была , вероятно, на 6–9 м выше, в основном за счет вкладов ледяных щитов Гренландии и Антарктики (GIS и AIS, соответственно), и маловероятно более чем на 10 м выше ( средняя степень достоверности ). Основываясь на новом понимании о геологических ограничениях после 5-го оценочного отчета МГЭИК (AR5), 25 м является вероятной верхней границей GMSL во время mPWP ( низкая достоверность ). Текущие неопределенности в реконструкции уровня моря и моделировании палео не позволяют сделать выводы относительно общих величин и темпов повышения уровня моря в прошлом (SLR). Более того, долгосрочные (многомилленовые) временные масштабы этих прошлых изменений климата и уровня моря, а также региональные климатические влияния, обусловленные изменениями орбитальной конфигурации Земли и обратными связями климатической системы, приводят к низкой достоверности при прямых сравнениях с изменениями в ближайшем будущем . {Перекрестная вставка 5 в главах 1, 4.2.2, 4.2.2.1, 4.2.2.5, SM 4.1}
Основываясь на новом понимании о геологических ограничениях после 5-го оценочного отчета МГЭИК (AR5), 25 м является вероятной верхней границей GMSL во время mPWP ( низкая достоверность ). Текущие неопределенности в реконструкции уровня моря и моделировании палео не позволяют сделать выводы относительно общих величин и темпов повышения уровня моря в прошлом (SLR). Более того, долгосрочные (многомилленовые) временные масштабы этих прошлых изменений климата и уровня моря, а также региональные климатические влияния, обусловленные изменениями орбитальной конфигурации Земли и обратными связями климатической системы, приводят к низкой достоверности при прямых сравнениях с изменениями в ближайшем будущем . {Перекрестная вставка 5 в главах 1, 4.2.2, 4.2.2.1, 4.2.2.5, SM 4.1}
Неклиматические антропогенные факторы, в том числе недавние и исторические демографические тенденции и тенденции развития поселений, а также антропогенное проседание, сыграли важную роль в увеличении подверженности низинных прибрежных сообществ и их уязвимости к SLR и явлениям экстремального уровня моря (ESL) ( очень высокое доверие ). В прибрежных дельтах, например, эти факторы изменили доступность пресной воды и наносов ( высокая степень достоверности ).В более широком смысле, в низколежащих прибрежных районах антропогенные изменения могут быть быстрыми и изменять береговые линии в течение коротких периодов времени, опережая эффекты SLR (, высокая достоверность, ). Адаптация может быть предпринята в краткосрочной и среднесрочной перспективе путем нацеливания на местные факторы воздействия и уязвимости, несмотря на неопределенность в отношении местных воздействий SLR в ближайшие десятилетия и далее (, высокая достоверность, ). {4.2.2.4, 4.3.1, 4.3.2.2, 4.3.2.3}
В прибрежных дельтах, например, эти факторы изменили доступность пресной воды и наносов ( высокая степень достоверности ).В более широком смысле, в низколежащих прибрежных районах антропогенные изменения могут быть быстрыми и изменять береговые линии в течение коротких периодов времени, опережая эффекты SLR (, высокая достоверность, ). Адаптация может быть предпринята в краткосрочной и среднесрочной перспективе путем нацеливания на местные факторы воздействия и уязвимости, несмотря на неопределенность в отношении местных воздействий SLR в ближайшие десятилетия и далее (, высокая достоверность, ). {4.2.2.4, 4.3.1, 4.3.2.2, 4.3.2.3}
Прибрежные экосистемы уже подвергаются воздействию сочетания SLR, других связанных с климатом изменений океана и неблагоприятных воздействий деятельности человека на океан и сушу ( высокая степень достоверности ).Однако приписать такое воздействие SLR остается проблематичным из-за влияния других связанных с климатом и неклиматических факторов, таких как развитие инфраструктуры и антропогенная деградация среды обитания ( высокая достоверность ). Прибрежные экосистемы, включая солончаки, мангровые заросли, покрытые растительностью дюны и песчаные пляжи, могут строиться вертикально и расширяться в поперечном направлении в ответ на SLR, хотя эта способность варьируется в зависимости от участка ( высокая достоверность ).Эти экосистемы предоставляют важные услуги, включая защиту прибрежных районов и среду обитания для разнообразной биоты. Однако в результате действий человека, которые фрагментируют среду обитания водно-болотных угодий и ограничивают миграцию в направлении суши, прибрежные экосистемы постепенно теряют способность адаптироваться к изменениям, вызванным климатом, и предоставлять экосистемные услуги, в том числе действовать в качестве защитных барьеров (, высокая достоверность, ). {4.3.2.3}
Прибрежные экосистемы, включая солончаки, мангровые заросли, покрытые растительностью дюны и песчаные пляжи, могут строиться вертикально и расширяться в поперечном направлении в ответ на SLR, хотя эта способность варьируется в зависимости от участка ( высокая достоверность ).Эти экосистемы предоставляют важные услуги, включая защиту прибрежных районов и среду обитания для разнообразной биоты. Однако в результате действий человека, которые фрагментируют среду обитания водно-болотных угодий и ограничивают миграцию в направлении суши, прибрежные экосистемы постепенно теряют способность адаптироваться к изменениям, вызванным климатом, и предоставлять экосистемные услуги, в том числе действовать в качестве защитных барьеров (, высокая достоверность, ). {4.3.2.3}
Прибрежный риск является динамичным и увеличивается из-за широко наблюдаемых изменений в прибрежной инфраструктуре, уровне жизни сообществ, сельском хозяйстве и обитаемости ( высокая степень достоверности ). Как и в случае с прибрежными экосистемами, отнести наблюдаемые изменения и связанный с ними риск к SLR по-прежнему сложно. Драйверы и процессы, препятствующие атрибуции, включают демографические, ресурсные и земельные изменения, а также антропогенное проседание. {4.3.3, 4.3.4}
Как и в случае с прибрежными экосистемами, отнести наблюдаемые изменения и связанный с ними риск к SLR по-прежнему сложно. Драйверы и процессы, препятствующие атрибуции, включают демографические, ресурсные и земельные изменения, а также антропогенное проседание. {4.3.3, 4.3.4}
Разнообразные меры адаптации к воздействиям и рискам прибрежных районов были реализованы по всему миру, но в основном как реакция на текущий риск для прибрежных районов или пережитые бедствия ( с высокой достоверностью ). Меры жесткой береговой защиты (плотины, насыпи, морские стены и барьеры от нагонов) широко распространены, обеспечивая предсказуемые уровни безопасности в северо-западной Европе, Восточной Азии и вокруг многих прибрежных городов и дельт. Экосистемная адаптация (EbA) продолжает набирать обороты во всем мире, обеспечивая множество сопутствующих выгод, но все еще существует низкая договоренность о ее стоимости и долгосрочной эффективности. Развитие, которое относится к созданию новых земель путем застройки в море (например, мелиорация земель), имеет долгую историю в большинстве районов с плотным прибрежным населением . Меры адаптации, такие как системы раннего предупреждения (EWS) для событий ESL, широко распространены. Отступление наблюдается, но в основном ограничивается небольшими сообществами или проводится с целью создания новой среды обитания водно-болотных угодий. {4.4.2.3, 4.4.2.4, 4.4.2.5}
Меры адаптации, такие как системы раннего предупреждения (EWS) для событий ESL, широко распространены. Отступление наблюдается, но в основном ограничивается небольшими сообществами или проводится с целью создания новой среды обитания водно-болотных угодий. {4.4.2.3, 4.4.2.4, 4.4.2.5}
Проекции
Будущее повышение GMSL, вызванное тепловым расширением, таянием ледников и ледяных щитов и изменениями запасов воды на суше, в значительной степени зависит от того, какой сценарий выбросов будет следовать репрезентативному пути концентрации (RCP).По прогнозам, SLR в конце века будет быстрее при всех сценариях, включая те, которые совместимы с достижением долгосрочной цели по температуре, установленной в Парижском соглашении. GMSL поднимется от 0,43 м (0,29 — 0,59 м, вероятно диапазон; RCP2.6) до 0,84 м (0,61 — 1,10 м, вероятно дальность; RCP8,5 ) к 2100 году ( средняя достоверность ) относительно 1986 — 2005. После 2100 года уровень моря будет продолжать повышаться в течение столетий из-за продолжающегося поглощения тепла глубинными океанами и потери массы ГИС и АИС, и будет оставаться повышенным в течение тысяч лет ( высокая достоверность ). Согласно RCP8.5 оценки для 2100 года выше, а диапазон неопределенности больше, чем в AR5. К концу столетия Антарктика может внести до 28 см SLR (RCP8.5, верхний предел диапазона , вероятно, ) (, средняя достоверность, ). Оценки SLR выше вероятного диапазона также представлены здесь для лиц, принимающих решения с низкой толерантностью к риску.{SR1.5, 4.1, 4.2.3.2, 4.2.3.5}
После 2100 года уровень моря будет продолжать повышаться в течение столетий из-за продолжающегося поглощения тепла глубинными океанами и потери массы ГИС и АИС, и будет оставаться повышенным в течение тысяч лет ( высокая достоверность ). Согласно RCP8.5 оценки для 2100 года выше, а диапазон неопределенности больше, чем в AR5. К концу столетия Антарктика может внести до 28 см SLR (RCP8.5, верхний предел диапазона , вероятно, ) (, средняя достоверность, ). Оценки SLR выше вероятного диапазона также представлены здесь для лиц, принимающих решения с низкой толерантностью к риску.{SR1.5, 4.1, 4.2.3.2, 4.2.3.5}
Согласно RCP8.5, скорость SLR будет 15 мм в год –1 (10 — 20 мм в год –1 , вероятно диапазон) в 2100 году , и мог превышать несколько см в год –1 в 22 веке. Эти высокие показатели затрудняют реализацию адаптационных мер, требующих длительного времени, но это еще не было изучено подробно. {4.2.3.2, 4.4.2.2.3}
{4.2.3.2, 4.4.2.2.3}
Процессы, контролирующие время потери шельфового ледника в будущем и пространственную протяженность нестабильности ледяного покрова, могут увеличить вклад Антарктиды в SLR до значений, превышающих диапазон , вероятно, в столетиях и в более длительных временных масштабах ( низкая достоверность ) . Эволюция САИ после конца 21 века характеризуется глубокой неопределенностью, поскольку в моделях ледникового покрова отсутствуют реалистичные представления некоторых основных физических процессов.Немногочисленные доступные модельные исследования, относящиеся к временным шкалам от веков до тысячелетий, указывают на многометровое (2,3–5,4 м) повышение уровня моря для RCP8.5 ( низкая достоверность ). Имеется низкая достоверность пороговых температур для нестабильности ледяного покрова и скорости повышения GMSL, которую они могут вызвать. {Перекрестная вставка 5 в главе 1, перекрестная вставка 8 в главе 3 и разделы 4. 1, 4.2.3.1.1, 4.2.3.1.2, 4.2.3.6}
1, 4.2.3.1.1, 4.2.3.1.2, 4.2.3.6}
Повышение уровня моря не является равномерным в глобальном масштабе и варьируется в зависимости от региона.Вклады теплового расширения, динамики океана и потери льда на суше вызовут отклонения в регионах примерно на ± 30% вокруг подъема GMSL. Отличия от глобального среднего могут составлять более ± 30% в областях с быстрым вертикальным перемещением земель, в том числе вызванных местными антропогенными факторами, такими как добыча подземных вод ( с высокой достоверностью ). Оседание воды, вызванное деятельностью человека, в настоящее время является наиболее важной причиной изменения относительного повышения уровня моря (RSL) во многих регионах дельты.В то время как сравнительная важность повышения RSL, обусловленного климатом, со временем будет возрастать, эти данные об антропогенном оседании подразумевают, что учет местных процессов имеет решающее значение для прогнозов воздействий уровня моря в локальных масштабах (, высокая достоверность, ). {4.2.1.6, 4.2.2.4}
{4.2.1.6, 4.2.2.4}
Из-за прогнозируемого повышения GMSL исторически редкие ESL (например, сегодняшнее столетнее событие) станут обычным явлением к 2100 году для всех RCP ( высокая достоверность ). Многие низколежащие города и небольшие острова на большинстве широт будут ежегодно испытывать такие явления к 2050 году. Ожидается, что снижение выбросов парниковых газов (ПГ), предусмотренное в сценариях с низким уровнем выбросов (например, RCP2.6), резко снизит, но не устранит риск до низкого уровня. -межные побережья и острова с событий SLR и ESL. Сценарии с низким уровнем выбросов приводят к более медленным темпам SLR и допускают более широкий диапазон вариантов адаптации. Для первой половины 21 века различия в событиях ESL между сценариями невелики, что облегчает планирование адаптации.{4.2.2.5, 4.2.3.4}
Неклиматические антропогенные факторы будут продолжать увеличивать подверженность и уязвимость прибрежных сообществ к будущим событиям SLR и ESL в отсутствие серьезных усилий по адаптации по сравнению с сегодняшним днем ( высокая достоверность ). {4.3.4, перекрестная вставка 9}
{4.3.4, перекрестная вставка 9}
Ожидаемые воздействия SLR на прибрежные экосистемы в течение столетия включают сокращение среды обитания, утрату функциональности и биоразнообразия, а также боковую и внутреннюю миграцию.Воздействие будет усугубляться в случаях мелиорации земель и когда антропогенные барьеры предотвращают внутреннюю миграцию болот и мангровых зарослей и ограничивают доступность и перемещение наносов ( высокая степень достоверности ). Было обнаружено, что при благоприятных условиях болота и мангровые заросли идут в ногу с высокими темпами SLR (например,> 10 мм в год-1), но эта способность значительно варьируется в зависимости от таких факторов, как воздействие волн на местности, диапазон приливов, отложения. улавливание, общая доступность наносов и прибрежное выдавливание (высокая степень достоверности). {4.3.3.5.1}
В отсутствие адаптации более интенсивные и частые явления ЭПС вместе с тенденциями развития прибрежных районов увеличат ожидаемые ежегодные убытки от наводнений на 2-3 порядка к 2100 году ( высокая степень достоверности ). Однако хорошо спроектированная береговая защита очень эффективна для снижения ожидаемого ущерба и рентабельна для городских и густонаселенных регионов, но, как правило, недоступна для сельских и более бедных районов ( высокая степень достоверности ). Эффективная защита требует вложений от десятков до нескольких сотен миллиардов долларов США в год во всем мире ( с высокой степенью достоверности ). Хотя инвестиции в густонаселенные и городские районы, как правило, рентабельны (, высокая степень достоверности, ), сельским и более бедным районам будет сложно позволить себе такие инвестиции, при этом относительные годовые затраты для некоторых малых островных государств составляют несколько процентов ВВП (, высокая достоверность ). ). Даже при хорошо продуманной жесткой защите сохраняется риск возможных катастрофических последствий в случае выхода из строя защиты.{4.3.4, 4.4.2.2, 4.4.3.2, перекрестная вставка 9}
Однако хорошо спроектированная береговая защита очень эффективна для снижения ожидаемого ущерба и рентабельна для городских и густонаселенных регионов, но, как правило, недоступна для сельских и более бедных районов ( высокая степень достоверности ). Эффективная защита требует вложений от десятков до нескольких сотен миллиардов долларов США в год во всем мире ( с высокой степенью достоверности ). Хотя инвестиции в густонаселенные и городские районы, как правило, рентабельны (, высокая степень достоверности, ), сельским и более бедным районам будет сложно позволить себе такие инвестиции, при этом относительные годовые затраты для некоторых малых островных государств составляют несколько процентов ВВП (, высокая достоверность ). ). Даже при хорошо продуманной жесткой защите сохраняется риск возможных катастрофических последствий в случае выхода из строя защиты.{4.3.4, 4.4.2.2, 4.4.3.2, перекрестная вставка 9}
Риск, связанный с SLR (включая эрозию, затопление и засоление) , как ожидается, значительно возрастет к концу этого века вдоль всех низколежащих побережий в отсутствие серьезных дополнительных усилий по адаптации ( очень высокое доверие ). В то время как ожидается, что только городские атоллы и некоторые арктические сообщества будут испытывать от умеренного до высокого риска по сравнению с сегодняшним днем при низком уровне выбросов, риск от почти высокого до очень высокого ожидается во всех низколежащих прибрежных районах в верхней части , вероятно, Диапазон для путей с высоким уровнем выбросов ( средний уровень достоверности ).Однако переход от умеренного к высокому и от высокого к очень высокому риску будет варьироваться от одного прибрежного района к другому (, высокая достоверность, ). В то время как более низкая скорость SLR дает больше возможностей для адаптации, ожидается, что преимущества адаптации будут различаться в зависимости от прибрежных условий. Хотя амбициозная адаптация не обязательно устранит риск SLR в конце века (, средняя степень достоверности, ), она поможет выиграть время во многих местах и, следовательно, заложить прочную основу для адаптации после 2100 года.{4.
В то время как ожидается, что только городские атоллы и некоторые арктические сообщества будут испытывать от умеренного до высокого риска по сравнению с сегодняшним днем при низком уровне выбросов, риск от почти высокого до очень высокого ожидается во всех низколежащих прибрежных районах в верхней части , вероятно, Диапазон для путей с высоким уровнем выбросов ( средний уровень достоверности ).Однако переход от умеренного к высокому и от высокого к очень высокому риску будет варьироваться от одного прибрежного района к другому (, высокая достоверность, ). В то время как более низкая скорость SLR дает больше возможностей для адаптации, ожидается, что преимущества адаптации будут различаться в зависимости от прибрежных условий. Хотя амбициозная адаптация не обязательно устранит риск SLR в конце века (, средняя степень достоверности, ), она поможет выиграть время во многих местах и, следовательно, заложить прочную основу для адаптации после 2100 года.{4. 1.3, 4.3.4, вставка 4.1, SM4.2}
1.3, 4.3.4, вставка 4.1, SM4.2}
Выбор и реализация ответов
Все типы ответов на SLR, включая защиту, приспособление, EbA, продвижение и отступление, играют важную и синергетическую роль в интегрированном и упорядоченном ответе на SLR ( высокая степень достоверности ) . Жесткая защита и продвижение (застройка в море) экономически эффективны в большинстве городских условий, сталкивающихся с нехваткой земли (, высокая степень достоверности, ), но могут привести к увеличению воздействия в долгосрочной перспективе.Там, где доступно достаточно места, EbA может как снизить прибрежные риски, так и обеспечить множество других преимуществ (, средняя степень достоверности, ). Такие жилые помещения, как защищенные от наводнения здания и EWS для мероприятий ESL, часто являются недорогими и очень рентабельными во всех контекстах (, высокая достоверность, ). Там, где прибрежные риски уже высоки, а размер и плотность населения низки или после прибрежного бедствия, отступление может быть особенно эффективным, хотя и проблематичным в социальном, культурном и политическом плане. {4.4.2.2, 4.4.2.3, 4.4.2.4, 4.4.2.5, 4.4.2.6, 4.4.3}
{4.4.2.2, 4.4.2.3, 4.4.2.4, 4.4.2.5, 4.4.2.6, 4.4.3}
Ожидается, что технические пределы жесткой защиты будут достигнуты при сценариях высоких выбросов (RCP8.5) за пределами 2100 (высокая степень достоверности) и биофизические пределы для EbA могут возникнуть в 21 веке, но экономические и социальные барьеры возникают задолго до конца века ( средняя степень достоверности ). Экономические проблемы жесткой защиты возрастают с повышением уровня моря и сделают адаптацию недоступной до достижения технических пределов ( высокая степень достоверности ).Ожидается, что драйверы, отличные от SLR, будут вносить больший вклад в биофизические пределы EbA. Для кораллов ограничения могут быть достигнуты в этом столетии из-за закисления океана и потепления океана, а для приливных водно-болотных угодий — из-за загрязнения и инфраструктуры, ограничивающей их внутреннюю миграцию. Ожидается, что ограничения на приспособление появятся задолго до того, как появятся пределы защиты. Пределы отступления не определены, что отражает пробелы в исследованиях. Социальные барьеры (включая проблемы управления) на пути адаптации уже встречаются.{4.4.2.2, 4.4.2.3., 4.4.2.3.2, 4.4.2.5, 4.4.2.6, 4.4.3, перекрестная вставка 9}
Пределы отступления не определены, что отражает пробелы в исследованиях. Социальные барьеры (включая проблемы управления) на пути адаптации уже встречаются.{4.4.2.2, 4.4.2.3., 4.4.2.3.2, 4.4.2.5, 4.4.2.6, 4.4.3, перекрестная вставка 9}
Выбор и реализация мер реагирования на SLR ставит перед обществом серьезные проблемы управления и трудный социальный выбор, который по своей сути является политическим и ценностным ( высокая степень достоверности ). Большая неопределенность в отношении SLR после 2050 года и ожидаемое существенное воздействие ставят под сомнение устоявшуюся практику планирования и принятия решений и вводят необходимость координации внутри и между уровнями управления и сферами политики.Ответы на SLR также вызывают обеспокоенность по поводу справедливости в отношении маргинализации наиболее уязвимых и потенциально могут спровоцировать или усугубить социальный конфликт (, высокая степень достоверности, ). Выбор и реализация ответных мер еще более затруднены из-за нехватки ресурсов, неприятных компромиссов между безопасностью, сохранением и экономическим развитием, множественных способов формулирования « проблемы повышения уровня моря », властных отношений и различных прибрежных заинтересованных сторон, имеющих конфликт интересов в будущем. развитие активно используемых прибрежных зон ( высокая достоверность ).{4.4.2, 4.4.3}
развитие активно используемых прибрежных зон ( высокая достоверность ).{4.4.2, 4.4.3}
Несмотря на большую неопределенность в отношении SLR после 2050 года, адаптационные решения могут быть приняты сейчас, чему способствуют методы анализа решений, специально разработанные для устранения неопределенности ( с высокой степенью достоверности ). Эти методы отдают предпочтение гибким ответам (т. Е. Тем, которые могут быть адаптированы с течением времени) и периодически корректируемым решениям (т. Е. Адаптивному принятию решений). Вместо стандартных критериев ожидаемой полезности они используют критерии устойчивости (то есть эффективность при различных обстоятельствах) для оценки альтернативных ответов ( с высокой достоверностью ).Одним из примеров является анализ путей адаптации, который превратился в недорогой инструмент для оценки долгосрочных прибрежных реакций как последовательности адаптивных решений перед лицом динамического прибрежного риска, характеризующегося глубокой неопределенностью ( среднее количество доказательств, высокое согласие ). Диапазон SLR, который следует учитывать при принятии решений, зависит от толерантности к риску заинтересованных сторон, при этом заинтересованные стороны, чья толерантность к риску низкая, также учитывают SLR выше, чем вероятный диапазон . {4.1, 4.4.4.3}
Диапазон SLR, который следует учитывать при принятии решений, зависит от толерантности к риску заинтересованных сторон, при этом заинтересованные стороны, чья толерантность к риску низкая, также учитывают SLR выше, чем вероятный диапазон . {4.1, 4.4.4.3}
Накопленный на сегодняшний день опыт адаптации показывает, что использование подходящей для местных условий комбинации анализа решений, планирования землепользования, участия общественности и подходов к разрешению конфликтов может помочь в решении проблем управления, возникающих при реагировании на SLR ( высокая степень достоверности ). Эффективное реагирование на SLR зависит, во-первых, от долгосрочной перспективы при принятии краткосрочных решений, явного учета неопределенности местных рисков после 2050 года ( с высокой степенью достоверности ) и создания возможностей управления для решения сложных проблем SLR риск ( среднее количество доказательств, высокое согласие ). Во-вторых, улучшенная координация ответных мер по SLR по масштабам, секторам и областям политики может помочь в устранении воздействия и риска SLR (, высокая достоверность, ).В-третьих, уделение первоочередного внимания социальной уязвимости и равенству подкрепляет усилия по содействию справедливой и справедливой устойчивости к изменению климата и устойчивому развитию (, высокая степень достоверности, ), и этому может помочь создание безопасных общественных площадок для значимого общественного обсуждения и разрешения конфликтов ( среднее количество доказательств, высокая степень согласия ). Наконец, осведомленность и понимание общественности о рисках и ответных мерах по УЛР можно улучшить, опираясь на системы местных, коренных и научных знаний, а также на социальное обучение о рисках и возможностях реагирования на УЛС, характерных для данной местности (, высокая достоверность, ).{4.4.4.2, 4.4.5, таблица 4.9}
Во-вторых, улучшенная координация ответных мер по SLR по масштабам, секторам и областям политики может помочь в устранении воздействия и риска SLR (, высокая достоверность, ).В-третьих, уделение первоочередного внимания социальной уязвимости и равенству подкрепляет усилия по содействию справедливой и справедливой устойчивости к изменению климата и устойчивому развитию (, высокая степень достоверности, ), и этому может помочь создание безопасных общественных площадок для значимого общественного обсуждения и разрешения конфликтов ( среднее количество доказательств, высокая степень согласия ). Наконец, осведомленность и понимание общественности о рисках и ответных мерах по УЛР можно улучшить, опираясь на системы местных, коренных и научных знаний, а также на социальное обучение о рисках и возможностях реагирования на УЛС, характерных для данной местности (, высокая достоверность, ).{4.4.4.2, 4.4.5, таблица 4.9}
Достижение целей Организации Объединенных Наций в области устойчивого развития (ЦУР) и определение путей развития, устойчивого к изменению климата, частично зависит от амбициозных и устойчивых усилий по смягчению последствий, направленных на сдерживание УУЗ, в сочетании с эффективными адаптационными действиями по снижению воздействия и риска УЛР ( средний объем доказательств, высокая степень согласия ).
% PDF-1.4
%
989 0 объект
>
endobj
xref
989 822
0000000016 00000 н.
0000019028 00000 п.
0000019233 00000 п.
0000019269 00000 п.
0000029443 00000 п.
0000029603 00000 п.
0000029795 00000 п.
0000029944 00000 н.
0000030136 00000 п.
0000030283 00000 п.
0000030474 00000 п.
0000030621 00000 п.
0000030816 00000 п.
0000030964 00000 п.
0000031159 00000 п.
0000031309 00000 п.
0000031504 00000 п.
0000031654 00000 п.
0000031849 00000 п.
0000031999 00000 п.
0000032194 00000 п.
0000032344 00000 п.
0000032539 00000 п.
0000032689 00000 п.
0000032884 00000 п.
0000033033 00000 п.
0000033227 00000 н.
0000033376 00000 п.
0000033570 00000 п.
0000033718 00000 п.
0000033913 00000 п.
0000034061 00000 п.
0000034255 00000 п.
0000034405 00000 п.
0000034567 00000 п.
0000034717 00000 п.
0000034880 00000 п.
0000035031 00000 п.
0000036239 00000 п.
0000037446 00000 н.
0000038648 00000 п.
0000039846 00000 п.
0000040703 00000 п.
0000040812 00000 п. 0000040923 00000 п.
0000041201 00000 п.
0000041814 00000 п.
0000041984 00000 п.
0000042751 00000 п.
0000043493 00000 п.
0000043583 00000 п.
0000043844 00000 п.
0000044367 00000 п.
0000044660 00000 п.
0000045252 00000 п.
0000057949 00000 п.
0000069504 00000 п.
0000079483 00000 п.
0000087838 00000 п.
0000095296 00000 п.
0000102636 00000 н.
0000102788 00000 н.
0000109720 00000 н.
0000118017 00000 н.
0000165311 00000 н.
0000174918 00000 н.
0000230479 00000 п.
0000278442 00000 н.
0000278513 00000 н.
0000278599 00000 н.
0000282087 00000 н.
0000282353 00000 п.
0000282535 00000 н.
0000282950 00000 н.
0000338431 00000 н.
0000338702 00000 н.
0000339288 00000 п.
0000340246 00000 н.
0000340287 00000 н.
0000340974 00000 п.
0000341159 00000 н.
0000341455 00000 н.
0000341635 00000 н.
0000342255 00000 н.
0000342440 00000 н.
0000342624 00000 н.
0000343231 00000 н.
0000343416 00000 н.
0000344028 00000 н.
0000344212 00000 н.
0000344397 00000 н.
0000344582 00000 н.
0000040923 00000 п.
0000041201 00000 п.
0000041814 00000 п.
0000041984 00000 п.
0000042751 00000 п.
0000043493 00000 п.
0000043583 00000 п.
0000043844 00000 п.
0000044367 00000 п.
0000044660 00000 п.
0000045252 00000 п.
0000057949 00000 п.
0000069504 00000 п.
0000079483 00000 п.
0000087838 00000 п.
0000095296 00000 п.
0000102636 00000 н.
0000102788 00000 н.
0000109720 00000 н.
0000118017 00000 н.
0000165311 00000 н.
0000174918 00000 н.
0000230479 00000 п.
0000278442 00000 н.
0000278513 00000 н.
0000278599 00000 н.
0000282087 00000 н.
0000282353 00000 п.
0000282535 00000 н.
0000282950 00000 н.
0000338431 00000 н.
0000338702 00000 н.
0000339288 00000 п.
0000340246 00000 н.
0000340287 00000 н.
0000340974 00000 п.
0000341159 00000 н.
0000341455 00000 н.
0000341635 00000 н.
0000342255 00000 н.
0000342440 00000 н.
0000342624 00000 н.
0000343231 00000 н.
0000343416 00000 н.
0000344028 00000 н.
0000344212 00000 н.
0000344397 00000 н.
0000344582 00000 н. 0000344767 00000 н.
0000344951 00000 н.
0000345136 00000 п.
0000345319 00000 п.
0000345504 00000 н.
0000345689 00000 н.
0000345873 00000 н.
0000346058 00000 н.
0000346242 00000 п.
0000346427 00000 н.
0000346612 00000 н.
0000346797 00000 н.
0000346982 00000 п.
0000347167 00000 н.
0000347351 00000 п.
0000347535 00000 н.
0000347719 00000 п.
0000347902 00000 н.
0000348085 00000 п.
0000348270 00000 н.
0000348455 00000 н.
0000348640 00000 н.
0000348824 00000 н.
0000349009 00000 н.
0000349194 00000 п.
0000349378 00000 п.
0000349562 00000 н.
0000349745 00000 н.
0000349929 00000 н.
0000350114 00000 н.
0000350298 00000 н.
0000350483 00000 н.
0000350667 00000 н.
0000350852 00000 н.
0000351037 00000 п.
0000351221 00000 н.
0000351405 00000 н.
0000351590 00000 н.
0000351775 00000 н.
0000351958 00000 н.
0000352142 00000 н.
0000352328 00000 н.
0000352513 00000 н.
0000352700 00000 н.
0000352887 00000 н.
0000353073 00000 н.
0000353261 00000 н.
0000353448 00000 н.
0000344767 00000 н.
0000344951 00000 н.
0000345136 00000 п.
0000345319 00000 п.
0000345504 00000 н.
0000345689 00000 н.
0000345873 00000 н.
0000346058 00000 н.
0000346242 00000 п.
0000346427 00000 н.
0000346612 00000 н.
0000346797 00000 н.
0000346982 00000 п.
0000347167 00000 н.
0000347351 00000 п.
0000347535 00000 н.
0000347719 00000 п.
0000347902 00000 н.
0000348085 00000 п.
0000348270 00000 н.
0000348455 00000 н.
0000348640 00000 н.
0000348824 00000 н.
0000349009 00000 н.
0000349194 00000 п.
0000349378 00000 п.
0000349562 00000 н.
0000349745 00000 н.
0000349929 00000 н.
0000350114 00000 н.
0000350298 00000 н.
0000350483 00000 н.
0000350667 00000 н.
0000350852 00000 н.
0000351037 00000 п.
0000351221 00000 н.
0000351405 00000 н.
0000351590 00000 н.
0000351775 00000 н.
0000351958 00000 н.
0000352142 00000 н.
0000352328 00000 н.
0000352513 00000 н.
0000352700 00000 н.
0000352887 00000 н.
0000353073 00000 н.
0000353261 00000 н.
0000353448 00000 н. 0000354054 00000 н.
0000354240 00000 н.
0000354425 00000 н.
0000355011 00000 н.
0000355196 00000 н.
0000355791 00000 н.
0000355977 00000 н.
0000356552 00000 н.
0000356737 00000 н.
0000356924 00000 н.
0000357110 00000 н.
0000357294 00000 н.
0000357480 00000 н.
0000357664 00000 н.
0000357850 00000 н.
0000358036 00000 н.
0000358221 00000 н.
0000358407 00000 н.
0000358593 00000 н.
0000358778 00000 н.
0000358964 00000 н.
0000359148 00000 н.
0000359333 00000 п.
0000359519 00000 п.
0000359705 00000 н.
0000359891 00000 н.
0000360077 00000 н.
0000360262 00000 н.
0000360447 00000 н.
0000360631 00000 н.
0000360815 00000 н.
0000361000 00000 н.
0000361186 00000 п.
0000361372 00000 н.
0000361558 00000 н.
0000361742 00000 н.
0000361928 00000 н.
0000362114 00000 п.
0000362299 00000 н.
0000362484 00000 н.
0000362668 00000 н.
0000362853 00000 н.
0000363038 00000 н.
0000363223 00000 н.
0000363409 00000 н.
0000363594 00000 н.
0000363780 00000 п.
0000363966 00000 н.
0000354054 00000 н.
0000354240 00000 н.
0000354425 00000 н.
0000355011 00000 н.
0000355196 00000 н.
0000355791 00000 н.
0000355977 00000 н.
0000356552 00000 н.
0000356737 00000 н.
0000356924 00000 н.
0000357110 00000 н.
0000357294 00000 н.
0000357480 00000 н.
0000357664 00000 н.
0000357850 00000 н.
0000358036 00000 н.
0000358221 00000 н.
0000358407 00000 н.
0000358593 00000 н.
0000358778 00000 н.
0000358964 00000 н.
0000359148 00000 н.
0000359333 00000 п.
0000359519 00000 п.
0000359705 00000 н.
0000359891 00000 н.
0000360077 00000 н.
0000360262 00000 н.
0000360447 00000 н.
0000360631 00000 н.
0000360815 00000 н.
0000361000 00000 н.
0000361186 00000 п.
0000361372 00000 н.
0000361558 00000 н.
0000361742 00000 н.
0000361928 00000 н.
0000362114 00000 п.
0000362299 00000 н.
0000362484 00000 н.
0000362668 00000 н.
0000362853 00000 н.
0000363038 00000 н.
0000363223 00000 н.
0000363409 00000 н.
0000363594 00000 н.
0000363780 00000 п.
0000363966 00000 н. 0000364152 00000 н.
0000364337 00000 н.
0000364523 00000 п.
0000364709 00000 н.
0000364895 00000 н.
0000365081 00000 н.
0000365267 00000 н.
0000365453 00000 н.
0000365639 00000 п.
0000365824 00000 н.
0000366008 00000 н.
0000366193 00000 н.
0000366821 00000 н.
0000367007 00000 н.
0000367191 00000 н.
0000367374 00000 н.
0000367560 00000 н.
0000367744 00000 н.
0000367929 00000 н.
0000368114 00000 н.
0000368300 00000 н.
0000368484 00000 н.
0000368670 00000 н.
0000368855 00000 н.
0000369040 00000 н.
0000369225 00000 н.
0000369411 00000 п.
0000369596 00000 н.
0000369782 00000 н.
0000369965 00000 н.
0000370151 00000 п.
0000370337 00000 н.
0000370522 00000 н.
0000370707 00000 н.
0000370893 00000 н.
0000371078 00000 н.
0000371262 00000 н.
0000371447 00000 н.
0000371632 00000 н.
0000371816 00000 н.
0000372000 00000 н.
0000372186 00000 н.
0000372370 00000 н.
0000372556 00000 н.
0000372742 00000 н.
0000372928 00000 н.
0000373113 00000 н.
0000373298 00000 н.
0000364152 00000 н.
0000364337 00000 н.
0000364523 00000 п.
0000364709 00000 н.
0000364895 00000 н.
0000365081 00000 н.
0000365267 00000 н.
0000365453 00000 н.
0000365639 00000 п.
0000365824 00000 н.
0000366008 00000 н.
0000366193 00000 н.
0000366821 00000 н.
0000367007 00000 н.
0000367191 00000 н.
0000367374 00000 н.
0000367560 00000 н.
0000367744 00000 н.
0000367929 00000 н.
0000368114 00000 н.
0000368300 00000 н.
0000368484 00000 н.
0000368670 00000 н.
0000368855 00000 н.
0000369040 00000 н.
0000369225 00000 н.
0000369411 00000 п.
0000369596 00000 н.
0000369782 00000 н.
0000369965 00000 н.
0000370151 00000 п.
0000370337 00000 н.
0000370522 00000 н.
0000370707 00000 н.
0000370893 00000 н.
0000371078 00000 н.
0000371262 00000 н.
0000371447 00000 н.
0000371632 00000 н.
0000371816 00000 н.
0000372000 00000 н.
0000372186 00000 н.
0000372370 00000 н.
0000372556 00000 н.
0000372742 00000 н.
0000372928 00000 н.
0000373113 00000 н.
0000373298 00000 н. 0000373484 00000 н.
0000373670 00000 н.
0000374263 00000 н.
0000374447 00000 н.
0000375025 00000 н.
0000375209 00000 н.
0000375788 00000 н.
0000375972 00000 н.
0000376156 00000 н.
0000376727 00000 н.
0000376911 00000 н.
0000377095 00000 п.
0000377279 00000 н.
0000377463 00000 н.
0000377648 00000 н.
0000377831 00000 н.
0000378015 00000 н.
0000378197 00000 н.
0000378380 00000 н.
0000378563 00000 н.
0000378746 00000 н.
0000378930 00000 н.
0000379114 00000 н.
0000379297 00000 н.
0000379480 00000 н.
0000379665 00000 н.
0000379849 00000 н.
0000380032 00000 н.
0000380216 00000 н.
0000380398 00000 н.
0000380582 00000 н.
0000380765 00000 н.
0000380948 00000 н.
0000381132 00000 н.
0000381314 00000 н.
0000381496 00000 н.
0000381680 00000 н.
0000381863 00000 н.
0000382047 00000 н.
0000382231 00000 н.
0000382415 00000 н.
0000382599 00000 н.
0000382783 00000 н.
0000382967 00000 н.
0000383151 00000 п.
0000383335 00000 н.
0000383519 00000 н.
0000383704 00000 н.
0000373484 00000 н.
0000373670 00000 н.
0000374263 00000 н.
0000374447 00000 н.
0000375025 00000 н.
0000375209 00000 н.
0000375788 00000 н.
0000375972 00000 н.
0000376156 00000 н.
0000376727 00000 н.
0000376911 00000 н.
0000377095 00000 п.
0000377279 00000 н.
0000377463 00000 н.
0000377648 00000 н.
0000377831 00000 н.
0000378015 00000 н.
0000378197 00000 н.
0000378380 00000 н.
0000378563 00000 н.
0000378746 00000 н.
0000378930 00000 н.
0000379114 00000 н.
0000379297 00000 н.
0000379480 00000 н.
0000379665 00000 н.
0000379849 00000 н.
0000380032 00000 н.
0000380216 00000 н.
0000380398 00000 н.
0000380582 00000 н.
0000380765 00000 н.
0000380948 00000 н.
0000381132 00000 н.
0000381314 00000 н.
0000381496 00000 н.
0000381680 00000 н.
0000381863 00000 н.
0000382047 00000 н.
0000382231 00000 н.
0000382415 00000 н.
0000382599 00000 н.
0000382783 00000 н.
0000382967 00000 н.
0000383151 00000 п.
0000383335 00000 н.
0000383519 00000 н.
0000383704 00000 н. 0000383888 00000 н.
0000384072 00000 н.
0000384254 00000 н.
0000384436 00000 н.
0000384620 00000 н.
0000384804 00000 н.
0000384987 00000 н.
0000385171 00000 п.
0000385354 00000 н.
0000385537 00000 н.
0000385722 00000 н.
0000385904 00000 н.
0000386088 00000 н.
0000386272 00000 н.
0000386456 00000 п.
0000386640 00000 н.
0000386824 00000 н.
0000387007 00000 н.
0000387189 00000 п.
0000387373 00000 п.
0000387556 00000 н.
0000387741 00000 н.
0000387925 00000 п.
0000388108 00000 п.
0000388291 00000 п.
0000388475 00000 п.
0000388658 00000 н.
0000388842 00000 н.
0000389026 00000 н.
0000389210 00000 п.
0000389393 00000 п.
0000389577 00000 н.
0000389762 00000 н.
0000389947 00000 н.
00003
0000383888 00000 н.
0000384072 00000 н.
0000384254 00000 н.
0000384436 00000 н.
0000384620 00000 н.
0000384804 00000 н.
0000384987 00000 н.
0000385171 00000 п.
0000385354 00000 н.
0000385537 00000 н.
0000385722 00000 н.
0000385904 00000 н.
0000386088 00000 н.
0000386272 00000 н.
0000386456 00000 п.
0000386640 00000 н.
0000386824 00000 н.
0000387007 00000 н.
0000387189 00000 п.
0000387373 00000 п.
0000387556 00000 н.
0000387741 00000 н.
0000387925 00000 п.
0000388108 00000 п.
0000388291 00000 п.
0000388475 00000 п.
0000388658 00000 н.
0000388842 00000 н.
0000389026 00000 н.
0000389210 00000 п.
0000389393 00000 п.
0000389577 00000 н.
0000389762 00000 н.
0000389947 00000 н.
00003
00000 н. 00003 00000 н. 00003
00000 н. 0000390865 00000 н. 0000391049 00000 н. 0000391233 00000 н. 0000391416 00000 н. 0000391597 00000 н. 0000391780 00000 н. 0000391965 00000 н. 0000392148 00000 п. 0000392332 00000 н. 0000392515 00000 н. 0000392699 00000 н.
0000393253 00000 н.
0000393439 00000 н.
0000393982 00000 н.
0000394167 00000 н.
0000394718 00000 н.
0000394904 00000 н.
0000395441 00000 п.
0000395626 00000 н.
0000395813 00000 н.
0000396357 00000 н.
0000396543 00000 н.
0000396728 00000 н.
0000397254 00000 н.
0000397439 00000 н.
0000397966 00000 н.
0000398152 00000 н.
0000398681 00000 н.
0000398866 00000 н.
0000399053 00000 н.
0000399239 00000 н.
0000399425 00000 н.
0000399609 00000 н.
0000399794 00000 н.
0000399980 00000 н.
0000400166 00000 н.
0000400350 00000 н.
0000400535 00000 п.
0000400721 00000 н.
0000400905 00000 н.
0000401091 00000 н.
0000401276 00000 н.
0000401460 00000 н.
0000401645 00000 н.
0000401830 00000 н.
0000402015 00000 н.
0000402201 00000 н.
0000402386 00000 н.
0000402571 00000 н.
0000402756 00000 н.
0000402940 00000 н.
0000403125 00000 н.
0000403311 00000 н.
0000403497 00000 н.
0000403683 00000 н.
0000403869 00000 н.
0000404055 00000 н.
0000404241 00000 н.
0000392699 00000 н.
0000393253 00000 н.
0000393439 00000 н.
0000393982 00000 н.
0000394167 00000 н.
0000394718 00000 н.
0000394904 00000 н.
0000395441 00000 п.
0000395626 00000 н.
0000395813 00000 н.
0000396357 00000 н.
0000396543 00000 н.
0000396728 00000 н.
0000397254 00000 н.
0000397439 00000 н.
0000397966 00000 н.
0000398152 00000 н.
0000398681 00000 н.
0000398866 00000 н.
0000399053 00000 н.
0000399239 00000 н.
0000399425 00000 н.
0000399609 00000 н.
0000399794 00000 н.
0000399980 00000 н.
0000400166 00000 н.
0000400350 00000 н.
0000400535 00000 п.
0000400721 00000 н.
0000400905 00000 н.
0000401091 00000 н.
0000401276 00000 н.
0000401460 00000 н.
0000401645 00000 н.
0000401830 00000 н.
0000402015 00000 н.
0000402201 00000 н.
0000402386 00000 н.
0000402571 00000 н.
0000402756 00000 н.
0000402940 00000 н.
0000403125 00000 н.
0000403311 00000 н.
0000403497 00000 н.
0000403683 00000 н.
0000403869 00000 н.
0000404055 00000 н.
0000404241 00000 н. 0000404426 00000 н.
0000404610 00000 н.
0000404796 00000 н.
0000404982 00000 н.
0000405168 00000 н.
0000405353 00000 п.
0000405539 00000 н.
0000405724 00000 н.
0000405909 00000 н.
0000406092 00000 н.
0000406278 00000 н.
0000406463 00000 н.
0000406649 00000 п.
0000406834 00000 н.
0000407019 00000 п.
0000407203 00000 н.
0000407388 00000 н.
0000407574 00000 н.
0000407758 00000 н.
0000407944 00000 н.
0000408129 00000 н.
0000408314 00000 н.
0000408498 00000 п.
0000408684 00000 н.
0000408869 00000 н.
0000409054 00000 н.
0000409240 00000 н.
0000409426 00000 п.
0000409610 00000 н.
0000409795 00000 н.
0000409981 00000 н.
0000410167 00000 н.
0000410352 00000 п.
0000410535 00000 п.
0000410719 00000 п.
0000410904 00000 н.
0000411089 00000 н.
0000411274 00000 н.
0000411459 00000 н.
0000411644 00000 п.
0000411828 00000 н.
0000412013 00000 н.
0000412199 00000 н.
0000412383 00000 п.
0000412568 00000 н.
0000412753 00000 н.
0000412937 00000 н.
0000413123 00000 п.
0000404426 00000 н.
0000404610 00000 н.
0000404796 00000 н.
0000404982 00000 н.
0000405168 00000 н.
0000405353 00000 п.
0000405539 00000 н.
0000405724 00000 н.
0000405909 00000 н.
0000406092 00000 н.
0000406278 00000 н.
0000406463 00000 н.
0000406649 00000 п.
0000406834 00000 н.
0000407019 00000 п.
0000407203 00000 н.
0000407388 00000 н.
0000407574 00000 н.
0000407758 00000 н.
0000407944 00000 н.
0000408129 00000 н.
0000408314 00000 н.
0000408498 00000 п.
0000408684 00000 н.
0000408869 00000 н.
0000409054 00000 н.
0000409240 00000 н.
0000409426 00000 п.
0000409610 00000 н.
0000409795 00000 н.
0000409981 00000 н.
0000410167 00000 н.
0000410352 00000 п.
0000410535 00000 п.
0000410719 00000 п.
0000410904 00000 н.
0000411089 00000 н.
0000411274 00000 н.
0000411459 00000 н.
0000411644 00000 п.
0000411828 00000 н.
0000412013 00000 н.
0000412199 00000 н.
0000412383 00000 п.
0000412568 00000 н.
0000412753 00000 н.
0000412937 00000 н.
0000413123 00000 п. 0000413309 00000 н.
0000413495 00000 н.
0000413681 00000 н.
0000413867 00000 н.
0000414053 00000 н.
0000414239 00000 н.
0000414425 00000 н.
0000414610 00000 н.
0000414795 00000 н.
0000414981 00000 п.
0000415167 00000 н.
0000415353 00000 п.
0000415539 00000 н.
0000415724 00000 н.
0000415909 00000 н.
0000416094 00000 н.
0000416279 00000 н.
0000416464 00000 н.
0000416649 00000 н.
0000416833 00000 н.
0000417019 00000 н.
0000417203 00000 н.
0000417387 00000 н.
0000417571 00000 н.
0000417757 00000 н.
0000417942 00000 н.
0000418126 00000 н.
0000418310 00000 п.
0000418496 00000 н.
0000418681 00000 п.
0000418865 00000 н.
0000419050 00000 н.
0000419234 00000 н.
0000419420 00000 н.
0000419606 00000 н.
0000419792 00000 н.
0000419978 00000 н.
0000420163 00000 н.
0000420349 00000 н.
0000420535 00000 н.
0000420721 00000 н.
0000420903 00000 н.
0000421088 00000 н.
0000421273 00000 н.
0000421459 00000 н.
0000421643 00000 н.
0000421829 00000 н.
0000422014 00000 н.
0000413309 00000 н.
0000413495 00000 н.
0000413681 00000 н.
0000413867 00000 н.
0000414053 00000 н.
0000414239 00000 н.
0000414425 00000 н.
0000414610 00000 н.
0000414795 00000 н.
0000414981 00000 п.
0000415167 00000 н.
0000415353 00000 п.
0000415539 00000 н.
0000415724 00000 н.
0000415909 00000 н.
0000416094 00000 н.
0000416279 00000 н.
0000416464 00000 н.
0000416649 00000 н.
0000416833 00000 н.
0000417019 00000 н.
0000417203 00000 н.
0000417387 00000 н.
0000417571 00000 н.
0000417757 00000 н.
0000417942 00000 н.
0000418126 00000 н.
0000418310 00000 п.
0000418496 00000 н.
0000418681 00000 п.
0000418865 00000 н.
0000419050 00000 н.
0000419234 00000 н.
0000419420 00000 н.
0000419606 00000 н.
0000419792 00000 н.
0000419978 00000 н.
0000420163 00000 н.
0000420349 00000 н.
0000420535 00000 н.
0000420721 00000 н.
0000420903 00000 н.
0000421088 00000 н.
0000421273 00000 н.
0000421459 00000 н.
0000421643 00000 н.
0000421829 00000 н.
0000422014 00000 н. 0000422200 00000 н.
0000422385 00000 п.
0000422569 00000 н.
0000422753 00000 п.
0000422938 00000 п.
0000423123 00000 п.
0000423308 00000 п.
0000423494 00000 н.
0000423679 00000 н.
0000423865 00000 н.
0000424050 00000 н.
0000424235 00000 н.
0000424421 00000 н.
0000424606 00000 н.
0000424792 00000 н.
0000424976 00000 н.
0000425162 00000 п.
0000425348 00000 н.
0000425533 00000 н.
0000425718 00000 н.
0000425903 00000 н.
0000426089 00000 н.
0000426275 00000 н.
0000426459 00000 н.
0000426643 00000 н.
0000426829 00000 н.
0000427014 00000 н.
0000427199 00000 н.
0000427385 00000 н.
0000427571 00000 н.
0000427757 00000 н.
0000427943 00000 н.
0000428129 00000 н.
0000428314 00000 п.
0000428499 00000 н.
0000428684 00000 н.
0000428870 00000 н.
0000429054 00000 н.
0000429240 00000 н.
0000429425 00000 н.
0000429611 00000 н.
0000429795 00000 н.
0000429978 00000 н.
0000430162 00000 п.
0000430345 00000 п.
0000430530 00000 н.
0000431068 00000 н.
0000431252 00000 н.
0000422200 00000 н.
0000422385 00000 п.
0000422569 00000 н.
0000422753 00000 п.
0000422938 00000 п.
0000423123 00000 п.
0000423308 00000 п.
0000423494 00000 н.
0000423679 00000 н.
0000423865 00000 н.
0000424050 00000 н.
0000424235 00000 н.
0000424421 00000 н.
0000424606 00000 н.
0000424792 00000 н.
0000424976 00000 н.
0000425162 00000 п.
0000425348 00000 н.
0000425533 00000 н.
0000425718 00000 н.
0000425903 00000 н.
0000426089 00000 н.
0000426275 00000 н.
0000426459 00000 н.
0000426643 00000 н.
0000426829 00000 н.
0000427014 00000 н.
0000427199 00000 н.
0000427385 00000 н.
0000427571 00000 н.
0000427757 00000 н.
0000427943 00000 н.
0000428129 00000 н.
0000428314 00000 п.
0000428499 00000 н.
0000428684 00000 н.
0000428870 00000 н.
0000429054 00000 н.
0000429240 00000 н.
0000429425 00000 н.
0000429611 00000 н.
0000429795 00000 н.
0000429978 00000 н.
0000430162 00000 п.
0000430345 00000 п.
0000430530 00000 н.
0000431068 00000 н.
0000431252 00000 н.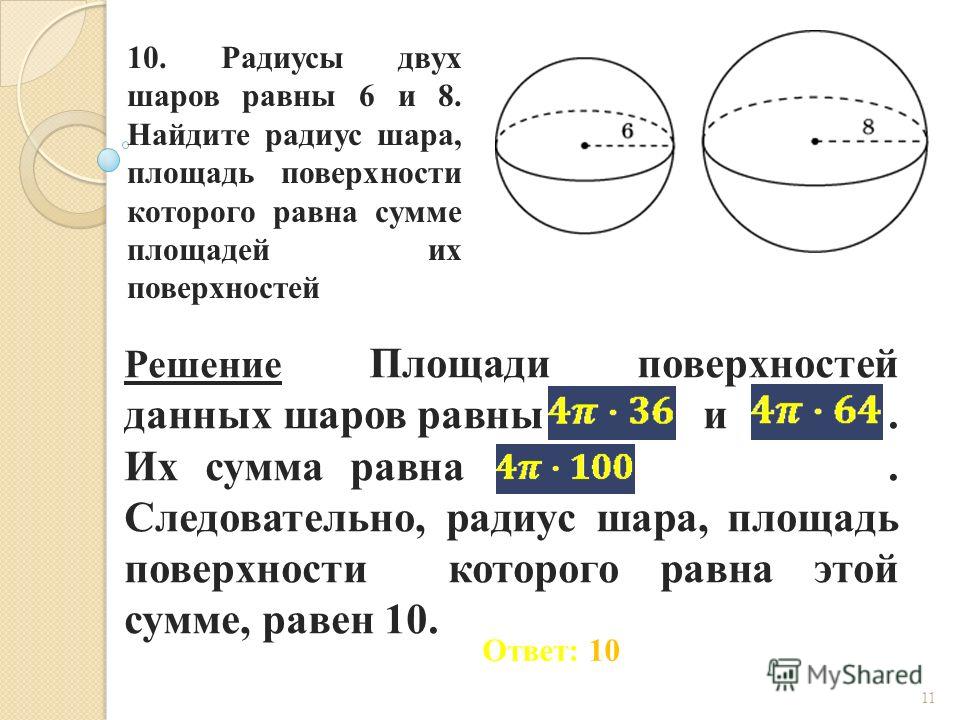 0000431781 00000 н.
0000431963 00000 н.
0000432148 00000 н.
0000432682 00000 н.
0000432866 00000 н.
0000433392 00000 н.
0000433574 00000 н.
0000433759 00000 п.
0000433943 00000 н.
0000434127 00000 н.
0000434310 00000 п.
0000434493 00000 п.
0000434676 00000 н.
0000434860 00000 н.
0000435044 00000 н.
0000435229 00000 п.
0000435412 00000 н.
0000435596 00000 п.
0000435779 00000 п.
0000435963 00000 н.
0000436146 00000 п.
0000436330 00000 н.
0000436512 00000 н.
0000436695 00000 н.
0000436879 00000 н.
0000437063 00000 н.
0000437248 00000 п.
0000437432 00000 н.
0000437616 00000 п.
0000437799 00000 н.
0000437982 00000 п.
0000438166 00000 п.
0000438350 00000 н.
0000438534 00000 п.
0000438718 00000 п.
0000438902 00000 н.
0000439086 00000 н.
0000439269 00000 н.
0000439454 00000 п.
0000439638 00000 н.
0000439821 00000 н.
0000440005 00000 н.
0000440188 00000 п.
0000440372 00000 п.
0000440554 00000 н.
0000440738 00000 п.
0000440920 00000 н.
0000441104 00000 н.
0000431781 00000 н.
0000431963 00000 н.
0000432148 00000 н.
0000432682 00000 н.
0000432866 00000 н.
0000433392 00000 н.
0000433574 00000 н.
0000433759 00000 п.
0000433943 00000 н.
0000434127 00000 н.
0000434310 00000 п.
0000434493 00000 п.
0000434676 00000 н.
0000434860 00000 н.
0000435044 00000 н.
0000435229 00000 п.
0000435412 00000 н.
0000435596 00000 п.
0000435779 00000 п.
0000435963 00000 н.
0000436146 00000 п.
0000436330 00000 н.
0000436512 00000 н.
0000436695 00000 н.
0000436879 00000 н.
0000437063 00000 н.
0000437248 00000 п.
0000437432 00000 н.
0000437616 00000 п.
0000437799 00000 н.
0000437982 00000 п.
0000438166 00000 п.
0000438350 00000 н.
0000438534 00000 п.
0000438718 00000 п.
0000438902 00000 н.
0000439086 00000 н.
0000439269 00000 н.
0000439454 00000 п.
0000439638 00000 н.
0000439821 00000 н.
0000440005 00000 н.
0000440188 00000 п.
0000440372 00000 п.
0000440554 00000 н.
0000440738 00000 п.
0000440920 00000 н.
0000441104 00000 н. 0000441288 00000 н.
0000441473 00000 н.
0000441656 00000 н.
0000441840 00000 н.
0000442022 00000 н.
0000442206 00000 н.
0000442390 00000 н.
0000442574 00000 н.
0000442758 00000 н.
0000442942 00000 н.
0000443126 00000 н.
0000443310 00000 н.
0000443495 00000 н.
0000443679 00000 н.
0000443863 00000 н.
0000444047 00000 н.
0000444231 00000 п.
0000444414 00000 н.
0000444597 00000 н.
0000444781 00000 н.
0000444965 00000 н.
0000445148 00000 п.
0000445331 00000 п.
0000445515 00000 н.
0000445698 00000 п.
0000445882 00000 н.
0000446066 00000 н.
0000446250 00000 н.
0000446434 00000 н.
0000446618 00000 н.
0000446802 00000 н.
0000446986 00000 н.
0000447170 00000 н.
0000447354 00000 н.
0000447539 00000 н.
0000447723 00000 н.
0000447907 00000 н.
0000448091 00000 н.
0000448275 00000 н.
0000448459 00000 н.
0000448642 00000 н.
0000448826 00000 н.
0000449010 00000 н.
0000449194 00000 н.
0000449378 00000 н.
0000449563 00000 н.
0000449747 00000 н.
0000449931 00000 н.
0000441288 00000 н.
0000441473 00000 н.
0000441656 00000 н.
0000441840 00000 н.
0000442022 00000 н.
0000442206 00000 н.
0000442390 00000 н.
0000442574 00000 н.
0000442758 00000 н.
0000442942 00000 н.
0000443126 00000 н.
0000443310 00000 н.
0000443495 00000 н.
0000443679 00000 н.
0000443863 00000 н.
0000444047 00000 н.
0000444231 00000 п.
0000444414 00000 н.
0000444597 00000 н.
0000444781 00000 н.
0000444965 00000 н.
0000445148 00000 п.
0000445331 00000 п.
0000445515 00000 н.
0000445698 00000 п.
0000445882 00000 н.
0000446066 00000 н.
0000446250 00000 н.
0000446434 00000 н.
0000446618 00000 н.
0000446802 00000 н.
0000446986 00000 н.
0000447170 00000 н.
0000447354 00000 н.
0000447539 00000 н.
0000447723 00000 н.
0000447907 00000 н.
0000448091 00000 н.
0000448275 00000 н.
0000448459 00000 н.
0000448642 00000 н.
0000448826 00000 н.
0000449010 00000 н.
0000449194 00000 н.
0000449378 00000 н.
0000449563 00000 н.
0000449747 00000 н.
0000449931 00000 н. 0000450115 00000 п.
0000450299 00000 н.
0000450483 00000 н.
0000450667 00000 н.
0000450851 00000 п.
0000451035 00000 п.
0000451217 00000 н.
0000451401 00000 п.
0000451586 00000 н.
0000451768 00000 н.
0000451952 00000 п.
0000452135 00000 п.
0000452319 00000 п.
0000452502 00000 н.
0000452685 00000 н.
0000452867 00000 н.
0000453051 00000 н.
0000453234 00000 н.
0000453417 00000 н.
0000453601 00000 п.
0000453783 00000 н.
0000453967 00000 н.
0000454151 00000 п.
0000454335 00000 п.
0000454518 00000 п.
0000454700 00000 н.
0000454884 00000 н.
0000455068 00000 н.
0000455252 00000 н.
0000455436 00000 н.
0000455621 00000 н.
0000455804 00000 н.
0000455987 00000 н.
0000456170 00000 н.
0000456352 00000 п.
0000456534 00000 н.
0000456717 00000 н.
0000456900 00000 н.
0000457083 00000 н.
0000457267 00000 н.
0000457450 00000 н.
0000457635 00000 н.
0000457819 00000 п.
0000458003 00000 н.
0000458187 00000 н.
0000458371 00000 п.
0000458554 00000 н.
0000458737 00000 н.
0000450115 00000 п.
0000450299 00000 н.
0000450483 00000 н.
0000450667 00000 н.
0000450851 00000 п.
0000451035 00000 п.
0000451217 00000 н.
0000451401 00000 п.
0000451586 00000 н.
0000451768 00000 н.
0000451952 00000 п.
0000452135 00000 п.
0000452319 00000 п.
0000452502 00000 н.
0000452685 00000 н.
0000452867 00000 н.
0000453051 00000 н.
0000453234 00000 н.
0000453417 00000 н.
0000453601 00000 п.
0000453783 00000 н.
0000453967 00000 н.
0000454151 00000 п.
0000454335 00000 п.
0000454518 00000 п.
0000454700 00000 н.
0000454884 00000 н.
0000455068 00000 н.
0000455252 00000 н.
0000455436 00000 н.
0000455621 00000 н.
0000455804 00000 н.
0000455987 00000 н.
0000456170 00000 н.
0000456352 00000 п.
0000456534 00000 н.
0000456717 00000 н.
0000456900 00000 н.
0000457083 00000 н.
0000457267 00000 н.
0000457450 00000 н.
0000457635 00000 н.
0000457819 00000 п.
0000458003 00000 н.
0000458187 00000 н.
0000458371 00000 п.
0000458554 00000 н.
0000458737 00000 н.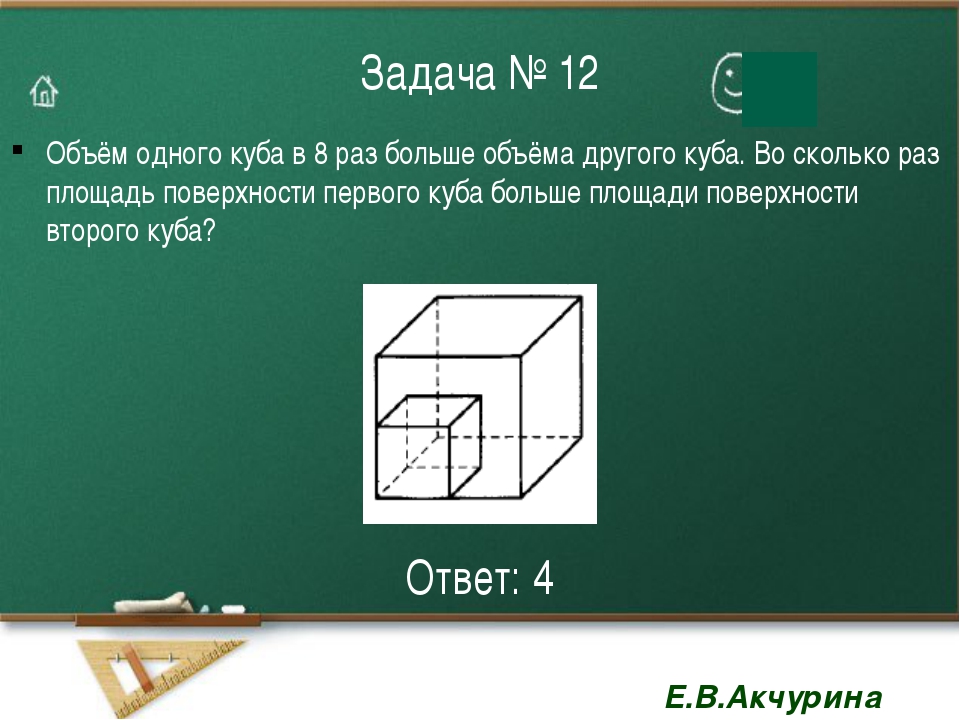 0000458919 00000 н.
0000459102 00000 п.
0000459285 00000 п.
0000459468 00000 н.
0000459651 00000 п.
0000459836 00000 н.
0000460020 00000 н.
0000460204 00000 н.
0000460387 00000 н.
0000460571 00000 п.
0000460755 00000 н.
0000460939 00000 п.
0000461123 00000 н.
0000461305 00000 н.
0000461489 00000 н.
0000461672 00000 н.
0000461857 00000 н.
0000462041 00000 н.
0000462224 00000 н.
0000462408 00000 п.
0000462592 00000 н.
0000462776 00000 н.
0000462959 00000 н.
0000463143 00000 п.
0000463327 00000 н.
0000463511 00000 н.
0000463694 00000 н.
0000463879 00000 п.
0000464062 00000 н.
0000464247 00000 н.
0000464432 00000 н.
0000464617 00000 н.
0000464802 00000 н.
0000464986 00000 н.
0000465171 00000 п.
0000465356 00000 п.
0000465541 00000 п.
0000465726 00000 н.
0000465911 00000 н.
0000466096 00000 н.
0000466281 00000 п.
0000466466 00000 н.
0000466651 00000 п.
0000466836 00000 н.
0000467021 00000 п.
0000467205 00000 н.
0000467390 00000 н.
0000467575 00000 н.
0000458919 00000 н.
0000459102 00000 п.
0000459285 00000 п.
0000459468 00000 н.
0000459651 00000 п.
0000459836 00000 н.
0000460020 00000 н.
0000460204 00000 н.
0000460387 00000 н.
0000460571 00000 п.
0000460755 00000 н.
0000460939 00000 п.
0000461123 00000 н.
0000461305 00000 н.
0000461489 00000 н.
0000461672 00000 н.
0000461857 00000 н.
0000462041 00000 н.
0000462224 00000 н.
0000462408 00000 п.
0000462592 00000 н.
0000462776 00000 н.
0000462959 00000 н.
0000463143 00000 п.
0000463327 00000 н.
0000463511 00000 н.
0000463694 00000 н.
0000463879 00000 п.
0000464062 00000 н.
0000464247 00000 н.
0000464432 00000 н.
0000464617 00000 н.
0000464802 00000 н.
0000464986 00000 н.
0000465171 00000 п.
0000465356 00000 п.
0000465541 00000 п.
0000465726 00000 н.
0000465911 00000 н.
0000466096 00000 н.
0000466281 00000 п.
0000466466 00000 н.
0000466651 00000 п.
0000466836 00000 н.
0000467021 00000 п.
0000467205 00000 н.
0000467390 00000 н.
0000467575 00000 н. 0000467760 00000 н.
0000467945 00000 н.
0000468130 00000 н.
0000468314 00000 н.
0000468498 00000 п.
0000468683 00000 п.
0000468868 00000 н.
0000469053 00000 н.
0000469238 00000 п.
0000469423 00000 н.
0000469608 00000 н.
0000469792 00000 н.
0000469977 00000 н.
0000470161 00000 п.
0000470346 00000 п.
0000470531 00000 п.
0000470716 00000 н.
0000470901 00000 н.
0000471085 00000 н.
0000471270 00000 н.
0000472919 00000 н.
0000473204 00000 н.
0000473699 00000 н.
0000474913 00000 н.
0000478342 00000 н.
0000478605 00000 н.
0000479024 00000 н.
0000480473 00000 п.
0000480886 00000 н.
0000481167 00000 н.
0000481611 00000 н.
0000481663 00000 н.
0000485040 00000 н.
0000485453 00000 н.
0000485505 00000 н.
0000486029 00000 н.
0000486248 00000 н.
0000486476 00000 н.
0000486704 00000 н.
0000486917 00000 н.
0000487154 00000 н.
0000487391 00000 н.
0000487610 00000 н.
0000487838 00000 н.
0000488066 00000 н.
0000488285 00000 н.
0000488546 00000 н.
0000488597 00000 н.
0000467760 00000 н.
0000467945 00000 н.
0000468130 00000 н.
0000468314 00000 н.
0000468498 00000 п.
0000468683 00000 п.
0000468868 00000 н.
0000469053 00000 н.
0000469238 00000 п.
0000469423 00000 н.
0000469608 00000 н.
0000469792 00000 н.
0000469977 00000 н.
0000470161 00000 п.
0000470346 00000 п.
0000470531 00000 п.
0000470716 00000 н.
0000470901 00000 н.
0000471085 00000 н.
0000471270 00000 н.
0000472919 00000 н.
0000473204 00000 н.
0000473699 00000 н.
0000474913 00000 н.
0000478342 00000 н.
0000478605 00000 н.
0000479024 00000 н.
0000480473 00000 п.
0000480886 00000 н.
0000481167 00000 н.
0000481611 00000 н.
0000481663 00000 н.
0000485040 00000 н.
0000485453 00000 н.
0000485505 00000 н.
0000486029 00000 н.
0000486248 00000 н.
0000486476 00000 н.
0000486704 00000 н.
0000486917 00000 н.
0000487154 00000 н.
0000487391 00000 н.
0000487610 00000 н.
0000487838 00000 н.
0000488066 00000 н.
0000488285 00000 н.
0000488546 00000 н.
0000488597 00000 н. 0000489020 00000 н.
0000489239 00000 н.
0000489458 00000 н.
0000489677 00000 н.
0000490799 00000 н.
0000491358 00000 н.
0000491410 00000 н.
0000492100 00000 н.
0000493525 00000 н.
0000494279 00000 н.
0000494331 00000 п.
0000495073 00000 н.
0000495293 00000 н.
0000495344 00000 н.
0000495645 00000 н.
0000496596 00000 н.
0000496824 00000 н.
0000496949 00000 н.
0000497037 00000 н.
0000497112 00000 н.
0000497416 00000 н.
0000497488 00000 н.
0000497590 00000 н.
0000497696 00000 н.
0000497770 00000 н.
0000497904 00000 н.
0000497978 00000 п.
0000498098 00000 н.
0000498172 00000 н.
0000498315 00000 н.
0000498389 00000 н.
0000498553 00000 п.
0000498705 00000 н.
0000498876 00000 н.
0000498948 00000 н.
0000499050 00000 н.
0000499192 00000 п.
0000499316 00000 н.
0000499388 00000 н.
0000499462 00000 н.
0000499644 00000 н.
0000499718 00000 н.
0000499906 00000 н.
0000499978 00000 н.
0000500169 00000 н.
0000500241 00000 н.
0000500357 00000 н.
0000500495 00000 н.
0000489020 00000 н.
0000489239 00000 н.
0000489458 00000 н.
0000489677 00000 н.
0000490799 00000 н.
0000491358 00000 н.
0000491410 00000 н.
0000492100 00000 н.
0000493525 00000 н.
0000494279 00000 н.
0000494331 00000 п.
0000495073 00000 н.
0000495293 00000 н.
0000495344 00000 н.
0000495645 00000 н.
0000496596 00000 н.
0000496824 00000 н.
0000496949 00000 н.
0000497037 00000 н.
0000497112 00000 н.
0000497416 00000 н.
0000497488 00000 н.
0000497590 00000 н.
0000497696 00000 н.
0000497770 00000 н.
0000497904 00000 н.
0000497978 00000 п.
0000498098 00000 н.
0000498172 00000 н.
0000498315 00000 н.
0000498389 00000 н.
0000498553 00000 п.
0000498705 00000 н.
0000498876 00000 н.
0000498948 00000 н.
0000499050 00000 н.
0000499192 00000 п.
0000499316 00000 н.
0000499388 00000 н.
0000499462 00000 н.
0000499644 00000 н.
0000499718 00000 н.
0000499906 00000 н.
0000499978 00000 н.
0000500169 00000 н.
0000500241 00000 н.
0000500357 00000 н.
0000500495 00000 н.

 Во сколько раз увеличится объем шара, если его радиус увеличить в пять раз?
Во сколько раз увеличится объем шара, если его радиус увеличить в пять раз? Объем одного шара в 2197 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Объем одного шара в 2197 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго? Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,44. Найдите объем шара.
Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,44. Найдите объем шара.
Leave A Comment