Действие магнитного поля на движущийся заряд. Сила Лоренца
Действие магнитного поля на движущийся заряд. Сила Лоренца
«Физика — 11 класс»
Магнитное поле действует с силой на движущиеся заряженные частицы, в то числе и на проводники с током.
Какова же сила, действующая на одну частицу?
1.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика X. Лоренца, создавшего электронную теорию строения вещества.
Силу Лоренца можно найти с помощью закона Ампера.
Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:
Так как сила (сила Ампера), действующая на участок проводника со стороны магнитного поля
равна F = | I | BΔl sin α,
а сила тока в проводнике равна
где
q — заряд частиц
n — концентрация частиц (т.е. число зарядов в единице объема)
v — скорость движения частиц
S — поперечное сечение проводника.
тогда получаем:
На каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:
где α — угол между вектором скорости и вектором магнитной индукции.
Сила Лоренца перпендикулярна векторам и .
2.
Направление силы Лоренца
Направление силы Лоренца определяется с помощью того же правила левой руки, что и направление силы Ампера:
Если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца F

3.
Если в пространстве, где движется заряженная частица, существует одновременно и электрическое поле, и магнитное поле, то суммарная сила, действующая на заряд, равна:
= эл + л
где сила, с которой электрическое поле действует на заряд q, равна Fэл = q.
4.
Значит сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости.
Под действием силы Лоренца меняется лишь направление скорости частицы.
5.
Движение заряженной частицы в однородном магнитном поле
Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля.
Магнитное поле не меняет модуль скорости движущейся частицы, значит остается неизменным и модуль силы Лоренца.
Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что
В однородном магнитном поле заряженная частица равномерно движется по окружности радиусом r.
Согласно второму закону Ньютона
Тогда радиус окружности, по которой движется частица, равен:
Время, за которое частица делает полный оборот (период обращения), равно:
6.
Использование действия магнитного поля на движущийся заряд.
Действие магнитного поля на движущийся заряд используют в телевизионных трубках-кинескопах, в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.
Сила Лоренца используется в циклотроне — ускорителе заряженных частиц для получения частиц с большими энергиями.
На действии магнитного поля основано также и устройство масс-спектрографов, позволяющих точно определять массы частиц..
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Магнитное поле. Физика, учебник для 11 класса — Класс!ная физика
Магнитное поле и взаимодействие токов — Магнитная индукция. Линии магнитной индукции — Модуль вектора магнитной индукции. Сила Ампера — Электроизмерительные приборы. Громкоговоритель — Действие магнитного поля на движущийся заряд. Сила Лоренца — Магнитные свойства вещества — Примеры решения задач — Краткие итоги главы
class-fizika.ru
FTF 3 semestr.ISAEV / 17
ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ТОКИ
2.1. Сила Лоренца. Движение заряженной частицы в однородном постоянном магнитном поле
Основные формулы
· Сила, действующая на электрический заряд , движущийся со скоростьюв магнитном поле
, (18)
где – вектор магнитной индукции поля.
· Модуль силы, действующей на заряженную частицу, движущуюся в магнитном поле
, (19)
где – модуль заряда частицы;– модуль вектора скорости;– модуль вектора индукции магнитного поля,– угол между векторамии.
· Направление силы определяется по правилу левой руки:
если ладонь левой руки расположить так, чтобы в нее входил вектор магнитной индукции , а четыре вытянутых пальца направить вдоль скорости движения положительного заряда (против направления движения отрицательного заряда), то отогнутый на 90° большой палец покажет направление силы, действующей на заряд.
· Если заряд движется в области, где существуют одновременно электрическое и магнитное поля, то на него действует полная сила
, (20)
формула (20) называется формулой Лоренца.
Методические рекомендации
1. Полная электромагнитная сила (сила Лоренца), действующая на заряд, определяется формулой (20). Данная формула справедлива как для постоянных, так и для переменных электрических и магнитных полей.
Эту силу разделяют на электрическую и магнитную составляющие. Если заряженная частица находится только в магнитном поле, то силу, определяемую выражением (18), обычно и называют силой Лоренца.
Важная особенность силы Лоренца – она всегда перпендикулярна вектору скорости заряда и поэтому не совершает над зарядом работы. Следовательно, в постоянном магнитном поле энергия движущейся заряженной частицы всегда постоянна.
Разделение полной электромагнитной силы на электрическую и магнитную зависит от выбора системы отсчета, так как магнитная составляющая силы Лоренца меняется при переходе от одной системы отсчета к другой, а значит, меняется и электрическая составляющая.
2. Под действием силы Лоренца заряженные частицы движутся в магнитном поле по криволинейным траекториям. Характер движения частицы в магнитном поле зависит от угла между первоначальным направлением скорости движения частицы и направлением линий индукции магнитного поля.
· Если скорость частицы перпендикулярна линиям магнитной индуции, то частица движется по круговой траектории (рис. 23).
Радиус окружности траектории
;
Рис. 23
период вращения частицы по окружности:
,
где – масса частицы;– модуль скорости частицы;– модуль вектора индукции магнитного поля;– модуль электрического заряда.
· Если заряженная частица движется вдоль линий магнитной индукции, сила Лоренца на нее не действует и характер ее движения не меняется.
· Если угол между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции (рис. 24).
Рис. 24
– тангенциальная составляющая скорости ;;
– нормальная составляющая скорости; ;
– шаг винтовой линии; .
3. При движении заряженной частицы в области пространства, занятой одновременно и электрическим и магнитным полями характер ее движения зависит от направления этих полей и величины сил, действующих с их стороны, а также от скорости частицы.
► Векторы ивзаимно-перпендикулярны и скоростьположительно заряженной частицы перпендикулярна силовым линиям этих полей. В этом случае на частицу действуют две силы: электрическаяи магнитная, которые могут быть как сонаправлены, так и противоположно направлены. Если силы противоположно направлены и равны по модулю (), то частица будет двигаться равномерно и прямолинейно, согласно первому закону Ньютона.
В случае если силы не уравновешивают друг друга, то движение частицы будет сложным: она будет двигаться с ускорением вдоль линии напряженности электрического поля и совершать вращательное движение вокруг линии индукции магнитного поля.
Если силы, действующие на движущуюся заряженную частицу сонаправлены, то движение частицы также будет представлять суперпозицию двух движений: прямолинейного с ускорением вдоль линий вектора и вращательного вокруг линий вектора.
► Частица влетает в область пространства параллельно векторам и. В этом случае на нее действует только электрическая сила(сила Лоренца, так каки). Под действием этой силычастица движется прямолинейно с ускорением.
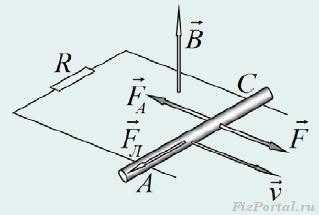
Пусть цилиндрический проводник движется в постоянном магнитном поле, так что вектор скорости v перпендикулярен оси цилиндра, а вектор индукции магнитного поля B перпендикулярен, как оси проводника, так и его скорости (рис. 509).
Вместе с проводником движутся и свободные заряды, находящиеся внутри него. Со стороны магнитного поля на эти заряды будут действовать силы Лоренца, направленные, в соответствии правила левой руки, вдоль оси проводника. В установившемся режиме сила Лоренца FЛ = qvB, действующая на частицу, будет уравновешена силой со стороны электрического поля Fэл = qE. Приравнивая эти силы, определим напряженность электрического поля в проводнике
Так сила Лоренца одинакова во всех точках проводника, то и электрическая сила также должна быть постоянна, то есть возникшее электрическое поле является однородным. Это электрическое поле можно также характеризовать разностью потенциалов между торцами цилиндра, которая равна
где l − длина проводника. Сила Лоренца, действующая на свободные заряды в проводнике, может являться сторонней силой, то есть приводить к возникновению электрического тока в замкнутом контуре, если его подключить к движущемуся проводнику.
 Вся
система помещена в однородное магнитное
поле, вектор индукции которого B перпендикулярен
плоскости шин. Для упрощения будем
считать, что сопротивления шин и
движущегося проводника (перемычки)
пренебрежимо малы по сравнению с
сопротивлением соединяющего
резистора R.
Если
к подвижному проводнику приложить
внешнюю силу F,
как показано на рисунке, то он придет в
движение. Под действие силы Лоренца
свободные заряды в проводнике придут
в движение, создавая избыточные заряды
на концах. Эти заряды создадут электрическое
поле во всем контуре, образованном
перемычкой, шинами и соединяющим
резистором, поэтому в контуре возникнет
электрический ток.
Вся
система помещена в однородное магнитное
поле, вектор индукции которого B перпендикулярен
плоскости шин. Для упрощения будем
считать, что сопротивления шин и
движущегося проводника (перемычки)
пренебрежимо малы по сравнению с
сопротивлением соединяющего
резистора R.
Если
к подвижному проводнику приложить
внешнюю силу F,
как показано на рисунке, то он придет в
движение. Под действие силы Лоренца
свободные заряды в проводнике придут
в движение, создавая избыточные заряды
на концах. Эти заряды создадут электрическое
поле во всем контуре, образованном
перемычкой, шинами и соединяющим
резистором, поэтому в контуре возникнет
электрический ток.
ЭДС равна произведению силы Лоренца на расстояние между шинами
По закону Ома сила возникшего в цепи электрического тока равна
Так как по проводнику идет электрический ток, то на него со стороны магнитного поля действует сила Ампера, равная
Уравнение второго закона Ньютона для перемычки имеет вид (в проекции на направление вектора скорости):
Под действием этих сил сначала перемычка будет двигаться ускорено, причем с увеличением скорости модуль ускорения будет уменьшаться, наконец, перемычка станет двигаться с постоянной скоростью, которая называется скоростью установившегося движения v. Величину этой скорости можно найти из условия F = FA, из которого следует
За промежуток времени Δt перемычка смещается на расстояние Δx = vΔt, следовательно, внешняя сила при этом совершает работу
За это же время на резисторе выделится количество теплоты равное
Взаимодействие двух параллельных проводников с током |
|
Пусть b – расстояние между двумя параллельными, бесконечно длинными проводниками (рис. 2.2). Задачу следует решать так: один из проводников создаёт магнитное поле, второйнаходится в этом поле. Магнитная индукция, создаваемая током на расстоянииb от него:
Рис. 2.2 Если илежат в одной плоскости, то угол междуипрямой, следовательно. Тогда сила, действующая на элементтока,
На каждую единицу длины проводника действует сила
(разумеется, со стороны первого проводника на второй действует точно такая же сила).
|
studfiles.net
Силы в электрическом поле. Силы, действующие на точечный заряд, диполь и непрерывно распределенный заряд. Силы, действующие на диэлектрик и проводник. Энергетический метод определения сил.
На точечный заряд в электрическом поле действует сила:
.
На непрерывно распределенный заряд:
,
объемная плотность сил:
.
Объемные силы, действующие на диэлектрик – это сумма сил, действующих на диполи внутри диэлектрика.
— особенно для жидкостей и газов.
Под действием элементарных сил на малые объемы эти элементы сдвигаются в направление роста . На поверхности раздела сила всегда направлена в сторону диэлектрика с меньшим.
Силы в магнитном поле: , объемная плотность сил. У диамагнетиков, поэтому сила направлена в сторону уменьшения магнитного поля.
Работа, которая совершается током, не является результатом превращения кинетической энергии электронов в другие виды энергии. Носитель энергии – не электроны, а поля. В частном случае джоулева тепла кинетическая энергия электрона не является промежуточной формой энергии.
Пусть — объемная плотность тепловой мощности, выделяемой в проводнике. Покажем, что:. Джоулево тепло, выделяемое в объеме,.
, . Получаем:
. Получаем 3 интеграла:
.
Окончательно получаем:
.
Здесь 1-я скобка – энергия поля (электрическое + магнитное), а производное – изменение этой энергии в объеме .
, здесь — вектор Умова-Пойнтинга, или же плотность потока.
Изменение энергии в объеме равно работе энергии тока проводимости и потоку энергии через , которая ограничивает. Работа, производимая в замкнутом объеме, совершается за счет потока энергии через поверхность, ограничивающую объем.
Для плоской волны, у которой иколеблются в фазе, в любой момент времени, откуда можно получить вектор Умова-Пойнтинга. Рассмотрим в качестве примера отрезок проводника, по которому течет ток:
.
Из закона полного тока можно получить
поле на расстоянии
от центра:.
Тогда поток через поверхность цилиндра
– это поток Умова-Пойнтинга..
Это поток энергии, которая втекает в
объемчерез поверхность.
Т.е. энергия электромагнитного поля
втекает в боковую поверхность проводника
и выделяется в виде тепла Джоуля-Ленца.
Если в пределах проводника действуют
сторонние силы, то в замкнутой цепи
постоянного тока энергия от участков,
где действуют сторонние силы, передается
другим участкам цепи не вдоль проводников,
а через окружающее пространство в виде
потоков энергии.
Как видно из рисунка, поток вектора Умова-Пойнтинга направлен вне провода.
Закон электромагнитной индукции Фарадея. Дифференциальная формулировка закона электромагнитом индукции Фарадея.
Электрические токи создают вокруг себя магнитное поле. Связь магнитного поля с током привела к многочисленным попыткам возбудить ток в контуре с помощью электромагнитного поля. Эта фундаментальная задача была решена в 1831 г. английским физиком М.Фарадеем, открывшим явление электромагнитной индукции. Оно заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.
Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и ЭДС электромагнитной индукции определяются только скоростью изменения магнитного потока. Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре ЭДС:
.
Правило Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.
studfiles.net
Как определить направление силы Лоренца ? от чего зависит сила лоренца ? Естественные науки
В самом деле, XIX век во многом перевернул представления ученых о строении мира и подтолкнул к множеству удивительных открытий и изобретений. Именно на этой волне и возник повышенный интерес к электричеству.
Открытия следовали одно за другим. Электрической силе и магнетизму приписывались самые фантастические свойства. Исследования ученых обрастали самыми невероятными слухами, но тем не менее все это в целом подхлестнуло небывалый интерес к научной деятельности и науке в частности.
Наука привлекала как никогда много различных людей, так произошло и с Андре-Мари Ампером. Он родился в Лионе в семье обычного торговца. Получил всего лишь домашнее образование, но поскольку Андре-Мари имел доступ к семейной библиотеке, то благодаря усердию и стремлению к знаниям, он самостоятельно выучил латынь с единственной целью — прочесть работы великих математиков.
Андре-Мари Ампер кроме занятий научной деятельностью сделал ощутимую карьеру в системе образования. При Наполеоне Бонапарте он был назначен на пост генерального инспектора университетов Франции.
В 1827 году увидела свет его фундаментальная работа «Теория электродинамических явлений, выведенная исключительно из опыта», где автор объединил свои исследования и дал им математические определения.
В своем труде Ампер описал принципы взаимодействия постоянных токов. Они были исследованы Андре-Мари Ампером еще в 1820 году. В результате экспериментов и расчетов Андре-Мари Ампер пришел к некоторым выводам. Ученый заметил, что направление тока, текущего в параллельных проводниках, оказывает влияние на их притяжение. Если Ампер пускал ток в двух проводниках в одном направлении, то они притягивались. Когда ток пускался в одном и проводников в обратном направлении, он отталкивался от другого проводника. Полученная информация легла в основу всем известного закона Ампера.
Суть эксперимента заключалась в выявлении силы притяжения или отталкивания, зависящей от направления движения электрического тока в двух проводниках.
Кроме того, ученый заметил, что если пропускать достаточно сильный электрический ток по проводникам, то их смещение хорошо видно невооруженным глазом. Будучи математиком, Ампер измерил и установил, что механическое взаимодействие имеет силу, пропорциональную силе тока и зависящую от расстояния между проводниками. Чем это расстояние больше, тем сила механического взаимодействия меньше. Так эксперимент навел Ампера на мысль о существовании магнитных полей, порождаемых электрическим током. В этом и состоит закон Ампера.
www.kakprosto.ru
Силы, действующие на заряженную частицу в электромагнитном поле. Сила Лоренца.
Мы уже знаем, что на проводник с током, помещенный в магнитное поле, действует сила Ампера. Но ток в проводнике – есть направленное движение зарядов. Отсюда напрашивается вывод, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, от которых это действие передается уже самому проводнику. Этот вывод подтверждается, в частности, еще и тем, что пучок свободно летящих заряженных частиц отклоняется магнитным полем.
Сила
Ампера, действующая на элемент тока в
магнитном поле с индукцией  :
:
,
где
α – угол между направлением тока в
проводнике и вектором .
.
Пусть – скорость упорядоченного движения
зарядов в проводнике;q –
заряд носителя тока (в металлах q = — e).
Для элемента тока можем написать:
– скорость упорядоченного движения
зарядов в проводнике;q –
заряд носителя тока (в металлах q = — e).
Для элемента тока можем написать:
dNq ,
,
где n = dN/dV – концентрация зарядов, dN – число зарядов в элементе объема dV = Sdl. Тогда, сила, действующая в магнитном поле на один заряд, будет:
или
в векторном виде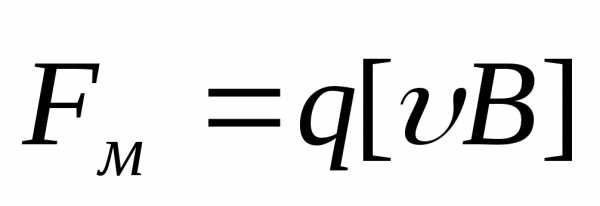 .
.
Эту силу называют силой Лоренца (Lorentz H., 1853-1928).
Свойства силы Лоренца:
сила Лоренца действует только на движущуюся заряженную частицу;
 и
одновременно
и
одновременно  ;
;поскольку
 ,
то сила Лоренцане
совершает работу, а следовательно, не может изменить энергию частицы.
,
то сила Лоренцане
совершает работу, а следовательно, не может изменить энергию частицы.
Полная сила, действующая на заряженную частицу в электромагнитном поле (которую также называют силой Лоренца) есть: .
4.3. Движение заряженной частицы в однородном постоянном магнитном поле.
В
данном случае 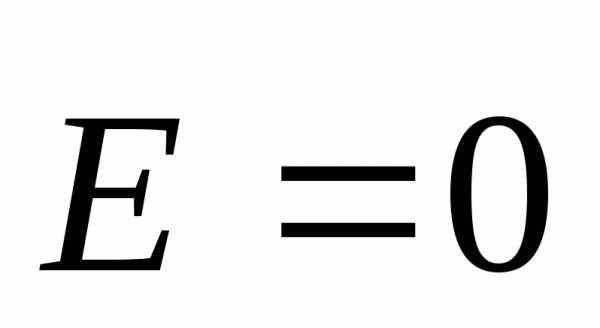 и сила Лоренца имеет только магнитную
составляющую
и сила Лоренца имеет только магнитную
составляющую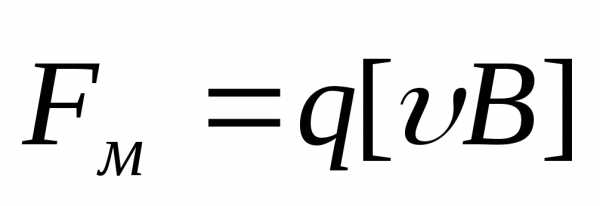 .
Уравнением движения частицы, записанном
в декартовой системе координат, в этом
случае является:
.
Уравнением движения частицы, записанном
в декартовой системе координат, в этом
случае является: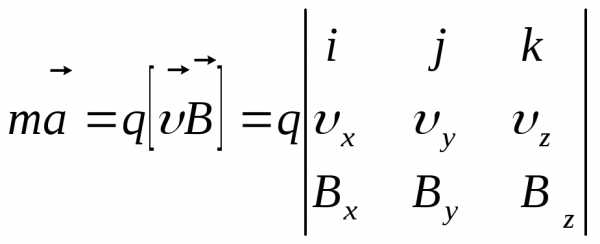 .
.
Рассмотрим сначала случай, когда частица влетает под прямым углом к силовым линиям магнитного поля (рис. 4.6.).
Рисунок
4.6. Движение
заряженной частицы в магнитном поле
(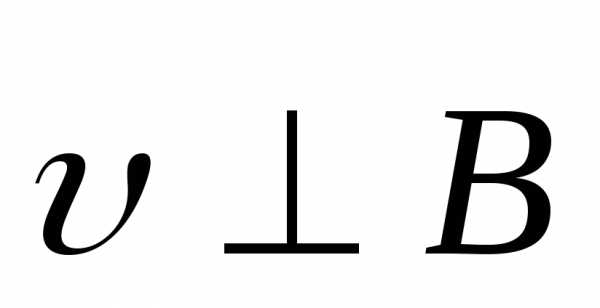 ).
).
В системе координат, показанной на рисунке ,, и уравнение движения принимает вид:
,
откуда
следует, что вектор полного ускорения частицы  лежит в плоскости, перпендикулярной
вектору
лежит в плоскости, перпендикулярной
вектору .
Легко убедиться также в том, что вектор
ускорения
.
Легко убедиться также в том, что вектор
ускорения перпендикулярен вектору скорости
частицы
перпендикулярен вектору скорости
частицы и составляет вместе с вектором
и составляет вместе с вектором правую
тройку векторов (как и должно быть по
свойствам силы Лоренца). Действительно,
правую
тройку векторов (как и должно быть по
свойствам силы Лоренца). Действительно,
.
Таким образом, ускорение частицы в каждый момент времени t направлено к центру кривизны траектории и играет роль нормального (центростремительного) ускорения. Модуль ускорения равен:
.
Траекторией
движения является окружность,
радиусR которой находим из условия: 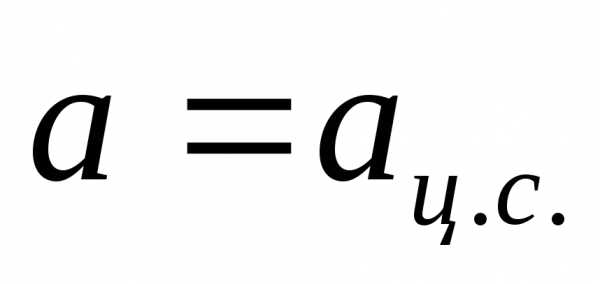 ,
то есть
,
то есть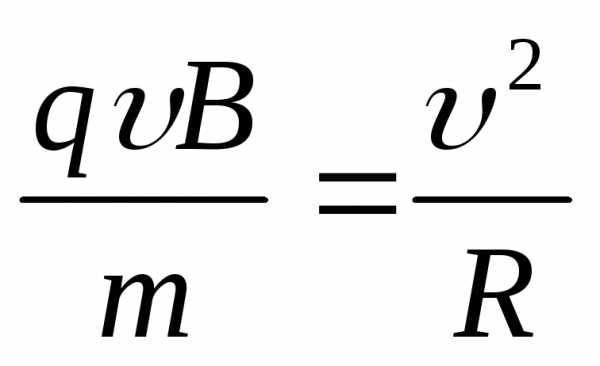 ,
откуда:
,
откуда: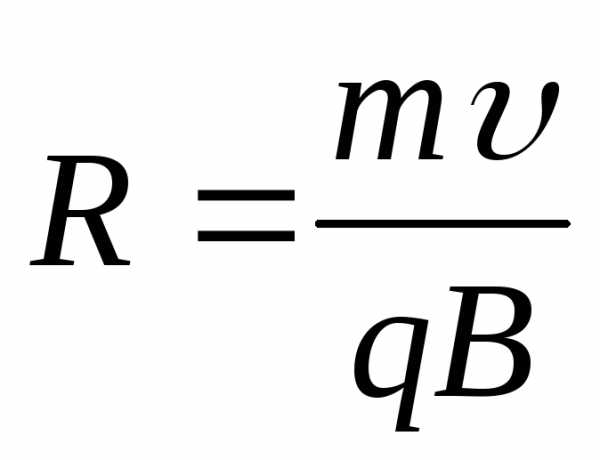 .
.
Период обращения частицы

Отметим,
что период обращения и соответственно
угловая скорость движения частицы не
зависят от линейной скорости  .
.
Рассмотрим теперь случай, когда частица влетает под углом α к силовым линиям магнитного поля.

Разложим
вектор скорости  на
две составляющие:
на
две составляющие: — параллельную вектору
— параллельную вектору и
и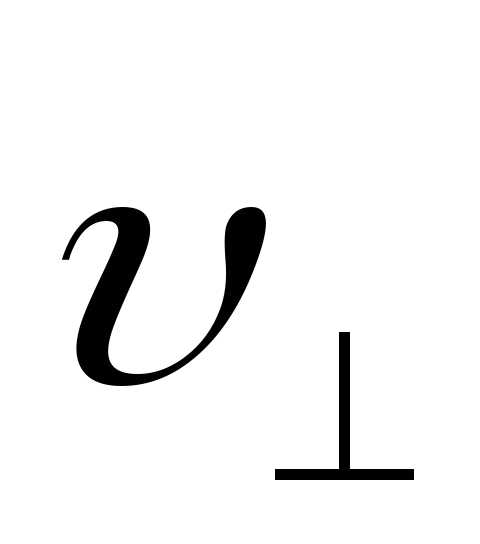 — перпендикулярную
— перпендикулярную .
Поскольку составляющая силы Лоренца в
направлении
.
Поскольку составляющая силы Лоренца в
направлении равна нулю, она не может повлиять на
величину
равна нулю, она не может повлиять на
величину .
Что касается составляющей
.
Что касается составляющей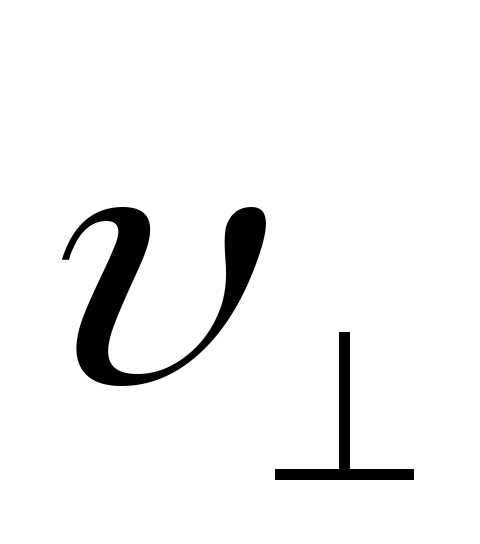 ,
то этот случай был рассмотрен выше.
Таким образом, движение частицы можно
представить как наложениедвух движений:
одного – равномерного
перемещения вдоль направления силовых линий поля
со скоростью
,
то этот случай был рассмотрен выше.
Таким образом, движение частицы можно
представить как наложениедвух движений:
одного – равномерного
перемещения вдоль направления силовых линий поля
со скоростью  ,
второго –равномерного
вращения в плоскости, перпендикулярной
,
второго –равномерного
вращения в плоскости, перпендикулярной  .
В итоге траекторией движения будетвинтовая
линия.
.
В итоге траекторией движения будетвинтовая
линия.
Шаг
винтовой линии определяется по формуле:
,
где 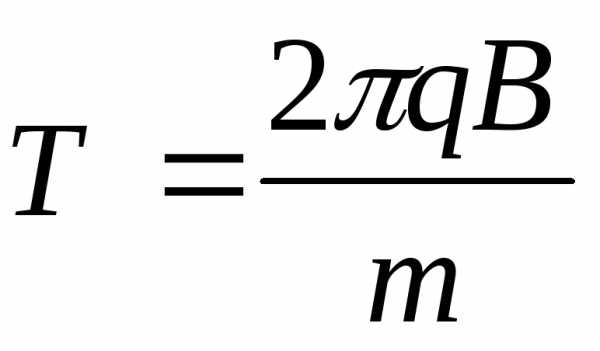 .Радиус
витка находим
по формуле:
.Радиус
витка находим
по формуле:
Направление,
в котором закручивается винтовая линия,
зависит от знака заряда частицы. Если
заряд частицы положительный,
то винтовая линия закручивается против часовой
стрелки, если смотреть вдоль
направления  ,
и наоборот –по часовой стрелке, если заряд частицы отрицательный.
,
и наоборот –по часовой стрелке, если заряд частицы отрицательный.
studfiles.net
Сила Лоренца и ее воздействие на электрический заряд
Электрические заряды, движущиеся в определенном направлении, создают вокруг себя магнитное поле, скорость распространения которого в вакууме равно скорости света, а в других средах чуть меньше. Если движение заряда происходит во внешнем магнитном поле, то между внешним магнитным полем и магнитным полем заряда возникает взаимодействие. Так как электрический ток – это направленное движение заряженных частиц, то сила, которая будет действовать в магнитном поле на проводник с током, будет являться результатом отдельных (элементарных) сил, каждая из которых прикладывается к элементарному носителю заряда.
Процессы взаимодействия внешнего магнитного поля и движущихся зарядов исследовались Г. Лоренцом, который в результате многих своих опытов вывел формулу для расчета силы, действующей на движущуюся заряженную частицу со стороны магнитного поля. Именно поэтому силу, которая действует на движущийся в магнитном поле заряд, называют силой Лоренца.
Сила, действующая на проводник стоком (из закона Ампера), будет равна:
По определению сила тока равна I = qn (q – заряд, n – количество зарядов, проходящее через поперечное сечение проводника за 1 с). Отсюда следует:
Где: n0 – содержащееся в единице объема количество зарядов, V – их скорость движения, S – площадь поперечного сечения проводника. Тогда:
Подставив данное выражение в формулу Ампера, мы получим:
Данная сила будет действовать на все заряды, находящиеся в объеме проводника: V = Sl. Количество зарядов, присутствующих в данном объеме будет равно:
Тогда выражение для силы Лоренца будет иметь вид:
Отсюда можно сделать вывод, что сила Лоренца, действующая на заряд q, который двигается в магнитном поле, пропорциональна заряду, магнитной индукции внешнего поля, скорости его движения и синусу угла между V и В, то есть:
За направление движения заряженных частиц принимают направление движения положительных зарядов. Поэтому направление данной силы может быть определено с помощью правила левой руки.
Сила, действующая на отрицательные заряды, будет направлена в противоположную сторону.
Сила Лоренца всегда направлена перпендикулярно скорости V движения заряда и поэтому работу она не совершает. Она изменяет только направление V, а кинетическая энергия и величина скорости заряда при его движении в магнитном поле остаются неизменными.
Когда заряженная частица движется одновременно в магнитном и электрическом полях, на него будет действовать сила:
Где Е – напряженность электрического поля.
Рассмотрим небольшой пример:
Электрон, прошедший ускоряющую разность потенциалов 3,52∙103 В, попадает в однородное магнитное поле перпендикулярно линиям индукции. Радиус траектории r = 2 см, индукция поля 0,01 Т. Определить удельный заряд электрона.
Решение:
Удельный заряд – это величина, равная отношению заряда к массе, то есть e/m.
В магнитном поле с индукцией В на заряд, движущийся со скоростью V перпендикулярно линиям индукции, действует сила Лоренца FЛ = BeV. Под ее действием заряженная частица будет перемещаться по дуге окружности. Так как при этом сила Лоренца вызовет центростремительное ускорение, то согласно 2-му закону Ньютона можно записать:
Кинетическую энергию, которая будет равна mV2/2, электрон приобретает за счет работы А сил электрического поля (А = eU), подставив в уравнение получим:
Преобразовав эти соотношения и исключив из них скорость, получим формулу для определения удельного заряда электрона:
Подставив исходные данные, выраженные в СИ, получим:
Проверяем размерность:
И кому интересно — видео о движении заряженных частиц:
elenergi.ru
1.4. Сила Лоренца. Правило левой руки для определения направления силы Лоренца
Силу,
действующую на движущуюся заряженную
частицу со стороны магнитного поля,
называют силой
Лоренца.
Опытным путём установлено, что сила,
действующая в магнитном поле на заряд  ,
перпендикулярна векторам
,
перпендикулярна векторам и
и ,
а ее модуль определяется формулой:
,
а ее модуль определяется формулой:
,
где  – угол между векторами
– угол между векторами  и
и .
.
Направление
силы Лоренца  определяется правилом левой руки (рис. 6):
определяется правилом левой руки (рис. 6):
если
вытянутые пальцы расположить по
направлению скорости положительного
заряда, а силовые линии магнитного поля
будут входить в ладонь, то отогнутый
большой палец укажет направление силы 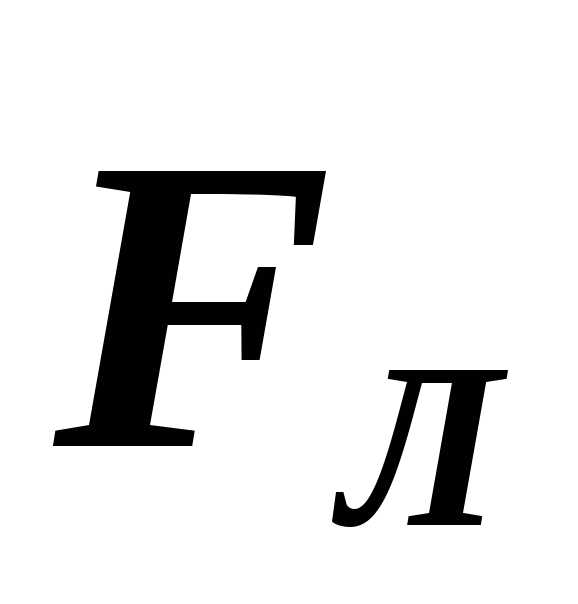 ,
действующей на заряд со стороны магнитного
поля.
,
действующей на заряд со стороны магнитного
поля.
Для
отрицательного заряда направление 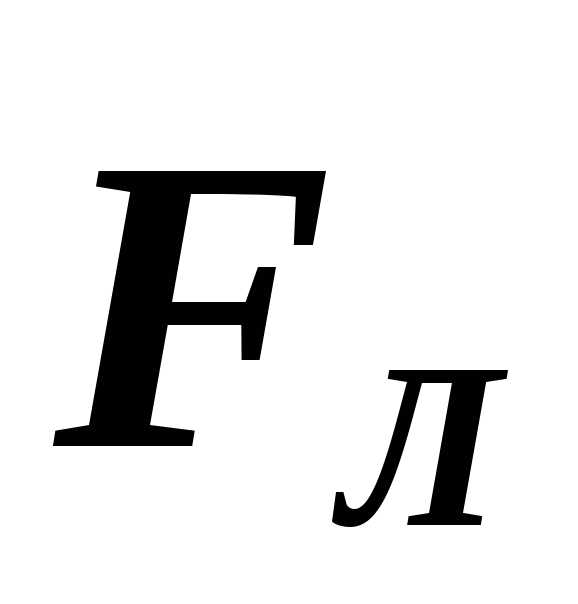 следует изменить на противоположное.
следует изменить на противоположное.

Рис. 6. Правило левой руки для определения направления силы Лоренца.
1.5. Сила Ампера. Правило левой руки для определения направления силы Ампера
Экспериментально установлено, что на проводник с током, находящийся в магнитном поле, действует сила, получившая название силы Ампера (см. п. 1.3.). Направление силы Ампера (рис. 4) определяется правилом левой руки (см. п. 1.3).
Модуль силы Ампера вычисляется по формуле
,
где 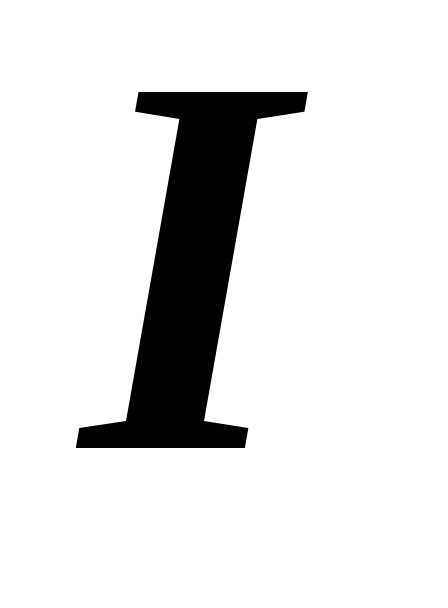 –
сила тока в проводнике,
–
сила тока в проводнике, —
индукция магнитного поля,
—
индукция магнитного поля,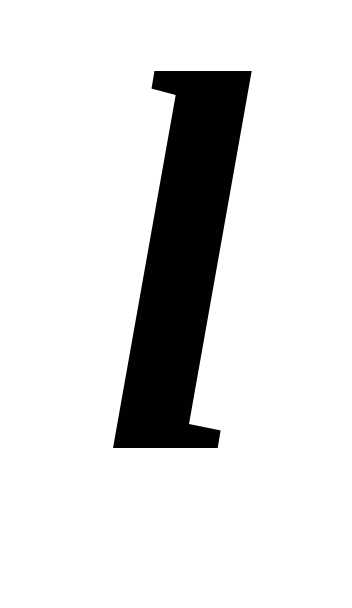 —
длина проводника,
—
длина проводника, —
угол между направлением тока и вектором
—
угол между направлением тока и вектором .
.
1.6. Магнитный поток
Магнитным
потоком  сквозь
замкнутый контур называется скалярная
физическая величина, равная произведению
модуля вектора
сквозь
замкнутый контур называется скалярная
физическая величина, равная произведению
модуля вектора  на площадь
на площадь контура и на косинус угла
контура и на косинус угла между
вектором
между
вектором  и
нормалью
и
нормалью 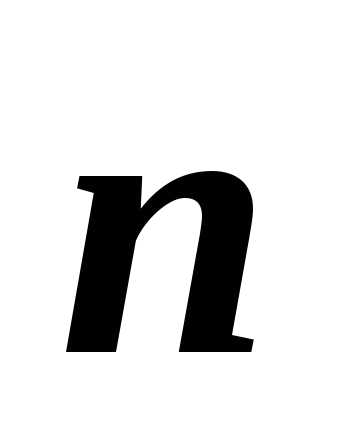 к контуру (рис. 7):
к контуру (рис. 7):

Рис. 7. К понятию магнитного потока
Магнитный
поток наглядно можно истолковать как
величину, пропорциональную числу линий
магнитной индукции, пронизывающих
поверхность площадью  .
.
Единицей магнитного потока является вебер .
Магнитный поток в 1 Вб создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
1 Вб =1 Тл·м2.
2. Электромагнитная индукция
2.1. Явление электромагнитной индукции
В 1831г. Фарадей обнаружил физическое явление, получившее название явления электромагнитной индукции (ЭМИ), заключающееся в том, что при изменении магнитного потока, пронизывающего контур, в нем возникает электрический ток. Полученный Фарадеем ток называется индукционным.
Индукционный ток можно получить, например, если постоянный магнит вдвигать внутрь катушки, к которой присоединен гальванометр (рис. 8, а). Если магнит вынимать из катушки, возникает ток противоположного направления (рис. 8, б).
Индукционный ток возникает и в том случае, когда магнит неподвижен, а движется катушка (вверх или вниз), т.е. важна лишь относительность движения.
Но не при всяком движении возникает индукционный ток. При вращении магнита вокруг его вертикальной оси тока нет, т.к. в этом случае магнитный поток сквозь катушку не изменяется (рис. 8, в), в то время как в предыдущих опытах магнитный поток меняется: в первом опыте он растет, а во втором – уменьшается (рис. 8, а, б).
Направление индукционного тока подчиняется правилу Ленца:
возникающий в замкнутом контуре индукционный ток всегда направлен так, чтобы создаваемое им магнитное поле противодействовало причине, его вызывающей.
Индукционный ток препятствует внешнему потоку при его увеличении и поддерживает внешний поток при его убывании.
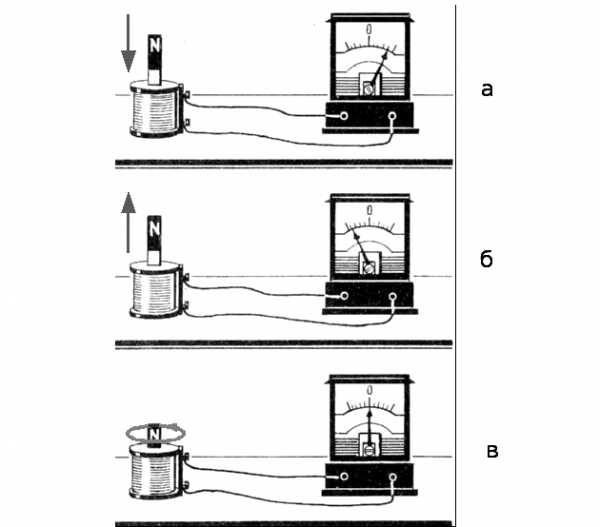
Рис. 8. Явление электромагнитной индукции
Ниже
на левом рисунке (рис. 9) индукция внешнего
магнитного поля  ,
направленного «от нас» (+) растет
(
,
направленного «от нас» (+) растет
(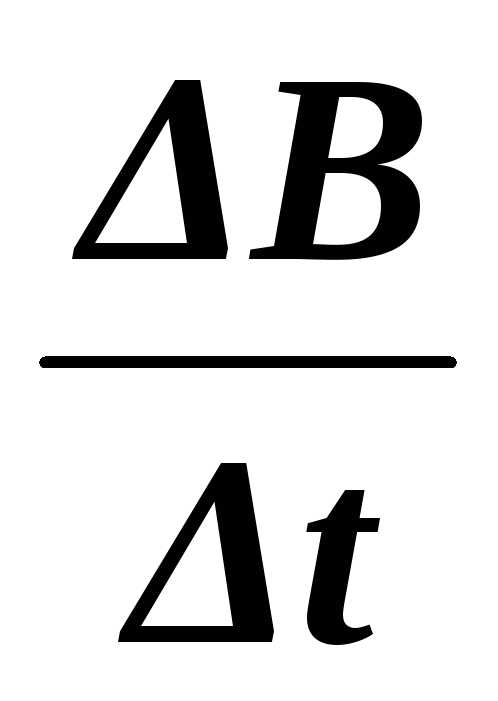 >0),
на правом – убывает (
>0),
на правом – убывает (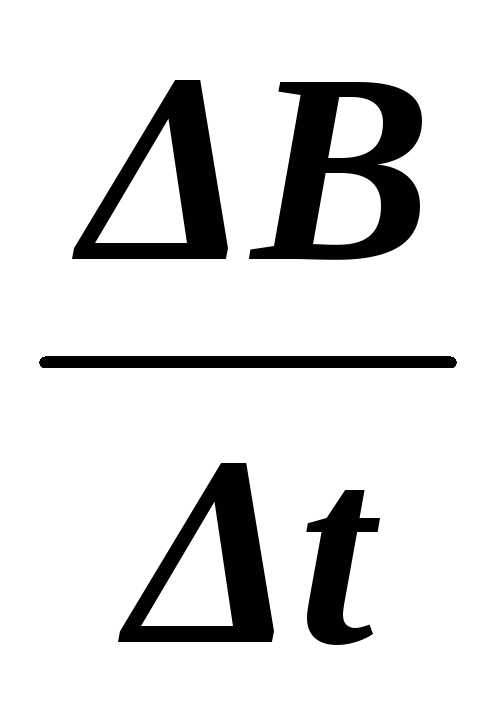 <0).
Видно, чтоиндукционный
ток направлен так, что его собственное магнитное поле препятствует изменению внешнего
магнитного потока, вызвавшего этот ток.
<0).
Видно, чтоиндукционный
ток направлен так, что его собственное магнитное поле препятствует изменению внешнего
магнитного потока, вызвавшего этот ток.

Рис. 9. К определению направления индукционного тока
studfiles.net

 и
одновременно
и
одновременно 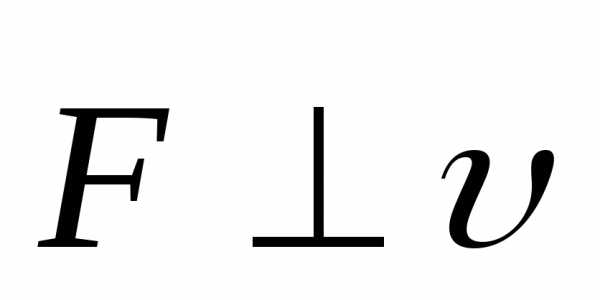 ;
;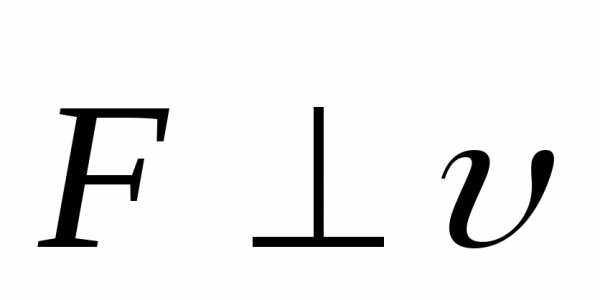 ,
то сила Лоренцане
совершает работу, а следовательно, не может изменить энергию частицы.
,
то сила Лоренцане
совершает работу, а следовательно, не может изменить энергию частицы.
Leave A Comment