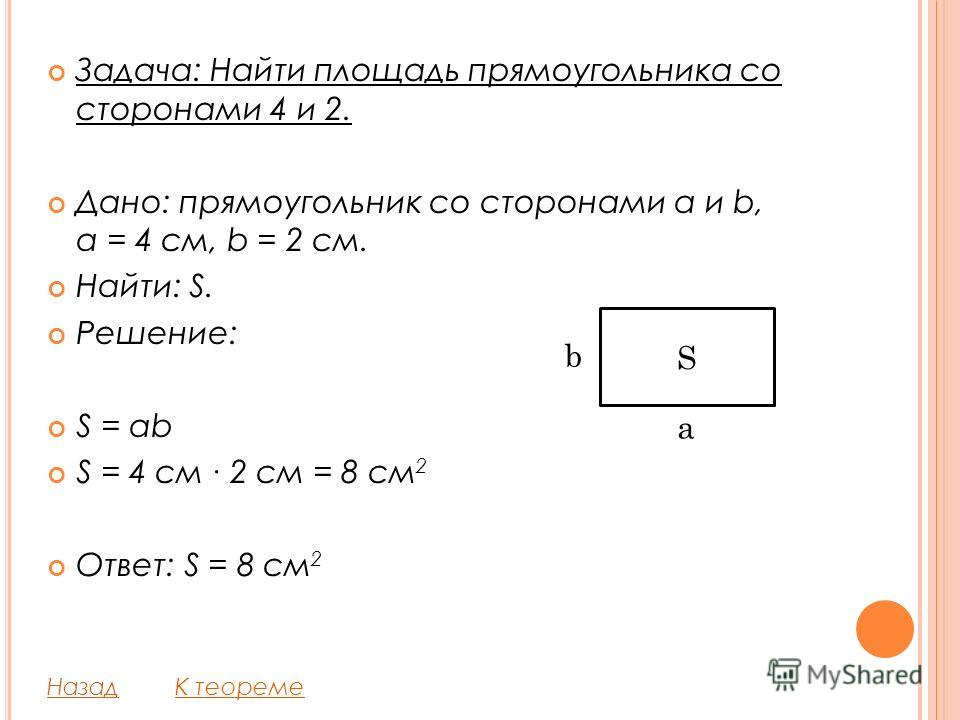
Как найти площадь прямоугольника – 9 формул с лайфхаками и примерами
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности.
 Корень из 16 = 4 см.
Корень из 16 = 4 см. - Умножаю корень разности на известную сторону: 16*9 = 144 см.
Ответ: 144 см.
Обратите внимание
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
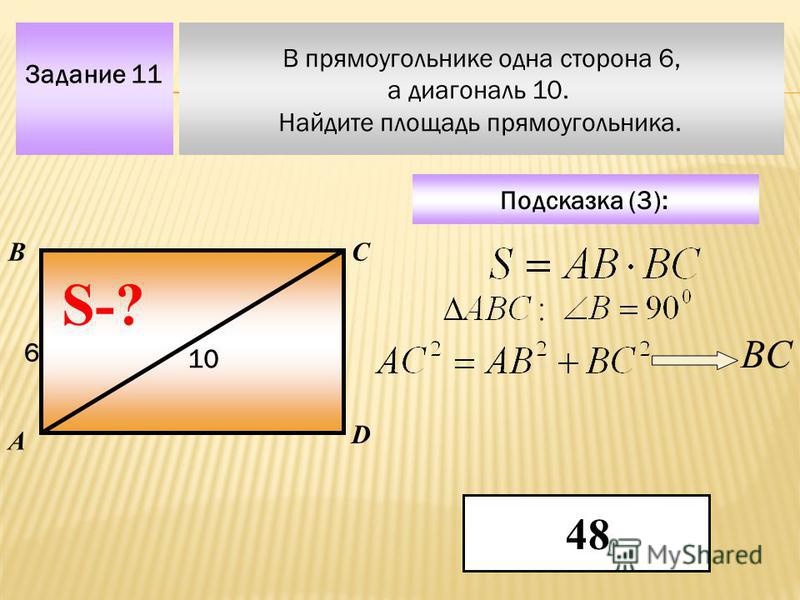
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
Действия:
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Ответ: 48 см.
Лайфхак
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
Другой способ:
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).

- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Ответ: 48 см.
Помните
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
Ответ: 12 см.
По стороне и периметру – 2 способ
Действия такие:
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.

- Делю разность на два: 140/2 = 70 см.
Ответ: 70 см.
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
Действия:
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
Ответ: 25 см.
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
Ответ: 36 см.
По радиусу описанной окружности и углу между диагоналями – второй способ
Действия:
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.

- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Ответ: 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯВаш браузер устарел рекомендуем обновить его до последней версии
или использовать другой более современный.
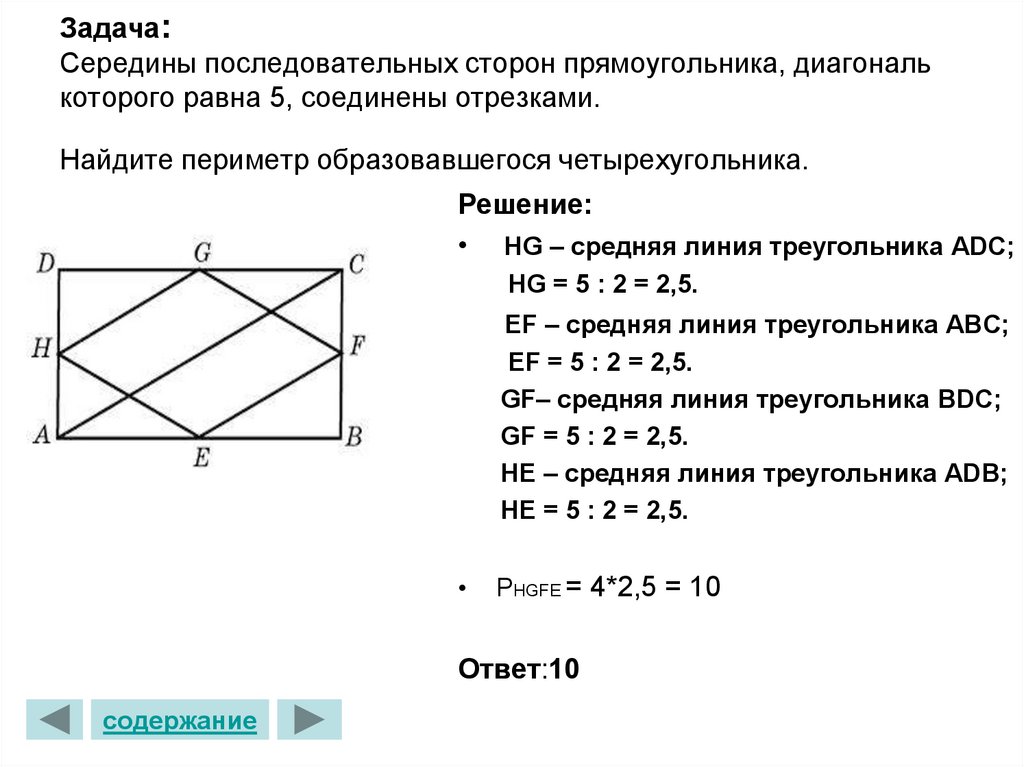
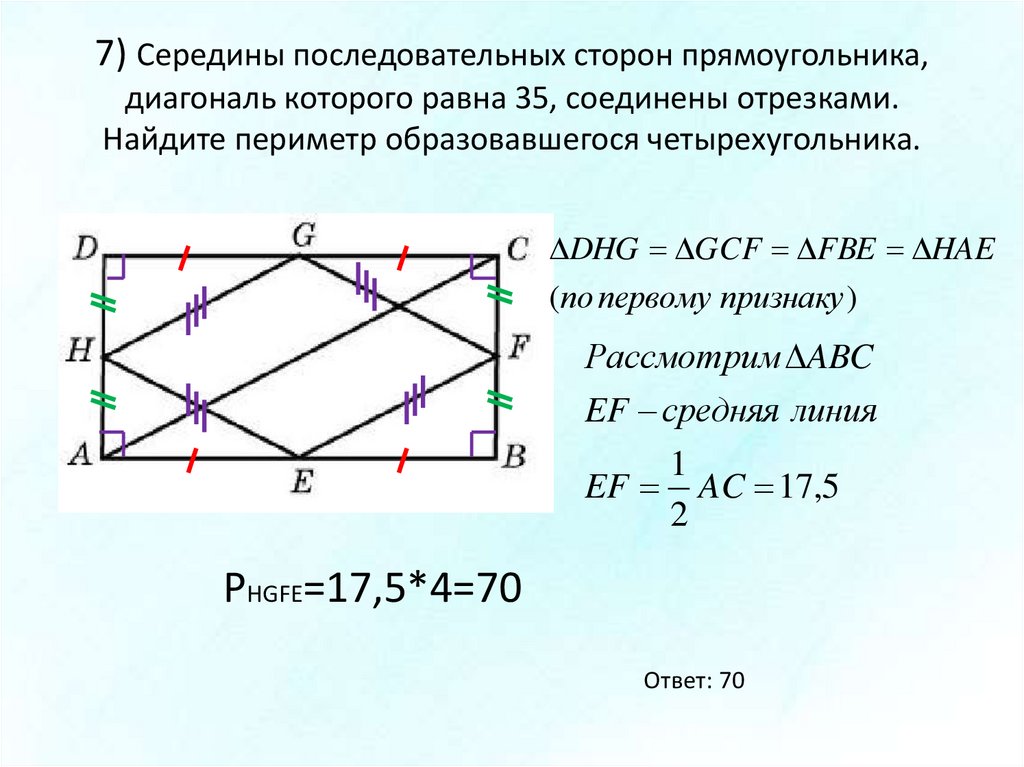
Задания к зачету по теме «Площади» 8 класс (гуманитаный)
Задания к зачету по теме: « Площадь» (8 класс. Глава VI.)
Карточка № 1
Теоретическая часть.
1. Сформулируйте основные свойства площадей многоугольников.
2. Сформулируйте и докажите теорему о вычислении площади прямоугольника.

1. В прямоугольном треугольнике катеты равны 15 и 20 см. Найти площадь
2. Найти высоты параллелограмма со сторонами 10 и 6 см, если его площадь равна
30 см.
3. Диагонали трапеции взаимно перпендикулярны и равны 4 и 10 см. Найти площадь трапеции.
4. Найдите площадь ромба по его диагоналям 8 и 12 см.
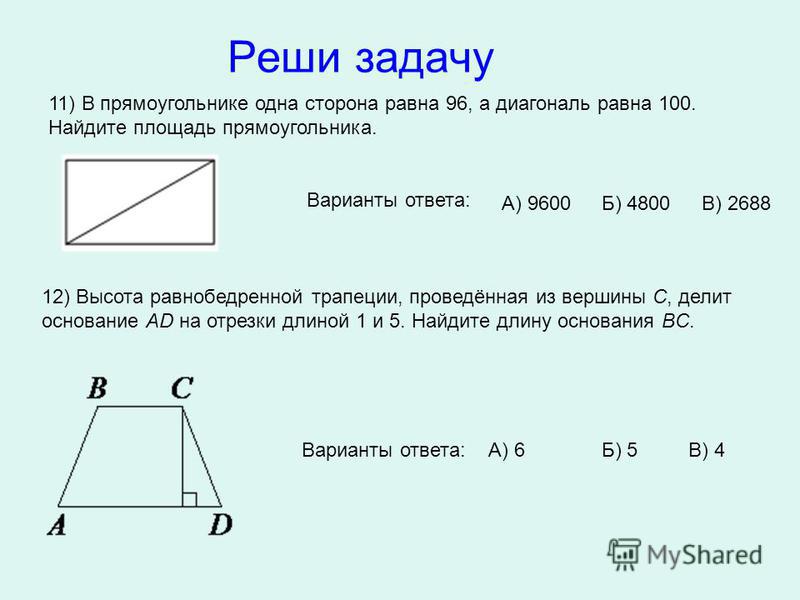
5. В прямоугольнике одна сторона равна 10, другая сторона равна 14. Найдите диагональ и площадь прямоугольника.
Карточка № 2
Теоретическая часть.
1. Какой треугольник называется прямоугольным ? Как вычислить площадь прямоугольного треугольника по его катетам?
2. Сформулируйте и докажите теорему о вычислении площади параллелограмма.
Практическая часть.
1.
Найти
площадь прямоугольного треугольника, если его гипотенуза равна 20 см, а один из
катетов 12 см.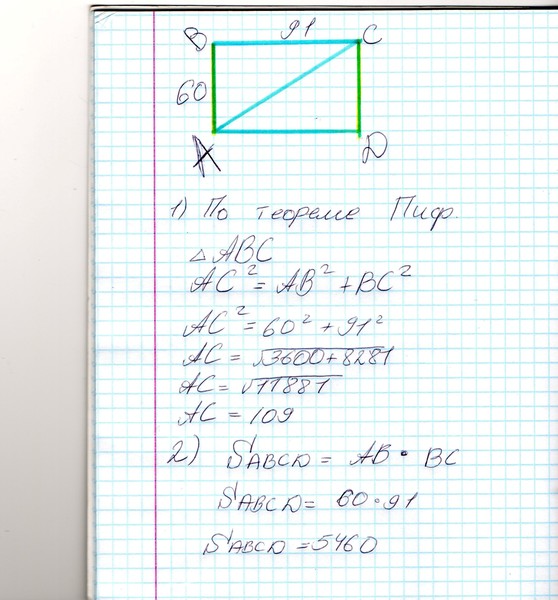
2. Одна из сторон параллелограмма равна 20, а опущенная на нее высота равна 23. Найдите площадь параллелограмма.
3.
Одна из
боковых сторон трапеции перпендикулярна основанию.
Найти площадь трапеции, если один из её углов равен 45, а длина боковых сторон
равны 6 и 8 см.
4. В ромбе сторона равна 10, одна из диагоналей 12 . Найдите другую диагональ и площадь ромба.
5. В прямоугольнике одна сторона равна 1, другая сторона равна 17. Найдите диагональ и площадь прямоугольника.
Карточка № 3
Теоретическая часть.
1. Какие треугольники называются пифагоровыми? Приведите примеры пифагоровых треугольников.
2. Сформулируйте и докажите теорему о вычислении площади треугольника.
Практическая часть.
1.
Прямоугольный треугольник
с катетами 5 и 12 см. Найдите площадь и периметр треугольника
Найдите площадь и периметр треугольника
2. Одна из сторон параллелограмма равна 16, а опущенная на нее высота равна 25. Найдите площадь параллелограмма.
3. Основания трапеции равны 4 и 25, одна из боковых сторон равна , а угол между ней и одним из оснований равен . Найдите площадь трапеции.
4. Сторона ромба равна 29, а диагональ равна 42. Найдите площадь ромба.
5. В прямоугольнике одна сторона равна 13, другая сторона равна 9. Найдите диагональ и площадь прямоугольника.
Карточка № 4
Теоретическая часть.
1. Какой треугольник называется египетским? Объясните.
2. Сформулируйте и докажите теорему о вычислении площади трапеции
Практическая часть.
1.
Найдите
площадь равнобедренного треугольника с боковой стороной 17 см и основанием 16
см.
2. Одна из сторон параллелограмма равна 19, а опущенная на нее высота равна 27. Найдите площадь параллелограмма
3. Основания трапеции равны 16 и 18, одна из боковых сторон равна , а угол между ней и одним из оснований равен . Найдите площадь трапеции.
4. Периметр ромба равен 28, а один из углов равен . Найдите площадь ромба.
5. В прямоугольнике одна сторона равна 13, периметр равен 62. Найдите площадь прямоугольника.
Карточка № 5
Теоретическая часть.
1. Сформулируйте теорему об отношении площадей двух треугольников, имеющих по равному углу.
2. Сформулируйте и докажите теорему Пифагора.
Практическая часть.
1. Найдите площадь правильного треугольника со стороной 8 см.
2.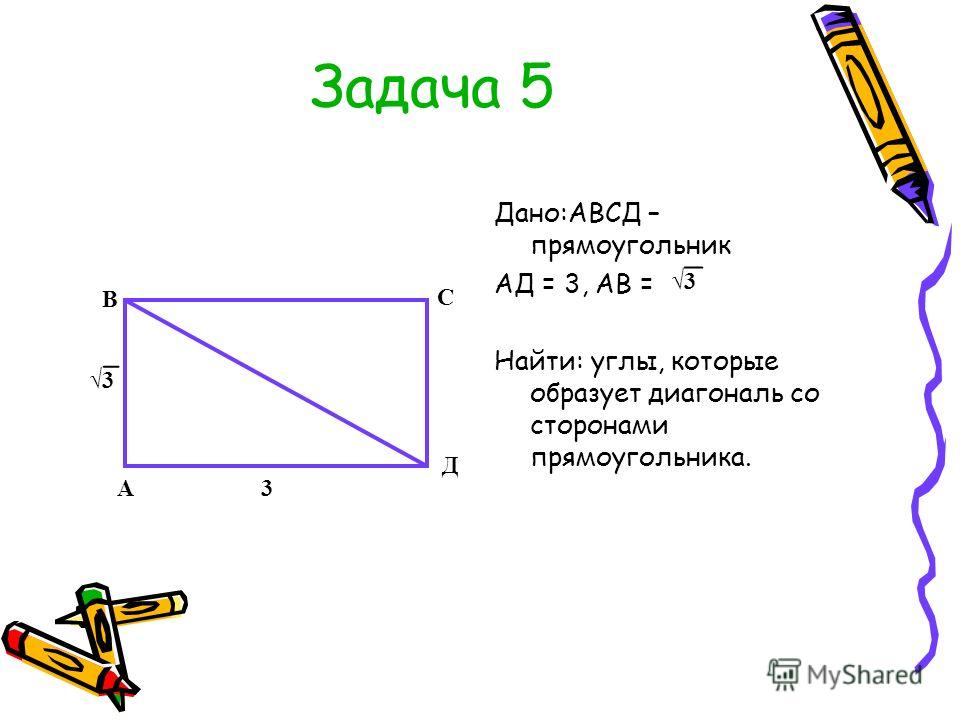 Стороны
параллелограмма равны 12 и 15 см. Высота проведённая к большей стороне, равна 8
см. Найти вторую высоту параллелограмма.
Стороны
параллелограмма равны 12 и 15 см. Высота проведённая к большей стороне, равна 8
см. Найти вторую высоту параллелограмма.
3. Основания трапеции равны 21 и 22, одна из боковых сторон равна , а угол между ней и одним из оснований равен . Найдите площадь трапеции.
4. В ромбе сторона равна 33, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен . Найдите площадь ромба.
5. В прямоугольнике одна сторона равна 14, периметр равен 54. Найдите площадь прямоугольника.
Карточка № 6
Теоретическая часть.
1. Сформулируйте теорему, обратную теореме Пифагора.
2. Сформулируйте и докажите теорему о вычислении площади прямоугольника.
Практическая часть.
1.
В прямоугольном треугольнике один из катетов равен , угол, лежащий напротив него, равен , а гипотенуза равна 34.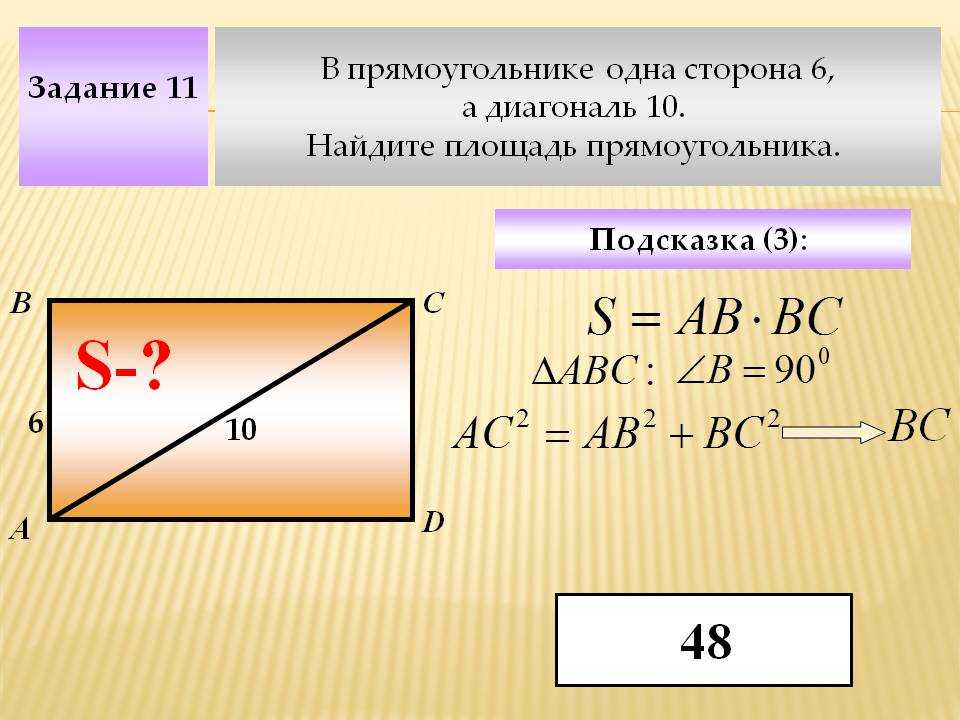
2. Диагональ параллелограмма, равная 13 см, перпендикулярна стороне равной 12 см. Найдите площадь параллелограмма.
3. Основания трапеции равны 9 и 24, одна из боковых сторон равна , а угол между ней и одним из оснований равен . Найдите площадь трапеции.
4. Сторона ромба равна 73, а диагональ равна 110. Найдите площадь ромба.
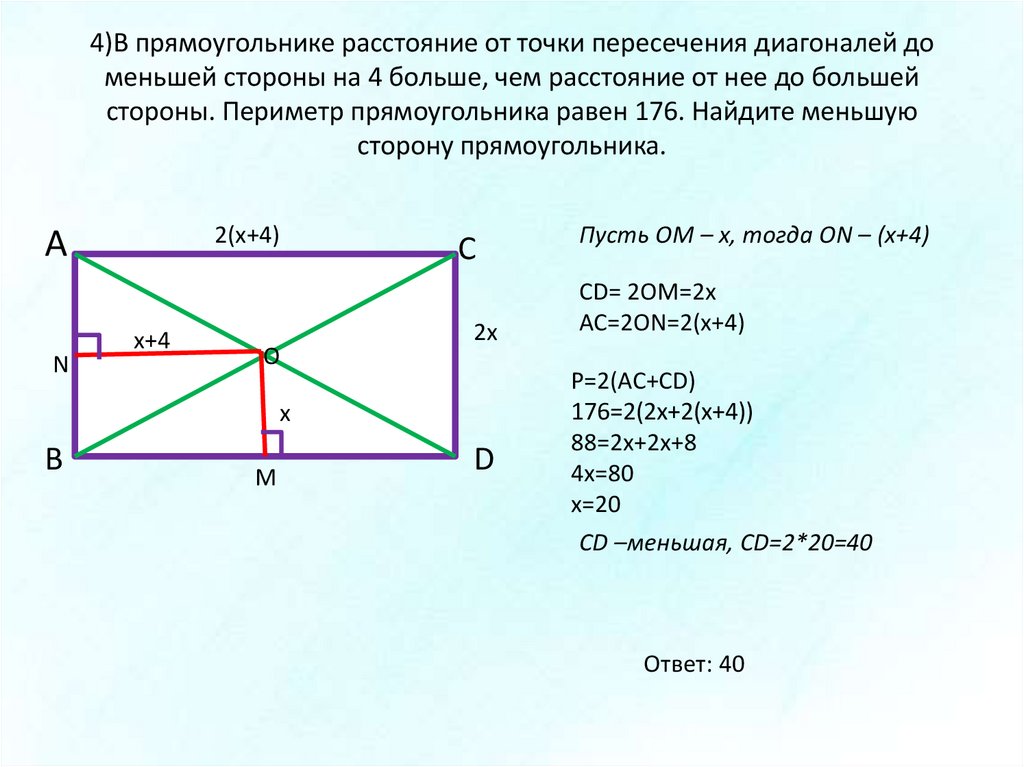
5. В прямоугольнике диагональ равна 92, а угол между ней и одной из сторон равен , длина этой стороны равна 46. Найдите площадь прямоугольника.
Карточка № 7
Теоретическая часть.
1. Сформулируйте основные свойства площадей многоугольников.
2. Сформулируйте и докажите теорему о вычислении площади прямоугольника.
Практическая часть.
1.
Периметр
равнобедренного треугольника равен 392, а основание — 192.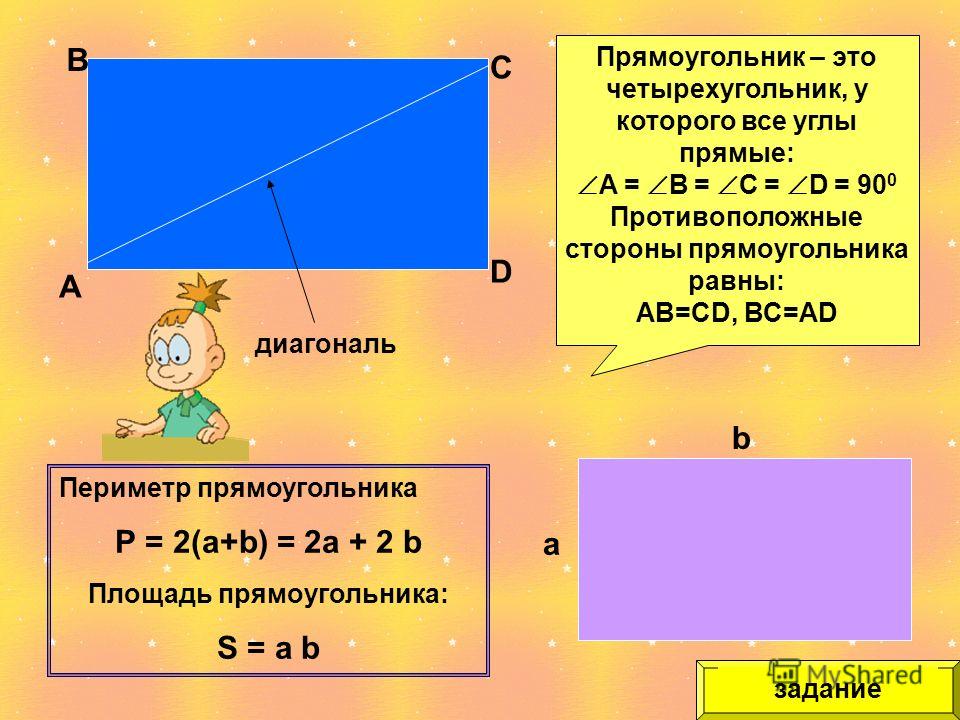 Найдите площадь
треугольника.
Найдите площадь
треугольника.
2. Стороны параллелограмма равны 12 и 15 см. Высота проведённая к большей стороне, равна 8 см. Найти вторую высоту параллелограмма.
3. Основания трапеции равны 4 и 12, одна из боковых сторон равна , а угол между ней и одним из оснований равен . Найдите площадь трапеции
4. Периметр ромба равен 128, а один из углов равен . Найдите площадь ромба
5. В прямоугольнике одна сторона равна 84, а диагональ равна 91. Найдите площадь прямоугольника
Карточка № 8
Теоретическая часть.
1. Какие треугольники называются пифагоровыми? Приведите примеры пифагоровых треугольников.
2. Сформулируйте и докажите теорему Пифагора.
Практическая часть
1.
В треугольнике
одна из сторон равна 2, а опущенная на нее высота — 17.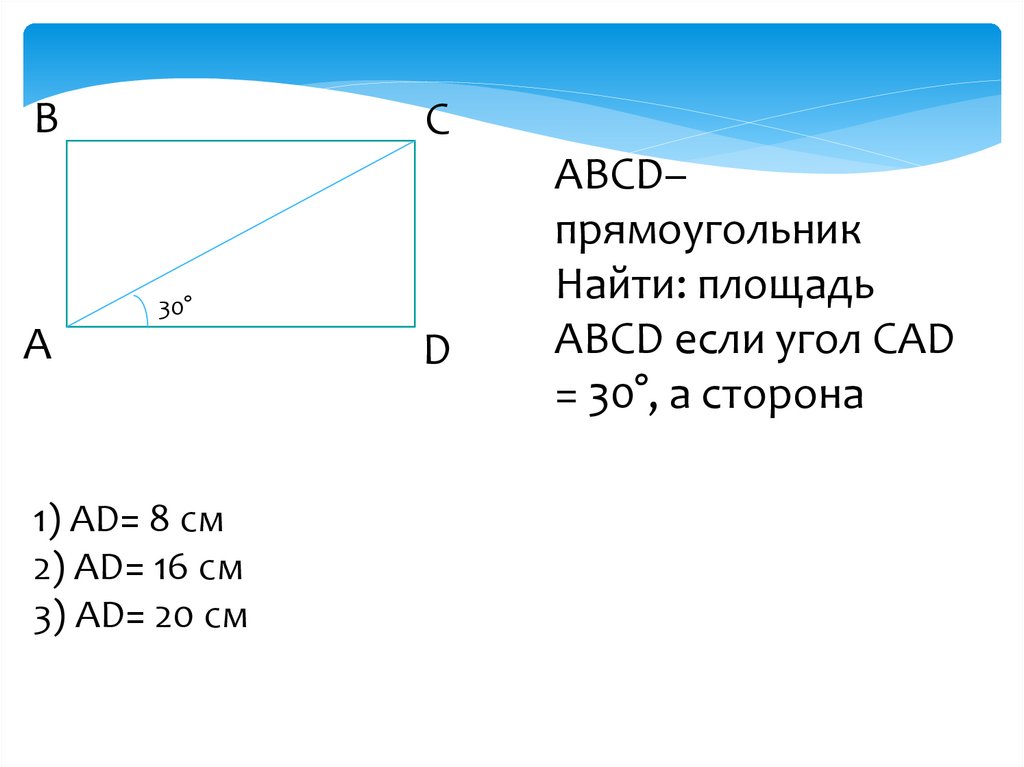 Найдите площадь
треугольника.
Найдите площадь
треугольника.
2. Смежные стороны параллелограмма равны 14 см и 12 см, а его острый угол равен .Найдите площадь параллелограмма
3. Основания трапеции равны 1 и 17, одна из боковых сторон равна , а угол между ней и одним из оснований равен . Найдите площадь трапеции.
4. В ромбе сторона равна 38, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен . Найдите площадь ромба.
5. В прямоугольнике одна сторона равна 52, а диагональ равна 65. Найдите площадь прямоугольника
Карточка № 9
Теоретическая часть.
1. Сформулируйте теорему об отношении площадей двух треугольников, имеющих по равному углу .
2. Сформулируйте и докажите теорему о вычислении площади трапеции
Практическая часть.
1.
Периметр равнобедренного треугольника равен 216, а основание — 96. Найдите площадь треугольника
Найдите площадь треугольника
2. Стороны параллелограмма равны 24 см и 18 см, а его площадь равна 144 см². Найдите высоты параллелограмма
3. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°
4. Сторона ромба равна 95, а диагональ равна 114. Найдите площадь ромба.
5. В прямоугольнике диагональ равна 42, а угол между ней и одной из сторон равен . Найдите площадь прямоугольника.
Карточка № 10
Теоретическая часть.
1. Какой треугольник называется египетским? Объясните.
2. Сформулируйте и докажите теорему о вычислении площади треугольника.
Практическая часть.
1. Периметр равностороннего треугольника равен 114. Найдите его площадь
2.
Стороны
параллелограмма равны 10 см и 12 см, а один из углов 150°. Найдите площадь параллелограмма
Найдите площадь параллелограмма
3. Высота трапеции равна 7 см, а одно из оснований в 5 раз больше другого. Найти основания трапеции, если её площадь равна 84 см².
4. В ромбе сторона равна 22, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен . Найдите площадь ромба.
5. В прямоугольнике диагональ равна 96, угол между ней и одной из сторон равен , длина этой стороны . Найдите площадь прямоугольника.
Карточка № 11
Теоретическая часть.
1. Сформулируйте теорему, обратную теореме Пифагора.
2. Сформулируйте и докажите теорему о вычислении площади параллелограмма.
Практическая часть.
1. В равнобедренном треугольнике боковая сторона равна 94, а угол, лежащий напротив основания, равен . Найдите площадь треугольника.
2. Высоты
параллелограмма равны 2 см и 6 см, а его площадь равна 48 см². Найдите длины сторон параллелограмма
Высоты
параллелограмма равны 2 см и 6 см, а его площадь равна 48 см². Найдите длины сторон параллелограмма
3. В прямоугольной трапеции основания равны 6 см и 9 см, а большая боковая сторона равны 5 см. Найти площадь трапеции.
4. В ромбе сторона равна 54, одна из диагоналей — 54, а угол, из которого выходит эта диагональ, равен . Найдите площадь ромба.
5. В прямоугольнике одна сторона равна 45, а диагональ равна 53. Найдите площадь прямоугольника.
Карточка № 12
Теоретическая часть.
1. Какой треугольник называется прямоугольным ? Как вычислить площадь прямоугольного треугольника по его катетам?
2. Сформулируйте и докажите теорему о вычислении площади прямоугольника.
Практическая часть.
1. Высота
равностороннего треугольника равна 7. Найдите его площадь.
Найдите его площадь.
2. Высоты параллелограмма равны 12 см и 9 см, а его площадь равны 36 см². Найдите длины сторон параллелограмма.
3. В равнобедренной трапеции основания равны 6 см и 14 см, а боковая сторона равна 5 см. Найти площадь трапеции.
4. Сторона ромба равна 90, а диагональ равна 144. Найдите площадь ромба.
5. В прямоугольнике диагональ равна 4, а угол между ней и одной из сторон равен , длина этой стороны равна 2. Найдите площадь прямоугольника.
Карточка № 13
Теоретическая часть.
1. Сформулируйте основные свойства площадей многоугольников.
2. Сформулируйте и докажите теорему о вычислении площади параллелограмма.
Практическая часть.
1.
В прямоугольном треугольнике один из катетов равен 10, а острый
угол, прилежащий к нему, равен . Найдите площадь
треугольника.
Найдите площадь
треугольника.
2. Стороны параллелограмма равны 8 см и 14 см, а один из углов 30°. Найдите площадь параллелограмма
3. Разность оснований трапеции равна 6 см, а высота равна 8 см. Найти основания трапеции, если её площадь равна 56 см².
4. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, из которого выходит эта диагональ, равен . Найдите площадь ромба.
5. В прямоугольнике одна сторона равна 16, периметр равен 58. Найдите площадь прямоугольника.
Карточка № 14
Теоретическая часть.
1. Сформулируйте теорему, обратную теореме Пифагора.
2. Сформулируйте и докажите теорему о вычислении площади трапеции.
Практическая часть.
1. Сторона равностороннего треугольника равна 48. Найдите его площадь.
2.
Периметр
параллелограмма равен 66 см. Два угла параллелограмма относятся как 1:5, а
стороны 2:9. Найдите площадь параллелограмма.
Два угла параллелограмма относятся как 1:5, а
стороны 2:9. Найдите площадь параллелограмма.
3. Высота трапеции в 3 раза меньше одного из оснований и в 5 раз меньше другого. Найти основания трапеции, если её площадь равна 100 см².
4. В ромбе сторона равна 68, одна из диагоналей — 68, а угол, лежащий напротив этой диагонали, равен . Найдите площадь ромба.
5. В прямоугольнике одна сторона равна 15, а диагональ равна 17. Найдите площадь прямоугольника
Карточка № 15
Теоретическая часть.
1. Какой треугольник называется египетским? Объясните.
2. Сформулируйте и докажите теорему Пифагора.
Практическая часть
1. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен . Найдите площадь треугольника.
2.
Периметр
параллелограмма равен 32 см. Найдите площадь параллелограмма, если один из углов на больше
прямого угла, а одна из сторон равна 6 см.
Найдите площадь параллелограмма, если один из углов на больше
прямого угла, а одна из сторон равна 6 см.
3. Высота, проведенная из вершины тупого угла прямоугольной трапеции, отсекает квадрат, площадь которого равна 16 см². Найти площадь трапеции, если её тупой угол равен 135°
4. В ромбе сторона равна 16, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен . Найдите площадь ромба.
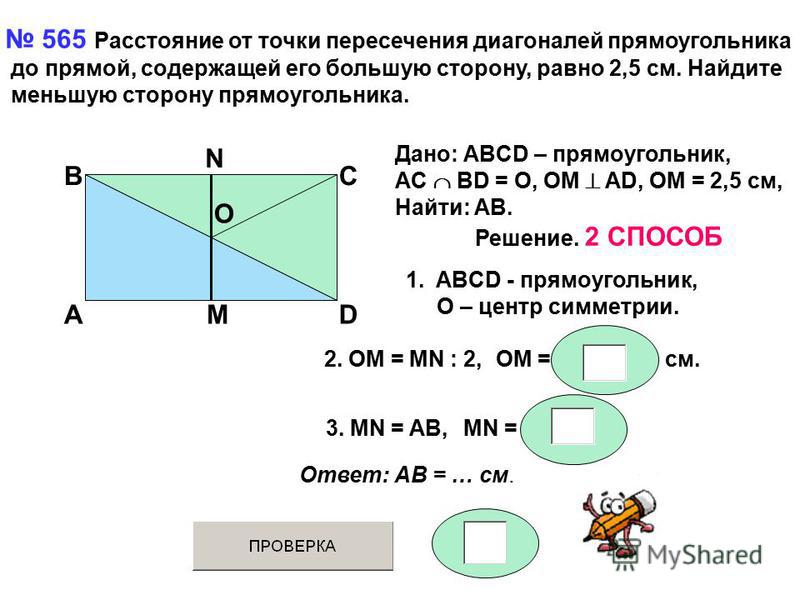
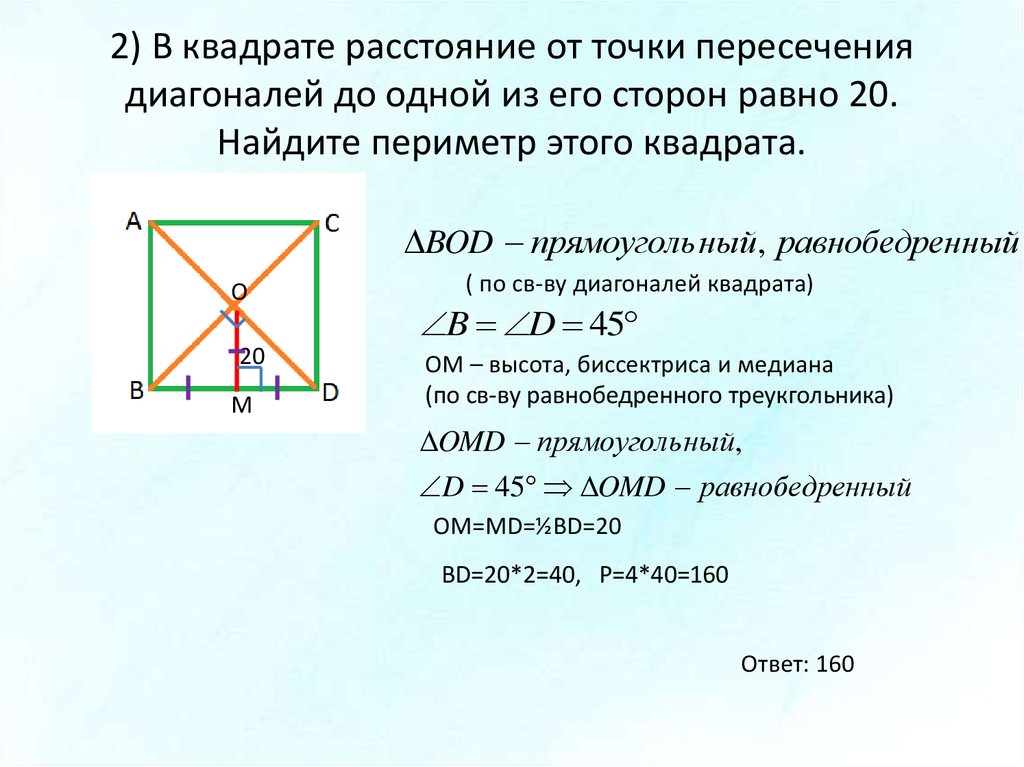
5. Расстояние от точки пересечения диагоналей прямоугольника до одной из его сторон в 8 раз меньше этой стороны. Найдите площадь прямоугольника, если его периметр равен 80 см.
Карточка № 16
Теоретическая часть.
1. Какой треугольник называется прямоугольным ? Как вычислить площадь прямоугольного треугольника по его катетам?
2. Сформулируйте и докажите теорему о вычислении площади треугольника.
Практическая часть
1. Найдите
площадь треугольника со сторонами 17, 65 и 80 см.
Найдите
площадь треугольника со сторонами 17, 65 и 80 см.
2. В параллелограмме острый угол равен 30°. Биссектриса этого угла делит сторону параллелограмма на отрезки 14 см и 9 см, считая от вершины тупого угла. Найдите площадь параллелограмма
3. Острый угол равнобокой трапеции равен 45о. Сумма длин ее боковых сторон и меньшего основания равна 18√2 см. Найдите высоту и площадь трапеции, если ее диагональ является биссектрисой угла при основании.
4. В ромбе сторона равна 54, одна из диагоналей — 54, а угол, из которого выходит эта диагональ, равен . Найдите площадь ромба.
5. Расстояние от точки пересечения диагоналей прямоугольника до одной из его сторон на 8 см меньше этой стороны. Найдите площадь прямоугольника, если его периметр равен 88 см.
Карточка № 17
Теоретическая часть.
1. Какой треугольник называется прямоугольным ? Как вычислить площадь прямоугольного треугольника по его катетам?
2. Сформулируйте
и докажите теорему Пифагора.
Сформулируйте
и докажите теорему Пифагора.
Практическая часть
1. Стороны треугольника равны 8см, 10см, 12см. Найдите площадь треугольника
2. Стороны параллелограмма равны 24 см и 52 см, а один из углов 30°. Найдите площадь параллелограмма
3. Боковые стороны прямоугольной трапеции равны 7 и 25 см, а меньшее основание – 2 см. Найдите площадь трапеции.
4. В ромбе сторона равна 44, одна из диагоналей — 44, а угол, из которого выходит эта диагональ, равен . Найдите площадь ромба.
5. Площади квадратов, построенных на сторонах прямоугольника, равны 64 см² и 121 см². Найдите площадь прямоугольника.
Карточка № 18
Теоретическая часть.
1. Какие треугольники называются пифагоровыми? Приведите примеры пифагоровых треугольников.
2.
Сформулируйте
и докажите теорему о вычислении площади прямоугольника.
Практическая часть
1. Площадь прямоугольного равнобедренного треугольника равна 16 см2. Найдите гипотенузу этого треугольника.
2. Смежные стороны параллелограмма равны 28 см и 24 см, а его острый угол равен .Найдите площадь параллелограмма
3. В равнобедренной трапеции основания равны 12 см и 20 см, а боковая сторона 5 см. Найдите площадь трапеции.
4. В ромбе сторона равна 44, одна из диагоналей — 44, а угол, из которого выходит эта диагональ, равен . Найдите площадь ромба.
5. Найдите площадь прямоугольника, если его периметр равен 144 см, а стороны относятся как 5:7.
Карточка № 19
Теоретическая часть.
1. Сформулируйте теорему, обратную теореме Пифагора.
2. Сформулируйте и докажите теорему о вычислении площади параллелограмма.
Практическая часть.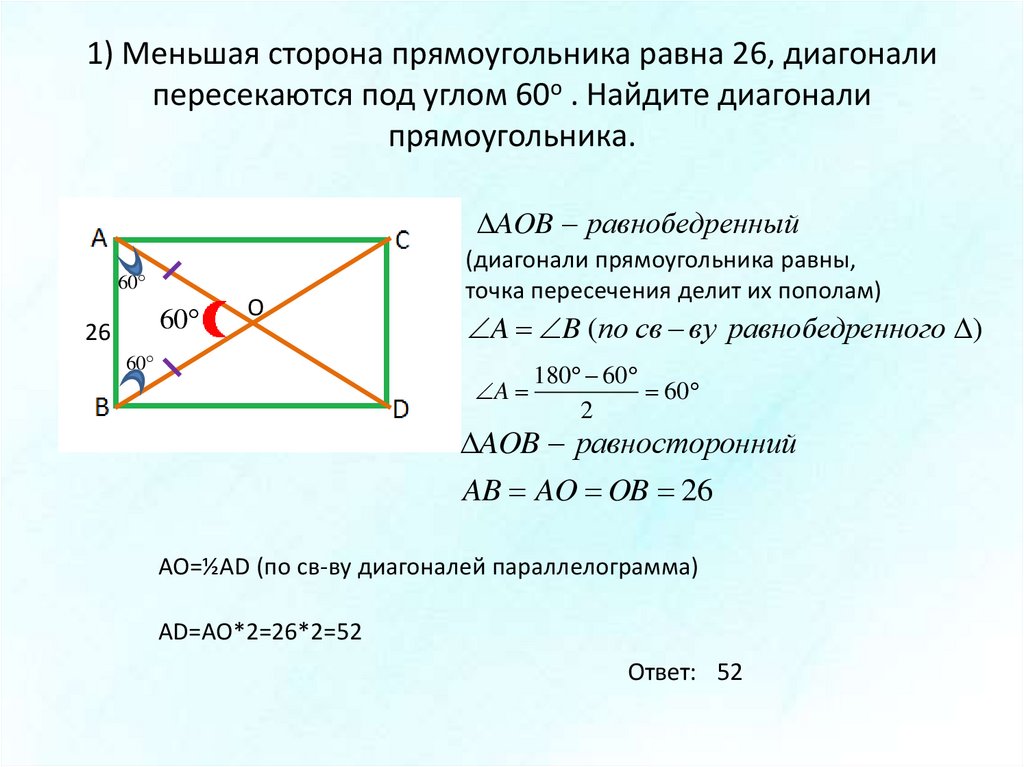
1. Боковая сторона равнобедренного треугольника равна 15 см, а основание 24 см. Чему равна площадь треугольника?
2. Высоты параллелограмма равны 5 см и 4 см, а периметр равен 42 см. Найдите площадь параллелограмма.
3. В прямоугольной трапеции основания равны 22 и 6 см, а большая боковая сторона 20 см. Найдите площадь трапеции
4. Одна из диагоналей ромба на 4 см больше другой, а площадь ромба равна 96 см2. Найдите стороны ромба.
5. Найдите площадь прямоугольника, если его периметр равен 74 см, а разность сторон 17 см.
Карточка № 20
Теоретическая часть.
1. Какой треугольник называется прямоугольным ? Как вычислить площадь прямоугольного треугольника по его катетам?
2. Сформулируйте и докажите теорему Пифагора.
Практическая часть.
3. Площадь
прямоугольного треугольника равна 24 м2, один катет которого в 3
раза больше другого. Найдите гипотенузу треугольника.
Площадь
прямоугольного треугольника равна 24 м2, один катет которого в 3
раза больше другого. Найдите гипотенузу треугольника.
4. Диагональ параллелограмма равна его стороне. Найдите площадь параллелограмма, если его большая его сторона равна 15,2 см, а один из углов равен
5. Найдите площадь равнобедренной трапеции, у которой основания равны 16см и 18см, а боковая сторона составляет с одним из оснований угол в
6. В ромбе сторона равна 10, одна из диагоналей —10, а угол, из которого выходит эта диагональ, равен . Найдите площадь ромба.
7. Найти площадь квадрата, если его периметр равен 4 см.
Калькулятор площади прямоугольника
Создано Bogna Szyk и Hanna Pamula, PhD
Отзыв от Jack Bowater
Последнее обновление: 09 февраля 2023 г.
Содержание:- Что такое прямоугольник?
- Как найти площадь прямоугольника?
- Формулы прямоугольника
- Вычисление прямоугольника: найти A (площадь)
- Вычисление прямоугольника: найти P (периметр)
- Вычисление прямоугольника: найти D (диагональ)
- Золотой прямоугольник
- Свойства прямоугольника
- Прямоугольник и другие формы.
 Является ли квадрат прямоугольником?
Является ли квадрат прямоугольником? - Странный забавный факт: какая страна имеет самую прямоугольную форму в мире?
- Прямоугольные узоры
- Прямоугольники в повседневной жизни: прямоугольная форма тела, прямоугольный бассейн, прямоугольная скатерть… прямоугольный бассейн или окно, эта площадь прямоугольного калькулятора решит вашу проблему в мгновение ока!
Все, что вам нужно сделать, это ввести длину и ширину (или диагональ) и позволить этому прямоугольнику вычислить значения P (периметр) и A (площадь).
Продолжайте читать, если вы хотите понять, что такое прямоугольник, вас интересует определение прямоугольника, формулы и свойства прямоугольника… Или вы просто хотите узнать, как найти площадь прямоугольника.
Что такое прямоугольник?
Прямоугольник четырехугольник с четырьмя прямыми углами . Мы можем также определить его по-другому: параллелограмм, содержащий прямой угол — если один угол прямой, другие должны быть такими же.
 При этом каждая сторона прямоугольника имеет ту же длину, что и противоположная ей сторона. Он также имеет неравные смежные стороны, в отличие от квадрата, частного случая прямоугольника.
При этом каждая сторона прямоугольника имеет ту же длину, что и противоположная ей сторона. Он также имеет неравные смежные стороны, в отличие от квадрата, частного случая прямоугольника.Если вы немного знаете латынь, название фигуры обычно многое объясняет. Слово прямоугольник происходит от латинского rectangulus . Это комбинация rectus (что означает «правильно, прямо») и angulus (угол), поэтому он может служить простым основным определением прямоугольника.
Прямоугольник является примером четырехугольника. Вы можете использовать наш четырехугольник калькулятор, чтобы найти площадь других типов четырехугольника.
Как найти площадь прямоугольника?
На изображении выше показан обычный прямоугольник. У него четыре стороны и четыре прямых угла. Длины его сторон обозначены a и b , а длина диагонали обозначена д .
Если все стороны прямоугольника имеют одинаковую длину, мы называем его квадратом .

Площадь прямоугольника — это пространство, ограниченное его сторонами или, другими словами, в пределах периметра прямоугольника. Чтобы найти площадь прямоугольника, все, что вам нужно сделать, это умножить стороны прямоугольника
aиb:Площадь = a × bФормулы прямоугольника
Наш калькулятор прямоугольника имеет следующие реализованные формулы :
Для площади прямоугольника :
A = a × bДля периметра прямоугольника :
P = 2 × (a + b)Для диагонали прямоугольника :
d² = a² + b²
d = √(a² + b²)
Расчет прямоугольника: найти A (площадь)
Как мы знаем формулу площади прямоугольника
A = a × b, покажем на примере, как можно вычислить это свойство:- Выберите длину прямоугольника – например,
a = 5 см.
- Определите ширину прямоугольника – например,
b = 6 см. - Умножьте эти два значения:
A = 5 см × 6 см = 30 см². - Площадь прямоугольника 30 см².
Расчет прямоугольника: найти P (периметр)
Давайте узнаем, как найти периметр прямоугольника. Как обычно, периметр — это сумма всех сторон фигуры:
P = a + b + a + b…что можно записать как:
P = 2 × (a + b)Возьмем для примера тот же прямоугольник:
- Выбираем длину прямоугольника –
a = 5 смв нашем случае. - Определите ширину прямоугольника – например,
b = 6 см. - Сложите эти два значения:
a + b = 5 + 6 = 11 см. - Умножьте результат на 2:
P = 2 × 11 = 22 см. - Вот так! Периметр нашего прямоугольника равен 22 см.
Расчет прямоугольника: найти D (диагональ)
Диагональ прямоугольника — это отрезок, соединяющий две противоположные вершины прямоугольника.
 Вычислим длину диагонали примерного прямоугольника:
Вычислим длину диагонали примерного прямоугольника:- Выберем длину прямоугольника – например,
а = 5 см. - Определите ширину прямоугольника – например,
b = 6 см. - Вычислить
aв степени двойки:a² = 25 см². - Вычислите
bв степени двойки:b² = 36 см². - Сложите эти два значения:
a² + b² = 25 + 36 = 61 см². - Наконец, извлеките квадратный корень из результата:
d = √(a² + b²) = √61 ~ 7,81 см. - Длина диагонали 7,81 см.
Естественно, вместо того, чтобы вычислять все эти значения вручную, вы можете использовать эту область калькулятора прямоугольника. Вы также можете использовать его в обратном порядке — например, для вычисления ширины прямоугольника с известными длиной и периметром.
Золотой прямоугольник
На рисунке выше показан особый тип прямоугольника, называемый золотым прямоугольником (узнайте с помощью нашего калькулятора золотого прямоугольника).
 Такой прямоугольник удовлетворяет следующему условию:
Такой прямоугольник удовлетворяет следующему условию:(a + b) / a = a / b = ϕ, где φ — золотое сечение, равное 1,618. Узнайте больше об этом особом соотношении с помощью нашего калькулятора золотого сечения.
Как вы, наверное, помните из калькулятора отношений, отношение — это отношение между двумя величинами, часто представленное в виде дроби.
Знаете ли вы, что можно построить золотой треугольник, используя только линейку и циркуль ? Это всего несколько шагов!
- Нарисовать квадрат.
- Проведите линию от середины одной стороны квадрата до противоположного угла. Наш калькулятор средней точки может помочь вам с этим шагом.
- Нарисуйте круг с радиусом, равным этой линии, с центром в средней точке, как показано на рисунке выше.
- Точка, в которой круг встречается с расширенной стороной квадрата, является следующим углом золотого прямоугольника.
- Найдите последнюю вершину и завершите золотой прямоугольник.

Таадааах! Это было не так сложно, не так ли?
Свойства прямоугольника
Прямоугольники обладают многими интересными свойствами:
- Цикличность – это означает, что все углы лежат на одной окружности.
- Равноугольный – все его углы равны 90 градусам.
- Прямолинейный – его стороны сходятся под прямым углом.
- Две линии отражательной симметрии – вертикаль и горизонталь через центр.
- Две диагонали, которые делят друг друга пополам . Длину диагонали можно найти по теореме Пифагора.
- Противоположные стороны прямоугольника параллельны друг другу и имеют одинаковую длину.
Другие менее известные прямоугольные свойства:
- Пересечение диагоналей — это центр описанной окружности — существует окружность с центром в этой точке, которая проходит через четыре угла.

- В прямоугольнике с разной длиной сторон (попросту говоря, не в квадрате) невозможно провести вписанную окружность.
- Прямые, соединяющие середины сторон прямоугольника, образуют ромб, площадь которого составляет половину площади прямоугольника. Стороны фигуры параллельны диагоналям.
Можно придумать и свои собственные свойства, например, о вращении прямоугольника – по стороне или диагонали, чтобы получился цилиндр или конус соответственно.
Прямоугольник против других форм. Является ли квадрат прямоугольником?
TL;DR:
- Является ли квадрат прямоугольником? ДА .
- Является ли прямоугольник параллелограммом? ДА .
- Является ли прямоугольник ромбом? В целом – НЕТ. Только если это квадрат (все углы ромба 90 градусов).
- Является ли ромб прямоугольником? В целом – НЕТ. Только если это квадрат (все стороны прямоугольника равны по длине).

- Является ли прямоугольник четырехугольником? ДА , конечно.
- Является ли прямоугольник трапецией? ДА .
Хотите знать, является ли квадрат прямоугольником или прямоугольник параллелограммом? Взгляните на рисунок ниже, и у вас больше не должно быть никаких сомнений относительно отношений между четырехугольниками:
Источник: WikimediaКак читать эту диаграмму? Начнем с нашего прямоугольника. Непосредственно к фигуре присоединены три фигуры: квадрат, параллелограмм и равнобедренная трапеция. Итак, если фигура находится выше интересующей нас формы, например, квадрата или прямоугольника, мы можем сказать, что:
- Каждый квадрат является прямоугольником и квадрат является частным случаем прямоугольника .
Для двух других фигур можно сказать аналогично:
- Каждый прямоугольник есть параллелограмм и прямоугольник есть частный случай параллелограмма .

- Каждый прямоугольник является трапецией и прямоугольник является частным случаем трапеции .
Странный забавный факт: какая страна имеет самую прямоугольную форму в мире?
Существует множество различных рейтингов, оценивающих страны по площади, населению, уровню образования или лауреатам Нобелевской премии.
Но задумывались ли вы когда-нибудь, , кто победит в конкурсе на самую прямоугольную страну? Австралийский геостатистик Дэвид Бэрри рассчитал параметр прямоугольности для всех стран мира и составил рейтинг.
Он выяснил, что самой прямоугольной страной является Египет, тогда как титул «наименее прямоугольной страны в мире» достается Мальдивским островам (впрочем, автор допускает, что расчеты для стран, состоящих из множества мелких островов, могут быть ужасно неверными). Взгляните на таблицу ниже и проверьте первые десять стран, а также наименее прямоугольные.
Высшие баллы по рейтингу прямоугольности.
 Индекс 1 — идеальный прямоугольник, 0 — бесконечное число бесконечно малых островков. Таблица адаптирована с веб-страницы г-на Барри как изображение мира ниже.
Индекс 1 — идеальный прямоугольник, 0 — бесконечное число бесконечно малых островков. Таблица адаптирована с веб-страницы г-на Барри как изображение мира ниже.Rank
Country
Roundness
Image
1
Egypt
0.955
2
Vatican
0.948
3
Sint Maarten
0.937
4
Lesotho
0,936
5
Йемен
Yeamen
902 - 999999999999999902
999999999902 9000
- 999999999902
9000 9000 2
.  28
286
Ghana
0.924
7
Macedonia
0.921
8
Côte d’ivoire
0,919
9 99999999902 - 999
- 999902
.19
10
Nauru
0.917
…
169
USA
0.735
…
206
Tuvalu
0.
 240
240207
Marshall Islands
0.201
208
Maldives
0.018
Egypt является лидером, но это не должно удивлять никого, кто проверяет форму этой страны на карте. USA находится в середине рейтинга, в основном из-за эксцентричности Аляски и Гавайев. Сбивает с толку то, что вторая самая прямоугольная страна — Ватикан — является в то же время четвертой самой круглой страной, и Польша , 5 место по округлости, 9 место по прямоугольности.
Как вообще возможно быть прямоугольным и круглым одновременно?! Как вы можете догадаться, все дело в определении прямоугольности и округлости, которое может быть неадекватным для сложных или разбросанных форм — и такими примерами обычно являются границы стран, содержащие острые края, маленькие острова или колонии где-то на другой стороне.
 земного шара.
земного шара.Если вам интересна эта тема, вы можете ознакомиться с этим объяснением и обсуждением результатов.
Можно подумать, что мир было бы легче рисовать, если бы каждая страна была прямоугольником… Или нет?
Шаблоны прямоугольников
Форма прямоугольника используется во многих периодических шаблонах мозаики. Его можно использовать для стен из кирпича, напольной плитки, тротуара или различной мозаики. Ниже вы найдете несколько популярных рисунков:
- Перевязка стопкой – самый распространенный и простой узор укладки плитки, так как плитка укладывается прямыми линиями.
- Текучая связка – типична для дорожных покрытий, плитки и кирпичной кладки.
- Елочка – с таким рисунком хорошо смотрятся деревянные полы.
- Корзиночное плетение – часто используется для коридоров или дорожек на открытом воздухе.
Конечно, плитка бывает всех форм и размеров – довольно популярны шестиугольные и восьмиугольные с квадратами.
 Для пятиугольника форма должна быть неправильной, чтобы образовался мозаичный узор.
Для пятиугольника форма должна быть неправильной, чтобы образовался мозаичный узор.Прямоугольники в повседневной жизни: прямоугольное телосложение, прямоугольный бассейн, прямоугольная скатерть…
Телосложение типа — одна из самых искомых задач, связанных с прямоугольниками. Все, что вам нужно сделать, это измерить свой бюст, талию, бедра и высоту бедер и ввести значения в инструмент. Тогда вы получите информацию о том, какая у вас форма тела.
Например, прямоугольная фигура определяется как «мальчишеский» тип телосложения — ваши бедра, талия и бюст примерно одного размера. Ваше тело имеет правильные пропорции и спортивный вид.
Удивительно, но нас окружают прямоугольные объекты. Вот почему наш калькулятор прямоугольников может быть полезен не только на уроках математики, но и в решении повседневных задач. Конечно, идеального прямоугольника в реальности не найти, так как он всегда имеет третье измерение; но если оно мало по сравнению с двумя другими измерениями, приближение достаточно хорошее.

Прямоугольные скатерти – зная размеры вашего стола, вы можете узнать, какая скатерть нужна или сколько кружева или подшивочной ленты вам потребуется.
Двери или оконное стекло – шторм или мяч для гольфа разбили ваше оконное стекло? Рассчитайте площадь и оцените стоимость ремонта, учитывая цену за кв.м или кв.м.
Экраны электронных устройств — планшетов, смартфонов, телевизоров — используйте этот калькулятор площади прямоугольника, чтобы оценить, сколько места на стене займет ваш экран — или насколько большой экран телефона, который вы хотите купить.
Доски, зеркала, рамы, холст, листы бумаги, блокноты, конверты, деньги, флажки, прямоугольные бассейны… Это бесконечный список!
Посмотри. Можете ли вы найти больше прямоугольных объектов вокруг вас? Что вы можете!
FAQ
Как найти периметр и площадь прямоугольника?
Чтобы найти периметр, нужно сложить все стороны прямоугольника:
P = a + b + a + bЧтобы найти площадь прямоугольника, нужно умножить меньшую и длинную стороны :
A = a × bКакова площадь прямоугольника размером 3 фута на 4 дюйма?
Это 144 квадратных дюйма ! Чтобы найти площадь этого прямоугольника, вам нужно:
- Преобразовать футов в дюймы.
 3 фута равны 36 дюймам.
3 фута равны 36 дюймам. - Умножьте на ширину и длину прямоугольника. Площадь равна 4 умножить на 36.
- Проверьте свой результат в нашем калькуляторе площади прямоугольника!
Как определить, является ли фигура прямоугольником?
Фигура является прямоугольником, если:
- Имеет два измерения – длину и ширину.
- У него четыре стороны, образующие четыре угла.
- Все углы прямые (90°).
- Противоположные стороны прямоугольника параллельны друг другу и имеют одинаковую длину.
Bogna Szyk и Hanna Pamuła, PhD
Длина (A)
Ширина (B)
Область (A)
Периметр (P)
Diagonal (D)
Проверка 23d 23d GeomTrate GEOMTROAT. 📏
ПлощадьПлощадь полумесяцаЦентр масс… Еще 20 к площади прямоугольника
Перейти к вычислению площади прямоугольника
Перейти к вычислению периметра прямоугольника
Перейти к вычислению периметра прямоугольника
Перейти к диагонали прямоугольника
Перейти к вычислению диагонали Прямоугольник
Перейти к применению этих вычислений в реальной жизни
Вернуться на страницу калькуляторов
Как вычислить площадь прямоугольникаЕсли вам нужно найти площадь и периметр прямоугольника, этот калькулятор вам пригодится.
 инструмент, который вам понадобится.
инструмент, который вам понадобится.Просто введя длину и ширину, этот калькулятор почти мгновенно найдет периметр (P) и площадь (A).
Если вас интересуют калькуляторы для различных других форм, вы можете посмотреть другие наши удобные калькуляторы. Но вы можете остаться здесь и узнать больше о нахождении площади прямоугольника.
Прямоугольник имеет четыре угла по 90 градусов. Если длины всех сторон одинаковы, то прямоугольник также является квадратом. Длины сторон будут указаны как a или b , или вы можете использовать l и w для «длины» и «ширины». Диагональ, идущая от одной вершины к противоположной, делящей прямоугольник на два квадрата, называется диагональю и обозначается как d .
Вот основные формулы, используемые калькулятором.
Площадь (A) = a (b)
Периметр (расстояние вокруг внешней стороны прямоугольника) = a + a + b + b или 2 a + 2 b и обозначается как (P)
Диагональ равна d ² = a ² + b ², что является теоремой Пифагора (см.
 наш калькулятор теоремы Пифагора).
наш калькулятор теоремы Пифагора).Пример вычисления площади прямоугольника:
Предположим, что длина равна а = 6 дюймов, а ширина равна b = 4 дюйма
A = a * b , поэтому A = 6(4) = 24 дюйма²
Используя те же размеры, мы можем вычислить периметр.
Периметр равен 2 a + 2 b , поэтому в этом примере периметр
P = 2(6) + 2(4) = 20 дюймов
Чтобы найти диагональ, используя те же размеры:
d ² = 6² + 4² = 36 + 16 = 52
Возьмите квадратный корень из обеих сторон, и диагональ d будет приблизительно 7,2 дюйма
Эти примеры иллюстрируют, как вычислить площадь, периметр и диагональ прямоугольника вручную, но если вы предпочитаете использовать калькулятор для получения более быстрых результатов или просто для проверки своей работы, не стесняйтесь делать это. Отличительной особенностью калькулятора является то, что вы можете найти либо длину, либо ширину, если знаете периметр и длину одной из сторон.

На этой странице показано, как измерять площадь прямоугольника. Мы рассмотрим следующие темы:
Каковы площадь, периметр и диагональ прямоугольника?
Как вычислить площадь, периметр и диагональ прямоугольника?
Реальное приложение для вычисления площади, периметра и диагонали прямоугольника
Площадь прямоугольникаПредставьте площадь прямоугольника в виде клеток внутри прямоугольника. Прямоугольник ниже имеет покрытую площадь 12 «квадратов»
Пространство внутри двумерной формы — это площадь или количество закрытой формы.На этой диаграмме показаны ширина, длина и площадь прямоугольника:
Вычисление площади прямоугольникаЧтобы найти площадь прямоугольника, нужно умножить длину и ширину прямоугольника.
 . Мы можем получить площадь прямоугольника по следующей формуле:
. Мы можем получить площадь прямоугольника по следующей формуле:A = L * W
A — площадь, L — длина, W — ширина.
Пример 1Вычислите площадь прямоугольника, имеющего длину 7 сантиметров и ширину 5 сантиметров.
Формула:A = L * W
ОТВЕТ:A = 35. Данная длина ( L ). W ). При умножении вы получите 35 в качестве вашей площади.
Периметр прямоугольникаПосмотрите на изображение ниже, человек ходит вокруг коробки. Путь, который он проходит от начальной точки и обратно, является периметром. Зная длину и ширину прямоугольника, мы можем теперь получить периметр прямоугольника. Обе противоположные стороны прямоугольника конгруэнтны, что означает, что сложив эти стороны, мы можем вычислить периметр.
Вычисление периметра прямоугольникаСложив все стороны прямоугольника, мы теперь можем получить его периметр.
 Вот уравнение для получения периметра прямоугольника:
Вот уравнение для получения периметра прямоугольника:P = L + W + L + W
Поскольку мы знаем, что обе противоположные стороны прямоугольника идентичны, мы можем упростить уравнение, используя это уравнение :
P = 2L + 2W
Пример 1Найдите периметр прямоугольника, длина которого 12 сантиметров, а ширина 7 сантиметров.
Формула:P = L + W + L + W или
P = 2L + 2W
. 12 + 7 илиP = 2(12) + 2(7)
Ответ будет P = 38. Прибавив 12 ( L ) + 7 ( W ) + 12 ( ) ) + 7 ( W ) , вы получите 38. Перемножив длину ( L ) и ширину ( W ) на 2, затем сложив частное, вы получите тот же ответ.
Диагональ прямоугольникаЕсли присмотреться, прямоугольник представляет собой комбинацию двух прямых углов.
 {2}}\)
\(D = \sqrt{34}\)
{2}}\)
\(D = \sqrt{34}\)D = 5,83
Реальные приложения для получения площади прямоугольникаМолодожены хотят положить плитку на пол в главной спальне. Комната имеет длину 20 футов и ширину 30 футов. Плитка, которую они выбрали, имеет длину 24 дюйма и ширину 36 дюймов. Решите, сколько плиток нужно, чтобы заполнить главную спальню.
Советы:
1. Найдите площадь, занимаемую главной спальней.
2. Вычислите площадь плитки
3. Выберите единицу измерения. В этом примере будут использоваться ноги.
Solution:A = L * W
A = 20 ft x 30 ft
A = 600 ft²
Tip:
Прежде чем мы получим площадь каждой плитки, переведем футы в дюймы
Пример преобразования:
1 Фут = 12 дюймов
2 фута = 24 дюйма
3 фута = 36 дюймов
Площадь 1 The Tile = L × W 9003 777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777.
 = 2 × 3
= 2 × 3 Площадь 1 плитки = 6 футов²
Это означает, что каждая плитка имеет площадь 6 футов² и должна покрывать площадь комнаты, которая составляет 600 футов². Итак, 6 × 100 = 600,
Количество плиток, необходимых для заполнения главной спальни, составляет 600.
Реальные приложения для получения периметра прямоугольникаФермер хочет добавить клетку для своих цыплят. Он хочет добавить новый забор возле своего дома и свободное пространство длиной 30 метров и шириной 16 метров. Найдите периметр свободного пространства.
Решение:P = 2L + 2W
Ответ:Периметр = 2(Длина свободного пространства) + 2(Ширина свободного пространства)
P = 2(30) + 2(16) P = 6 00023 9 00003 9 + 32
P = 92
Периметр свободного пространства 92 метра.


 Корень из 16 = 4 см.
Корень из 16 = 4 см.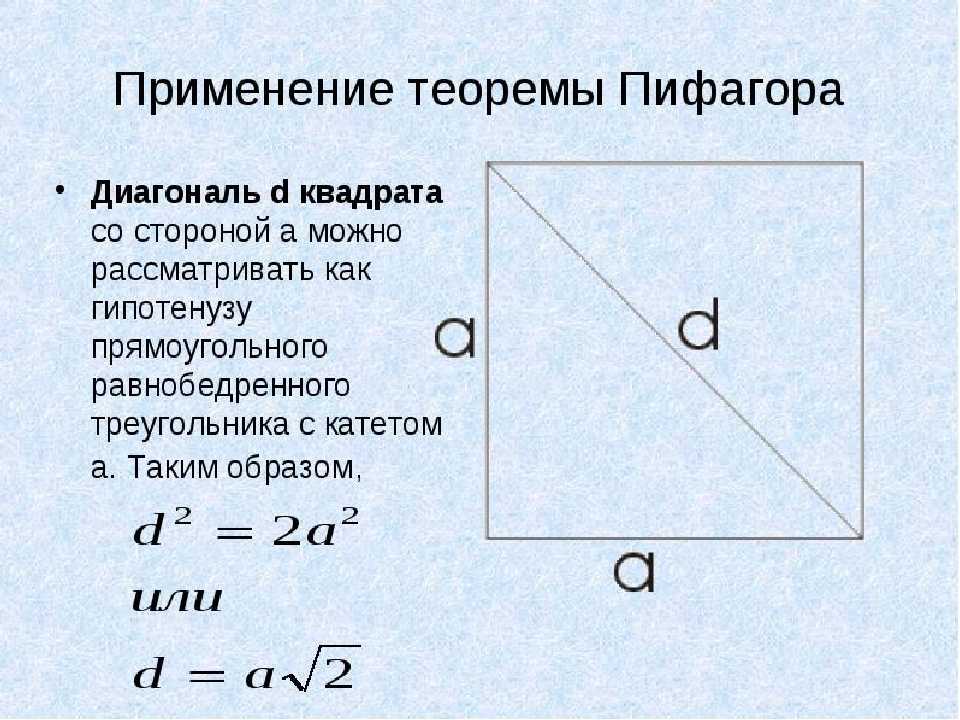

 Является ли квадрат прямоугольником?
Является ли квадрат прямоугольником? При этом каждая сторона прямоугольника имеет ту же длину, что и противоположная ей сторона. Он также имеет неравные смежные стороны, в отличие от квадрата, частного случая прямоугольника.
При этом каждая сторона прямоугольника имеет ту же длину, что и противоположная ей сторона. Он также имеет неравные смежные стороны, в отличие от квадрата, частного случая прямоугольника.
 Вычислим длину диагонали примерного прямоугольника:
Вычислим длину диагонали примерного прямоугольника: Такой прямоугольник удовлетворяет следующему условию:
Такой прямоугольник удовлетворяет следующему условию:

 Индекс 1 — идеальный прямоугольник, 0 — бесконечное число бесконечно малых островков. Таблица адаптирована с веб-страницы г-на Барри как изображение мира ниже.
Индекс 1 — идеальный прямоугольник, 0 — бесконечное число бесконечно малых островков. Таблица адаптирована с веб-страницы г-на Барри как изображение мира ниже.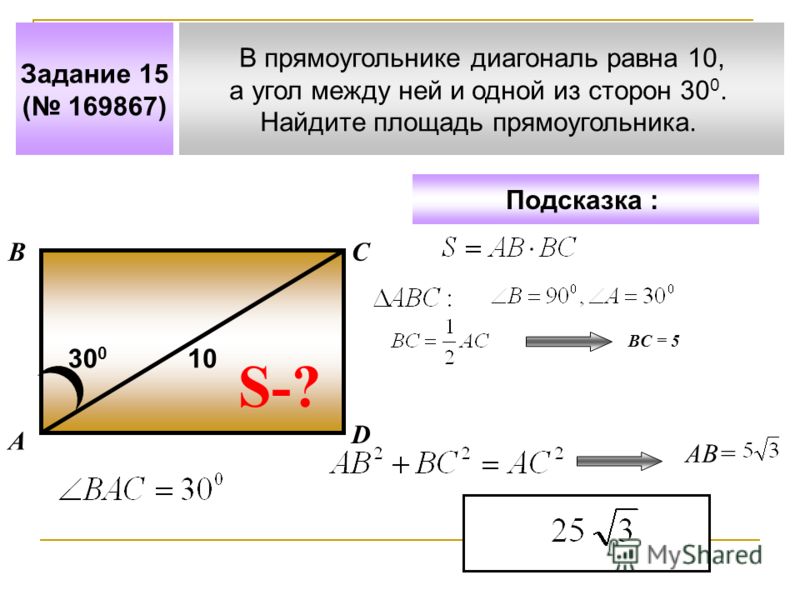 28
28 240
240 земного шара.
земного шара. Для пятиугольника форма должна быть неправильной, чтобы образовался мозаичный узор.
Для пятиугольника форма должна быть неправильной, чтобы образовался мозаичный узор.
 3 фута равны 36 дюймам.
3 фута равны 36 дюймам.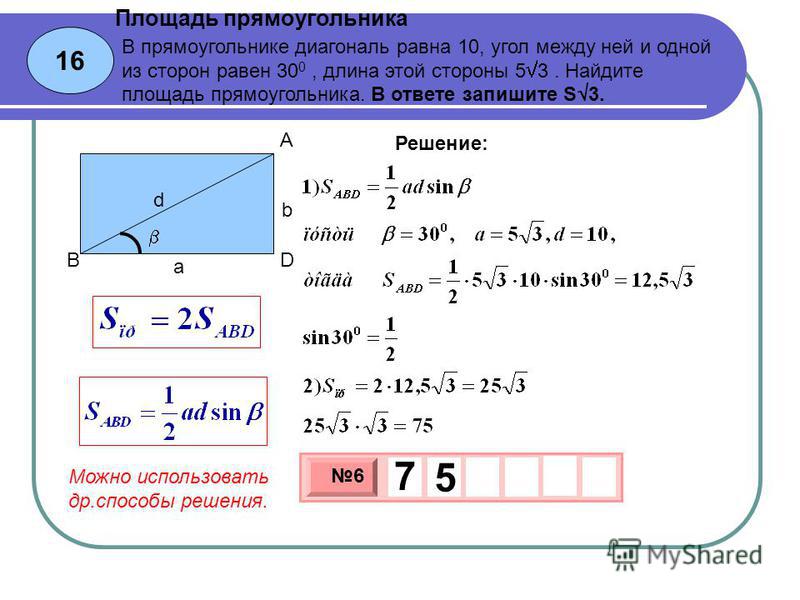 инструмент, который вам понадобится.
инструмент, который вам понадобится.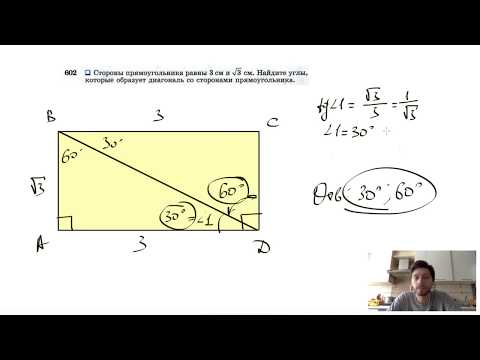 наш калькулятор теоремы Пифагора).
наш калькулятор теоремы Пифагора).
 . Мы можем получить площадь прямоугольника по следующей формуле:
. Мы можем получить площадь прямоугольника по следующей формуле: Вот уравнение для получения периметра прямоугольника:
Вот уравнение для получения периметра прямоугольника: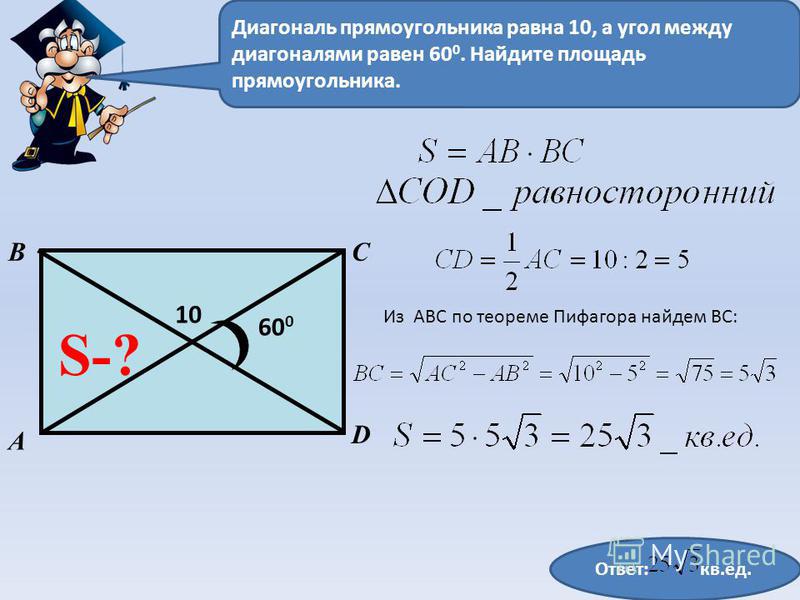 {2}}\)
\(D = \sqrt{34}\)
{2}}\)
\(D = \sqrt{34}\) = 2 × 3
= 2 × 3 
Leave A Comment