Краткое причастие — определение, окончание, формы
Научим писать без ошибок и интересно рассказывать
Начать учиться
У причастия и прилагательного есть общие свойства, одно из них — полная и краткая формы. В этой статье расскажем, как определить краткое причастие, раскроем его синтаксические и грамматические особенности.
Понятие причастия
Причастие — это часть речи или особая форма глагола, которая обозначает признак предмета по действию и отвечает на вопросы прилагательного. Согласно одной из версий, называется оно так, потому что причастно к свойствам глагола и прилагательного.
Примеры причастий:
- решенный — образовано от глагола«решить»
- приглашенный — от глагола «пригласить».

У причастий, как и у некоторых прилагательных, есть не только полная, но и краткая форма:
- обожаемая — обожаема;
- приклеенный — приклеен;
- запертый — заперт.
Ответим на самый популярный вопрос: «Какие причастия имеют краткую форму?». Ее имеют только страдательные причастия, которые обозначают признак по действию другого объекта.
Демоурок по русскому языку
Пройдите тест на вводном занятии и узнайте, какие темы отделяют вас от «пятёрки» по русскому.
Понятие краткого причастия
Краткое причастие — это грамматическая форма, которую образует полное страдательное причастие настоящего или прошедшего времени. Обозначает признак предмета по действию.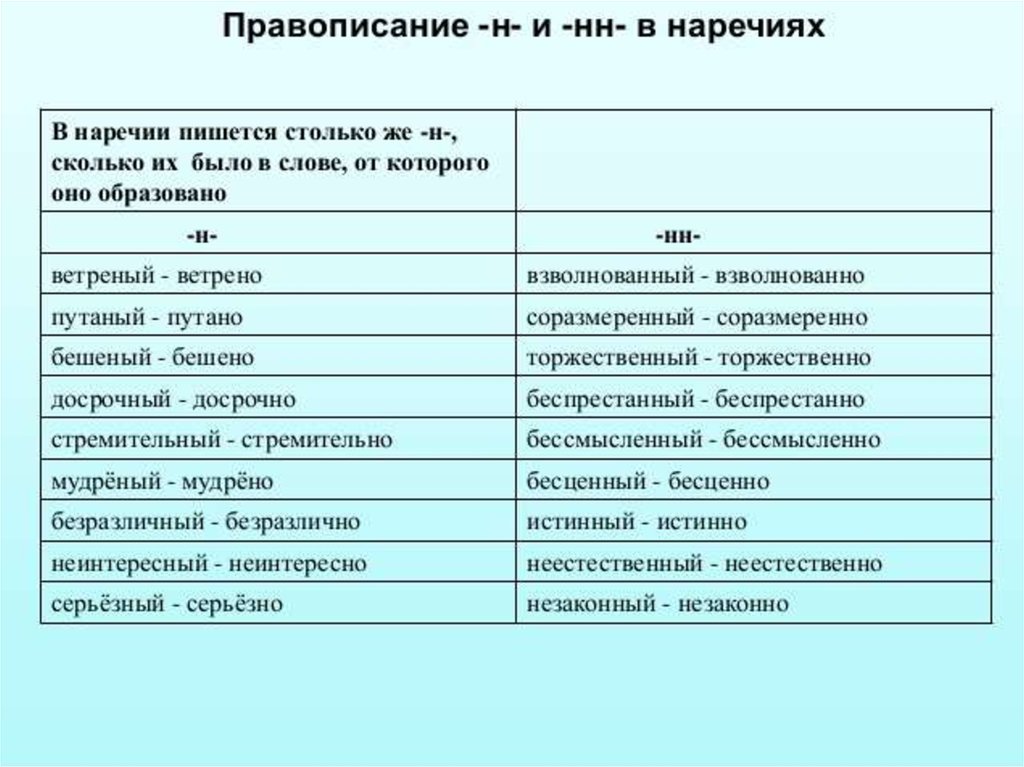
Вопросы кратких причастий: «каков?», «какова?», «каково?», «каковы?», а также «что сделан?», «что сделано?», «что сделана?», «что сделаны?». Они схожи с вопросами полной формы:
- заявление (что сделано?) озвучено,
- картина (что сделана?) нарисована,
- кабинет (что сделан?) отремонтирован.
В русском языке краткие формы образуют только страдательные причастия настоящего и прошедшего времени с суффиксами
При образовании краткой формы происходит усечение окончания, а суффиксам -енн- и -нн- соответствуют суффиксы -ен- и -н-.
Вот как это выглядит:
Запоминаем!
Краткие причастия всегда пишутся с одной буквой «н».
Курсы подготовки к ЕГЭ по русскому языку в онлайн-школе Skysmart — без стресса и на реальных экзаменационных заданиях. Попробуйте бесплатно на вводном уроке!
Суффиксы | Примеры кратких причастий | |
Краткие причастия настоящего времени | -ем-/-ом- | управляем (от управляемый) выполняем (от выполняемый) читаем (от читаемый) |
-им- | храним (от хранимый) слышим (от слышимый) зависим (от зависимый) | |
Краткие причастия прошедшего времени | -ен- | завешен (от завешенный) ухожен (от ухоженный) принесен (от принесенный) |
-н- | сделан (от сделанный) указан (от указанный) | |
-т- | покрыт (от покрытый) разбит (от разбитый) спет (от спетый) |
Краткое страдательное причастие можно заменить однокоренным глаголом в форме прошедшего времени:
- стена (какова?) покрашена — стена, которую покрасили;
- дело (каково?) сделано — дело, которое сделали.

Особенности изменения кратких причастий
Краткие причастия изменяются по родам и числам, в словосочетаниях согласуются с существительными и местоимениями.
Запоминаем!
Краткое причастие не изменяется по падежам, как и краткая форма прилагательного.
Единственное число | Множественное число | |||
окончание | примеры | окончание | примеры | |
Мужской род | нулевое | украшаем вымыт брошен | -ы | украшаемы вымыты брошены |
Женский род | -а | украшаема вымыта брошена | ||
Средний род | -о | украшаемо вымыто брошено | ||
Роль кратких причастий в предложении
В предложениях и словосочетаниях причастия должны согласоваться с другими членами предложения. В частности, с существительными и местоимениями, которые они определяют.
В частности, с существительными и местоимениями, которые они определяют.
В предложении составное именное сказуемое чаще располагается после подлежащего. Рассмотрим примеры:
Шпаргалки для родителей по русскому
Все формулы по русскому языку под рукой и бесплатно
Лидия Казанцева
Автор Skysmart
К предыдущей статье
260.4K
Разряды имен прилагательных
К следующей статье
396.7K
Чередование гласных в корне
Получите план развития речи и письма на бесплатном вводном уроке
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Н и НН в причастиях, правописание в суффиксах, примеры и правила
3. 9
9
Средняя оценка: 3.9
Всего получено оценок: 4680.
3.9
Средняя оценка: 3.9
Всего получено оценок: 4680.
При написании причастий часто допускаются ошибки, в частности, при использовании -Н- и -НН-. В данной статье приведены правила написания одной и двух Н в причастиях и отглагольных прилагательных с примерами, а также важные моменты, на которые стоит обратить внимание.
Материал подготовлен совместно с учителем высшей категории Кучминой Надеждой Владимировной.
Опыт работы учителем русского языка и литературы — 27 лет.
Страдательные причастия прошедшего времени образуются при помощи суффиксов
-нн-/-енн-, поэтому при написании их часто путают с отглагольными прилагательными, делая характерные ошибки. Для правильного употребления н и нн в причастиях необходимо запомнить:
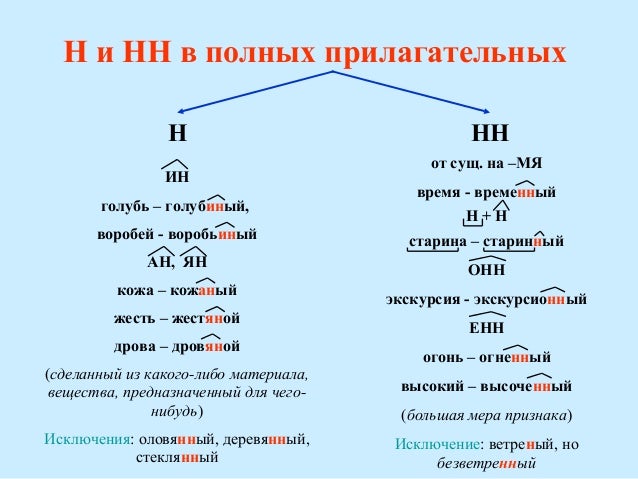
- Две буквы н пишутся в суффиксах полных страдательных причастий прошедшего времени.
- Одна н в причастиях пишется только в случаях, когда причастие употребляется в краткой форме.

Таблица Особенности правописания н и нн в причастиях
| НН | Н | ||
| Правило | Примеры | Правило | Примеры |
| причастие имеет приставку (кроме не-) | убранная комната, сделанное задание, вспаханное поле | в кратких причастиях, образованных от полных страдательных причастий прошедшего времени путем усечения части основы и окончания | задание сделано учеником, зверь ранен охотником в лапу, грибы маринованы, лошадь подкована |
| причастие употребляется с зависимыми от него словами (в составе причастного оборота) | жаренный мальчиками на костре картофель, раненный охотником в лапу зверь, сушенные дедушкой на чердаке яблоки | ||
| причастия, образованные от глаголов совершенного вида без приставки | брошенные вещи, данный стариком совет, решенный вопрос | ||
| Причастие образовано от глаголов с суффиксами -ова-/-ева-/-ирова- | маринованные грибы, отремонтированная машина, подкованная лошадь | ||
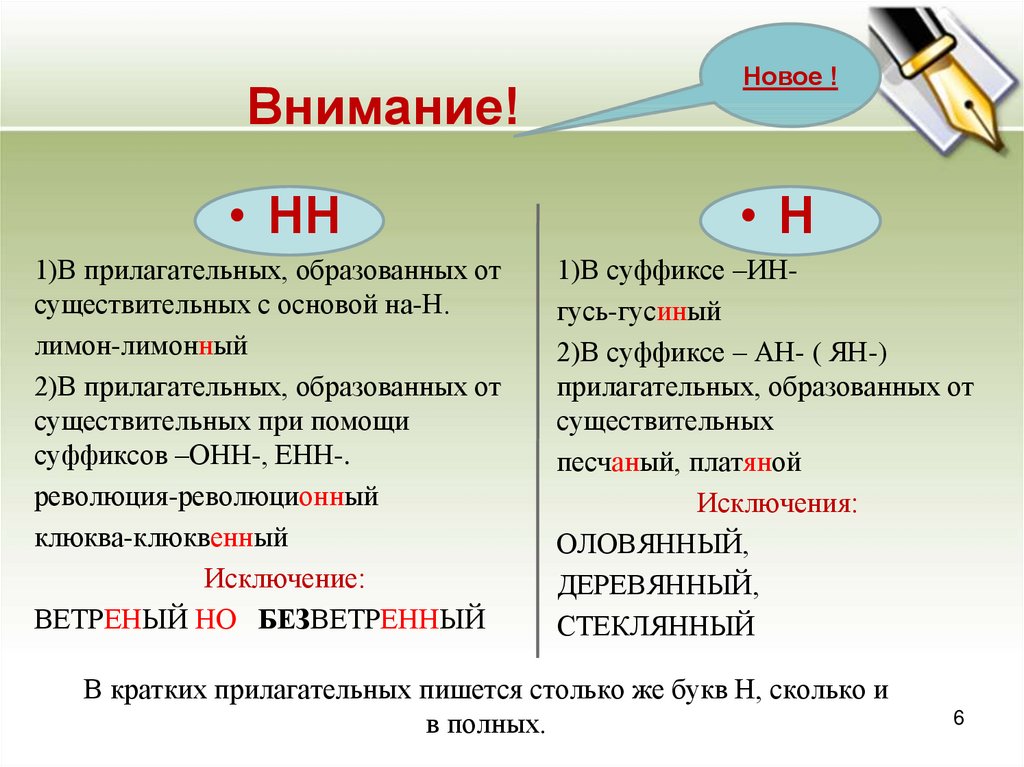
Важно! Полные страдательные причастия прошедшего времени всегда употребляются с двумя н. Слова, в которых пишется одна н, обычно являются бывшими причастиями, которые перешли в прилагательные и утратили значение признака по действию (печеное мясо, кипяченая вода).
Слова, в которых пишется одна н, обычно являются бывшими причастиями, которые перешли в прилагательные и утратили значение признака по действию (печеное мясо, кипяченая вода).
Доска почёта
Чтобы попасть сюда — пройдите тест.
Оценка статьи
3.9
Средняя оценка: 3.9
Всего получено оценок: 4680.
А какая ваша оценка?
Что такое алгоритм k ближайших соседей?
Алгоритм K-ближайших соседей
Алгоритм k-ближайших соседей, также известный как KNN или k-NN, представляет собой непараметрический классификатор с контролируемым обучением, который использует близость для классификации или прогнозирования группировки отдельных точек данных. Хотя его можно использовать как для задач регрессии, так и для задач классификации, обычно он используется в качестве алгоритма классификации, основанного на предположении, что похожие точки могут быть найдены рядом друг с другом.
Для задач классификации метка класса присваивается на основе большинства голосов, т.е. используется метка, которая чаще всего представлена вокруг данной точки данных. Хотя технически это считается «многочисленным голосованием», термин «мажоритарное голосование» чаще используется в литературе. Различие между этими терминологиями заключается в том, что для «голосования большинством» технически требуется большинство, превышающее 50%, что в первую очередь работает, когда есть только две категории. Когда у вас есть несколько классов, например. четыре категории, не обязательно 50% голосов, чтобы сделать вывод о классе; вы можете присвоить метку класса при голосовании более 25%. Университет Висконсин-Мэдисон хорошо резюмирует это с помощью примера здесь (PDF, 1,2 МБ) (ссылка находится за пределами ibm.com).
В задачах регрессии используется та же концепция, что и в задачах классификации, но в этом случае для предсказания классификации берется среднее значение k ближайших соседей. Основное отличие здесь в том, что классификация используется для дискретных значений, а регрессия — для непрерывных. Однако, прежде чем можно будет провести классификацию, необходимо определить расстояние. Чаще всего используется евклидово расстояние, о котором мы поговорим ниже.
Основное отличие здесь в том, что классификация используется для дискретных значений, а регрессия — для непрерывных. Однако, прежде чем можно будет провести классификацию, необходимо определить расстояние. Чаще всего используется евклидово расстояние, о котором мы поговорим ниже.
Также стоит отметить, что алгоритм KNN также является частью семейства моделей «ленивого обучения», что означает, что он сохраняет только обучающий набор данных, а не проходит этап обучения. Это также означает, что все вычисления происходят во время классификации или предсказания. Поскольку он в значительной степени зависит от памяти для хранения всех своих обучающих данных, его также называют методом обучения на основе экземпляров или памяти.
Эвелин Фикс и Джозеф Ходжес приписывают первоначальные идеи относительно модели KNN в этой статье 1951 года (PDF, 1,1 МБ) (ссылка находится за пределами ibm.com), а Томас Ковер расширяет их концепцию в своем исследовании (PDF, 1 МБ) (ссылка находится за пределами ibm. com), «Классификация шаблонов ближайших соседей». Хотя он не так популярен, как когда-то, он по-прежнему остается одним из первых алгоритмов, которые изучают в науке о данных, благодаря своей простоте и точности. Однако по мере роста набора данных KNN становится все менее эффективным, что снижает общую производительность модели. Он обычно используется для простых систем рекомендаций, распознавания образов, интеллектуального анализа данных, прогнозов финансовых рынков, обнаружения вторжений и многого другого.
com), «Классификация шаблонов ближайших соседей». Хотя он не так популярен, как когда-то, он по-прежнему остается одним из первых алгоритмов, которые изучают в науке о данных, благодаря своей простоте и точности. Однако по мере роста набора данных KNN становится все менее эффективным, что снижает общую производительность модели. Он обычно используется для простых систем рекомендаций, распознавания образов, интеллектуального анализа данных, прогнозов финансовых рынков, обнаружения вторжений и многого другого.
Вычислить KNN: метрики расстояния
Напомним, что целью алгоритма k-ближайших соседей является определение ближайших соседей заданной точки запроса, чтобы мы могли присвоить этой точке метку класса. Для этого у KNN есть несколько требований:
Определите ваши показатели расстояния
Чтобы определить, какие точки данных находятся ближе всего к заданной точке запроса, потребуется расстояние между точкой запроса и другими точками данных. быть рассчитаны. Эти метрики расстояния помогают формировать границы решений, которые разбивают точки запроса на разные регионы. Обычно вы видите границы решений, визуализированные с помощью диаграмм Вороного.
быть рассчитаны. Эти метрики расстояния помогают формировать границы решений, которые разбивают точки запроса на разные регионы. Обычно вы видите границы решений, визуализированные с помощью диаграмм Вороного.
Хотя существует несколько мер расстояния, которые вы можете выбрать, в этой статье рассматриваются только следующие:
Евклидово расстояние (p=2): оцененные векторы. Используя приведенную ниже формулу, он измеряет прямую линию между точкой запроса и другой измеряемой точкой.
Манхэттенское расстояние (p=1) : Это также еще одна популярная метрика расстояния, которая измеряет абсолютное значение между двумя точками. Его также называют расстоянием такси или расстоянием до городских кварталов, поскольку оно обычно визуализируется с помощью сетки, иллюстрирующей, как можно перемещаться от одного адреса к другому по улицам города.
Расстояние Минковского : Эта мера расстояния является обобщенной формой евклидовых и манхэттенских метрик расстояния. Параметр p в приведенной ниже формуле позволяет создавать другие показатели расстояния. Евклидово расстояние представлено этой формулой, когда p равно двум, а манхэттенское расстояние обозначается p, равным единице.
Параметр p в приведенной ниже формуле позволяет создавать другие показатели расстояния. Евклидово расстояние представлено этой формулой, когда p равно двум, а манхэттенское расстояние обозначается p, равным единице.
Расстояние Хэмминга: Этот метод обычно используется с булевыми или строковыми векторами, определяя точки, в которых векторы не совпадают. В результате его также называют показателем перекрытия. Это можно представить следующей формулой:
Например, если бы у вас были следующие строки, расстояние Хэмминга было бы равно 2, поскольку различаются только два значения.
Вычисление KNN: определение k
Значение k в алгоритме k-NN определяет, сколько соседей будет проверено для определения классификации конкретной точки запроса. Например, если k=1, экземпляр будет отнесен к тому же классу, что и его единственный ближайший сосед. Определение k может быть уравновешивающим действием, поскольку разные значения могут привести к переоснащению или недообучению. Более низкие значения k могут иметь высокую дисперсию, но низкое смещение, а большие значения k могут привести к высокому смещению и более низкой дисперсии. Выбор k будет в значительной степени зависеть от входных данных, поскольку данные с большим количеством выбросов или шума, вероятно, будут работать лучше при более высоких значениях k. В целом, рекомендуется иметь нечетное число для k, чтобы избежать связей в классификации, а тактика перекрестной проверки может помочь вам выбрать оптимальное k для вашего набора данных.
Более низкие значения k могут иметь высокую дисперсию, но низкое смещение, а большие значения k могут привести к высокому смещению и более низкой дисперсии. Выбор k будет в значительной степени зависеть от входных данных, поскольку данные с большим количеством выбросов или шума, вероятно, будут работать лучше при более высоких значениях k. В целом, рекомендуется иметь нечетное число для k, чтобы избежать связей в классификации, а тактика перекрестной проверки может помочь вам выбрать оптимальное k для вашего набора данных.
k-ближайшие соседи и python
Чтобы углубиться, вы можете узнать больше об алгоритме k-NN с помощью Python и scikit-learn (также известного как sklearn). Наш учебник в Watson Studio поможет вам изучить базовый синтаксис этой библиотеки, которая также содержит другие популярные библиотеки, такие как NumPy, pandas и Matplotlib. Следующий код является примером того, как создавать и прогнозировать с помощью модели KNN:
из sklearn.neighbors import KNeighborsClassifier
model_name = ‘K-Nearest Neighbor Classifier’
knnClassifier = KNeighborsClassifier(n_neighbors = 5, metric = ‘minkowski’, p=2)
knn_model = Pipeline(steps=[(‘preprocessor’, preprocessorForFeatures), (‘classifier’, knnClassifier)])
knn_model. fit(X_train , y_train)
fit(X_train , y_train)
y_pred = knn_model.predict(X_test)
Применение k-NN в машинном обучении
Алгоритм k-NN использовался в различных приложениях, в основном в классификации. Вот некоторые из этих вариантов использования:
— Предварительная обработка данных : наборы данных часто содержат пропущенные значения, но алгоритм KNN может оценить эти значения в процессе, известном как вменение пропущенных данных.
— Механизмы рекомендаций : Алгоритм KNN, использующий данные о посещениях веб-сайтов, был использован для предоставления пользователям автоматических рекомендаций по дополнительному контенту. Это исследование (ссылка находится за пределами ibm.com) показывает, что пользователь относится к определенной группе, и на основе поведения пользователей этой группы ему даются рекомендации. Однако, учитывая проблемы масштабирования с KNN, этот подход может быть не оптимальным для больших наборов данных.
— Финансы : Он также использовался в различных финансовых и экономических случаях. Например, в одном документе (PDF, 391 КБ) (ссылка находится за пределами ibm.com) показано, как использование KNN в кредитных данных может помочь банкам оценить риск кредита для организации или отдельного лица. Он используется для определения кредитоспособности заемщика. В другом журнале (PDF, 447 КБ) (ссылка находится за пределами ibm.com) освещается его использование в прогнозировании фондового рынка, обменных курсов валют, торговле фьючерсами и анализе отмывания денег.
— Здравоохранение : KNN также применялся в сфере здравоохранения, делая прогнозы риска сердечных приступов и рака простаты. Алгоритм работает, вычисляя наиболее вероятные экспрессии генов.
— Распознавание шаблонов : KNN также помог в выявлении шаблонов, например, в классификации текста и цифр (ссылка находится за пределами ibm.com). Это было особенно полезно при идентификации рукописных номеров, которые вы могли найти на формах или почтовых конвертах.
Преимущества и недостатки алгоритма KNN
Как и любой алгоритм машинного обучения, k-NN имеет свои сильные и слабые стороны. В зависимости от проекта и приложения это может быть или не быть правильным выбором.
Преимущества — Простота реализации : Учитывая простоту и точность алгоритма, это один из первых классификаторов, который изучит новый специалист по данным.
— Легко адаптируется : По мере добавления новых обучающих выборок алгоритм корректируется с учетом любых новых данных, поскольку все обучающие данные сохраняются в памяти.
— Несколько гиперпараметров : KNN требует только значения k и метрики расстояния, что является низким по сравнению с другими алгоритмами машинного обучения.
Недостатки — Плохо масштабируется : Поскольку KNN является ленивым алгоритмом, он требует больше памяти и места для хранения данных по сравнению с другими классификаторами.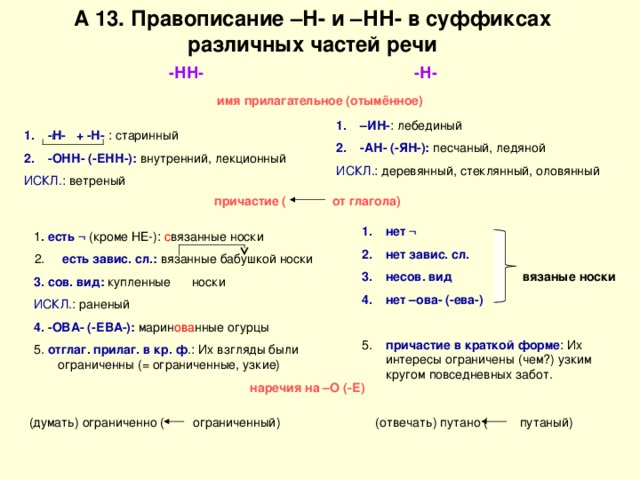 Это может быть затратно как с точки зрения времени, так и денег. Больше памяти и хранилища повысит бизнес-расходы, а для обработки большего объема данных может потребоваться больше времени. Хотя для устранения неэффективности вычислений были созданы различные структуры данных, такие как Ball-Tree, в зависимости от бизнес-задачи может подойти другой классификатор.
Это может быть затратно как с точки зрения времени, так и денег. Больше памяти и хранилища повысит бизнес-расходы, а для обработки большего объема данных может потребоваться больше времени. Хотя для устранения неэффективности вычислений были созданы различные структуры данных, такие как Ball-Tree, в зависимости от бизнес-задачи может подойти другой классификатор.
— Проклятие размерности : Алгоритм KNN имеет тенденцию становиться жертвой проклятия размерности, что означает, что он плохо работает с многомерными входными данными. Это иногда также называют пиковым явлением (PDF, 340 МБ) (ссылка находится за пределами ibm.com), когда после того, как алгоритм достигает оптимального количества функций, дополнительные функции увеличивают количество ошибок классификации, особенно когда выборка размер меньше.
— Склонен к переоснащению : Из-за «проклятия размерности» KNN также более склонен к переоснащению. Хотя для предотвращения этого используются методы выбора признаков и уменьшения размерности, значение k также может влиять на поведение модели.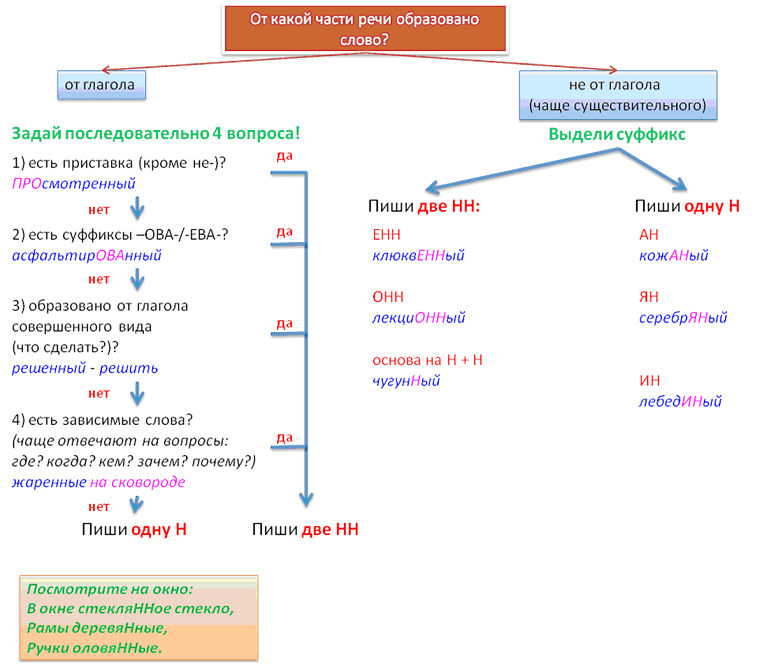 Более низкие значения k могут перекрыть данные, тогда как более высокие значения k имеют тенденцию «сглаживать» значения прогноза, поскольку они усредняют значения по большей площади или окрестностям. Однако, если значение k слишком велико, оно может не соответствовать данным.
Более низкие значения k могут перекрыть данные, тогда как более высокие значения k имеют тенденцию «сглаживать» значения прогноза, поскольку они усредняют значения по большей площади или окрестностям. Однако, если значение k слишком велико, оно может не соответствовать данным.
IBM Cloud Pak for Data — это открытая расширяемая платформа данных, которая обеспечивает структуру данных, позволяющую сделать все данные доступными для ИИ и аналитики в любом облаке.
Студия IBM WatsonСоздавайте, запускайте и управляйте моделями ИИ. Подготавливайте данные и создавайте модели в любом облаке с помощью открытого исходного кода или визуального моделирования. Прогнозируйте и оптимизируйте свои результаты.
IBM Db2 в облаке Узнайте о Db2 on Cloud — полностью управляемой облачной базе данных SQL, настроенной и оптимизированной для обеспечения надежной работы.
Следующие шаги
k-NN Node и IBM Cloud Pak для данных
Cloud Pak for Data — это набор инструментов, помогающих подготовить данные для внедрения ИИ. Узел k-NN — это метод моделирования, доступный в IBM Cloud Pak for Data, который упрощает разработку прогностических моделей. Плагин развертывается в любом облаке и легко интегрируется в существующую облачную инфраструктуру.



 Итак, для этой идентификации мы можем использовать алгоритм KNN, так как он работает с мерой сходства. Наша модель KNN найдет сходные черты нового набора данных с изображениями кошек и собак и, основываясь на наиболее сходных характеристиках, поместит его в категорию кошек или собак.
Итак, для этой идентификации мы можем использовать алгоритм KNN, так как он работает с мерой сходства. Наша модель KNN найдет сходные черты нового набора данных с изображениями кошек и собак и, основываясь на наиболее сходных характеристиках, поместит его в категорию кошек или собак.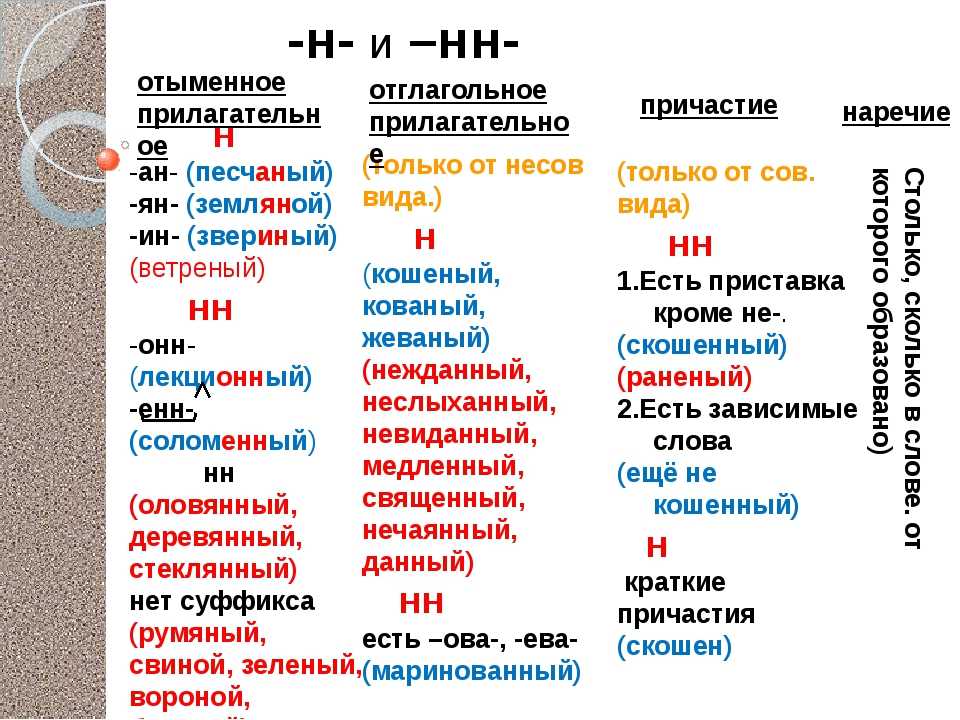



 После масштабирования функций наш тестовый набор данных будет выглядеть так:
После масштабирования функций наш тестовый набор данных будет выглядеть так: neighbors импортировать KNeighborsClassifier
classifier = KNeighborsClassifier (n_neighbors = 5, метрика = ‘Минковский’, p = 2)
classifier.fit(x_train, y_train)
neighbors импортировать KNeighborsClassifier
classifier = KNeighborsClassifier (n_neighbors = 5, метрика = ‘Минковский’, p = 2)
classifier.fit(x_train, y_train) Ниже приведен код для него:
Ниже приведен код для него: colors импортировать ListedColormap
x_set, y_set = x_train, y_train
x1, x2 = nm.meshgrid(nm.arange(начало = x_set[:, 0].min() — 1, стоп = x_set[:, 0].max() + 1, шаг = 0,01),
nm.arange(начало = x_set[:, 1].min() — 1, стоп = x_set[:, 1].max() + 1, шаг = 0,01))
mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape),
альфа = 0,75, cmap = ListedColormap((‘красный’,’зеленый’ )))
mtp.xlim (x1.min(), x1.max())
mtp.ylim (x2.min(), x2.max())
для i, j в перечислении (nm.unique (y_set)):
mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1],
c = ListedColormap((‘красный’, ‘зеленый’))(i), метка = j)
mtp.title(‘Алгоритм K-NN (обучающий набор)’)
mtp.xlabel(‘Возраст’)
mtp.ylabel(‘Ориентировочная зарплата’)
mtp.легенда()
mtp.show()
colors импортировать ListedColormap
x_set, y_set = x_train, y_train
x1, x2 = nm.meshgrid(nm.arange(начало = x_set[:, 0].min() — 1, стоп = x_set[:, 0].max() + 1, шаг = 0,01),
nm.arange(начало = x_set[:, 1].min() — 1, стоп = x_set[:, 1].max() + 1, шаг = 0,01))
mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape),
альфа = 0,75, cmap = ListedColormap((‘красный’,’зеленый’ )))
mtp.xlim (x1.min(), x1.max())
mtp.ylim (x2.min(), x2.max())
для i, j в перечислении (nm.unique (y_set)):
mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1],
c = ListedColormap((‘красный’, ‘зеленый’))(i), метка = j)
mtp.title(‘Алгоритм K-NN (обучающий набор)’)
mtp.xlabel(‘Возраст’)
mtp.ylabel(‘Ориентировочная зарплата’)
mtp.легенда()
mtp.show() Это можно понять по пунктам ниже:
Это можно понять по пунктам ниже: Е. Тестовый набор данных. Код остался прежним, за исключением некоторых незначительных изменений: например, x_train и y_train будут заменены на x_test и y_test .
Е. Тестовый набор данных. Код остался прежним, за исключением некоторых незначительных изменений: например, x_train и y_train будут заменены на x_test и y_test . 
Leave A Comment