Самостоятельные работы по геометрии по темам «Четырехугольники. Площадь» № 1-9 (8 класс)
Геометрия 8 класс. Самостоятельная работа № 1.
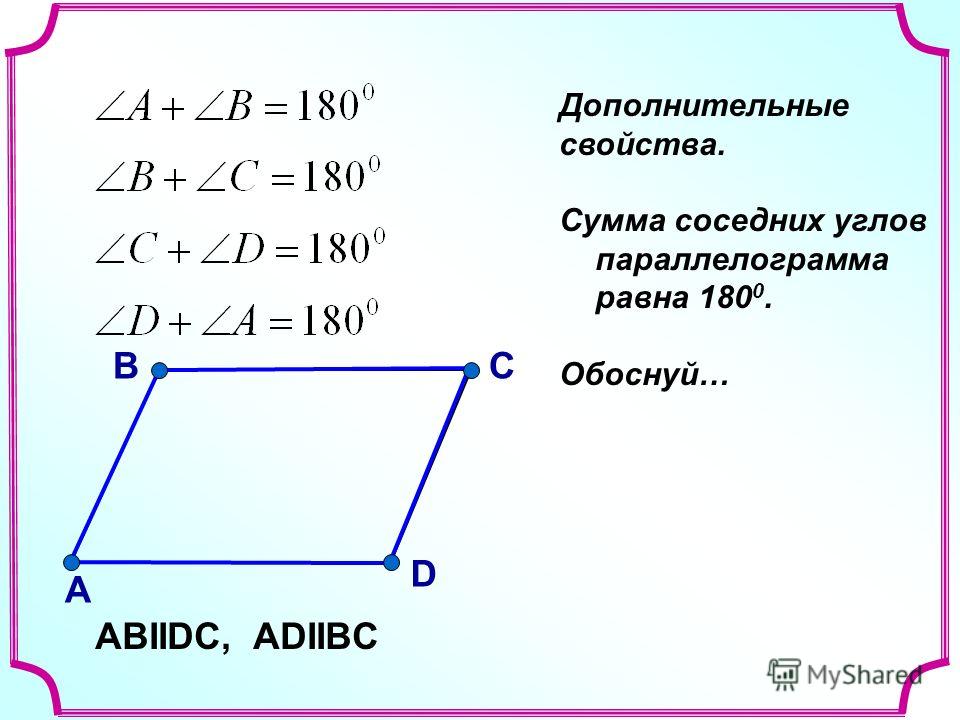
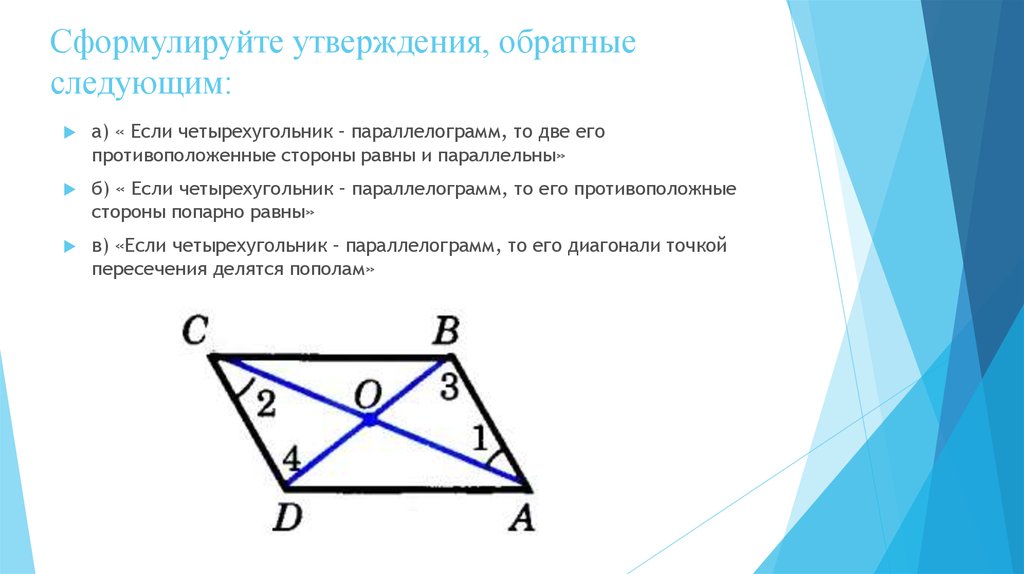
Свойства параллелограмма
Вариант 1.
1. Найдите сумму углов выпуклого семиугольника.
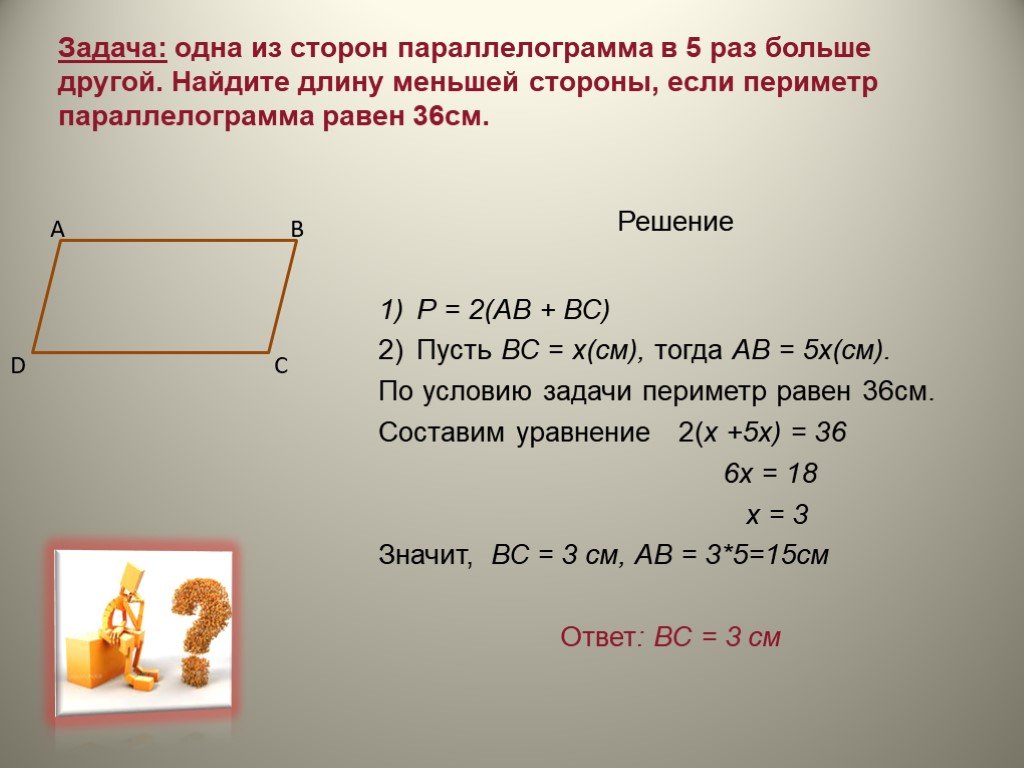
2. Найдите периметр параллелограмма, длины сторон которого равны 5см и 9 см.
3. Диагональ параллелограмма составляет со сторонами параллелограмма углы в 40 и 80 градусов. Найдите углы параллелограмма.
4. Стороны параллелограмма относятся как 2:5, а его периметр равен 56 см. Найдите стороны параллелограмма.
Вариант 2.
1. Найдите сумму углов выпуклого восьмиугольника.
2. Найдите сторону параллелограмма, если длина смежной с ней стороны равна 41 см, а периметр параллелограмма равен 100 см.
3. Высота параллелограмма составляет со стороной параллелограмма угол 27 градусов. Найдите углы параллелограмма.
4. Разность
сторон параллелограмма равна 6 см, а его периметр равен 52 см. Найдите стороны
параллелограмма.
Найдите стороны
параллелограмма.
Вариант 3.
1. Сколько сторон имеет выпуклый многоугольник, если каждый его угол равен 120 градусов?
2. В параллелограмме MNPQ проведена биссектриса ML острого угла М. Точка L лежит на стороне NP. Отрезок LP равен 3 дм, боковая сторона PQ равна 8 дм. Найдите периметр параллелограмма MNPQ.
3. Найдите углы параллелограмма, если известно, что острый угол относится к тупому углу как 4:5.
4. В параллелограмме АВСD проведена диагональ ВD. Угол АВD равен 48 градусов, а угол СВD равен 62 градуса. Найдите углы параллелограмма.
Вариант 4.
1. Сколько сторон имеет выпуклый многоугольник, если каждый его угол равен 135 градусов?
2. В параллелограмме MNPQ проведена биссектриса NL тупого угла N. Точка L лежит на стороне MQ. Отрезок LQ равен 8 дм, боковая сторона QP равна 14 дм. Найдите периметр параллелограмма MNPQ.
3. Найдите
углы параллелограмма, если известно, что острый угол относится к тупому углу
как 1:8.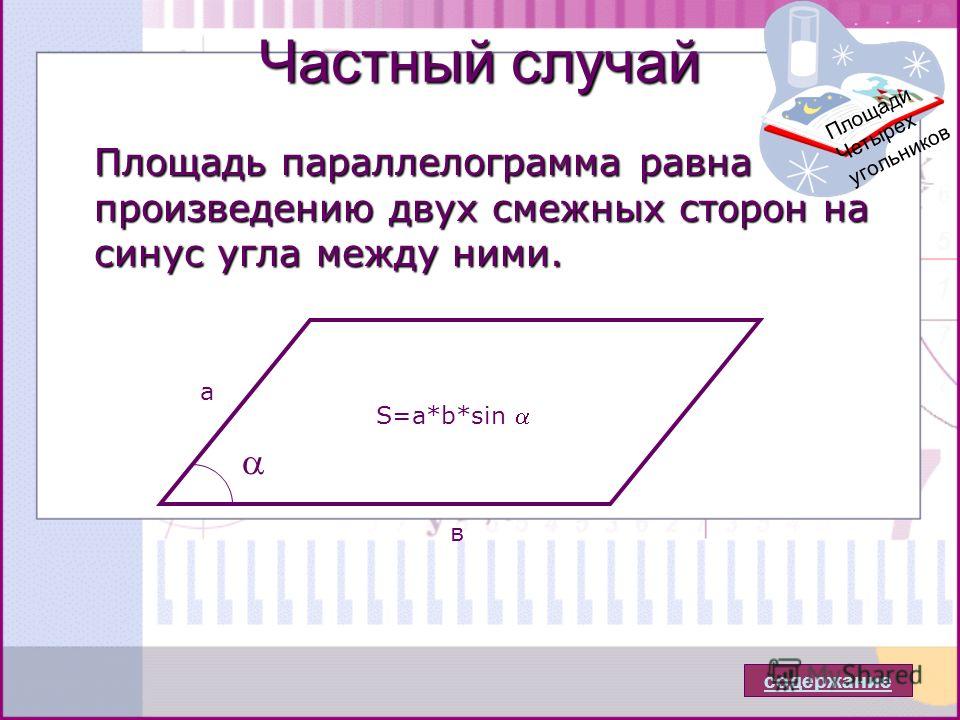
4. В параллелограмме АВСD проведен отрезок АЕ (точка Е лежит на стороне ВС). Известно, что угол ЕАD равен 55 градусов, а DС = ВЕ. Найдите углы параллелограмма.
Геометрия 8 класс. Самостоятельная работа № 2.
Трапеция.
Вариант 1.
1. Углы при большем основании трапеции равны 75 и 43 градуса. Найдите углы при меньшем основании.
2. Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основанию
Вариант 2.
1. Тупой угол равнобедренной трапеции равен 108 градусов. Найдите оставшиеся углы этой трапеции.
2. Докажите, что в равнобедренной трапеции углы при каждом основании равны.
Вариант 3.
1. В прямоугольной трапеции АВСD меньшее основание ВС перпендикулярно боковой стороне АВ. Диагональ АС равна боковой стороне СD, угол АСD равен 40 градусов. Найдите углы этой трапеции.
2. Докажите,
что трапеция равнобедренная, если диагонали трапеции равны.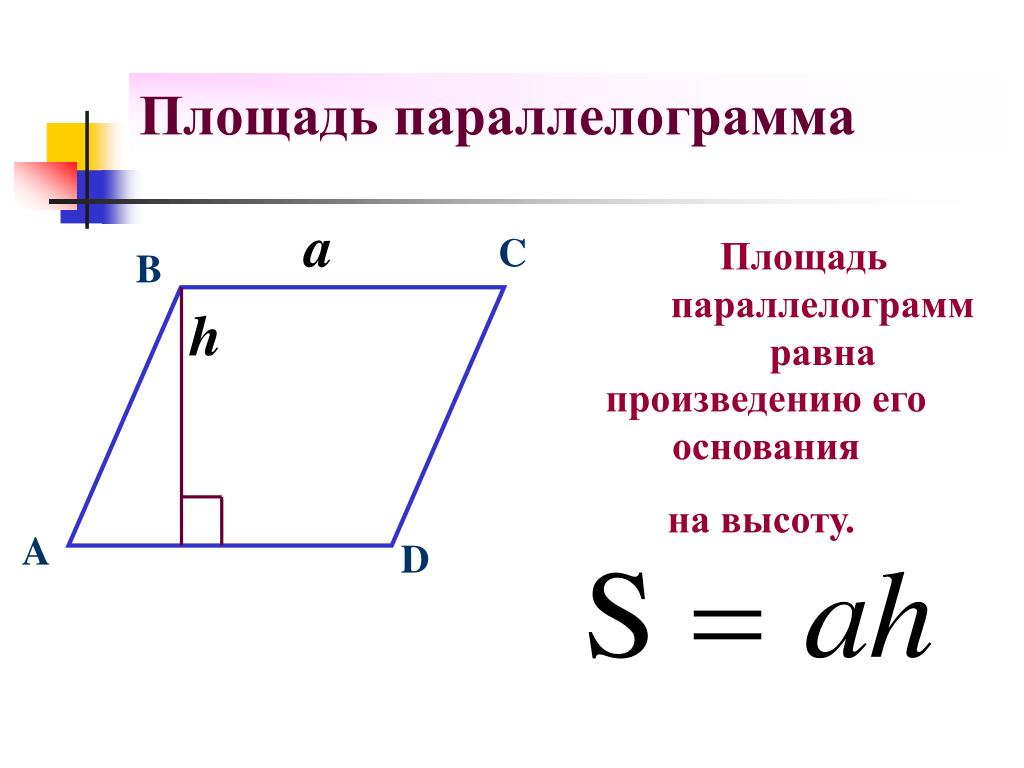
Вариант 4.
1. В прямоугольной трапеции АВСD большее основание АD перпендикулярно боковой стороне АВ. Диагональ АС равна боковой стороне СD, угол АСВ равен 32 градуса. Найдите углы этой трапеции.
2. Докажите, что трапеция равнобедренная, если углы при основании равны.
Геометрия 8 класс. Самостоятельная работа № 3.
Прямоугольник. Ромб. Квадрат.
Осевая и центральная симметрия.
Вариант 1.
1. Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 30 см.
2. В ромбе одна из диагоналей равна стороне. Определите углы ромба.
3. В равнобедренный прямоугольный треугольник, каждый катет которого равен 26 см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.
4. Какие из букв A, D, O, Q, X, Z, W имеют центр симметрии?
Вариант 2.
1. Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его большая сторона равна 40 см.
2. Стороны ромба образуют с его диагоналями углы, разность которых равна 35 градусов. Определите углы ромба.
3. В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.
4. Какие из букв A, D, J, Q, R, Z имеют ось симметрии?
Вариант 3.
1. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 8 см дальше, чем от большей стороны. Периметр прямоугольника равен 128 см. Определите его стороны.
2. Углы, образуемые стороной ромба с его диагоналями, относятся как 2:7. Определите углы ромба.
3.
В
квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна
вершина прямоугольника и стороны прямоугольника параллельны диагоналям
квадрата.
4. Сколько осей симметрии имеет отрезок; луч?
Вариант 4.
1. Задан прямоугольник АВСD. Точка М – середина стороны ВС. Прямые МА и МD взаимно перпендикулярны. Периметр прямоугольника АВСD равен 72 м. Определите его стороны.
2. Углы, образуемые стороной ромба с его диагоналями, относятся как 4:5. Определите углы ромба.
3. В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна 72см.
4. Сколько центров симметрии имеет отрезок; прямая?
Решение задач по теме «Четырехугольники».
1. Диагонали
прямоугольника АВСD пересекаются в точке О, угол АВО
равен 36 градусам.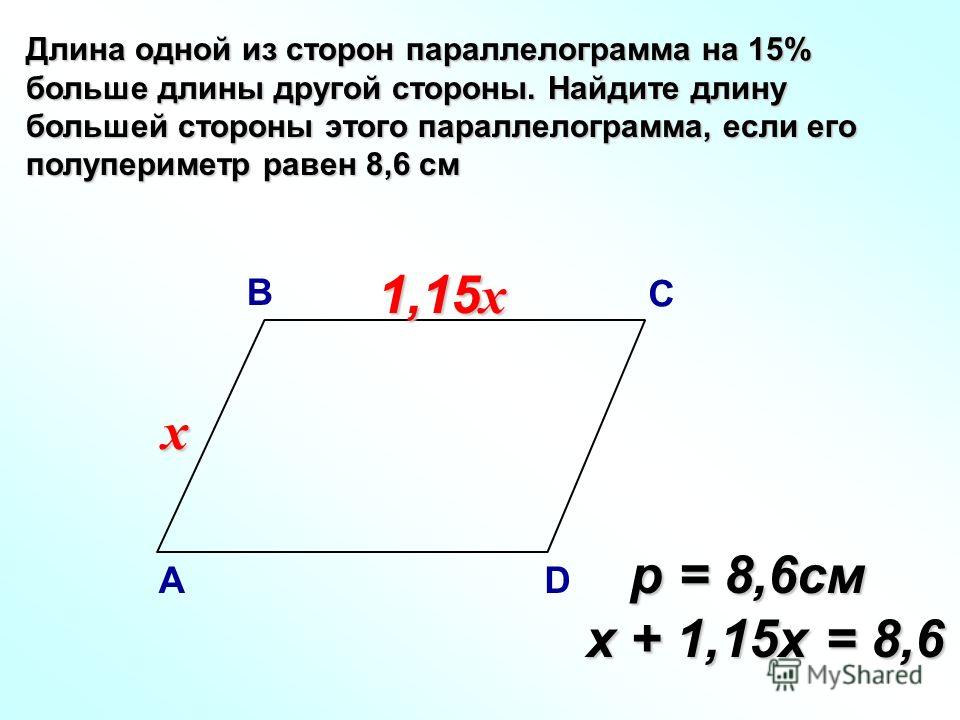 Найдите угол АОD.
Найдите угол АОD.
2. Найдите углы прямоугольной трапеции, если один из его углов равен 20 градусам.
3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма.
4. В равнобедренной трапеции сумма углов при большем основании равна 96 градусов. Найдите углы трапеции.
5. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма
6. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4:5.
7. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон.
8. В трапеции АВСD диагональ ВD перпендикулярна боковой стороне АВ, угол АDВ равен углу ВDС и равен 30 градусам. Найдите длину АD, если периметр трапеции 60 см.
Задача № 1.
Диагонали
ромба KMNP
пересекаются в точке О. Найдите углы треугольника KOM,
если угол MNP равен 80 градусам.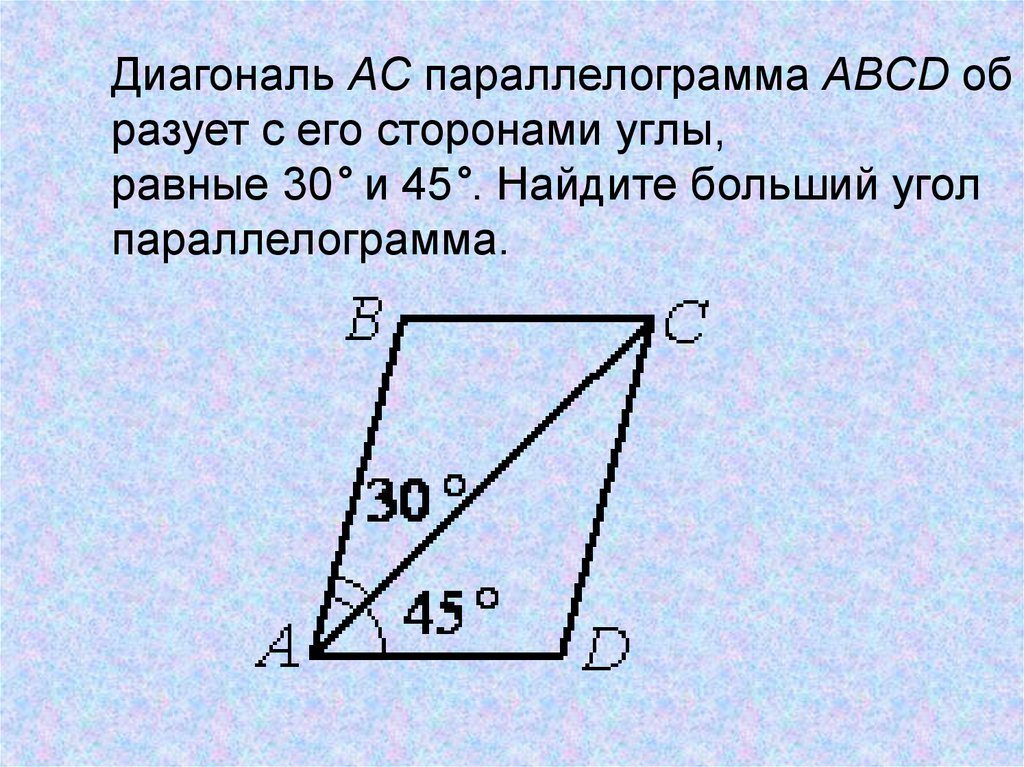
Задача № 2.
В параллелограмме КMNP проведена биссектриса угла МКР, которая пересекает сторону MN в точке Е.
А) Докажите, что треугольник КМЕ – равнобедренный.
Б) Найдите сторону КР, если МЕ равно 10 см, а периметр параллелограмма равен 52 см.
Задача №3.
Через вершину С прямоугольника АВСD проведена прямая, параллельная диагонали ВD и пересекающая прямую АВ в точке М. Через току М проведена прямая, параллельная диагонали АС и пересекающая прямую ВС в точке N. Найдите периметр четырехугольника ACMN, если диагональ ВD равна 8 см.
Задача № 4.
Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке М, лежащей на стороне ВС. Луч DМ пересекает прямую АВ в точке N. Найдите периметр параллелограмма АВСD, если AN равно 10 см.
Самостоятельная работа № 4
Площадь квадрата и прямоугольника
Вариант 1.
1. Найдите площадь квадрата, если его сторона равна 9,1 дм.
2. Найдите
сторону квадрата, площадь которого равна площади прямоугольника со сторонами 18
см и 50 см.
3. Как изменится площадь квадрата, если его сторону уменьшить в три раза?
Вариант 2.
1. Найдите площадь квадрата, если его сторона равна 2.
2. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 32 см и 25 см.
3. Как изменится площадь квадрата, если его сторону увеличить в два раза?
Вариант 3.
1. Найдите сторону квадрата, если его площадь равна 18 дм².
2. Определите стороны прямоугольника, если они относятся как 2:3, а площадь равна 294 см²?
3. Как изменится площадь прямоугольника, если одну его сторону увеличить в 4 раза, а другую уменьшить в два раза?
Вариант 4.
1. Найдите диагональ квадрата, если его площадь равна 128 дм².
2. Определите площадь прямоугольника, если разность его сторон составляет 18 см, а периметр равен 92 см.
3. Как изменится площадь прямоугольника, если одну его сторону увеличить в 3 раза, а другую уменьшить в 9 раз?
Самостоятельная работа № 5
Площадь параллелограмма и треугольника
Вариант 1 .
1. Найдите площадь параллелограмма, у которого основание равно 21 см, а высота 12 см.
2. Сторона ромба равно 10 дм, а его тупой угол равен 150°. Найдите площадь ромба.
3. Найдите площадь прямоугольного треугольника, если его катеты равны 21 см и 34 см.
Вариант 2.
1. Найдите площадь параллелограмма, у которого диагональ, равная 23 см перпендикулярна стороне параллелограмма, длина которой равна 7 см.
2. Периметр ромба равен 24 дм, а его острый угол равен 30°. Найдите площадь ромба.
3. Найдите катеты прямоугольного треугольника, если они относятся как 7:8 и площадь треугольника равна 112 ².
Вариант 3.
1. Найдите площадь параллелограмма, если известны длины его сторон: 12 см и 9 см и угол 30° между ними..
2. Высота ромба равна 12 дм, а его его тупой угол равен 150°. Найдите площадь ромба.
3. В
равнобедренном треугольнике боковая сторона, равная 32 см составляет с
основанием угол 75°. Найдите площадь треугольника.
Найдите площадь треугольника.
Вариант 4.
1. Найдите площадь параллелограмма, если известны длины двух его сторон: 4 15 см и угол 45° между ними.
2. Тупой угол ромба больше острого в пять раз. Стороны ромба равны 18 дм. Найдите площадь ромба.
3. В треугольнике заданы два угла: 75° и 30°. Сторона, лежащая против угла 75°, равна 32 см. Найдите площадь треугольника.
Самостоятельная работа № 6
Площадь трапеции.
Вариант 1.
1. Сумма оснований трапеции равна 7 см, а её высота – 4 см. Найдите площадь трапеции.
2. В равнобедренной трапеции разность оснований равна 10 см, меньшее основание равно 9 см, а высота – 12 см. Найдите площадь трапеции.
Вариант 2.
1. Площадь трапеции равна 24 см². Найдите сумму оснований трапеции, если её высота равна 6 см.
2. В
равнобедренной трапеции основания равны 38 см и 72 см, а тупой угол равен 135°.
Найдите площадь трапеции.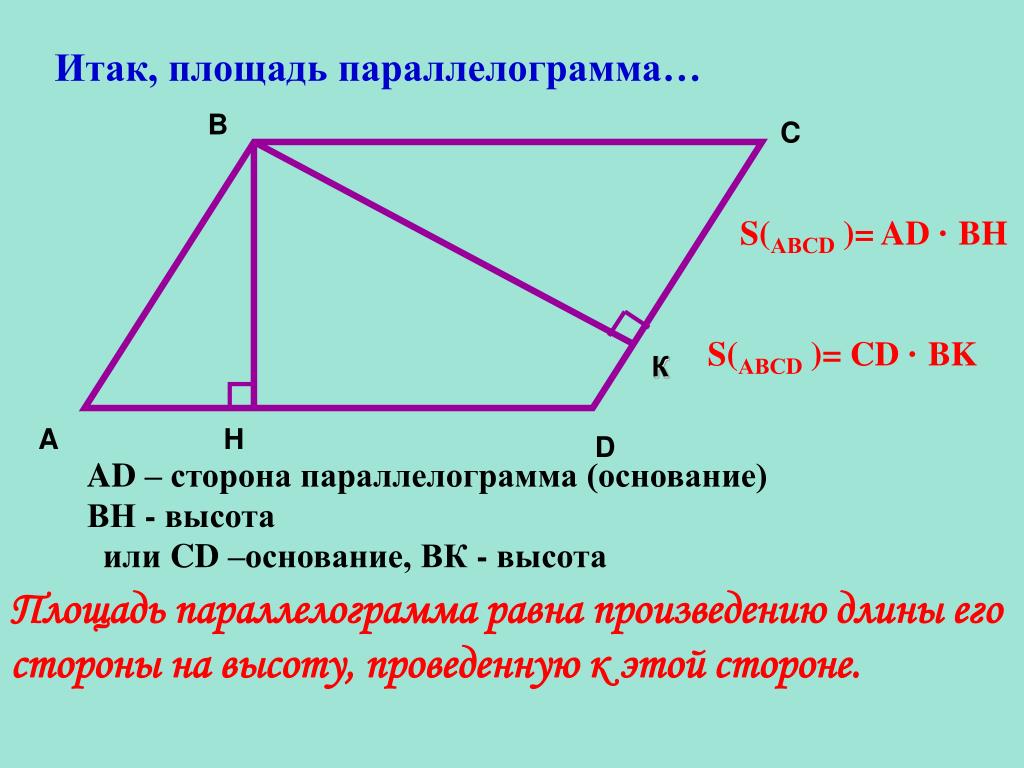
Вариант 3.
1. Площадь трапеции равна 81 см², а её высота равна 9 см. Найдите основания трапеции, если их разность равна 12 см.
2. В равнобедренной трапеции PQRS угол равен 45°, RT – высота трапеции, PT = 11см, TS =6 см. Найдите площадь трапеции.
Вариант 4.
1. В равнобедренной трапеции основания равны 3 и 7, а острый угол равен 45°. Найдите площадь трапеции.
2. В прямоугольной трапеции острый угол равен 30°, сумма оснований равна 18 дм, а сумма боковых сторон – 15 дм. Найдите площадь трапеции.
Самостоятельная работа № 7.
Теорема Пифагора.
Вариант 1.
1. Найдите гипотенузу прямоугольного треугольника, если его катеты равны 8 и 15 м.
2. В равнобедренном треугольнике боковая сторона 51 см, а основание 48 см. Определите высоту треугольника.
3. Найдите
сторону ромба, диагонали которого равны 24 дм и 70 дм.
Вариант 2.
1. Найдите катет прямоугольного треугольника, если его гипотенуза и другой катет равны и 2 м.
2. Найдите площадь треугольника, стороны которого равны 15 см, 15 см, 24 см.
3. Найдите диагональ ромба, если его сторона равна 15 дм, а вторая диагональ равна 24 дм.
Вариант 3.
1. Найдите катет прямоугольного треугольника, лежащий против угла в 60°, если его гипотенуза равна 8м.
2. Найдите наименьшую высоту прямоугольного треугольника, катеты которого равны 14 см, 48 см.
3. В равнобедренной трапеции основания равны 20 см и 48 см, боковая сторона равна 50 см. Найдите высоту трапеции.
Вариант 4.
1. Найдите катет прямоугольного треугольника, прилежащий углу в 30°, если его гипотенуза равна 12 м.
2. Найдите наименьшую высоту прямоугольного треугольника, катет и гипотенуза которого равны 24 см и 26 см.
3. В
равнобедренной трапеции сумма оснований равна 50 см, боковая сторона равна 25
см, а высота – 20 см.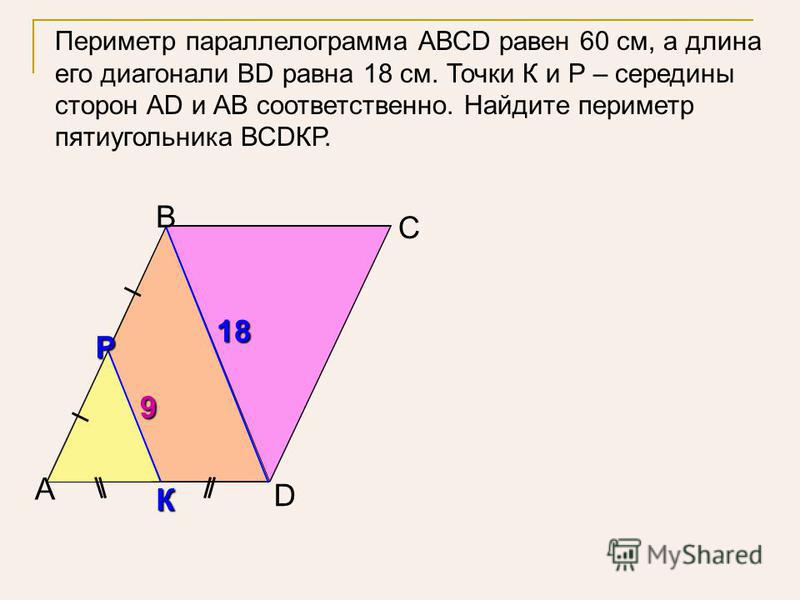 Найдите основания трапеции.
Найдите основания трапеции.
Самостоятельная работа
Площади геометрических фигур.
Вариант 1.
1. Сторона параллелограмма равна 21 см, а высота, проведенная к ней, равна 15 см. Найдите площадь параллелограмма.
2. Сторона треугольника равна 5 см, а высота, проведенная к ней, в 2 раза больше стороны. Найдите площадь треугольника.
3. В трапеции основания равны 6 см и 10 см, а высота равна полусумме оснований. Найдите площадь трапеции.
4. Стороны параллелограмма равны 6 см и 8см, а угол между ними равен 30°. Найдите площадь параллелограмма.
5. Диагонали ромба относятся друг к другу как 2:3, а их сумма равна 25 см. Найдите площадь ромба.
Вариант 2.
1. Сторона параллелограмма равна 17 см, а его площадь равна 187 см². найдите высоту, проведенную к данному основанию.
2. Сторона
треугольника равна 18 см, а высота, проведенная к ней, в три раза меньше
стороны.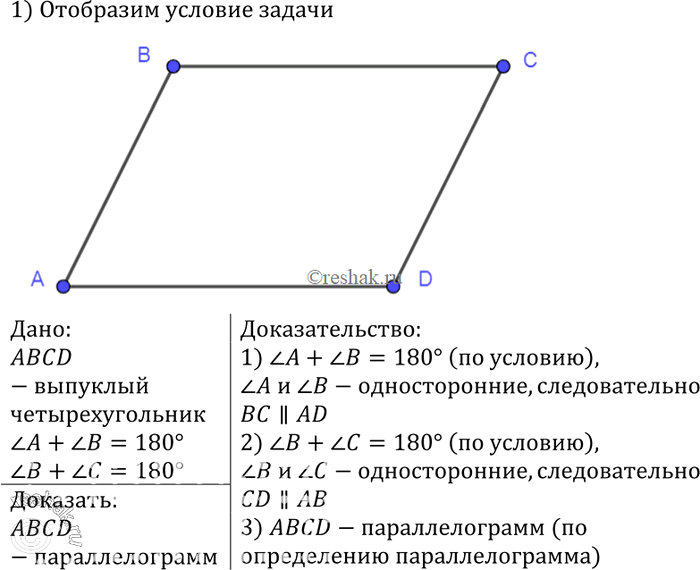 Найдите площадь треугольника.
Найдите площадь треугольника.
3. В трапеции основания равны 4 см и 12 см, а высота равна полусумме оснований. Найдите площадь трапеции.
4. Стороны параллелограмма равны 4 см и 7см, а угол между ними равен 150°. Найдите площадь параллелограмма.
5. Диагонали ромба относятся друг к другу как 3:5, а их разность равна 8 см. Найдите площадь ромба.
Вариант 3.
1. В равнобедренном треугольнике АВС высота ВН равна 12 см, а основание АС в три раза больше высоты ВН. Найдите площадь треугольника АВС.
2. В параллелограмме АВСD стороны равны 14см и 8 см, высота, проведенная к большей стороне, равна 4 см. Найдите площадь параллелограмма и вторую высоту.
3. Площадь трапеции равна 320 см², а высота трапеции равна 8 см. Найдите основания трапеции, если длина одного из оснований составляет 60% от длины другого.
4.
В треугольнике АВС стороны АВ и ВС равны
соответственно 14 см и 18 см. Сторона АВ продолжена за точку А на отрезок АМ,
равный АВ.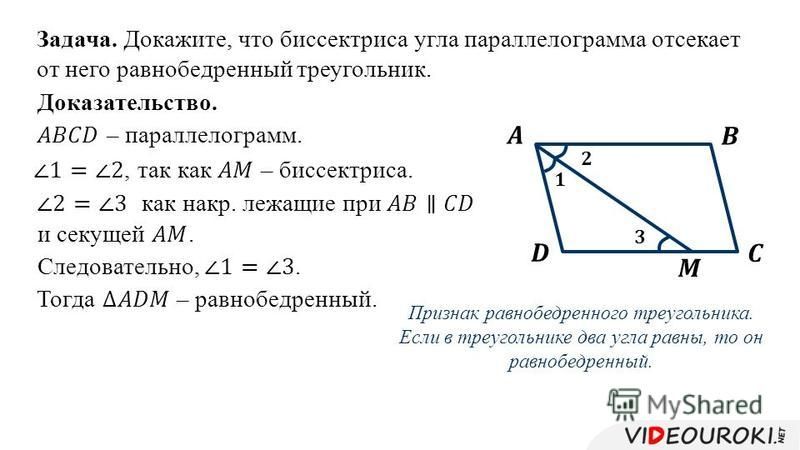 Сторона ВС продолжена за точку С на отрезок КС, равный половине ВС.
Найдите площадь треугольника МВК, если площадь треугольника АВС равна 126 см².
Сторона ВС продолжена за точку С на отрезок КС, равный половине ВС.
Найдите площадь треугольника МВК, если площадь треугольника АВС равна 126 см².
5. В ромбе АВСК из вершин В и С опущены высоты ВМ и СН на прямую АК. Найдите площадь четырехугольника МВСН, если площадь ромба равна 67 см².
Тест Параллелограмм 8 класс с ответами
Тесты по геометрии 8 класс. Тема: «Параллелограмм»
Правильный вариант ответа отмечен знаком +
1. Из фигур, изображённых на рисунках, нужно выбрать параллелограмм.
2. Выбрать верное продолжение высказывания: «Параллелограммом называется…».
— фигура, у которой все стороны равны;
— четырёхугольник, с противоположными параллельными сторонами;
+ четырёхугольник, у которого противолежащие стороны попарно параллельны и равны;
— фигура, с попарно перпендикулярными сторонами.
3. Следует выбрать правильное завершение предложения: «Противоположные углы параллелограмма.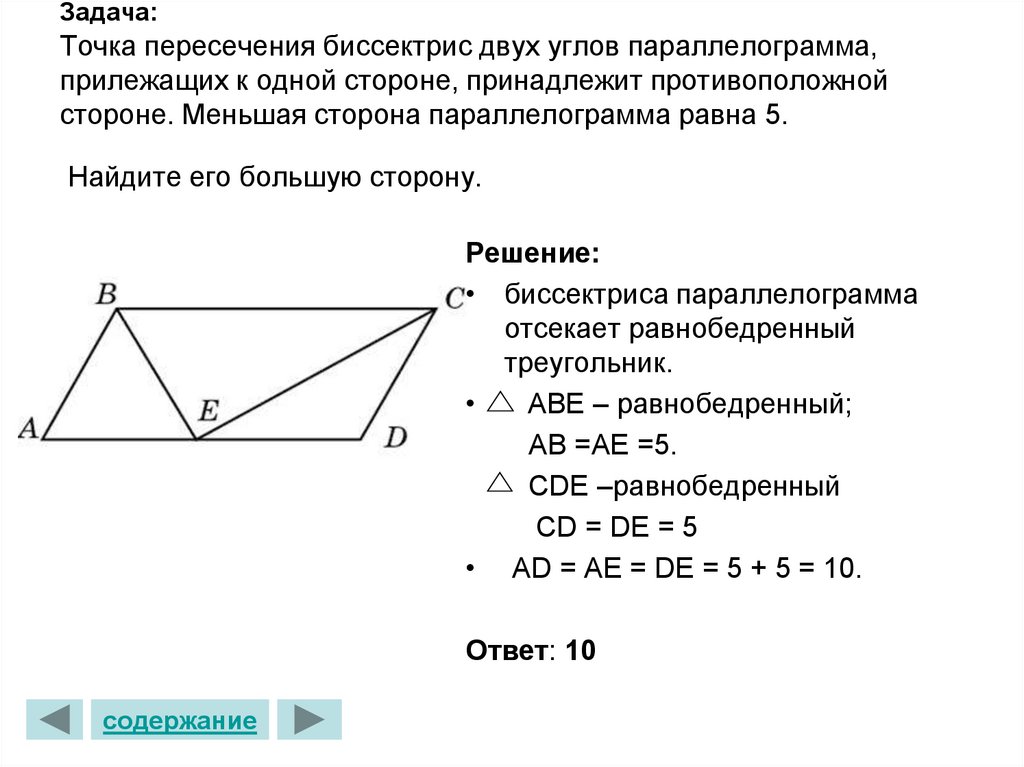 ..».
..».
— трудно сказать без рисунка;
— не равны;
— равны 90о;
+ равны.
4. Какое существует свойство о диагоналях параллелограмма?
— диагонали параллелограмма параллельны;
— в параллелограмме диагонали равны;
+ диагонали параллелограмма точкой пересечения делятся пополам;
— в параллелограмме диагонали перпендикулярны друг другу.
5. Указать равные углы параллелограмма ERTB. EA - биссектриса.
— ∠Е и ∠В;
— ∠Т и ∠2;
— ∠1 и ∠3;
+ ∠2 и ∠4.
6. Завершить предложение: «Если в четырёхугольнике противоположные стороны попарно равны и параллельны, то этот четырёхугольник …».
— многоугольник;
— трапеция;
— равносторонний треугольник;
+ параллелограмм.
7. На рисунке изображён параллелограмм ZVBN. Какие из его сторон равны?
— ZN и ZB;
+ ZV и NB;
— VB и BN;
— BN и NZ.
8. Дан параллелограмм AVSN. Какие стороны данного параллелограмма параллельны?
+ AV и SN;
— VS и AS;
— AN и SN;
— AS и SN.
9. «Параллелограмм — это … четырёхугольник». На месте пропуска в высказывании должно быть:
+ выпуклый;
— невыпуклый;
— нет верного варианта ответа;
— ни тот, ни другой.
тест 10. Изображён параллелограмм KMNP. Требуется ответить, какие из его углов равны?
— ∠K и ∠M;
+ ∠K и ∠N;
— ∠N и ∠P;
— ∠P и ∠K.
11. Периметр параллелограмма равен 68 см. Одна из сторон в 3 раза больше смежной с ней. Чему равна длина смежной стороны?
— 8 см;
— 9 см;
+ 8,5 см;
— 34 см.
12. Известен периметр параллелограмма. Он равен 68 см. Одна из смежных сторон больше другой в 3 раза. Чему она равна?
+ 25,5 см;
— 34 см;
— 8,5 см;
— 2,8 см.
13. В параллелограмме CVFD разность двух смежных сторон равна 8. Периметр равен 64 см. Длины сторон равны:
В параллелограмме CVFD разность двух смежных сторон равна 8. Периметр равен 64 см. Длины сторон равны:
— 12 и 25;
— 20 и 14;
+ 20 и 12;
— 32 и 24.
14. Дан параллелограмм CVFD. Сторона CD на 4 см больше отрезка CV. Периметр параллелограмма известен. Он равен 72 см. Чему равна длина отрезка CV?
+ 18 см;
— 31 см;
— 20 см;
-68 см.
15. В параллелограмме CVFD, сторона CD больше на 4 см отрезка CV. Периметр равен 72 см. Длина отрезка CD?
— 64 см;
-24 см;
— 35 см;
+ 22 см.
16. В параллелограмме ZXAS, ∠Z = 30o, перпендикуляр XH к стороне ZS равняется 7 см. Чему равна длина отрезка ZX?
+ 14 см;
— 21 см;
— 7 см;
— 16 см.
17. Дан параллелограмм ZXAS, перпендикуляр к прямой ZS, XH = 7 см. ∠Z = 30o. Периметр параллелограмма равен 52 см. Сторона ZS равна:
— 18 см;
— 14 см;
+ 12 см;
— 16 см.
18. Чему равен ∠M в параллелограмме MNKP, если ∠N = 82o?
— 120o;
+ 98o;
— 92o;
— 95о.
19. Чему равен ∠Z в параллелограмме MNZP, если ∠M=2∠N?
— 60o;
— 90o;
— 30o;
+ 120о.
тест-20. В параллелограмме MNZP ∠M=2∠N. Чему равен ∠P?
— 120o;
+ 60o;
— 92o;
— 95о.
21. Сумма углов в параллелограмме равна:
— 120o;
— 180o;
+ 360o;
— 90о.
22. Завершить высказывание: «В параллелограмме противолежащие углы …».
— известны;
— не известны;
— не равны;
+ равны.
23. Свойство, не характерное для биссектрисы одного из углов параллелограмма:
+ делить противолежащую сторону на 2 равных отрезка;
— делить угол пополам;
— соединять точку противолежащей стороны и угол параллелограмма;
— отсекать от параллелограмма равнобедренный треугольник.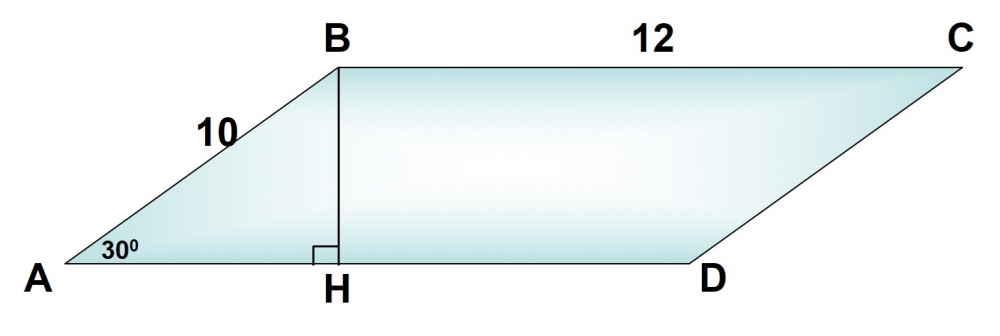
24. Почему биссектриса одного из углов параллелограмма отсекает от него равнобедренный треугольник?
— потому, что в получившемся треугольнике соответственные углы равны;
+ при основании полученного треугольника односторонние углы равны;
— соответствующие углы отсечённого треугольника равны;
— все углы полученного треугольника равны.
25. В параллелограмме ADCF из угла А к стороне DC проведена биссектриса AK. Она делит DC на отрезки DK=16, KC=10. Сторона AD равна:
+ 16 см;
— 10 см;
— 26 см;
— 20 см.
26. ADCF – параллелограмм. Угол А соединён с DC биссектрисой AK. Она делит сторону DC на отрезки DK=17, KC=9. Длина стороны CF равна:
— 13 см;
— 9 см;
— 26 см;
+ 17 см.
27. Дан параллелограмм ADCF с биссектрисой AK угла А, проведённой к стороне DC. Прямая DC делится на отрезки DK=16 см, KC=9 см. Чему равен периметр параллелограмма?
-25 см;
— 50 см;
+ 82 см;
— 41 см.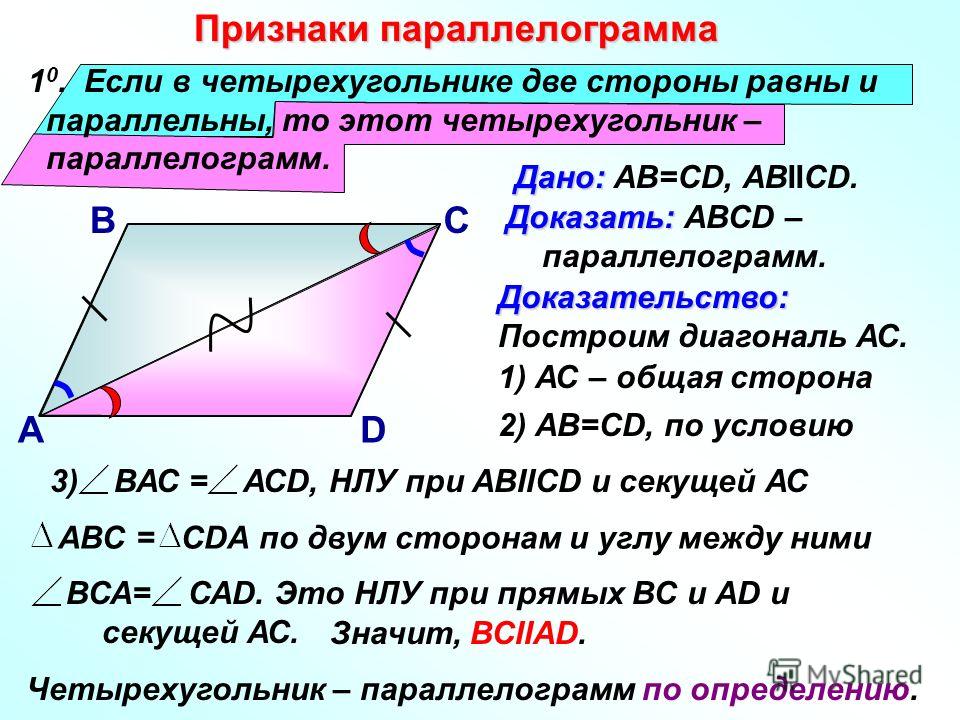
28. В параллелограмме MNPJ проведён перпендикуляр NH к стороне MJ. Угол N равен 30°, MH=8, HJ=5. Требуется найти периметр параллелограмма.
+ 58 см;
— 29 см;
— 26 см;
— 32 см.
29. Дан параллелограмм MNPJ. NH – перпендикуляр к стороне MJ. Угол N равен 30°, HM=8, JH=5. Требуется указать чему равна длина отрезка NM.
+ 16 см;
— 8 см;
— 13 см;
— 15 см.
тест_30. MNPJ – параллелограмм. Перпендикуляр NH проведён к стороне MJ. Угол N равен 30°, MH=10, HJ=5. Требуется выбрать верную схему нахождения отрезка NH.
+ x2= 162-82;
— x =162-82;
— x=16-8;
— x2= 16-8.
Как найти длину стороны параллелограмма
Все математические ресурсы GRE
13 Диагностические тесты 452 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
GRE Math Help » Геометрия » Плоская геометрия » Четырехугольники » Параллелограммы » Как найти длину стороны параллелограмма
Сумма двух оснований в параллелограмме равна Прилегающая сторона к основаниям равна длине одного из двух оснований. Найдите длину стороны, примыкающей к основаниям.
Найдите длину стороны, примыкающей к основаниям.
Возможные ответы:
Правильный ответ:
Объяснение:
В этой задаче вам говорят, что сумма двух оснований в параллелограмме равна Поскольку два основания должны быть эквивалентны, каждая сторона должна быть равна: . Кроме того, в задаче указано, что смежные стороны — это длина оснований. Следовательно, смежная с основанием сторона должна быть равна:
Сообщить об ошибке
Используя параллелограмм, показанный выше, найдите сумму двух сторон, прилегающих к основанию.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти одну из сторон, примыкающих к основанию, сначала обратите внимание, что внутренние треугольники, представленные красными вертикальными линиями, должны иметь высоту и длину основания Затем примените формулу: чтобы найти длину одной стороны .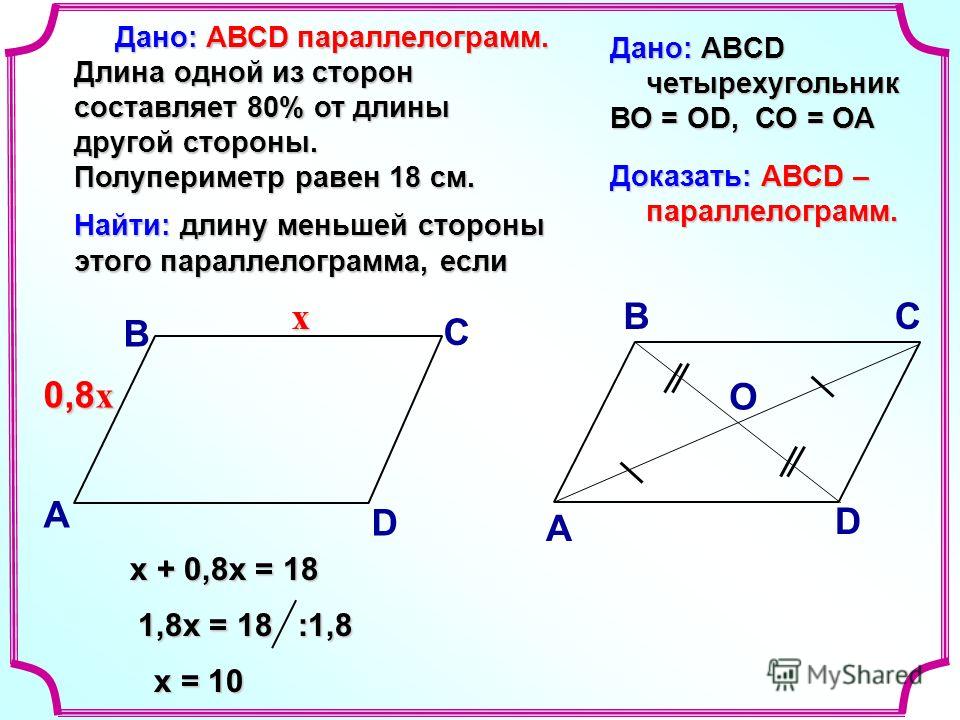
Таким образом, решение:
Таким образом, сумма двух сторон: Периметр параллелограмма равен . Найдите сумму двух сторон, примыкающих к основанию.
Возможные ответы:
Правильный ответ:
Объяснение:
Параллелограмм должен иметь два набора конгруэнтных/параллельных противоположных сторон. Этот параллелограмм должен иметь две стороны размером и две стороны основания длиной . В этом вопросе вам предоставляется информация о том, что параллелограмм имеет основание и общий периметр . Таким образом, работайте в обратном направлении, используя формулу периметра, чтобы найти сумму двух смежных сторон основания.
, где и – размеры смежных сторон.
Таким образом, решение:
Сообщить об ошибке
Основание параллелограмма равно . Периметр параллелограмма равен . Найдите длину стороны, примыкающей к основанию.
Периметр параллелограмма равен . Найдите длину стороны, примыкающей к основанию.
Возможные ответы:
Правильный ответ:
Объяснение:
Параллелограмм должен иметь два набора конгруэнтных/параллельных противоположных сторон. Следовательно, этот параллелограмм должен иметь две стороны с размером и две стороны основания, каждая из которых имеет длину Поскольку в вопросе указаны периметр и одна длина основания, действуйте в обратном направлении, используя формулу периметра:
, где и – размеры смежных сторон.
Таким образом, решение:
Проверка:
Отчет о ошибке
Параллелограмма имеет базовое измерение. Периметр параллелограмма равен . Найдите длину стороны, примыкающей к основанию.
Возможные ответы:
Правильный ответ:
Объяснение:
Параллелограмм должен иметь два набора конгруэнтных/параллельных противоположных сторон. Этот параллелограмм должен иметь две стороны размером и две стороны основания длиной . В этом вопросе вам предоставляется информация о том, что параллелограмм имеет основание и общий периметр . Таким образом, работайте в обратном направлении, используя формулу периметра, чтобы найти длину одной недостающей стороны, примыкающей к основанию.
Этот параллелограмм должен иметь две стороны размером и две стороны основания длиной . В этом вопросе вам предоставляется информация о том, что параллелограмм имеет основание и общий периметр . Таким образом, работайте в обратном направлении, используя формулу периметра, чтобы найти длину одной недостающей стороны, примыкающей к основанию.
, где и – размеры смежных сторон.
Таким образом, решение:
Сообщить об ошибке
Параллелограмм имеет основание . Периметр параллелограмма равен . Найдите сумму двух сторон, примыкающих к основанию.
Возможные ответы:
Правильный ответ:
Объяснение:
Параллелограмм должен иметь два набора конгруэнтных/параллельных противоположных сторон. Этот параллелограмм должен иметь две стороны размером и две стороны основания длиной .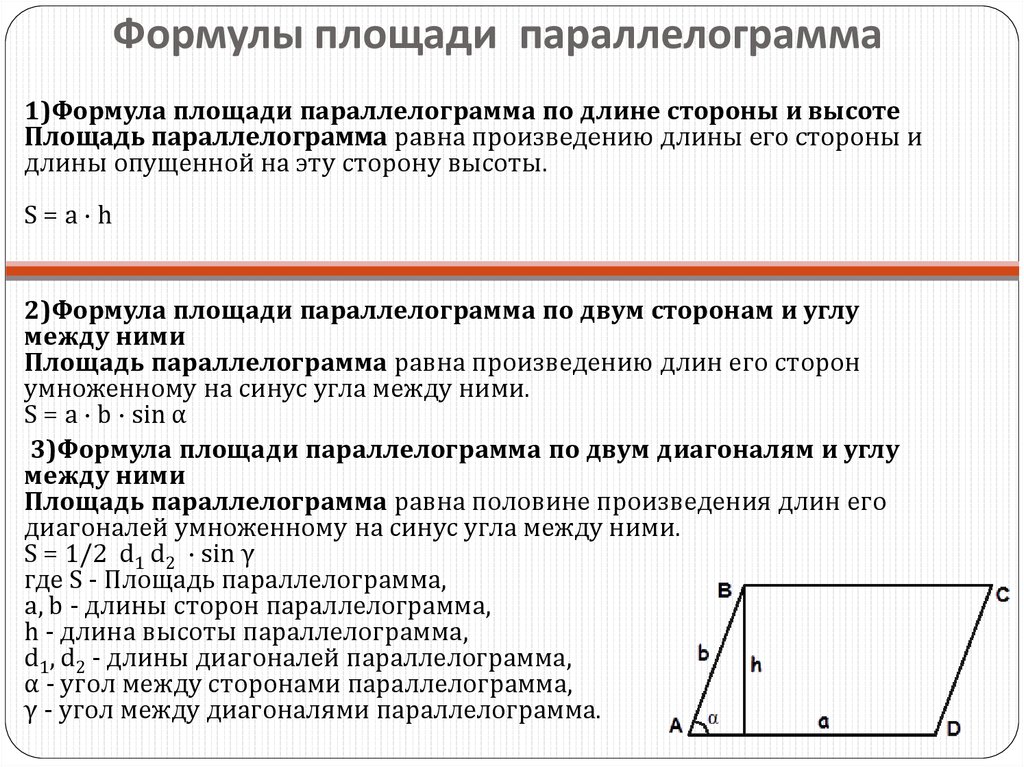 В этом вопросе вам предоставляется информация о том, что параллелограмм имеет основание и общий периметр . Таким образом, работайте в обратном направлении, используя формулу периметра, чтобы найти сумму двух смежных сторон основания.
В этом вопросе вам предоставляется информация о том, что параллелограмм имеет основание и общий периметр . Таким образом, работайте в обратном направлении, используя формулу периметра, чтобы найти сумму двух смежных сторон основания.
, где и – размеры смежных сторон.
Таким образом, решение:
Сообщить об ошибке
Основание параллелограмма равно . Сторона, примыкающая к основанию, имеет длину . Найдите периметр параллелограмма.
Возможные ответы:
Правильный ответ:
Объяснение:
Параллелограмм должен иметь два набора конгруэнтных/параллельных противоположных сторон. Следовательно, этот параллелограмм должен иметь две стороны размером и две стороны основания длиной . Для нахождения периметра параллелограмма применим формулу:
, где и – размеры смежных сторон.
Таким образом, решение:
Сообщить об ошибке
Базовое измерение параллелограмма равно . Периметр параллелограмма равен . Найдите размер стороны, примыкающей к основанию.
Возможные ответы:
Правильный ответ:
Объяснение:
Параллелограмм должен иметь два набора конгруэнтных/параллельных противоположных сторон. Следовательно, этот параллелограмм должен иметь две стороны размером и две стороны основания длиной . Однако, чтобы решить эту проблему, вы должны сначала преобразовать предоставленное измерение периметра из футов в дюймы. Поскольку дюйм равен футу, футы равны дюймам.
Теперь вы можете работать в обратном порядке, используя формулу:
, где и – размеры смежных сторон.
Таким образом, решение:
Отчет о ошибке
Используя параллелограмму, показанную выше, найдите длину стороны
Возможные ответы:
: .
Объяснение:
Параллелограмм должен иметь два набора конгруэнтных/параллельных противоположных сторон. Следовательно, этот параллелограмм должен иметь две стороны с размером и две стороны основания, каждая из которых имеет длину Поскольку в вопросе указаны периметр и одна длина основания, действуйте в обратном направлении, используя формулу периметра:
, где и – размеры смежных сторон.
Таким образом, решение:
Сообщить об ошибке
Параллелограмм имеет основание . Периметр параллелограмма равен . Найдите сумму двух сторон, примыкающих к основанию.
Возможные ответы:
Правильный ответ:
Объяснение:
Параллелограмм должен иметь два набора конгруэнтных/параллельных противоположных сторон. Этот параллелограмм должен иметь две стороны размером и две стороны основания длиной . В этом вопросе вам предоставляется информация о том, что параллелограмм имеет основание и общий периметр . Таким образом, работайте в обратном направлении, используя формулу периметра, чтобы найти сумму двух смежных сторон основания.
Этот параллелограмм должен иметь две стороны размером и две стороны основания длиной . В этом вопросе вам предоставляется информация о том, что параллелограмм имеет основание и общий периметр . Таким образом, работайте в обратном направлении, используя формулу периметра, чтобы найти сумму двух смежных сторон основания.
, где и – размеры смежных сторон.
Таким образом, решение:
Отчет о ошибке
← Предыдущий 1 2 Следующие →
Уведомление об авторских правах
All GRE Math Resources
13 Испытания диагностики. 452 практических теста Вопрос дня Карточки Learn by Concept
Калькулятор площади параллелограмма
Автор: Hanna Pamuła, PhD
Отзыв от Bogna Szyk и Steven Wooding
Последнее обновление: 02 февраля 2023 г.
Содержание:- Формулы площади параллелограмма
- Как использовать этот калькулятор площади параллелограмма?
- Часто задаваемые вопросы
Если у вас возникли проблемы с геометрией параллелограмма, проверьте этот калькулятор площади параллелограмма (а также его брат-близнец, калькулятор периметра параллелограмма).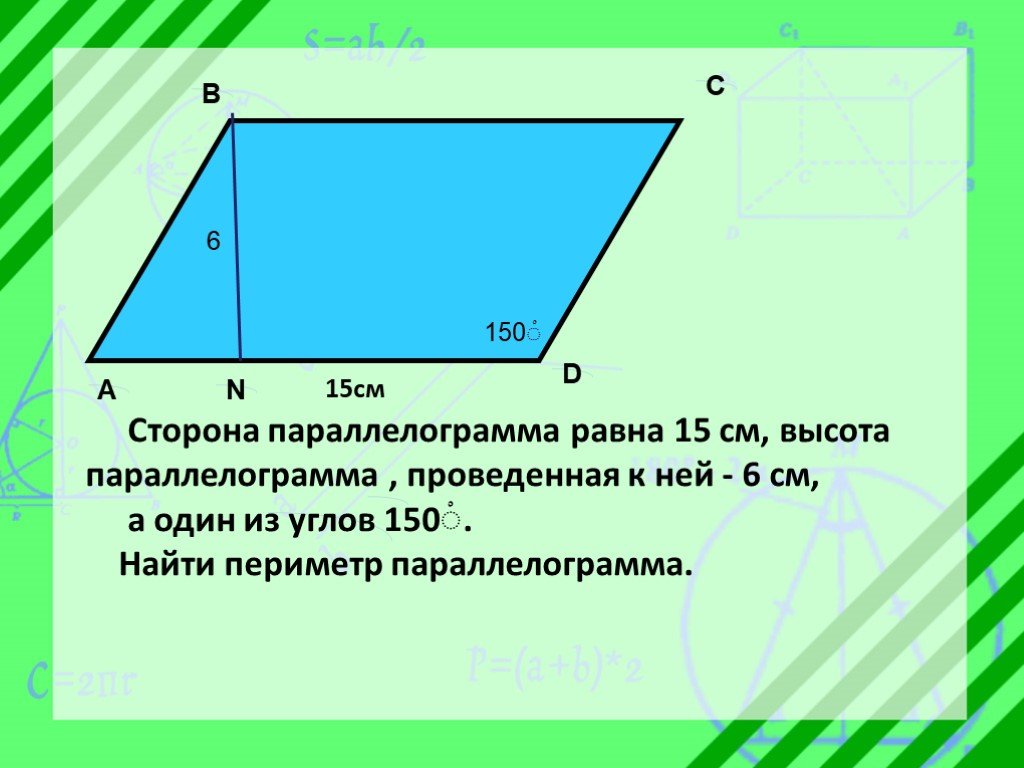
Хотите ли вы вычислить площадь по основанию и высоте, сторонам и углу или диагоналям параллелограмма и углу между ними, вы находитесь в правильном месте. Не спрашивайте, как найти площадь параллелограмма; просто попробуйте калькулятор!
Ниже вы можете узнать, как работает инструмент — формулы площади параллелограмма и четкое объяснение — все, что вам нужно, чтобы понять тему.
Формулы площади параллелограмма
Параллелограмм — это простой четырехугольник с двумя парами параллельных сторон. Каждый прямоугольник является параллелограммом, так же как каждый ромб и квадрат. Помните, это не работает наоборот!
Какие формулы использует калькулятор площади параллелограмма?
Площадь с учетом основания и высоты
площадь = основание × высотаВы что-то заметили? Формула площади параллелограмма почти такая же, как и для прямоугольника! Почему это так? Взгляните на рисунок: параллелограмм можно разделить на трапецию и прямоугольный треугольник и превратить в прямоугольник.

Узнайте больше о площади прямоугольника с помощью нашего калькулятора площади прямоугольника.
Площадь с учетом сторон и угла между ними
площадь = a × b × sin(угол)
Это звонит в колокол? Эта формула пришла из тригонометрии и используется, например, в нашем калькуляторе площади треугольника — параллелограмм можно рассматривать как два конгруэнтных треугольника. Смежные углы в параллелограмме являются дополнительными, поэтому вы можете выбрать любой угол, который вы хотите, потому что sin(угол) = sin(180° - угол) .
Площадь данных диагоналей параллелограмма и угла между ними
площадь = ½ × e × f × sin(угол)Формула тоже взята из тригонометрии. Хотите знать, откуда оно?
Разделите параллелограмм на два треугольника и предположите, что наша диагональ
eявляется «базой» для обоих новых треугольников.
Какова высота этого треугольника? Используйте функцию синуса. Это
(f/2) × sin(угол)!Площадь треугольника равна нашему «основанию»
eумноженному на высоту:e × (f/2) × sin(угол)Параллелограмм состоит из двух таких треугольников, поэтому его площадь равна
e × f × sin(angle).
Как пользоваться этим калькулятором площади параллелограмма?
Вы все еще не уверены, что наш калькулятор площади параллелограмма работает? Мы покажем вам шаг за шагом:
Посмотрите на свое упражнение. Что дано, что неизвестно? Выберите нужную часть калькулятора для ваших нужд . Предположим, что мы хотим вычислить площадь, зная диагонали параллелограмма и угол между диагоналями.
Введите указанные значения в правые поля . Примите 5 дюймов, 13 дюймов и 30° для первой диагонали, второй диагонали и угла между ними соответственно.

Калькулятор отображает площадь параллелограмма значением . В нашем случае это 32,5 дюйма².
Ознакомьтесь с нашими калькуляторами площади для других фигур, таких как калькулятор площади ромба, калькулятор площади круга и калькулятор площади трапеции.
Часто задаваемые вопросы
Как найти площадь параллелограмма, зная его смежные стороны?
Чтобы определить площадь по смежным сторонам параллелограмма, необходимо также знать угол между сторонами . Тогда можно применить формулу: площадь = a × b × sin(α) , где a и b — стороны, а α — угол между ними.
Как найти площадь параллелограмма по диагоналям?
Площадь параллелограмма можно определить по его диагоналям, если вы также знаете угол между диагоналями .
Если e и f — длины диагоналей и φ — угол между ними, то площадь можно вычислить следующим образом: площадь = ½ × e × f × sin(φ) .


Leave A Comment