Найдите объем многогранника изображенного на рисунке: Решение №2959 Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).

Решутест. Продвинутый тренажёр тестов

Решутест. Продвинутый тренажёр тестов

• Главная
• ЕГЭ
• Математика профильная
• Стереометрия
• Объём и площадь поверхности нестандартных многогранников

Решил заданий

Не решил заданий

Осталось заданий

История решения

6743 — не приступал 6681 — не приступал 4096 — не приступал 7442 — не приступал 8387 — не приступал 5223 — не приступал 6315 — не приступал 4454 — не приступал 8065 — не приступал 4330 — не приступал 4668 — не приступал 1920 — не приступал 2343 — не приступал 5420 — не приступал 3078 — не приступал 2404 — не приступал 2991 — не приступал

Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.

Примеры ответов: 7 или здесьисейчас или 3514

Раскрыть Скрыть

№1

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

№2

Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

№3

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/π.

№4

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

№5

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

№6

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).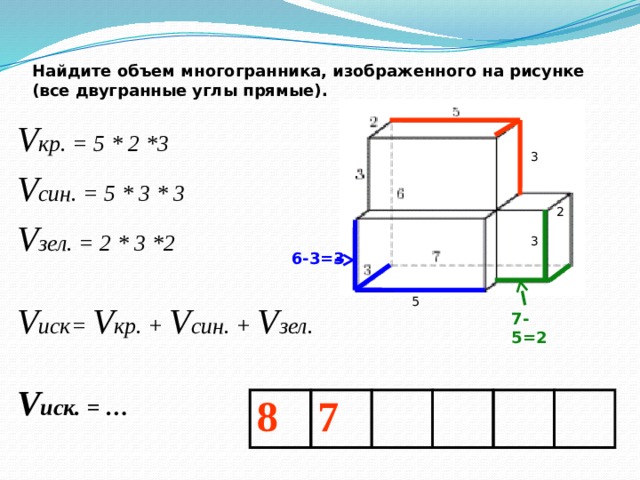

№7

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

№8

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности получившегося многогранника.

№9

Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

№10

Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах (в виде числа).

№11

Найдите тангенс угла B₂A₂C₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

№12

Найдите квадрат расстояния между вершинами B₂ и D₃ многогранника, изображенного на рисунке.

Все двугранные углы многогранника прямые.

№13

Найдите квадрат расстояния между вершинами B и D₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

№14

Найдите квадрат расстояния между вершинами A и C₃ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

№15

Найдите угол EAD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах (в виде числа).

№16

Найдите квадрат расстояния между вершинами D и C₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

№17

Найдите угол D₂EF многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.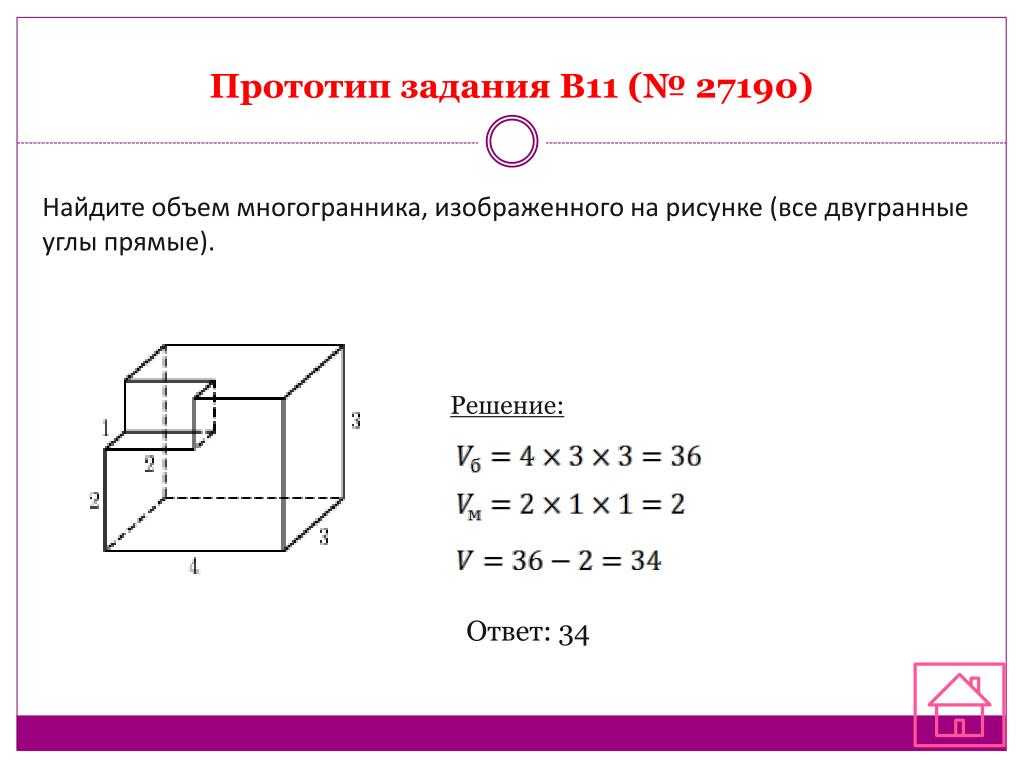

Так твой прогресс будет сохраняться.

Регистрация

Мы отправили код на:

Изменить

Получить код повторно через 00:00

Я прочитал(-а) Политику конфиденциальности и согласен(-на) с правилами использования моих персональных данных

Ништяк!

Решено верно

Браво!

Решено верно

Крутяк!

Решено верно

Зачёт!

Решено верно

Чётко!

Решено верно

Бомбезно!

Решено верно

Огонь!

Решено верно

Юхууу!

Решено верно

Отпад!

Решено верно

Шикарно!

Решено верно

Блестяще!

Решено верно

Волшебно!

Решено верно

Готовимся к ЕГЭ. Стереометрия — презентация онлайн

2. Урок 5

Задание 8: типы 1-6

3. Задание 8: стереометрия

Куб
Прямоугольный параллелепипед
Элементы составных многогранников
Площадь поверхности составного многогранника
Объем составного многогранника
Призма
Пирамида
Цилиндр
Конус
Шар
Комбинации тел

4.

Задание 8, тип 1: куб

5. Задание 8, тип 1: куб

1. Площадь поверхности куба равна 18. Найдите его
диагональ.
2. Если каждое ребро куба увеличить на 1, то его площадь
поверхности увеличится на 54. Найдите ребро куба.
3. Диагональ куба равна √12. Найдите его объем.
4. Площадь поверхности куба равна 24. Найдите его объем.
5. В кубе ABCDA1B1C1D1 точка K — середина ребра
AA1, точка L — середина ребра A1D1, точка M —
середина ребра A1B1. Найдите угол MLK. Ответ дайте в
градусах.

6. Задание 8, тип 2: Прямоугольный параллелепипед

7. Задание 8, тип 2: Прямоугольный параллелепипед

1. Два ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 3 и 4. Площадь
поверхности этого параллелепипеда равна 94. Найдите
третье ребро, выходящее из той же вершины.
2. Площадь грани прямоугольного параллелепипеда
равна 12. Ребро, перпендикулярное этой грани, равно
4. Найдите объем параллелепипеда
3. Объем прямоугольного параллелепипеда равен 24.
Одно из его ребер равно 3. Найдите площадь грани
параллелепипеда, перпендикулярной этому ребру.

8. Задание 8, тип 2: Прямоугольный параллелепипед

4. Два ребра прямоугольного параллелепипеда, выходящие
из одной вершины, равны 2, 4. Диагональ параллелепипеда
равна 6. Найдите объем параллелепипеда.
5. Найдите объем многогранника, вершинами которого
являются точки A, D, A1, B, C, B1 прямоугольного
параллелепипеда ABCDA1B1C1D1, у которого AB=3,
AD=4, AA1=5
6. В прямоугольном параллелепипеде ABCDA1B1C1D1
ребро AB=2, ребро AD=√5, ребро AA1=2.Точка K —
середина ребра BB1. Найдите площадь сечения,
проходящего через точки A1, D и K/

9. Задание 8, тип 3: Элементы составных многогранников

1. На рисунке изображён многогранник, все
двугранные углы многогранника прямые. Найдите
расстояние между вершинами А и С2.

10. Задание 8, тип 3: Элементы составных многогранников

2. Найдите квадрат расстояния между вершинами D и
C2 многогранника, изображенного на рисунк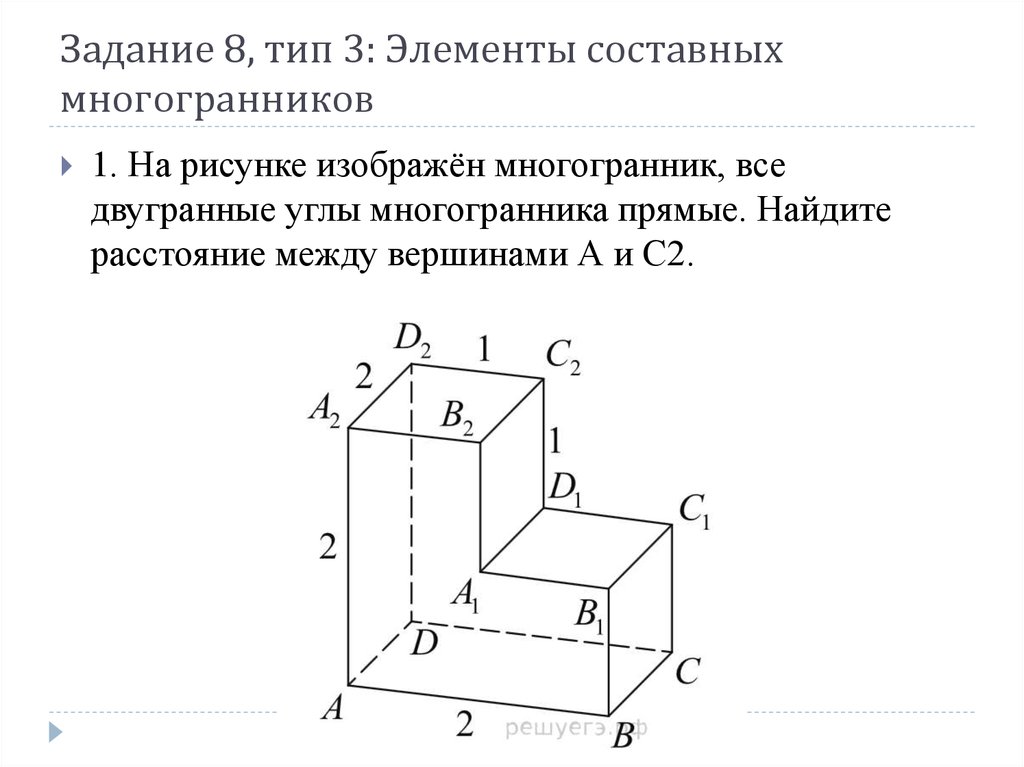е. Все
двугранные углы многогранника прямые.

11. Задание 8, тип 3: Элементы составных многогранников

3. Найдите угол CAD2 многогранника, изображенного
на рисунке. Все двугранные углы многогранника
прямые. Ответ дайте в градусах.

12. Задание 8, тип 3: Элементы составных многогранников

4. На рисунке изображён многогранник, все
двугранные углы многогранника прямые. Найдите
квадрат расстояния между вершинами B2 и D3.

13. Задание 8, тип 3: Элементы составных многогранников

5. Найдите угол D2EF многогранника, изображенного
на рисунке. Все двугранные углы многогранника
прямые. Ответ дайте в градусах.

14. Задание 8, тип 4: Площадь поверхности составного многогранника

1. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы
прямые).

15. Задание 8, тип 4: Площадь поверхности составного многогранника

2. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы
прямые).

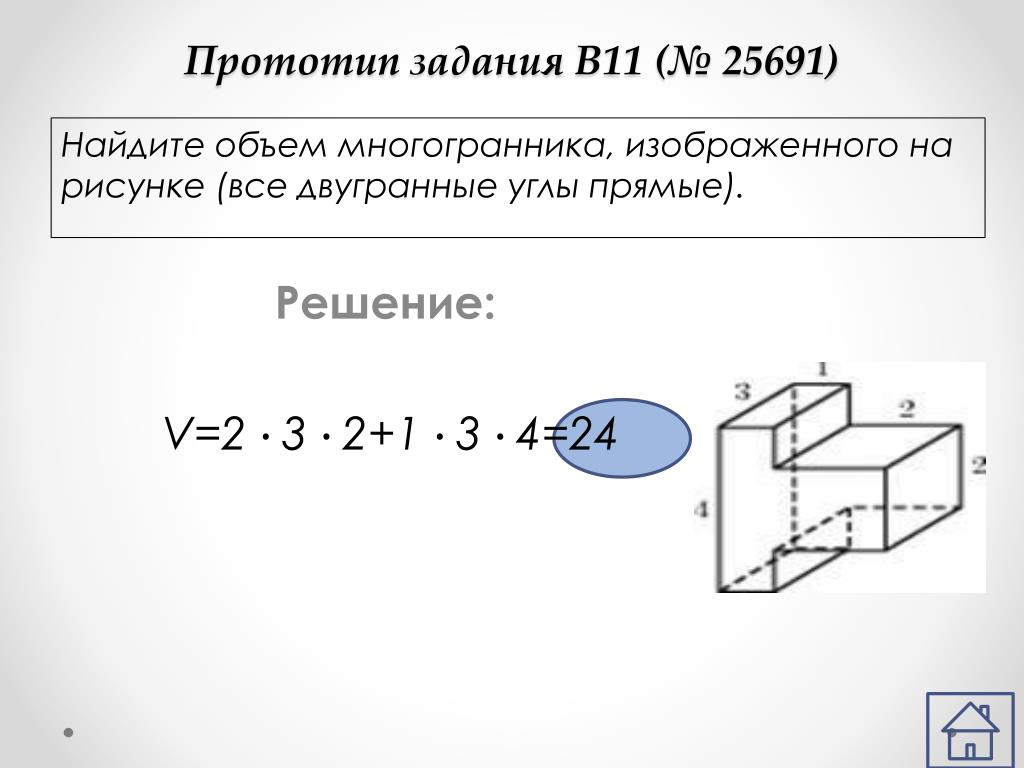
16. Задание 8, тип 4: Площадь поверхности составного многогранника

3. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы
прямые).

17. Задание 8, тип 4: Площадь поверхности составного многогранника

4. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы
прямые).

18. Задание 8, тип 5: Объем составного многогранника

1. Найдите объем многогранника, изображенного на
рисунке (все двугранные углы многогранника
прямые).

19. Задание 8, тип 5: Объем составного многогранника

2. Найдите объем пространственного креста,
изображенного на рисунке и составленного из
единичных кубов.

20. Задание 8, тип 5: Объем составного многогранника

3. Найдите объем многогранника, изображенного на
рисунке (все двугранные углы прямые).

21. Задание 8, тип 5: Объем составного многогранника

4. Найдите объем многогранника, изображенного на
рисунке (все двугранные углы прямые).

22. Задание 8, тип 5: Объем составного многогранника

5. Найдите объем многогранника, изображенного на
рисунке (все двугранные углы прямые).

23. Задание 8, тип 6: призма

1. В сосуд, имеющий форму правильной треугольной
призмы, налили воду. Уровень воды достигает 80 см. На
какой высоте будет находиться уровень воды, если ее
перелить в другой такой же сосуд, у которого сторона
основания в 4 раза больше, чем у первого? Ответ выразите
в см.

24. Задание 8, тип 6: призма

25. Задание 8, тип 6: призма

2. Найдите площадь поверхности прямой призмы, в
основании которой лежит ромб с диагоналями,
равными 6 и 8, и боковым ребром, равным 10.
3. Основанием прямой треугольной призмы служит
прямоугольный треугольник с катетами 6 и 8.
Площадь ее поверхности равна 288. Найдите высоту
призмы.

26. Задание 8, тип 6: призма

4. Через среднюю линию основания треугольной
призмы, объем которой равен 32, проведена
плоскость, параллельная боковому ребру. 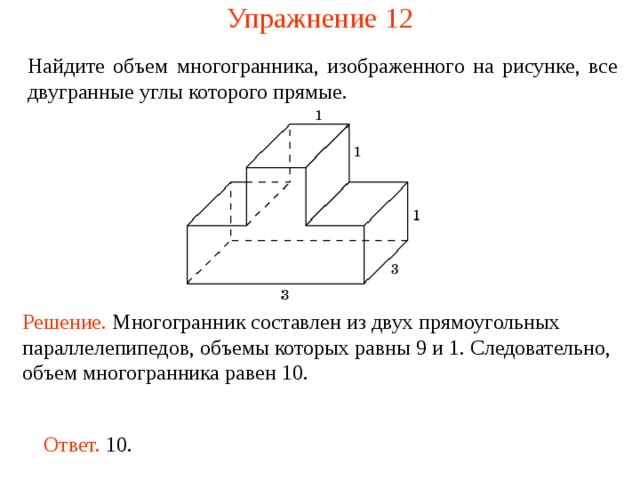Найдите
объем отсеченной треугольной призмы.

27. Задание 8, тип 6: призма

28. Задание 8, тип 6: призма

5. Найдите площадь боковой поверхности правильной
шестиугольной призмы, сторона основания которой
равна 5, а высота – 10.

29. Задание 8, тип 6: призма

6. Найдите объем многогранника, вершинами которого
являются точки A, B, C, D, A1, B1, C1, D1 правильной
шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь
основания которой равна 6, а боковое ребро равно 2.

30. Задание 8, тип 6: призма

7. Найдите расстояние между вершинами А и D
прямоугольного параллелепипеда, для которого AB =
5, AD = 4, AA = 3.

Как найти объем многогранника

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

ACT Math Help » Геометрия » Твердая геометрия » Другие многогранники » Как найти объем многогранника

У Роберто есть бассейн в форме прямоугольной призмы.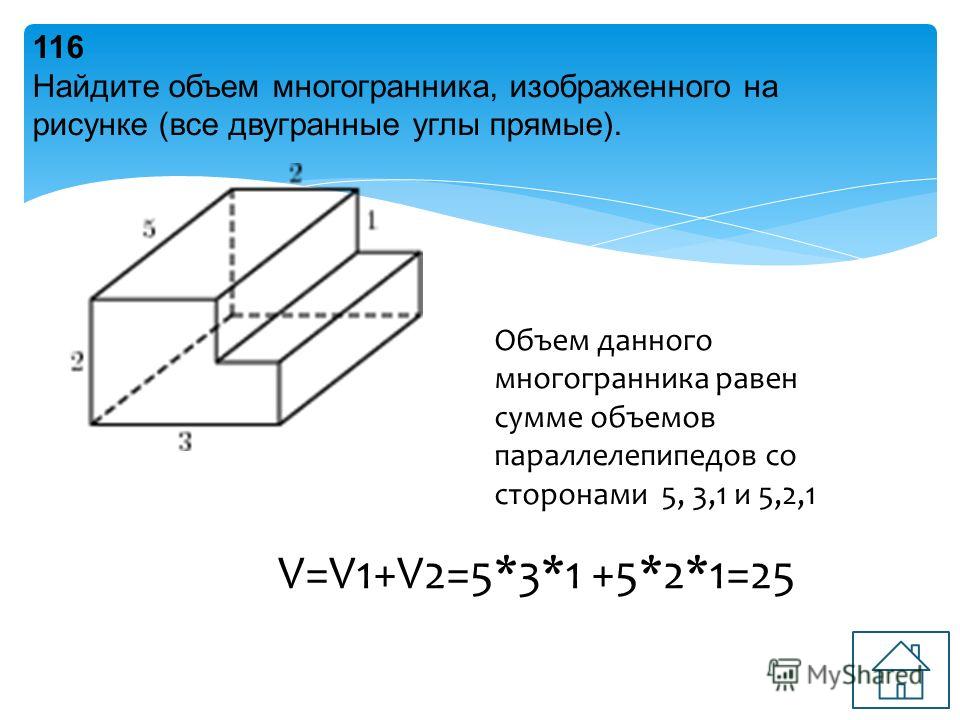 Его бассейн имеет метры в ширину, метры в длину и метры в глубину. Ему нужно наполнить бассейн к лету, а его шланг наполняется со скоростью  кубических метров в час. За сколько часов Роберто наполнит бассейн?

Возможные ответы:

Правильный ответ:

Пояснение:

Сначала найдите объем бассейна. Для прямоугольной призмы формула объема следующая:

Для бассейна

кубических метров

Теперь, поскольку шланг наполняет только кубические метры в час, разделите общий объем на долго бассейн будет заполняться.

Наполнение бассейна из шланга займет несколько часов.

Сообщить об ошибке

Мэтт испек прямоугольный торт на день рождения своей мамы. Торт был дюймов в длину, дюймов в ширину и дюймов в высоту. Если он разрежет торт на кусочки длиной в несколько дюймов, шириной в несколько дюймов и высотой в несколько дюймов, сколько кусков торта он сможет разрезать?

Возможные ответы:

Правильный ответ:

Пояснение:

Сначала найдите объем торта. Для прямоугольной призмы

Затем найдите объем каждого отдельного среза.

Теперь разделите объем всего торта на объем кусочка, чтобы узнать, сколько кусочков торта может разрезать Мэтт.

Сообщить об ошибке

Куб имеет площадь поверхности . Каков его объем?

Возможные ответы:

Правильный ответ:

Пояснение:

Сначала найдите длины сторон куба.

Напомним, что площадь поверхности куба определяется следующим уравнением:

, где  – длина стороны.

Подставляя площадь поверхности, заданную уравнением, мы можем найти длину стороны куба.

Теперь вспомним, что объем куба определяется следующим уравнением:

Сообщить об ошибке угловая призма. Найдите значение .

Возможные ответы:

Правильный ответ:

Объяснение:

Объем прямоугольной призмы задается следующим уравнением:

Теперь, для заданного вопроса, высота равна .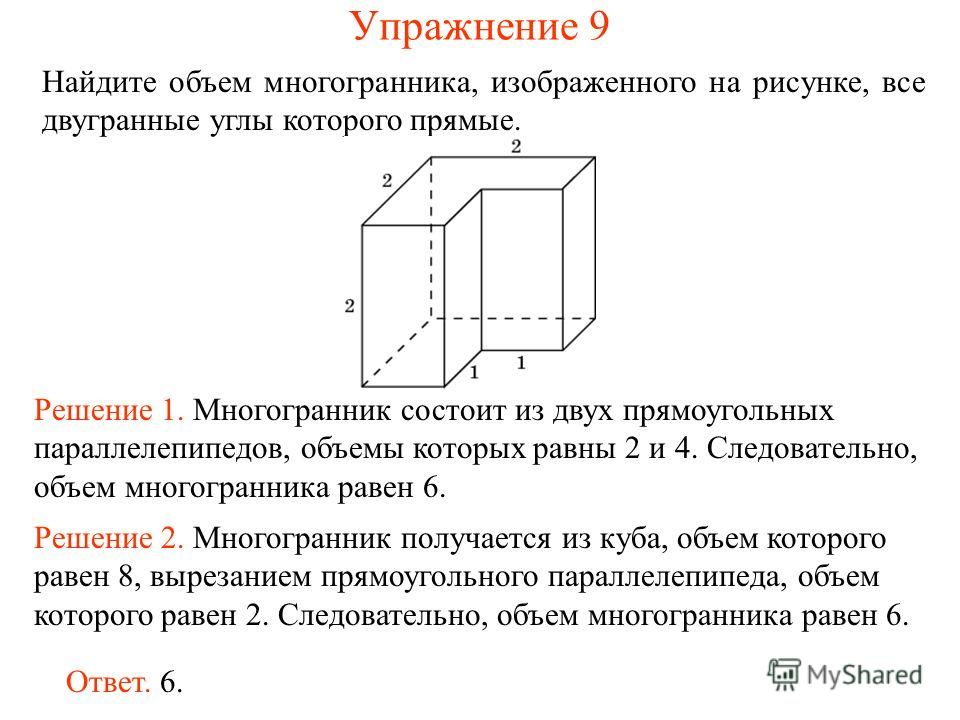

Поскольку площадь основания представляет собой прямоугольный треугольник, мы можем подставить данные значения, чтобы найти .

Сообщить об ошибке

Показанная ниже палатка имеет форму треугольной призмы. Каков объем этой палатки в кубических футах?

Возможные ответы:

Правильный ответ:

Объяснение:

Объем прямоугольной призмы определяется следующим уравнением:

Сообщить об ошибке

Высота коробки вдвое больше ширины и половины длины. Если объем коробки , какова длина коробки?

Возможные ответы:

Правильный ответ:

Объяснение:

Для прямоугольной призмы формула для объема выглядит следующим образом:

Теперь мы знаем, что высота в два раза больше ширины.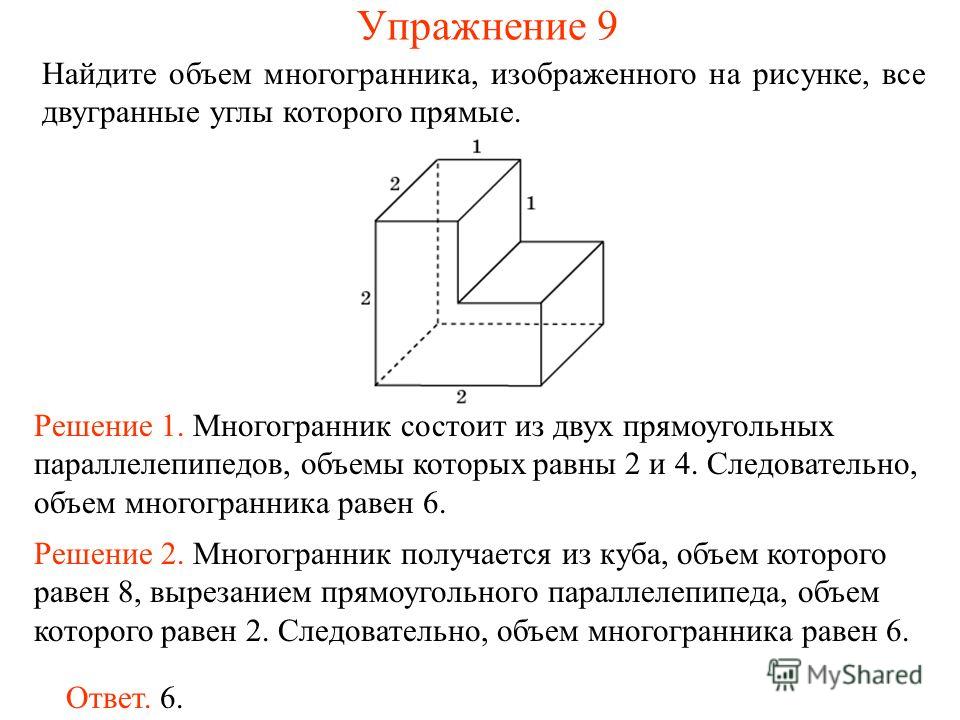 Мы можем переписать это как:

Мы также знаем, что высота равна половине его длины. Это можно записать так:

Теперь мы можем подставить значения длины, ширины и высоты в единицу высоты, чтобы найти высоту.

Задача состоит в том, чтобы найти длину коробки. Подставьте значение высоты в более раннее уравнение, которое мы написали ранее, чтобы представить отношение между высотой и длиной.

Сообщить об ошибке

Найдите в кубических дюймах объем тетраэдра с площадью поверхности .

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала нам нужно найти длину стороны тетраэдра.

Мы можем использовать площадь поверхности, чтобы найти длину стороны. Напомним, что формула для нахождения поверхности тетраэдра:

, где  – длина стороны.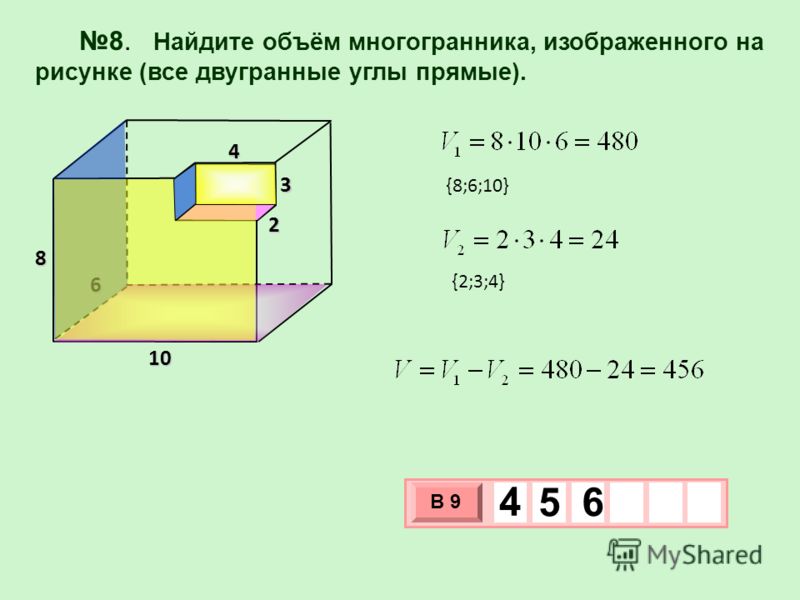

Теперь вспомните формулу для нахождения объема тетраэдра:

Сообщить об ошибке

Сьюзен купила плитку шоколада который пришел в контейнере в форме треугольной призмы, показанной ниже. Если контейнер полностью заполнен шоколадом в кубических дюймах, какой объем шоколада купила Сьюзен?

Возможные ответы:

Правильный ответ:

Объяснение:

Объем прямоугольной треугольной призмы определяется следующим уравнением:

Сообщить об ошибке . Если пластик, необходимый для изготовления игральных костей, стоит кубический сантиметр, сколько стоит Трою изготовление одного игрального кубика?

Возможные ответы:

Правильный ответ:

Пояснение:

Сначала найдите объем кубика.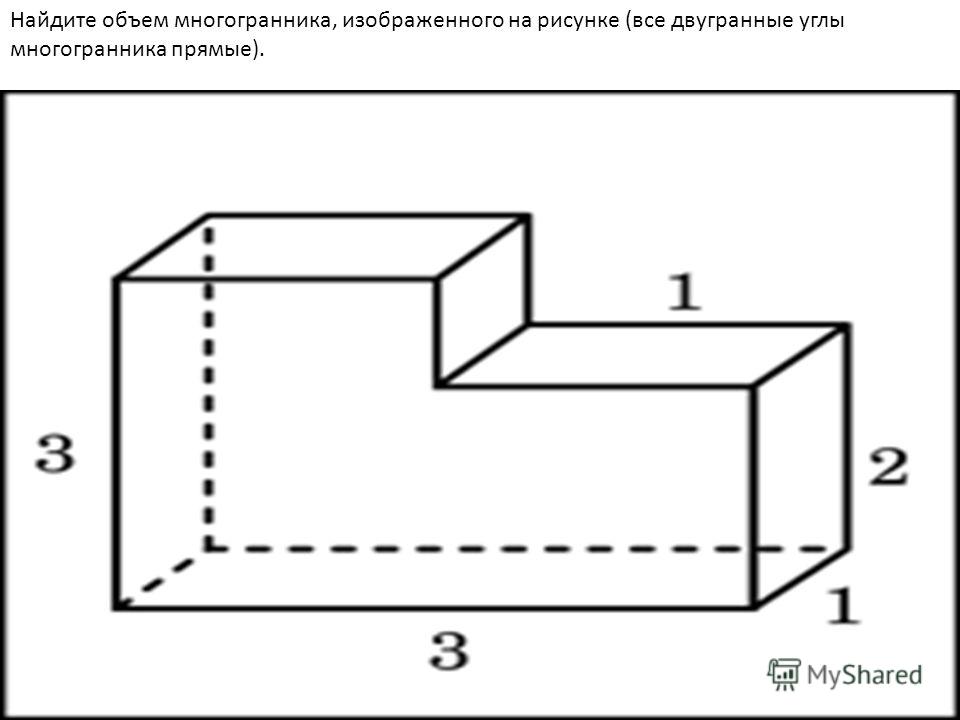 Для куба объем имеет следующую формулу:

Поскольку каждый кубический сантиметр стоит, вам нужно будет умножить это число на , чтобы получить стоимость каждого кубика.

Сообщить об ошибке

Пирамида помещена внутрь куба так, что они имеют общее основание и высоту. Если площадь поверхности куба равна , каков объем пирамиды в квадратных футах?

Возможные ответы:

Правильный ответ:

Пояснение:

Сначала нам нужно найти длину стороны куба.

Напомним, что площадь поверхности куба определяется следующим уравнением:

, где  – длина стороны.

Подставляя площадь поверхности, заданную уравнением, мы можем найти длину стороны куба.

Теперь, поскольку пирамида и куб имеют общее основание, мы знаем, что пирамида должна быть прямоугольной.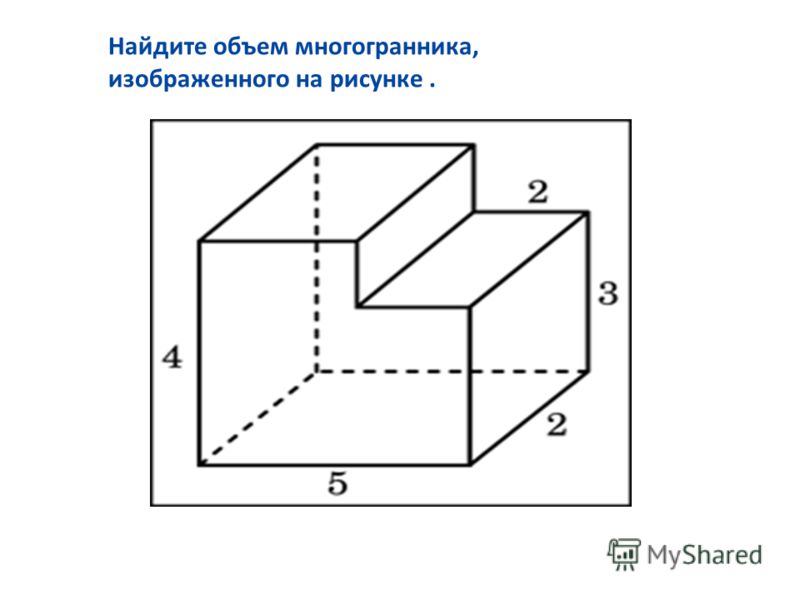

Вспомните, как найти объем пирамиды:

Теперь, поскольку пирамида имеет ту же высоту, что и куб, высота пирамиды также равна .

Сообщить об ошибке

← Назад 1 2 Далее →

Уведомление об авторских правах

Все ресурсы ACT Math

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Учитесь по концепции

Вычисление объема и поверхности в трехмерной геометрии

 

Ключевые термины

 

o         Многогранник

o         Грань

o         Край

o         Призма

o         Правая призма

 

Объективы

 

o         Распознавать многогранники и призмы и уметь анализировать простые примеры этих рисунков

o        Знать, как использовать формулы объема и площади поверхности для сфер и цилиндров

 

 

Сначала рассмотрим объем и площадь поверхности некоторых простых трехмерных фигур, затем перейдем к составным трехмерным фигурам.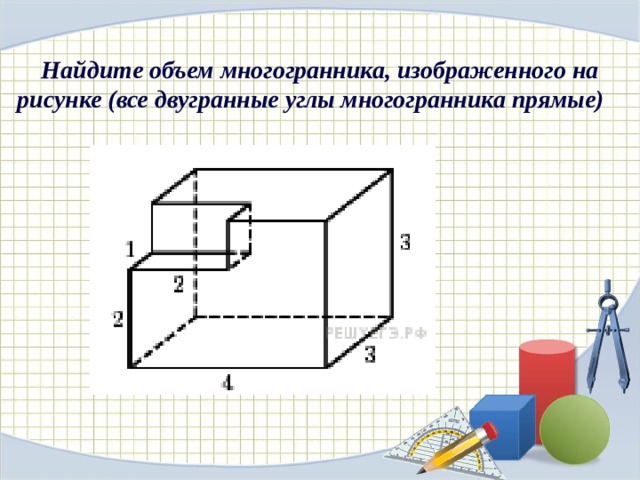

 

Объем и площадь поверхности

 

Мы рассмотрим два основных типа геометрических тел: многогранники и сферы. Многогранник — это, по сути, —-сторонняя сплошная фигура — трехмерный аналог многоугольника. Некоторые примеры многогранников показаны ниже.

 

                   

 

Многогранники определяются своими гранями , которые являются областями многоугольника, ребрами, которые являются сегментами линий, очерчивающими грани и, следовательно, многогранник, и вершины, которые определяются так же, как и предназначены для полигонов. Особый тип многогранника — это призма , представляющая собой многогранник с одинаковыми (и параллельными) вершиной и низом. Если стороны призмы встречаются с верхом и низом под прямым углом, то она называется прямой призмой . Два многогранника в левой части приведенного выше ряда примеров являются призмами — мы можем увидеть это более точно, используя пунктирные линии, чтобы показать части, которые находятся вне поля зрения.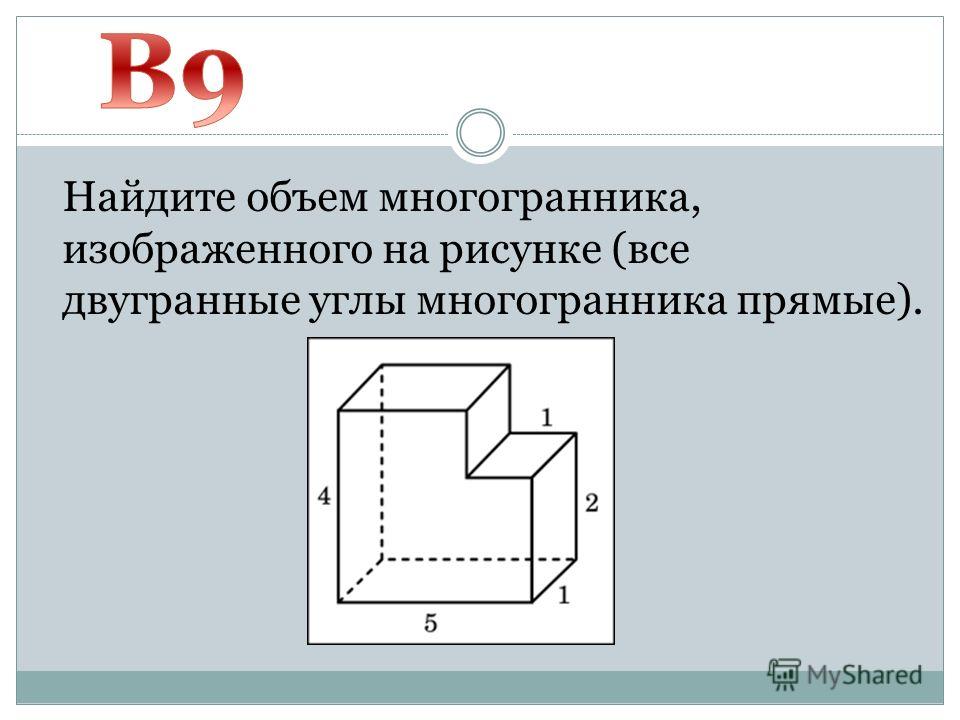

 

                                             

 

Опять же, обратите внимание, что верхняя и нижняя грани (основания) идентичны; кроме того, это на самом деле прямые призмы (при условии, что углы, образованные между сторонами и основаниями, прямые, как они выглядят на диаграммах). Очевидно, том V прямой призмы — это просто площадь A основания, умноженная на высоту h сторон, как показано ниже для куба (шестигранной призмы).

 

 

Но что, если призма не правильная? Применяется та же формула. Давайте посмотрим, почему это так, снова используя шестигранную призму. Мы будем смотреть на эту фигуру «с торца» так, чтобы ее глубина была перпендикулярна поверхности страницы (другими словами, два основания не видны). Из определения призмы мы знаем, что противоположные отрезки (ребра) конгруэнтны.

 

                                                            

 

s разделить тело, как показано ниже, образуя два треугольных тела и одно прямоугольное тело. Обратите внимание, что пунктирная линия также является высотой призмы.

 

                                                             

 

Из свойств прямоугольников известно следующее.

 

                                                         

 

Таким образом, по условию SSS мы знаем, что два треугольника конгруэнтны. Обозначим фигуру следующим образом, заметив, что основание b фигуры равно b ₁ + b ₂ .

 

Хотите узнать больше? Почему бы не пройти онлайн-курс по геометрии?

                                                        

 

Теперь мы можем вычислить площадь этой грани фигуры.

 

 

Но площадь оснований не меняется между правым и неправильным вариантами призмы. Другими словами, глубина в этом случае и в случае правильной призмы (при одинаковой ориентации) одинакова. Соответственно и объем одинаковый. Хотя мы продемонстрировали этот факт только для шестигранных призм, то же самое относится ко всем призмам: объем равен площади основания, умноженной на высоту.

 

 

Практическая задача : Вычислите объем призмы, показанной ниже.

 

 

Решение : Многогранник на диаграмме идентифицирован как призма. На основании прямых углов в основании (и, следовательно, обоих оснований) мы можем идентифицировать основания как прямоугольники с длиной 4 единицы и шириной 9 единиц. Таким образом, площадь основания призмы равна 36 квадратных единиц. Высота призмы показана на схеме как 4 единицы. Таким образом, мы можем вычислить объем V призмы следующим образом.

 

V = bh = (36 шт. ² )(4 шт.) = 144 шт. ³

 

90 004  

Объем общих многогранников может быть трудно вычислить, поэтому мы не будем рассмотреть их в любой большей глубины.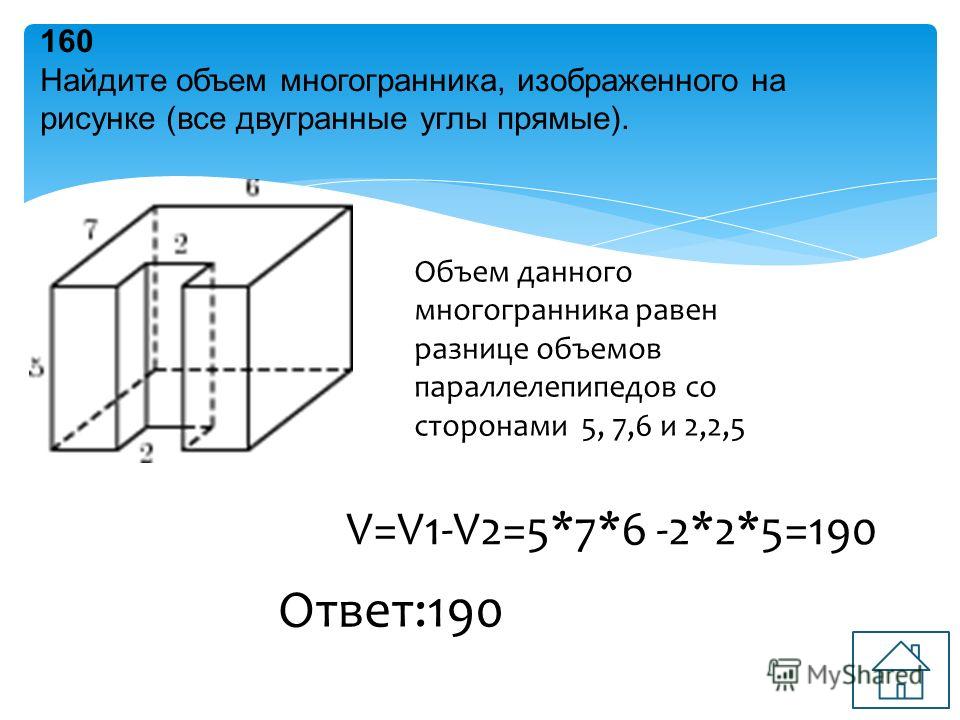 Формулы есть в книгах и в интернете, правда, для некоторых многогранников.

 

Еще один параметр, который мы можем рассчитать, — это площадь поверхности фигуры. Независимо от многогранника, площадь поверхности — это просто сумма площадей всех граней фигуры. Например, в случае куба (шестигранной призмы) площадь поверхности просто в шесть раз больше площади любой грани (все грани имеют одинаковую площадь, поскольку все ребра конгруэнтны). (Или, если каждое ребро имеет длину s , площадь поверхности 6 s ² .)

 

 

Практическая задача : Расчет Определите площадь поверхности призмы из предыдущей практической задачи, предполагая, что фигура только наклонена. Направо.

 

Решение : Посмотрите еще раз на призменную диаграмму в первой практической задаче. Мы можем найти площадь поверхности, вычислив площадь каждой грани. Мы уже знаем, что каждое основание имеет площадь 36 квадратных единиц.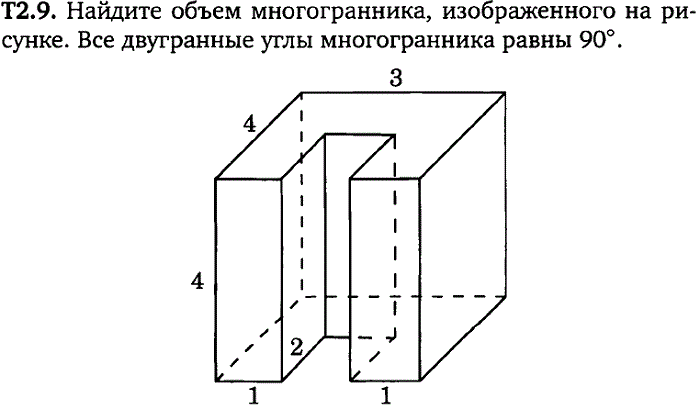 Остаются четыре неизвестные стороны. Задача говорит нам, что фигура наклонена только вправо (показана на диаграмме ниже дугой) — таким образом, единственные непрямые углы находятся на передней и задней гранях. Эти две грани являются параллелограммами. Левая и правая грани — прямоугольники.

 

 

Площадь левой и правой граней равна произведению 4 и 5 единиц, или 20 квадратных единиц. Передняя и задняя грани представляют собой параллелограммы с основанием в 9 единиц и высотой в 4 единицы, поэтому каждая имеет площадь 36 квадратных единиц. Теперь найдем общую площадь поверхности S .

S = (36 + 36) + (20 + 20) + (36 + 36) = 184 единицы ³

Сферы — это еще один тип трехмерных фигур, объем и площадь поверхности которых можно вычислить относительно легко. Сфера является трехмерным аналогом окружности и определяется точкой центра O и радиусом r . Сфера — это множество всех точек, находящихся на расстоянии r от O . Пример сферы показан ниже.

 

 

Как и в случае с кругами, сложно вывести формулы геометрически, но формулы хорошо известны. Том V и площадь поверхности S даны ниже для сферы радиусом r .

 

 

Подобной фигурой является (круглый) цилиндр, который имеет два конгруэнтных круглых основания и трубчатое тело, как показано ниже. Цилиндр определяется радиусом основания r и высотой h .

 

 

Аналогично призме объем V цилиндра есть произведение площади его основания на высоту.

 

V = πr ² h

 

Площадь поверхности немного сложнее, но ее можно рассчитать по формуле просто расширяя наши текущие знания. Мы знаем, что длина окружности основания равна 2 πr ; таким образом, если мы просто умножим эту формулу на ч , мы получим площадь поверхности «бочки» цилиндра.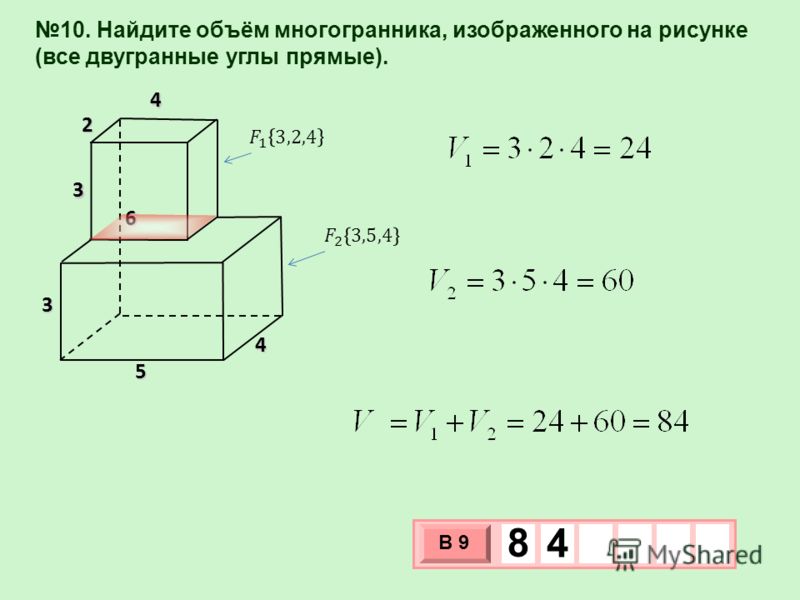 Теперь нам нужно только добавить площадь оснований, которая в два раза больше площади любого круглого основания. Общая площадь S означает следующее.

 

S = 2 πrh + πr ² + πr ² = 2( πrh + πr ² )

 

 

Практическая задача : Цилиндр высотой 16 футов и радиусом 5 футов закрыт с каждого конца полусферой (половиной сферы), как показано ниже. Какова площадь поверхности и объем фигуры?

 

                                                                   

 

90 004 Решение : Мы уже знаем, как вычислить площадь поверхности стороны цилиндра: 2 πrh . Мы также должны рассчитать площадь поверхности двух полусферических крышек. Обратите внимание, что «основание» полушарий представляет собой поперечное сечение полной сферы. Поскольку это поперечное сечение имеет радиус 5 футов, оба полушария имеют одинаковый радиус. Площадь поверхности обоих полушарий вместе равна тогда просто площади поверхности полной сферы радиусом 5 футов. Площадь этой поверхности равна 4 πr ² . Теперь мы можем вычислить площадь поверхности фигуры.

 

S = 2 π (5)(16) + 4 π (5) ² = 160 π + 100 π = 260 π ≈ 816,8 фута ²

 

Чтобы вычислить объем, просто найдите объем цилиндра плюс объем сферы радиусом 5 футов.

 

 

 

Составные фигуры в трех измерениях

 

Работа с составными фигурами в трех измерениях требует почти тех же принципов, что и для работы с составными фигурами в двух измерениях. Например, вычисление объема прямоугольного твердого тела со сферическим пустым пространством просто включает вычитание объема сферы из общего объема внутри прямоугольной области. Кроме того, наш подход к разделению сложных фигур на более простые и легкие в управлении фигуры применим и к трехмерным фигурам.