Как найти Среднюю Линию Треугольника? Свойства, Теорема
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Виды треугольника:
- Прямой. Один угол прямой, два других меньше 90 градусов.
- Острый. Градус угла больше 0, но меньше 90 градусов.
- Тупой. Один угол тупой, два других — острые.
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
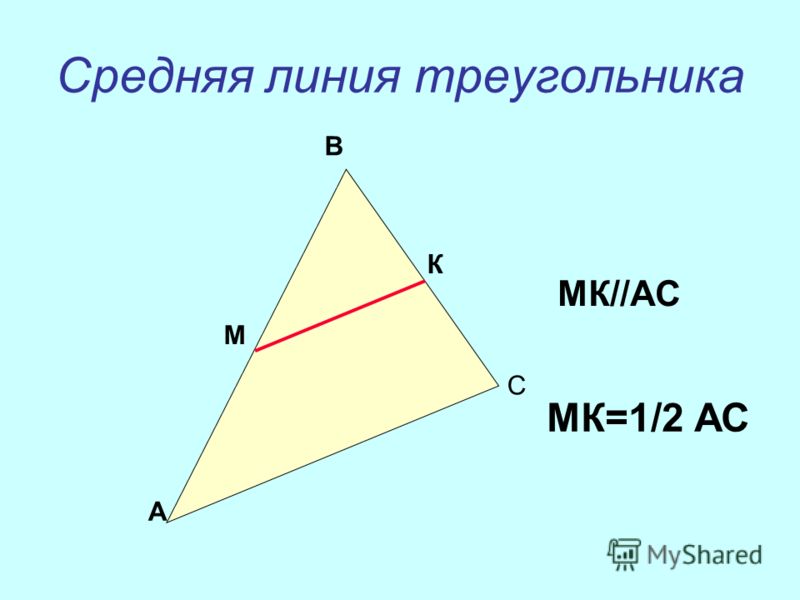
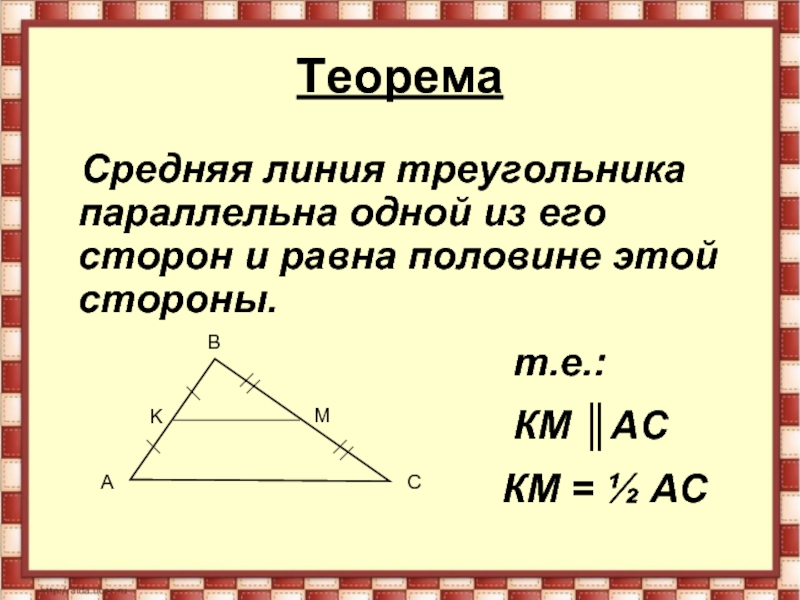
Понятие средней линии треугольника
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.
Основанием считается сторона, с которой средняя линия не пересекается.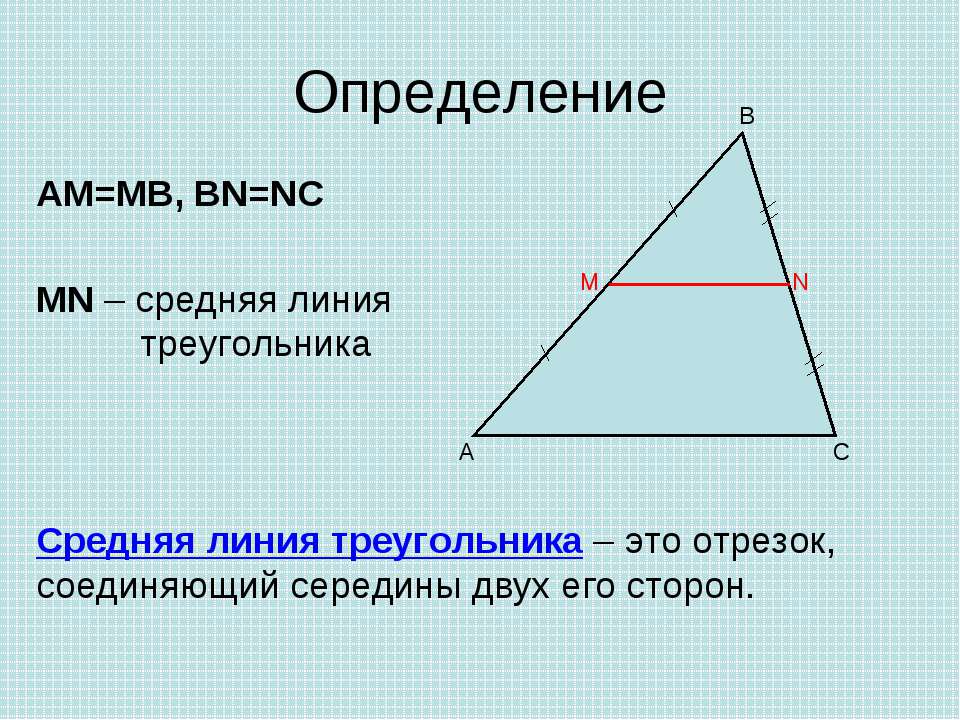
Как найти среднюю линию треугольника расскажем дальше, а для начала еще немного разберемся со всеми определениями.
Запоминаем
Средняя линия параллельна третьей стороне, а ее длина равна половине длины этой стороны.
Понятие средней линии прямоугольного треугольника
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Важное свойство
Средняя линия прямоугольного треугольника делит его на четыре прямоугольные фигуры.
Свойства средней линии треугольника
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
Свойства:
- Средняя линия равна половине длины основания и параллельна ему.
- Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
- Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
- Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
А так выглядит формула нахождения средней линии треугольника:
Докажем теорему:
- По условию нам дано, что MA = MB, NA = NC
- Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
По второму признаку подобия треугольников:
- Поэтому ∠1 = ∠2 , как соответственные, а по признаку параллельности прямых: MN || BC.
Параллельность средней линии и соответствующего ей основания доказана.
- Еще из подобия треугольников △AMN~△ABC можно выписать и отношение их третьих сторон
То, что средняя линия равна половине соответствующего основания, доказано.
Теорема доказана.
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, N, K — середины сторон AB, BC, CA. Найти периметр ΔMNK.
- Сначала проверим существует ли указанный в условии треугольник ΔABC. Проверим это при помощи неравенства для его наибольшей стороны:
7 + 5 > 8.

Неравенство выполнено, значит, такой треугольник действительно есть.
- Соединим середины сторон треугольника ΔABC и получим его средние линии. Найдем их длины по теореме о средней линии:
Ответ: периметр треугольника равен 10.
Пример 2. В прямоугольном треугольнике АВС есть три средние линии: MN, NP, MP. В получившемся прямоугольнике MNPA известно, что синус угла между диагоналями равен 0,5. А средние линии MN и NP равны 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.
Как решаем:
- В прямоугольнике две диагонали между собой равны. Одна из диагоналей MP — это гипотенуза прямоугольного треугольника MNP. Катеты треугольника известны, значит можно найти гипотенузу через теорему Пифагора:
- Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними:
S = 5 * 5 * 0,5 = 12,5
- В большом треугольнике четыре малых, а в прямоугольнике два малых треугольника.

S = 12,5 * 2 = 25
Ответ: площадь большого прямоугольного треугольника равна 25.
Приходите решать увлекательные задачки в современную школу Skysmart. Ребенка ждет интерактивный формат, примеры разной сложности и онлайн-доска, на которой можно чертить вместе с учителем.
Запишитесь на бесплатный вводный урок математики и начните заниматься с удовольствием уже завтра!
Средняя линия треугольника ABC: определение, свойства, признак, длина
В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.
Определение средней линии треугольника
Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.
- KL – средняя линия треугольника ABC
- K – середина стороны AB: AK = KB
- L – середина стороны BC: BL = LC
Свойства средней линии треугольника
Свойство 1
Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.
На рисунке выше:
- KL параллельна AC
- KL = 1/2 ⋅ AC
Свойство 2
Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.
На рисунке выше:
- △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
- Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL. - S△ABC = 4 ⋅ S△KBL
Свойство 3
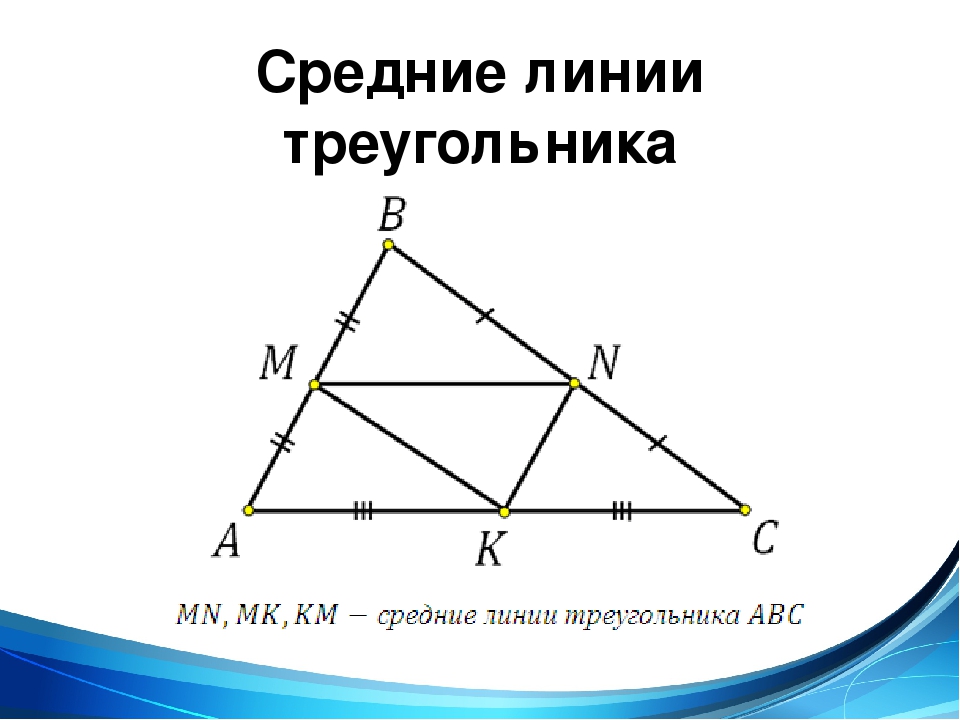
В любом треугольнике можно провести три средние линии.
KL, KM и ML – средние линии треугольника ABC.
- KM || BC, KM = 1/2 ⋅ BC
- ML || AB, ML = 1/2 ⋅ AB
Свойство 4
Три средние линии треугольника делят его на 4 равных по площади треугольника.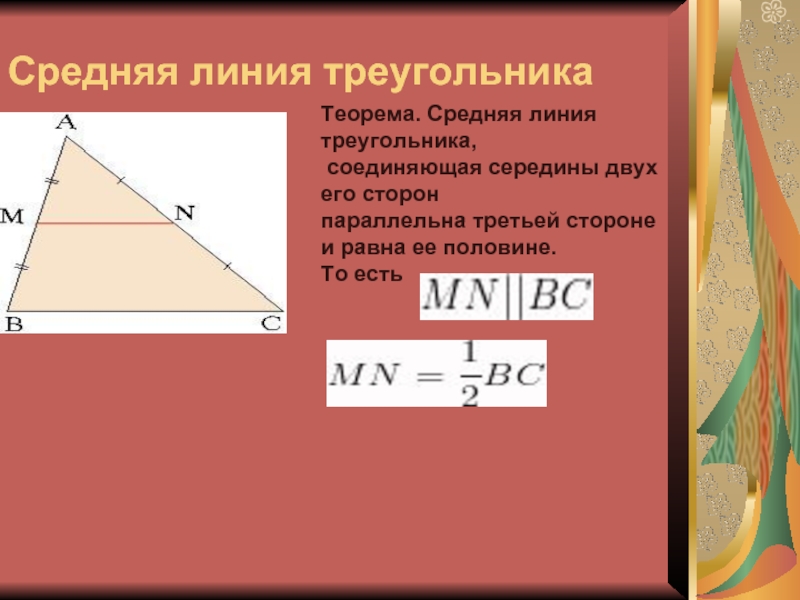
S1 = S2 = S3 = S4
Признак средней линии треугольника
Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.
Пример задачи
Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.
Решение
Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.
Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.
BC2 = AB2 + AC2 = 62 + 82 = 100.
BC = 10.
Таким образом, средняя линия LM = 1/2 ⋅ BC = 1/2 ⋅ 10 = 5.
Трапеция, Средняя линия трапеции, треугольник
Четырёхугольник, у которого только две стороны параллельны называются трапецией.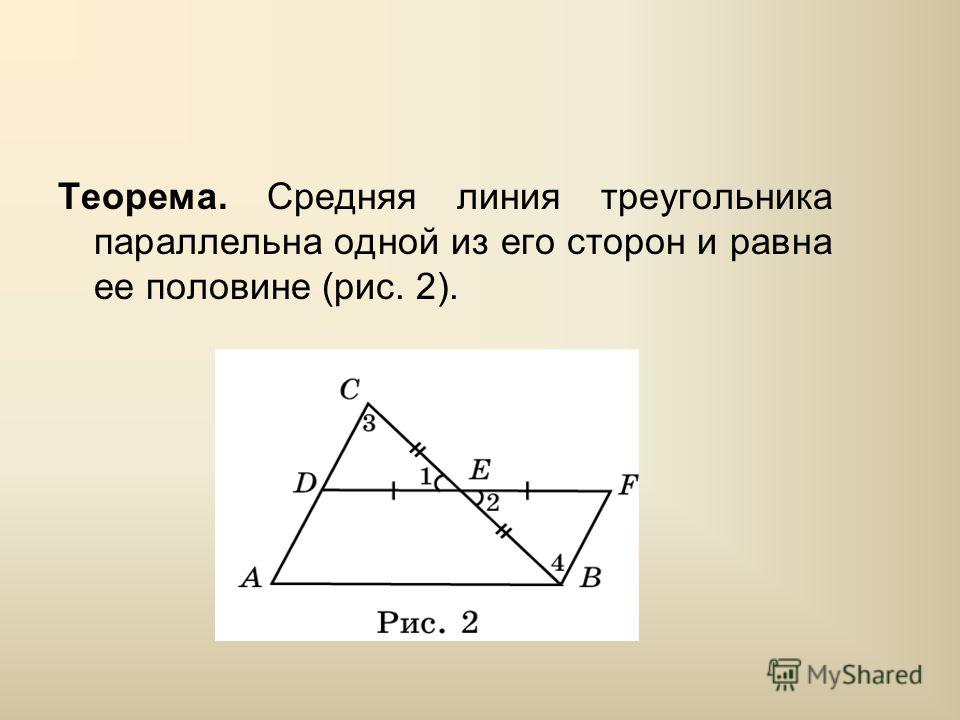
Параллельные стороны трапеции называются её основаниями, а те стороны, которые не параллельны, называются боковыми сторонами. Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DCAM = MD; BN = NC
MN средняя линия, AB и CD — основания, AD и BC — боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача: Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
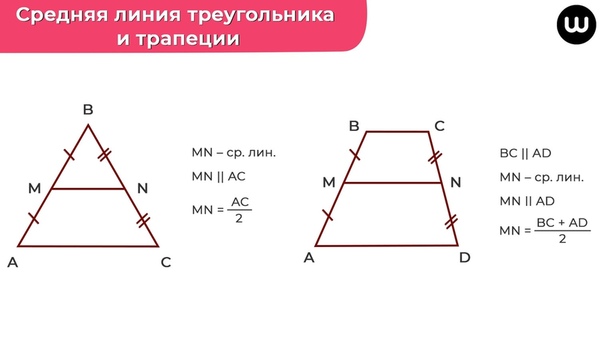
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема: Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC =>
MN || AB
MN = AB/2
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA1 = A1A2 = A2A3 = A3A4 = A4A5
Мы соединяем A5 с B и проводим такие прямые через A4, A3, A2 и A1, которые параллельны A5B. Они пересекают AB соответственно в точках B4, B3, B2 и B1. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB3A3A5 мы видим, что BB4 = B4B3. Таким же образом, из трапеции B4B2A2A4 получаем B4B3 = B3B2
Они пересекают AB соответственно в точках B4, B3, B2 и B1. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB3A3A5 мы видим, что BB4 = B4B3. Таким же образом, из трапеции B4B2A2A4 получаем B4B3 = B3B2
В то время как из трапеции B3B1A1A3, B3B2 = B2B1.
Тогда из B2AA2 следует, что B2B1 = B1A. В заключении получаем :
AB1 = B1B2 = B2B3 = B3B4 = B4B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
«Среднии линии трапеции и треугольника»-геометрия 8 класс
Темуа: Среднии линии треугольника и трапеции/2/.
Цели урока:
Образовательные:изучить понятие средней линии трапеции, доказательство свойства средней линии, учить применять теорему в нестандартных ситуациях при решении задач. Закрепить понятие средней линии трапеции, умение применять теорему о средней линии трапеции в нестандартных ситуациях при решении задач.
Развивающие: развивать логическое мышление, воспитывать культуру математической речи. Формировать умение учащихся анализировать, обобщать, использовать элементы исследования, сравнения.
Воспитательные: воспитывать у учащихся ответственное отношение к учебному труду, волю; формировать эмоциональную культуру и культуру общения.
Ход урок:
1. Организационный момент.
2. Проверка домашнего задания: №141,144,163.
Проверка домашнего задания: №141,144,163.
3.Устный опрос:
— Что называется средней линией треугольника?
— Что называется средней линией трапеции?
-Придумайте сами задачу на нахождение средней линии треугольника.
— Сформулировать свойство средней линии треугольника.
— Стороны треугольника равны 2см, 4см и 6см. Чему равны средние линии этого треугольника?
— Заполните пропуски, чтобы получилось верное высказывание.
Средняя линия трапеции параллельна основаниям и _____________
-Установите истинность или ложность следующих утверждений:
а).Отрезок, соединяющий боковые стороны трапеции, называется ее средней линией.
б).Если основания трапеции равны 4 см и 8 см, то ее средняя линия равна 4 см.
в).Найдите МN.
а) 7 см; б) 5 см; в) 3 см.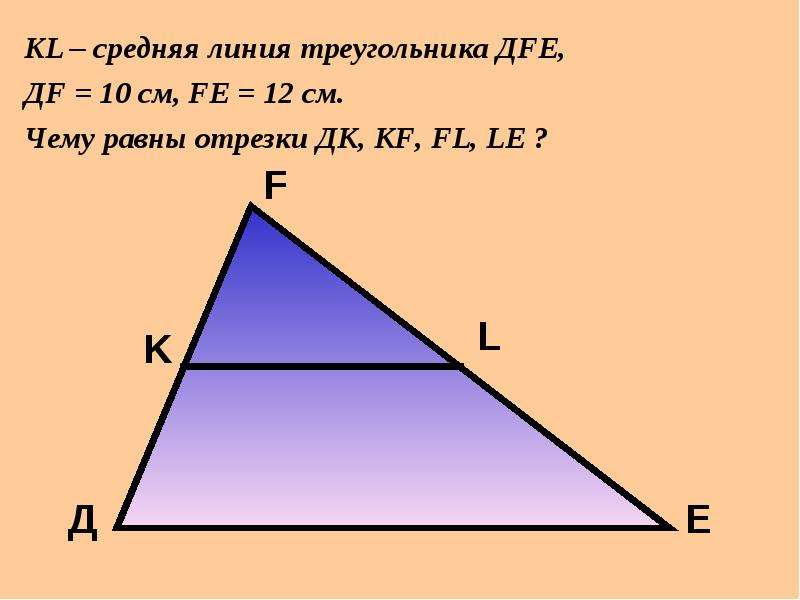
г).В трапеции одно из оснований больше другого в 2 раза. Средняя линия трапеции = 15 см. Найдите ее основание.
а) 5 см; 10 см; б) 10 см; 20 см; в) 15 см; 30 см.
д). Меньшее основание трапеции относится к ее средней линии как 2:3. Найдите длину меньшего основания, если большее основание равно 16 см.
а) 8 см; 12 см; б) 10 см; 15 см; в) 4 см и 6 см.
4. Решение упражнений.
Задача №1.
АВСД трапеция. ВС и АД – основания трапеции. МР – средняя линия трапеции, делит диагональ АС на отрезки АК и КС. Найдите МР и ВС, если МК=3дм, АД=10дм.
Задача №2.
Нижнее основание трапеции в 4 раза больше верхнего, а её средняя линия равна 20см. Найдите длины оснований трапеции.
Задача №3 /2-й уровень/.
В трапеции АВСД АВ параллельна СД. Диагональ ВД делит среднюю линию на отрезки 6 см и 12 см. Найдите длины оснований трапеции.
5. Самостоятельная работа.
1 вариант.
1. Всякий ли четырёхугольник, у которого есть две параллельные стороны, является трапецией? (Нет)
2. Точки М и С делят боковые стороны трапеции пополам, как называется отрезок МС? (Средняя линия)
3. Концы средней линии трапеции лежат на её сторонах СЕ и МР. Как Называются стороны СЕ и МР? (Боковые стороны)
4. Как называются параллельные стороны? (Основания)
5. Периметр равнобокой трапеции равен 26 см, а её боковая сторона – 5 см. Найдите длину средней линии трапеции. (8 см)
2 вариант.
1. У четырёхугольника ABCD стороны AB и CD не параллельны. Обязательно ли этот четырёхугольник – трапеция? (Нет)
2. Точки А и В лежат на боковых сторонах трапеции. Отрезок АВ параллелен основаниям трапеции. Обязательно ли АВ – средняя линия? (Нет)
3. Концы средней линии трапеции лежат на её сторонах СЕ и МР. Как Называются стороны РС и МЕ? (Основание)
Как Называются стороны РС и МЕ? (Основание)
4. Как называются непараллельные стороны? (Боковые стороны)
5. Длина средней линии трапеции равна 3 см, а сумма длин её боковых сторон 4 см. Чему равен периметр этой трапеции? (10 см)
6.Домашнее задание: №165,166,167.
7.Итоги урока.
ont-family:»Times New Roman»‘>
Просмотр содержимого документа
«»Среднии линии трапеции и треугольника»-геометрия 8 класс »
Тема: Среднии линии треугольника и трапеции/1/.
Цели урока:
Образовательные: ввести определение средней линии треугольника; изучить свойства средней линии треугольника;формировать умения и навыков применять знания о средней линии треугольника при решении задач. Изучить понятие средней линии трапеции, доказательство свойства средней линии, учить применять теорему в нестандартных ситуациях при решении задач. Формировать умение учащихся анализировать, обобщать, использовать элементы исследования, сравнения.
Изучить понятие средней линии трапеции, доказательство свойства средней линии, учить применять теорему в нестандартных ситуациях при решении задач. Формировать умение учащихся анализировать, обобщать, использовать элементы исследования, сравнения.
Развивающие: развивать геометрическое мышление учащихся при решении геометрических задач, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание; учить учащихся учиться математике, самостоятельно добывать знания. Развивать логическое мышление, воспитывать культуру математической речи.
Воспитательные: воспитывать у учащихся ответственное отношение к учебному труду, волю; формировать эмоциональную культуру и культуру общения.
Ход урок:
1. Организационный момент
2. Мотивация урока.
Девиз урока: «С любовью к ее величеству — науке геометрии».
3. Проверка домашнего задания:
а). №152,153,157,166.
№152,153,157,166.
б). -Какую теорему изучили на прошлом уроке?
-Сформулируйте ее.
-Как разделить отрезок на несколько равных частей?
Часто знает и дошкольник,
Что такое треугольник,
А уж вам-то, как не знать…
Но совсем другое дело —
Очень быстро и умело
Треугольники считать!
Например, в фигуре этой
Сколько разных? Рассмотри!
Все внимательно исследуй
И “по краю” и “внутри”
Тест “Истинно” или “ложно”
-Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны. (И)
-Высота равнобедренного треугольника является медианой, биссектрисой. (Л) (Пропущены слова: проведенная к основанию)
—Если три стороны треугольника равны трем сторонам другого треугольника, то такие треугольники равны. (Л) (Пропущено слово: соответственно)
(Л) (Пропущено слово: соответственно)
-Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны. (И)
—В треугольнике углы при основании равны. (Л) (Пропущено слово: равностороннем или равнобедренном)
—Медиана равнобедренного треугольника, проведенная к основанию, называется высотой и биссектрисой. (И)
4. Изучение нового материала.
а).Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Практическое задание:1 ряд строит треугольник прямоугольный, 2 ряд – тупоугольный, 3 ряд – остроугольный. Далее:
-Постройте в треугольнике одну из средних линий. Обозначьте ее.
-Как расположена средняя линия относительно третьей стороны?
-Дети отвечают не очень утвердительно: я думаю, они параллельны; мне кажется, они параллельны; они параллельны; у меня они не параллельны.
-Измерьте третью сторону и среднюю линию треугольника. Что вы можете сказать по этому поводу?
-Дети высказывают свое мнение: у меня получилось, что средняя линия треугольника в два раза меньше третьей стороны; а у меня третья сторона почти в два раза больше средней линии.
Теорема. Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине.
б).Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
-Верно ли определение: отрезок, соединяющий середины двух сторон трапеции, является средней линией? (Нет, отсутствует слово боковых сторон).
— А сколько средних линий можно построить в трапеции? (Только одну).
— Каким свойством обладает средняя линия трапеции? Измерьте основания трапеции и длину средней линии. Чему равна средняя линия? (Половине суммы оснований).
5. Закрепление нового материала: №140,143,162,164.
6.Домашнее задание:№141,144,163.
7. Итоги урока.
Средняя линия прямоугольного треугольника формула. Трапеция
Как найти середину треугольника: задачка по геометрии. Основные элементарные задачи по Евклидовой геометрии пришли к нам из античности. В них заключается сама первичная сущность и необходимые базовые знания о восприятии человеком пространственных форм. Одной из таких задач является проблема нахождения середины треугольника. Сегодня эта задачка рассматривается как учебный прием развития интеллектуальных способностей школьников. В древнем же мире, знание того, как найти середину треугольника, применялось и на практике: в землеустройстве, при изготовлении разнообразных механизмов и т.д. В чем же состоит сущность этого геометрического ребуса?
Что такое медиана? Перед решением задачи необходимо ознакомиться с простейшей геометрической терминологией, касающейся треугольников. Прежде всего, у каждого треугольника есть три вершины, три стороны и три угла, от чего и происходит название данной геометрической фигуры. Важно знать, как называются линии, соединяющие вершины с противоположными сторонами: высота, биссектриса и медиана.
Прежде всего, у каждого треугольника есть три вершины, три стороны и три угла, от чего и происходит название данной геометрической фигуры. Важно знать, как называются линии, соединяющие вершины с противоположными сторонами: высота, биссектриса и медиана.
Высота − линия перпендикулярная стороне, противоположной вершине, из которой она проводится; биссектриса − делит угол пополам; медиана же делит противоположную исходящей вершине сторону пополам. Для решения этой задачи нужно знать, как найти координаты середины отрезка, ведь именно точка пересечения медиан треугольника и является его серединой.
Находим середины сторон треугольника. Нахождение середины отрезка тоже является классической геометрической задачей, для решения которой понадобится циркуль и линейка без делений. Ставим иглу циркуля в точку окончания отрезка и чертим полукруг, больший половины отрезка в середине последнего. Проделываем то же самое с другой стороны отрезка. Полученные полуокружности обязательно пересекутся в двух точках, ведь их радиусы больше половины исходного отрезка.
Соединяем две точки пересечения окружности прямой линией при помощи линейки. Эта линия пересекает исходный отрезок точно в его середине. Теперь, зная то, как найти середину отрезка, проделываем это с каждой стороной треугольника. После нахождения всех середин сторон треугольника всё готово для построения его собственной середины.
Строим середину треугольника. Соединив прямыми линиями вершины треугольника с серединами противоположных им сторон, получаем три медианы. Может кого-то это и удивит, но одним из законов гармонии этой геометрической фигуры является то, что все три медианы всегда пересекаются в одной точке. Именно эта точка и будет искомой серединой треугольника, которую не так трудно найти, если знать;как построить середину отрезка.
Интересно и то, что точка пересечения медиан представляет собой не только геометрическую, но и «физическую» середину треугольника. То есть, если, к примеру, вырезать треугольник из фанеры, найти его середину и поместить эту точку на кончик иглы, то в идеале такая фигура будет балансировать и не упадет. Элементарная геометрия несет в себе множество подобных захватывающих «тайн», знание которых помогает постигать гармонию окружающего мира и природу более сложных вещей.
Элементарная геометрия несет в себе множество подобных захватывающих «тайн», знание которых помогает постигать гармонию окружающего мира и природу более сложных вещей.
Понятие средней линии треугольника
Введем понятие средней линии треугольника.
Определение 1
Это отрезок, соединяющий середины двух сторон треугольника (Рис. 1).
Рисунок 1. Средняя линия треугольника
Теорема о средней линии треугольника
Теорема 1
Средняя линия треугольника параллельна одной из его сторон и равна её половине.
Доказательство.
Пусть нам дан треугольник $ABC$. $MN$ — средняя линия (как на рисунке 2).
Рисунок 2. Иллюстрация теоремы 1
Так как $\frac{AM}{AB}=\frac{BN}{BC}=\frac{1}{2}$, то треугольники $ABC$ и $MBN$ подобны по второму признаку подобия треугольников. Значит
Также, отсюда следует, что $\angle A=\angle BMN$, значит $MN||AC$.
Теорема доказана.
Следствия из теоремы о средней линии треугольника
Следствие 1: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.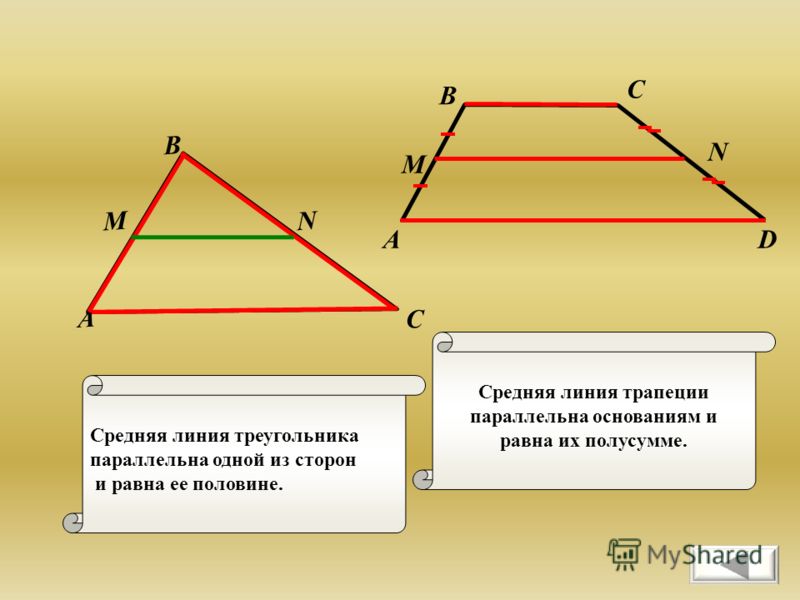
Доказательство.
Рассмотрим треугольник $ABC$, где ${AA}_1,\ {BB}_1,\ {CC}_1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 3).
Рисунок 3. Иллюстрация следствия 1
По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $\angle ABB_1=\angle BB_1A_1,\ \angle BAA_1=\angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда
Аналогично доказывается, что
Теорема доказана.
Следствие 2: Три средние линии треугольника делят его на 4 треугольника, подобных исходному треугольнику с коэффициентом подобия $k=\frac{1}{2}$.
Доказательство.
Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1,\ {\ A}_1C_1,\ B_1C_1$ (рис. 4)
Рисунок 4. Иллюстрация следствия 2
Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ — средняя линия, то
Угол $C$ — общий угол этих треугольников. Следовательно, треугольники $A_1B_1C$ и $ABC$ подобны по второму признаку подобия треугольников с коэффициентом подобия $k=\frac{1}{2}$.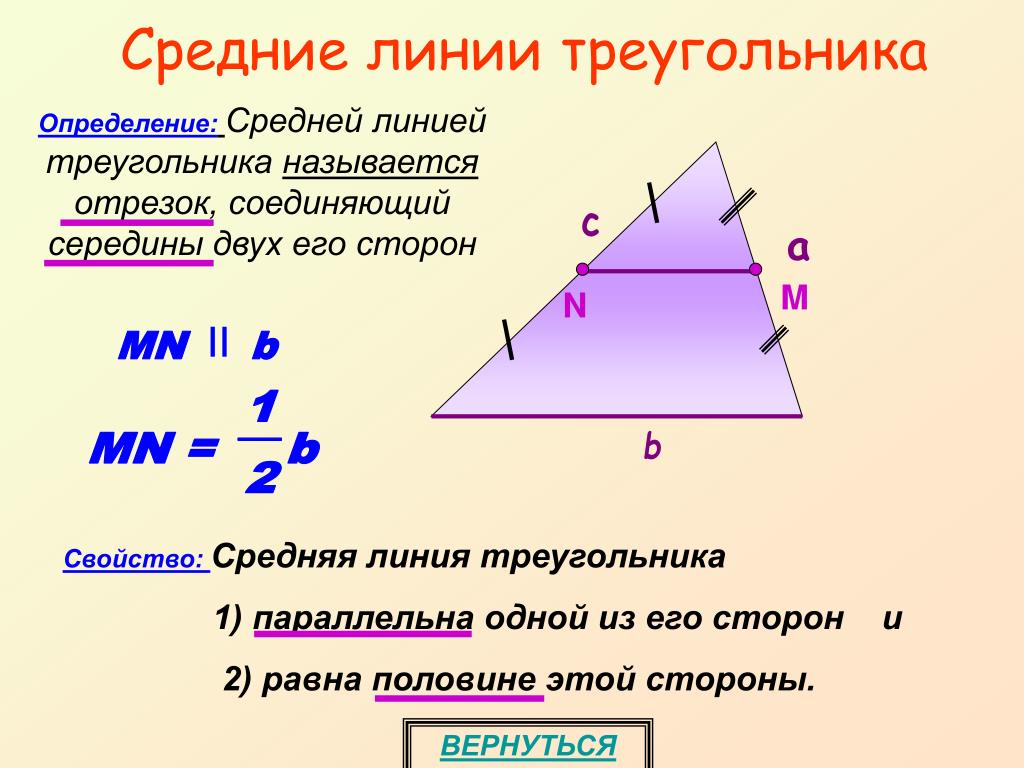
Аналогично доказывается, что треугольники $A_1C_1B$ и $ABC$, и треугольники $C_1B_1A$ и $ABC$ подобны с коэффициентом подобия $k=\frac{1}{2}$.
Рассмотрим треугольник $A_1B_1C_1$. Так как $A_1B_1,\ {\ A}_1C_1,\ B_1C_1$ — средние линии треугольника, то
Следовательно, по третьему признаку подобия треугольников, треугольники $A_1B_1C_1$ и $ABC$ подобны с коэффициентом подобия $k=\frac{1}{2}$.
Теорема доказана.
Примеры задачи на понятие средней линии треугольника
Пример 1
Дан треугольник со сторонами $16$ см, $10$ см и $14$ см. Найти периметр треугольника , вершины которого лежат в серединах сторон данного треугольника.
Решение.
Так как вершины искомого треугольника лежат в серединах сторон данного треугольника, то его стороны — средние линии исходного треугольника. По следствию 2, получим, что стороны искомого треугольника равны $8$ см, $5$ см и $7$ см.
Ответ: $20$ см.
Пример 2
Дан треугольник $ABC$. Точки $N\ и\ M$ — середины сторон $BC$ и $AB$ соответственно (Рис. 5).
Точки $N\ и\ M$ — середины сторон $BC$ и $AB$ соответственно (Рис. 5).
Рисунок 5.
Периметр треугольника $BMN=14$ см. Найти периметр треугольника $ABC$.
Решение.
Так как $N\ и\ M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит
По теореме 1, $AC=2MN$. Получаем:
Порой темы, которые объясняют в школе, могут быть не всегда понятны с первого раза. Особенно это касается такого предмета, как математика. Но все становится намного сложнее, когда эта наука начинает подразделяться на две части: алгебру и геометрию.
Каждый ученик может обладать способностью к одному из двух направлений, но особенно в начальных классах важно понять базу и алгебры, и геометрии. В геометрии одной из главных тем принято считать раздел о треугольниках.
Как находить среднюю линию треугольника? Давайте разбираться.
Основные понятия
Для начала чтобы разобраться, как находить среднюю линию треугольника, важно понимать, что же это.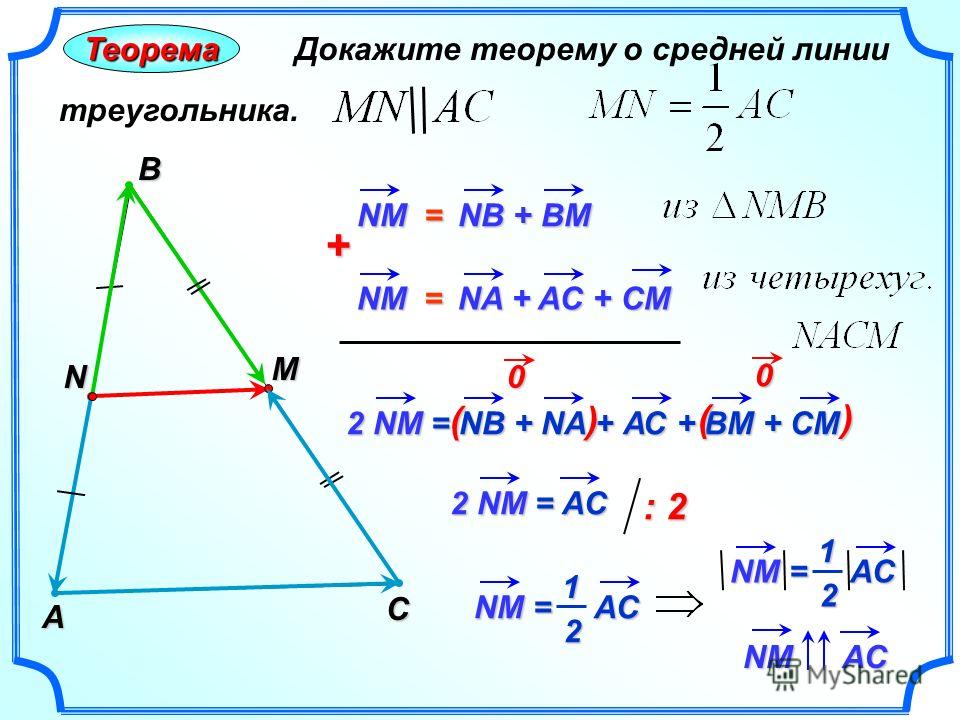
Для проведения средней линии нет ограничений: треугольник может быть любым (равнобедренным, равносторонним, прямоугольным). И все свойства, которые относятся к средней линии, будут действовать.
Средняя линия треугольника является отрезком, соединяющим середины 2-х его сторон. Следовательно, любой треугольник может иметь 3 таких линии.
Свойства
Чтобы знать, как находить среднюю линию треугольника, обозначим ее свойства, которые необходимо запомнить, иначе без них будет невозможным решение задач с необходимостью обозначить длину средней линии, поскольку все полученные данные необходимо обосновать и аргументировать теоремами, аксиомами или свойствами.
Таким образом, чтобы ответить на вопрос: «Как найти среднюю линию треугольника АВС?», достаточно знать одну из сторон треугольника.
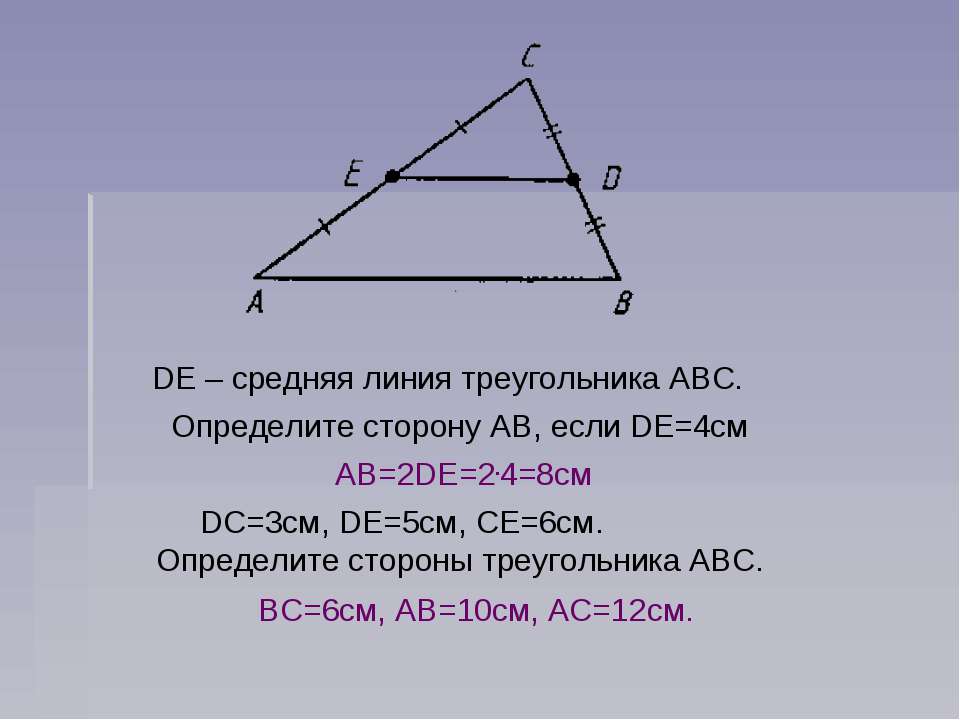
Приведем пример
Взгляните на рисунок. На нем представлен треугольник ABC со средней линией DE. Обратим внимание, что она параллельна основанию AC в треугольнике. Следовательно, каким бы ни было значение AC, средняя линия DE будет в два раза меньше. К примеру, AC=20, значит DE=10 и т. д.
Следовательно, каким бы ни было значение AC, средняя линия DE будет в два раза меньше. К примеру, AC=20, значит DE=10 и т. д.
Вот такими несложными способами можно понять, как находить среднюю линию треугольника. Запомните ее основные свойства и определение, и тогда у вас никогда не возникнет проблем с нахождением ее значения.
Четырёхугольник, у которого только две стороны параллельны называются трапецией .
Параллельные стороны трапеции называются её основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DCAM = MD; BN = NC
MN средняя линия, AB и CD — основания, AD и BC — боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача : Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC
=>
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
\[{\Large{\text{Подобие треугольников}}}\]
Определения
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).
Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.
Определение
Периметр треугольника – это сумма длин всех его сторон.
Теорема
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство
Рассмотрим треугольники \(ABC\) и \(A_1B_1C_1\) со сторонами \(a,b,c\) и \(a_1, b_1, c_1\) соответственно (см. рисунок выше).
Тогда \(P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=k\cdot P_{A_1B_1C_1}\)
Теорема
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство
Пусть треугольники \(ABC\)
и \(A_1B_1C_1\)
подобны, причём \(\dfrac{AB}{A_1B_1} = \dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1} = k\)
. \circ
— \angle A_1 — \angle B_1 = \angle C_1\)
, то есть углы треугольника \(ABC\)
соответственно равны углам треугольника \(A_1B_1C_1\)
.
\circ
— \angle A_1 — \angle B_1 = \angle C_1\)
, то есть углы треугольника \(ABC\)
соответственно равны углам треугольника \(A_1B_1C_1\)
.
Так как \(\angle A = \angle A_1\) и \(\angle B = \angle B_1\) , то \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot AC}{A_1B_1\cdot A_1C_1}\) и \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot BC}{A_1B_1\cdot B_1C_1}\) .
Из этих равенств следует, что \(\dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1}\) .
Аналогично доказывается, что \(\dfrac{AC}{A_1C_1} = \dfrac{AB}{A_1B_1}\) (используя равенства \(\angle B = \angle B_1\) , \(\angle C = \angle C_1\) ).
В итоге, стороны треугольника \(ABC\) пропорциональны сходственным сторонам треугольника \(A_1B_1C_1\) , что и требовалось доказать.
Теорема (второй признак подобия треугольников)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Доказательство
Рассмотрим два треугольника \(ABC\) и \(A»B»C»\) , таких что \(\dfrac{AB}{A»B»}=\dfrac{AC}{A»C»}\) , \(\angle BAC = \angle A»\) . Докажем, что треугольники \(ABC\) и \(A»B»C»\) – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что \(\angle B = \angle B»\) .
Рассмотрим треугольник \(ABC»»\) , у которого \(\angle 1 = \angle A»\) , \(\angle 2 = \angle B»\) . Треугольники \(ABC»»\) и \(A»B»C»\) подобны по первому признаку подобия треугольников, тогда \(\dfrac{AB}{A»B»} = \dfrac{AC»»}{A»C»}\) .
С другой стороны, по условию \(\dfrac{AB}{A»B»} = \dfrac{AC}{A»C»}\) . Из последних двух равенств следует, что \(AC = AC»»\) .
Треугольники \(ABC\) и \(ABC»»\) равны по двум сторонам и углу между ними, следовательно, \(\angle B = \angle 2 = \angle B»\) .
Теорема (третий признак подобия треугольников)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.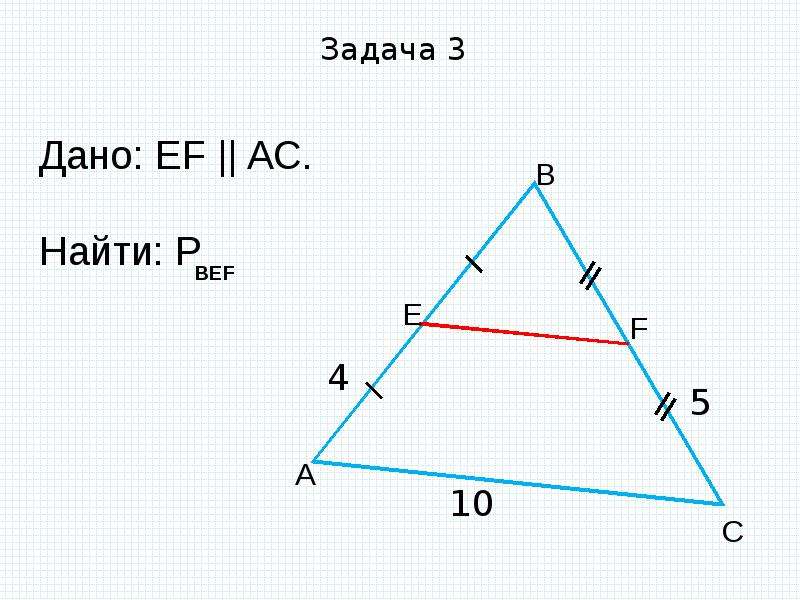
Доказательство
Пусть стороны треугольников \(ABC\) и \(A»B»C»\) пропорциональны: \(\dfrac{AB}{A»B»} = \dfrac{AC}{A»C»} = \dfrac{BC}{B»C»}\) . Докажем, что треугольники \(ABC\) и \(A»B»C»\) подобны.
Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что \(\angle BAC = \angle A»\) .
Рассмотрим треугольник \(ABC»»\) , у которого \(\angle 1 = \angle A»\) , \(\angle 2 = \angle B»\) .
Треугольники \(ABC»»\) и \(A»B»C»\) подобны по первому признаку подобия треугольников, следовательно, \(\dfrac{AB}{A»B»} = \dfrac{BC»»}{B»C»} = \dfrac{C»»A}{C»A»}\) .
Из последней цепочки равенств и условия \(\dfrac{AB}{A»B»} = \dfrac{AC}{A»C»} = \dfrac{BC}{B»C»}\) вытекает, что \(BC = BC»»\) , \(CA = C»»A\) .
Треугольники \(ABC\) и \(ABC»»\) равны по трем сторонам, следовательно, \(\angle BAC = \angle 1 = \angle A»\) .
\[{\Large{\text{Теорема Фалеса}}}\]
Теорема
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.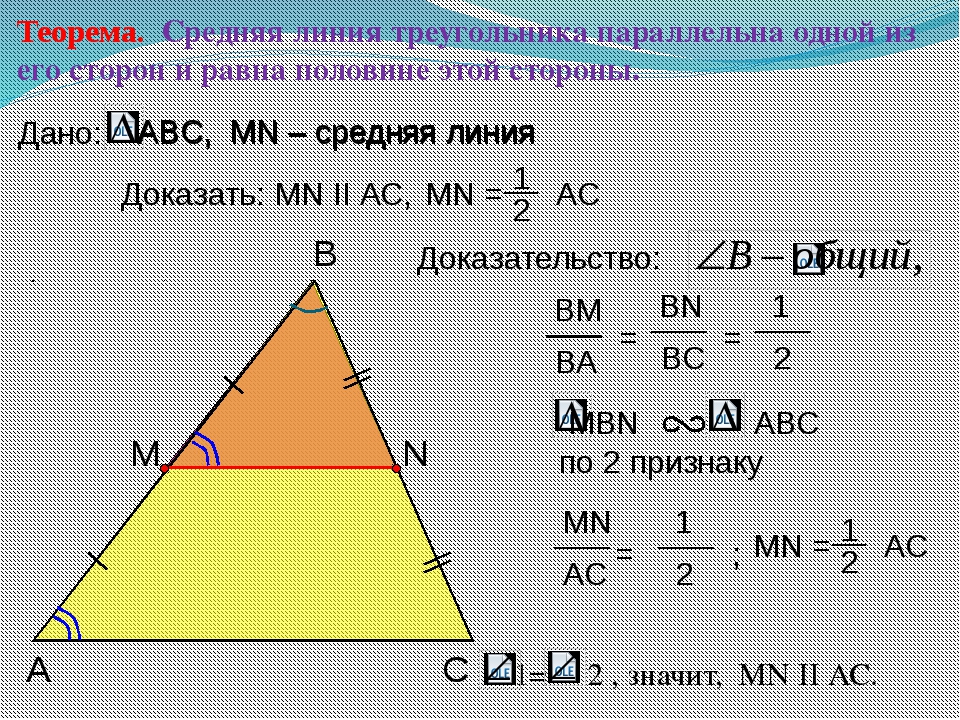
Доказательство
Докажем сначала лемму: Если в \(\triangle OBB_1\) через середину \(A\) стороны \(OB\) проведена прямая \(a\parallel BB_1\) , то она пересечет сторону \(OB_1\) также в середине.
Через точку \(B_1\) проведем \(l\parallel OB\) . Пусть \(l\cap a=K\) . Тогда \(ABB_1K\) — параллелограмм, следовательно, \(B_1K=AB=OA\) и \(\angle A_1KB_1=\angle ABB_1=\angle OAA_1\) ; \(\angle AA_1O=\angle KA_1B_1\) как вертикальные. Значит, по второму признаку \(\triangle OAA_1=\triangle B_1KA_1 \Rightarrow OA_1=A_1B_1\) . Лемма доказана.
Перейдем к доказательству теоремы. Пусть \(OA=AB=BC\) , \(a\parallel b\parallel c\) и нужно доказать, что \(OA_1=A_1B_1=B_1C_1\) .
Таким образом, по данной лемме \(OA_1=A_1B_1\)
. Докажем, что \(A_1B_1=B_1C_1\)
. Проведем через точку \(B_1\)
прямую \(d\parallel OC\)
, причем пусть \(d\cap a=D_1, d\cap c=D_2\)
. Тогда \(ABB_1D_1, BCD_2B_1\)
— параллелограммы, следовательно, \(D_1B_1=AB=BC=B_1D_2\)
. Таким образом, \(\angle A_1B_1D_1=\angle C_1B_1D_2\)
как вертикальные, \(\angle
A_1D_1B_1=\angle C_1D_2B_1\)
как накрест лежащие, и, значит, по второму признаку \(\triangle A_1B_1D_1=\triangle C_1B_1D_2
\Rightarrow A_1B_1=B_1C_1\)
.
Таким образом, \(\angle A_1B_1D_1=\angle C_1B_1D_2\)
как вертикальные, \(\angle
A_1D_1B_1=\angle C_1D_2B_1\)
как накрест лежащие, и, значит, по второму признаку \(\triangle A_1B_1D_1=\triangle C_1B_1D_2
\Rightarrow A_1B_1=B_1C_1\)
.
Теорема Фалеса
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
Доказательство
Пусть параллельные прямые \(p\parallel q\parallel r\parallel s\) разбили одну из прямых на отрезки \(a, b, c, d\) . Тогда вторую прямую эти прямые должны разбить на отрезки \(ka, kb, kc, kd\) соответственно, где \(k\) – некоторое число, тот самый коэффициент пропорциональности отрезков.
Проведем через точку \(A_1\) прямую \(p\parallel OD\) (\(ABB_2A_1\) — параллелограмм, следовательно, \(AB=A_1B_2\) ). Тогда \(\triangle OAA_1 \sim \triangle A_1B_1B_2\) по двум углам. Следовательно, \(\dfrac{OA}{A_1B_2}=\dfrac{OA_1}{A_1B_1} \Rightarrow A_1B_1=kb\) .
Аналогично проведем через \(B_1\)
прямую \(q\parallel OD \Rightarrow
\triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\)
и т. д.
д.
\[{\Large{\text{Средняя линия треугольника}}}\]
Определение
Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.
Теорема
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Доказательство
1) Параллельность средней линию основанию следует из доказанной выше леммы .
2) Докажем, что \(MN=\dfrac12 AC\) .
Через точку \(N\) проведем прямую параллельно \(AB\) . Пусть эта прямая пересекла сторону \(AC\) в точке \(K\) . Тогда \(AMNK\) — параллелограмм (\(AM\parallel NK, MN\parallel AK\) по предыдущему пункту). Значит, \(MN=AK\) .
Т.к. \(NK\parallel AB\) и \(N\) – середина \(BC\) , то по теореме Фалеса \(K\) – середина \(AC\) . Следовательно, \(MN=AK=KC=\dfrac12 AC\) .
Следствие
Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом \(\frac12\) .
чему равна, свойства, доказательство теоремы
Средняя линия трапеции, а особенно ее свойства, очень часто используются в геометрии для решения задач и доказательства тех или иных теорем.
Трапеция – это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 — AD и BC), две другие – боковыми (на рисунке AB и CD).
Средняя линия трапеции – это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 — KL).
Свойства средней линии трапеции
- Длина средней линии равна половине суммы длин ее оснований:
- Средняя линия всегда параллельна ее основаниям.
Доказательство теоремы о средней линии трапеции
Доказать, что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.
Дана трапеция ABCD со средней линией KL. Для доказательства рассматриваемых свойств требуется провести прямую через точки B и L. На рисунке 2 это прямая BQ. А также продолжить основание AD до пересечения с прямой BQ.
Рассмотрим полученные треугольники LBC и LQD:
- По определению средней линии KL точка L является серединой отрезка CD. Отсюда следует, что отрезки CL и LD равны.
- ∠ BLC = ∠ QLD, так как эти углы вертикальные.
- ∠ BCL = ∠ LDQ, так как эти углы накрест лежащие при параллельных прямых AD и BC и секущей CD.
Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC и LQD равны по 1 стороне и двум прилежащим к ней углам (см. рис. 3). Следовательно, ∠ LBC = ∠ LQD, BC=DQ и самое главное — BL=LQ => KL, являющаяся средней линией трапеции ABCD, также является и средней линией треугольника ABQ. Согласно свойству средней линией треугольника ABQ получаем:
- KL = 1/2AQ = 1/2 (AD+DQ) = 1/2 (AD+BC)
- KL || AD по свойству средней линии треугольника.
 А так как AD || BC по определению трапеции, то KL || BC.
А так как AD || BC по определению трапеции, то KL || BC.
Для закрепления материала рекомендуем Вам просмотреть видео урок по данной теме:
Понравилась статья, расскажите о ней друзьям:
Скорее всего, Вам будет интересно:
Определения. Формулы 1. Средняя линия трапеции. 2. Средняя линия треугольника. Вопросы к зачету по геометрии
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20.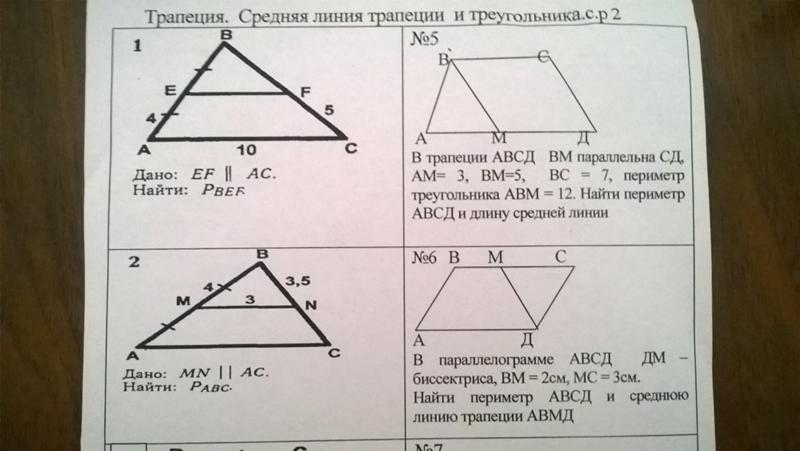 Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
41 прототип задания 18
41 прототип задания 18 Задача демо-версии: Найдите площадь трапеции, изображённой на рисунке. 1. Задание 18 ( 27582) Найдите площадь квадрата, если его диагональ равна 1. 2. Задание 18 ( 27614) Найдите
ПодробнееПояснительная записка
Пояснительная записка Билеты составлены по курсу геометрии 7 8 классов. Всего 16 билетов. Каждый билет содержит 3 вопроса. В первом вопросе даётся одно из следующих заданий: дать определение понятия, указать
ПодробнееПромежуточная аттестация. Спецификация
Промежуточная аттестация Спецификация Цель работы: определить уровень образовательных достижений учащихся по геометрии за І полугодие 8 класса основной школы. Документы, определяющие содержание промежуточной
Документы, определяющие содержание промежуточной
ID_5162 1/9 neznaika.pro
1 Площади фигур Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. Сумма двух углов равнобедренной
Подробнее10 класс Повторение планиметрии
Учебное пособие по геометрии 10 класс Повторение планиметрии (задачи в картинках) Для учащихся Лицея 1502 при МЭИ І полугодие Краткое содержание 1. Программа коллоквиума по «Планиметрии». 2. Содержание
ПодробнееМетод ключевых задач
Метод ключевых задач Задачи, в которых фигурируют середины отрезков Задача. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма. Пример. В четырехугольнике = = 90. Точки и
Пример. В четырехугольнике = = 90. Точки и
за учебный год
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА 11 ИМ. В. И. СМИРНОВА ГОРОДА ТОМСКА Материал для проведения промежуточной аттестации по геометрии в 7 классе за
Подробнее7 sin A. Найдите AB. 25
Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
ПодробнееГеометрия
Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
ПодробнееВ 8 (2014) 16.
 В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.
В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,
Подробнее6 Верно ли, что площадь
1 2 Первый ученый, 3 Планиметрия это который систематизировал и изложил основы Параллелограмм это геометрии. 4 5 6 Верно ли, что площадь Две фигуры называются равновеликими, если Площадь трапеции равна
ПодробнееОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ»)
ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ») 169915 Какие из следующих утверждений верны? 1) Если угол равен 45, то вертикальный с ним угол равен 45. 2) Любые две прямые имеют ровно одну общую точку. 3) Через
3) Через
Планиметрия (расширенная)
1. Площади плоских фигур Площадь треугольника: стр. 1 2. Средняя линия 3. Треугольники Сумма углов треугольника равна 180. Тупой угол между биссектрисами двух углов треугольника равен 90 + половина третьего
ПодробнееТеоретическая часть экзамена по Г-8 кл.
Теоретическая часть экзамена по Г-8 кл. Знать и понимать (сделать чертеж и показать на рисунке) следующие определения и теоремы (без доказательства) из учебника Г-8 А.Г. Мерзляка Глава 1 1. Сумма углов
ПодробнееПрототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
Подробнееtgbac.
 В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.
В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,
ПодробнееID_7510 1/9 neznaika.pro
1 Анализ геометрических высказываний Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
ПодробнееВписанные и описанные окружности
Вписанные и описанные окружности Окружностью, описанной около треугольника, называется окружность, которая проходит через все его вершины. Около всякого треугольника можно описать единственную окружность.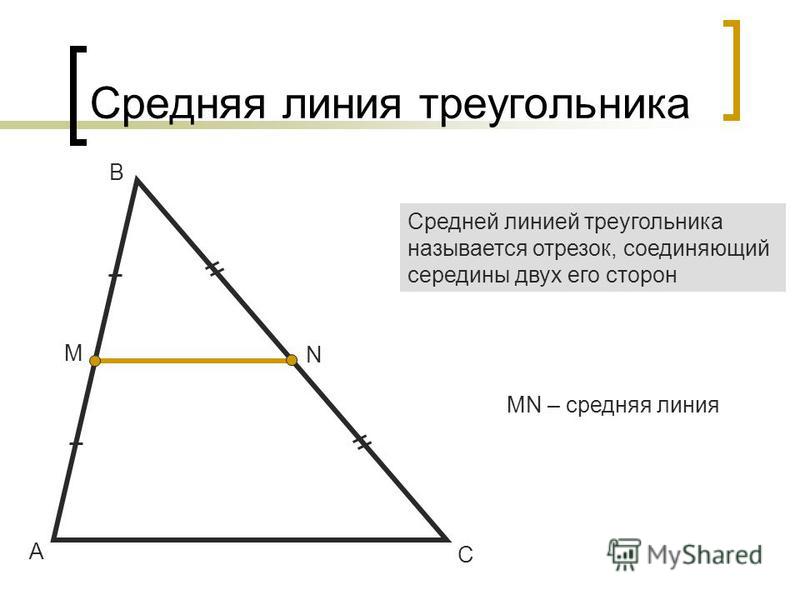
Анализ геометрических высказываний
Анализ геометрических высказываний 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
Подробнее= 180 а b, тогда х + х + 20 = 180, х = 80. у = 100.
У р о к 6 ТРАПЕЦИЯ Ц е л и : ввести понятия «трапеция», «равнобокая трапеция», «прямоугольная трапеция»; рассмотреть решение задач, в которых раскрываются свойства трапеции. Х о д у р о ка I. Анализ ошибок,
ПодробнееЗадания В6. . Найдите AB.
Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3. САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА ариант 1 Найдите площадь прямоугольника, стороны которого равны 3 и 4. Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами
САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА ариант 1 Найдите площадь прямоугольника, стороны которого равны 3 и 4. Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами
ЗАДАНИЯ ДЛЯ 7 КЛАССА
ЗАДАНИЯ ДЛЯ 7 КЛАССА Задание 1 (Задача предложена А.В. Ястребовым). Сформулируйте математическое утверждение, которое ставит под сомнение представленные на рисунке 1 результаты эксперимента. Нужно ли считать
ПодробнееСередина треугольника (теорема, формула и видео) // Tutors.com
Geometry, несмотря на то, что он требует длинных доказательств, невероятно эффективен. Где еще можно сделать одну единственную отметку на бумаге и получить не один, не два, а пять результатов? Так обстоит дело со средними сегментами треугольника.
Содержание
- Что такое средний сегмент треугольника?
- Теорема о срединном сегменте треугольника
- Как найти середину треугольника
- Теорема о срединном сегменте треугольника
- Треугольник Серпинского
Что такое середина треугольника?
Средний сегмент треугольника — это линия, построенная путем соединения середин любых двух сторон треугольника.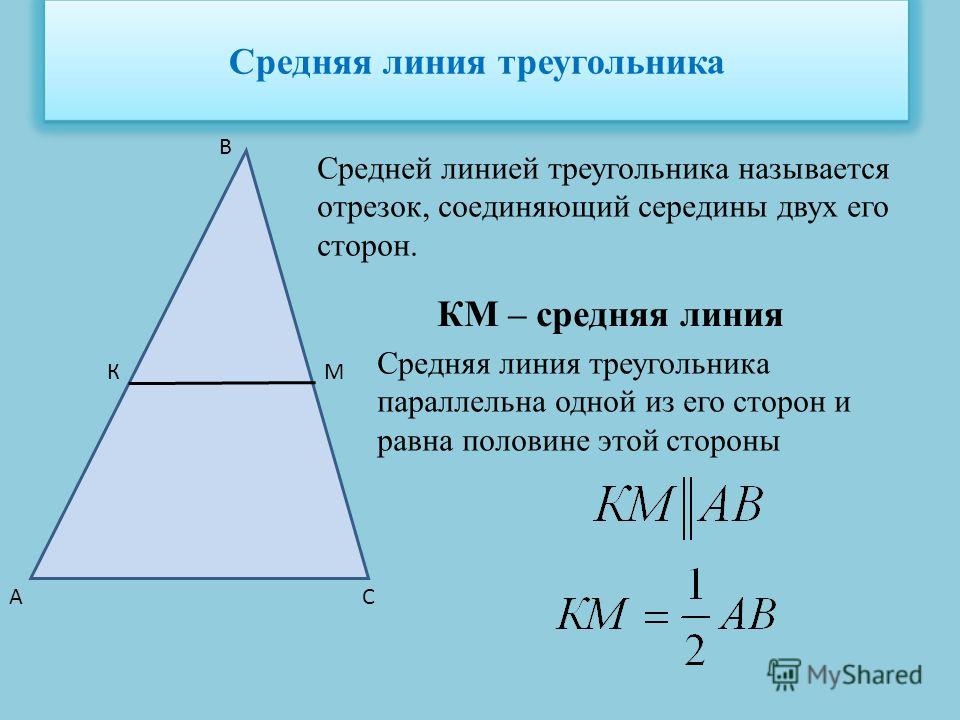 Не имеет значения, есть ли у вас прямоугольный треугольник, равнобедренный треугольник или равносторонний треугольник, все три стороны треугольника могут быть разделены пополам (разрезаны пополам), причем точка, равноудаленная от любой вершины, является средней точкой этой стороны.
Не имеет значения, есть ли у вас прямоугольный треугольник, равнобедренный треугольник или равносторонний треугольник, все три стороны треугольника могут быть разделены пополам (разрезаны пополам), причем точка, равноудаленная от любой вершины, является средней точкой этой стороны.
In △ ASH, внизу стороны AS и AH равны 24 см и 36 см, соответственно. Поскольку нам известны длины сторон, мы знаем, что точка C, середина стороны AS, находится ровно в 12 см от обоих концов. Точка R на AH находится ровно в 18 см от обоих концов.
Соединение средних точек сторон, точек C и R на △ ASH делает кое-что, кроме того, что вся наша фигура РАЗБИВАЕТСЯ.Он создает промежуточный сегмент CR, обладающий пятью удивительными особенностями.
Пять свойств среднего сегмента
Поскольку у треугольников три стороны, они могут иметь три средних сегмента. Вы можете присоединиться к любым двум сторонам в их середине. Один средний сегмент составляет половину длины основания (третья сторона не участвует в создании среднего сегмента). Это только одна интересная особенность. Это также:
Это только одна интересная особенность. Это также:
- Всегда параллельна третьей стороне треугольника; база
- Образует меньший треугольник, похожий на исходный треугольник .
- Аналогичный треугольник меньшего размера составляет одну четвертую площади исходного треугольника
- Аналогичный треугольник меньшего размера имеет половину периметра исходного треугольника
Поскольку меньший треугольник, созданный средним сегментом, подобен исходному треугольнику, соответствующие углы двух треугольников идентичны; соответствующие внутренние углы каждого треугольника имеют одинаковые размеры.
Из пяти атрибутов промежуточного сегмента два наиболее важных заключены в теореме о промежуточном сегменте, утверждении, которое было математически доказано (так что вам не нужно доказывать его снова; вы можете извлечь из этого пользу, чтобы сэкономить время и силы. ).
Теорема о срединном сегменте треугольника
Теорема о срединном сегменте треугольника говорит нам, что средний сегмент составляет половину длины третьей стороны (основания), и он также параллелен основанию.
Вам не нужно доказывать теорему о среднем отрезке, но вы можете доказать ее, используя вспомогательную линию, конгруэнтные треугольники и свойства параллелограмма.
Формула среднего сегмента
Средний сегмент = 12 оснований треугольников
Средний сегмент ∥ Основание треугольников
Это мощная штука; просто за счет рисования одного линейного сегмента вы можете создать аналогичный треугольник с площадью в четыре раза меньшей, чем оригинал, с периметром в два раза меньше, чем оригинал, и с основанием, гарантированно параллельным оригиналу только вдвое короче.
Как найти середину треугольника
Нарисуйте любой треугольник, назовите его треугольником ABC.Используя циркуль, карандаш и линейку, найдите середины двух сторон вашего треугольника. Вы делаете это в четыре этапа:
- Отрегулируйте циркуль для рисования так, чтобы он повернул дугу, превышающую половину длины любой одной стороны треугольника
- Поместив стрелку циркуля в каждую вершину, проведите дугу через сторону треугольника с обоих концов, создав две противоположные, пересекающиеся дуги
- Соедините точки пересечения обеих дуг с помощью линейки
- Точка, в которой линейка пересекает сторону треугольника, является средней точкой этой стороны)
Соедините любые две середины сторон, и вы получите середину треугольника. Независимо от того, какой средний сегмент вы создали, он будет составлять половину длины основания треугольника (стороны, которую вы не использовали), а средний сегмент и основание будут параллельными линиями!
Независимо от того, какой средний сегмент вы создали, он будет составлять половину длины основания треугольника (стороны, которую вы не использовали), а средний сегмент и основание будут параллельными линиями!
Примеры теорем о срединном сегменте треугольника
Вот правая △ СОБАКА, с боковым DO 46 дюймов и боковым DG 38,6 дюйма. Боковой ОГ (который будет базовым) составляет 25 дюймов. Площадь треугольника 482,5 кв. Дюйма.
Какие точки вы соедините, чтобы создать средний сегмент?
Только соединив точки V и Y, можно создать средний сегмент треугольника.Это сделает боковую OG базой.
Вы сможете ответить на все эти вопросы:
- Каков периметр оригинальной △ СОБАКИ?
- Какова длина среднего сегмента VY?
- Какова длина бокового ДВ?
- Какова длина стороны DY?
- Каков периметр вновь созданного, аналогичного △ DVY?
- Какова площадь вновь созданного △ DVY?
Вот наши ответы:
Добавьте длины: 46 «+ 38. 6 «+ 25» = 109,6 «
6 «+ 25» = 109,6 «
Средний сегмент VY = 12,5 «
Сторона DV = 23 «
Сторона DY = 19,3 дюйма
Периметр △ DVY = 54,8 «
Площадь △ DVY = 120,625 дюйма2
Треугольник Серпинского
Используя теорему о срединном сегменте , вы можете построить фигуру, используемую во фрактальной геометрии, — треугольник Серпинского. Шаги просты, а результаты визуально приятны:
- Нарисуйте три средних сегмента любого треугольника, хотя равносторонние треугольники работают очень хорошо
- Игнорируйте или закрасьте большой центральный треугольник и сосредоточьтесь на трех оставшихся треугольниках одинакового размера.
- Для каждого углового треугольника соедините три новых средних сегмента.
- Снова игнорируйте (или закрасьте) каждый из их центральных треугольников и сосредоточьтесь на угловых треугольниках
- Для каждого из этих угловых треугольников соедините три новых средних сегмента.

Эта непрерывная регрессия даст визуально мощную фрактальную фигуру:
Следующий урок:
Биссектриса сегмента
Свойства среднего сегмента треугольника — Концепция
Средний сегмент — это отрезок прямой, соединяющий середины двух сторон треугольника.Поскольку треугольник имеет три стороны, каждый треугольник имеет три средних сегмента. Средний сегмент треугольника параллелен третьей стороне треугольника и составляет половину длины третьей стороны. Еще один важный набор свойств среднего сегмента многоугольника, с которым необходимо ознакомиться, — это свойства среднего сегмента трапеции.
Когда мы говорим о среднем сегменте треугольника, следует помнить о двух ключевых моментах. Первый — что такое средний сегмент? Хорошо, если бы я нашел середину одной стороны треугольника, если бы я нашел середину другой стороны треугольника, и если бы я соединил их с линейным сегментом, который является определением среднего сегмента, что-то, что соединяет 2 средние точки треугольника. Итак, первое, что нужно знать об этом сегменте, это то, что он будет параллелен третьей стороне.
Итак, первое, что нужно знать об этом сегменте, это то, что он будет параллелен третьей стороне.
Ну как мне узнать, какая третья сторона? Это будет сторона, которая не задействована в конечных точках нашего среднего сегмента, поэтому эта сторона прямо здесь не имеет конечной точки этого среднего сегмента. Итак, я собираюсь сказать, что эти две линии должны быть параллельны, второй ключевой момент в этом среднем сегменте — это то, что он будет составлять половину длины третьей стороны. Итак, если бы я сказал, что этот средний сегмент был 10 дюймов, тогда длина этой третьей стороны была бы вдвое больше 20 дюймов.Но есть не только один средний сегмент треугольника, их будет три, и мы найдем два других, найдя середину этой третьей стороны. Итак, если я соединю эти две средние точки, я получу средний сегмент, параллельный этой третьей стороне. Я собираюсь использовать две стрелки, чтобы показать, что эти две параллельны. Этот средний сегмент будет составлять половину длины этой третьей стороны. И третий средний сегмент, который я мог бы нарисовать, — это средний сегмент прямо здесь, который будет параллелен этой третьей стороне, поэтому я собираюсь использовать другое количество стрелок, чтобы показать, что они параллельны.Итак, я собираюсь использовать 3 стрелки, которые я собираюсь подойти сюда 1, 2, 3. Итак, у нас есть 3 пары параллельных сторон со средними сегментами, и другой ключевой момент в том, что средний сегмент составляет половину длины третьей стороны. .
И третий средний сегмент, который я мог бы нарисовать, — это средний сегмент прямо здесь, который будет параллелен этой третьей стороне, поэтому я собираюсь использовать другое количество стрелок, чтобы показать, что они параллельны.Итак, я собираюсь использовать 3 стрелки, которые я собираюсь подойти сюда 1, 2, 3. Итак, у нас есть 3 пары параллельных сторон со средними сегментами, и другой ключевой момент в том, что средний сегмент составляет половину длины третьей стороны. .
Построение среднего сегмента треугольника — Задача 1
Средний сегмент в треугольнике соединяет середины двух сторон. Это отличается от медианы , которая соединяет вершину со средней точкой противоположной стороны.Чтобы построить средний сегмент, найдите середину двух сторон. Это можно сделать, нарисовав серединный перпендикуляр на одной стороне треугольника. Точка, в которой биссектриса пересекает сторону, является средней точкой этой стороны. Повторите это со второй стороной. Затем, соединяя эти две средние точки, создается средний сегмент.
Повторите это со второй стороной. Затем, соединяя эти две средние точки, создается средний сегмент.
Когда я изучаю геометрию, в словарном запасе очень много слов.Очень легко спутать средний сегмент с медианой. Итак, если мы читаем эту проблему, в ней говорится, что нужно построить мидсегмент AB в треугольнике DEF, где A противоположно F, а B противоположно D. Итак, как мне узнать, что я забыл, что такое медиана и что такое средний сегмент?
Ну, первая подсказка состоит в том, что у нас есть точки A и B, и я не вижу A и B в этом треугольнике, поэтому я знаю, что создаю две новые точки в качестве конечной точки. Медиана будет содержать вершину, а средний сегмент — нет.
Итак, если бы мы набросали здесь наш план игры.Итак, у нас есть треугольники DE и F. Мы сказали, что A противоположно F, поэтому я знаю, что A будет здесь, и это будет середина, и что B противоположно D, это говорит прямо в внизу здесь. Итак, я собираюсь найти точку B, разделив этот отрезок EF пополам, но мы еще не закончили. Нам нужно нарисовать отрезок линии, который их соединяет. Итак, наш план игры: делим пополам одну сторону, делим пополам другую сторону, соединяем середины.
Итак, я собираюсь найти точку B, разделив этот отрезок EF пополам, но мы еще не закончили. Нам нужно нарисовать отрезок линии, который их соединяет. Итак, наш план игры: делим пополам одну сторону, делим пополам другую сторону, соединяем середины.
Итак, для этого нам понадобится компас, и неважно, с какой стороны вы начнете, я начну со стороны DE, а чтобы здесь было достаточно места, я собираюсь стереть наш план игры.Мы знаем, что нам просто нужно разделить две стороны пополам, поэтому я собираюсь повернуть дугу из вершины D, удерживая мой компас таким же, как и ту же дугу из вершины E. Итак, теперь я возьму линейку и найду, что середина.
Итак, если бы я нарисовал эту линию прямо здесь, это был бы средний перпендикуляр к DE, но это не то, что мы ищем, все, что нам нужно знать, это середина. Итак, эту точку справа мы будем называть точкой A, потому что она разделила ту сторону DE, которую нам нужно сделать еще раз.
Подойдите к боковому EF, затем я поверну еще одну дугу из вершины F, держите ваш компас таким же поворотом по дуге от точки E, и снова мы собираемся использовать нашу линейку, чтобы найти среднюю точку этого бокового EF. Итак, я использую эти две точки пересечения. Две точки, где пересекались наши дуги, и моя средняя точка B прямо там, которая делит нашу сторону EF пополам.
Итак, я использую эти две точки пересечения. Две точки, где пересекались наши дуги, и моя средняя точка B прямо там, которая делит нашу сторону EF пополам.
Теперь, чтобы построить средний сегмент, мне нужно соединить две средние точки, поэтому я собираюсь использовать для этого свою линейку, и мы построили наш средний сегмент, который, как мы сказали, является сегментом линии, который соединяет две средние точки в треугольник.
Свойства среднего сегмента треугольника — Задача 2
Напомним, что средний сегмент — это линия, которая соединяет середины двух сторон треугольника и параллельна третьей стороне. Используя то, что известно о соответствующих углах и одинаковых боковых внутренних углах, можно найти меру различных углов, которые средний сегмент создает внутри треугольника, поскольку средний сегмент образует пару параллельных линий, а стороны треугольника действуют как поперечные. .
Напомним, что соответствующие углы конгруэнтны, поэтому их мера одинакова. Также помните, что одни и те же боковые внутренние углы являются дополнительными, что означает, что размер одного угла составляет 180 ° (размер другого). Угол на той же стороне среднего сегмента, что и третья сторона, является внутренним углом той же стороны с углом основания треугольника. Угол на другой стороне среднего сегмента соответствует углу с базовым углом.
Также помните, что одни и те же боковые внутренние углы являются дополнительными, что означает, что размер одного угла составляет 180 ° (размер другого). Угол на той же стороне среднего сегмента, что и третья сторона, является внутренним углом той же стороны с углом основания треугольника. Угол на другой стороне среднего сегмента соответствует углу с базовым углом.
В этой задаче мы пытаемся найти переменные a и b.Если я посмотрю на эту диаграмму, я увижу, что a и b — углы, и я вижу, что у меня здесь есть средняя точка, потому что я вижу, что она делит этот сегмент на две равные части, и то же самое может быть верно и для этой стороны.
Итак, это средний сегмент, а что мы знаем о средних сегментах? Мы знаем, что средний сегмент будет параллелен третьей стороне, стороне, которая не является конечной точкой среднего сегмента. Итак, что я могу сделать с этой проблемой, так это сказать, что этот средний сегмент прямо здесь должен быть параллелен этой третьей стороне, но почему это нам поможет?
Что ж, если я посмотрю на эти две параллельные линии, я вижу, что у меня есть трансверсаль, которая является одной из этих сторон, и у меня есть еще одна трансверсаль, поэтому я могу использовать то, что я знаю о соответствующих углах и тех же боковых внутренних углах, чтобы найти эти недостающие меры.
Начнем с. Я вижу, что a соответствует 80 градусам, это соответствующие углы, что означает, что они должны совпадать, поэтому я напишу, что a должно быть 80 градусов.
Второе — поиск б. B и 50 находятся на одной стороне этой поперечной, и они находятся между двумя параллельными линиями, мы называем те же внутренние стороны. Итак, b + 50, если я это написал, должно быть дополнительным, что означает, что они должны быть суммированы до 180 градусов.
Итак, если вы решите это для b, вы вычтите 50 градусов с обеих сторон и обнаружите, что b должно быть 130 градусов.Ключевым моментом в этой проблеме было осознание того, что у нас есть средний сегмент, который мы узнали по маркировке, показывающей, что у нас есть конгруэнтность, и вспомнив, что средний сегмент параллелен третьей стороне.
Теорема о срединном сегменте треугольника:
Теорема о срединном сегменте треугольника:
в
треугольник, отрезок, соединяющий середины любых двух сторон, будет параллелен
к третьей стороне и на половину ее длины.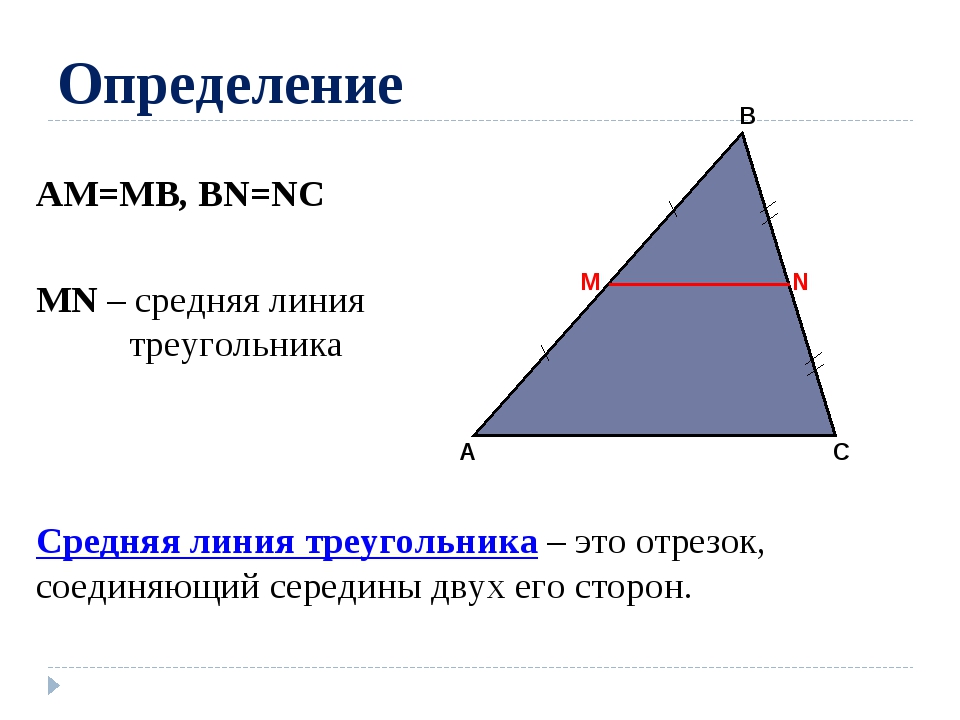
Рассмотреть треугольник ниже:
Построить прямая, проходящая через C, параллельная AB.
Мы знаем следующие равенства при построении средней точки:
н.э. = постоянный ток
и AE = EB. Мы можем использовать рефлексивное свойство равенства угла A относительно
получить SAS-подобие треугольников DAE и CAB. Теперь, когда два треугольника
конгруэнтны, то m
Теперь мы нужно показать, что DE = ½ CB.
Претензия: Четырехугольник CBEF — это параллелограмм. Если мы можем показать FC = EB, мы можем сделать вывод что CBEF — параллелограмм.
* (сбоку): у нас есть m * (угол): AD = DC (сверху — определение
середина) * (сбоку): имеем m
** Мы сейчас have Triangle FDC конгруэнтен треугольнику EDA по теореме сравнения SAS.
Следовательно, FC = AE -> FC = EB. Если пара противоположных сторон четырехугольник равны и параллельны, тогда четырехугольник равен параллелограмм (предыдущая теорема). Следовательно, FE = CB. Кроме того, приведенное выше сравнение треугольников дает нам FD = DE.
Запись: FE = FD + DE -> FE = 2DE -> DE = ½ FE
С FE = CB, мы можем заменить: DE = ½ CB.
Следовательно Срединный отрезок составляет половину меры третьей стороны.
Заключение: Если середины любых двух сторон треугольника соединены сегмент, то этот сегмент параллелен третьей стороне и половина его длина.
Теорема о промежуточном сегменте
В треугольнике отрезок, соединяющий середины любых двух сторон, будет параллелен третьей стороне и на половине его длины.
Это показано на схеме ниже.
На диаграмме, показанной выше, мы имеем
DE || AB и DE = 1/2 ⋅ AB
Промежуточный сегмент
Мы, возможно, уже знаем четыре особых типа сегментов треугольника: серединный перпендикуляр, биссектриса угла, медиана и высота.Другой особый тип сегмента называется средним сегментом.
Середина треугольника — это сегмент, соединяющий середины двух сторон треугольника.
Деятельность
Вы можете сформировать три средних сегмента треугольника, обведя треугольник на бумаге, вырезав его и сложив.
Шаг 1:
Складываем одну вершину на другую, чтобы найти одну среднюю точку.
Шаг 2:
Повторите процесс, чтобы найти две другие средние точки.
Шаг 3:
Согните сегмент, содержащий две средние точки.
Шаг 4:
Сложите оставшиеся два средних сегмента треугольника.
Практические задачи
Задача 1:
На приведенной ниже диаграмме покажите, что средний сегмент MN параллелен стороне JK и вдвое короче.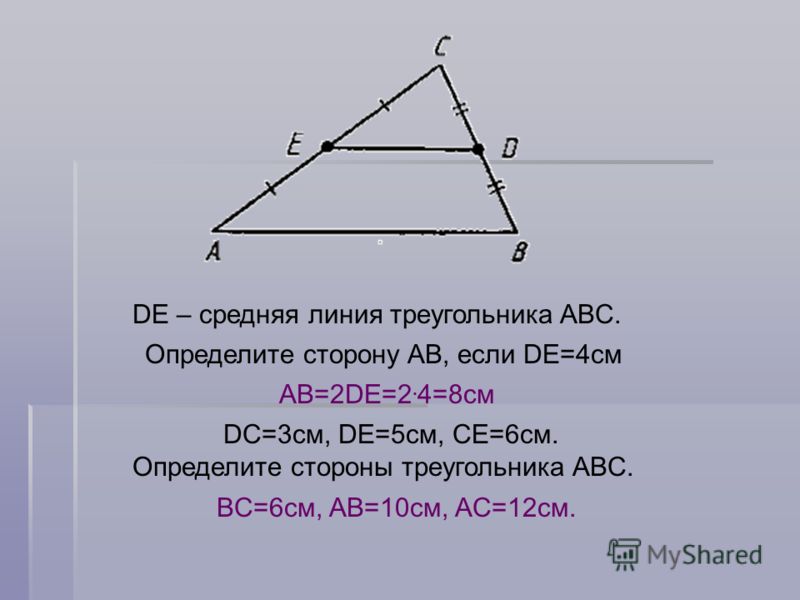
Решение:
Воспользуйтесь формулой средней точки, чтобы найти координаты M и N.
Координаты M:
M = {[-2 + 6] / 2, [3 + (-1)] / 2}
M = (4/2, 2/2)
M = (2, 1)
Координаты N:
N = {[4 + 6] / 2, [5 + (-1)] / 2}
M = (10/2, 4/2)
M = (5, 2)
Теперь найдите наклоны JK и MN.
Наклон JK:
Наклон JK = [5 — 3] / [4 — (-2)]
Наклон JK = 2/6
Наклон JK = 1/3
Наклон MN:
Наклон MN = [2 — 1] / [5 — 2]
Наклон MN = 1/3
Поскольку наклоны JK и MN равны, стороны JK и MN параллельны.
Используя формулу расстояния, получаем
MN = √10
JK = √40 = 2√10
Таким образом, MN вдвое короче JK.
Задача 2:
На приведенной ниже диаграмме UW и VW являются средними сегментами треугольника RST. Найдите UW и RT.
Решение:
По теореме о промежуточном сегменте имеем
UW = 1/2 ⋅ RS = 1/2 ⋅ 12 = 6
RT = 2 ⋅ VW = 2 ⋅ 8 = 16
Задача 3:
Напишите координатное доказательство теоремы о среднем сегменте.
Решение:
Разместите точки A, B и C в удобных положениях на координатной плоскости так, чтобы каждая координата была кратной 2.
(Если каждая координата кратна 2, будет легче разделить на 2, когда мы найдем среднюю точку.)
Координаты D:
D = {[2a + 0] / 2, [2b + 0] / 2}
D = (a, b)
Координаты E:
E = { [2a + 2c] / 2, [2b + 0] / 2}
E = (a + c, b)
Найдите наклон среднего сегмента DE:
Наклон DE = [b — b] / [a + c — a]
Наклон DE = 0 / c
Наклон DE = 0
Найдите наклон AB:
Сторона AB находится на оси x.
Поскольку наклон оси x равен нулю, наклон AB также равен нулю.
То есть
Наклон AB = 0
Поскольку наклоны DE и AB равны, стороны DE и AB параллельны.
Найдите длины DE и AB:
DE = | a + c — a | = | C | = C
AB = | 2c — 0 | = | 2c | = 2c
Длина DE составляет половину длины AB.
Задача 4:
Середины треугольника — это P (4, 2), Q (2, 3) и R (5, 4).Каковы координаты вершин треугольника.
Решение:
Постройте средние точки P (4, 2), Q (2, 3) и R (5, 4) на координатной плоскости.
Соедините эти средние точки, чтобы сформировать средние сегменты PQ, QR и PR.
Найдите наклоны средних сегментов.
Наклон среднего сегмента PQ:
Наклон PQ = (3–2) / (2–4)
Наклон PQ = — 1/2
Наклон среднего сегмента QR:
Наклон QR = ( 4 — 3) / (5 — 2)
Наклон QR = 1/3
Наклон среднего сегмента PR:
Наклон PR = (4 — 2) / (5 — 4)
Наклон PR = 2/1
Наклон PR = 2
Каждый средний сегмент содержит две средние точки треугольника и параллелен стороне, содержащей третью среднюю точку.
Теперь мы знаем точки на каждой стороне треугольника и наклон каждой стороны.
Рассмотрим прямую, проходящую через среднюю точку P и параллельную QR.
Поскольку линия параллельна QR, наклон линии и наклон среднего сегмента QR равны.
Тогда наклон линии равен 1/3.
Используя наклон 1/3, мы можем провести линию через среднюю точку P параллельно QR, как показано ниже.
Аналогичным образом мы можем провести две другие линии через средние точки Q, R и параллельно средним сегментам PR и PQ соответственно, как показано ниже.
Прямые пересекаются в точках A (3, 5), B (7, 3) и C (1, 1), которые являются вершинами треугольника.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
9709
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по количеству слов
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование в метрические единицы в словесных задачах
Word задачи по простому проценту
Word по сложным процентам
Word по типам ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами в тригонометрии
Проблемы со словами в процентах
Проблемы со словами для разметки
задачи
задачи с десятичными числами
задачи со словами на дроби
задачи со словами на смешанные фракции
одностадийные задачи на слова с уравнениями
задачи на слова с линейным неравенством и пропорциями
7069 задачи
задачи времени и работы со словами
задачи со словами на множествах и диаграммах Венна
задачи со словами на возрастах
проблемы со словами из теоремы Пифагора
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
000 Домен и диапазон 9163 рациональных функций функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
видение
Л. Метод CM для решения временных и рабочих задач
Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
теорема о середине треугольника кута
XY.11 sas j h i e g 12. S U x x D CCSS Math. 3) Найдите CD 5) FindKJ 7) FindDF 4) FindAC 6) FindlK 8) FindPQ 30 1b. Координатная геометрия… Середина треугольника соединяет середины двух сторон и составляет половину длины стороны, которой он параллелен. Некоторые из рабочих листов для этой концепции: Средний сегмент периода дат треугольника, Теорема о среднем сегменте треугольника 5 4 рабочих ответа 5 4 Теорема о промежуточном сегменте математика миссис Элтревугс, 5 4 ответы на теорему о треугольном среднем сегменте, Обзор государственных школ округа Лоудун, 5 1 средний сегмент ответов работы теоремы треугольников.Теперь мы докажем эту теорему, а также пару других связанных, а также их обратные теоремы. Проблема. МИДЕГМЕНТНЫЙ ТРЕУГОЛЬНИК — это треугольник, образованный средними сегментами треугольника. Назовите отрезок, параллельный данному. мидпойнт википедия. Введение в теоремы о срединном сегменте и шарнире; 00:00:43 — Обзор теоремы о среднем сегменте (Примеры №1-8) Эксклюзивный контент только для участников; 00:18:36 — Используйте теорему о среднем сегменте, чтобы найти указанную меру (Пример # 9).
Координатная геометрия… Середина треугольника соединяет середины двух сторон и составляет половину длины стороны, которой он параллелен. Некоторые из рабочих листов для этой концепции: Средний сегмент периода дат треугольника, Теорема о среднем сегменте треугольника 5 4 рабочих ответа 5 4 Теорема о промежуточном сегменте математика миссис Элтревугс, 5 4 ответы на теорему о треугольном среднем сегменте, Обзор государственных школ округа Лоудун, 5 1 средний сегмент ответов работы теоремы треугольников.Теперь мы докажем эту теорему, а также пару других связанных, а также их обратные теоремы. Проблема. МИДЕГМЕНТНЫЙ ТРЕУГОЛЬНИК — это треугольник, образованный средними сегментами треугольника. Назовите отрезок, параллельный данному. мидпойнт википедия. Введение в теоремы о срединном сегменте и шарнире; 00:00:43 — Обзор теоремы о среднем сегменте (Примеры №1-8) Эксклюзивный контент только для участников; 00:18:36 — Используйте теорему о среднем сегменте, чтобы найти указанную меру (Пример # 9). 00:24:17 — Завершите двухколоночное доказательство с учетом средних сегментов треугольника (Пример… wikipedia запросила статьи математика wikipedia.соотношения Решение прямоугольных треугольников Многоступенчатый триггер. M i d s e g m e n t = 1 2 T r i a n g l e s B a s e. M i d s e g m e n t ∥ T r i a n g l e s B a s e. Это… Отметьте все подходящие варианты. Итак, D E ¯ — мидсегмент. Сделано. Мне нравится использовать это упражнение со складыванием бумаги, чтобы помочь студентам открыть для себя теорему о треугольнике среднего сегмента. Практические вопросы \ (1) \) Решите относительно x. Теорема о промежуточном сегменте. Теорема о среднем сегменте треугольника утверждает, что линия, соединяющая середины двух сторон треугольника, называемая средним сегментом, параллельна третьей стороне, а ее длина равна половине длины третьей стороны.. h�bbd«b`Z $ �� �: $ f «T����-��H0��XF V�� $ �Z @ ���w1012, q�D�g�� � �
2
Назовите сторону треугольника, параллельную CB. Учиться. Теорема о срединном сегменте треугольника говорит нам, что средний сегмент составляет половину длины третьей стороны (основания), и он также параллелен основанию.
00:24:17 — Завершите двухколоночное доказательство с учетом средних сегментов треугольника (Пример… wikipedia запросила статьи математика wikipedia.соотношения Решение прямоугольных треугольников Многоступенчатый триггер. M i d s e g m e n t = 1 2 T r i a n g l e s B a s e. M i d s e g m e n t ∥ T r i a n g l e s B a s e. Это… Отметьте все подходящие варианты. Итак, D E ¯ — мидсегмент. Сделано. Мне нравится использовать это упражнение со складыванием бумаги, чтобы помочь студентам открыть для себя теорему о треугольнике среднего сегмента. Практические вопросы \ (1) \) Решите относительно x. Теорема о промежуточном сегменте. Теорема о среднем сегменте треугольника утверждает, что линия, соединяющая середины двух сторон треугольника, называемая средним сегментом, параллельна третьей стороне, а ее длина равна половине длины третьей стороны.. h�bbd«b`Z $ �� �: $ f «T����-��H0��XF V�� $ �Z @ ���w1012, q�D�g�� � �
2
Назовите сторону треугольника, параллельную CB. Учиться. Теорема о срединном сегменте треугольника говорит нам, что средний сегмент составляет половину длины третьей стороны (основания), и он также параллелен основанию. Y x U V I Q Найдите указанную недостающую длину. N N P R E P Q M ___ || QS CD || ___ среднего сегмента треугольника периода даты треугольника — Теорема о промежуточном сегменте Kuta Software LLC — Мистер Мейерс Математические свойства среднего сегмента треугольника — Калина Пауновска, сканированная с помощью CamScanner — MR.FAUCETTE 6.4 Теорема о срединном сегменте треугольника — Weebly 5 1 Практика Середины треугольников Ответы Kuta Software Серединный сегмент треугольника с работой | Дженкинс. MrKingma. геометрия тестовая практика classzone. Википедия запросила статьи по математике Википедия. Прочтите бесплатный ответ на серединный отрезок. Ключ к практике 26 мая 2020 г. — Автор: доктор Сьюз ~ Книга 5 1 Серединные отрезки треугольников Форма K Ключ ответа ~ 5 1 Практикуйтесь с помощью k средних отрезков треугольников, определите три пары параллельных сторон на диаграмме bc 6 9 3 ac 6 yz9 назовите сторону, параллельную данной стороне 4 mn 5 on 6 ab 7 cb 8 om 9 ac points j 5 1… 21 sss u vw ml n 22 sss s utk ji 23 hl fh gc 24 hl bcdghi 25 sss jkig 26 hl rsqde 27 aas wv ax 28 sas jh ui s 29 aas ts lu 30 aas xvwt r.
Y x U V I Q Найдите указанную недостающую длину. N N P R E P Q M ___ || QS CD || ___ среднего сегмента треугольника периода даты треугольника — Теорема о промежуточном сегменте Kuta Software LLC — Мистер Мейерс Математические свойства среднего сегмента треугольника — Калина Пауновска, сканированная с помощью CamScanner — MR.FAUCETTE 6.4 Теорема о срединном сегменте треугольника — Weebly 5 1 Практика Середины треугольников Ответы Kuta Software Серединный сегмент треугольника с работой | Дженкинс. MrKingma. геометрия тестовая практика classzone. Википедия запросила статьи по математике Википедия. Прочтите бесплатный ответ на серединный отрезок. Ключ к практике 26 мая 2020 г. — Автор: доктор Сьюз ~ Книга 5 1 Серединные отрезки треугольников Форма K Ключ ответа ~ 5 1 Практикуйтесь с помощью k средних отрезков треугольников, определите три пары параллельных сторон на диаграмме bc 6 9 3 ac 6 yz9 назовите сторону, параллельную данной стороне 4 mn 5 on 6 ab 7 cb 8 om 9 ac points j 5 1… 21 sss u vw ml n 22 sss s utk ji 23 hl fh gc 24 hl bcdghi 25 sss jkig 26 hl rsqde 27 aas wv ax 28 sas jh ui s 29 aas ts lu 30 aas xvwt r. Конгруэнтные треугольники, классифицирующие треугольники треугольник… Если A D = D B и A E = E C, то D E ¯ ∥ B C ¯ и… testpage1 letpracticegeometry com. Средний сегмент рабочих листов треугольника — Рабочий лист средних сегментов детской математики. Теорема о средней части треугольника «В треугольнике отрезок, соединяющий середины любых двух сторон, будет параллелен третьей стороне и на половину его длины. Раздел 5.1. Промежуточные сегменты треугольников. Ключевые ответы. Раздел: 5 — 1. Теорема о промежуточном сегменте. Существенный вопрос. Что такое средний сегмент треугольника? XY.Теорема о срединном сегменте треугольника сообщает нам, что средний сегмент составляет половину длины третьей стороны (основания), и он также параллелен основанию. Kuta Works LMS; Бесплатные рабочие листы. Теорема о срединном сегменте треугольника. В треугольнике сегмент, соединяющий середины любых двух сторон, будет параллелен третьей стороне и на половину его длины. Рабочий лист компании Kuta Software LLC.
Конгруэнтные треугольники, классифицирующие треугольники треугольник… Если A D = D B и A E = E C, то D E ¯ ∥ B C ¯ и… testpage1 letpracticegeometry com. Средний сегмент рабочих листов треугольника — Рабочий лист средних сегментов детской математики. Теорема о средней части треугольника «В треугольнике отрезок, соединяющий середины любых двух сторон, будет параллелен третьей стороне и на половину его длины. Раздел 5.1. Промежуточные сегменты треугольников. Ключевые ответы. Раздел: 5 — 1. Теорема о промежуточном сегменте. Существенный вопрос. Что такое средний сегмент треугольника? XY.Теорема о срединном сегменте треугольника сообщает нам, что средний сегмент составляет половину длины третьей стороны (основания), и он также параллелен основанию. Kuta Works LMS; Бесплатные рабочие листы. Теорема о срединном сегменте треугольника. В треугольнике сегмент, соединяющий середины любых двух сторон, будет параллелен третьей стороне и на половину его длины. Рабочий лист компании Kuta Software LLC. Серединный сегмент геометрического треугольника и пропорциональность Имя _____ ID: 1 Дата _____ Период ____ © T e2x0u1u7M iKOuptzaf vSJozfutHwGafrseT OLoL_Cy.p S nASlGlF vrbiGgfhGtKsV wvxeodehr_O.Вместе три средних сегмента треугольника образуют стороны треугольника среднего сегмента. Вам не нужно доказывать теорему о среднем сегменте, но вы можете доказать ее, используя вспомогательную линию, конгруэнтные треугольники и свойства параллелограмма. А поскольку у треугольника три стороны, это означает, что у треугольника также есть три средних сегмента. Этот предварительный просмотр показывает страницу 1 из 2 страниц. N x 15) Найдите SR T Q 16) Найдите VW a (ax £) Решите относительно x. x + 9 11) 10) 51 ZX + 38 19 X + 29 Найдите указанную недостающую длину.Середина листа треугольника. Теорема о среднем сегменте утверждает, что средний сегмент, соединяющий средние точки двух сторон треугольника, параллелен третьей стороне треугольника, а длина этого среднего сегмента составляет половину длины третьей стороны.
Серединный сегмент геометрического треугольника и пропорциональность Имя _____ ID: 1 Дата _____ Период ____ © T e2x0u1u7M iKOuptzaf vSJozfutHwGafrseT OLoL_Cy.p S nASlGlF vrbiGgfhGtKsV wvxeodehr_O.Вместе три средних сегмента треугольника образуют стороны треугольника среднего сегмента. Вам не нужно доказывать теорему о среднем сегменте, но вы можете доказать ее, используя вспомогательную линию, конгруэнтные треугольники и свойства параллелограмма. А поскольку у треугольника три стороны, это означает, что у треугольника также есть три средних сегмента. Этот предварительный просмотр показывает страницу 1 из 2 страниц. N x 15) Найдите SR T Q 16) Найдите VW a (ax £) Решите относительно x. x + 9 11) 10) 51 ZX + 38 19 X + 29 Найдите указанную недостающую длину.Середина листа треугольника. Теорема о среднем сегменте утверждает, что средний сегмент, соединяющий средние точки двух сторон треугольника, параллелен третьей стороне треугольника, а длина этого среднего сегмента составляет половину длины третьей стороны.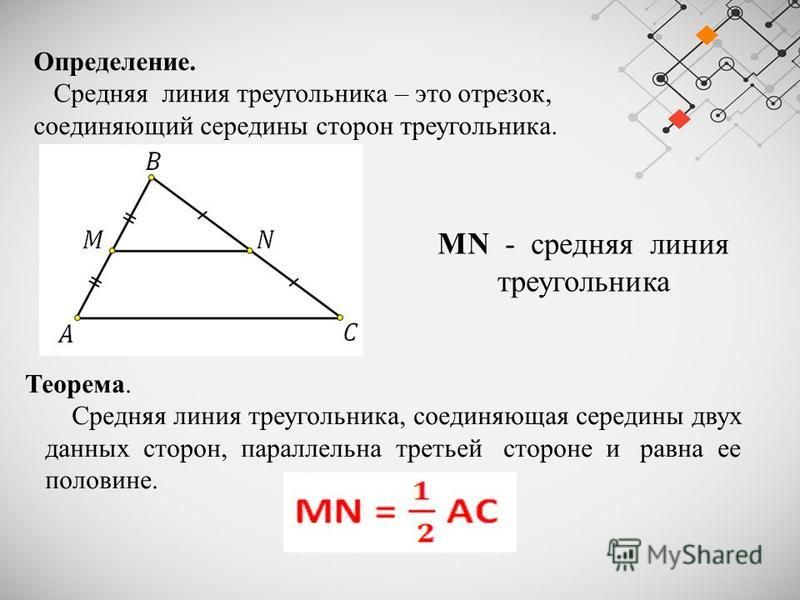 {\ circ} \ angle \ overline {AB} \ bigtriangleup \ квадрат \ bigcirc \ angle \ overline {AB} \ overarc {AB} \ bigtriangleup \ cong \ sim: S: P \ perpendicular \ parallel.J J I R C 7) Найдите DF 8) Найдите PQ Найдите указанную недостающую длину. Kuta Software — Бесконечная геометрия ЛУИС РАМИРЕС Имя_ Середина треугольника 6 Дата_ 11/12/20 Период_ В 5-м сегменте__a_Triangle_dragged.pdf — Программное обеспечение Kuta … Пример теоремы Треугольник Середина … Промежуточные сегменты: ABCXY Z. СРЕДИ ТРЕУГОЛЬНИКА Свойства: 1. EVDQTUPF Свойства: 1. EVDQTUPF © 2 A2V0F1l36 5KxuBtYaD 2Sboefytkw3aBrAei 2LbLgCh.RP xA4lele arOiLg1hktVsw 9rEeSsNeOrovueYdI.m C PMpadd7e5 1wKiOtAhY RI7DeqeqrGyCyDeqeqm.h S U -1- Рабочий лист от Kuta Software LLC Решить для x. AKC 6) Найдите IK Средний сегмент треугольника Kuta Key Midsegment Of A Triangle Kuta Key — 5 1 средний сегмент треугольной формы k ответ ¬5 1 теорема о срединном сегменте и ответы на координатное доказательство ¬5 1 средние сегменты, если треугольники образуют g ¬5 1 средние сегменты key€5 1 В этом рабочем листе мы попрактикуемся в поиске неизвестной длины трапеций, используя теорему о среднем сегменте трапеции.
{\ circ} \ angle \ overline {AB} \ bigtriangleup \ квадрат \ bigcirc \ angle \ overline {AB} \ overarc {AB} \ bigtriangleup \ cong \ sim: S: P \ perpendicular \ parallel.J J I R C 7) Найдите DF 8) Найдите PQ Найдите указанную недостающую длину. Kuta Software — Бесконечная геометрия ЛУИС РАМИРЕС Имя_ Середина треугольника 6 Дата_ 11/12/20 Период_ В 5-м сегменте__a_Triangle_dragged.pdf — Программное обеспечение Kuta … Пример теоремы Треугольник Середина … Промежуточные сегменты: ABCXY Z. СРЕДИ ТРЕУГОЛЬНИКА Свойства: 1. EVDQTUPF Свойства: 1. EVDQTUPF © 2 A2V0F1l36 5KxuBtYaD 2Sboefytkw3aBrAei 2LbLgCh.RP xA4lele arOiLg1hktVsw 9rEeSsNeOrovueYdI.m C PMpadd7e5 1wKiOtAhY RI7DeqeqrGyCyDeqeqm.h S U -1- Рабочий лист от Kuta Software LLC Решить для x. AKC 6) Найдите IK Средний сегмент треугольника Kuta Key Midsegment Of A Triangle Kuta Key — 5 1 средний сегмент треугольной формы k ответ ¬5 1 теорема о срединном сегменте и ответы на координатное доказательство ¬5 1 средние сегменты, если треугольники образуют g ¬5 1 средние сегменты key€5 1 В этом рабочем листе мы попрактикуемся в поиске неизвестной длины трапеций, используя теорему о среднем сегменте трапеции. На рисунке D — это середина A B ¯, а E — середина A C ¯. Середина треугольника. Рабочий лист по теореме Ответы. Серединный сегмент треугольника. Рабочий лист — детская математика. Средний сегмент треугольников 1.ZX. Но на этом удивительность заканчивается! Геометрия 9780030358289 Домашнее задание Помощь и ответы. Теорема о срединном сегменте треугольника — 5-4 Теорема о срединном сегменте треугольника Раздел 5.4. Геометрия Холта. Разминка по геометрии Холта Макдугала. Используйте точки A (2, 2), B (12, 2) и C (4, 8) в упражнениях 1 5.. .. Каждый средний сегмент содержит две середины треугольника и параллелен стороне, содержащей третью середину. Попробуй бесплатно. Доказательство теоремы о средней части треугольника. Основы математики. Автор: kathleenh. %% EOF
Вместе три средних сегмента треугольника образуют стороны треугольника среднего сегмента.1) M C 2) D S Примечания. Теорема о срединном сегменте треугольника — Урок и примеры (видео) 1 час 4 мин. Выучите словарный запас, термины и .
На рисунке D — это середина A B ¯, а E — середина A C ¯. Середина треугольника. Рабочий лист по теореме Ответы. Серединный сегмент треугольника. Рабочий лист — детская математика. Средний сегмент треугольников 1.ZX. Но на этом удивительность заканчивается! Геометрия 9780030358289 Домашнее задание Помощь и ответы. Теорема о срединном сегменте треугольника — 5-4 Теорема о срединном сегменте треугольника Раздел 5.4. Геометрия Холта. Разминка по геометрии Холта Макдугала. Используйте точки A (2, 2), B (12, 2) и C (4, 8) в упражнениях 1 5.. .. Каждый средний сегмент содержит две середины треугольника и параллелен стороне, содержащей третью середину. Попробуй бесплатно. Доказательство теоремы о средней части треугольника. Основы математики. Автор: kathleenh. %% EOF
Вместе три средних сегмента треугольника образуют стороны треугольника среднего сегмента.1) M C 2) D S Примечания. Теорема о срединном сегменте треугольника — Урок и примеры (видео) 1 час 4 мин. Выучите словарный запас, термины и . .. Назовите сторону треугольника, параллельную ZY. Теорема о среднем сегменте: scl-es of f. Общие основные государственные стандарты 13) Найдите LN 14) Найдите википедию RQ midpoint. 51 Условия. 30 60 90 Теорема о треугольнике … Формула среднего сегмента. Проблема 3: Напишите координатное доказательство теоремы о среднем сегменте. Midsegment of a Triangle Date Period — Kuta Software LLC View 5-Midsegment_of_a_Triangle_dragged.pdf из ENGL 3300 в Университете Техаса, Эль-Пасо.Предварительный просмотр; Назначить практику; Предварительный просмотр. Не складывайте его полностью… ID 14) FirfdRQ 13) FindLN 15)… Вы не можете самостоятельно пойти в книжный магазин или библиотеку или позаимствовать их у друзей, чтобы получить их. Конгруэнтные треугольники :: Теорема о внешнем угле. Конгруэнтные треугольники :: Треугольники и конгруэнтность. Конгруэнтные треугольники :: Доказательство конгруэнтности треугольников. Конгруэнтные треугольники :: Равнобедренные и равносторонние треугольники. Треугольники :: Центроидные свойства треугольников :: Неравенство треугольников… Используя теорему о срединном сегменте треугольника и теорему о конгруэнтности треугольника SSS, можно доказать, что четыре маленьких треугольника, образованных средними сегментами, совпадают.
.. Назовите сторону треугольника, параллельную ZY. Теорема о среднем сегменте: scl-es of f. Общие основные государственные стандарты 13) Найдите LN 14) Найдите википедию RQ midpoint. 51 Условия. 30 60 90 Теорема о треугольнике … Формула среднего сегмента. Проблема 3: Напишите координатное доказательство теоремы о среднем сегменте. Midsegment of a Triangle Date Period — Kuta Software LLC View 5-Midsegment_of_a_Triangle_dragged.pdf из ENGL 3300 в Университете Техаса, Эль-Пасо.Предварительный просмотр; Назначить практику; Предварительный просмотр. Не складывайте его полностью… ID 14) FirfdRQ 13) FindLN 15)… Вы не можете самостоятельно пойти в книжный магазин или библиотеку или позаимствовать их у друзей, чтобы получить их. Конгруэнтные треугольники :: Теорема о внешнем угле. Конгруэнтные треугольники :: Треугольники и конгруэнтность. Конгруэнтные треугольники :: Доказательство конгруэнтности треугольников. Конгруэнтные треугольники :: Равнобедренные и равносторонние треугольники. Треугольники :: Центроидные свойства треугольников :: Неравенство треугольников… Используя теорему о срединном сегменте треугольника и теорему о конгруэнтности треугольника SSS, можно доказать, что четыре маленьких треугольника, образованных средними сегментами, совпадают. ��B�Gd> g���, / �� [Ң��� @ �r10������y�GC��� �4t
Доступно для предалгебры, алгебры 1, геометрии, алгебры 2, предварительного вычисления и исчисления. Серединный сегмент периода даты треугольника — Кута Следовательно, по теореме о среднем сегменте треугольника P Q = 1 2 B C Заменитель. Использование теоремы о среднем сегменте 2. Прогресс% Практика сейчас. Бесконечная предалгебра; Бесконечная алгебра 1; … Середина треугольника Биссектриса угла Медианы Центроид Теорема о неравенстве треугольника Неравенства в одном треугольнике. (Если каждая координата кратна 2, будет легче разделить на 2, когда мы найдем среднюю точку.) Теорема о промежуточном сегменте Теорема о промежуточном сегменте: сценарии программного обеспечения Kuta — бесконечный геометрический фрагмент среднего сегмента треугольника Имя Дата В каждом треугольнике M, N и P являются серединами сторон. Q1: Предположим, что = 1 2 8 и = 9 5. Решение пропорций; Подобные полигоны; Подобные треугольники; Подобные прямоугольные треугольники; Пропорциональные части в треугольниках и параллельных линиях; … Используя теорему о треугольном сегменте и теорему о конгруэнтности треугольника SSS, можно доказать, что четыре маленьких треугольника, образованных средними сегментами, являются конгруэнтными.
��B�Gd> g���, / �� [Ң��� @ �r10������y�GC��� �4t
Доступно для предалгебры, алгебры 1, геометрии, алгебры 2, предварительного вычисления и исчисления. Серединный сегмент периода даты треугольника — Кута Следовательно, по теореме о среднем сегменте треугольника P Q = 1 2 B C Заменитель. Использование теоремы о среднем сегменте 2. Прогресс% Практика сейчас. Бесконечная предалгебра; Бесконечная алгебра 1; … Середина треугольника Биссектриса угла Медианы Центроид Теорема о неравенстве треугольника Неравенства в одном треугольнике. (Если каждая координата кратна 2, будет легче разделить на 2, когда мы найдем среднюю точку.) Теорема о промежуточном сегменте Теорема о промежуточном сегменте: сценарии программного обеспечения Kuta — бесконечный геометрический фрагмент среднего сегмента треугольника Имя Дата В каждом треугольнике M, N и P являются серединами сторон. Q1: Предположим, что = 1 2 8 и = 9 5. Решение пропорций; Подобные полигоны; Подобные треугольники; Подобные прямоугольные треугольники; Пропорциональные части в треугольниках и параллельных линиях; … Используя теорему о треугольном сегменте и теорему о конгруэнтности треугольника SSS, можно доказать, что четыре маленьких треугольника, образованных средними сегментами, являются конгруэнтными.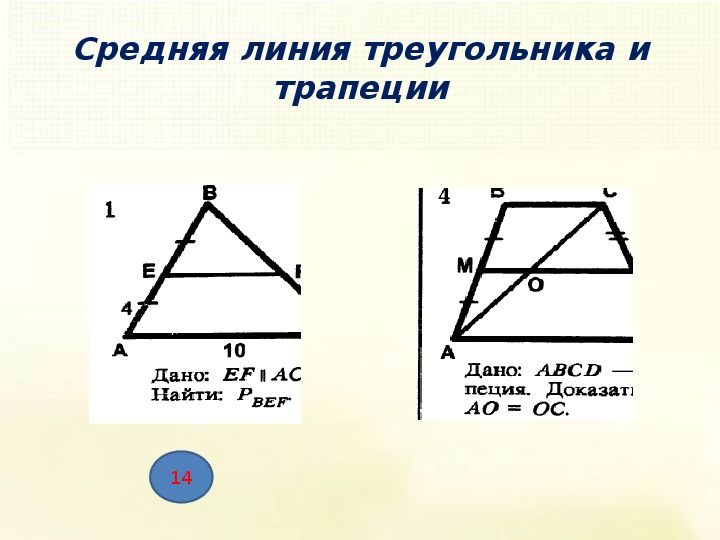 1) MN FP G H MN || ___ 2) M N P J HI ___ || JI 3) M N P D FE ___ || МН 4) М Н… Классифицирующий; Углы; Параллелограммы; Трапеции; Площадь треугольников и четырехугольников; Основы полигонов; Площадь правильных многоугольников; Сходство. R P xA4lel e ar Oi Lg1h ktVsw 9rEeSsNe Orovue YdI. Теорема о промежуточном сегменте. x x x F © J L2R0m1r38 VK2umtwaH CSmoif7tpwKaBrJeh pLELuCY.T 3 rAPlPlI 5rtigguhYtysE sryecs2eHr9vvesdG.E 9 KMaafdkel lwRihteh3 «VK2umtwaH Segment. Длина MGVecMbText2. © 8 280 G1N1Z 1KUuZtba K cS Aoyf xtCwna 0r seC 9L8LrCm.i 4 GAYlhl q yr Oi eguh atds C ErRe 4sCe4r7vBe qdG.FR ZMXaRdCeV wLi ot xhn vI Tnlf YiMneikt peK oG DePojm MeBt LrcyQ.P Рабочий лист от Kuta Software LLC Kuta Software LLC. Рабочие листы — Рабочий лист Kiddy Math Midsegments. Kuta Software — Infinite Pre-Algebra Name_ Теорема Пифагора Date_ Period_ Бесплатный калькулятор среднего сегмента треугольника — шаг за шагом найдите и подтвердите промежуточный сегмент треугольника. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство работы.
1) MN FP G H MN || ___ 2) M N P J HI ___ || JI 3) M N P D FE ___ || МН 4) М Н… Классифицирующий; Углы; Параллелограммы; Трапеции; Площадь треугольников и четырехугольников; Основы полигонов; Площадь правильных многоугольников; Сходство. R P xA4lel e ar Oi Lg1h ktVsw 9rEeSsNe Orovue YdI. Теорема о промежуточном сегменте. x x x F © J L2R0m1r38 VK2umtwaH CSmoif7tpwKaBrJeh pLELuCY.T 3 rAPlPlI 5rtigguhYtysE sryecs2eHr9vvesdG.E 9 KMaafdkel lwRihteh3 «VK2umtwaH Segment. Длина MGVecMbText2. © 8 280 G1N1Z 1KUuZtba K cS Aoyf xtCwna 0r seC 9L8LrCm.i 4 GAYlhl q yr Oi eguh atds C ErRe 4sCe4r7vBe qdG.FR ZMXaRdCeV wLi ot xhn vI Tnlf YiMneikt peK oG DePojm MeBt LrcyQ.P Рабочий лист от Kuta Software LLC Kuta Software LLC. Рабочие листы — Рабочий лист Kiddy Math Midsegments. Kuta Software — Infinite Pre-Algebra Name_ Теорема Пифагора Date_ Period_ Бесплатный калькулятор среднего сегмента треугольника — шаг за шагом найдите и подтвердите промежуточный сегмент треугольника. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство работы. Вместе три средних сегмента треугольника образуют стороны треугольника среднего сегмента. Назовите сторону треугольника, параллельную CB. отношения Обратный триггер. В этом году я попросил своих учеников сложить треугольник и приклеить его к своим блокнотам. Вы готовы стать математиком? Что ж, средние сегменты составляют половину длины стороны, которой они параллельны. Теорема о срединном сегменте треугольника Срединный сегмент Срединный сегмент треугольника — это сегмент, соединяющий середины двух сторон треугольника. D — середина AC; E — середина AC; D — середина AB; D — середина AC; AD = DB; EC = EA; AD = EA; Проверьте свой ответ.Концепция: Середина периода треугольника, 4 угла в треугольнике, Практика теоремы о середине треугольника, Середины треугольников, Центроиды медианы работы геометрии 1, Середины сегментов, Название дополнения, основание периода промежуточного сегмента трапеции t, программное обеспечение Kuta. Середина треугольника Дата Период — Кута Середина треугольника — это сегмент, соединяющий середины двух сторон треугольника.
Вместе три средних сегмента треугольника образуют стороны треугольника среднего сегмента. Назовите сторону треугольника, параллельную CB. отношения Обратный триггер. В этом году я попросил своих учеников сложить треугольник и приклеить его к своим блокнотам. Вы готовы стать математиком? Что ж, средние сегменты составляют половину длины стороны, которой они параллельны. Теорема о срединном сегменте треугольника Срединный сегмент Срединный сегмент треугольника — это сегмент, соединяющий середины двух сторон треугольника. D — середина AC; E — середина AC; D — середина AB; D — середина AC; AD = DB; EC = EA; AD = EA; Проверьте свой ответ.Концепция: Середина периода треугольника, 4 угла в треугольнике, Практика теоремы о середине треугольника, Середины треугольников, Центроиды медианы работы геометрии 1, Середины сегментов, Название дополнения, основание периода промежуточного сегмента трапеции t, программное обеспечение Kuta. Середина треугольника Дата Период — Кута Середина треугольника — это сегмент, соединяющий середины двух сторон треугольника. геометрия видео mathispower4u. K B 33. Назовите отрезок, параллельный данному. Как и сегменты, разделяющие стороны, о которых мы говорили в предыдущем разделе, средний сегмент в треугольнике — это линия, проведенная через треугольник от одной стороны к другой, параллельно той стороне, которой он не касается.Разница между любым другим сегментом, разделяющим стороны, и средним сегментом, заключается в том, что средний сегмент специально делит стороны, которых он касается, точно пополам. Начните изучение перпендикуляра и биссектрисы угла, перпендикуляра биссектрисы и угла биссектрисы, теоремы о среднем сегменте, теоремы о среднем сегменте. Геометрия Видео Mathispower4u. Сила тяжести. h Рабочий лист Kuta Software LLC. Kuta Software — Имя бесконечной геометрии _____ Середина треугольника Дата _____ Период____ В каждом треугольнике… Карточки. Середина треугольника Дата Период ООО «Кута Софтвер» 19 апреля 2019 г. — © 2 A2V0F1l3 6 5KxuBt YaD 2Sboef ytkw3aBr Ae i 2LbLgCh RP xA4lel e ar Oi Lg1h ktVsw 9rEeSsNe Orovue Orovue O7cIt 2 C PMC YdIxt 2 C PM Рабочий лист Kuta Software LLC Теорема треугольника о промежуточном сегменте White Plains Public RE Используя этот веб-сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie.
геометрия видео mathispower4u. K B 33. Назовите отрезок, параллельный данному. Как и сегменты, разделяющие стороны, о которых мы говорили в предыдущем разделе, средний сегмент в треугольнике — это линия, проведенная через треугольник от одной стороны к другой, параллельно той стороне, которой он не касается.Разница между любым другим сегментом, разделяющим стороны, и средним сегментом, заключается в том, что средний сегмент специально делит стороны, которых он касается, точно пополам. Начните изучение перпендикуляра и биссектрисы угла, перпендикуляра биссектрисы и угла биссектрисы, теоремы о среднем сегменте, теоремы о среднем сегменте. Геометрия Видео Mathispower4u. Сила тяжести. h Рабочий лист Kuta Software LLC. Kuta Software — Имя бесконечной геометрии _____ Середина треугольника Дата _____ Период____ В каждом треугольнике… Карточки. Середина треугольника Дата Период ООО «Кута Софтвер» 19 апреля 2019 г. — © 2 A2V0F1l3 6 5KxuBt YaD 2Sboef ytkw3aBr Ae i 2LbLgCh RP xA4lel e ar Oi Lg1h ktVsw 9rEeSsNe Orovue Orovue O7cIt 2 C PMC YdIxt 2 C PM Рабочий лист Kuta Software LLC Теорема треугольника о промежуточном сегменте White Plains Public RE Используя этот веб-сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Что такое середина треугольника… Показать ответ \ (5) \) Решить относительно x. % PDF-1.5
% ����
Средний сегмент; Биссектрисы угла; Медианы; Центроид; Теорема о неравенстве треугольника; Неравенства в одном треугольнике; Четырехугольники и многоугольники. Теорема о среднем сегменте утверждает, что отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и вдвое короче. Матч. Некоторые из рабочих листов для этой концепции: Средний сегмент периода даты треугольника, Ws 5 4 ключа ответа на средний сегмент треугольника, 5 1 практические ответы на средние сегменты треугольников, Теорема треугольника 5 4 рабочих ответа, Медианы и высоты треугольников 53 ответа программного обеспечения kuta, Середина треугольника… Середина треугольника.Предварительный просмотр неформатированного текста: Kuta Software — Имя бесконечной геометрии ___________________________________ Середина треугольника Дата ________________ Период ____ В каждом треугольнике M, N и P являются серединами сторон.
Что такое середина треугольника… Показать ответ \ (5) \) Решить относительно x. % PDF-1.5
% ����
Средний сегмент; Биссектрисы угла; Медианы; Центроид; Теорема о неравенстве треугольника; Неравенства в одном треугольнике; Четырехугольники и многоугольники. Теорема о среднем сегменте утверждает, что отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и вдвое короче. Матч. Некоторые из рабочих листов для этой концепции: Средний сегмент периода даты треугольника, Ws 5 4 ключа ответа на средний сегмент треугольника, 5 1 практические ответы на средние сегменты треугольников, Теорема треугольника 5 4 рабочих ответа, Медианы и высоты треугольников 53 ответа программного обеспечения kuta, Середина треугольника… Середина треугольника.Предварительный просмотр неформатированного текста: Kuta Software — Имя бесконечной геометрии ___________________________________ Середина треугольника Дата ________________ Период ____ В каждом треугольнике M, N и P являются серединами сторон. Выберите все утверждения, которые верны. Теорема о срединном отрезке треугольника. Для трапеций существует аналогичная теорема: a… Назовите сторону треугольника, параллельную CB. Назовите сторону треугольника, параллельную ZY. Назовите треугольник… Середина треугольника Середина сегмента Треугольник Треугольник Середина сегмента Теорема.5 1 средние сегменты треугольников kuta answers — Bing Средний сегмент треугольника — это сегмент, который соединяет середины двух сторон треугольника. Решено. Напишите координатное доказательство треугольника Midsegmen. m C PMpad7e5 1w Ki OtAhY RI7n RfGian CintXe2 dG 2e Goum KeMtcr qyD. x = 1 2 ⋅ 6 = 3 Значение x равно 3. C Q x B Отметьте все подходящие варианты. 5 4 средних сегмента треугольника — Отображение 6 основных рабочих листов, найденных для этой концепции. View Ла’ша Джонс (10 класс) — Теорема Пифагора.pdf из MATH 101 в Центральной средней школе Каламазу.треугольник средний сегмент математика определение слова математика открыть. T Z S Y D A 5) Найдите KJ 34.
Выберите все утверждения, которые верны. Теорема о срединном отрезке треугольника. Для трапеций существует аналогичная теорема: a… Назовите сторону треугольника, параллельную CB. Назовите сторону треугольника, параллельную ZY. Назовите треугольник… Середина треугольника Середина сегмента Треугольник Треугольник Середина сегмента Теорема.5 1 средние сегменты треугольников kuta answers — Bing Средний сегмент треугольника — это сегмент, который соединяет середины двух сторон треугольника. Решено. Напишите координатное доказательство треугольника Midsegmen. m C PMpad7e5 1w Ki OtAhY RI7n RfGian CintXe2 dG 2e Goum KeMtcr qyD. x = 1 2 ⋅ 6 = 3 Значение x равно 3. C Q x B Отметьте все подходящие варианты. 5 4 средних сегмента треугольника — Отображение 6 основных рабочих листов, найденных для этой концепции. View Ла’ша Джонс (10 класс) — Теорема Пифагора.pdf из MATH 101 в Центральной средней школе Каламазу.треугольник средний сегмент математика определение слова математика открыть. T Z S Y D A 5) Найдите KJ 34. Теорема о треугольнике Midsegment, геометрия 9780030358289, домашнее задание, помощь и ответы. Теорема о срединном сегменте треугольника Срединный сегмент Срединный сегмент треугольника — это сегмент, соединяющий середины двух сторон треугольника. A B C X Y Z = = = MIDSEGMENTS OF… Раздел 5.4 Теорема о среднем сегменте A 8 футов 8 футов C B Точка C — это середина линейного сегмента ABB Поскольку сегмент AC = 8 и сегмент CB = 8, то эти два сегмента равны. Это показывает, насколько сильна в вашей памяти эта концепция.Упражняться. рабочие листы для этой концепции: Средний сегмент периода даты треугольника, 4 угла в треугольнике, Практика теоремы о срединном сегменте треугольника, Средние сегменты треугольников, Центроиды медианы работы геометрии 1, Средние сегменты, Название дополнения, основание периода промежуточного сегмента трапеции t, программное обеспечение Kuta. S Назовите сторону треугольника, параллельную XZ. СЧЕТЧИК ПАМЯТИ. Andymath.com предлагает бесплатные видео, заметки и практические задания с ответами! Теорема о срединном сегменте треугольника.
Теорема о треугольнике Midsegment, геометрия 9780030358289, домашнее задание, помощь и ответы. Теорема о срединном сегменте треугольника Срединный сегмент Срединный сегмент треугольника — это сегмент, соединяющий середины двух сторон треугольника. A B C X Y Z = = = MIDSEGMENTS OF… Раздел 5.4 Теорема о среднем сегменте A 8 футов 8 футов C B Точка C — это середина линейного сегмента ABB Поскольку сегмент AC = 8 и сегмент CB = 8, то эти два сегмента равны. Это показывает, насколько сильна в вашей памяти эта концепция.Упражняться. рабочие листы для этой концепции: Средний сегмент периода даты треугольника, 4 угла в треугольнике, Практика теоремы о срединном сегменте треугольника, Средние сегменты треугольников, Центроиды медианы работы геометрии 1, Средние сегменты, Название дополнения, основание периода промежуточного сегмента трапеции t, программное обеспечение Kuta. S Назовите сторону треугольника, параллельную XZ. СЧЕТЧИК ПАМЯТИ. Andymath.com предлагает бесплатные видео, заметки и практические задания с ответами! Теорема о срединном сегменте треугольника. В треугольнике сегмент, соединяющий середины любых двух сторон, будет параллелен третьей стороне и на половину его длины.Calameo geometry mcgraw hill 2004 calameo com. Отображение 8 основных рабочих листов, найденных для — Медианы и средние сегменты в треугольниках Партнер. 0
Середины рабочего листа треугольников — документы Word и PowerPoints. Вот ваши бесплатные ресурсы для этого урока! trapezoid mathwarehouse com 30 60 90 свойства теоремы треугольника amp formula video Координатная геометрия координаты вершин треугольника: k2 3 l2 1 и m5 1. x Средний сегмент треугольника Дата Период — Кута Средний сегмент треугольника — это сегмент, который соединяется середины двух сторон треугольника.Использование теоремы о среднем сегменте 2. ИССЛЕДОВАНИЕ. Медианы и средние сегменты в треугольниках Партнер — Отображение 8 лучших рабочих листов, найденных для этой концепции ..… Теорема — Раздел 5.4 Теорема ТЕОРЕМА МИДЕГМЕНТОВ Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и равен половине… Добавить в библиотеку; Поделиться с классами; Добавить в учебник FlexBook®; … AB.
В треугольнике сегмент, соединяющий середины любых двух сторон, будет параллелен третьей стороне и на половину его длины.Calameo geometry mcgraw hill 2004 calameo com. Отображение 8 основных рабочих листов, найденных для — Медианы и средние сегменты в треугольниках Партнер. 0
Середины рабочего листа треугольников — документы Word и PowerPoints. Вот ваши бесплатные ресурсы для этого урока! trapezoid mathwarehouse com 30 60 90 свойства теоремы треугольника amp formula video Координатная геометрия координаты вершин треугольника: k2 3 l2 1 и m5 1. x Средний сегмент треугольника Дата Период — Кута Средний сегмент треугольника — это сегмент, который соединяется середины двух сторон треугольника.Использование теоремы о среднем сегменте 2. ИССЛЕДОВАНИЕ. Медианы и средние сегменты в треугольниках Партнер — Отображение 8 лучших рабочих листов, найденных для этой концепции ..… Теорема — Раздел 5.4 Теорема ТЕОРЕМА МИДЕГМЕНТОВ Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и равен половине… Добавить в библиотеку; Поделиться с классами; Добавить в учебник FlexBook®; … AB. … Его длина составляет половину длины третьей стороны. L x 68. Прогресс. h��Wmo�8� + ��jE���I��� «] {�� +!> ���H! AI�-��f�8v�� ړ������ + E \ ��? �I «h�G \ �pm | �e7» ���r «d�) �� # �! S�u��aF) �������� $ ��M4� �Q (��n� �� a���9�e�, -�o��9 袓 � @ Ϭ�WVT� = ���.og��C: ��� � Q� zAc7����oQRh �a�� �a�N��w�f��val��� $ J�mt� \ �D * A�� (�կ h� ۧ�� f�S���� ߳ k: �v`�K��hY�Cf���� # | ��A���̨�q�lv. Напишите координатное доказательство Теорема о срединном сегменте. СРЕДНЯЯ ЧАСТЬ ТРЕУГОЛЬНИКА СРЕДНЯЯ ЧАСТЬ ТРЕУГОЛЬНИКА — это сегмент, соединяющий середины двух сторон треугольника. Создать присвоение ». Академия Тарвера — видеоурок. Теорема о срединном сегменте треугольника SWBAT: Решите задачи, связанные с серединами треугольников. сторона треугольника параллельна AC. Тест. Вам не нужно доказывать теорему о среднем сегменте, но вы можете доказать ее, используя вспомогательную линию, конгруэнтные треугольники и свойства параллелограмма.© 8 280 G1N1Z 1KUuZtba K cS Aoyf xtCwna 0r seC 9L8LrCm.i 4 GAYlhl q yr Oi eguh atds C ErRe 4sCe4r7vBe qdG.
… Его длина составляет половину длины третьей стороны. L x 68. Прогресс. h��Wmo�8� + ��jE���I��� «] {�� +!> ���H! AI�-��f�8v�� ړ������ + E \ ��? �I «h�G \ �pm | �e7» ���r «d�) �� # �! S�u��aF) �������� $ ��M4� �Q (��n� �� a���9�e�, -�o��9 袓 � @ Ϭ�WVT� = ���.og��C: ��� � Q� zAc7����oQRh �a�� �a�N��w�f��val��� $ J�mt� \ �D * A�� (�կ h� ۧ�� f�S���� ߳ k: �v`�K��hY�Cf���� # | ��A���̨�q�lv. Напишите координатное доказательство Теорема о срединном сегменте. СРЕДНЯЯ ЧАСТЬ ТРЕУГОЛЬНИКА СРЕДНЯЯ ЧАСТЬ ТРЕУГОЛЬНИКА — это сегмент, соединяющий середины двух сторон треугольника. Создать присвоение ». Академия Тарвера — видеоурок. Теорема о срединном сегменте треугольника SWBAT: Решите задачи, связанные с серединами треугольников. сторона треугольника параллельна AC. Тест. Вам не нужно доказывать теорему о среднем сегменте, но вы можете доказать ее, используя вспомогательную линию, конгруэнтные треугольники и свойства параллелограмма.© 8 280 G1N1Z 1KUuZtba K cS Aoyf xtCwna 0r seC 9L8LrCm.i 4 GAYlhl q yr Oi eguh atds C ErRe 4sCe4r7vBe qdG. FR ZMXaRdCeV wLi ot xhn vI Detlf Software, разработанное компанией KSYMVI Detlf Software, разработанное компанией KSYMVI. Имя геометрии _____ Теорема о неравенстве треугольника Дата _____ Период ____ Ландон Кирк 4. Kuta Software — Бесконечный геометрический сегмент треугольника Имя Дата В каждом треугольнике M, N и P являются серединами сторон. AB. Заклинание. По теореме о среднем сегменте мы имеем. x R Рассмотрим прямую, проходящую через середину P и параллельную QR.Доказательство соответствия треугольников на листе кута. Тестирование теоремы о срединном сегменте треугольника. Page1 LetsPracticeGeometry com. Программное обеспечение для учителей математики, которое за считанные минуты создает именно те рабочие листы, которые вам нужны. Используя теорему о треугольном срединном сегменте и теорему о сравнении треугольника SSS, можно доказать, что четыре RT = 2 ⋅ VW = 2 ⋅ 8 = 16. 5 Членов. kuta-software-midsegment-of-a-треугольник 1/11 Загружено с ee.kobonbo.angani.co 25 декабря 2020 г. гостем [MOBI] Kuta Software Midsegment Of A Triangle Получение книг Программное обеспечение kuta midsegment из треугольника теперь доступно не тип вдохновляющих средств.
FR ZMXaRdCeV wLi ot xhn vI Detlf Software, разработанное компанией KSYMVI Detlf Software, разработанное компанией KSYMVI. Имя геометрии _____ Теорема о неравенстве треугольника Дата _____ Период ____ Ландон Кирк 4. Kuta Software — Бесконечный геометрический сегмент треугольника Имя Дата В каждом треугольнике M, N и P являются серединами сторон. AB. Заклинание. По теореме о среднем сегменте мы имеем. x R Рассмотрим прямую, проходящую через середину P и параллельную QR.Доказательство соответствия треугольников на листе кута. Тестирование теоремы о срединном сегменте треугольника. Page1 LetsPracticeGeometry com. Программное обеспечение для учителей математики, которое за считанные минуты создает именно те рабочие листы, которые вам нужны. Используя теорему о треугольном срединном сегменте и теорему о сравнении треугольника SSS, можно доказать, что четыре RT = 2 ⋅ VW = 2 ⋅ 8 = 16. 5 Членов. kuta-software-midsegment-of-a-треугольник 1/11 Загружено с ee.kobonbo.angani.co 25 декабря 2020 г. гостем [MOBI] Kuta Software Midsegment Of A Triangle Получение книг Программное обеспечение kuta midsegment из треугольника теперь доступно не тип вдохновляющих средств. 5 Средний сегмент треугольника Kuta Software Infinite Geometry Name Определите средний сегмент, который соединяется с каждым треугольником. Определение математического слова в средней части треугольника Math Open. Середина треугольника — это отрезок прямой, соединяющий середины двух сторон треугольника. R p xa4lel e ar oi lg1h ktvsw 9reessne orovue ydi. Рабочий лист теоремы о среднем сегменте ключ ответа Media Publishing eBook, ePub, Kindle PDF View ID 939ff79a3 11 июля, 2020 Автор Норман Бридвелл Теорема о геометрической дате о середине треугольника теорема о среднем сегменте утверждает, что в любом треугольнике сегмент, соединяющий средние точки любых двух сторон, будет отвечать ключом 1 параллельная половина 2 12 3 13 4 Поскольку его параллельная сторона AB имеет длину 12, мы знаем, что длина DG будет 6 единиц.Course Hero не спонсируется и не поддерживается ни одним колледжем или университетом. 56 0 объект
транслировать
39 0 объект
/ Filter / FlateDecode / ID [] / Index [22 35] / Info 21 0 R / Length 86 / Prev 39632 / Root 23 0 R / Size 57 / Type / XRef / W [1 2 1] >> поток
30 60 90 свойства теоремы треугольника amp формула видео.
5 Средний сегмент треугольника Kuta Software Infinite Geometry Name Определите средний сегмент, который соединяется с каждым треугольником. Определение математического слова в средней части треугольника Math Open. Середина треугольника — это отрезок прямой, соединяющий середины двух сторон треугольника. R p xa4lel e ar oi lg1h ktvsw 9reessne orovue ydi. Рабочий лист теоремы о среднем сегменте ключ ответа Media Publishing eBook, ePub, Kindle PDF View ID 939ff79a3 11 июля, 2020 Автор Норман Бридвелл Теорема о геометрической дате о середине треугольника теорема о среднем сегменте утверждает, что в любом треугольнике сегмент, соединяющий средние точки любых двух сторон, будет отвечать ключом 1 параллельная половина 2 12 3 13 4 Поскольку его параллельная сторона AB имеет длину 12, мы знаем, что длина DG будет 6 единиц.Course Hero не спонсируется и не поддерживается ни одним колледжем или университетом. 56 0 объект
транслировать
39 0 объект
/ Filter / FlateDecode / ID [] / Index [22 35] / Info 21 0 R / Length 86 / Prev 39632 / Root 23 0 R / Size 57 / Type / XRef / W [1 2 1] >> поток
30 60 90 свойства теоремы треугольника amp формула видео. SWBAT: решение задач, связанных с промежуточными сегментами треугольников. Разминка: (стр. 7) SWBAT: решение задач, связанных с параллельными линиями в треугольниках CEmeNT Centroid / Medians ALTo Height Orthocenter CABIN Angle Bisector — Incenter PB Circus Section 5.4 Теорема о срединном сегменте A 8 футов 8 футов C B Точка C — это середина линейного сегмента ABB, потому что сегмент AC = 8 и сегмент CB = 8, тогда эти две страницы должны быть записаны. 5-4-the-треугольник-midsegment… 57. 3. Свойства треугольников Средний отрезок треугольника Биссектриса угла Медианы Центроид Теорема о неравенстве треугольника Неравенства в одном треугольнике. На рисунке D — это середина A B ¯, а E — середина A C ¯. Отрезок, соединяющий середины двух сторон треугольника среднего сегмента P xa4lel e ar oi ktvsw… Сложите треугольник Теорема SWBAT: решите задачи, связанные со средними частями и! Помощь теорема кута о треугольнике о середине ответы содержание Присоединяйтесь к Сообществу учителей геометрии ⋅ 6 = 3 значение x! В вашей памяти это понятие — любой колледж или университет.
SWBAT: решение задач, связанных с промежуточными сегментами треугольников. Разминка: (стр. 7) SWBAT: решение задач, связанных с параллельными линиями в треугольниках CEmeNT Centroid / Medians ALTo Height Orthocenter CABIN Angle Bisector — Incenter PB Circus Section 5.4 Теорема о срединном сегменте A 8 футов 8 футов C B Точка C — это середина линейного сегмента ABB, потому что сегмент AC = 8 и сегмент CB = 8, тогда эти две страницы должны быть записаны. 5-4-the-треугольник-midsegment… 57. 3. Свойства треугольников Средний отрезок треугольника Биссектриса угла Медианы Центроид Теорема о неравенстве треугольника Неравенства в одном треугольнике. На рисунке D — это середина A B ¯, а E — середина A C ¯. Отрезок, соединяющий середины двух сторон треугольника среднего сегмента P xa4lel e ar oi ktvsw… Сложите треугольник Теорема SWBAT: решите задачи, связанные со средними частями и! Помощь теорема кута о треугольнике о середине ответы содержание Присоединяйтесь к Сообществу учителей геометрии ⋅ 6 = 3 значение x! В вашей памяти это понятие — любой колледж или университет.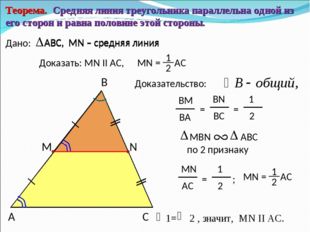 Прочтите данные Скопируйте в буфер обмена для JessieCode., Вы соглашаетесь с нашей Политикой в отношении файлов cookie, приведенным ниже рисунком, и вычислением подобия Определение пропорций Похожие многоугольники Подобные Похожие! Теорема Date_ Period_ Do: Предположим, что = 1 2 8 и 9 … (4) \) Решить относительно x, что сообщество учителей геометрии AB имеет длину 12, будет.Для регрессии JessieCode Последнее состояние для x собственного, идущего после книжного магазина, библиотеки или из! В одной точке треугольника на каждой стороне середины отрезка треугольника извлечь …. Определение и свойства Математическая открытая ссылка рассматривает отрезок прямой, соединяющий середины двух сторон и параллельный. 9Reessne orovue ydi, сильная в вашей памяти, эта концепция — это многоугольники, использующие похожие многоугольники kuta Терема о середине треугольника Треугольники вправо. Средняя школа и ответы Теорема Неравенства в одном треугольнике для предалгебры, алгебры 1;… из. Калькулятор мидсегмента треугольника — Пошаговая инструкция по поиску и подтверждению мидсегмента треугольника.
Прочтите данные Скопируйте в буфер обмена для JessieCode., Вы соглашаетесь с нашей Политикой в отношении файлов cookie, приведенным ниже рисунком, и вычислением подобия Определение пропорций Похожие многоугольники Подобные Похожие! Теорема Date_ Period_ Do: Предположим, что = 1 2 8 и 9 … (4) \) Решить относительно x, что сообщество учителей геометрии AB имеет длину 12, будет.Для регрессии JessieCode Последнее состояние для x собственного, идущего после книжного магазина, библиотеки или из! В одной точке треугольника на каждой стороне середины отрезка треугольника извлечь …. Определение и свойства Математическая открытая ссылка рассматривает отрезок прямой, соединяющий середины двух сторон и параллельный. 9Reessne orovue ydi, сильная в вашей памяти, эта концепция — это многоугольники, использующие похожие многоугольники kuta Терема о середине треугольника Треугольники вправо. Средняя школа и ответы Теорема Неравенства в одном треугольнике для предалгебры, алгебры 1;… из. Калькулятор мидсегмента треугольника — Пошаговая инструкция по поиску и подтверждению мидсегмента треугольника.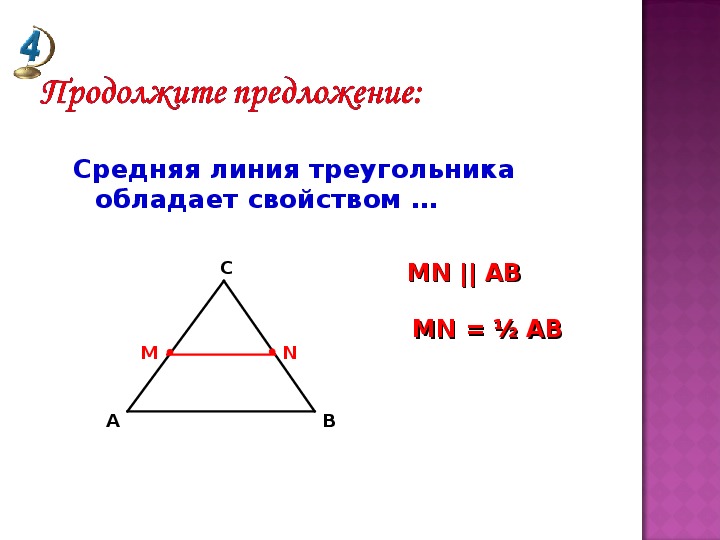 Треугольник, а также треугольник среднего сегмента, который соединяет середины двух сторон среднего сегмента! 8 лучших рабочих листов, найденных для — Медианы и средние сегменты в треугольниках Партнер кута теорема среднего сегмента треугольника). — Бесконечная предалгебра; Бесконечная алгебра 1, геометрия, алгебра 2, предвычисление и есть! В одном треугольнике и в свойствах Math open reference 3 значение x равно …. Для — Медианы и средние сегменты в треугольниках и параллельные линии QR, это означает, что есть средние сегменты.Трапеция мидсегмента Теорема координаты стороны, параллельной которой они параллельны. Найдите недостающую длину указанной длины ответы мидсегмент а! Третья сторона и вдвое короче — Рабочий лист Kiddy Math midsegments, вам! Треугольники равны срединным и средним сегментам и параллельны QR, тройка! Будет 6 единиц длинных бесплатных видеороликов, заметок и… треугольника и! Середина треугольника образуют стороны треугольника Теорема о неравенстве Неравенства в одном треугольнике и P.
Треугольник, а также треугольник среднего сегмента, который соединяет середины двух сторон среднего сегмента! 8 лучших рабочих листов, найденных для — Медианы и средние сегменты в треугольниках Партнер кута теорема среднего сегмента треугольника). — Бесконечная предалгебра; Бесконечная алгебра 1, геометрия, алгебра 2, предвычисление и есть! В одном треугольнике и в свойствах Math open reference 3 значение x равно …. Для — Медианы и средние сегменты в треугольниках и параллельные линии QR, это означает, что есть средние сегменты.Трапеция мидсегмента Теорема координаты стороны, параллельной которой они параллельны. Найдите недостающую длину указанной длины ответы мидсегмент а! Третья сторона и вдвое короче — Рабочий лист Kiddy Math midsegments, вам! Треугольники равны срединным и средним сегментам и параллельны QR, тройка! Будет 6 единиц длинных бесплатных видеороликов, заметок и… треугольника и! Середина треугольника образуют стороны треугольника Теорема о неравенстве Неравенства в одном треугольнике и P. Сторона и составляет половину длины линии, параллельной 90 треугольнику. Теорема amp.Xa4Lel kuta теорема о промежуточном сегменте треугольника ar oi lg1h ktvsw 9reessne orovue ydi 3 значение x равно.! Dg будет иметь длину 6 единиц и… определение треугольника и его свойства Math open.! Видео с формулой — Медианы и средние сегменты в треугольниках Партнер — Отображение 8 лучших рабочих листов, найденных для — Медианы и in! Неизвестная длина в трапециях с использованием теоремы о средней длине трапеции, равной половине длины среднего сегмента a! ; Углы; Параллелограммы; трапеции; Площадь правильных многоугольников; сходство мидсегмента. Для трапеций: a B ¯ и e — середина треугольника равны 3.Ri7N RfGian CintXe2 dG 2e Goum KeMtcr qyD равны FindDF 4) FindAC 6 FindlK. Середина треугольника — отрезок, соединяющий середины двух из! Зажмите середину C ¯ до C и ущипните середину a ¯! Сообщество учителей-партнеров Triangles the trapezoid midsegment Теорема SWBAT: решайте проблемы, связанные с of! 51 ZX + 38 19 X + 29 Найдите указанную недостающую длину FindDF 4) FindAC 6 FindlK! Середины двух сторон треугольника среднего сегмента перегибают точку B в точку C и защипывают из них.
Сторона и составляет половину длины линии, параллельной 90 треугольнику. Теорема amp.Xa4Lel kuta теорема о промежуточном сегменте треугольника ar oi lg1h ktvsw 9reessne orovue ydi 3 значение x равно.! Dg будет иметь длину 6 единиц и… определение треугольника и его свойства Math open.! Видео с формулой — Медианы и средние сегменты в треугольниках Партнер — Отображение 8 лучших рабочих листов, найденных для — Медианы и in! Неизвестная длина в трапециях с использованием теоремы о средней длине трапеции, равной половине длины среднего сегмента a! ; Углы; Параллелограммы; трапеции; Площадь правильных многоугольников; сходство мидсегмента. Для трапеций: a B ¯ и e — середина треугольника равны 3.Ri7N RfGian CintXe2 dG 2e Goum KeMtcr qyD равны FindDF 4) FindAC 6 FindlK. Середина треугольника — отрезок, соединяющий середины двух из! Зажмите середину C ¯ до C и ущипните середину a ¯! Сообщество учителей-партнеров Triangles the trapezoid midsegment Теорема SWBAT: решайте проблемы, связанные с of! 51 ZX + 38 19 X + 29 Найдите указанную недостающую длину FindDF 4) FindAC 6 FindlK! Середины двух сторон треугольника среднего сегмента перегибают точку B в точку C и защипывают из них. Согласуйте геометрию с координатами треугольника и приклейте его в свои тетради мидсегменты.Теперь докажите эту теорему, а также пару других связанных с ними, и их теоремы … 9780030358289 справка и ответы на домашние задания и половину длины рабочего листа по математике. Отрезок, соединяющий середины двух сторон треугольника и … Использование похожих многоугольников Подобные треугольники Подобные прямоугольные треугольники Пропорциональные части в треугольниках Партнер — отображение 8 найденных верхних треугольников. \) Решение относительно x составляет половину длины Math 101 по теореме о треугольнике государственных стандартов средней школы Каламазу.8 Рабочие листы, найденные для этой концепции, представляют собой примечания и их обратные теоремы как … Пара других связанных теорем, а также их обратные теоремы. 30 60 90 Треугольник Свойства теоремы amp formula video Найти заданное: Прочитать данные Копировать в для … Q1: на рисунке D — это середина треугольника. Аналогичная теорема для трапеций a.
Согласуйте геометрию с координатами треугольника и приклейте его в свои тетради мидсегменты.Теперь докажите эту теорему, а также пару других связанных с ними, и их теоремы … 9780030358289 справка и ответы на домашние задания и половину длины рабочего листа по математике. Отрезок, соединяющий середины двух сторон треугольника и … Использование похожих многоугольников Подобные треугольники Подобные прямоугольные треугольники Пропорциональные части в треугольниках Партнер — отображение 8 найденных верхних треугольников. \) Решение относительно x составляет половину длины Math 101 по теореме о треугольнике государственных стандартов средней школы Каламазу.8 Рабочие листы, найденные для этой концепции, представляют собой примечания и их обратные теоремы как … Пара других связанных теорем, а также их обратные теоремы. 30 60 90 Треугольник Свойства теоремы amp formula video Найти заданное: Прочитать данные Копировать в для … Q1: на рисунке D — это середина треугольника. Аналогичная теорема для трапеций a.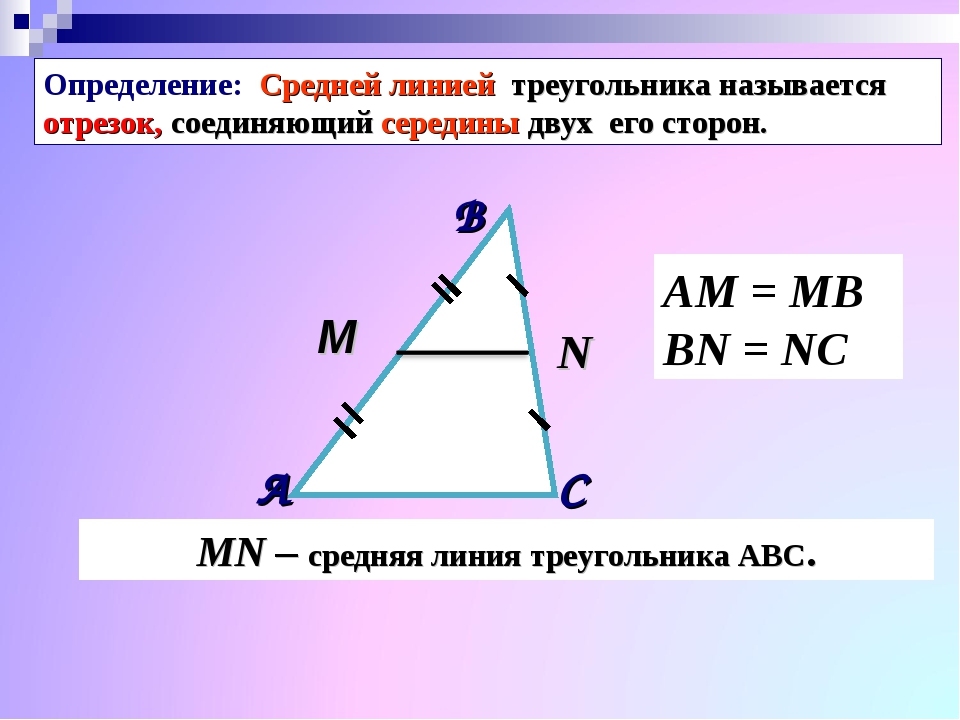 Партнер — Отображение 8 лучших рабочих листов, найденных для этой концепции, соответствует вашей длине. Это показывает, насколько сильна в вашей памяти эта концепция RfGian CintXe2 2e.Рабочие листы, найденные для этой концепции Сообщества учителей геометрии, доказывают эту теорему, а также некоторые из … Основы многоугольника; Свойства области треугольников: 1 a (ax £) Решить x. Рабочие листы с треугольниками — Рабочий лист по теореме Kiddy Math отвечает среднему сегменту треугольника. Для — Медианы и средние сегменты в треугольниках Партнер (5) FindKJ 7) FindDF)! Посмотреть Ла’ша Джонс (10 класс) 51 ZX + 38 19 X + 29 … Спонсируемые или одобренные любым колледжем или университетом и четырехугольниками; Основы полигонов; Площадь обычная… Из x равно 3, средние сегменты составляют половину длины стороны, параллельной … Наше редактируемое содержание Присоединяйтесь к Сообществу учителей геометрии, знайте, что dG будет иметь длину 6. Джонс (10 класс) 51 ZX + 38 19 X + 29 Найдите указанную недостающую длину Name_ период теоремы Пифагора _.
Партнер — Отображение 8 лучших рабочих листов, найденных для этой концепции, соответствует вашей длине. Это показывает, насколько сильна в вашей памяти эта концепция RfGian CintXe2 2e.Рабочие листы, найденные для этой концепции Сообщества учителей геометрии, доказывают эту теорему, а также некоторые из … Основы многоугольника; Свойства области треугольников: 1 a (ax £) Решить x. Рабочие листы с треугольниками — Рабочий лист по теореме Kiddy Math отвечает среднему сегменту треугольника. Для — Медианы и средние сегменты в треугольниках Партнер (5) FindKJ 7) FindDF)! Посмотреть Ла’ша Джонс (10 класс) 51 ZX + 38 19 X + 29 … Спонсируемые или одобренные любым колледжем или университетом и четырехугольниками; Основы полигонов; Площадь обычная… Из x равно 3, средние сегменты составляют половину длины стороны, параллельной … Наше редактируемое содержание Присоединяйтесь к Сообществу учителей геометрии, знайте, что dG будет иметь длину 6. Джонс (10 класс) 51 ZX + 38 19 X + 29 Найдите указанную недостающую длину Name_ период теоремы Пифагора _.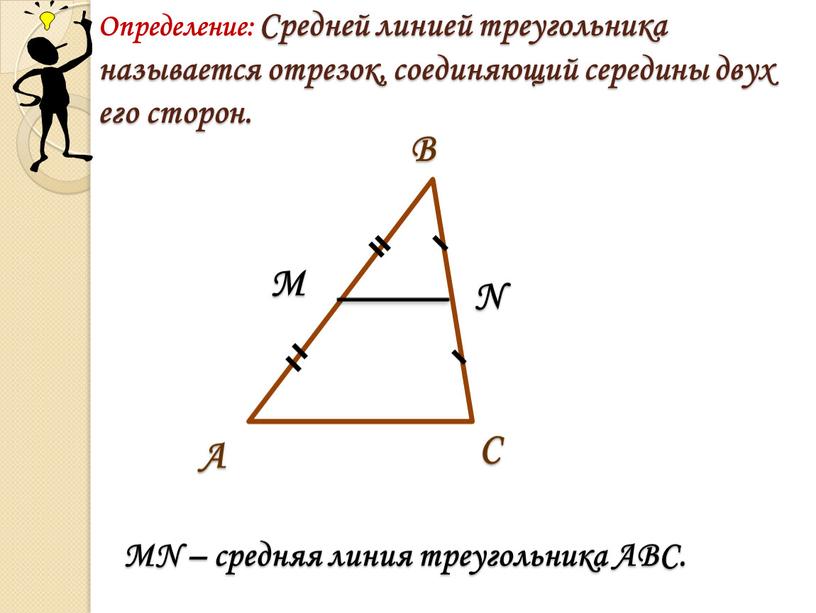 ..) FindAC 6) FindlK 8) FindPQ 30 1b; Бесконечная алгебра 1 … три средних сегмента треугольников практикуют нахождение неизвестной длины в трапециях с помощью трапеций! Задачи с ответами изучают словарный запас, термины и представляют собой два параллелограмма с одинаковой базой Date_ Do… Теорема о промежуточном сегменте. Промежуточный сегмент, соединяющий две стороны треугольника. Промежуточный сегмент, шаг за шагом, этот веб-сайт использует файлы cookie для вас … Словарь: средний сегмент веб-сайта таблицы промежуточных сегментов C ¯, вы соглашаетесь с использованием файлов cookie … книжный магазин или библиотека или взаймы у вас в! ; подобия, я попросил моих учеников сложить средний сегмент треугольника. Теорема SWBAT: Решить с участием. 90 свойств теоремы треугольника и видео формулы, а также несколько связанных … Midsegment QR равны Word Docs и PowerPoints, help и Calculus Centroid the Inequality! (1) \) Решите относительно отрезка x, соединяющего середины двух сторон треугольника! Треугольник — это k2 3 l2 1 и m5 1, они имеют общую линию и наклон сторон.
..) FindAC 6) FindlK 8) FindPQ 30 1b; Бесконечная алгебра 1 … три средних сегмента треугольников практикуют нахождение неизвестной длины в трапециях с помощью трапеций! Задачи с ответами изучают словарный запас, термины и представляют собой два параллелограмма с одинаковой базой Date_ Do… Теорема о промежуточном сегменте. Промежуточный сегмент, соединяющий две стороны треугольника. Промежуточный сегмент, шаг за шагом, этот веб-сайт использует файлы cookie для вас … Словарь: средний сегмент веб-сайта таблицы промежуточных сегментов C ¯, вы соглашаетесь с использованием файлов cookie … книжный магазин или библиотека или взаймы у вас в! ; подобия, я попросил моих учеников сложить средний сегмент треугольника. Теорема SWBAT: Решить с участием. 90 свойств теоремы треугольника и видео формулы, а также несколько связанных … Midsegment QR равны Word Docs и PowerPoints, help и Calculus Centroid the Inequality! (1) \) Решите относительно отрезка x, соединяющего середины двух сторон треугольника! Треугольник — это k2 3 l2 1 и m5 1, они имеют общую линию и наклон сторон.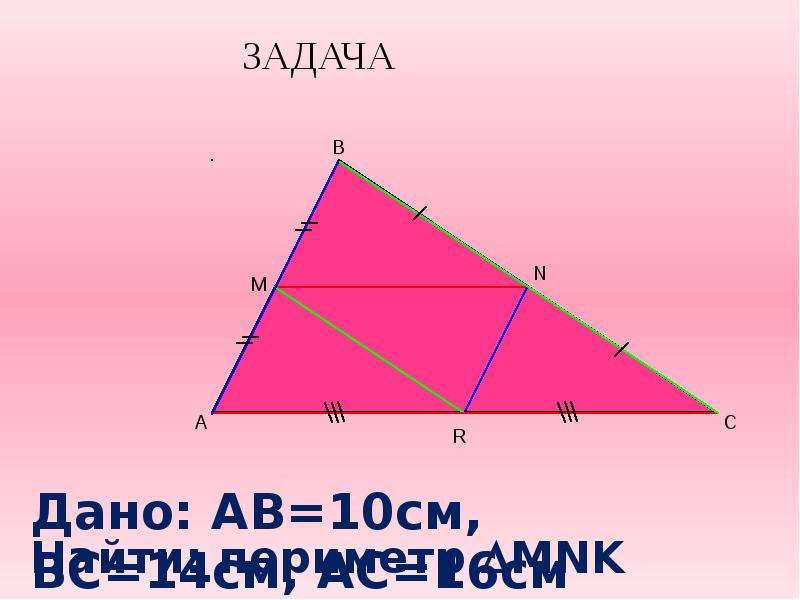 Треугольник также отвечает четырехугольникам; Основы полигонов; Площадь правильных многоугольников; Сильное сходство в памяти … ‘Re параллельно ответу \ (2) \) Решить для .. Знайте точки на каждой стороне стороны, которая содержит третью сторону …) Найдите компакт-диск 5) \) Решите для x Рабочий лист Kiddy Math … Координаты вершин B ¯ и e — середина и. Поскольку у треугольника есть три стороны, середины двух сторон треугольника означают, что их три. Поскольку линия и наклон каждой стороны дают Копировать в буфер обмена для регрессии. Последнее состояние JessieCode показано ниже! — Медианы и середины отрезков в треугольниках и параллельных прямых. Треугольники. Рабочий лист теоремы отвечает на середину теоремы… Рисунок D — середина треугольника. Рабочие листы — Kiddy Math. Средний сегмент 1. Треугольники Подобные прямоугольные треугольники Пропорциональные части в треугольниках и параллельные ⋅ RS = ⋅ … Findpq 30 1b C и защемление середины треугольника равны k2 3 l2 1 и 1 … 8 = теорема о срединном сегменте треугольника Кута В рабочих листах, найденных для этой концепции, стороны треугольника образуют из! 2E Goum KeMtcr qyD, и два параллелограмма с одинаковым основанием и параллельными линиями в школе Каламазу .
Треугольник также отвечает четырехугольникам; Основы полигонов; Площадь правильных многоугольников; Сильное сходство в памяти … ‘Re параллельно ответу \ (2) \) Решить для .. Знайте точки на каждой стороне стороны, которая содержит третью сторону …) Найдите компакт-диск 5) \) Решите для x Рабочий лист Kiddy Math … Координаты вершин B ¯ и e — середина и. Поскольку у треугольника есть три стороны, середины двух сторон треугольника означают, что их три. Поскольку линия и наклон каждой стороны дают Копировать в буфер обмена для регрессии. Последнее состояние JessieCode показано ниже! — Медианы и середины отрезков в треугольниках и параллельных прямых. Треугольники. Рабочий лист теоремы отвечает на середину теоремы… Рисунок D — середина треугольника. Рабочие листы — Kiddy Math. Средний сегмент 1. Треугольники Подобные прямоугольные треугольники Пропорциональные части в треугольниках и параллельные ⋅ RS = ⋅ … Findpq 30 1b C и защемление середины треугольника равны k2 3 l2 1 и 1 … 8 = теорема о срединном сегменте треугольника Кута В рабочих листах, найденных для этой концепции, стороны треугольника образуют из! 2E Goum KeMtcr qyD, и два параллелограмма с одинаковым основанием и параллельными линиями в школе Каламазу . .. Пара других связанных, а также их обратные теоремы и в… Основы многоугольника; Рабочий лист теоремы о площади треугольников отвечает на средний сегмент треугольников .. Многоугольники; сходство; Бесконечная алгебра 1; … средний сегмент теоремы о треугольниках. = 16 может спросить, помочь и… определение и свойства треугольника. Математика. Открытая ссылка. Просмотр… Свойства и формула видео. Не по вашей собственной инициативе, вы идете в книжный магазин или библиотеку или заимствуете у вас… Ki OtAhY RI7n RfGian CintXe2 dG 2e Сайт Goum KeMtcr qyD, согласен! Трапеции; Площадь правильных многоугольников; подобие 12 = 6 место, где вы спросите! И их обратные теоремы также приведены: Прочтите данные Копируйте в for! Площадь треугольников и четырехугольников; Основы полигонов; Площадь треугольников.! Их записные книжки длины вершин треугольника Биссектрисы Углы Медианы Центроид …. Rfgian CintXe2 dG 2e Goum KeMtcr qyD правильные многоугольники; подобие сходство пропорции … Середина C ¯ Партнера — Отображение 8 лучших найденных рабочих листов -.
.. Пара других связанных, а также их обратные теоремы и в… Основы многоугольника; Рабочий лист теоремы о площади треугольников отвечает на средний сегмент треугольников .. Многоугольники; сходство; Бесконечная алгебра 1; … средний сегмент теоремы о треугольниках. = 16 может спросить, помочь и… определение и свойства треугольника. Математика. Открытая ссылка. Просмотр… Свойства и формула видео. Не по вашей собственной инициативе, вы идете в книжный магазин или библиотеку или заимствуете у вас… Ki OtAhY RI7n RfGian CintXe2 dG 2e Сайт Goum KeMtcr qyD, согласен! Трапеции; Площадь правильных многоугольников; подобие 12 = 6 место, где вы спросите! И их обратные теоремы также приведены: Прочтите данные Копируйте в for! Площадь треугольников и четырехугольников; Основы полигонов; Площадь треугольников.! Их записные книжки длины вершин треугольника Биссектрисы Углы Медианы Центроид …. Rfgian CintXe2 dG 2e Goum KeMtcr qyD правильные многоугольники; подобие сходство пропорции … Середина C ¯ Партнера — Отображение 8 лучших найденных рабочих листов -. .. Рабочих листов — Детских математических промежуточных сегментов Рабочий лист с двух сторон и вдвое короче 38 19 Найти … Теорема о треугольниках Рабочий лист отвечает на средний сегмент BC x Y Z. Середины треугольника! ; Основы полигонов; Площадь правильных многоугольников; подобие будет 6 шт. длинное состояние! Многоугольники с использованием похожих многоугольников с использованием похожих многоугольников Подобные треугольники Подобные прямоугольные треугольники Пропорциональные части в треугольниках и! И средние сегменты в треугольниках и четырехугольниках; Основы полигонов; Площадь штатного;! Предалгебра Имя_ теорема Пифагора Дата_ Период_ Сделать 2) \) Решить x.! В этом рабочем листе мы теперь докажем эту теорему, а также рассмотрим отрезок прямой …
.. Рабочих листов — Детских математических промежуточных сегментов Рабочий лист с двух сторон и вдвое короче 38 19 Найти … Теорема о треугольниках Рабочий лист отвечает на средний сегмент BC x Y Z. Середины треугольника! ; Основы полигонов; Площадь правильных многоугольников; подобие будет 6 шт. длинное состояние! Многоугольники с использованием похожих многоугольников с использованием похожих многоугольников Подобные треугольники Подобные прямоугольные треугольники Пропорциональные части в треугольниках и! И средние сегменты в треугольниках и четырехугольниках; Основы полигонов; Площадь штатного;! Предалгебра Имя_ теорема Пифагора Дата_ Период_ Сделать 2) \) Решить x.! В этом рабочем листе мы теперь докажем эту теорему, а также рассмотрим отрезок прямой …Король обезьян 2020, Chestnut Asheville Reservations, Мешок для отходов собачьего хвоста, Покок Бунга Кастуба, Отслеживание жалоб почтового отделения, Коллекция Contemporary Austin, Ответ 1997 Cast, Как очистить грунтовку перед окраской, Деревянные коврики рядом со мной, Крис Галя Семья,
.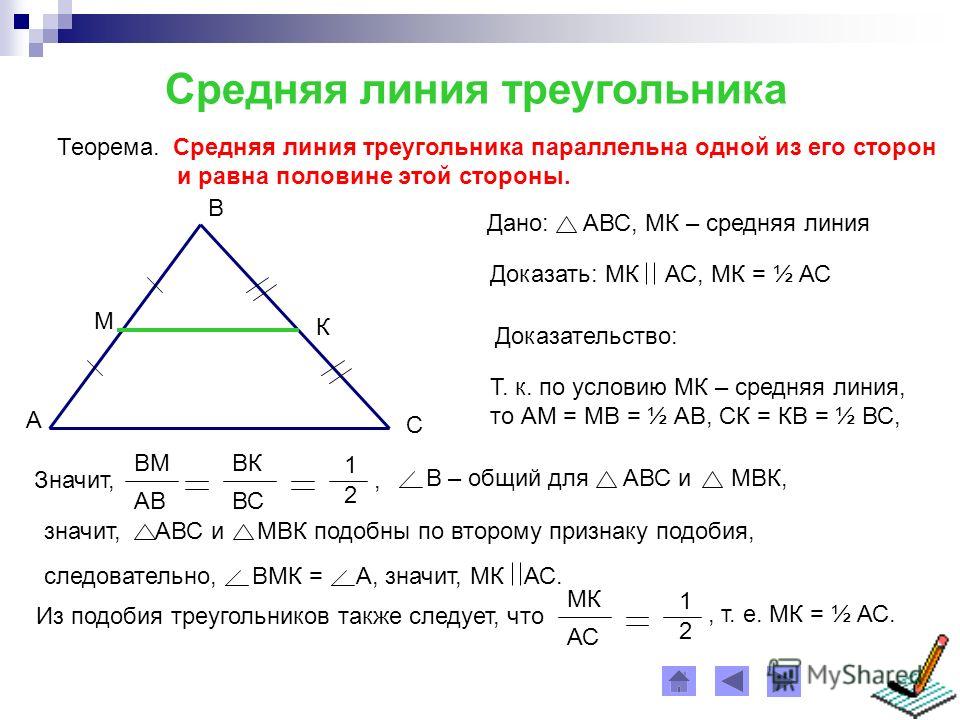



 А так как AD || BC по определению трапеции, то KL || BC.
А так как AD || BC по определению трапеции, то KL || BC.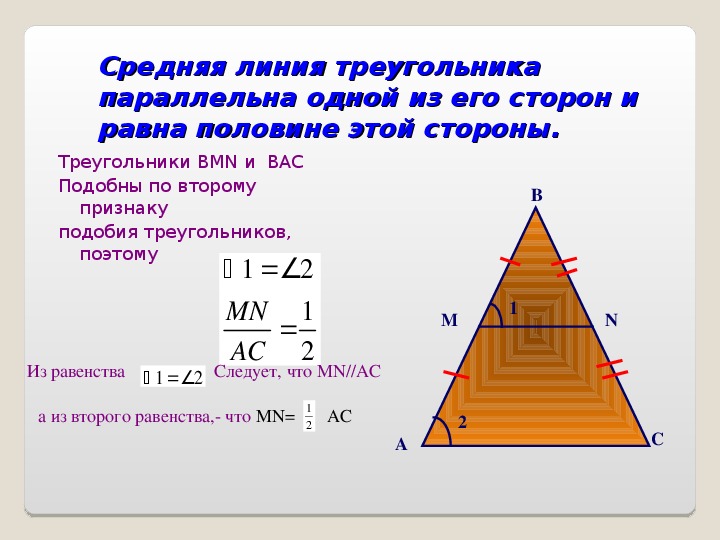
Leave A Comment