253 вариант Алекса Ларина. Разбор ЕГЭ математика 2019
Дано натуральное четырехзначное число n, в записи которого нет нулей. Для этого числа составим дробь $$f(n)$$ , в числителе которой само число n , а в знаменателе – произведение всех цифр числа n.
А) Приведите пример такого числа , для которого $$f(n)=\frac{643}{160}$$
Б) Существует ли такое n, что $$f(n)=\frac{343}{160}$$ ?
В) Какое наименьшее значение может принимать дробь $$f(n)$$, если она равна несократимой дроби со знаменателем 160?
Пусть число $$M=10^{3}a+10^{2}b+10c+d$$, $$0<a,b,c,d<9 \in N$$
A) $$\frac{643}{160}=\frac{643*k}{160*k}$$. $$M=643k$$ ; $$abcd=160k$$
Разложим 160: $$160=2^{5}*5$$. С учетом , что $$a,b,c,d \in N$$ и $$a,b,c,d \in [1;9]$$, то среди чисел точно есть 5. Рассмотрим умножение 643 на натуральное $$k\geq 2$$.
$$643*2=1286$$ — нет 5
$$643*3=1929$$ — нет 5
$$643*4=2572$$. При этом 2*5*7*2=140 не кратно 160.
$$643*5=3215\Rightarrow$$ $$3*2*1*5=30$$ — не подходит.
$$643*6=3858\Rightarrow$$ $$3*8*5*8=960=160*6$$ — подходит
Т.е. пример числа: 3858
B) Рассмотрим сначала наименьшее возможное f(n) . С учетом , что $$160=2^{5}*5$$ и $$a,b,c,d$$ – натуральные, меньшие 10, то возможные a,b,c и d : $$1,4,8,5$$; $$2,2,8,5$$; $$2,4,4,5$$ . При этом $$\frac{M}{abcd}\rightarrow min$$, при $$abcd\rightarrow max$$. Пусть k-множитель, который бы сокращался . $$k_{max}=18=2*3^{2}$$ т.к. тогда бы $$1\rightarrow 9$$; $$4\rightarrow 8$$ и M состояло бы из цифр $$9,8,8,5$$ (очевидно, что наибольшее k именно для множителей $$1,4,8,5$$) . При k>18 получим, что одна из цифр станет больше 9. При этом k — число составное.
Рассмотрим их. $$k=18\Rightarrow$$ $$a,b,c,d: 9,8,8,5$$. Но $$9+8+8+5=30$$, число 30 не делится нацело на 9, значит при сокращении на k мы не получим знаменатель 160.
$$k=16$$; $$a,b,c,d\Rightarrow$$ $$8,8,8,5$$. Комбинации с этими цифрами:
$$\frac{5888}{160*16}=\frac{368}{160}$$ — сократима дальше
$$\frac{8588}{160*16}=\frac{2147}{640}$$ — нет знаменателя 160
$$\frac{8858}{160*16}=\frac{4429}{1280}$$
$$\frac{8885}{160*16}$$ — не делится на 16
$$k=14$$: $$a,b,c,d: 7,8,8,5$$. Аналогично предыдущему нет чисел.
$$k=12$$: $$a,b,c,d :6,8,8,5$$. При использовании данных чисел наименьшее $$f(n)=\frac{5868}{160*12}=\frac{489}{160}$$
249 вариант Алекса Ларина. Разбор ЕГЭ математика 2019
Найдите все значения параметра a , при каждом из которых система уравнений
$$\left\{\begin{matrix}y(ax-1)=2|x+1|+2xy\\ xy+1=x-y\end{matrix}\right.$$
имеет решения
$$\left\{\begin{matrix}y(ax-1)=2\left | x+1 \right |+2xy\\xy+1=x-y\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y(ax-1-2x)=2\left | x+1 \right |\\y(x+1)=x-1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y=\frac{2\left | x+1 \right |}{ax-1-2x}\\y=\frac{x-1}{x+1}\end{matrix}\right.$$
Приравняем правые части функций: $$\frac{2\left | x+1 \right |}{ax-1-2x}=\frac{x-1}{x+1}$$. Раскрываем модуль:
1) $$x+1\geq 0\Leftrightarrow x\geq -1\Leftrightarrow$$$$2(x+1)^{2}=(ax-1-2x)(x-1)\Leftrightarrow$$$$2x^{2}+4x+2=ax^{2}-ax-x+1-2x^{2}+2x\Leftrightarrow$$$$x^{2}(a-4)+x(-a-3)-1=0$$. Чтобы были корни, дискриминант должен быть неотрицательным: $$D=a^{2}+6a+9+4a-16=a^{2}+10a-7\geq 0$$. Так же корень из дискриминанта должен находится: $$D_{1}=100+28=128$$. Получаем: $$a_{1,2}=\frac{-10\pm \sqrt{128}}{2}=-5\pm 4\sqrt{2}$$
$$a \in (-\infty ; -5-4\sqrt{2}]\cup [-5+4\sqrt{2};+\infty )(*)$$ — условие возможного существованиях корней.
При этом имеем параболу $$f(x)=x^{2}(a-4)+x(-a-3)-1$$. Рассмотрим случай, когда ни один корень не попадает в $$x\geq -1$$ (противоположный необходимому нам. То есть, найдя решения для данного случая, нам необходимо будет взять оставшийся промежуток. Например: пусть решением получим$$(0;1)$$, тогда для нахождения решений, чтобы хотя бы один корень попадал в промежуток от -1, мы возьмем $$(-\infty;0]\cup[1;+\infty)$$. Тогда абцисса вершины должна быть меньше -1, т.е. $$\frac{a+3}{2(a-4)}<-1$$ и если ветви вверх, то $$f(-1)>0$$ ветви вниз , то $$f(-1)<0$$
Обоснование:
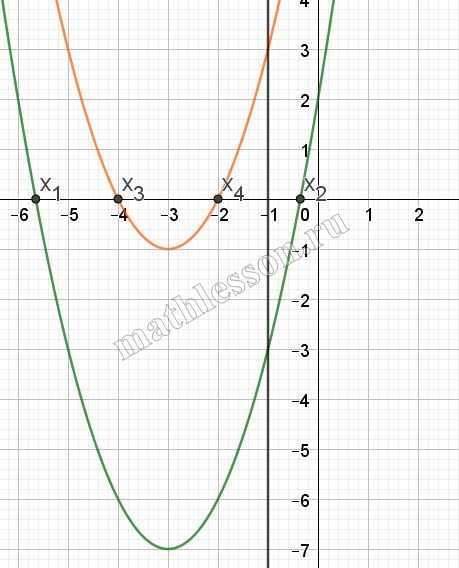
Как видим, если ветви направлены вверх и f(-1)<0, то будет точно один корень, который попадет в промежуток от -1 до плюс бесконечности ($$x_{2}$$)
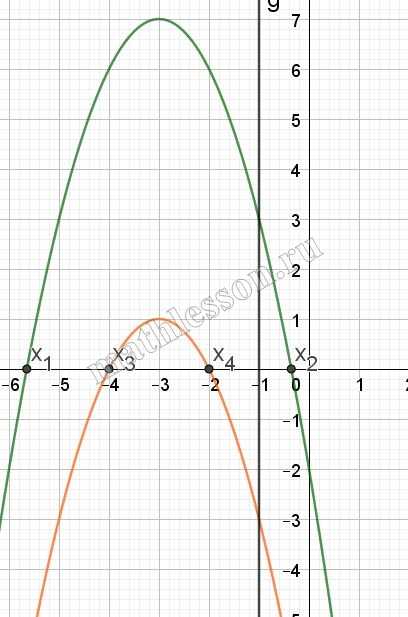
Как видим, если ветви направлены вниз и f(-1)>0, то будет точно один корень, который попадет в промежуток от -1 до плюс бесконечности ($$x_{2}$$)
Т.е. $$\left\{\begin{matrix} a-4>0\\ (a-4)+a+3-1>0\end{matrix}\right.$$ и $$\left\{\begin{matrix}a-4<0 & & \\(a-4)+a+3-1<0& &\end{matrix}\right.$$ или $$(a-4)(2a-2)>0$$
Получаем : $$\left\{\begin{matrix}\frac{a+3}{2(a+4)}<-1\\(a-4)(a-1)>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{a+3+2a-8}{a-4}<0\\(a-4)(a-1)>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{3a-5}{a-4}<0\\(a-4)(a-1)>0\end{matrix}\right.$$
Пересечений нет, значит случай невозможен и хотя бы один корень $$\geq -1$$. Тогда с учетом (*): $$a\in (-\infty ; -5-4\sqrt{2}]\cup [-5+4\sqrt{2}; +\infty )$$
2) $$x+1<0\Rightarrow x<-1$$. Аналогично п.1
$$-2(x+1)^{2}=(ax-1-2x)(x-1)\Leftrightarrow$$$$-2x^{2}-4x-2=ax^{2}-ax-x+1-2x^{2}+2x\Leftrightarrow$$$$ax^{2}+x(-a+5)+3=0\Leftrightarrow$$$$D=a^{2}-100+25-12a=a^{2}-22a+25\geq 0\Leftrightarrow$$$$D=484-100=384\Leftrightarrow$$$$a_{1,2}=\frac{22\pm \sqrt{384}}{2}=11\pm 4\sqrt{6}\Leftrightarrow$$$$a \in (-\infty ; 11-4\sqrt{6}]\cup [11+4\sqrt{6};+\infty )$$
Имеем параболу: $$f(x)=ax^{2}+x(5-a)+3$$
Пусть оба корня $$>-1$$, тогда $$x_{0}\geq -1$$. И при ветвях вверх $$f(-1)\geq 0$$, при ветвях вних $$f(-1)\leq 0$$, т.е. $$\left\{\begin{matrix}a> 0\\a-5+a+3\geq 0\end{matrix}\right.$$ и $$\left\{\begin{matrix}a <0\\a-5+a+3\leq 0\end{matrix}\right.$$.Или $$a(2a-2)\geq 0$$. Тогда: $$\left\{\begin{matrix}\frac{a-5}{2a}\geq -1\\a(a-1)\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{a-5+2a}{2a}\geq 0\\a(a-1)\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{3a-5}{2a}\geq 0\\a(a-1)\geq 0\end{matrix}\right.$$
Т.е. $$a \in (-\infty ; 0]\cup [\frac{5}{3};+\infty )(3)$$ с учетом $$a \in (-\infty ; 11-4\sqrt{6}]\cup [11+4\sqrt{6};+\infty )$$ и то, что промежуток (3) нас не удовлетворяет (мы должны взять наоборот $$(0;\frac{5}{3})$$ имеем:
т.е. $$a\in (0; 11-4\sqrt{6}]$$
Сравним $$4\sqrt{2}-5$$ и $$11-4\sqrt{6}$$:
$$(4\sqrt{2}-5)^{2}=32-40\sqrt{2}+25=57-40\sqrt{2}\approx 0,43$$
$$(11-4\sqrt{6})^{2}=121-88\sqrt{6}+96=217-88\sqrt{6}\approx 1,44$$
Объединим с (*) , тогда

т.е. $$a \in (-\infty ;-5-4\sqrt{2}]\cup (0; +\infty )$$
mathlesson.ru
261 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
А) Приведите пример такого двухзначного числа A, что последние цифры числа A2 составляют число А.
Б) Может ли такое двухзначное число А заканчиваться на 1?
В) Найдите все такие трёхзначные числа A, что последние три цифры числа A2 составляют число А.
A) Все числа, что при возведении в квадрат имеют аналогичную цифру в единицах , как и первоначальное оканчиваются на 0,1,5 или 6 ($$0^{2}=0$$ ;$$1^{2}=1$$; $$5^{2}=25$$; $$6^{2}=36$$). Возьмем число 25: $$25^{2}=625\Rightarrow$$ подходит
Б) Самый простой способ рассмотреть двузначное числа, оканчивающиеся на 1: $$11^{2}=121$$; $$21^{2}=441$$; $$31^{2}=961$$; $$41^{2}=1681$$; $$51^{2}=2601$$; $$61^{2}=3721$$; $$71^{2}=5041$$; $$81^{2}=6561$$; $$91^{2}=8281$$. Видим , что не может .
B) Пусть дано трёхзначное число x. При возведении такого числа в квадрат мы получим числа 4х, 5-ти или 6-ти значимые . Следовательно, чтобы данное $$x^{2}$$ оканчивалось на x должно выполняться условие: $$x^{2}-1000K=x$$, где $$K \in N$$ $$\Leftrightarrow$$ $$x^{2}-x=1000K\Leftrightarrow$$ $$x(x-1)=2^{3}*5^{3}K$$
Следовательно, x и x-1 числа последовательные натуральные, одно из них четное, второе –нет . При этом одно из них вида $$2^{3}*m$$, второе $$5^{3}*n$$, где m и n -делители $$K$$ ($$K_{max }=998$$). Рассмотрим 1 случай: $$x=2^{3}m$$, тогда $$x-1=2^{3}m-1$$ и оно трехзначное кратное 125:
$$2^{3}m-1=125\Rightarrow$$ $$2^{3}m=126\Rightarrow m \notin N$$
$$2^{3}m-1=250\Rightarrow$$ $$2^{3}m=251\Rightarrow m \notin N$$
$$2^{3}m-1=375\Rightarrow$$ $$2^{3}m=376\Rightarrow m =47$$
$$2^{3}m-1=500\Rightarrow$$ $$^{3}m=501\Rightarrow m \notin N$$
$$2^{3}m-1=625 \Rightarrow$$ $$2^{3}m=626 \Rightarrow m \notin N$$
$$2^{3}m-1=750\Rightarrow$$ $$2^{3}m=751\Rightarrow m \notin N$$
$$2^{3}m-1=875\Rightarrow$$ $$2^{3}m=876\Rightarrow m \notin N$$
Т.е. одно число равно 376. Рассмотрим 2-ой случай : $$x=5^{3} *n \Rightarrow$$ $$x-1=5^{3} *n-1$$, и оно трехзначное , кратное 8 :
$$n=1 \Rightarrow x-1=124$$,не кратно 8
$$n=2\Rightarrow x-1=249$$, не кратное 8
$$n=3 \Rightarrow x-1=374$$, не кратно 8
$$n=5 \Rightarrow x-1=624$$ $$\Rightarrow$$ кратно 8 $$\Rightarrow$$ $$x =625$$
$$n=7 \Rightarrow$$ $$x-1=724$$ , не кратно 8
$$n=9 \Rightarrow$$ $$x-1>100$$
Четыре n не рассматриваем, т.к. x-1 нечетно и не кратно 8 . Получим 2 числа: 376 и 625.
mathlesson.ru
260 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
В пирамиде SBCD каждое ребро равно 3. На ребре SB взята точка А так, что SA:AB=1:2.
А) В каком отношении плоскость ACD делит объем пирамиды?
Б) Найдите радиус сферы, описанной около пирамиды SACD.
A) 1) Пусть SO — высота SBCD. Опустим $$AM\perp (BCD)$$, тогда $$\DeltaAMB\sim \Delta SOB$$: $$\frac{AM}{SO}=\frac{AB}{SB}=\frac{2}{3}$$
2) $$V_{SBCD}=\frac{1}{3} SO*S_{BCD}$$; $$V_{ABCD}=\frac{1}{3} AM*S_{BCD}\Rightarrow$$$$V_{ABCD}=\frac{AM}{SO}*V_{SBCD}=\frac{2}{3}V_{SBCD}\Rightarrow$$, пусть V — оставшаяся часть: $$V=\frac{1}{3}V_{SBCD}\Rightarrow$$ $$\frac{V_{ABCD}}{V}=\frac{2}{1}$$
Б) 1) $$CA=AD\Rightarrow$$ $$\Delta ACD$$ — равнобедренный. Из $$\Delta SAC$$: $$CA=\sqrt{CS^{2}+SA^{2}-2 CS*SA *\cos S}=\sqrt{7}$$
2) Рассмотрим пирамиду SADC, введем ортогальную систему координат , как показано на рисунке, где N — центр, описанной окружности около $$\Delta SCD$$
3) Центр сферы будет лежать на оси Oz. Пусть Q — центр сферы, тогда $$Q (0;0;z)$$ и QS=QA (как радиусы сферы). Зададим координаты QS и QA; $$A(NA_{x}; O; AA_{x})$$, где $$A_{x}$$ — проекция A на (SDC) ; $$S(NS;0;0)$$
4) из $$\Delta CSD$$: $$SH=SD* \sin D=3*\frac{\sqrt{3}}{2}$$; $$SN=\frac{2}{3} SH=\sqrt{3}\Rightarrow$$ $$S(\sqrt{3}; 0;0)$$
Из $$\Delta ADC$$: $$AH=\sqrt{AD^{2}-HD^{2}}=\frac{\sqrt{19}}{2}$$; Из $$\Delta ASH$$: $$\cos S=\frac{AS^{2}+SH^{2}-AH^{2}}{2 AS*SH}=\frac{1}{\sqrt{3}}\Rightarrow$$ $$\sin S=\frac{\sqrt{2}}{\sqrt{3}}\Rightarrow$$ $$SA_{x}=AS*\cos S=\frac{1}{\sqrt{3}}\Rightarrow$$ $$NA_{x}=NS-SA_{x}=\frac{2\sqrt{3}}{3}$$; $$AA_{x}=SA*\sin S=\frac{\sqrt{2}}{\sqrt{3}}$$. Тогда A $$(\frac{2\sqrt{3}}{3};0; \frac{\sqrt{2}}{\sqrt{3}})$$, следовательно:
$$QS(\sqrt{3}-0;0-0; 0-z)=(\sqrt{3};0;-z)$$ и $$QA(\frac{2\sqrt{3}}{3}-0;0-0;\frac{\sqrt{2}}{\sqrt{3}}+z)=(\frac{2\sqrt{3}}{3};0; \frac{\sqrt{2}}{\sqrt{3}}+z)$$
Тогда длины: $$\left | QS \right |=\sqrt{(\sqrt{3})^{2}+(-z)^{2}}$$ и $$\left | QA \right |=\sqrt{(\frac{2\sqrt{3}}{3})^{2}+(\frac{\sqrt{2}}{\sqrt{3}}+z)^{2}}$$. В итоге получим:
$$QS^{2}=QA^{2}\Leftrightarrow$$ $$3+z^{2}=\frac{4}{3}+\frac{2}{3}+\frac{2\sqrt{2}}{\sqrt{3}}z+z^{2}\Leftrightarrow$$ $$\frac{2\sqrt{2}}{\sqrt{3}}z=1\Leftrightarrow$$ $$z=\frac{\sqrt{3}}{2\sqrt{2}}$$
Тогда $$QS=\sqrt{(\sqrt{3})^{2}+(\frac{\sqrt{3}}{2\sqrt{2}})^{2}}=$$$$\sqrt{\frac{27}{8}}=\frac{3}{2}\sqrt{\frac{3}{2}}$$
mathlesson.ru
265 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
В основании пирамиды с вершиной S лежит прямоугольник, центр которого находится на высоте пирамиды. Плоскость пересекает боковые ребра пирамиды в точках P, Q, M и N так, что Р и М – противоположные вершины четырехугольника PQMN. Известно, что $$SP=7$$, $$SM=\frac{7}{6}$$, $$SQ+SN=\frac{25}{6}$$, $$SQ>SN$$
А) Найдите SQ и SN
Б) Найдите, в каком отношении плоскость делит высоту пирамиды, если дополнительно известно, что боковое ребро пирамиды равно 10.
A) 1)Через P проведем плоскость параллельную (ABC): $$PQ_{1}M_{1}N{1})$$$$\Rightarrow$$ $$SP=SQ=SM_{1}=SN_{1}=7$$. Пусть H –центр ABCD $$\Rightarrow$$ SH –высота пирамиды; $$SH\cap (PQMN)=O$$, $$SH\cap (PQ_{1}M_{1}N_{1})=O_{1}$$ ; $$MM_{1}=SM_{1}-SM=\frac{35}{6}$$
2) Из $$\Delta SM_{1}P$$: $$M_{1}Q_{1}=O_{1}P\Rightarrow$$ по т. Менелая для $$\Delta MPM_{1}$$ : $$\frac{SO}{OO_{1}}*\frac{O_{1}P}{PM_{1}}*\frac{M_{1}M}{MS}=1\Leftrightarrow$$ $$\frac{SO}{OO_{1}}*\frac{1}{2}*\frac{35}{6}:\frac{7}{6}=1\Leftrightarrow$$ $$\frac{SO}{OO_{1}}=\frac{2}{5}$$
3) Рассмотрим $$\Delta SQ_{1}N_{1}$$: пусть $$SQ=x\Rightarrow$$ $$SN=\frac{25-x}{6}$$; Построим $$N_{2}Q_{2}\left | \right |N_{1}Q_{1}\Rightarrow$$ $$\Delta SON_{2}\sim \Delta SO_{1}N_{1}\Rightarrow$$ $$\frac{SN_{2}}{N_{2}N_{1}}=\frac{SO}{OO_{1}}=\frac{2}{5}$$. Т.е. $$SN_{1}=7$$, то $$SN_{2}=2=SQ_{2}$$, тогда $$N_{2}N=SN_{2}-SN=2-(\frac{25}{6}-x)=x-\frac{13}{6}$$; $$Q_{2}Q=SQ-SQ_{2}=x-2$$
По т. Менелая для $$\Delta NSQ$$: $$\frac{N_{2}O}{OQ_{2}}*\frac{Q_{2}Q}{QS}*\frac{SN}{NN_{2}}=1$$$$\Leftrightarrow$$ $$\frac{1}{1}*\frac{x-2}{x}*\frac{\frac{25}{6}-x}{x-\frac{13}{6}}=1$$$$\Leftrightarrow$$ $$(x-2)(\frac{25}{6}-x)=x(x-\frac{13}{6})|*6$$$$\Leftrightarrow$$ $$12x^{2}-50x+50=0\Leftrightarrow$$ $$6x^{2}-25x+25=0\Leftrightarrow$$ $$\left[\begin{matrix}x_{1}=\frac{5}{2}\\x_{2}=\frac{5}{3}\end{matrix}\right.$$
$$\frac{5}{3}$$ не подходит, т.к. $$\frac{25}{6}-\frac{5}{3}=\frac{5}{2}$$ и $$\frac{5}{3}<\frac{5}{2}$$, а по условию $$SQ>SN\Rightarrow$$ $$SQ=\frac{5}{2}$$; $$SN=\frac{5}{3}$$
Б) 1) Рассмотрим $$\Delta SHD$$: $$SQ_{2}=2$$; $$Q_{2}Q_{1}=5$$; $$Q_{1}D=SD-SQ_{1}=10-7=3\Rightarrow$$ $$Q_{2}D=5+3=8$$
2) $$\Delta SOQ_{2}\sim \Delta SHD\Rightarrow$$ $$\frac{SO}{OH}=\frac{SQ_{2}}{Q_{2}D}=\frac{2}{8}=\frac{1}{4}$$
mathlesson.ru
246 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Найдите все значения параметра , при которых система $$\left\{\begin{matrix}\log_{2} (3-x+y)=\log_{2} (25-6x+7y)\\ y+2=(x-2a)^{2}+a+2x\end{matrix}\right.$$ имеет ровно два решения
Рассмотрим область определения данной системы. Так как даны логарифмы, то: $$\left\{\begin{matrix}3-x+y>0\\25-6x+7y>0\end{matrix}\right.\Rightarrow$$ $$\left\{\begin{matrix}y>x-3\\y>\frac{6x-25}{7}\end{matrix}\right.$$ (желтым выделено решение для первого неравенства, синим — для второго, серым — их пересечение)
Рассмотрим первое уравнение системы:
$$\log_{2}(8(3-x+y))=\log_{2}(25-6x+7y)\Leftrightarrow$$$$24-8x+8y=25-6x+7y\Leftrightarrow$$$$y=2x+1 (1)$$
Построим график данной функции с учетом области определения:
Как видим, чтобы было два пересчения, x должен быть больше 4 (иначе часть прямой лежит вне области определения)
Подставим (1) во второе:$$2+2x+1=(x-2a)^{2}+a+2x\Leftrightarrow$$$$(x-2a)^{2}=3-a$$
Так как число в квадрате, то правая часть уравнения должна быть больше нуля (если равна нулю, то корень всего один): $$3-a>0\Rightarrow a<3$$
Рассмотрим график второгой функции:
$$y+2=x^{2}-4ax+2a^{2}+a+2x\Leftrightarrow$$$$y=x^{2}+x(2-4a)+4a^{2}+a-2$$
Найдем вершину параболы:
$$x_{0}=-\frac{2(1-2a)}{2}=2a-1$$
$$y_{0}=4a^{2}-4a+1-2(2a-1)^{2}+4a^{2}+a-2=8a^{2}-3a-1-8a^{2}+8a-2=5a-3$$
Рассмотрим возможное расположение графика с учетом области определения:
Как видим, координата y вершины параболы должна быть больше -8, а х больше -3 (если будет левее, то отно пересечение точно не попадет в область определения) :
$$\left\{\begin{matrix}2a-1>-3\\5a-3>-8\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}a>-1\\a>-1\end{matrix}\right.$$
С учетом того, что $$a<3$$, получаем: $$a \in (-1;3)$$
mathlesson.ru
248 вариант Алекса Ларина. Разбор ЕГЭ математика 2019
При изучении темы «Среднее арифметическое» в классе из 34 учащихся раздали синие и красные карточки, при этом каждый из учеников получил хотя бы одну карточку, но не более одной каждого цвета. На каждой карточке написано одно целое число от 0 до 20 (на различных карточках могут быть записаны одинаковые числа). Среднее арифметическое по всем розданным карточкам оказалось равным 15 по каждому цвету в отдельности. Затем каждый ученик назвал наибольшее из чисел на своих карточках (если ему досталась одна карточка, то он назвал число, написанное на этой карточке). Среднее арифметическое всех названных чисел оказалось равно S.
а) Приведите пример, когда S<15
б) Могло ли S быть равным 9?
в) Найдите наименьшее значение S , если по две карточки получили 17 учеников.
A) Пусть у 30 человек и синие, и красные , но каждой из которых по 16 , у двух синие с О и у двух красных с О
Синие: $$\frac{30*16+2*0}{32}=15$$
Красные :$$\frac{30*16+2*0}{32}=15$$
Условие среднего арифметического выполняются : $$S=\frac{30*16+4*0}{34}<15\Rightarrow$$ да
Б) Пусть:
k людей , у которых и синие и красные
a-сумма всех чисел у людей только с одной карточкой
b-сумма максимальных чисел у людей с двумя карточками
c-минимальных
Так как средняя для синих и красных отдельно составляет 15, то и среднее для всех вообще чисел равно 15.
При этом всего было выдано $$34+k$$ карточек. Значит общая сумма $$15(34+k)=510+15k$$ . С другой стороны эту же сумму можно представить как $$a+b+c$$: $$a+b+c=510+15k(1)$$. При этом $$a+b=9*34=306$$ . Подставим в (1): $$306+c=510+15k\Leftrightarrow$$ $$c=204+15k$$
С другой стороны $$c\leq 20k$$ ( сумма наименьших будет максимальна если на всех карточках число 20)
Получаем: $$204+15k\leq 20k\Leftrightarrow$$ $$5k\geq 204\Leftrightarrow$$ $$k\geq 40,8$$ но $$k\leq 34$$, следовательно , нет.
B) Аналогично, $$a+b =34S, a+b+c=15(34+17)$$.Тогда $$34S+c=765\Rightarrow$$ $$S=\frac{765-c}{34}$$. Очевидно , что $$S\Rightarrow min$$, при $$c\Rightarrow max$$, т.е. $$S\geq \frac{765-17*20}{34}=12,5$$
Найдем такой пример :
У нас 17 человек с карточками красными и синими на каждой из которых по 20, тогда сумма на все оставшиеся карточки (по одной) составит :
$$765-2*340=85$$. При этом она приходится на 17 человек с одной карточкой . Пусть y-сумма на синих, тогда 85-y-на красных. Учитывая среднее 15 для синих и красных :
$$\left\{\begin{matrix}340+y=15(17+N)\\340+85-y=15(17+17-N)\end{matrix}\right.$$, Где N-число синих , тогда красных 17-N (речь идет об одиночных карточках)
$$\left\{\begin{matrix}\frac{340+y}{15}=17+N\\\frac{425-y}{15}=34-N\end{matrix}\right.$$
Слева должны быть натуральные числа, т.е. 340+y и 435-y делятся нацело на 15 . При y=20 получим :
$$\frac{340+20}{15}=\frac{360}{15}=24=17+N\Rightarrow N=7$$
$$\frac{425-20}{15}=27$$
Условия выполнились, следовательно , если у 17 человек синие и красные с числами 20, у 17 человек только синие с общей суммой 20( например 1+2+3+4+5+2+3) и у 10 только красных с суммой 65 (7+7+7+7+7+7+7+7+7+2), то S=12,5
mathlesson.ru

Leave A Comment