ЕГЭ-2022, математика. Все задачи с решениями

Каким был ЕГЭ по математике в 2022 году?

Мы знаем, что в 2022 году формат ЕГЭ по математике изменился. Поменялась нумерация заданий. Добавились новые задачи: №9 (Функции и графики) и № 10 (Теория вероятностей). И в первой части стало на 1 задачу меньше.

Во второй части ЕГЭ также произошли изменения.

«Экономическая» задача, которая теперь под № 15, оценивается уже не в 3, а только в 2 первичных балла.

А вот задача по стереометрии, №13, наоборот, «подорожала» и теперь оценивается в 3 балла.

Расскажем о заданиях 2 части ЕГЭ, задачах 13-18, а затем подробно разберем различные типы таких задач.
Задание 12, уравнения. Все стандартно, просто тригонометрия.

Задание 13, стереометрия. По сравнению с прошлыми годами сложность значительно выше. Здесь и теорема Менелая, и произвольная призма, и пересечение сфер.

Задача 14, неравенство. Все стандартно – показательное неравенство, замена переменной. Помним о секретах решения таких задач! Сделав замену, сначала полностью решаем неравенство для новой переменной, затем возвращаемся к первоначальной.

Задача 15, экономическая. В 2022 году были только кредиты и вклады. Обошлись без задач на оптимизацию.

Задача 16, планиметрия. Простые задания, без затей. Подобные треугольники, теорема косинусов, свойство биссектрисы треугольника, в общем, обязательная школьная программа по геометрии.

Задание 17, задачи с параметрами. Составители вариантов порадовали разнообразием: был и графический метод, и аналитический. И решение квадратных уравнений с параметрами. И в каждом задании присутствовали модули, так что кто эту тему не знает, надо повторить!

Изучить «параметры» с нуля можно с помощью

Видеокурса Анны Малковой

Полный курс, 26 часов видео, 13 видеоуроков. 11 методов решения задач с параметрами.

И наконец, задание 18, задачи на числа и их свойства. Все типы заданий – новые, нестандартные. Числа на круге, использование делимости и остатков.

Освоить эту необычную задачу можно с помощью видеокурса Анны Малковой.

Полный курс, 10 видеоуроков по 2 часа. 11 методов решения задач на числа и их свойства.

А теперь подробно о каждом задании ЕГЭ-2022, 2 часть.

Уравнения на EГЭ -2022 по математике, задача 12

Cтереометрия на EГЭ-2022 по математике, задача 13

Hеравенства на EГЭ-2022 по математике, задача 14

Экономические задачи и финансовая математика на ЕГЭ-2022, задача 15

Планиметрия на EГЭ-2022 по математике, задача 16

Задачи с параметрами на ЕГЭ-2022: модули, окружности, квадратные уравнения

Задача 18 на числа и их свойства на ЕГЭ-2022 по математике

 

Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «ЕГЭ-2022, математика. Все задачи с решениями» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.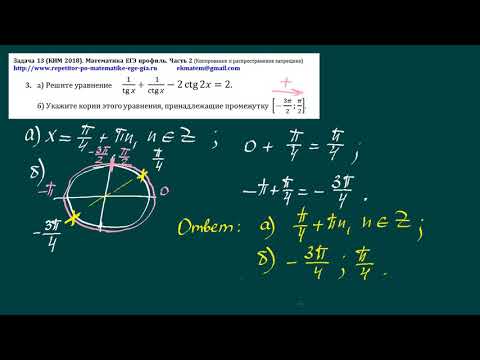

Публикация обновлена: 08.04.2023

ЕГЭ по математике 2022 — задания с развернутым ответом

Задания ЕГЭ с развернутым ответом — самые сложные в экзамене по любому предмету. А о математике так вообще ходят легенды! Выпускники настолько боятся этих задач, что даже не пытаются к ним готовиться, пропускают, не читая, во время экзамена. И это стоит им стольких баллов!

Что из себя представляют задания с развернутым ответом в ЕГЭ по математике?

Вторая часть экзамена по профильной математике целиком состоит из заданий ЕГЭ с развернутым ответом — от №12 до №18. Они проверяют углубленное знание предмета, поэтому без решения хотя бы их части невозможно получить 80+ баллов.

Задание №12 — это решение сложного уравнения и определение корней в рамках обозначенного отрезка. За него можно получить максимум 2 балла.

Задание №13 — это геометрическая задача на доказательство утверждения и нахождение одного из показателей. Максимальный балл — 3.

Задание №14 — это решение сложного неравенства (например, логарифмического). Максимальный балл — 2.

Задание №15 — классическая экономическая задача. За нее можно получить до 2 баллов.

Задание №16 — сложная геометрическая задача, с которой справляются только 2.7% выпускников. Проверяется примерно то же, что в №13, и приносит также 3 балла.

Задание №17 — это решение системы уравнений. При этом, нужно будет найти все возможные переменные, соответствующие заданному условию (например, положительные, при которых система имеет только одно решение). Максимальный балл — 4.

Задание №18 — это работа с теорией чисел, в которой придется руководствоваться не только знаниями, но и старым добрым логическим подбором. Максимальный балл — 4.

В чем их основная сложность?

Задания ЕГЭ с развернутым ответом №12, 14, 15  самые легкие из второй части, поэтому их желательно научиться решать в первую очередь. Они принесут дополнительные баллы и позволят получить высокий результат на экзамене.

А вот №16–18 — номера повышенной сложности, с которыми удается справиться далеко не каждому выпускнику. Для их решения потребуется основательная подготовка.

При этом, при подготовке и решении второй части ЕГЭ по математике нужно помнить об оформлении и доказательной базе. Забытое ОДЗ при решении уравнения или неравенства или непоясненное действие при доказательстве может стоить драгоценных баллов!

Как решать задания с развернутым ответом?

Решать задания ЕГЭ с развернутым ответом нужно с самых простых задач: например, с простых алгебраических вычислений (№12, 14). После подготовки и регулярного нарешивания они не займут на самом экзамене много времени. После можно выполнить экономическую задачу и все, что получается решить. В оставшееся время нужно проверить ответы и попытаться решить оставшееся.

При подготовке можно руководствоваться правилами оформления прошлого года, но нужно помнить про изменившуюся нумерацию!

Почему стоит браться за эти задачи?

Большинство выпускников в принципе не берется за решение второй части, поэтому правильно решенная первая часть и задачи из второй — сильное конкурентное преимущество. Именно они станут залогом 90+ за математику и позволят поступить на бюджет в самые престижные вузы страны.

Что говорит статистика?

И преимущество перед другими будет действительно колоссальным, потому что по статистике правильно решают задачи второй части единицы:

  • около 30% — за №12,
  • около 2% — за №13,
  • около 12% — за №14,
  • около 15% — за №15,
  • около 2,7% — за №16,
  • около 1% — за №17 и №18.

Без подготовки решить вторую часть по математике практически нереально. Именно этим объясняются неутешительные проценты выполнения номеров и средние баллы по предмету. Но такая сложность — это конкурентное преимущество подготовившихся учеников, которое поможет поступить в вуз мечты!

Математика — Задания высокого качества

Иногда учитель может дополнить материалы учебного плана, принятого школьным округом, уроком, основанным на заданиях. В других случаях учитель может захотеть заменить за урок. Высококачественные задания ценны своей глубиной мышления, возможностями для командной работы и возможностями для улучшения объяснений и рассуждений учащихся. В сочетании с хорошей учебной рутиной качественное задание является ценным обучающим опытом.

Иллюстративная математика — это веб-сайт с заданиями, сопоставленными с каждым из основных государственных стандартов, K-12. Многие из задач являются выдающимися, хотя они просты. Задания IM предлагают версию для печати для учащихся, а также страницу для учителей с «комментариями» о том, как подходить к обучению заданию. Многие задачи IM подходят для учебной программы «5 практик».

Illustrative Mathematics также предлагает бесплатную учебную программу по математике для 6, 7 и 8 классов.

Задания MARS ориентированы на оценивание, поэтому они снабжены оценочной рубрикой. Их также можно использовать в качестве качественной задачи в среде, не связанной с оцениванием. Они перечислены по уровням обучения, по требуемой степени независимости и по Общему базовому стандарту.

MARS также публикует уроки формирующего оценивания (классные задания).

Задания из 3-х актов предназначены для того, чтобы решение задач по математике было похоже на рассказ. В акте 1 учащиеся наблюдают за математической ситуацией, формулируют математический вопрос и делают первые предположения о решении этого вопроса. В акте 2 учащиеся решают, какая еще информация им нужна для решения их проблемы. Учитель предоставляет дополнительную информацию, а учащиеся занимаются математикой, чтобы решить задачу и уточнить свои предполагаемые ответы. В акте 3 раскрывается ответ на вопрос, и учащиеся размышляют об успешности своего процесса и возможных источниках ошибок. .»

Акт 1 «Зубочистки» Дэна Мейера.мова

Акт 1 «Зубочистки» Дэна Мейера

3-актные задания были созданы и опубликованы многими учителями.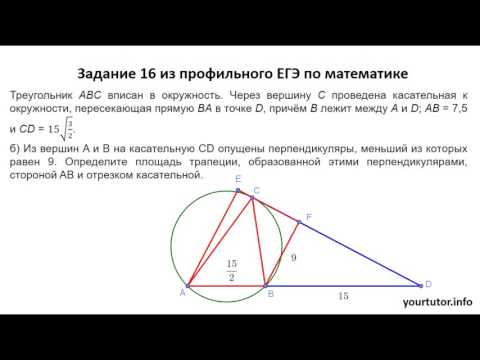 Ниже приведены списки заданий, опубликованных каждым учителем.

  • Дан Мейер. Актовые задачи (хорошо для элементарного!)

Другие источники проблемных уроков и высококачественных задач

  • Emergent Math (Geoff Krall) Карты на основе проблемной программы

  • Проблемная поиска (Роберт Kaplinsk Каплинский — Уроки

  • Оценка 180 — уроки по стандарту

Обоснование решения

На уроках математики учителям следует побуждать учащихся концентрировать внимание не только на правильном ответе; учащиеся должны понимать процесс и лежащие в его основе понятия, чтобы получить правильный ответ (Johnson & Watson, 2011). Другими словами, учащиеся должны найти и обосновать свои решения.

Чтобы обосновать решение, учащиеся должны уметь использовать соответствующий математический язык, чтобы обосновать конкретный подход, используемый для решения проблемы. Каждый раз, когда учащийся предлагает «решение» в попытке решить проблему, это «решение» необходимо обосновать. То есть учащийся должен объяснить, откуда он знает, что его «решение» правильное.

Обоснование решения также может возникнуть в контексте обсуждения математики в классе, когда учащиеся должны будут устно объяснить свои решения.

Чтобы помочь учащимся обосновать свои решения, учитель может:

  • есть класс обсуждение того, что значит обосновать решение

    • Учитель может попросить некоторых учащихся обрисовать в общих чертах, как они могут обосновать конкретное решение из предыдущего урока.

    Может быть полезно обсудить ключевую терминологию, связанную с изучаемой математической темой, чтобы стимулировать студентов к обсуждению. Эти ключевые термины можно найти в классе и записать на доске.

  • предложите учащимся задачу и попросите их решить ее, записывая свои обоснования

  • попросите учащихся работать в парах, чтобы обосновать свои решения

  • попросите пары поделиться и дать конструктивную обратную связь относительно обоснований друг друга.


В приведенном ниже примере показано, как эту стратегию можно применить к классу 10-го класса по линейным уравнениям.

Сценарий: взимание платы за выполнение задачи


Сравните два следующих расчета платы за услугу, где C означает стоимость (в долларах) выполнения задачи, а t — время, затраченное (в часах) на выполнение задачи:

Определите, когда первое уравнение дешевле второго

C = 25t + 200
C = 30t +150

Разработка решения


Учащиеся будут работать над решением задачи. Либо графически, либо путем решения одновременных уравнений время, для которого затраты равны, составляет 10 часов.

Примечание. Время, в течение которого первая ставка меньше второй, считается временем, превышающим 10 часов.

Обсуждение в классе


Обсудите в классе, что значит обосновывать решение. Попросите некоторых студентов обрисовать, как они могли бы обосновать свое конкретное решение.