На левом рисунке представлены векторы скорости и ускорения тела какой: На левом рисунке представлены векторы скорости и ускорения тела. Какой из четырёх векторов на правом рисунке указывает направление

Тест Импульс тела 9 класс

24.10.2020 Физика Тесты9 класс

Тест Импульс тела 9 класс с ответами. Тест включает 10 заданий.

1. Тело массой m движется со скоростью v. Как найти импульс тела?

1) ^mv2/₂
2) ^mv/₂
3) mv
4) mv

2. На левом рисунке представлены векторы скорости и ускорения тела. Какой из четырех векторов на правом рисунке указывает направление импульса тела?

1) 1
2) 2
3) 3
4) 4

3. На рисунке представлена траектория движения мяча, брошенного под углом к горизонту. Куда направлен импульс мяча в высшей точке траектории? Сопротивление воздуха пренебрежимо мало.

1) 1
2) 2
3) 3
4) 4

4. Какое тело имеет импульс, равный нулю?

1) взлетающая ракета
2) ракета, летающая по круговой орбите
3) книга, лежащая на парте

4) парашютист, движущийся равномерно вниз

5. Два шарика массой по 200 г движутся навстречу друг другу с одинаковыми скоростями. Выберите верное(-ые) утверждение(-я).

А. Импульсы этих шаров равны.
Б. Проекции импульсов этих шаров равны.
В. Модули импульсов этих шаров равны.

1) только А
2) только Б
3) только В
4) А и Б

6. Алюминиевый и стальной бруски одинакового объема двигаются по гладкой горизонтальной поверхности в одну сто­рону с одинаковыми скоростями. Сравните импульсы этих брусков. (ρ_ал. = 2,7 г/см³; ρ_ст.

= 7,8 г/см³)

1) импульс алюминиевого бруска больше
2) импульс стального бруска больше
3) импульсы брусков одинаковы
4) среди ответов нет правильного

7. Чему равен импульс тела массой 400 г при скорости 4 м/с?

1) 1,6 кг·м/с
2) 0,8 кг·м/с
3) 32 кг·м/с
4) 64 кг·м/с

8. Чему равен импульс автомобиля, если его масса 1 т и он движется со скоростью 72 км/ч?

1) 72 кг·м/с
2) 20 000 кг·м/с
3) 20 кг·м/с
4) 72 000 кг·м/с

9. Каким импульсом обладает ворона, сидящая на заборе высотой 2,5 м? Масса вороны 500 г.

1) 1,25 кг·м/с
2) 0 кг·м/с
3) 250 кг·м/с
4) 5 кг·м/с

10. Легковой автомобиль и грузовик движутся со скоростями 30 м/с и 20 м/с соответственно. Масса автомобиля 1000 кг. Какова масса грузовика, если отношение импульса грузовика к импульсу автомобиля равно 2?

1) 3000 кг
2) 4500 кг
3) 1500 кг
4) 1000 кг

Ответы на тест Импульс тела 9 класс
1-4
2-1
3-3
4-3
5-3
6-2
7-1
8-2
9-2
10-1

PDF версия для печати
Тест по физике Импульс тела 9 класс
(150 Кб)

Опубликовано: 24.10.2020 Обновлено: 24.10.2020

Поделись с друзьями

Найти:

на левом рисунке представлены векторы скорости и ускорения тела. какой из четырех векторов на правом рисунке указывает направление вектора силы, действующей на это тело?

Последние вопросы

• Физика

  6 минут назад

  Если российские учителя математики/физики/химии поправляют английские названия букв латиницы на французские, это норма?

• Физика

  47 минут назад

  Помогите с физикой пожалуйста 7 класс.

• Физика

  47 минут назад

  Тело массой 5000 кг расположено на наклонной плоскости диной 8м и высотой 3м. Какую силу надо приложить к телу, чтобы удержать его на плоскости, если сила направлена параллельно наклонной плоскости. Коэффициент трения покоя принять равным 0,02.

• Физика

  1 час назад

  Помогите пж с домашним заданием

• Физика

  1 час назад

  Помогите, пожалуйста, очень срочно!!!

• Физика

  1 час назад

  В каком случае к лампы и показания вольтметра при нахождении выводов обмоток будут наибольшими (наименьшими)?​

• Физика

  1 час назад

  5. -2 кг/м3 на стенки сосуда, если средняя скорость движения его молекул равна 400 м/с?

• Физика

  2 часа назад

  Физика 7 класс

• Физика

  2 часа назад

  Допоможіть будь ласка . Спам блокую

• Физика

  2 часа назад

  Помогите посчитать формулу

• Физика

  3 часа назад

  якій зміні маси відповідає зміна повної енергії тіла на 900 дж​

• Физика

  3 часа назад

  Физика, домашняя работа

• Физика

  4 часа назад

  Физика помогите срочно 8 класс

Все предметы

Выберите язык и регион

English

United States

Polski

Polska

Português

Brasil

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Русский

Россия

How much to ban the user?

1 hour 1 day 100 years

Ускорение

Как упоминалось ранее в Уроке 1, объект, движущийся в равномерном круговом движении, движется по окружности с равномерной или постоянной скоростью. Вектор скорости постоянен по величине, но изменяется по направлению. Поскольку скорость для такого движения постоянна, у многих студентов возникает неправильное представление об отсутствии ускорения. «Ведь, — могут сказать они, — если бы я вел машину по кругу с постоянной скоростью 20 миль в час, то скорость не уменьшается и не увеличивается, следовательно, не должно быть ускорения». В основе этого распространенного студенческого заблуждения лежит ошибочное убеждение, что ускорение связано со скоростью, а не со скоростью. Но дело в том, что ускоряющийся объект — это объект, изменяющий свою скорость. А поскольку скорость — это вектор, который имеет как величину, так и направление, изменение либо величины, либо направления представляет собой изменение скорости. По этой причине можно с уверенностью заключить, что объект, движущийся по кругу с постоянной скоростью, действительно ускоряется. Он ускоряется, потому что направление вектора скорости меняется.

 

Геометрический

Доказательство Внутреннего Ускорения

Чтобы понять это на более глубоком уровне, нам придется объединить определение ускорения с обзором некоторых основных векторных принципов.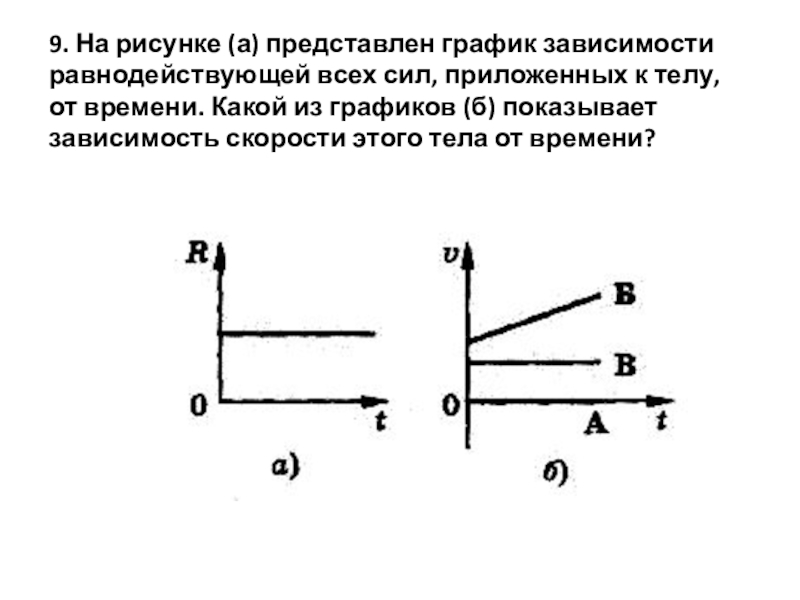 Вспомним из раздела 1 курса физики, что ускорение как величина определяется как скорость, с которой изменяется скорость объекта. Таким образом, он рассчитывается с использованием следующего уравнения:

, где v _i представляет собой начальную скорость, а v _f представляет конечную скорость через некоторое время

t . Числитель уравнения находится путем вычитания одного вектора ( v _i ) из второго вектора ( v _f ). Но сложение и вычитание векторов друг из друга осуществляется совершенно иначе, чем сложение и вычитание скалярных величин. Рассмотрим случай, когда объект движется по кругу вокруг точки C, как показано на диаграмме ниже. За время t секунд объект переместился из точки A в точку B. За это время скорость изменилась с v _i до v _f . Процесс вычитания v _i из v _f показан на векторной диаграмме; этот процесс приводит к изменению скорости.

 

Направление вектора ускорения

Обратите внимание на приведенную выше диаграмму, что существует изменение скорости для объекта, движущегося по кругу с постоянной скоростью. Внимательное рассмотрение вектора изменения скорости на приведенной выше диаграмме показывает, что он указывает вниз и влево. В середине дуги, соединяющей точки А и В, изменение скорости направлено к точке С — центру окружности. Ускорение объекта зависит от этого изменения скорости и находится в том же направлении, что и это изменение скорости. Ускорение объекта совпадает с направлением вектора изменения скорости; ускорение также направлено к точке С — центру окружности. Объекты, движущиеся по кругу с постоянной скоростью, ускоряются к центру круга.

Ускорение объекта часто измеряется с помощью устройства, известного как акселерометр. Простой акселерометр состоит из объекта, погруженного в жидкость, например воду.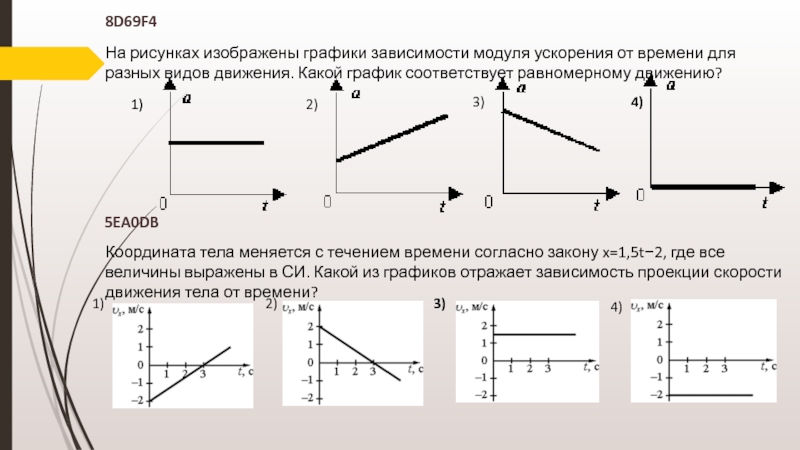 Рассмотрим запечатанный сосуд, наполненный водой. Пробка, прикрепленная к крышке шнурком, может служить акселерометром. Чтобы проверить направление ускорения объекта, движущегося по кругу, банку можно перевернуть и прикрепить к концу короткого отрезка деревянного бруска 2×4. Второй акселерометр, построенный таким же образом, можно прикрепить к противоположному концу 2×4. Если 2х4 и акселерометры прижать к вращающейся платформе и крутить по кругу, направление ускорения можно четко увидеть по направлению наклона пробок. Когда комбинация пробка-вода вращается по кругу, пробка наклоняется к центру круга. Наименее массивный из двух объектов всегда наклоняется в направлении ускорения. В случае с пробкой и водой пробка менее массивна (в пересчете на миллилитр) и поэтому испытывает большее ускорение. Имея меньшую инерцию (из-за меньшей массы в пересчете на миллилитр), пробка меньше всего сопротивляется ускорению и, таким образом, наклоняется внутрь банки к центру круга. Это наблюдаемое свидетельство того, что объект, движущийся по окружности с постоянной скоростью, испытывает ускорение, направленное к центру окружности.

 

Еще один простой самодельный акселерометр включает в себя зажженную свечу, расположенную вертикально по центру открытого стекла. Если стакан держать горизонтально и в покое (так что ускорения нет), то пламя свечи распространяется вверх. Однако, если вы держите систему стекло-свеча вытянутой рукой и вращаете ее по кругу с постоянной скоростью (такой, что пламя испытывает ускорение), то пламя свечи больше не будет простираться вертикально вверх. Вместо этого пламя отклоняется от вертикального положения. Это означает, что есть ускорение, когда пламя движется по круговой траектории с постоянной скоростью. Отклонение пламени будет в сторону ускорения. Это можно объяснить, утверждая, что горячие газы пламени менее массивны (в расчете на миллилитр) и, следовательно, имеют меньшую инерцию, чем окружающие его более холодные газы. Следовательно, более горячие и легкие газы пламени испытывают большее ускорение и будут наклоняться в направлении ускорения. Тщательное изучение пламени показывает, что пламя будет направлено к центру круга, что указывает, таким образом, не только на ускорение; но что есть внутреннее ускорение. Это еще одно наблюдаемое свидетельство, указывающее на то, что объекты, движущиеся по кругу с постоянной скоростью, испытывают ускорение, направленное к центру круга.

Итак, до сих пор мы видели геометрическое доказательство и две реальные демонстрации этого внутреннего ускорения. В этот момент это становится решением ученика верить или не верить. Разумно ли, что тело, движущееся по окружности, испытывает ускорение, направленное к центру окружности? Можете ли вы придумать логическую причину верить, скажем, в отсутствие ускорения или даже во внешнее ускорение, испытываемое объектом, движущимся по равномерному круговому движению? В следующей части Урока 1 будут представлены дополнительные логические доказательства в поддержку понятия внутренней силы для объекта, движущегося по окружности.

 

 

Мы хотели бы предложить…

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения Uniform Circular Motion. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащимся в интерактивном режиме исследовать векторы скорости, ускорения и силы для объекта, движущегося по кругу.

Посетите: Интерактивный сайт Uniform Circular Motion

Проверьте свое понимание

1. Ниже показаны начальная и конечная скорости мяча в два разных момента времени. Направление мяча указано стрелкой. Для каждого случая укажите, есть ли ускорение. Объясните, почему да или почему нет. Укажите направление ускорения.

а.
Ускорение: да или нет? Объяснять.	Если есть ускорение, то в каком направлении?

б.
Ускорение: да или нет? Объяснять.	Если есть ускорение, то в каком направлении?

в.
Ускорение: да или нет? Объяснять.	Если есть ускорение, то в каком направлении?

д.
Ускорение: да или нет? Объяснять.	Если есть ускорение, то в каком направлении?

эл.
Ускорение: да или нет? Объяснять.	Если есть ускорение, то в каком направлении?

 

2. Объясните связь между вашими ответами на приведенные выше вопросы и рассуждениями, используемыми для объяснения того, почему можно сказать, что объект, движущийся по кругу с постоянной скоростью, испытывает ускорение.

 

3. Диззи Смит и Гектор Вектор все еще обсуждают №1e. Диззи говорит, что мяч не ускоряется, потому что его скорость не меняется. Гектор говорит, что поскольку мяч изменил свое направление, значит, есть ускорение. С кем ты согласен? Аргументируйте позицию, объяснив несоответствие в аргументации другого студента.

 

 

4. Назовите три элемента управления автомобилем, которые позволяют ему ускоряться.

 

 

Для вопросов #5-#8: Объект движется в по часовой направлении по окружности с постоянной скоростью. Используйте свое понимание понятий скорости и ускорения, чтобы ответить на следующие четыре вопроса. Используйте схему, показанную справа.

5. Какой из приведенных ниже векторов представляет направление вектора скорости, когда объект находится в точке B на окружности?

 

 

6. Какой из приведенных ниже векторов представляет направление вектора ускорения, когда объект находится в точке C на окружности?

 

 

7. Какой из приведенных ниже векторов представляет направление вектора скорости, когда объект находится в точке C на окружности?

 

 

8. Какой из приведенных ниже векторов представляет направление вектора ускорения, когда объект находится в точке А на окружности?

 

 

 

 

Следующий раздел:

Перейти к следующему уроку:

6.2 Равномерное круговое движение | Техасский шлюз

Цели обученияЦентростремительное ускорениеЦентростремительная силаРешение задач на центростремительное ускорение и центростремительную силуПрактические заданияПроверьте свое понимание

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Описывать центростремительное ускорение и связывать его с линейным ускорением
• Опишите центростремительную силу и свяжите ее с линейной силой
• Решение задач на центростремительное ускорение и центростремительную силу

«>

Основные термины раздела

центробежная сила	центростремительное ускорение	центростремительная сила
равномерное круговое движение

Центростремительное ускорение

В предыдущем разделе мы определили круговое движение. Простейшим случаем кругового движения является равномерное круговое движение, когда объект движется по круговому пути с постоянной скоростью . Обратите внимание, что, в отличие от скорости, линейная скорость объекта в круговом движении постоянно меняется, потому что он всегда меняет направление. Из кинематики мы знаем, что ускорение есть изменение скорости либо по величине, либо по направлению, либо по тому и другому. Следовательно, объект, совершающий равномерное круговое движение, всегда ускоряется, даже если величина его скорости постоянна.

Вы сами испытываете это ускорение каждый раз, когда едете в машине, когда она поворачивает за угол. Если вы держите руль неподвижно во время поворота и двигаетесь с постоянной скоростью, вы выполняете равномерное круговое движение. Что вы заметите, так это ощущение скольжения (или отбрасывания, в зависимости от скорости) от центра поворота. Это не реальная сила, действующая на вас — это происходит только потому, что ваше тело хочет продолжать движение по прямой линии (согласно первому закону Ньютона), в то время как автомобиль сворачивает с этой прямолинейной траектории. Внутри машины создается впечатление, что вас выталкивает из центра поворота. Эта фиктивная сила известна как центробежная сила. Чем круче кривая и чем больше ваша скорость, тем заметнее становится этот эффект.

На рис. 6.7 показан объект, движущийся по круговой траектории с постоянной скоростью. Направление мгновенной тангенциальной скорости показано в двух точках вдоль траектории. Ускорение направлено в сторону изменения скорости; в этом случае он указывает примерно на центр вращения. (Центр вращения находится в центре кругового пути). Если представить, что ΔsΔs становится все меньше и меньше, то ускорение направит точно на к центру вращения, но этот случай трудно изобразить. Назовем ускорение тела, движущегося равномерно по окружности, центростремительным ускорением a _c , потому что центростремительный означает центр, ищущий .

Рис. 6.7 Показаны направления скорости объекта в двух разных точках, и видно, что изменение скорости ΔvΔv указывает приблизительно на центр кривизны (см. маленькую вставку). Для чрезвычайно малого значения ΔsΔs ΔvΔv указывает точно на центр круга (но это трудно нарисовать). Поскольку ac=Δv/Δtac=Δv/Δt, ускорение также направлено к центру, поэтому a _c называется центростремительным ускорением.

Теперь, когда мы знаем, что направление центростремительного ускорения направлено к центру вращения, давайте обсудим величину центростремительного ускорения. Для объекта, движущегося со скоростью v по круговой траектории с радиусом r , модуль центростремительного ускорения равен

.

ac=v2r.ac=v2r.

Центростремительное ускорение больше на высоких скоростях и в крутых поворотах (меньший радиус), как вы могли заметить, управляя автомобилем, потому что автомобиль фактически толкает вас к центру поворота. Но немного удивительно, что a _c пропорционально квадрату скорости. Это означает, например, что ускорение в четыре раза больше при движении по кривой на скорости 100 км/ч, чем на скорости 50 км/ч.

Мы также можем выразить a _c через величину угловой скорости. Подставляя v=rωv=rω в приведенное выше уравнение, мы получаем ac=(rω)2r=rω2ac=(rω)2r=rω2. Следовательно, величина центростремительного ускорения через величину угловой скорости равна

6,9.ас=rω2.ac=rω2.

Советы по достижению успеха

Уравнение, выраженное в форме a _c = rω ² , полезно для решения задач, в которых известна угловая скорость, а не тангенциальная скорость.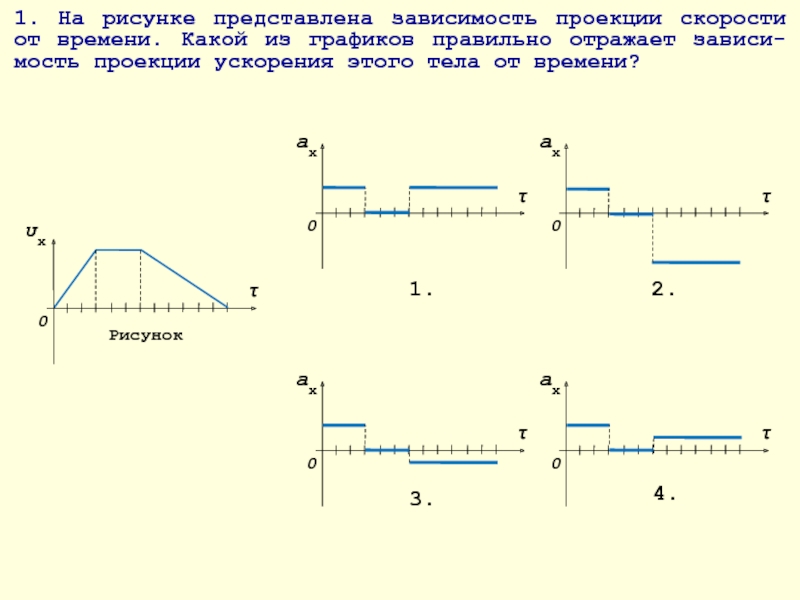

Виртуальная физика

Движение божьей коровки в 2D

В этой симуляции вы экспериментируете с положением, скоростью и ускорением божьей коровки в круговом и эллиптическом движении. Переключите тип движения с линейного на круговой и наблюдайте за векторами скорости и ускорения. Затем попробуйте эллиптическое движение и обратите внимание, как векторы скорости и ускорения отличаются от векторов кругового движения.

Рисунок 6.8 Щелкните здесь для моделирования

Проверка хватки

Каков угол между ускорением и скоростью при равномерном круговом движении? Какое ускорение испытывает тело при равномерном движении по окружности?

1. Угол между ускорением и скоростью равен 0°, и тело испытывает линейное ускорение.
2. Угол между ускорением и скоростью равен 0°, и тело испытывает центростремительное ускорение.
3. Угол между ускорением и скоростью равен 90°, и тело испытывает линейное ускорение.
4. Угол между ускорением и скоростью равен 90°, и тело испытывает центростремительное ускорение.

Центростремительная сила

Поскольку объект, совершающий равномерное круговое движение, испытывает постоянное ускорение (за счет изменения направления), из второго закона Ньютона мы знаем, что на объект должна действовать постоянная результирующая внешняя сила.

Любая сила или комбинация сил может вызвать центростремительное ускорение. Всего несколько примеров: натяжение веревки на шаре, сила земного притяжения на Луне, трение между дорогой и шинами автомобиля, когда он движется по кривой, или нормальная сила американских горок. след на тележке во время петли.

Любая результирующая сила, вызывающая равномерное круговое движение, называется центростремительной силой. Центростремительная сила направлена ​​к центру вращения, как и центростремительное ускорение. Согласно второму закону Ньютона, результирующая сила вызывает ускорение массы согласно формуле F _net = м a . Для равномерного кругового движения ускорение равно центростремительному ускорению: a = a _c . Следовательно, величина центростремительной силы F _c , это Fc=macFc=mac.

Используя две разные формы уравнения для величины центростремительного ускорения, ac=v2/rac=v2/r и ac=rω2ac=rω2, мы получаем два выражения, включающие величину центростремительной силы F _c . Первое выражение в терминах тангенциальной скорости, второе в терминах угловой скорости: Fc=mv2rFc=mv2r и Fc=mrω2Fc=mrω2.

Обе формы уравнения зависят от массы, скорости и радиуса кругового пути. Вы можете использовать любое более удобное выражение для центростремительной силы. Второй закон Ньютона также гласит, что объект будет ускоряться в том же направлении, что и результирующая сила. По определению центростремительная сила направлена ​​к центру вращения, поэтому объект также будет ускоряться по направлению к центру.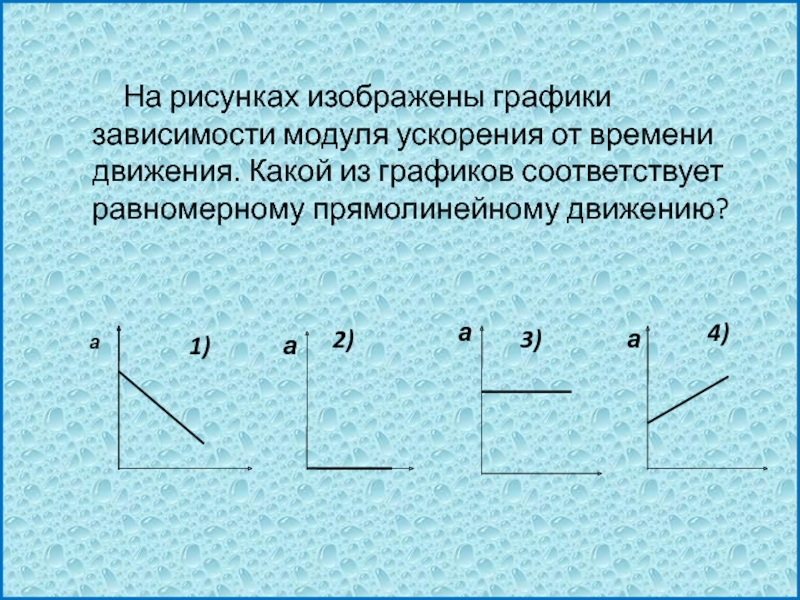 Прямая линия, проведенная от кругового пути к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание, что если вы решите первое выражение для р , получается

r=mv2Fc.r=mv2Fc.

Из этого выражения мы видим, что при данной массе и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть крутую кривую.

Рисунок 6.9 На этом рисунке сила трения f служит центростремительной силой F _c . Центростремительная сила перпендикулярна тангенциальной скорости и вызывает равномерное круговое движение. Чем больше центростремительная сила F _c , тем меньше радиус кривизны r и тем острее кривая. Нижняя кривая имеет ту же скорость v , но большая центростремительная сила F _c создает меньший радиус r′r′.

Watch Physics

Центростремительная сила и интуиция ускорения

В этом видео объясняется, почему центростремительная сила создает центростремительное ускорение и равномерное круговое движение. Он также охватывает разницу между скоростью и скоростью и показывает примеры равномерного кругового движения.

Проверка на хват

Представьте, что вы раскачиваете йойо по вертикали по часовой стрелке перед собой, перпендикулярно направлению, в котором вы смотрите. Теперь представьте, что веревка рвется как раз в тот момент, когда йо-йо достигает крайнего нижнего положения, ближайшего к полу. Что из следующего описывает путь йо-йо после разрыва струны?

1. Йо-йо полетит вверх в направлении центростремительной силы.
2. Йо-йо полетит вниз в направлении действия центростремительной силы.
3. Йо-йо полетит влево в направлении тангенциальной скорости.
4. Йо-йо полетит вправо в направлении тангенциальной скорости.

Решение задач центростремительного ускорения и центростремительной силы

Чтобы получить представление о типичных величинах центростремительного ускорения, мы проведем лабораторную работу, оценив центростремительное ускорение теннисной ракетки, а затем в нашем первом рабочем примере сравним центростремительное ускорение автомобиля, совершающего поворот, с гравитационным ускорением. Для второго рабочего примера мы рассчитаем силу, необходимую для поворота автомобиля по кривой.

Snap Lab

Оценка центростремительного ускорения

В этом упражнении вы измерите размах клюшки для гольфа или теннисной ракетки, чтобы оценить центростремительное ускорение конца клюшки или ракетки. Вы можете сделать это в замедленном темпе.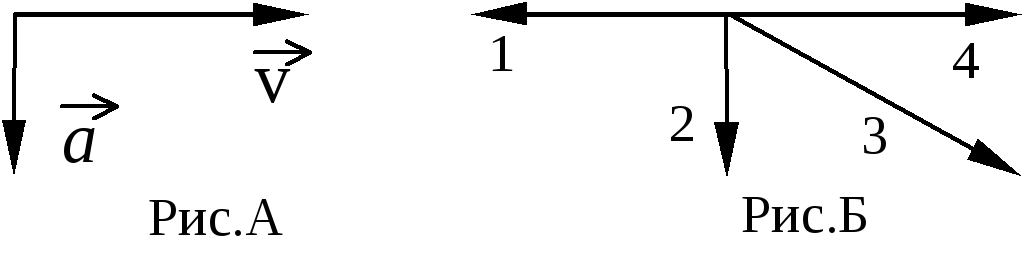 Напомним, что уравнение для центростремительного ускорения имеет вид ac=v2rac=v2r или ac=rω2ac=rω2.

Материалы

• Одна теннисная ракетка или клюшка для гольфа
• Один таймер
• Одна линейка или рулетка

Процедура

1. Работа с партнером. Стойте на безопасном расстоянии от партнера, когда он или она размахивает клюшкой для гольфа или теннисной ракеткой.
2. Опишите движение качелей — это равномерное круговое движение? Почему или почему нет?
3. Постарайтесь, чтобы качание было как можно ближе к равномерному круговому движению. Какие коррективы должен был внести ваш партнер?
4. Измерьте радиус кривизны. Что вы измеряли физически?
5. Используя таймер, найдите либо линейную, либо угловую скорость, в зависимости от того, какое уравнение вы решите использовать.
6. Каково приблизительное центростремительное ускорение на основе этих измерений? Как вы думаете, насколько они точны? Почему? Как вы и ваш партнер можете сделать эти измерения более точными?

Проверка на хватку

Было ли полезнее использовать уравнение ac=v2rac=v2r или ac=rω2ac=rω2 в этом упражнении? Почему?

1. Должно быть проще использовать ac=rω2ac=rω2, потому что измерение угловой скорости путем наблюдения было бы проще.
2. Должно быть проще использовать ac=v2rac=v2r, поскольку было бы проще измерить тангенциальную скорость посредством наблюдения.
3. Должно быть проще использовать ac=rω2ac=rω2, потому что измерение угловой скорости путем наблюдения будет затруднено.
4. Должно быть проще использовать ac=v2rac=v2r, потому что измерение тангенциальной скорости путем наблюдения будет затруднено.

Рабочий пример

Сравнение центростремительного ускорения автомобиля, огибающего кривую, с ускорением под действием силы тяжести

Автомобиль движется по кривой радиусом 500 м со скоростью 25,0 м/с (около 90 км/ч). Чему равно центростремительное ускорение автомобиля? Сравните центростремительное ускорение для этой довольно плавной кривой, снятой на скорости шоссе, с ускорением под действием силы тяжести ( г ).

Стратегия

Поскольку дана линейная, а не угловая скорость, наиболее удобно использовать выражение ac=v2rac=v2r для нахождения величины центростремительного ускорения.

Решение

Ввод данных значений v = 25,0 м/с и r = 500 м в выражение для a _c дает =1,25 м/с2.ac=v2r=(25,0 м/с)2500 м=1,25 м/с2.

Обсуждение

Чтобы сравнить это с ускорением свободного падения ( г = 9,80 м/с ² ), возьмем соотношение ac/g=(1,25 м/с2)/(9,80 м/с2)=0,128ac/ g=(1,25 м/с2)/(9,80 м/с2)=0,128. Следовательно, ac=0,128gac=0,128g, что означает, что центростремительное ускорение составляет примерно одну десятую ускорения свободного падения.

Рабочий пример

Сила трения на автомобильных шинах, огибающих кривую

1. Рассчитайте центростремительную силу, действующую на автомобиль массой 900 кг, который огибает кривую радиусом 600 м на горизонтальной поверхности со скоростью 25,0 м/с.
2. Статическое трение предотвращает скольжение автомобиля. Найдите величину силы трения между шинами и дорогой, которая позволяет автомобилю пройти поворот без соскальзывания по прямой.

Стратегия и решение для (а)

Мы знаем, что Fc=mv2rFc=mv2r. Следовательно,

Fc=mv2r=(900 кг)(25,0 м/с)2600 m=938 N.Fc=mv2r=(900 кг)(25,0 м/с)2600 m=938 N.

Стратегия и решение для (b)

На изображении выше показаны силы, действующие на автомобиль при движении по кривой. На этой диаграмме автомобиль въезжает на страницу, как показано, и поворачивает налево. Трение действует влево, ускоряя автомобиль к центру кривой. Поскольку трение является единственной горизонтальной силой, действующей на автомобиль, в данном случае оно обеспечивает всю центростремительную силу. Следовательно, сила трения является центростремительной силой в этой ситуации и направлена ​​к центру кривой.

f=Fc=938 Nf=Fc=938 N

Обсуждение

Так как мы нашли силу трения в части (b), мы могли также найти коэффициент трения, так как f=µsN=µsmgf=µsN= мкг.

Практические задания

Каково центростремительное ускорение объекта со скоростью 12 м/с, движущегося по пути радиусом 2,0 м?

1. 6 м/с
2. 72 м/с
3. 6 м/с2
4. 72 м/с2

Рассчитайте центростремительное ускорение объекта, следующего по пути с радиусом кривизны 0,2 м и с угловой скоростью 5 рад/с.

1. 1 м/с
2. 5 м/с
3. 1 м/с ²
4. 5 м/с ²

Проверьте свое понимание

Упражнение 7

Что такое равномерное круговое движение?

1. Равномерное круговое движение — это когда объект ускоряется по круговой траектории с постоянно увеличивающейся скоростью.
2. Равномерное круговое движение — это когда объект движется по круговой траектории с переменным ускорением.
3. Равномерное круговое движение — это когда объект движется по круговой траектории с постоянной скоростью.
4. Равномерное круговое движение — это когда объект движется по круговой траектории с переменной скоростью.

Упражнение 8

Что такое центростремительное ускорение?

1. Ускорение объекта, движущегося по круговой траектории и направленного радиально к центру круговой орбиты
2. Ускорение объекта, движущегося по круговой траектории и направленного по касательной по круговой траектории
3. Ускорение объекта, движущегося по прямолинейному пути и направленного в направлении движения объекта
4. Ускорение объекта, движущегося по прямолинейному пути и направленного в сторону, противоположную движению объекта

Упражнение 9

Существует ли результирующая сила, действующая на объект, совершающий равномерное круговое движение?

1. Да, объект ускоряется, поэтому на него должна действовать результирующая сила.