Векторы примеры решения задач, формулы и онлайн калькуляторы
Содержание:
- Координаты вектора
- Длина (модуль) вектора
- Угол между векторами
- Разложение вектора по ортам координатных осей
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме — координаты вектора.
Пример
Запись $\overline{a}=(5 ;-2)$ означает, что вектор $\overline{a}$
имеет следующие координаты: абсцисса равна 5, ордината равна -2.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Заданы векторы $\overline{a}=(-3 ; 5)$ и $\overline{b}=(0 ;-1)$. Найти координаты вектора $\overline{c}=\overline{a}+\overline{b}$
Решение. $\overline{c}=\overline{a}+\overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$
Пример
Задание. Вектор $\overline{a}=(3 ;-2)$. Найти координаты вектора 2$\overline{a}$
Решение. $2 \overline{a}=2 \cdot(3 ;-2)=(2 \cdot 3 ; 2 \cdot(-2))=(6 ;-4)$
Пример
Задание. Найти координаты вектора $\overline{A B}$, если $A(-4 ; 2), B(1 ;-3)$
Решение. $\overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)$
Длина (модуль) вектора
Теоретический материал по теме — длина вектора.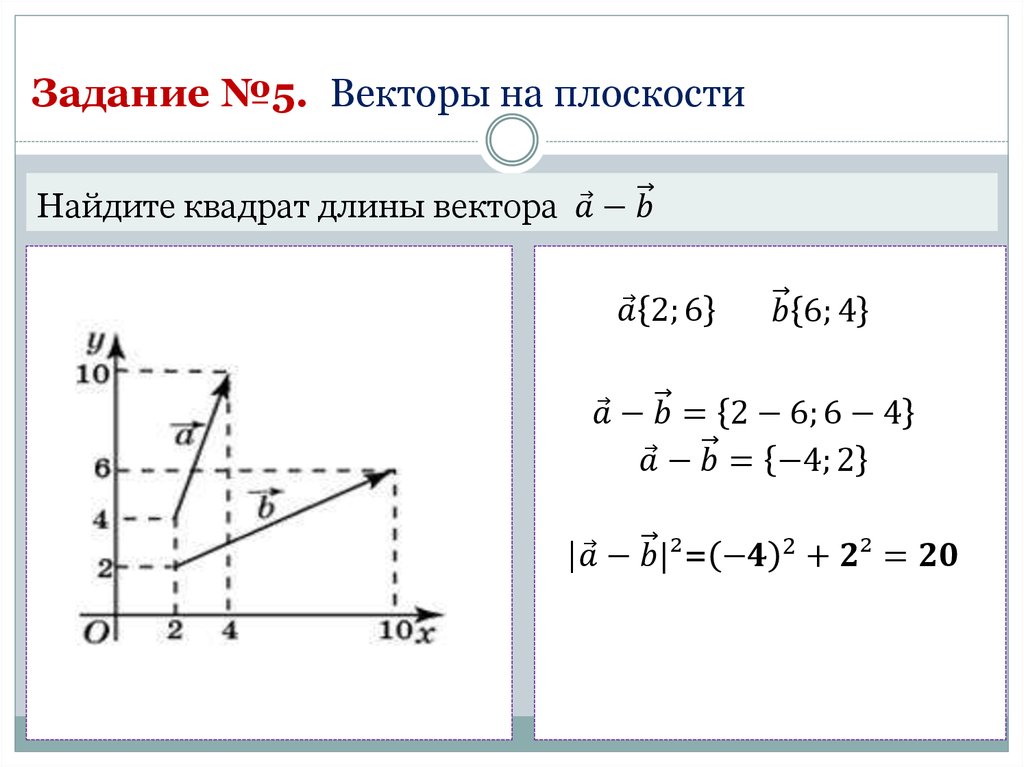 {\circ}$$
{\circ}$$
Разложение вектора по ортам координатных осей
Теоретический материал по теме — разложение вектора по ортам.
Пример
Задание. Зная разложения вектора $\overline{a}$ по базисной системе векторов: $\overline{a}=3 \overline{i}-\overline{k}$, записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что $\overline{a}=3 \overline{i}-0 \cdot \overline{j}-\overline{k}$, получаем, что $\overline{a}=(3 ; 0 ;-1)$
Пример
Задание. Вектор $\overline{a}$ задан своими координатами: $\overline{a}=(2 ;-1 ; 5)$. Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора — это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:
$\overline{a}=2 \overline{i}-\overline{j}+5 \overline{k}$
Скалярное произведение векторов
 {\circ}=6 \cdot \frac{1}{2}=3$
{\circ}=6 \cdot \frac{1}{2}=3$Пример
Задание. Найти скалярное произведение векторов $\overline{a}=(3 ;-1)$ и $\overline{b}=(-2 ; 7)$
Решение. Скалярное произведение
$\overline{a} \overline{b}=3 \cdot(-2)+(-1) \cdot 7=-6-7=-13$
Векторное произведение векторов
Теоретический материал по теме — векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов $\overline{a}=(6 ; 7 ; 10)$ и $\overline{b}=(8 ; 5 ; 9)$
Решение. Составляем определитель и вычисляем его:
$\overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|=$
$=\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)=$
$=13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26)$
Смешанное произведение векторов
Теоретический материал по теме — смешанное произведение векторов.
Пример
Задание. Вычислить объем пирамиды, построенной на векторах $\overline{a}=(2 ; 3 ; 5)$, $\overline{b}=(1 ; 4 ; 4)$, $\overline{c}=(3 ; 5 ; 7)$
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов $\overline{a}$, $\overline{b}$ и $\overline{c}$:
$(\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{lll}{2} & {3} & {5} \\ {1} & {4} & {4} \\ {3} & {5} & {7}\end{array}\right|=2 \cdot 4 \cdot 7+1 \cdot 5 \cdot 5+3 \cdot 4 \cdot 3-$
$-3 \cdot 4 \cdot 5-5 \cdot 4 \cdot 2-1 \cdot 3 \cdot 7=-4$
$$V_{пир}=\frac{1}{6}|(\overline{a}, \overline{b}, \overline{c})|=\frac{1}{6} \cdot 4=\frac{2}{3}$$
Читать первую тему — операции над векторами, раздела векторы.
Задачи с векторами
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2013-11-10
Задачи с векторами на ЕГЭ. Дорогие друзья! Вы знаете, что в состав экзамена по математике входят такие задания. Не факт, что такая задача попадёт именно вам, но готовиться к этому и понимать тему в любом случае нужно. На блоге мы уже рассмотрели несколько задач на сумму (разность) векторов, длину вектора, в этой же статье есть необходимая теория. Посмотрите её, прежде чем рассматривать задачи представленные ниже.
Дорогие друзья! Вы знаете, что в состав экзамена по математике входят такие задания. Не факт, что такая задача попадёт именно вам, но готовиться к этому и понимать тему в любом случае нужно. На блоге мы уже рассмотрели несколько задач на сумму (разность) векторов, длину вектора, в этой же статье есть необходимая теория. Посмотрите её, прежде чем рассматривать задачи представленные ниже.
Также загляните в справочник на блоге. Если нужно вспомнить, что такое абсцисса и ордината точки, тогда посмотрите эту статью. Кратко повторим:
Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты начала:
Формула для определения длины вектора, если известны координаты его начала и конца:
Формула для определения длины вектора, если известны его координаты:
27725. Вектор АВ с началом в точке A(2;4) имеет координаты (6;2). Найдите ординату точки B.
Как уже сказано координаты вектора находятся следующим образом: из соответствующих координат конца вычитаются координаты начала вектора. То есть:
Координаты вектора нам даны, координаты его начала тоже, значит:
Следовательно можем найти координаты точки В:
х2 – 2 = 6 у2 – 4 = 2
х2 = 8 у2 = 6
Таким образом, ордината точки В равна 6.
Ответ: 6
27726. Вектор АВ с началом в точке A(3;6) имеет координаты (9;3). Найдите сумму координат точки B.
Задача по процессу решения такая же как и предыдущая, но иначе поставлен вопрос. Вычисления так же находятся в пределах устного счёта. Ещё раз запишем координаты вектора, когда известны координаты его начала и конца:
Координаты вектора и координаты его начала даны, значит:
Можем найти координаты точки В:
х2 – 3 = 9 у2 – 6 = 3
х2 = 12 у2 = 9
Таким образом, сумма координат точки В равна 21.
Ответ: 21
27727. Вектор АВ с концом в точке B (5;3) имеет координаты (3;1). Найдите абсциссу и ординату точки A, также сумму её координат.
Нам известны координаты вектора и координаты его конца, значит:
Можем найти координаты точки А:
5 – х1 = 3 3 – у1 = 1
х1 = 2 у1 = 2
Таким образом, абсцисса точки А равна двум, ордината тоже равна двум, а сумма координат равна 2+2 = 4.
Ответ: 4
27731 Найдите квадрат длинны вектора a+b.
В данной задаче необходимо найти координаты вектора, который является суммой указанных векторов, затем найти его длину и возвести её в квадрат. Запишем формулу длины вектора, если известны его координаты:
Или в другой форме:
Найдём координаты вектора, который является суммой данных векторов. Для этого сначала найдём координаты данных векторов.
Рассмотрим вектор:
Рассмотрим вектор:
*Можно было глядя на эскиз сразу их записать, так как точки их начал совпадают с началом координат.
Теперь найдём координаты вектора являющегося их суммой:
(2 + 8; 6 + 4) = (10;10)
Таким образом, длина вектора являющегося суммой векторов a и b равна:
Следовательно квадрат длины будет равен 200.
*Имея опыт в решении подобных задач, можно сразу записывать:
Как видите, вычисления можно осуществить устно. Здесь для вас умышленно представлено подробное решение.
Ответ: 200
27733. Найдите квадрат длины вектора a – b.
Задача аналогична предыдущей. Необходимо найти координаты вектора, который является разностью представленных векторов, затем найти его длину и результат возвести в квадрат.
Координаты данных векторов нам уже известны (из предыдущей задачи):
Теперь найдём координаты вектора, который является их разностью:
(2 – 8; 6 – 4) = (–6;2)
Таким образом, длина вектора, который является разностью векторов
Следовательно квадрат её длины будет равен 40.
*Можно сразу записывать и вычислять:
Ответ: 40
27723.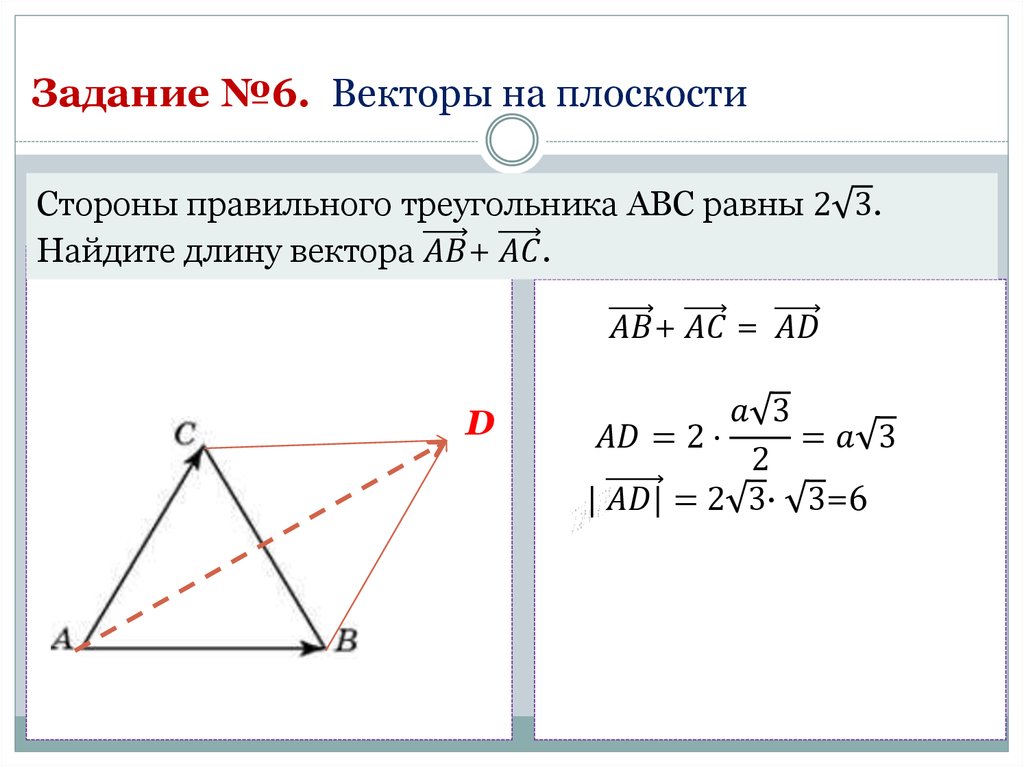 Найдите сумму координат вектора АВ.
Найдите сумму координат вектора АВ.
Посмотреть решение
27724.Вектор АВ с началом А(2;4) имеет координаты (6;2) Найдите абсциссу точки В.
Посмотреть решение
27730. Найдите сумму координат вектора а + b.
Посмотреть решение
27732. Найдите сумму координат вектора а–b.
Посмотреть решение
27736. Найдите сумму координат вектора а + b
Посмотреть решение
27739. Найдите квадрат длины вектора а–b.
Посмотреть решение
Вы убедились, что задачи с векторами на ЕГЭ это одни из самых простых заданий. Есть, конечно, задания со скалярным произведением векторов, но о они сложности не представляют, нужно лишь знать формулу скалярного произведения. Такие задачи мы также рассмотрим, не пропустите!
На этом всё. Если что-то непонятно, пишите. Успеха Вам!
С уважением, Александр Крутицких
Уроки сделаны… Мама охрипла… Сын оглох … Соседи выучили всё наизусть, собака пересказала!!!.
.
P.S: Делитесь этой статьёй в сетях.
Категория: Векторы | ЕГЭ-№1
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Исчисление II — Векторы (задачи о назначениях)
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.
Уведомление о проблемах с назначением
Пожалуйста, не пишите мне по электронной почте, чтобы получить решения и/или ответы на эти проблемы. Я не буду их раздавать ни при каких обстоятельствах и не буду отвечать на любые просьбы об этом. Цель этих задач состоит в том, чтобы инструкторы использовали их для заданий, а наличие легкодоступных решений / ответов побеждает эту цель.
Вот набор задач на присваивание для главы «Векторы» заметок «Исчисление II». Обратите внимание, что эти проблемы не имеют доступных решений. Они предназначены в основном для инструкторов, которые могут захотеть назначить набор задач для сдачи. Наличие доступных решений (или даже только окончательных ответов) лишило бы цели задачи.
Если вы ищете практические задачи (с доступными решениями), пожалуйста, ознакомьтесь с практическими задачами.
Вот список всех разделов, для которых были написаны задачи на задания, а также краткое описание материала, затронутого в примечаниях к этому конкретному разделу.
Основные понятия. В этом разделе мы введем некоторые общие обозначения для векторов, а также некоторые основные понятия о векторах, такие как величина вектора и единичные векторы. Мы также покажем, как найти вектор по его начальной и конечной точкам.
Векторная арифметика. В этом разделе мы обсудим математическую и геометрическую интерпретацию суммы и разности двух векторов. Мы также определяем и даем геометрическую интерпретацию скалярного умножения. Мы также даем некоторые из основных свойств векторной арифметики и вводим общие обозначения \(i\), \(j\), \(k\) для векторов.
Скалярное произведение. В этом разделе мы определим скалярное произведение двух векторов. Мы даем некоторые из основных свойств скалярных произведений и определяем ортогональные векторы и показываем, как использовать скалярное произведение, чтобы определить, являются ли два вектора ортогональными. В этом разделе мы также обсуждаем нахождение векторных проекций и направляющих косинусов.
В этом разделе мы также обсуждаем нахождение векторных проекций и направляющих косинусов.
Перекрестное произведение. В этом разделе мы определяем перекрестное произведение двух векторов и приводим некоторые основные факты и свойства перекрестных произведений.
Векторы Помощь с заданиями по физике, Векторы Помощь с домашними заданиями по физике, Задания Репетиторы онлайн
Задания по физике Домашнее задание, Векторы / Автор Задание по физике
Ускорение 14Е. Нарисуйте график, который является возможным описанием положения как функции времени для частицы, которая движется вдоль оси x и. при = 1 с имеет (а) нулевую скорость и положительное ускорение; (б) нулевая скорость и отрицательное ускорение; (c) отрицательная скорость и положительное ускорение: (d) отрицательная скорость и отрицательное ускорение. (e) Для которого …
Ускорение Подробнее »
Векторы / Автор Задание по физике
ВОПРОСЫ 1. Какое из следующих соотношений между ускорением a и перемещением x метелки включает ВГМ: (a) a = 0,5x, (b) a = 400×2, (c) a = -2Ox, ( г) а = -3×2? 2.
ВОПРОСЫ Подробнее »
Векторов / Автор Задание по физике
ВОПРОСЫ 1. Какое из следующих соотношений между ускорением a и перемещением x метелки включает ВГМ: (a) a = 0,5x (b) a = 400×2, (c) a = 2Ox, (d) a = -3×2 2. Учитывая x’ =·(2,0 м) cos(5t) для SHM и необходимо найти скорость в момент t = 2 с, следует ли заменить …
ВОПРОСЫ Подробнее »
Векторов / Автор Задание по физике
busincs Термин «оценка» подразумевает, что задача l’Mimatinj.l стоимость/стоимость или стоимость, ценная бумага или бизнес», «J11L» цена инвестора или «фирмы (покупателя) ) будет согласовываться с этим значением при оплате покупателю, «какой-либо актив/ценная бумага». Очевидно, что два разных покупателя могут иметь неодинаковую оценку для …
бизнесов Подробнее »
Векторов / Автор Задание по физике
УПРАЖНЕНИЯ ЗАДАЧИ ВЕКТОР 15E. Вектор имеет магнитуду 5,0 м и направлен на восток. Вектор b имеет величину 4,0 м и направлен в 35° к западу от севера. Каковы (а) величина и (б) направление b? Каковы (c) величина и (d) направление b o? (e) Нарисуйте векторную диаграмму …
Вектор имеет магнитуду 5,0 м и направлен на восток. Вектор b имеет величину 4,0 м и направлен в 35° к западу от севера. Каковы (а) величина и (б) направление b? Каковы (c) величина и (d) направление b o? (e) Нарисуйте векторную диаграмму …
УПРАЖНЕНИЯ ЗАДАЧИ ВЕКТОР Подробнее »
Векторов / Автор Задание по физике
УПРАЖНЕНИЯ ЗАДАЧИ ВЕКТОРЫ Решение находится в Руководстве по решениям для учащихся. www Решение доступно в Интернете по адресу: http://www.wiley.com/college/hrW Решение доступно в Interactive Learning Ware. Добавление векторов геометрически 1E. Рассмотрим два смещения, одно величиной 3 м, а другое величиной 4 м. Покажите, как векторы смещения могут быть объединены в …
УПРАЖНЕНИЯ ЗАДАЧИ ВЕКТОРЫ Подробнее »
Векторов / Автор Задание по физике
ОБЗОР И ОБЗОР ВЕКТОРЫ Скаляры и векторы Скаляры, такие как температура, имеют только величину. Они задаются числом с единицей C и подчиняются правилам арифметики и обычной алгебры. Векторы, например смещение, имеют как величину, так и направление (5 м, север) и подчиняются специальным правилам векторной алгебры.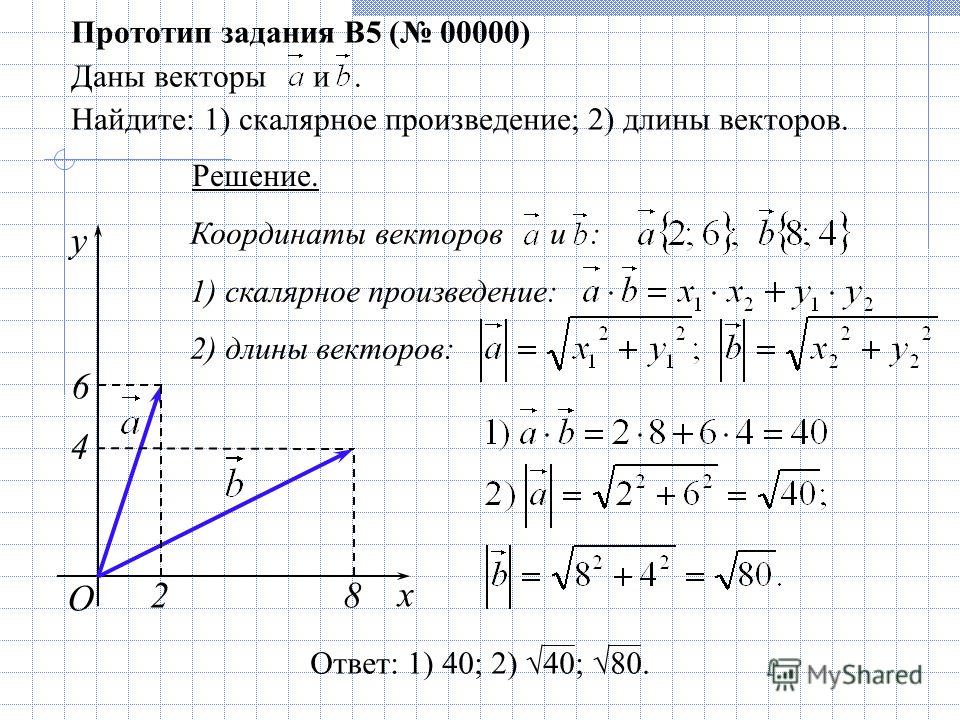 Добавление векторов геометрически Два вектора …
Добавление векторов геометрически Два вектора …
ОБЗОР И СВОДНЫЕ ВЕКТОРЫ Подробнее »
Векторов / Автор Задание по физике
ТАКТИКА РЕШЕНИЯ ПРОБЛЕМ Тактика 5: Распространенные ошибки при вычислении векторного произведения При нахождении векторного произведения распространены несколько ошибок. (I) Неспособность расположить векторы хвост к хвосту заманчива, когда на иллюстрации они представлены голова к хвосту: вы должны мысленно сдвинуть (или, лучше, перерисовать) один вектор в правильное расположение, не меняя его ориентации. (2) Неиспользование…
ТАКТИКА РЕШЕНИЯ ПРОБЛЕМ Подробнее »
Векторов / Автор Задание по физике
Пример задачи РЕШЕНИЕ. Ключевая идея состоит в том, что когда два вектора представлены в единичной векторной записи. мы можем найти их перекрестное произведение, используя закон распределения. Здесь это означает, что мы можем написать Затем мы оцениваем каждый термин, определяя направление с помощью правила правой руки.

 .
.
Leave A Comment