Можно ли описать около ромба окружность: Около любого ромба можно описать окружность

Высота равна радиусу вписанной окружности. Радиус вписанной окружности в ромб

Психология

Ромб – это параллелограмм, у которого все стороны равны. Следовательно, он наследует все свойства параллелограмма. А именно:

• Диагонали ромба взаимно перпендикулярны.
• Диагонали ромба являются биссектрисами его внутренних углов.

Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы противоположных сторон равны.
Следовательно, в любой ромб можно вписать окружность. Центр вписанной окружности совпадает с центром пересечения диагоналей ромба.
Радиус вписанной окружности в ромб можно выразить несколькими способами

1 способ. Радиуса вписанной окружности в ромб через высоту

Высота ромба равна диаметру вписанной окружности. Это следует из свойства прямоугольника, который образуют диаметр вписанной окружности и высота ромба – у прямоугольника противолежащие стороны равны.

Следовательно формула радиуса вписанной окружности в ромб через высоту:

2 способ.

Радиус вписанной окружности в ромб через диагонали

Площадь ромба можно выразить через радиус вписанной окружности
, где Р – периметр ромба. Зная, что периметр это сумма всех сторон четырехугольника имеем P= 4×а. Тогда
Но площадь ромба также равна половине произведения его диагоналей
Прировняв правые части формул площади, имеем следующее равенство
В результате получаем формулу, позволяющую вычислить радиус вписанной окружности в ромб чрез диагонали

Пример расчета радиуса окружности вписанной в ромб, если известны диагонали
Найти радиус окружности вписанной в ромб, если известно, что длина диагоналей 30 см и 40 см
Пусть ABCD -ромб, тогда AC и BD его диагонали. AC= 30 см, BD =40 см
Пусть точка О – это центр вписанной в ромб ABCD окружности, тогда она будет также являться и точкой пересечения его диагоналей, делящих их пополам.


т.к диагонали ромба пересекаются под прямым углом, то треугольник AOB прямоугольный.

Тогда по теореме Пифагора
, подставляем в формулу ранее полученные значения

AB = 25 см
Применив ранее выведенную формулу для радиуса описанной окружности в ромб, получаем

3 способ. Радиус вписанной окружности в ромб через отрезки m и n

Точка F – точка касания окружности со стороной ромба, которая делит ее на отрезки AF и BF . Пусть AF= m, BF=n.
Точка O – центр пересечения диагоналей ромба и центр вписанной в него окружности.
Треугольник AOB – прямоугольный, так как диагонали ромба пересекаются под прямым углом.
, т.к. является радиусом, проведенным в точку касания окружности. Следовательно OF – высота треугольника

AOB к гипотенузе. Тогда AF и BF – проекции катетов на гипотенузу.
Высота в прямоугольном треугольнике, опущенная на гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу.

Формула радиуса вписанной окружности в ромб через отрезки равна корню квадратному из произведения этих отрезков, на которые делит сторону ромба точка касания окружности

Окружность считается вписанной в границы правильного многоугольника, в случае, если лежит внутри него, касаясь при этом прямых, которые проходят через все стороны. Рассмотрим, как найти центр и радиус окружности. Центром окружности будет являться точка, в которой пересекаются биссектрисы углов многоугольника. Радиус рассчитывается: R=S/P; S – площадь многоугольника, Р – полупериметр окружности.

В треугольнике

В правильный треугольник вписывают лишь одну окружность, центр которой называется инцентром; он от всех сторон удалён на одинаковое расстояние и является местом пересечения биссектрис.

В четырёхугольнике

Часто приходится решать, как найти радиус вписанной окружности в эту геометрическую фигуру. Она должна быть выпуклой (если нет самопересечений). Окружность вписать в неё можно только в случае равенства сумм противоположных сторон: AB+CD=BC+AD.

При этом центр вписанной окружности, середины диагоналей, расположены на одной прямой (согласно теореме Ньютона). Отрезок, концы которого находятся там, где пересекаются противоположные стороны правильного четырёхугольника, лежит на этой же прямой, называемой прямой Гаусса. Центром окружности будет точка, в которой пересекаются высоты треугольника с вершинами, диагоналями (по теореме Брокара).

В ромбе

Им считается параллелограмм с одинаковой длиной сторон. Радиус окружности, вписываемой в него, можно рассчитать несколькими способами.

1. Чтобы сделать это правильно, найдите радиус вписанной окружности ромба, если известна площадь ромба, длина его стороны. Применяется формула r=S/(2Хa). К примеру, если площадь ромба составляет 200 мм кв., длина стороны 20 мм, то R=200/(2Х20), то есть, 5 мм.
2. Известен острый угол одной из вершин. Тогда необходимо использовать формулоу r=v(S*sin(α)/4). Например, при площади в 150 мм и известном угле в 25 градусов, R= v(150*sin(25°)/4) ≈ v(150*0,423/4) ≈ v15,8625 ≈ 3,983 мм.
3. Все углы в ромбе равны. В этой ситуации радиус окружности, вписанной в ромб, будет равен половине длины одной стороны данной фигуры. Если рассуждать по Евклиду, утверждающего, что сумма углов всякого четырёхугольника равна 360 градусов, то один угол будет равен 90 градусам; т. е. получится квадрат.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
  д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Если окружность располагается внутри угла и касается его сторон, её называют вписанной в этот угол.

Центр такой вписанной окружности располагается на биссектрисе этого угла .

Если же она лежит внутри выпуклого многоугольника и соприкасается со всеми его сторонами, она называется вписанной в выпуклый многоугольник.

Окружность, вписанная в треугольник, соприкасается с каждой стороной этой фигуры лишь в одной точке. В один треугольник возможно вписать лишь одну окружность.

Радиус такой окружности будет зависеть от следующих параметров треугольника:

1. Длин сторон треугольника.
2. Его площади.
3. Его периметра.
4. Величины углов треугольника.

Для того чтобы вычислить радиус вписанной окружности в треугольник, не всегда обязательно знать все перечисленные выше параметры, поскольку они взаимосвязаны между собой через тригонометрические функции.

Вычисление с помощью полупериметра

1. Если известны длины всех сторон геометрической фигуры (обозначим их буквами a, b и c), то вычислять радиус придётся путём извлечения квадратного корня.
2. Приступая к вычислениям, необходимо добавить к исходным данным ещё одну переменную — полупериметр (р). Его можно рассчитать, сложив все длины и полученную сумму разделив на 2. p = (a+b+c)/2. Таким образом можно существенно упростить формулу нахождения радиуса.
3. В целом формула должна включать в себя знак радикала, под который помещается дробь, знаменателем этой дроби будет величина полупериметра р.
4. Числителем данной дроби будет представлять собой произведение разностей (p-a)*(p-b)*(p-c)
5. Таким образом, полный вид формулы будет представлен следующим образом: r = √(p-a)*(p-b)*(p-c)/p).

Вычисление с учётом площади треугольника

Если нам известна площадь треугольника и длины всех его сторон, это позволит найти радиус интересующей нас окружности, не прибегая к извлечению корней.

1. Для начала нужно удвоить величину площади.
2. Результат делится на сумму длин всех сторон. Тогда формула будет выглядеть следующим образом: r = 2*S/(a+b+c).
3. Если воспользоваться величиной полупериметра, можно получить совсем простую формулу: r = S/p.

Расчёт с помощью тригонометрических функций

Если в условии задачи присутствует длина одной из сторон, величина противоположного угла и периметр, можно воспользоваться тригонометрической функцией — тангенсом. В этом случае формула расчёта будет иметь следующий вид:

r = (P /2- a)* tg (α/2), где r — искомый радиус, Р — периметр, а — значение длины одной из сторон, α — величина противоположного стороне, а угла.

Радиус окружности, которую необходимо будет вписывать в правильный треугольник, можно найти по формуле r = a*√3/6.

Окружность, вписанная в прямоугольный треугольник

В прямоугольный треугольник можно вписать только одну окружность . Центр такой окружности одновременно служит точкой пересечения всех биссектрис. Эта геометрическая фигура имеет некоторые отличительные черты, которые необходимо учесть, вычисляя радиус вписанной окружности.

1. Для начала необходимо выстроить прямоугольный треугольник с заданными параметрами. Построить такую фигуру можно по размеру её одной стороны и величинам двух углов или же по двум сторонам и углу между этими сторонами. Все эти параметры должны быть указаны в условии задачи. Треугольник обозначается как АВС, причём С — это вершина прямого угла. Катеты при этом обозначаются переменными, а и b , а гипотенуза — переменной с .
2. Для построения классической формулы и вычисления радиуса окружности необходимо найти размеры всех сторон описанной в условии задачи фигуры и по ним вычислить полупериметр. Если в условиях даются размеры двух катетов, по ним можно вычислить величину гипотенузы, исходя из теоремы Пифагора.
3. Если в условии дан размер одного катета и одного угла, необходимо понять, прилежащий этот угол или противолежащий. В первом случае гипотенуза находится с помощью теоремы синусов: с=a/sinСАВ , во втором случае применяют теорему косинусов с=a/cosCBA .
4. Когда все расчёты выполнены и величины всех сторон известны, находят полупериметр по формуле, описанной выше.
5. Зная величину полупериметра, можно найти радиус. Формула представляет собой дробь. Её числителем является произведение разностей полупериметра и каждой из сторон, а знаменателем -величина полупериметра.

Следует заметить, что числитель данной формулы является показателем площади. В этом случае формула нахождения радиуса гораздо упрощается — достаточно разделить площадь на полупериметр.

Определить площадь геометрической фигуры можно и в том случае, если известны оба катета. По сумме квадратов этих катетов находится гипотенуза, далее вычисляется полупериметр. Вычислить площадь можно, умножив друг на друга величины катетов и разделив полученное на 2.

Если в условиях даны длины и катетов и гипотенузы, определить радиус можно по очень простой формуле: для этого складываются длины катетов, из полученного числа вычитается длина гипотенузы. Результат необходимо разделить пополам.

Видео

Из этого видео вы узнаете, как находить радиус вписанной в треугольник окружности.

Не получили ответ на свой вопрос? Предложите авторам тему.

Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.

Для любой точки L , лежащей на окружности, действует равенство OL=R . (Длина отрезка OL равняется радиусу окружности).

Отрезок, который соединяет две точки окружности, является ее хордой .

Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D) . Диаметр можно вычислить по формуле: D=2R

Длина окружности вычисляется по формуле: C=2\pi R

Площадь круга : S=\pi R^{2}

Дугой окружности называется та ее часть, которая располагается между двух ее точек. {\circ}}

Используя радианную меру: CD = \alpha R

Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.

В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.

AN\cdot NB = CN \cdot ND

Касательная к окружности

Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.

Если же у прямой есть две общие точки, ее называют секущей .

Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.

Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.

AC = CB

Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}

\angle ADB = \angle AEB = \angle AFB

На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.

Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.

\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)

Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.

\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)

Вписанная окружность

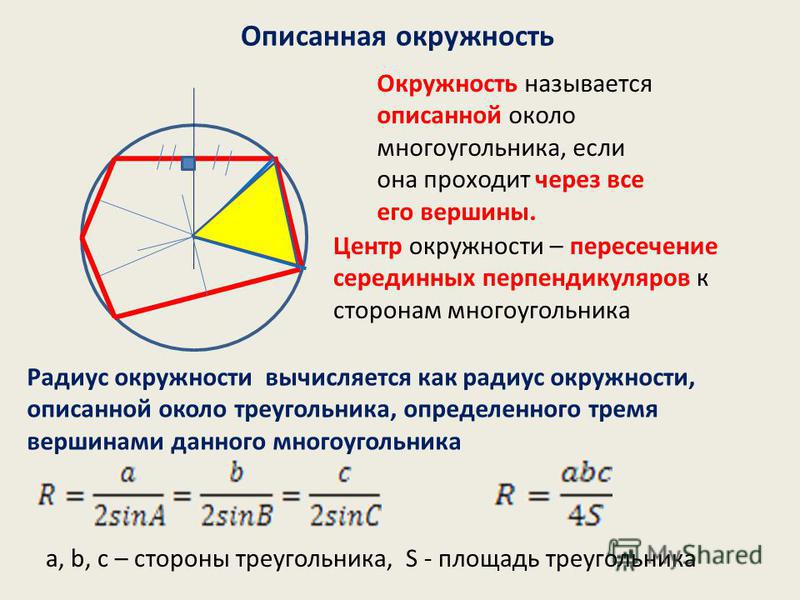
Вписанная окружность — это окружность, касающаяся сторон многоугольника.

В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.

Окружность может быть вписанной не в каждый многоугольник.

Площадь многоугольника с вписанной окружностью находится по формуле:

S = pr ,

p — полупериметр многоугольника,

r — радиус вписанной окружности.

Отсюда следует, что радиус вписанной окружности равен:

r = \frac{S}{p}

Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.

AB + DC = AD + BC

В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.

Радиус вписанной окружности вычисляется по формуле:

r = \frac{S}{p} ,

где p = \frac{a + b + c}{2}

Описанная окружность

Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}

Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.

Радиус описанной окружности можно вычислить по формулам:

R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}

R = \frac{abc}{4 S}

a , b , c — длины сторон треугольника,

S — площадь треугольника.

Теорема Птолемея

Под конец, рассмотрим теорему Птолемея.

Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.

AC \cdot BD = AB \cdot CD + BC \cdot AD

Вписанная и описанная окружность 8 класс онлайн-подготовка на Ростелеком Лицей

Вписанная и описанная окружность.

Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

Докажем следующее утверждение.

В любой треугольник можно вписать окружность.

 

 

Доказательство:

Мы знаем, что все биссектрисы треугольника пересекаются в одной точке – пусть в точке О. Проведем биссектрисы АО, ВО, СО. Точка их пересечения О равноудалена от сторон треугольника. Она равноудалена от сторон угла ∠А – АС и АВ, так как принадлежит биссектрисе этого угла. Аналогично она равноудалена от сторон углов ∠В и ∠С, таким образом, от трех сторон треугольника.

Опустим перпендикуляры из точки О на стороны треугольника – ОМ на сторону АС, OL – на ВС, ОК – на АВ. Эти перпендикуляры и будут расстояниями от точки О до сторон треугольника, и они равны: ОМ = ОL = OK.

Обозначим расстояние от точки О до сторон треугольника за r и рассмотрим окружность с центром в точке О и радиусом r.

Окружность касается прямой АВ, т.к. имеет с ней общую точку К, и радиус ОК, проведенный в эту точку, перпендикулярен прямой АВ. Аналогично окружность касается прямых АС и ВС. Таким образом, окружность касается всех тех сторон треугольника, значит, она вписана в треугольник.

Итак, три биссектрисы треугольника пересекаются в точке, являющейся центром вписанной окружности.

Отметим, что в треугольник можно вписать только одну окружность.

В отличие от треугольника не во всякий четырехугольник можно вписать окружность.

Рассмотрим, например, прямоугольник, не являющийся квадратом. Ясно, что в такой прямоугольник можно поместить окружность, касающуюся только трех его сторон.

Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством.

В любом описанном четырехугольнике суммы противоположных сторон равны.

Это свойство легко установить, используя рисунок, на котором одними и теми же буквами обозначены равные отрезки касательных.

 

 

АВ+СD = AD+BC

AB = x+y, BC = y+z, CD = z+u, AD = x+u

(x+y)+(z+u) = (y+z)+(x+u)

Раскроем скобки:

x+y+z+u = x+y+z+u

Это равенство верно для любых переменных, значит, АВ+СD = AD+BC.

Верно и обратное утверждение. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

Рассмотрим еще одну теорему, она касается точки пересечения серединных перпендикуляров треугольника. Мы знаем, что они пересекаются в одной точке, и эта точка совпадает с центром описанной около треугольника окружности.

Около любого треугольника можно описать окружность.

Итак, задан треугольник ⊿АВС. Проведем серединный перпендикуляр р₁ к стороне треугольника ВС, р₂ – к стороне АВ, р₃ – к стороне АС.

 

 

Серединные перпендикуляры пересекутся в точке Q.

Согласно теореме о свойствах серединных перпендикуляров, точка, принадлежащая серединному перпендикуляру к отрезку, равноудалена от концов отрезка. Отсюда QA = QC, т.к. точка Q принадлежит серединному перпендикуляру к отрезку АС. Аналогично QA = QB и QB = QC. Таким образом, точка Q равноудалена от вершин треугольника. Отсюда QA, QB, QC – радиусы окружности, описанной около треугольника ⊿АВС. Обозначим радиус за R. Точка пересечения серединных перпендикуляров – центр описанной окружности.

Отметим, что около треугольника можно описать только одну окружность.

Около четырехугольника не всегда можно описать окружность.

Например, нельзя описать окружность около ромба, не являющегося квадратом.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством.

В любом вписанном четырехугольнике сумма противоположных углов равна 180°.

 

 

Это свойство легко установить, если обратиться к рисунку и воспользоваться теоремой о вписанном угле.

∠А равен половине дуги ВСD,

∠C равен половине дуги ВАD.

Отсюда следует, что ∠А+∠С=12BCD+12BAD=12BCD+BAD=12·360°=180°.

Верна и обратная теорема.

Если сумма противоположных углов четырехугольника равна 180⁰, то около него можно описать окружность.

вписанных и описанных кругов и многоугольников на GMAT

By Mike MᶜGarry on 20 августа 2012 г. в GMAT Geometry

Вписанный и описанный

Еще один сложный тип геометрической диаграммы включает многоугольники «внутри» кругов или круги «внутри» многоугольников. Когда многоугольник находится «внутри» круга, каждая вершина должна лежать на круге:

На этой диаграмме в неправильный пятиугольник ABCDE вписан в круге, а круг описан вокруг вокруг пятиугольника. Мы также можем сказать: окружность описывает пятиугольник. Слово «вписанный» описывает внутреннюю форму, а слово «описанный» описывает внешнюю форму. Вот еще одна диаграмма с многоугольником снаружи.

 

Заметьте теперь, что каждая сторона этого неправильного пятиугольника является касательной к окружности. Теперь пятиугольник описан вокруг круга, а круг вписан в пятиугольник . В обоих случаях внешняя форма описывает, а внутренняя — вписанную.

 

Треугольники

Как это часто бывает при обсуждении многоугольников, треугольники являются особым случаем при обсуждении вписанных и описанных. Каждый возможный треугольник можно вписать в одну окружность и описать другую окружность . Эта «универсальная двойственность» не верна ни для каких других многоугольников более высокого порядка — она верна только для треугольников. Вот небольшая галерея треугольников, каждый из которых вписан в один круг и описывает другой круг.

Обратите внимание, что когда один угол особенно тупой, близкий к 180°, разница в размерах между описанной и вписанной окружностями становится довольно большой. Обратите также внимание: в случае прямоугольного треугольника, на втором изображении, гипотенуза треугольника является диаметром описанной окружности. Мы вернемся к этому моменту.

Четырехугольники

Многие четырехугольники нельзя ни вписать в окружность, ни описать в окружности: то есть нельзя построить окружность, проходящую через все четыре вершины, а также невозможно построить окружность, к которой примыкают все четыре стороны. касательная.

Некоторые четырехугольники, например продолговатый прямоугольник, можно вписать в окружность, но нельзя описать окружность. Другие четырехугольники, как и наклонный ромб, описывают окружность, но не могут быть вписаны в окружность.

Несколько элитных четырехугольников могут как описывать одну окружность, так и вписываться в другую окружность. Конечно, квадрат (внизу слева), самый элитный из всех четырехугольников, обладает этим свойством. Другой пример — «правильный воздушный змей» (внизу справа), воздушный змей с парой противоположных прямых углов:

Хотя это «двойное членство» верно для всех треугольников, оно ограничено некоторыми особыми случаями четырехугольников.

 

Высшие полигоны

То, что верно для четырехугольников, верно и для всех многоугольников более высокого порядка.

а. Большинство, подавляющее большинство не может ни описать круг, ни быть вписанным в него.

б. Некоторые можно вписать в круг, но нельзя описать круг.

в. Некоторые могут описать круг, но не могут быть вписаны в круг.

д. Немногие элиты могут как описывать круг, так и быть вписанными в него.

Эта последняя категория, элитные участники, всегда включает в себя правильный многоугольник. Подобно тому, как все треугольники имеют эту «двойную принадлежность», так и все правильные многоугольники. Вот галерея правильных многоугольников с вписанной окружностью и описанной окружностью.

Очевидно, что по мере увеличения числа сторон размеры двух кругов становятся все ближе и ближе.

Вопросы

GMAT о вписанных и описанных многоугольниках встречаются редко и могут проверить как ваше понимание терминологии, так и ваши навыки визуализации, описывая геометрическую ситуацию (например, «прямоугольник JKLM вписан в круг») и , а не , давая вам диаграмму. .

 

Частный случай: треугольник, вписанный в полуокружность

Это особый случай, который любят GMAT. Он появляется в OG13 (DS #118) и может легко появиться где-нибудь в разделе Quant вашего настоящего GMAT.

Если все, что вы знаете, это то, что KL — это диаметр окружности, этого достаточно, чтобы установить, что ∠J = 90° и что треугольник JKL — прямоугольный с KL в качестве гипотенузы. С другой стороны, если все, что вы знаете, это то, что треугольник JKL — прямоугольный с гипотенузой KL, этого достаточно, чтобы установить, что дуга KJL — полуокружность, а KL — диаметр. Это мощный набор идей, потому что выводы работают в обоих направлениях и потому что он неразрывно связывает две, казалось бы, несопоставимые идеи.

 

Кстати, этот пост является четвертым в серии из пяти статей. Вот и вся серия.

1) Знакомство с кругами на GMAT

2) Геометрия GMAT: окружности и углы

3) Круговые и линейные диаграммы на GMAT

4) Вписанные и описанные окружности и многоугольники на GMAT

5) Разделение кругов GMAT на части: длины дуг, секторы и число Пи

 

Практический вопрос

1) На схеме выше S — центр круга. Если QS = 5 и QR = 6, что такое PQ?

А. 7

Б. 8

С. 9

Д. 10

Э. 11

 

Объяснение практического вопроса

1) Во-первых, QS — это радиус, поэтому, если QS = 5, это означает, что PS = SR = 5, а диаметр PR = 10. Кроме того, поскольку PR — это диаметр, это означает, что треугольник PQR — прямоугольный, ∠PQR = 90°. Мы знаем две стороны этого прямоугольного треугольника: QR = 6 и PR = 10, поэтому мы можем использовать теорему Пифагора, чтобы найти третью сторону.

92 = 100 – 36 = 64

PQ = квадрат {64} = 8

Ответ = Б

 

Автор

← Предыдущий

Следующий →

9 наиболее распространенных форм и способы их идентификации

Вы, вероятно, многое узнали о формах, даже не задумываясь о том, что они из себя представляют. Но понимание того, что такое форма, невероятно удобно при сравнении ее с другими геометрическими фигурами, такими как плоскости, точки и линии.

В этой статье мы рассмотрим, что такое фигура, а также несколько распространенных форм, как они выглядят и основные формулы, связанные с ними.

 

Что такое форма?

Если кто-нибудь спросит вас, что такое фигура, вы, вероятно, сможете назвать несколько из них. Но «форма» имеет и особое значение — это не просто название кругов, квадратов и треугольников.

Форма — это форма объекта, а не то, сколько места он занимает или где он находится физически, а реальная форма, которую он принимает. Круг определяется не тем, сколько места он занимает или где вы его видите, а скорее фактической круглой формой, которую он принимает.

Фигура может быть любого размера и появляться где угодно; они ничем не ограничены, потому что фактически не занимают места. Это довольно сложно уложить в голове, но не думайте о них как о физических объектах — форма может быть трехмерной и занимать физическое пространство, например, пирамидальная подставка для книг или цилиндрическая банка из-под овсяных хлопьев, или он может быть двухмерным и не занимать физической комнаты , например треугольник, нарисованный на листе бумаги.

Тот факт, что он имеет форму, отличает форму от точки или линии.

Точка — это просто позиция; у него нет ни размера, ни ширины, ни длины, ни какого бы то ни было измерения.

Линия, с другой стороны, является одномерной. Он простирается бесконечно в любом направлении и не имеет толщины. Это не форма, потому что у нее нет формы.

Хотя мы можем представлять точки или линии в виде фигур, потому что нам нужно их видеть, на самом деле они не имеют никакой формы. Вот что отличает форму от других геометрических фигур — она двумерна или трехмерна, потому что имеет форму.

 

Кубы, подобные тем, что показаны здесь, представляют собой трехмерные формы квадратов — и то, и другое — формы!

 

6 основных типов двумерных геометрических фигур

Трудно изобразить форму, основываясь только на определении — что значит иметь форму , но не занимать место? Давайте рассмотрим несколько различных форм, чтобы лучше понять, что именно означает быть формой!

Мы часто классифицируем фигуры по количеству сторон.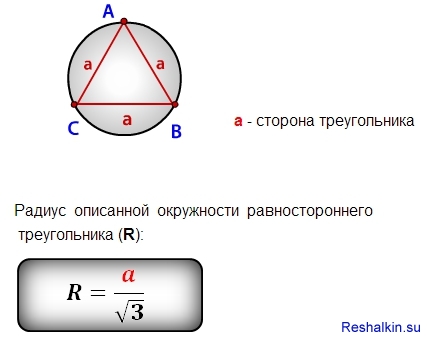 «Сторона» — это отрезок линии (часть линии), который составляет часть фигуры. Но у фигуры тоже может быть неоднозначное количество сторон.

 

Тип 1: Эллипсы

Эллипсы представляют собой круглые овальные формы, в которых заданная точка ( p ) имеет одинаковую сумму расстояний от двух разных фокусов.

 

Овал

Овал немного похож на смазанный круг — он не совсем круглый, а в некотором роде вытянутый. Однако классификация неточная. Есть много, много видов овалов, но общее значение состоит в том, что они имеют круглую форму, которая является удлиненной, а не идеально круглой, как круг. Овал — это любой эллипс, фокусы которого находятся в двух разных положениях.

Поскольку овал не идеально круглый, формулы, которые мы используем для их понимания, должны быть скорректированы.

Также важно отметить, что вычисление длины окружности овала довольно сложно, поэтому ниже нет уравнения длины окружности. Вместо этого используйте онлайн-калькулятор или калькулятор со встроенной функцией измерения окружности, потому что даже самые лучшие уравнения окружности, которые вы можете составить вручную, являются приблизительными.

Определения

• Большой радиус : расстояние от начала овала до самого дальнего края
• Малый радиус : расстояние от начала овала до ближайшего края

Формулы

• Площадь = $\Major \Radius*\Minor \Radius*π$

 

Круг

Сколько сторон у круга? Хороший вопрос! К сожалению, хорошего ответа нет, потому что «стороны» имеют больше общего с многоугольниками — двумерной формой, по крайней мере, с тремя прямыми сторонами и, как правило, по крайней мере с пятью углами. Наиболее знакомые фигуры — это многоугольники, но у кругов нет прямых сторон и явно не хватает пяти углов, поэтому они не являются многоугольниками.

 

Итак, сколько сторон у круга? Нуль? Один? На самом деле это не имеет значения — вопрос просто не относится к кругам.

Круг — это не многоугольник, но что это такое? Окружность — это двумерная фигура (у нее нет толщины и глубины), состоящая из кривой, которая всегда находится на одном и том же расстоянии от точки в центре. Овал имеет два фокуса в разных положениях, тогда как фокусы круга всегда находятся в одном и том же положении.

Определения

• Начало: центр окружности
• Радиус: расстояние от начала координат до любой точки на окружности
• Окружность: 92$

 

Тип 2: Треугольники

Треугольники — это простейшие многоугольники. У них три стороны и три угла, но они могут отличаться друг от друга. Возможно, вы слышали о прямоугольных или равнобедренных треугольниках — это разные типы треугольников, но все они имеют три стороны и три угла.

Поскольку существует много видов треугольников, существует лотов важных формул треугольника , многие из них сложнее других. Основы приведены ниже, но даже основы основаны на знании длины сторон треугольника. Если вы не знаете стороны треугольника, вы все равно можете вычислить его различные аспекты, используя углы или только некоторые из сторон.

Определения

• Вершина : точка пересечения двух сторон треугольника
• Основание : любая из сторон треугольника, обычно нижняя сторона
• Высота : расстояние по вертикали от основания до вершины, с которой оно не связано

Формулы

• Площадь = ${\основание*\высота}/2$
• Периметр = $\сторона a + \сторона b + \сторона c$

 

Тип 3: Параллелограммы

Параллелограмм — это фигура с равными противоположными углами, параллельными противоположными сторонами и параллельными сторонами одинаковой длины. Вы могли заметить, что это определение применимо к квадратам и прямоугольникам, потому что квадратов и прямоугольников также являются параллелограммами ! Если вы можете вычислить площадь квадрата, вы можете сделать это с любым параллелограммом.

Определения

• Длина : мера нижней или верхней стороны параллелограмма
• Ширина : мера левой или правой стороны параллелограмма

Формулы

• Площадь : $\длина*\высота$
• Периметр : $\Сторона 1 + \Сторона 2 + \Сторона 3 + \Сторона 4$
• В качестве альтернативы, Периметр : $\Сторона*4$

 

Прямоугольник

Прямоугольник — это фигура с параллельными противоположными сторонами и всеми углами в 90 градусов. Как тип параллелограмма, он имеет противоположные параллельные стороны.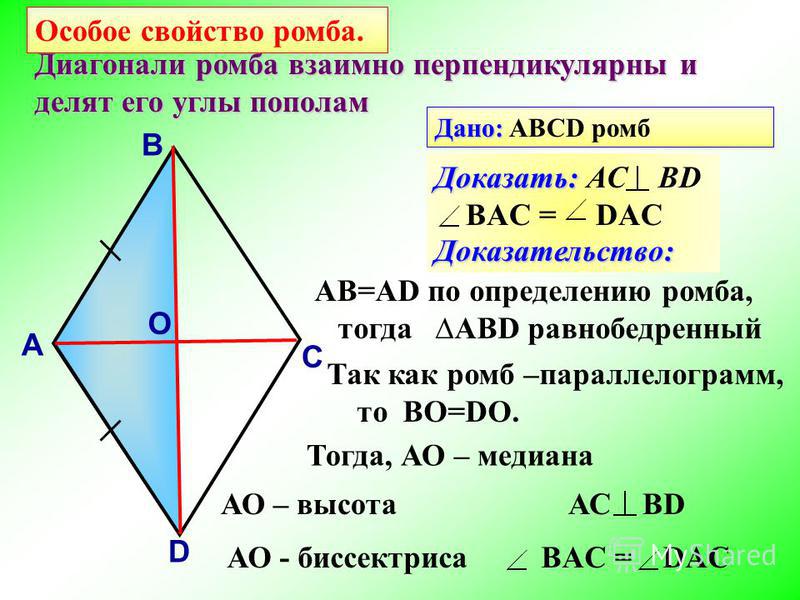 В прямоугольнике один набор параллельных сторон длиннее другого, что делает его похожим на вытянутый квадрат.

Поскольку прямоугольник является параллелограммом, вы можете использовать те же самые формулы для вычисления его площади и периметра.

 

Квадрат

Квадрат очень похож на прямоугольник, за одним заметным исключением: все его стороны имеют одинаковую длину. Как и прямоугольники, квадратов имеют все углы 90 градусов и параллельны противоположным сторонам. Это потому, что квадрат на самом деле является типом прямоугольника, который является типом параллелограмма!

По этой причине вы можете использовать те же формулы для вычисления площади или периметра квадрата, что и для любого другого параллелограмма.

 

Ромб

Как вы уже догадались, ромб — это разновидность параллелограмма. Отличие ромба от прямоугольника или квадрата в том, что его внутренние углы только такие же, как и их диагональные противоположности.

Из-за этого ромб немного похож на квадрат или прямоугольник, немного скошенный в сторону . Хотя периметр вычисляется таким же образом, это влияет на способ вычисления площади, поскольку высота уже не такая, как в квадрате или прямоугольнике.

Определение

• Диагональ : длина между двумя противоположными вершинами

Формулы

• Площадь = ${\Диагональ 1*\Диагональ 2}/2$

 

Тип 4: Трапеции

Трапеции — четырехсторонние фигуры с двумя противоположными параллельными сторонами. В отличие от параллелограмма, трапеция имеет только две противоположные параллельные стороны, а не четыре , что влияет на способ вычисления площади и периметра.

Определения

• Основание : любая из параллельных сторон трапеции
• Ножки : любая из сторон трапеции непараллельна
• Высота : расстояние от одной базы до другой

Формулы

• Площадь : $({\Base_1\length + \Base_2\length}/2)\altitude$
• Периметр : $\Base + \Base + \Leg + \Leg$

 

Тип 5: Пятиугольники

Пятиугольник — это пятиугольник. Обычно мы видим правильные пятиугольники, у которых все стороны и углы равны , но существуют и неправильные пятиугольники. Неправильный пятиугольник имеет неравные стороны и неравные углы и может быть выпуклым — без углов, направленных внутрь — или вогнутым — с внутренним углом более 180 градусов.

 

Поскольку форма более сложная, ее необходимо разделить на меньшие фигуры, чтобы вычислить ее площадь.

Определения

• Апофема : линия, проведенная из центра пятиугольника к одной из сторон, пересекающая сторону под прямым углом.

Формулы

• Периметр : $\Сторона 1 + \Сторона 2 + \Сторона 3 + \Сторона 4 + \Сторона 5$
• Площадь : ${\Perimeter*\Apothem}/2$

 

Тип 6: Шестиугольники

Шестиугольник — это шестиугольник, очень похожий на пятиугольник. Чаще всего мы видим правильные шестиугольники, но они, как и пятиугольники, также могут быть неправильными, выпуклыми или вогнутыми.

Как и в случае с пятиугольниками, формула площади шестиугольника значительно сложнее, чем у параллелограмма.

Формулы

• Периметр : $\Сторона 1 + \Сторона 2 + \Сторона 3 + \Сторона 4 + \Сторона 5 + \Сторона 6$
• Зона : ${3√3*\Сторона*2}/2$
• В качестве альтернативы, Зона : ${\Perimeter*\Apothem}/2$

 

Как насчет трехмерных геометрических фигур?

Существуют также трехмерные формы, которые имеют не только длину и ширину, но и глубину или объем. Это формы, которые вы видите в реальном мире, например, сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.

Трехмерные фигуры, естественно, более сложны, чем двумерные, с дополнительным измерением — количеством места, которое они занимают, а не только формой, — которое необходимо учитывать при расчете площади и периметра.

Математика, включающая 2D-формы, такие как приведенные выше, называется плоскостной геометрией, поскольку она имеет дело конкретно с плоскостями или плоскими формами .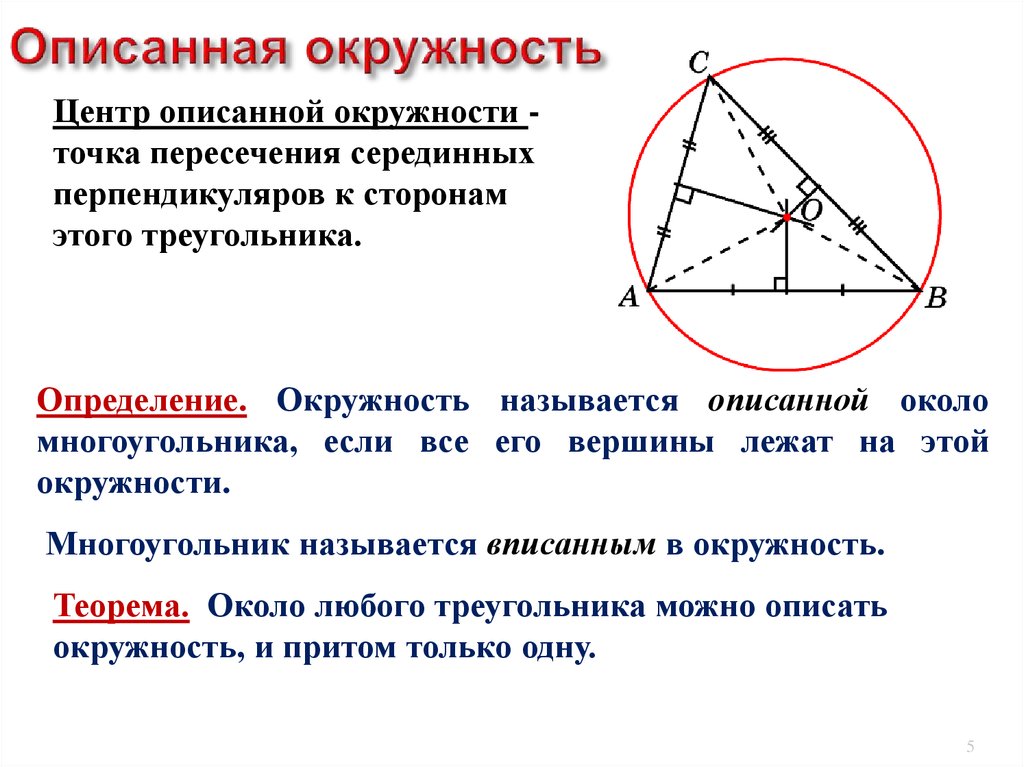 Математика, связанная с трехмерными формами, такими как сферы и кубы, называется твердотельной геометрией, потому что она имеет дело с твердыми телами, другими словами для трехмерных форм .

 

2D-формы составляют 3D-фигуры, которые мы видим каждый день!

 

3 основных совета по работе с фигурами

Существует так много типов фигур, что бывает сложно запомнить, какие из них есть какие, и как вычислить их площади и периметры. Вот несколько советов и приемов, которые помогут вам их запомнить!

 

#1: определение многоугольников

Некоторые фигуры являются многоугольниками, а некоторые нет. Один из самых простых способов определить, к какому типу формы относится предмет, — выяснить, является ли он многоугольником.

Многоугольник состоит из прямых линий, которые не пересекаются. Какие из фигур ниже являются многоугольниками, а какие нет?

 

Круг и овал не являются многоугольниками, а значит, их площадь и периметр вычисляются по-разному. Узнайте больше о том, как вычислить их с помощью $π$ выше!

 

#2: Проверка на наличие параллельных сторон

Если фигура, на которую вы смотрите, является параллелограммом, обычно легче вычислить его площадь и периметр, чем если это не параллелограмм. Но как определить параллелограмм?

В названии указано — параллельно. Параллелограмм представляет собой четырехугольник с двумя наборами параллельных сторон . Квадраты, прямоугольники и ромбы являются параллелограммами.

Квадраты и прямоугольники используют одни и те же базовые формулы для площади — длину, умноженную на высоту. Для них также очень легко найти периметр, так как вы просто складываете все стороны вместе.

С ромбами дело обстоит сложнее, потому что диагонали перемножаются и делятся на два.

Чтобы определить, на какой вид параллелограмма вы смотрите, спросите себя, имеет ли он все углы по 90 градусов.

Если да, то это либо квадрат, либо прямоугольник .