Модуль разности чисел: Сложение и вычитание модулей. Модуль разности, суммы, произведения чисел. Абсолютные величины дробей

Внеклассный урок — Модуль числа

Модуль числа

Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.

Например, модулем числа 5 является 5, модулем числа –5 тоже является 5.

То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.

Обозначается так: |5|, |х|, |а| и т.д.

Правило:

|а| = а, если а ≥ 0.

|а| = –а, если а < 0.

Пояснение:

|5| = 5
Читается так: модулем числа 5 является 5.

|–5| = –(–5) = 5
Читается так: модулем числа –5 является 5.

|0| = 0
Читается так: модулем нуля является ноль.

Свойства модуля:

1) Модуль числа есть неотрицательное число:

|а| ≥ 0

2) Модули противоположных чисел равны:

|а| = |–а|

3) Квадрат модуля числа равен квадрату этого числа:

|а|² = a²

4) Модуль произведения чисел равен произведению модулей этих чисел:

|а · b| = |а| · |b|

6) Модуль частного чисел равен отношению модулей этих чисел:

|а : b| = |а| : |b|

7) Модуль суммы чисел меньше или равен сумме их модулей:

|а + b| ≤ |а| + |b|

8) Модуль разности чисел меньше или равен сумме их модулей:

|а – b| ≤ |а| + |b|

9) Модуль суммы/разности чисел больше или равен модулю разности их модулей:

|а ± b| ≥ ||а| – |b||

10) Постоянный положительный множитель можно вынести за знак модуля:

|m · a| = m · |а|, m >0

11) Степень числа можно вынести за знак модуля:

|а^k| = |а|^k, если а^k существует

12) Если |а| = |b|, то a = ± b

Геометрический смысл модуля.

Модуль числа – это величина расстояния от нуля до этого числа.

Для примера возьмем снова число 5. Расстояние от 0 до 5 такое же, что и от 0 до –5 (рис.1). И когда нам важно знать только длину отрезка, то знак не имеет не только значения, но и смысла. Впрочем, не совсем верно: расстояние мы измеряем только положительными числами – или неотрицательными числами. Пусть цена деления нашей шкалы составляет 1 см. Тогда длина отрезка от нуля до 5 равна 5 см, от нуля до –5 тоже 5 см.

На практике часто расстояние отмеряется не только от нуля – точкой отсчета может быть любое число (рис.2). Но суть от этого не меняется. Запись вида |a – b| выражает расстояние между точками а и b на числовой прямой.

Пример 1. Решить уравнение |х – 1| = 3.

Решение.

Смысл уравнения в том, что расстояние между точками х и 1 равно 3 (рис.2). Поэтому от точки 1 отсчитываем три деления влево и три деления вправо – и наглядно видим оба значения х:
х₁ = –2, х₂ = 4.

Можем и вычислить.

│х – 1 = 3
│х – 1 = –3

↕

│х = 3 + 1
│х = –3 + 1

↕

│х = 4
│ х = –2.

Ответ: х₁ = –2; х₂ = 4.

Пример 2. Найти модуль выражения:

3√5 – 10.

Решение.

Сначала выясним, является ли выражение положительным или отрицательным. Для этого преобразуем выражение так, чтобы оно состояло из однородных чисел. Не будем искать корень из 5 – это довольно сложно. Поступим проще: возведем в корень 3 и 10. Затем сравним величину чисел, составляющих разность:

3 = √9. Следовательно, 3√5 = √9 · √5 = √45

10 = √100.

Мы видим, что первое число меньше второго. Значит, выражение отрицательное, то есть его ответ меньше нуля:

3√5 – 10 < 0.

Но согласно правилу, модулем отрицательного числа является это же число с противоположным знаком. У нас отрицательное выражение. Следовательно, надо поменять его знак на противоположный. Выражением, противоположным 3√5 – 10, является –(3√5 – 10). Раскроем в нем скобки – и получим ответ:

–(3√5 – 10) = –3√5 + 10 = 10 – 3√5.

Ответ:

|3√5 – 10| = 10 – 3√5.

Модуль числа, определение и свойства

Поможем понять и полюбить математику

Начать учиться

331.7K

Разберем сегодня, что значит модуль числа, как считать модуль и как обозначается модуль в математике. А также его свойства и, конечно же, примеры.

Определение модуля числа

Алгебра дает четкое определение модуля числа. Модуль числа в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».

Знак модуля: |a| = OA.

Разберем на примере:

Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.

Число 3 (длину отрезка OB) называют модулем числа −3.

Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).

Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.

Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

|a| > 0

2. Модуль положительного числа равен самому числу.

|a| = a, если a > 0

3. Модуль отрицательного числа равен противоположному числу.

|−a| = a

4. Модуль нуля равен нулю.

|0| = 0, если a = 0

5. Противоположные числа имеют равные модули.

|−a| = |a| = a

6. Модуль произведения равен произведению модулей этих чисел.

|a b| = |a| |b|, когда

a · b = 0

или

−(a · b), когда a · b < 0

7. Модуль частного равен частному от деления модуля числа числителя на модуль числа знаменателя:

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5.

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

Когда у нас есть два числа a и b, то их разность |a — b| равна расстоянию между ними на числовой прямой или длине отрезка АВ.

Расстояние от точки a до точки b равно расстоянию от точки b до точки a, тогда |a — b| = |b — a|.

Решим уравнение: |a — 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.

Уравнение имеет два решения: −1 и 7. Мы из 3 вычли 4 — и это один ответ, а также к 3 мы прибавили 4 — и это второй ответ.

Решим неравенство: |a + 7| < 4.

Эту запись читаем так: расстояние от точки a до точки −7 меньше четырех. Отмечаем на числовой прямой точки, удовлетворяющие этому условию:

Ответ в данном случае будет таким: (−11; −3).

Решим неравенство: |10 − x| ≥ 7.

Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.

Ответ: (−∞; 3] [17, +∞).

График функции

График функции равен y = |х|.

Для x > 0 имеем y = x.

Для x < 0 имеем y = −x. В результате получаем:

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

В контрольной работе или на ЕГЭ может встретиться задачка, в которой нужно вычислить √a² , где a – некоторое число или выражение.

При этом, √a²= |a|.

По определению арифметического квадратного корня √a² — это такое неотрицательное число, квадрат которого равен a² .

Оно равно a при а > 0 и −а, при а < 0 , т.

е. как раз |a|.

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Модуль рационального числа, примеры:

|-3,5| = 3,5

|2,27| = 2,27

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Юлия Герасимова

К предыдущей статье

417.2K

Квадратичная функция. Построение параболы

К следующей статье

200.3K

Деление десятичных дробей

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс

Абсолютное значение — общее руководство по математическим навыкам

Что это значит?

Определения:

Абсолютное значение (или модуль) | х | действительного числа x является неотрицательным значением x независимо от его знака.

Например, абсолютное значение 5 равно 5, а абсолютное значение -5 также равно 5. Абсолютное значение числа можно рассматривать как его расстояние от нуля по линии действительных чисел. Кроме того, абсолютная величина разности двух действительных чисел есть расстояние между ними.

Абсолютное значение обладает следующими четырьмя фундаментальными свойствами:

Неотрицательность $$|a| ≥ 0$$ Положительная определенность $$|a| = 0 ⇔ a = 0$$ Мультипликативность $$|ab| = |a||b|$$ Субаддитивность $$|a + b| ≤ |а| + |b|$$

Другие важные свойства абсолютного значения включают:

Идемпотентность (абсолютное значение абсолютного значения является абсолютным значением) $$||a|| = |a|$$ Симметрия $$|-a| = |a|$$ Тождество неразличимых (эквивалентно положительной определенности) $$|a — b| = 0 ⇔ a = b$$ Неравенство треугольника (эквивалентное субаддитивности) $$|a — b| ≤ |а — с| + |c — b|$$ Сохранение деления (эквивалентно мультипликативности) $$|a / b| = |а| / |б| \space\space if \space\space b ≠ 0$$ (эквивалент субаддитивности) $$|a — b| ≥ ||а| — |b||$$

Два других полезных свойства, касающихся неравенств: $$|a| ≤ b ⇔ -b ≤ a ≤ b$$ $$|a| ≥ b ⇔ a ≤ -b \space или \space b ≤ a$$

Эти соотношения можно использовать для решения неравенств, включающих абсолютные значения.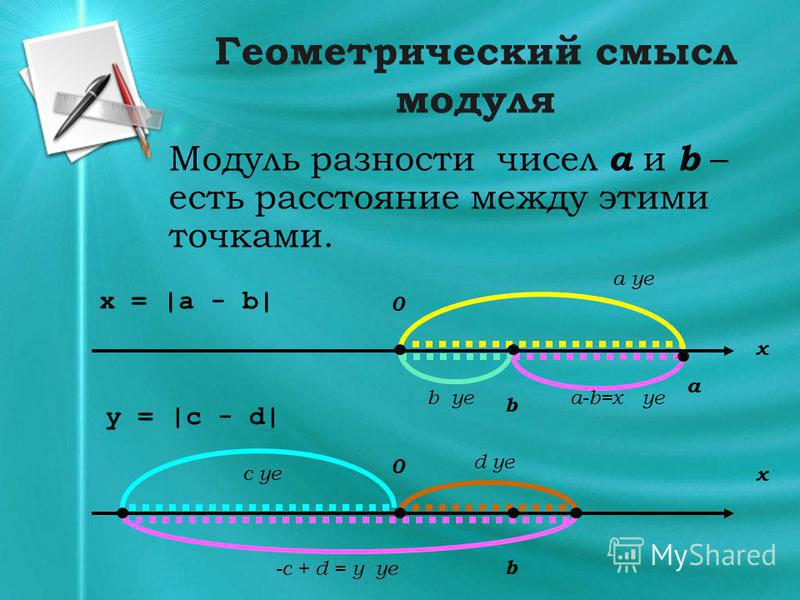 Например: $$|x — 3| ≤ 9 ⇔ -9 < x - 3 < 9$$ $$⇔ -6 < x < 12$$

From:en.wikipedia.org/wiki/Absolute_value

Как это выглядит?

Абсолютное значение 5 равно 5, это расстояние от 0,5 единиц.

Абсолютное значение -5 равно 5, это расстояние от 0,5 единиц.

$$|x| = 2 $$

$$|x| > 2$$

$$Для \space |x| < 2, -2 < x < 2$$ $$For \space |x| = 4, -4 = x = 4$$

|7| = 7 означает, что абсолютное значение 7 равно 7.

|-7| = 7 означает, что абсолютное значение -7 равно 7.

|-2 — x| означает абсолютное значение -2 минус x.

-|х| означает отрицательное значение абсолютного значения x.

Тебе пригодится…

Абсолютное значение действительных чисел встречается в самых разных математических установках, например, абсолютное значение также определяется для комплексных чисел, кватернионов, упорядоченных колец, полей и векторных пространств.

В реальной жизни абсолютное значение тесно связано с понятиями величины, расстояния и нормы. Подобно глубине океана, времени: 500 г. до н.э. в отличие от 500 г. н.э.

Видео

Абсолютное значение и числовые строки

Смотреть видео Академии Хана »
Продолжительность: 5:39

Видео

Абсолютное значение целых чисел

Смотреть видео Академии Хана »
Продолжительность: 2:22

Видео

Уравнения абсолютного значения

Смотреть видео Академии Хана »
Продолжительность: 10:41

Практические задачи

Абсолютные значения »

Абсолютные уравнения »

Как найти модуль комплексного числа

Как найти модуль комплексного числа

Как найти модуль комплексного числа?

Пусть z = a + ib — комплексное число.

Модуль или абсолютное значение z, обозначаемое | г | определяется как

Модуль свойств комплексных чисел

Свойство 1 :

Модуль суммы двух комплексных чисел всегда меньше или равен сумме их модулей.

Приведенное выше неравенство может быть немедленно распространено по индукции на любое конечное число комплексных чисел, т. е. для любых n комплексных чисел z ₁ , z ₂ , z ₃ , …, z _n

|z ₁ + z ₂ + z ₃ + … + zn | ≤ | я ₁ | + | я ₂ | + … + | я _н |

Недвижимость 2 :

Модуль разности двух комплексных чисел всегда больше или равен разности их модулей.

Свойство 3 :

Модуль произведения двух комплексных чисел равен произведению их модулей.

Свойство 4 :

Модуль отношения двух комплексных чисел равен отношению их модулей.

Давайте рассмотрим несколько примеров, основанных на приведенной выше концепции.

Пример 1:

Найдите модуль следующего комплексного числа

− 2 + 4i

Решение:

Пусть z = -2 + 4i

9 |z| = √(-2 + 4i)

|z| = √(-2) ² + 4 ²

= √4 + 16

= √20

⋅ 5)

= 2√5

Пример 2:

Найдите модуль следующего комплексного числа

2 − 3i

Решение:

Пусть z = 2 − 3i

|z| = √(2 — 3i)

|z| = √2 ² + (-3) ²

= √4 + 9

= √13

− 3 − 2i

Решение:

Пусть z = − 3 − 2i

|z| = √(− 3 − 2i)

|z| = √(-3) ² + (-2) ²

= √9 + 4

= √13

0073

Решение:

Пусть z = 4 + 3i

|z| = √(4 + 3i)

|z| = √4 ² + 3 ²

= √16 + 9

= √25

0009

= √5

Давайте рассмотрим следующий пример «Как найти модуль комплексного числа».

Внеклассный урок — Модуль числа