Модуль равнодействующей силы формула: Равнодействующая сил

Формула модуля равнодействующей силы, F

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Формулы по физике Формула модуля равнодействующей силы

Сила является вектором, то есть обладает как модулем (величиной) так и направлением. Однако чаще всего приходится иметь дело с телами, на которые действуют не одна, а несколько сил. Тогда рассматривают сумму всех сил, оказывающих действие на тело, такую сумму сил называют равнодействующей силой ():

Равнодействующая сила – это гипотетический (искусственный) параметр, который вводят для того, чтобы удобнее было производить расчеты.

Следует учитывать, что равнодействующая сила (как и любая сила) – это векторная величина, имеющая модуль и направление.

Модуль равнодействующей двух сил

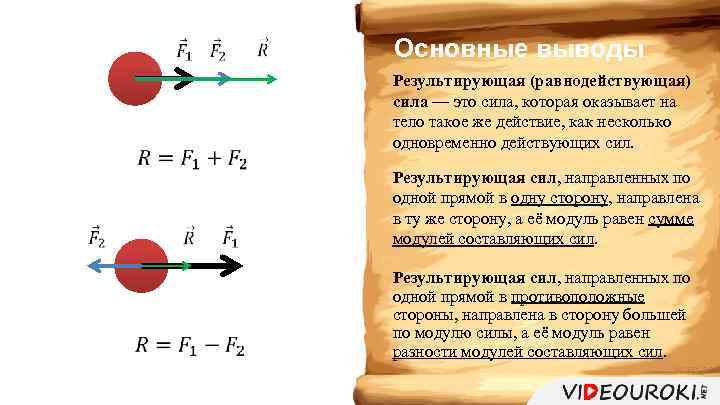
Допустим, тело находится под воздействием двух сил. Они направлены по одной прямой (рис.1).

Если силы имеют одинаковые направления (рис.1 (а)), то модуль равнодействующей вычисляется как:

На рис 1(б) силы направлены по одной прямой, но имеют противоположные направления. Формулой для вычисления модуля равнодействующей в таком случае будет выражение:

Рассмотрим случаи, когда две силы, действующие на тело, направлены под углом друг другу (рис.2).

В случае, который представлен на рис.2 (а) силы и направлены под углом 900 по отношению друг к другу. Модуль равнодействующей силы можно найти по теореме Пифагора:

Если угол между векторами сил и отличен от прямого угла, то модуль равнодействующей силы находят по теореме косинусов:

где – угол между векторами и

Модуль равнодействующей нескольких сил

Пусть на тело действуют силы: , тогда равнодействующая этих сил () находится в соответствии с формулой (1).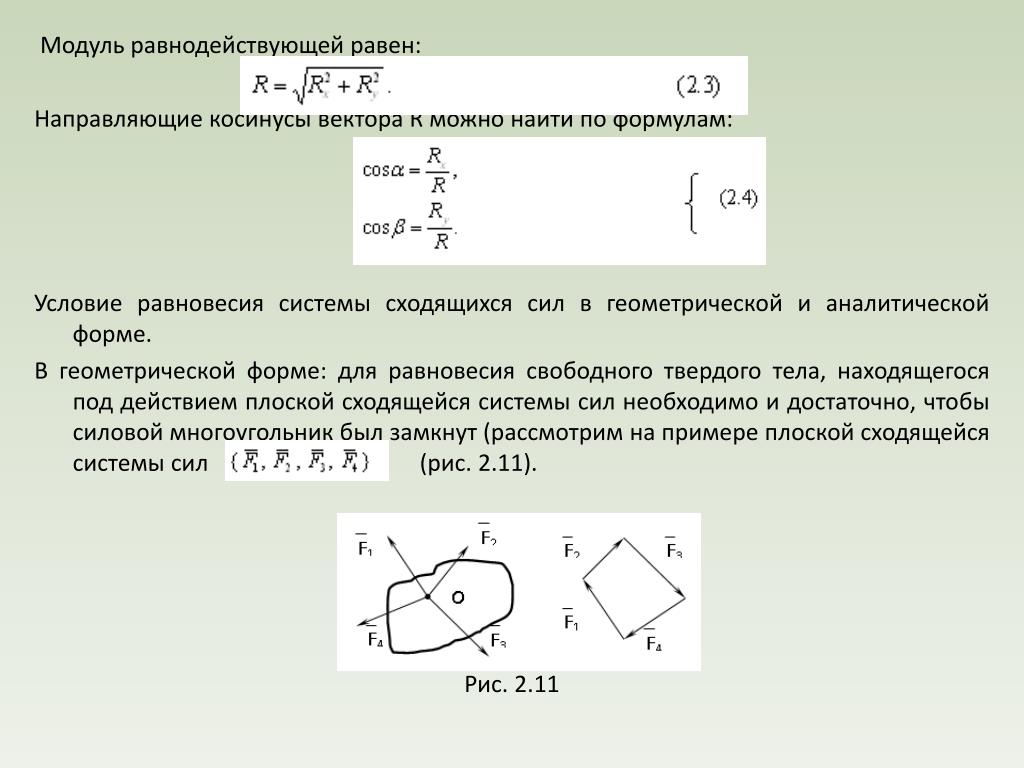 Для того чтобы вычислить модуль равнодействующей нескольких сил приложенных к телу выполняют следующую последовательность действий:

Вводят декартову систему координат, выбирают направления осей (X,Y).
Записывают проекции сил, действующих на тело на избранные оси:

Вычисляют проекции равнодействующей силы на оси X и Y, при этом складывают проекции сил по осям. Необходимо отметить, что суммирование проводят алгебраическое, то есть учитывают знаки проекций:
И в заключении модуль равнодействующей силы находят, применяя теорему Пифагора:

Примеры решения задач по теме «Модуль равнодействующей силы»

Понравился сайт? Расскажи друзьям!

Равнодействующая сила – формула, модуль, законы Ньютона

4.7

Средняя оценка: 4.

Всего получено оценок: 165.

Обновлено 31 Октября, 2021

4.7

Средняя оценка: 4.7

Всего получено оценок: 165.

Обновлено 31 Октября, 2021

Законы Ньютона – математическая абстракция. В реальности причиной движения или покоя тел, а также их деформации, выступают сразу несколько сил. Поэтому важным дополнениям к законам механики будет введение понятия равнодействующей силы и его применение.

О причинах изменений

Классическая механика разделена на два раздела – кинематику, при помощи уравнений описывающую траекторию движения тел, и динамику, которая разбирается с причинами изменения положения объектов или самих объектов.

Причиной изменений выступает некоторая сила, которая есть мера действия на тело других тел или силовых полей (например, электромагнитное поле или гравитация). К примеру, сила упругости вызывает деформацию тела, сила тяжести – падение тел на Землю.

Сила – это векторная величина, то есть, ее действие – направленное. 2}$

Теперь дадим строгое определение: равнодействующая сила есть векторная сумма всех сил, оказывающих влияние на тело.

Разберем правила треугольника и параллелограмма. Графически это выглядит так:

Рис. 3. Правило треугольника и параллелограмма.

Внешне они кажутся различными, но когда доходит до вычислений, сводятся к нахождению третьей стороны треугольника (или, что тоже самое, диагонали параллелограмма) по теореме косинусов.

Если сил больше двух, иногда удобней пользоваться правилом многоугольника. По своей сути – это всё тот же треугольник, только повторенный на одном рисунке некоторое количество раз. В случае, если по итогу контур получился замкнутым, общее действие сил равно нулю и тело покоится.

Задачи

На ящик, размещенный в центре декартовой прямоугольной системы координат, действуют две силы: $F_1 = (5, 0)$ и $F_2 = (3, 3)$. Рассчитать равнодействующую двумя методами: по правилу треугольника и при помощи покомпонентного сложения векторов. 2 + 2F_1F_2 sin45} = \sqrt{25 + 18 + 2 \cdot 5 \cdot 4,2 \cdot sin45} = 8,5 Н$
- На машину действуют три силы: $F_1 = (-5, 0)$, $F_2 = (-2, 0)$, $F_1 = (7,0)$. Какова их равнодействующая?
Решение
Достаточно сложить иксовые компоненты векторов:
$F = -5 – 2 + 7 = 0$
Что мы узнали?
В ходе урока было введено понятие равнодействующей сил и рассмотрены различные методы ее расчета, а также введена запись второго закона Ньютона для общего случая, когда количество сил неограниченно.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 165.
А какая ваша оценка?
Формула результирующей силы | Примеры и практические вопросы
- Формула
Дата последнего обновления: 14 апреля 2023 г.
•
Всего просмотров: 451,2 тыс. 1k
Когда действуют две или более сил на тело, то сумма всех сил, вызывающих результирующий эффект, является результирующей силой или результирующей силой. Поскольку сила является вектором, нам нужно взять векторную сумму всех сил, чтобы вычислить равнодействующую. Подходящая комбинация нескольких сил, действующих на тело, может дать нулевую результирующую, не вызывающую результирующего эффекта.

В общем случае, если \[{\vec F_1},\,\,{\vec F_2},\,\,{\vec F_3}\,\,….\]являются силами, действующими на тело, их результирующая сила \[\vec F\] определяется как:
\[\vec F = {\vec F_1} + {\vec F_2} + \,\,{\vec F_3}\,\,… .\]
В зависимости от числа действующих сил равнодействующая может быть получена геометрически, применяя закон треугольника, закон параллелограмма или закон сложения векторов многоугольника.

Обратите внимание, что величины сил нельзя складывать или вычитать, если они не коллинеарны.
Пример:
Найдите равнодействующую трех сил, показанных на рисунке.
Решение:
Пусть F1, F2 и F3 будут силами с величинами 50 Н, 10 Н и 70 Н. Также пусть направление вправо положительно. Затем;
F1 = 50 Н, F2 = 10 Н и F3 = – 70 Н
Результирующая сила: F = F1 + F2 + F3 = 50 + 10 – 70 = –10 Н
F = – 10 Н означает, результирующая сила равна 10 Н, действующая влево.
Пример: Двое друзей прикладывают силы к столу, как показано на рисунке, в каком направлении будет двигаться стол? 9{—1}}\left( {\frac{{15}}{8}} \right)\] с силой 8 Н. Стол будет двигаться в этом направлении.

Вопрос: На тело действуют три силы одинаковой величины. Затем выберите правильное утверждение.
Опции:
(a) Равнодействующая сила никогда не может быть равна нулю
(b) Равнодействующая может быть равна нулю, если все они коллинеарны
(c) Для нулевой равнодействующей одна сила должна быть противоположна комбинации два других.

(d) Равнодействующая трех равных сил всегда равна нулю.

Ответ: (с)
Недавно обновленные страницы. Формула – значение, расчет, решенные примеры и часто задаваемые вопросы
Формула энергии фотона – уравнение, график, приложения и часто задаваемые вопросы
Формула цилиндрического конденсатора – определение. Решенный пример и часто задаваемые вопросы
Формула трансформатора — эффективность, коэффициент трансформации, повышение и понижение
Формула радиоактивного распада — значение, уравнение, период полураспада и часто задаваемые вопросы
Электрические формулы — объяснение, примеры решений и часто задаваемые вопросы
Формула тепловой нагрузки — значение, расчет , Решенные примеры и часто задаваемые вопросы

Формула энергии фотона — уравнение, график, приложения и часто задаваемые вопросы
Формула цилиндрического конденсатора — определение. Решенный пример и часто задаваемые вопросы
Актуальные темы
Формула результирующего вектора.
Научитесь находить результирующий вектор.
Формула результирующего вектора используется для получения результирующего значения двух или более векторов. Это получается путем вычисления векторов на основе направлений друг относительно друга. Результирующая векторная формула имеет многочисленные приложения в физике, технике. Примером этого является взаимодействие многочисленных векторов силы на теле, где эта формула используется для получения результирующего вектора.
Что такое формула результирующего вектора?
Результирующая векторная формула бывает трех видов в зависимости от направления векторов. Эти формулы предназначены для векторов в одном и том же направлении, для векторов в противоположном направлении и для векторов, наклоненных друг к другу.
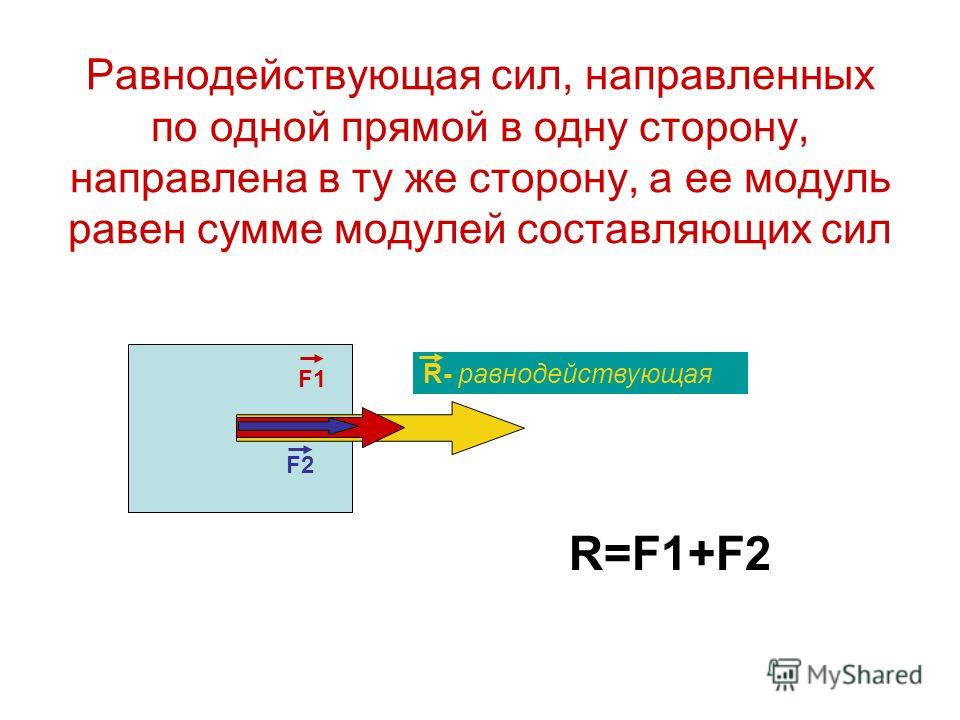
Формула 1 Можно просто сложить векторы в одном направлении, чтобы получить результирующий вектор. Здесь A, B — векторы в одном направлении, а R — результирующий вектор.
Р = А + В
Формула 2 Векторы в противоположном направлении вычитаются друг из друга, чтобы получить результирующий вектор. Здесь вектор B противоположен по направлению вектору A, а R — результирующий вектор.
R = A — B
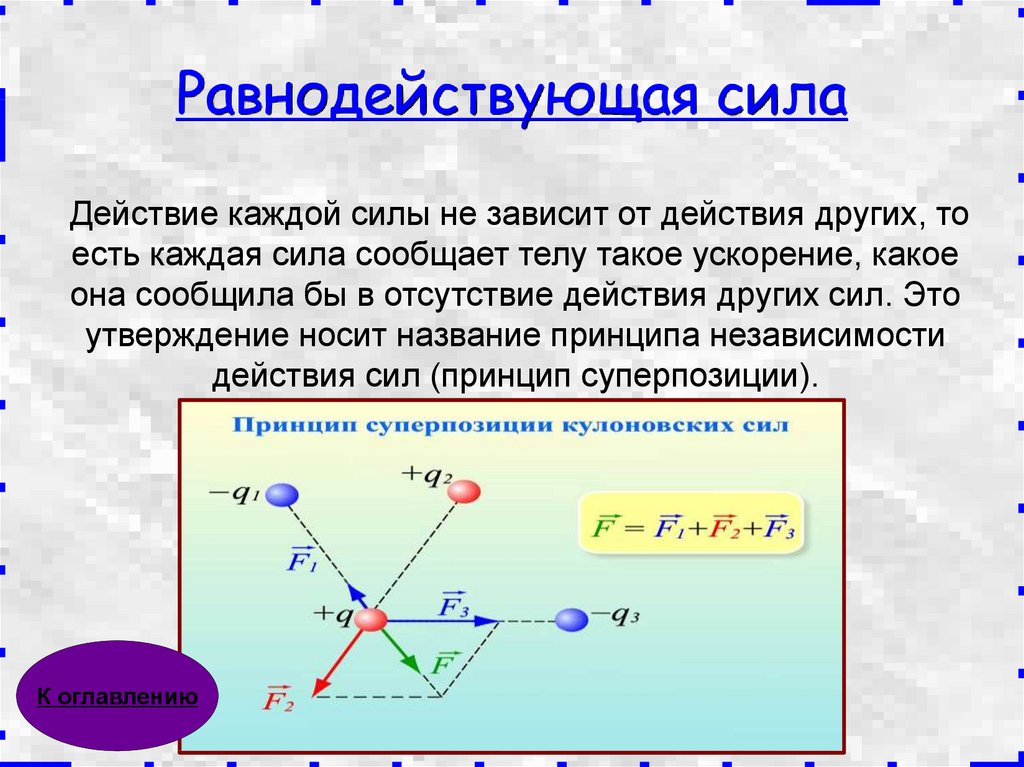
Формула 3 Векторы, наклоненные друг к другу, вычисляются по приведенной ниже формуле для получения результирующего вектора. Hre векторы A и B наклонены под углом Ø друг к другу, а R — результирующий вектор.
Р
² = А ² + B ² + 2ABCosØ
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запись на бесплатный пробный урок
Решенные примеры по формуле результирующего вектора
1. Пример 1: Найдите равнодействующую векторов 4i + 3j -5k и 8i + 6j — 10k.
  Решение:
  Даны два вектора:
  A = 4i + 3j — 5k и B = 8i + 6j — 10k
  Отношения направлений двух векторов находятся в равной пропорции, и, следовательно, два вектора имеют одинаковое направление.