Разбор тренировочного теста
Разбор тренировочного теста интернет-олимпиады по физике 2008/2009 года
11 класс. Кинематика
Вопрос № 1
По графику, представленному на рисунке, определите скорость движения велосипедиста через три секунды после начала движения.
Решение.
На рисунке представлен график зависимости пути от времени. График представляет собой прямую линию, значит, велосипедист двигался равномерно. Определим по графику величину пути, пройденного велосипедистом за фиксированный отрезок времени. Например, за 3 с велосипедист прошел 9 м. Скорость велосипедиста V = L / t = 9/3 = 3 м/с.
Вопрос № 2
Пешеход и велосипедист одновременно начали движение
навстречу. Их скорости равны V1 = 6 км/ч и V2 = 30 км/ч, соответственно.
Решение.
Определим скорость велосипедиста в системе отсчета пешехода V12 = V1 + V2 = 6 + 30 = 36 км/ч = 10 м/с. Итак, пешеход и велосипедист сближаются со скоростью 10 м/с, тогда их время движения до встречи t = L / V12 = 700/10 = 70 с.
Вопрос № 3
Автомобиль двигался со скоростью 15 м/с в течение 5 с. Какой путь он проехал за это время?
Решение.
Автомобиль двигался равномерно, поэтому пройденный путь L = V∙t = 15∙5 = 75 м.
Вопрос № 4
Брошенный вертикально вверх мяч возвращается в исходное положение. На рисунке представлен график его скорости от времени. В какой момент времени мяч достиг максимальной высоты?
Решение.
В момент, когда мяч достиг максимальной высоты, его скорость равна нулю. По графику, представленному на рисунке определяем, что скорость мяча равна нулю в момент времени t = 2 с.
Вопрос № 5
Какие из перечисленных выше величин векторные ? (Отметьте все векторные величины)
Решение.
Из перечисленных величин векторными являются скорость, ускорение и перемещение. Путь — величина скалярная.
Вопрос № 6
Спортсмен пробежал дистанцию 400 м по дорожке стадиона и возвратился к месту старта. Определите путь L, пройденный спортсменом, и модуль его перемещения S.
Решение.
Пройденный спортсменом путь L = 400 м. Модуль перемещения S = 0, так как спортсмен вернулся в точку, из которой он начал движение.
Вопрос № 7
Скорость тела, движущегося прямолинейно и равноускоренно,
изменилась при перемещении из точки 1 в точку 2 так, как показано на рисунке.
Решение.
Из рисунка видно, что модуль скорости тела при перемещении уменьшается, значит, вектор ускорения направлен навстречу движению, то есть налево.
Вопрос № 8
По графику зависимости модуля скорости от времени определите ускорение прямолинейно движущегося тела в момент времени t = 2 с.
Решение.
По графику определим изменение скорости тела за фиксированный момент времени. Например, за первые две секунды скорость тела изменилась на 6 м/с (с V0 = 3 м/с до Vt= 9 м/с). Ускорение a = (Vt – V0) / t = 6/2 = 3 м/с2.
Вопрос № 9
При равноускоренном движении автомобиля в течение пяти секунд его скорость увеличилась от 10 до 15 м/с. Чему равен модуль ускорения автомобиля?
Решение.
Вопрос № 10
Автомобиль стартует с места с постоянным ускорением а = 1 м/с2. Какой путь проходит автомобиль за первые десять секунд движения?
Решение.
Автомобиль движется равноускоренно без начальной скорости — пройденный путь L = a∙t2/2 = 1∙102/2 = 50 м.
Вопрос № 11
Плот равномерно плывет по реке со скоростью 3 км/ч. Сплавщик движется поперек плота со скоростью 4 км/ч. Какова скорость сплавщика в системе отсчета, связанной с берегом?
Решение.
Скорость сплавщика в в системе отсчета, связанной с берегом
Вопрос № 12
Вертолет поднимается вертикально вверх c
постоянной скоростью. Какова траектория движения точки на конце лопасти винта
вертолета в системе отсчета, связанной с корпусом вертолета?
Какова траектория движения точки на конце лопасти винта
вертолета в системе отсчета, связанной с корпусом вертолета?
Решение.
Представьте себе, что вы находитесь в кабине вертолета, то есть вы неподвижны относительно корпуса вертолета. В этом случае вы можете видеть, что любая точка винта вертолета описывает окружность.
Вопрос № 13
Тело движется вдоль оси Х по закону, представленному на рисунке, где х — координата в метрах, t — время в секундах. Определите модуль ускорения тела.
Решение.
Уравнение зависимости координаты от времени при прямолинейном равноускоренном движении в общем виде имеет вид Х(t) = X0 + V0х∙t + aх∙t2/2, где X0 — начальная координата, а V0х и aх— проекции начальной скорости и ускорения на ось Х.
Приравнивая члены, в которые входит t2, получим aх∙t2/2 = –4,5∙t2.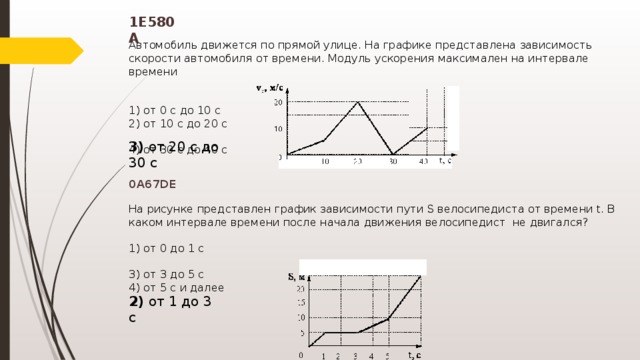 Откуда проекция ускорения aх
= –9 м/с2, а модуль ускорения a=
9 м/с2.
Откуда проекция ускорения aх
= –9 м/с2, а модуль ускорения a=
9 м/с2.
Вопрос № 14
На рисунке представлены графики зависимости модуля скорости от времени для четырех тел. Какое из этих тел (или какие тела) прошли наибольший путь?
Решение.
На рисунке показаны графики зависимости скорости движущихся
тел от времени. Как известно, пройденный телом путь представляет собой площадь,
лежащую под графиком скорости. Из рисунка видно, что фигура максимальной
площади лежит под графиком, для тела 4. Значит, за промежуток времени от 0 до t
Вопрос № 15
Тело движется прямолинейно. На рисунке представлен график скорости тела от времени. На каком промежутке (каких промежутках) времени проекция ускорения отрицательна?
Решение.
Проанализируем график:
1. на
промежутке времени от 0 до 1с скорость тела постоянна, поэтому а
2. на промежутке времени от 1с до 2с скорость тела уменьшается, поэтому проекция ускорения ах < 0;
3. на промежутке времени от 2с до 3с тело покоится, поэтому ах = 0;
4. на промежутке времени от 3с до 4с скорость тела увеличивается, поэтому проекция ускорения ах > 0.
Итак, проекция ускорения отрицательна на промежутке времени от 1с до 2с.
Вопрос № 16
Двигавшийся с начальной скоростью 20 м/с автомобиль
разгоняется с постоянным ускорением а = 2 м/с
Решение.
Для расчета пути можно воспользоваться формулой L = V0∙t + a∙t2/2
= 20∙5 + 2∙52/2 = 125 м.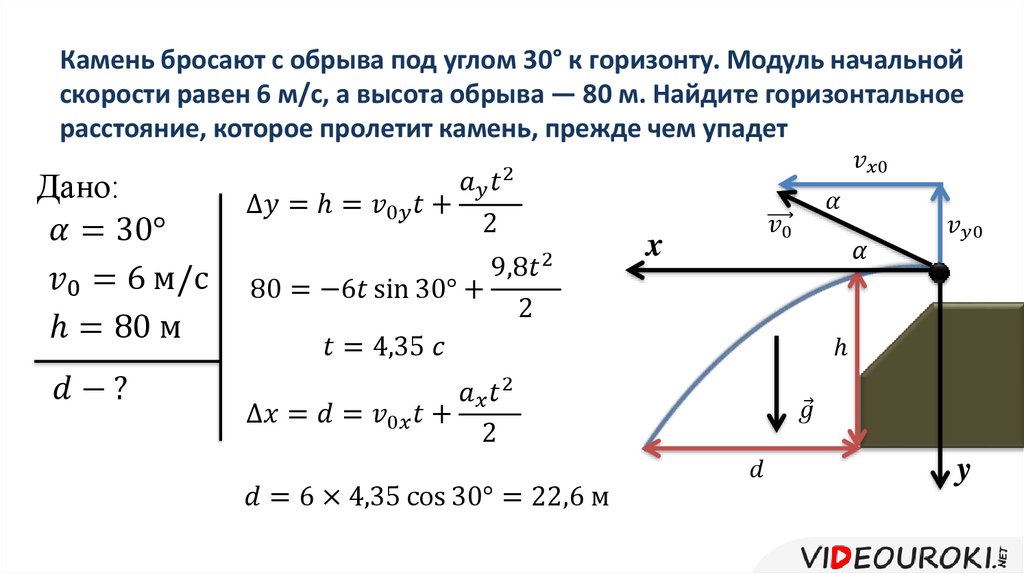
Гармонические колебания. | Объединение учителей Санкт-Петербурга
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Гармонические колебания.
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ | ||
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают. |
| |
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0. |
| |
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: . Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени. | ||
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе). |
| |
Скорость и ускорение при гармонических колебаниях. | ||
Согласно определению скорости, скорость – это производная от координаты по времени |
| |
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2. |
| |
Величина — максимальная скорость колебательного движения (амплитуда колебаний скорости). | ||
Следовательно, для скорости при гармоническом колебании имеем: , а для случая нулевой начальной фазы (см. | ||
Согласно определению ускорения, ускорение – это производная от скорости по времени: — вторая производная от координаты по времени. Тогда: . Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе). | ||
Величина — максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: , а для случая нулевой начальной фазы: (см. график). | ||
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения). | ||
Сравним выражения для смещения и ускорения при гармонических колебаниях: и . |
| |
Можно записать: — т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. | ||
Часто бывает удобно записывать уравнения для колебаний в виде: , где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: . Аналогично для скорости и ускорения. | ||
Теги:
конспект
Модуль скорости— Factorio Wiki
Модуль скорости увеличивает скорость машины на 20% и потребление энергии на 50%. Это означает, что за счет энергии машина производит больше изделий в минуту.
Машина будет потреблять больше энергии в секунду, но и работать будет быстрее. Поскольку затраты на энергию основаны на времени, а не на количестве операций, часть возросших затрат на энергию компенсируется сокращением времени на операцию.
Модуль скорости 1 требует значительного увеличения мощности для очень небольшого (менее половины стандартной скорости) увеличения пропускной способности, что является худшим показателем среди его группы. Напротив, модуль скорости 3 будет обеспечивать гораздо лучшую пропорцию пропускной способности при аналогичном недостатке потребляемой мощности по сравнению с этим модулем скорости уровня 1.
История
- 0.
 13.0 :
13.0 :- Модули поддержки чертежей.
- 0.12.1 :
- Изменено поведение автоматической вставки сборочных машин при использовании модулей скорости. Более высокая скорость с быстрыми рецептами позволит быстрее вставлять больше предметов.
- 0.7.1 :
- Модуль скорости не производит дополнительного загрязнения (кроме увеличения загрязнения от скорости).
- 0.7.0 :
- Добавлена механика загрязнения.
- 0.6.0 :
- Представлен
См. также
- Модули
- Модуль скорости 2
- Модуль скорости 3
Инструменты |
|
Электричество |
|
Добыча ресурсов |
|
Печи |
|
Производство |
|
модуля |
|
Космос |
|
Навигация |
|
Сверхскоростной модуль Lumedyne-XSMF Fast
XSMF — это высокоскоростной модуль, который ускоряет перезарядку системы флэш-памяти Lumedyne. Он подключается между батареей и остальной частью системы и сокращает время перезарядки при любых настройках мощности. Это не помогает системе Lumedyne стать ярче, но помогает ей намного быстрее перезаряжаться от питания от батареи или текущих параметров питания от сети переменного тока.
Он подключается между батареей и остальной частью системы и сокращает время перезарядки при любых настройках мощности. Это не помогает системе Lumedyne стать ярче, но помогает ей намного быстрее перезаряжаться от питания от батареи или текущих параметров питания от сети переменного тока.
Будьте первым кто оценит этот продукт
Производитель: Люмедин, Инк.
Артикул: XSMF
400,00 долларов США
Экстраскоростной модуль XSMF Fast предназначен для ускорения переработки системы флэш-памяти Lumedyne. Он крепится между батареей и блоком питания, чтобы сократить время перезарядки.
Нет переключателей, если они находятся между Pack и Battery, это автоматически ускоряет перезапуск системы. Модули скорости не делают систему ярче, это делают бустеры. Однако иногда, когда для повышения яркости системы используются усилители, а затем время перезарядки становится намного больше, добавление высокоскоростного модуля рядом с батареей в стек имеет огромное значение, сокращая это время быстрее.
Он весит около фунта и имеет высоту около двух дюймов и имеет металлические боковые стенки экрана, что позволяет продолжать переработку на очень высокой скорости без перегрева.
Поскольку XSMF имеет мощность рециркуляции 28 ампер, это более чем в три раза быстрее, чем скорость блока № 065 с тягой 7 ампер. Модели #065X, Packs и #067X Pack (оба типа Pack # с буквами X, M, L, Q или T имеют силу тока 14 ампер) при использовании XSMF работают более чем в два раза быстрее. Аккумуляторы #065Z или #067Z перезаряжаются при 28 амперах, как и наша текущая сверхбыстрая скорость перезарядки серии Next Generation и Signature, которая будет в два раза выше при использовании XSMF.
Высокоскоростные модули НЕ МОГУТ использоваться с пакетами действий или пакетом #068 660. Они не предназначены для использования с велосипедистами.
Этот высокоскоростной модуль будет работать с батареями любого размера, но Маленькие не рекомендуются для этого, потому что они будут разряжаться намного быстрее при такой большой нагрузке, и это не принесет им пользы в долгосрочной перспективе. С большими батареями вы должны ожидать примерно на 20-30% меньше вспышек на одну зарядку, когда вы перезаряжаете в два раза быстрее.
С большими батареями вы должны ожидать примерно на 20-30% меньше вспышек на одну зарядку, когда вы перезаряжаете в два раза быстрее.
Вы можете использовать этот высокоскоростной модуль с блоками питания переменного тока, которые мы в настоящее время предлагаем. Максимальная скорость меньшего источника переменного тока XPSU составляла 30 ампер, поэтому вы не сможете полностью раскрыть потенциал высокоскоростного модуля с большинством пакетов, даже если они будут намного быстрее, чем без модуля скорости. Однако, если у вас уже есть сверхбыстрый пакет или вы хотите максимально возможную скорость, вам понадобится база питания XACU Power Base на 60 ампер.
Несовместим с классическими адаптерами переменного тока, высокоскоростные модули ничего не делают со старыми продуктами с питанием от сети переменного тока #058.
На заметку: если вы очень быстро снимаете фотографа, который будет очень быстро использовать большую мощность на регулярной основе, срок службы обычных ламп-вспышек 800 нс может сократиться.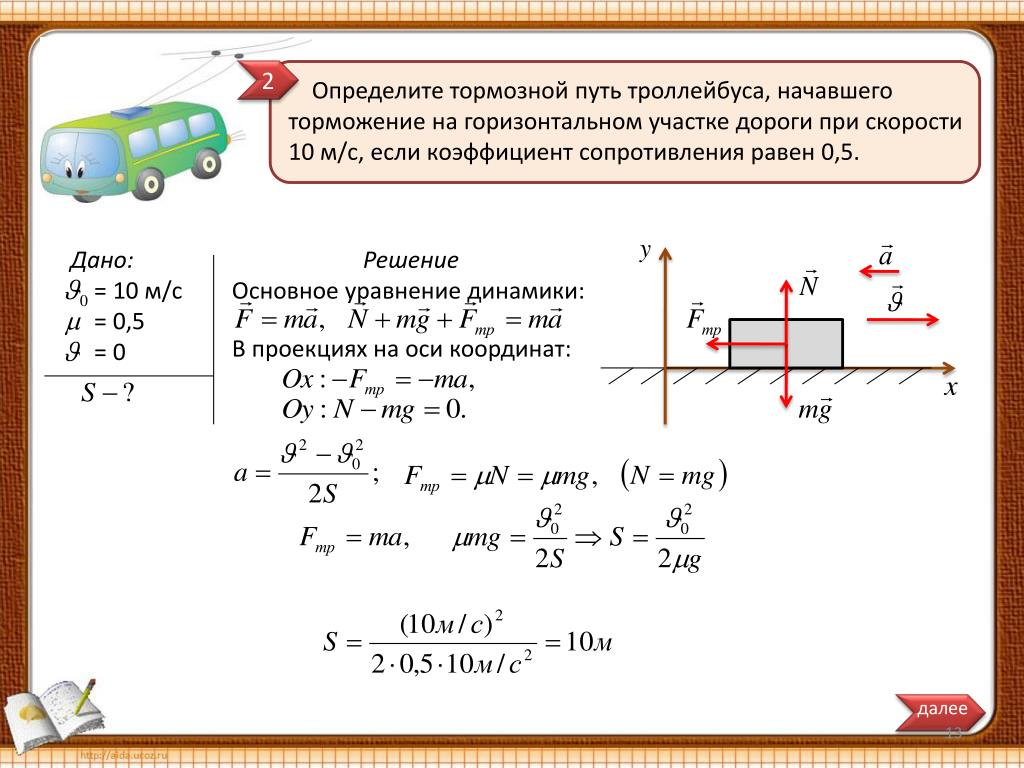



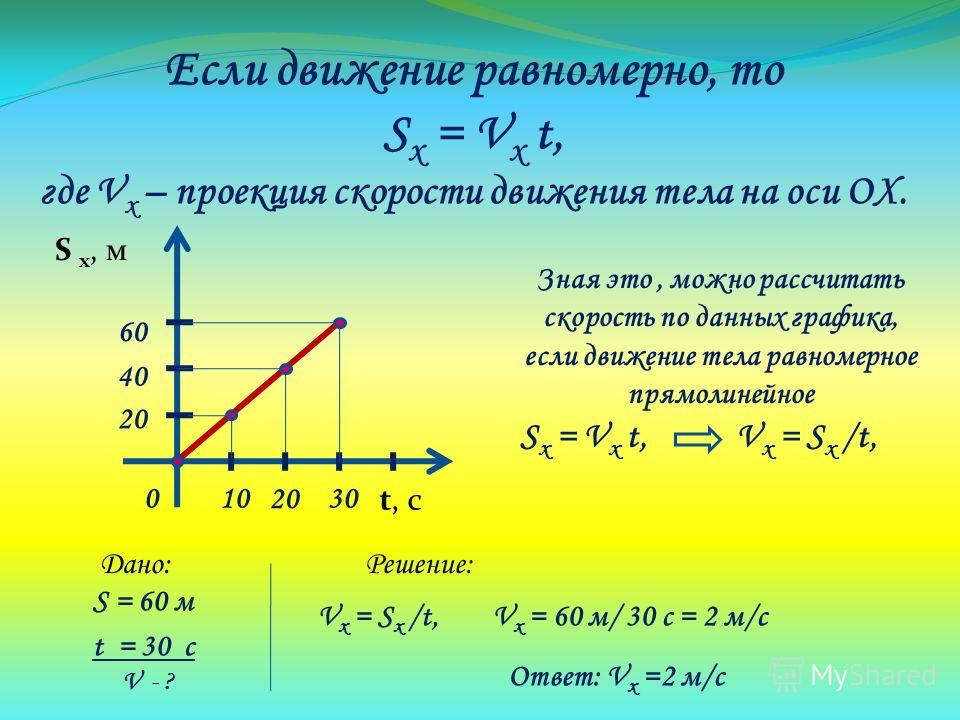 график).
график).

 13.0 :
13.0 :
Leave A Comment