Медиана равностороннего треугольника равна 9 корень из 3 найдите сторону этого треугольника: Биссектриса равностороннего треугольника равна 9√3. Найдите его сторону.

Биссектриса

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.

Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.

Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам: b : c =  x : y.

Высота

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

Медиана

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника.

Медианы треугольника пересекаются в одной точке и делятся в отношении 2:1 начиная от вершины треугольника: СO=2OL, BO=2OM.

Медиана разбивает треугольник на два треугольника одинаковой площади: S ABM = S BCM.

Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Равнобедренный треугольник

Две равные стороны называются боковыми сторонами, третья – основанием: KL и LM — боковые стороны (KL=LM), КМ — основание.

Углы при основании равнобедренного треугольника равны: К=М.

Высота, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой.

Прямоугольный треугольник

Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

с²=a²+b².

Синус угла – отношение противолежащего катета к гипотенузе: sin α=a:c.

Косинус угла – отношение прилежащего катета к гипотенузе: cos α=b:c.

Тангенс угла – отношение противолежащего катета к прилежащему катету: tg α=a:b=sin α : cos α.

Котангенс угла – отношение прилежащего катета к противолежащему катету: ctg α= cos α : sin α.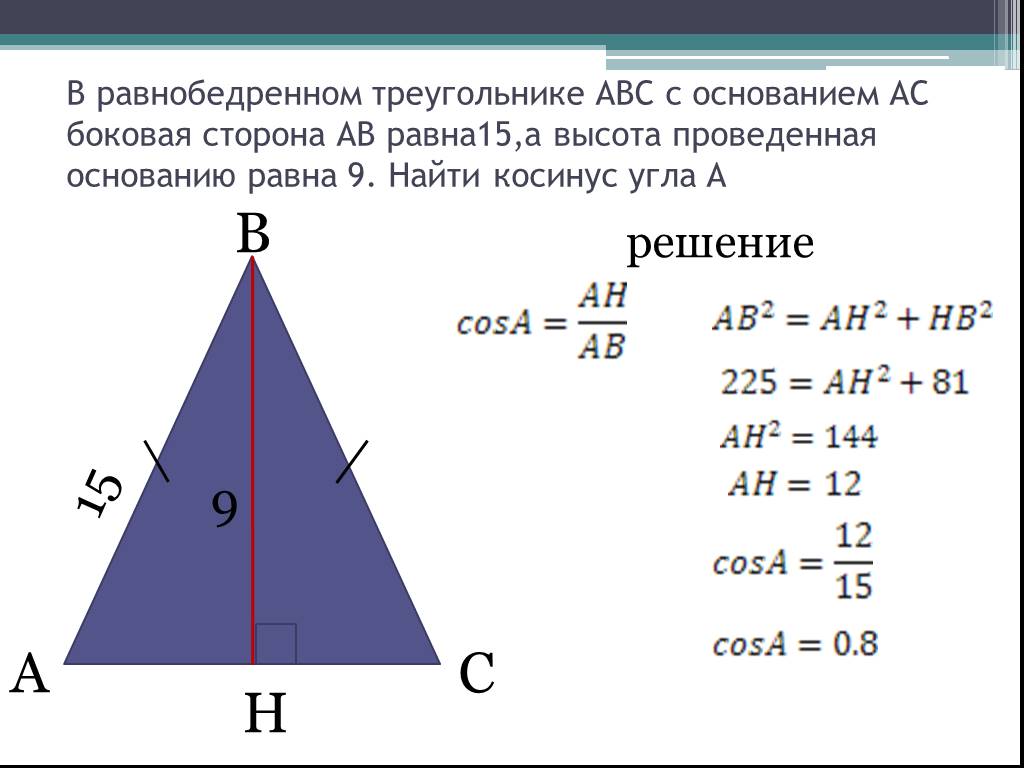

Гипотенуза прямоугольного треугольника является диаметром описанной окружности.

Радиус описанной около прямоугольного треугольника окружности: R=c:2.
Радиус вписанной в прямоугольный треугольник окружности: r=(a+b-c):2.

Квадрат высоты, проведенной к гипотенузе прямоугольного треугольника равен произведению проекций высоты на гипотенузу: h²=x*y.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности:

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

a² = b² + c² — 2bc cos А.

Площадь треугольника

 h – высота, проведенная к стороне а.

 a, b – стороны треугольника, γ – угол между ними.

 р – полупериметр, a, b, c – стороны треугольника.

S=pr, р – полупериметр, r – радиус вписанной окружности

S=abc : (4R), R — радиус описанной окружности

В прямоугольном треугольнике 

S=0,5ab, где a, b – катеты треугольника

В равностороннем треугольнике

УПРАЖНЕНИЯ

1. а) В прямоугольном треугольнике один из катетов равен 10 см, один из углов равен 45. Найдите второй катет.

    б) В прямоугольном треугольнике катеты равны. Найдите все углы треугольника.

Решение:

. Треугольник равнобедренный, т.к. два угла равны, тогда и катеты равны, т.е. второй катет равен 10 см.

Решение:
а) Треугольник АВС прямоугольный и А=180°-90°-60°=30°. 
    ВС=АВ:2=10:2=5 см (катет лежит против угла в 30

3. Найдите площадь равнобедренного треугольника со сторонами:
а) 6 см, 6 см, 8 см;     б) 10 см, 10 см, 12 см.
Решение:
а) по формуле Герона 

Ответ: 

4. а) В треугольнике АВС сторона АВ равна 10 см, расстояние от точки С до прямой АВ равно 6 см, сторона ВС равна 14 см. Найдите расстояние от точки А до прямой ВС.

Дано: АВС — треугольник;
d(C, AB)=6 см;
АВ=10 см; ВС=14 см
Найти: d(A, BC)

Решение:
1) Найдем площадь треугольника АВС:
S=CК*АВ:2=10*6:2=30 см2
2) Зная площадь треугольника АВС и сторону ВС, найдем высоту АМ, проведенную к этой стороне:
S=BC*AM:2; AM=30:14*2=30/7 = 4 2/7 см
Ответ: 4 2/7 см

    б) В равнобедренном прямоугольном треугольнике гипотенуза равна 10 см. Найдите площадь треугольника.

Дано: АВС — равнобедренный прямоугольный треугольник;
    ВН=4 см
  Найти: S — ?

Решение:
1) Т.к. треугольник АВС — равнобедренный, то высота ВН, проведенная к основанию является и медианой: АН=НС.

6. а) Периметр треугольника АВС равен 30 см. А=С и АВ больше АС на 3 см. Найдите стороны треугольника.
 б) Периметр треугольника АВС равен 36 см. А=С и АВ : АС как 3:2. Найдите стороны треугольника.

Решение:
а) 

Дано:
АВС — треугольник;
Р=30 см;
А=С;
АВ=АС+3 см.
Найти: АВ, ВС, АС

Решение:
1) Т.к. А=С, то треугольник АВС — равнобедренный и АВ=ВС.
2) Пусть х — основание треугольника АВС, тогда боковая сторона равна (х+3).
Р=АВ+ВС+АС=х+х+3+х+3; 3х+6=30, 3х=24, х=8 см — сторона АС.
АВ=ВС=8 + 3=11 см
Ответ: 8 см, 11 см, 11 см

7. а) В прямоугольном треугольнике один из катетов равен 6 см, а сумма второго катета и гипотенузы равна 18 см. Найдите площадь треугольника.   
    б) В прямоугольном треугольнике один из катетов равен 1,5 см, а разность гипотенузы и второго катета   равна 0,5 см. Найдите площадь треугольника.

Решение:
а) 1) Пусть катет равен х см, тогда гипотенуза равна (18 -х) см.
По теореме Пифагора:
62+х2=(18-х)2
36+х2=324-36х+х2
36х=288
х=8 (см) — катет прямоугольного треугольника
2) S=6*8:2=24 см2
Ответ: 24 см2

8. а) В равнобедренном треугольнике высота, проведенная к боковой стороне, делит ее на отрезки, равные 5 см и 4 см, считая от вершины треугольника. Найдите площадь треугольника.

    б) В треугольнике АВС АК — высота, ВК=СК=5 см. Найдите площадь треугольника, если АВ=12 см.
Решение:

а)

Дано: АВС — равнобедренный треугольник;

          АК — высота к боковой стороне;

         ВК= 5 см; КС= 4 см

Найти: S — ?

Решение:

1) Т.к. треугольник АВС — равнобедренный, то АВ=ВС=ВК+КС=5+4 = 9 см.

2) Треугольник АВК — прямоугольный, Зная гипотенузу АВ и катет ВК,  найдем катет АК:

АК2=АВ2-ВК2=81-25=56 

9. а) В прямоугольном треугольнике катеты равны 12 см и 9 см. Найдите биссектрису треугольника, проведенную к большему катету.
    б) В прямоугольном треугольнике один из катетов равен 6 см, а гипотенуза равна 10 см. Найдите биссектрису треугольника, проведенную к меньшему катету.
Решение:
а) 

Дано: АВС — прямоугольный треугольник;
АВ=12 см; АС=9 см;
СК — биссектриса
Найти: СК -?

Решение:
1) По теореме Пифагора найдем гипотенузу: ВС2=АВ2+АС2=144+81=225, ВС=15 см.
2) Т.к. СК — биссектриса, то АС:ВС=АК:КВ.
Пусть КВ=х, тогда АК=12-х.
9:15=(12-х):х,
9х=15(12-х),
8х=60,
х=7,5 см — ВК.
3) АК=12-7,5=4,5 см
4) Треугольник АКС — прямоугольный, по теореме Пифагора найдем КС:
КС2=АК2+АС2=101,25

10. а) В прямоугольном треугольнике проекции катетов на гипотенузу равны 25 см и 4 см. Найдите площадь треугольника.
      б) В прямоугольном треугольнике проекции катетов на гипотенузу равны 9 см и 16 см. Найдите площадь треугольника.
Решение:
а)

Дано:
АВС — прямоугольный треугольник;
АК — высота;
ВК=25 см; КС=4 см
Найти: S — ?

Решение:
1) Квадрат высоты, проведенной из вершины прямого угла к гипотенузе равен произведению ее проекций на гипотенузу: АК2=ВК*КС;  АК2=25*4=100, АК=10 см
2) ВС=ВК+КС=25+4=29 см 
3) S=АК*ВС:2=15*10:2=145 см2 
Ответ: 145 см2

11. а) В равнобедренном треугольнике боковые стороны равны 6 см, площадь треугольника равна 24 см2. Найдите сумму расстояний от точки на основании  треугольника до его боковых сторон.
      б) В равнобедренном треугольнике боковые стороны равны 12 см, площадь треугольника равна 56 см2. Найдите сумму расстояний от точки на основании  треугольника до его боковых сторон.
Решение:
а)

Дано: АВС- равнобедренный треугольник;
АВ=ВС=6 см;
S=24 cм2
О — точка на основании треугольника АВС
Найти: d(O, AB)+d(O, BC)

Решение:
1) Найдем площадь треугольника АВО:
S=OK*AB:2=OK*6:2=3OK;
2) Найдем площадь треугольника ВСО:
S=OМ*BС:2=OМ*6:2=3OМ;
3) Площадь треугольника АВС равна сумме площадей треугольников АВО и ВСО:
24=3ОК+3ОМ,
ОК+ОМ=24:3=8 см
Ответ: 8 см

12. а) В прямоугольном треугольнике катеты равны 9 см и 12 см. Найдите биссектрису, проведенную к гипотенузе.
      б) В прямоугольном треугольнике катеты равны 3 см и 4 см. Найдите биссектрису, проведенную к гипотенузе.
Решение:
а)

Дано: АВС- прямоугольный треугольник;
АВ=12 см; АС=9 см;
АК — биссектриса
Найти: АК — ?

Решение:
1) Найдем гипотенузу треугольника АВС:
ВС2=АВ2+АС2=81+144=225, ВС=15 см.
2) По свойству биссектрисы треугольника:
АС:АВ=КС:ВК.
Пусть КС= х см, тогда ВК=15-х см
9:12=х:(15-х),
12х=135-9х,
21х=135,
х=45/7.
3) Найдем АК по теореме косинусов:
cos С=АС:ВС=9/15=3/5
АК2=АС2+КС2-2АС*КС*cos С=677.

13. а) Найдите наибольшую высоту треугольника со сторонами 7 см, 5 см, 4 см.
      б) Найдите наименьшую высоту треугольника со сторонами 10 см, 12 см, 8 см.
Решение:
а)
1) Найдем площадь треугольника по формуле Герона:

2) Наибольшая высота проведена к меньшей стороне, следовательно высота проведена к стороне, равной 4 см. Зная площадь треугольника и сторону, к которой высота проведена, найдем высоту:
S=h*4:2, 

14. а) Докажите, что медианы треугольника пересекаются в одной точке.
      б) Докажите, что высоты треугольника пересекаются в одной точке.
Решение:

а)

Дано: АВС — треугольник;
АМ, ВК, СN — медианы
Доказать: медианы пересекаются в одной точке

Доказательство:
1) Докажем, что медианы точкой пересечения делятся в отношении 2:1, начиная от вершины:
Пусть точка Е — середина АО, точка F — середина СО.
Рассмотрим четырехугольник ENMF, его стороны NM и EF параллельны и равны, т.к. являются средними линиями треугольников АВС и АОС с общим основанием АС. Тогда ENMF — параллелограмм, следовательно, МО=ЕО, NO=OF (диагонали параллелограмма точкой пересечения делятся пополам). Т.к. АЕ=ЕО=ОМ, то АО:МО=2:1, аналогично СО:ОN=2:1.
2) Докажем, что и медиана ВК проходит через точку О:
Пусть медианы ВК и АМ пересекаются в точке Н. Тогда ВН:НК=2:1 и АН:НМ=2:1, но, тогда точки О и Н делят медиану АМ в отношении 2:1, следовательно, они совпадают и медиана ВК проходит через точку О. 

15. а) АК — биссектриса треугольника АВС. NK||AC, NM||BC,  К лежит на ВС, М лежит на АС, N лежит на АВ и AN=5 см, NB= 3 см, ВК= 4 см. Найти МС.
      б) АК — биссектриса треугольника АВС. NK||AC, NM||BC,  К лежит на ВС, М лежит на АС, N лежит на АВ и AN=6 см, СК= 8 см, ВК= 7 см. Найти МС.
Решение:
а)

Дано: АВС — треугольник;
АК — биссектриса;
NK||AC, NM||BC;
AN=5 см, NB= 3 см, ВК= 4 см
Найти:  МС — ?

Решение:
1) Рассмотрим треугольник ANK:
КАС=AKN как внутренние накрест лежащий при параллельных прямых NK и АС и секущей АК. По условию АК биссектриса и ВАК=КАС, следовательно ВАК=АКN и треугольник АNК — равнобедренный и AN=NK=5 cм.
2) Рассмотрим четырехугольник MNKC:
MNKC — параллелограмм, т.к. NK|| MC и NM || KC, следовательно NK=MC=5 cм
Ответ: 5 см

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Укажите медиану данного треугольника.

2. Определите, из какого набора отрезков можно построить треугольник:
а) 10 см, 2 см, 5 см;   б) 9 см, 9 см, 12 см;   в) 3 см, 4 см, 5 см.

3. Найдите площадь треугольника со сторонами 5 см, 7 см, 8 см.

4. Найдите сторону равностороннего треугольника, если его высота равна 8 см.

5. Острые углы в прямоугольном треугольнике относятся как 1:2. Найдите угол, лежащий напротив меньшего катета.

6. В треугольнике АВС проведена медиана АМ. Площадь треугольника АОС равна 64 см, где О — середина АМ. Найдите площадь треугольника АВС.

7. Найдите сторону треугольника ВС, если АС равно 12 см, АВ=6 см, а биссектриса внешнего угла при вершине А пересекается со стороной СВ в точке К и ВК=8 см.

8. В равнобедренном треугольнике, высота, проведенная к боковой стороне делит ее на отрезки 8 и 6 см, считая от вершины. Найдите площадь треугольника.

9. Внутри равностороннего треугольника взята точка К. Доказать, что сумма расстояний от этой точки до сторон треугольника постоянная величина.

10.  В треугольнике АВС проведены высоты АМ и СК к сторонам треугольника. АК=9 см, КВ=2 см, ВМ=3 см. Найдите величину МС.

Боковое ребро правильной треугольной призмы равно 9 см,а диагональ боковой грани равна 15 см. Найти площадь боковой и полной поверхности призмы — вопрос №2747798

27. 01.18

Посмотреть всех экспертов из раздела Учеба и наука

В баллоне объёмом 1,66^3 м находится 2 кг азота при давлении 10^5 Па.

Решено

Найдите наименьший положительный период функции y=sinx+cosx Прдробно, пожалуйста

Вычислить площадь треугольника с вершинами А(7;3;4), В(1;0;6), С(4;5;-2)

Медиана равностороннего треугольника равна 13√3.Найдите его сторону. Решение плиз

Пользуйтесь нашим приложением

Площадь равностороннего треугольника равна 9√3м2. Длина медианы (в м) составляет 9√3м2 है। Просмотреть еще ोगी?

Вопрос

Обновлено:26/04/2023

ПУБЛИКАЦИЯ ЧЕМПИОНА-2013 TIER-II PAPER(21)-УПРАЖНЕНИЕ

РЕКЛАМА

लि खित उत्तर

Пошаговое решение от экспертов, которое поможет вам в сомнениях оформление и отличные оценки на экзаменах.

Аб Падхаи каро бина адс ке

Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке!

संबंधित वीडियो

किसी समबाहु त्रिभु ज का क्षेत्रुफल 9√3м2 माध्यिका की लम्बाई ज्ञात करें?

25789893

Длина каждой стороны равностороннего треугольника, имеющего площадь 9√3см2:

642909236

Основанием прямой призмы является равносторонний треугольник со стороной 6 см. Если объем призмы 108 кв. тогда его высота равна एक लंब प्रिज्म का आधार 6 सेमी. भुजा वाला समबाहु त्रिभुज है। यदि प्रिज्म का आयतन 108 sqrt3 घन सेमी. है, तो उसकी ऊँचाई है-

645129546

Какова длина радиуса описанной окружности равностороннего треугольника, длина стороны которого равна 6 кв. см? एक समबाहु त्रिभुज जिसकी भुजा की लम्बाई 6 sqrt3 सेमी है, के परिवृत्त की त्रिज्या की लम्बाई कितनी होग ी?

645129661

Если высота равностороннего треугольника равна 10√3 см, площадь равна:
ुज की ऊंचाई 10√3 सेमी है, तो क्षेत्रफल ज्ञात करें |

645733593

Сторона равностороннего треугольника равна 4 см. Какова его площадь? 92 है। इसके विकर्ण की लंबाई कया है?

645733876

Какова площадь равностороннего треугольника со стороной 4 кв. 3 см? 43 . ?

645733880

Если высота равностороннего треугольника равна 12 см, то какова его площадь? यदि एक समबाह त्रिभुज की ऊंचाई 12 часов, तो त्रि भुज का क्षेत्रफल कितना है?

645733934

Основанием пирамиды является равносторонний треугольник со стороной 10м.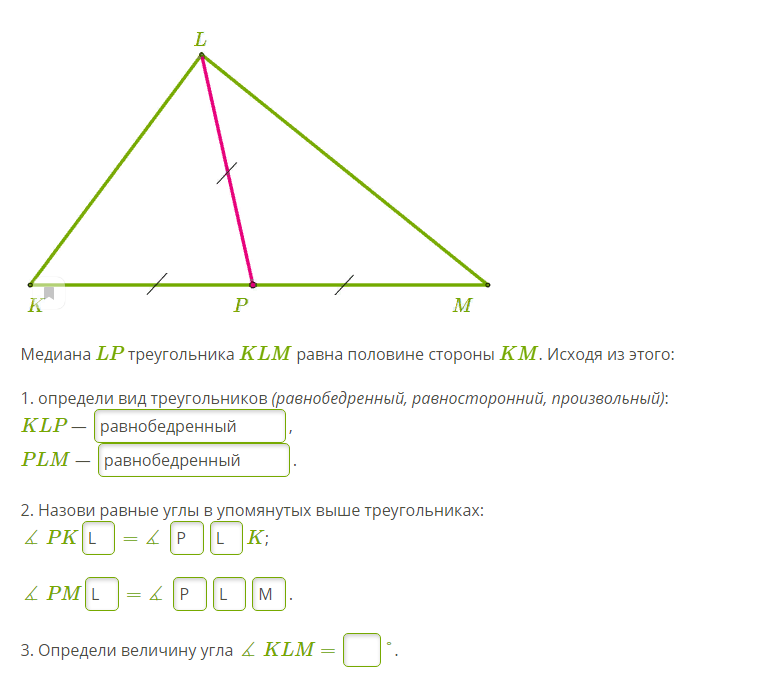 Если высота пирамиды 40 кв.м3, то объем пирамиды: ाह त्रिभुज है। यदि पिरामिड की ऊंचाई 40 sqrt3 मीटर है, तो पिरामिड का आ यतन क्या है 92 , то периметр треугольника равен: ग सेमी है, तो इस त्रिभुज का परिमाप कितना होगा ?

645734355

ABC — равносторонний треугольник со стороной 12 см, а AD — медиана. Найдите длину GD, если G — центр тяжести треугольника ABC. ABC एक समबाहु त्रिभुज है जिसके भुजा 12cm और AD मध्यिका है। GD की लंबाई ज्ञात करें यदि G, треугольник ABC का केन्द्रक है।

645734507

Если высота равностороннего треугольника равна 12 sqrt3 см, то его площадь будет: शीर्ष लम्ब 12 sqrt3 सेमी. है, तो उसका क्षेत्रफल कितना होगा? 9{2}\). Длина (в м) медианы

Темы

Правильный ответ:

\( \Большая сторона=\sqrt{36}=6 см \)

длина медианы \( \Large =\frac{\sqrt{3}}{ 2}(сторона) \)

\( \Large =\frac{\sqrt{3}}{2} \times 6=3\sqrt{3}cm \)

\(\textbf{Примечание:}\ ) В равностороннем треугольнике длина медианы, биссектрисы угла, высота равна \( \Large \frac{\sqrt{3}}{2} \) стороны

Часть решенных вопросов и ответов на измерения: >> Способности > > Измерение

Комментарии

Похожие вопросы

1). 360 кв.см и 250 кв.см — площади двух подобных треугольников. Если длина одной из сторон первого треугольника равна 8 см, то длина соответствующей стороны второго треугольника равна А). \( \Большой 6\frac{1}{5}см \) Б). \( \Большой 6\frac{1}{3}см \) С). \( \Большой 6\frac{2}{3}см \) Д). \( \Большой 6см\) 9{2}\)) треугольника есть А). 240 Б). 180 С). 360 Д). 120 — Просмотреть ответ 4). Три окружности радиуса a, b, c касаются друг друга внешним образом. Площадь треугольника, образованного соединением их центров, равна А). \( \Большой \sqrt{(a+b+c)abc} \) Б). \( \Большой (a+b+c)\sqrt{ab+bc+ca} \) С). \( \Большой ab+bc+ca \) Д). Ничего из вышеперечисленного — Просмотреть ответ 5). В равносторонний треугольник вписана окружность, а в эту окружность вписан квадрат. Отношение площадей треугольника и квадрата равно 9009{2}\) соответственно. Если АВ=5 см, то DE равно А). \(\sqrt{3}:4\) А). 6,5 см Б). 7,5 см С). 8,5 см Д). 5,5 см — Просмотреть ответ 9). \(C_{1}\) и \(C_{2}\) — две концентрические окружности с центром в точке O. Их радиусы равны 12 см и 3 см соответственно. B и C — точки касания двух касательных, проведенных к \(C_{2}\) из точки A, лежащей на окружности \(C_{1}\). Тогда площадь четырехугольника АВОС равна А). Share This Story, Choose Your Platform! FacebookTwitterLinkedInRedditWhatsappGoogle+TumblrPinterestVkEmail Related Posts Насморк при прорезывании зубов у детей: причины, симптомы и лечение Насморк при прорезывании зубов у детей: причины, симптомы и лечение Как развивать ребенка в 10 месяцев: игры и занятия для малыша Как развивать ребенка в 10 месяцев: игры и занятия для малыша Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов Когда и как вводить прикорм грудному ребенку: рекомендации педиатров Когда и как вводить прикорм грудному ребенку: рекомендации педиатров Leave A Comment Отменить ответ Comment Save my name, email, and website in this browser for the next time I comment.