Образовательный портал Лицей №14

  1. Двоичное кодирование, системы счисления

Основные определения

Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.

Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

Алфавит системы счисления — это используемый в ней набор цифр.

Основание системы счисления — это количество цифр в алфавите (мощность алфавита).

Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.

Любое целое число A, записанное в системе счисления с основанием p, можно представить в расширенной форме:

Правила перевода чисел из одной системы счисления в другую.

Перевод целых чисел в десятичную систему счисления из других систем счисления.

Для перевода целого числа, записанного в системе счисления с основанием p, в десятичную, нужно пронумеровать цифры его целой части справа налево, начиная с 0, затем найти произведение каждой цифры числа на степень основания, где показателем степени является номер цифры, и сложить полученные значения (то есть, нужно представить число в расширенной форме и вычислить).

Перевод целых десятичных чисел в другие системы счисления.

Для перевода целого десятичного числа в систему счисления с основанием p, нужно последовательно делить число и получающиеся частные на p, запоминая остатки, до тех пор, пока последнее частное не будет равно 0. После этого выписать полученные остатки в обратном порядке.

Также, для перевода целого десятичного числа в систему счисления с основанием p можно разложить это число на слагаемые, содержащие максимальную степень числа p и выписать коэффициенты (множители) при этих степенях. Вместо отсутствующей степени нужно записать 0.

Легко заметить, что множители при степенях p не что иное, как остатки от последовательного деления десятичного числа на p.

Кратные системы счисления

Для перевода восьмеричного числа в двоичную систему счисления достаточно заменить каждую цифру восьмеричного числа соответствующим трехразрядным двоичным числом.

Для перевода двоичного числа в восьмеричную систему счисления нужно разбить число на триады, начиная справа. Каждую триаду записать в виде одной восьмеричной цифры.

00000
11001
22010
33011
44100
55101
66110
77111

Перевод числа из шестнадцатеричной системы счисления в двоичную выполняется аналогично. Только в этом случае каждая цифра шестнадцатеричного числа заменяется соответствующим четырехразрядным двоичным числом.

Для перевода двоичного числа в шестнадцатеричную систему счисления нужно разбить число на тетрады, начиная справа. Каждую тетраду записать в виде одной шестнадцатеричной цифры.

000000
110001
220010
330011
440100
550101
660110
770111
881000
991001
10A1010
11B1011
12C1100
13D1101
14E1110
15F1111

Задачи

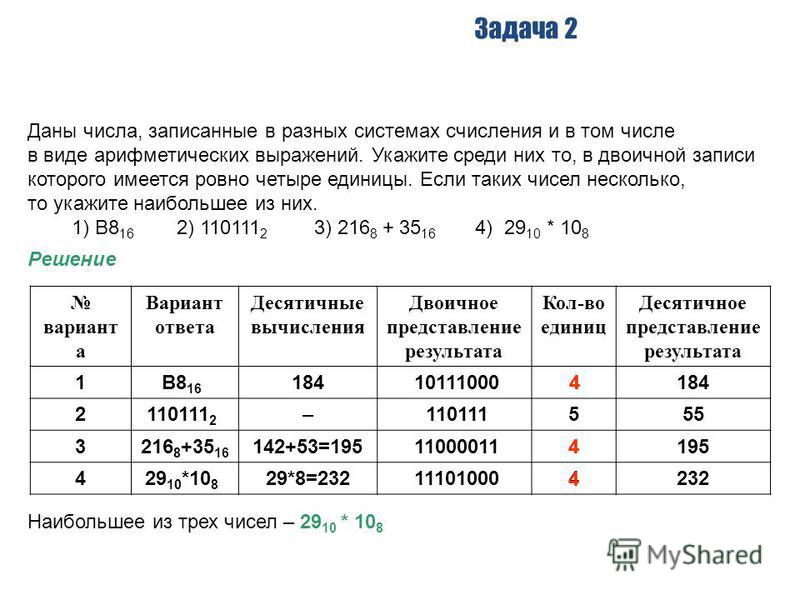
  1. Сколько единиц в двоичной записи десятичного числа 48?
    Решение:
    Переведём число 48 в двоичную систему счисления. Это можно сделать следующим образом:

    После того как последовательно было выполнено деление сначала самого числа, а затем получающихся частных на 2, следует выписать полученные остатки в обратном порядке. Таким образом, получаем:
    48 = 1100002
    Также, можно представить число 48 как сумму степеней двоек. Если какая-то степень двойки в сумме отсутствует, значит при ней пишем коэффициент 0.
    48 = 32 + 16 = 1·25 + 1·24+ 0·23 + 0·22 + 0·21 + 0·20 = 1100002
    Итак, в двоичной записи числа 48 содержится две единицы.
    Ответ: 2.
  2. Сколько нулей в двоичной записи десятичного числа 1021?
    [Я. Н. Зайдельман, М. А. Ройтберг, Информатика и ИКТ. Подготовка к ЕГЭ в 2019 году. Диагностические работы. ФГОС.— М.: МЦНМО, 2019.
    , стр 42, №1]
    Решение:
    а) Запишем число 1021 как сумму степеней двоек.
    1021 = 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 1 = 1·29+ 1·28 + 1·27 + 1·26 + 1·25 + 1·24 + 1·23 + 1·22 +0·21 + 1·20 = 1111111101 2
    б) Также можно заметить, что 1021 = 1024 – 3.
    1021 = 1024 – 3 = 1·210 – 3 = 100000000002 – 112 = 11111111012
    Выполним вычитание в двоичной системе счисления:
    100000000002
    — 112
    11111111012
    В записи числа присутствует одна цифра 0.
    Ответ: 1
  3. Сколько единиц в двоичной записи числа 77716? [Я. Н. Зайдельман, М. А. Ройтберг, Информатика и ИКТ. Подготовка к ЕГЭ в 2019 году. Диагностические работы. ФГОС.— М.: МЦНМО, 2019., стр 6, №1]
    Решение:
    а) Для того, чтобы определить количество единиц в двоичной записи числа 77716 можно сначала это число перевести в десятичную систему счисления, а затем из десятичной в двоичную.
    77716 → X10 → X2
    77716 = 7∙162 + 7∙161 + 7∙160 = 1792 + 112 + 7 = 1911
    1911 = 111011101112
    б) Лучше всего воспользоваться тем, что шестнадцатеричная и двоичная системы счисления являются кратными.
    77716 = 0111 0111 01112 = 111011101112
    7 = 1112
    Ответ: 9
  4. Вычислите значение выражения 6578 – 1AC16. В ответе запишите результат в десятичной системе счисления. [Тренировочная работа СтатГрад ИН1910401, №4 по информатике от 04.03.2020]
    Решение:
    Переведем уменьшаемое и вычитаемое в двоичную систему счисления.
    6 = 1102, 5 = 1012, 7 = 1112 .
    6578 = 110 101 1112
    A16 = 10 = 10102, C16 = 12 = 11002.
    Выполним вычитание в двоичной системе счисления:

    Переведем полученный результат в десятичную систему счисления:
    112 = 1∙21 + 1∙20 = 3
    Ответ: 3
  5. Выберите наибольшее из чисел: AA16, 2518, 100111012. В ответе запишите выбранное число в десятичной системе счисления. [Я. Н. Зайдельман, М. А. Ройтберг, Информатика и ИКТ. Подготовка к ЕГЭ в 2019 году. Диагностические работы. ФГОС.— М.: МЦНМО, 2019., стр 77, №1]
    Решение:
    Шестнадцатеричная и двоичная, восьмеричная и двоичная системы счисления являются кратными.
    AA16 = 1010 10102 , A16 = 10 =10102
    2518 = 10 101 0012 , 2 = 102 , 5 = 1012 , 1 = 12
    Выполним поразрядное сравнение.
    101010102
    101010012
    100111012
    Переведем найденное число в десятичную систему счисления:
    AA16 =10 ∙ 161 +0 ∙ 160 = 170
    Ответ: 170
  6. Даны 4 целых числа, записанные в двоичной системе: 10001011, 10111000, 10011011, 10110100. Сколько среди них чисел, больших, чем А416 +208? [Материалы ЕГЭ №1 К.Ю.Полякова, №47]
    Решение:
    Переведем оба слагаемых в двоичную систему счисления:
    A416 = 1010 01002
    208 = 10 0002
    Выполним сложение в двоичной системе счисления:
    101001002
    +
    100002
    101101002
    100010112, 101110002, 100110112, 101101002
    Ответ: 2
  7. Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит 6 единиц. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно. [Материалы ЕГЭ №1 К.Ю.Полякова, №56]
    Решение:
    Каждый разряд восьмеричного числа соответствует трем разрядам в двоичной системе счисления. Так как число четырехзначное, то в нем от 10 до 12 двоичных разрядов. Так как число должно получиться наименьшим, то последние пять разрядов и десятый разряд заполняем единицами, на остальных местах записываем нули.

    X8 = 10378
    Ответ: 1037
  8. Укажите наибольшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 9 значащих нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно. [Материалы ЕГЭ №1 К.Ю.Полякова, №67]
    Решение:
    Каждый разряд шестнадцатеричного числа соответствует четырем разрядам в двоичной системе счисления. Так как число четырехзначное, то в нем от 13 до 16 двоичных разрядов. Так как число должно получиться наибольшим, то на первых семи разрядах размещаем единицы, на остальных местах записываем нули.

    X16 = FE0016
    Ответ: FE00
  9. Определите количество натуральных чисел, удовлетворяющих неравенству: AA16 ≤ x < 4118. [Материалы ЕГЭ №1 К.Ю.Полякова, №99]
    Решение:
    Переведем числа AA16и 4118 в десятичную систему счисления.
    АА16 = 10·161 + 10·160 = 170
    4118 = 4·82 + 1·81 +1·80 = 4·64 + 9 = 265
    Количество чисел = 265 – 170 = 95
    Ответ: 95
  10. Определите количество натуральных чисел, удовлетворяющих неравенству: AB16 < x < 3448. [Материалы ЕГЭ №1 К.Ю.Полякова, №101]
    Решение:
    Переведем числа AВ16и 3448 в десятичную систему счисления.
    АB16 = 10·161 + 11·160 = 171
    3448 = 3·82 + 4·81 +4 ·80 = 3·64 + 32+4 = 228
    Количество чисел = 228 – 171 — 1 = 56
    Ответ: 56
  11. Определите количество натуральных чисел, удовлетворяющих неравенству: ( 6416 — 1E16 ) ≤ x ≤ ( 508 + 368 ). [Материалы ЕГЭ №1 К.Ю.Полякова, №98]

Решение:

Выполним арифметические действия.

Заметим, что E16 = 14.

Переведем результаты вычислений в десятичную систему счисления.

4616 =4∙16 + 6 = 70

1068 =1∙82 + 6 = 70

Количество чисел = 1

Ответ: 1

Информационные источники

  1. «ФИПИ. Открытый банк тестовых заданий», http://os.fipi.ru/tasks/5/a
  2. Материалы для подготовки к ЕГЭ по информатике К.Ю. Полякова, http://kpolyakov.spb.ru/school/ege.htm
  3. Образовательный портал «Решу ЕГЭ», https://ege.sdamgia.ru/
  4. Я.Н.Зайдельман , ЕГЭ 2020. Информатика и ИКТ. Подготовка к ЕГЭ в 2020 году. Диагностические работы. ФГОС. — М.: МЦНМО, 2019.
  5. Я. Н. Зайдельман, М. А. Ройтберг, Информатика и ИКТ. Подготовка к ЕГЭ в 2019 году. Диагностические работы. ФГОС.— М.: МЦНМО, 2019.

Перевод чисел из одной позиционной системы счисления в другую

Информатика. 10 класса. Босова Л.Л. Оглавление

§11. Перевод чисел из одной позиционной системы счисления в другую

11.1. Перевод целого десятичного числа в систему счисления с основанием q

Для перевода целого десятичного числа в систему счисления с основанием q следует:

1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего остатка.

Рассмотрим примеры перевода целых десятичных чисел в 2-ичную, 8-ричную и 16-ричную системы счисления.

Пример 1.

Пример 2.

Пример 3.

Пример 4. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись десятичного числа 22 оканчивается на 4.

Поскольку запись числа в системе счисления с основанием q заканчивается на 4, остаток от деления числа 22 на q равен 4: 22 mod q = 41). Следовательно, 18 mod q = 0. Это верно для q ? {18, 9, 6, 3, 2, 1}.

1) Операция mod — вычисление остатка от целочисленного деления.

Так как в новой системе счисления запись числа оканчивается на 4, то q > 4. Следовательно, условию задачи удовлетворяют основания: 18, 9 и 6.

11.2. Перевод целого десятичного числа в двоичную систему счисления

Перевод целого десятичного числа, безусловно, может осуществляться по рассмотренному выше универсальному алгоритму. Но для чисел в пределах десяти тысяч (особенно если число немного больше некоторой степени двойки) бывает удобно снова воспользоваться таблицей степеней двойки.

Например: 109610 = 1024 + 72 = 1024 + 64 + 8 = 100010010002.

Здесь мы представили число в виде суммы степеней двойки: сначала взяли максимально возможное значение, не превышающее исходное число (1024 < 1096), и нашли разность между исходным числом и этим значением (72). Затем выписали степень двойки, не превышающую эту разность, и т. д. Когда исходное число было представлено в виде суммы, мы построили его двоичное представление, записав 1 в разрядах, соответствующих слагаемым, вошедшим в сумму, и 0 — во всех остальных разрядах.

11.3. Перевод целого числа из системы счисления с основанием р в систему счисления с основанием q

Каждый из нас может выполнять арифметические операции в привычной десятичной системе счисления. Выполнять такие же операции в других системах счисления человеку непривычно, а поэтому и неудобно.

Для того чтобы перевести целое число из системы счисления с основанием р в систему счисления с основанием q, достаточно:

1) основание новой системы счисления выразить в исходной системе счисления и все последующие действия производить в исходной системе счисления;
2) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
3) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
4) составить число в новой системе счисления, записывая его, начиная с последнего остатка.

При необходимости перевести целое число из системы счисления с основанием р в систему счисления с основанием q можно попытаться воспользоваться описанным выше алгоритмом. Другой способ состоит в том, чтобы свести всё к хорошо знакомым действиям в десятичной системе счисления: перевести исходное число в десятичную систему счисления, после чего полученное десятичное число представить в требуемой системе счисления (рис. 3.3).

Рис. 3.3. Схема перевода целого числа из системы счисления с основанием р
в систему счисления с основанием q через десятичную систему счисления

Пример 5.

12345 = 1 • 53 + 2 • 52 + 3 • 51 + 4 • 50 = 19410 = 5226.

11.4. Перевод конечной десятичной дроби в систему счисления с основанием q

Для перевода конечной десятичной дроби в систему счисления с основанием q следует:

1) последовательно умножать данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или не будет достигнута требуемая точность представления числа;
2) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
3) составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

Пример 6. Переведём число 0,187510 в двоичную систему счисления.

Выполним умножение числа 0,187510 на 2:

Здесь жирным выделены цифры, участвующие в двоичном представлении дроби, а в скобках указан номер цифры в дроби.

0,187510 = 0,00112.

11.5. «Быстрый» перевод чисел в компьютерных системах счисления

Из курса информатики основной школы вы знаете, что в компьютерных науках широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления, благодаря чему их называют «компьютерными».

Между основаниями этих систем существует очевидная связь: 16 = 24, 8 = 23.

Способ «быстрого» перевода основан на том, что каждой цифре числа в системе счисления, основание которой q кратно степени двойки, соответствует число, состоящее из n (q = 2n) цифр в двоичной системе счисления. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетрадами) позволяет осуществлять быстрый перевод между этими системами счисления, не прибегая к арифметическим операциям.

Для того чтобы целое двоичное число записать в системе счисления с основанием q = 2n, достаточно:

1) данное двоичное число разбить справа налево на группы по n цифр в каждой;
2) если в последней левой группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = 2n.

Пример 7. Переведём число 110101001112 в восьмеричную систему счисления.
110101001112 — исходное число;

?11.010.100.111 — выделяем триады;

?011.010.100.111 — дополняем левую группу слева нулём;

?3.2.4.7 — выписываем восьмеричные цифры;

?32478 — результат.

Пример 8. Переведём число 16АС16 в двоичную систему счисления.
16АС16 — исходное число;

?0001.0110.1010.1100 — заменяем каждую цифру тетрадой;

?1.0110.1010.1100 — убираем слева незначащие нули;

?10110101011002 — результат.

Через двоичную систему счисления можно проводить быстрые переводы из восьмеричной системы счисления в шестнадцатеричную и обратно (рис. 3.4)

Рис. 3.4. Схема перевода целых чисел из восьмеричной системы счисления в шестнадцатеричную
и обратно через двоичную систему счисления

Пример 9. Выполним перевод восьмеричного 67 2528 числа в шестнадцатеричную систему счисления.
672528 — исходное число;

?110.111.010.101.010 — заменяем каждую цифру триадой;

?110.1110.1010.1010 — разбиваем двоичную строку справа налево на тетрады;

?0110. 1110.1010.1010 — дополняем левую группу слева нулём;

?6.Е.А.А — выписываем шестнадцатеричные цифры;

?6ЕАА16 — результат.

Аналогичные алгоритмы быстрого перевода существуют и для дробных чисел. Для того чтобы записать правильную двоичную дробь в системе счисления с основанием q = 2n, достаточно:

1) двоичное число разбить слева направо на группы по n цифр в каждой;
2) если в последней правой группе окажется меньше n разрядов, то её надо дополнить справа нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = 2n.

Пример 10. Число 0,1011000112 заменим равным ему шестнадцатеричным числом.
0,1011000112 — исходное число;

?0,1011.0001.1 — разбиваем двоичную строку слева направо на тетрады;

?0,1011. 0001.1000 — дополняем правую группу справа нулями;

?0,В.1.8 — выписываем шестнадцатеричные цифры;

?0,В1816 — результат.

Попытайтесь самостоятельно сформулировать алгоритм быстрого перевода произвольного двоичного числа в восьмеричную систему счисления. Примените алгоритм к числу 11101001000,110100102.

Пример 11. Выясним, сколько значащих нулей в двоичной записи восьмеричного числа 16018.

Для ответа на этот вопрос достаточно знать двоичные триады, соответствующие восьмеричным цифрам от 0 до 7 и выполнить «быстрый» перевод числа 16018 в двоичную систему счисления:

16018 = 001 110 000 0012 = 11100000012.

В двоичной записи 6 значащих нулей, а первые два нуля являются незначащими и не учитываются.

Пример 12. Среди четырёхзначных шестнадцатеричных чисел, двоичная запись которых содержит ровно 7 единиц, найдём:

1) наименьшее число;
2) наибольшее число.

Наименьшее четырёхзначное шестнадцатеричное число — это 100016 = 0001 0000 0000 00002, и его двоичное представление содержит всего одну единицу. Чтобы получить наименьшее число, удовлетворяющее условию задачи, оставшиеся шесть единиц следует разместить в самых младших разрядах. Получим 1 0000 ОО11 11112 = 103F16. Чтобы получить наибольшее число, удовлетворяющее условию задачи, оставшиеся шесть единиц следует разместить в самых старших разрядах. Получим 1111 1110 0000 00002 = FE0016.

А сколько всего таких четырёхзначных шестнадцатеричных чисел, двоичная запись которых содержит ровно 7 единиц?

САМОЕ ГЛАВНОЕ

Для перевода целого десятичного числа в систему счисления с основанием q следует:

1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего остатка.

В компьютерных науках широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления, благодаря чему их называют «компьютерными». Между основаниями этих систем существует очевидная связь: 16 = 24, 8 = 23.

Если основание системы счисления q кратно степени двойки (q = 2n), то любое число в этой системе счисления можно «быстро» перевести в двоичную систему счисления, выписав последовательно двоичные коды каждой из цифр, образующих исходное число. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетрадами) позволяет осуществлять быстрый перевод между этими системами счисления, не прибегая к арифметическим операциям.

Вопросы и задания

1. Переведите целые числа из десятичной системы счисления в двоичную систему счисления: 1) 1025; 2) 512; 3) 600.

2. Переведите целое число 1147 из десятичной системы счисления в системы счисления: 1) пятеричную; 2) восьмеричную; 3) шестнадцатеричную.

3. Переведите двоичные числа в восьмеричную систему счисления: 1) 1010001001011; 2) 1010,00100101.

4. Переведите двоичные числа в шестнадцатеричную систему счисления: 1) 1010001001011; 2) 1010,00100101.

5. Переведите числа в двоичную систему счисления: 1) 2668; 2) 26616.

6. Переведите числа из восьмеричной системы счисления в шестнадцатеричную: 1) 12754; 2) 1515.

7. Переведите числа из шестнадцатеричной системы счисления в восьмеричную: 1) 1АЕ2; 2) 1С1С.

8. Сравните числа: 1) 12516 и 1111000101012; 2) 7578 и 11100101012; 3) А2316 и 12328.

9. Сколько из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству 2218<С<9516? Какие числа? 1) 100101002; 2) 100101102; 3) 100100112; 4) 100011002.

10. Сколько значащих нулей в двоичной записи: 1) восьмеричного числа 2501; 2) шестнадцатеричного числа 12А?

11. Среди четырёхзначных восьмеричных чисел, двоичная запись которых содержит ровно 5 единиц, найдите: 1) наименьшее число; 2) наибольшее число.

12. Среди трёхзначных шестнадцатеричных чисел, двоичная запись которых содержит ровно 7 нулей, найдите: 1) наименьшее число; 2) наибольшее число.

13. Все 5-буквенные слова, составленные из букв О, П, Р, Т, записаны в алфавитном порядке и пронумерованы. Вот начало списка: 1. ООООО 2. ООООП 3. ООООР 4. ООООТ 5. ОООПО
Какие слова находятся в этом списке на 531-м и 787-м местах?

14. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись десятичного числа 82 оканчивается на 5.

§ 10. Представление чисел в позиционных системах счисления
§ 11. Перевод чисел из одной позиционной системы счисления в другую
§ 12.  Арифметические операции в позиционных системах счисления

Алгоритм

— Вычисление чисел, двоичное представление которых имеет точно требуемые числа 1

Вы правы, подозревая, что есть более эффективный способ.

Начнем с более простой подзадачи. Отсутствуют действительно умные идеи, нам нужно будет найти количество целых чисел в [n+1, 2n] , в двоичном представлении которых установлено ровно k бит. К короче, назовем такие целые числа «вес- к » целые числа (чтобы мотивировать эту терминологию, посмотрите вес Хэмминга). Мы можем сразу упростим нашу задачу подсчета: если мы можем посчитать все веса- k целых чисел в [0, 2n] и мы можем посчитать все веса — k целых чисел в [0, n] , мы можем вычесть один счет из другого, чтобы получить число веса- k целых чисел в [n+1, 2n] .

Таким образом, очевидная подзадача состоит в том, чтобы подсчитать, сколько существует весовых k целых чисел. в интервале

[0, n] , для заданных неотрицательных целых чисел k и n .

Стандартный метод решения проблемы такого рода — искать способ сломать разбить на более мелкие подзадачи того же типа; это один из аспектов то, что часто называют динамическим программированием. В этом случае есть простой способ при этом: рассмотрим четные числа в [0, n] и нечетные числа в [0, n] в отдельности. Каждое четное число m в [0, n] имеет точно такой же вес, как м/2 (потому что при делении на два мы всего лишь удаляем один ноль кусочек). Точно так же каждое нечетное число m имеет вес ровно на единицу больше, чем вес

(м-1)/2 . Если подумать о соответствующих базовых случаях, это приводит к следующему рекурсивному алгоритму (в данном случае реализованному на Python, но он должен легко переводиться на любой другой основной язык).

 по определению count_weights(n, k):
    """
    Возвращает количество целых чисел веса-k в ​​[0, n] (для n >= 0, k >= 0)
    """
    если к == 0:
        return 1 # 0 - единственное значение веса-0
    Элиф п == 0:
        return 0 # только с учетом 0, который не имеет положительного веса
    еще:
        from_even = count_weights(n//2, k)
        from_odd = count_weights((n-1)//2, k-1)
        возврат из_четного + из_нечетного

Здесь много места для ошибок, так что давайте проверим наш модный рекурсивный алгоритм.

алгоритм против чего-то менее эффективного, но более прямого (и, надеюсь, более очевидно правильно):

 вес определения (n):
    """
    Количество битов 1 в двоичном представлении n (для n >= 0).
    """
    вернуть корзину (n). count ('1')
определение count_weights_slow (n, k):
    """
    Возвращает количество целых чисел веса-k в ​​[0, n] (для n >= 0, k >= 0)
    """
    возвращаемая сумма (вес (m) == k для m в диапазоне (n + 1))

Результаты сравнения двух алгоритмов выглядят убедительно:

 >>> count_weights(100, 5)
11
>
 
>> count_weights_slow(100, 5)
11
>>> all(count_weights(n, k) == count_weights_slow(n, k)
... для n в диапазоне (1000) для k в диапазоне (10))
Истинный

Однако наша предположительно быстрая функция count_weights плохо масштабируется для нужные вам размеры:

 >>> count_weights(2**64, 5) # на моей машине это занимает несколько секунд
7624512
>>> count_weights(2**64, 6) # минут ...
74974368
>>> count_weights(2**64, 10) # перестал ждать. ..

Но здесь вступает в действие вторая ключевая идея динамического программирования: запоминайте! То есть вести учет результатов предыдущих вызовов, на случай, если нам потребуется использовать их снова. Получается, что цепочка рекурсивных вызовов

будет стремиться к . повторять много звонков, так что есть смысл запоминать. В Питоне это тривиально легко сделать с помощью декоратора functools.lru_cache . вот наш новый версия количество_весов . Все, что изменилось, это дополнительная строка вверху:

 @lru_cache(maxsize=None)
определение count_weights (n, k):
    """
    Возвращает количество целых чисел веса-k в ​​[0, n] (для n >= 0, k >= 0)
    """
    если к == 0:
        return 1 # 0 - единственное значение веса-0
    Элиф п == 0:
        return 0 # только с учетом 0, который не имеет положительного веса
    еще:
        from_even = count_weights(n//2, k)
        from_odd = count_weights((n-1)//2, k-1)
        возврат из_четного + из_нечетного

Теперь снова тестируя эти более крупные примеры, мы получаем результаты намного быстрее, без заметной задержки.

 >>> count_weights(2**64, 10)
151473214816
>>> count_weights(2**64, 32)
18326241409425

>>> count_weights(5853459801720308837, 27)
356506415596813420

Итак, теперь у нас есть эффективный способ подсчета, у нас есть обратная задача для решить: учитывая k и m , найти n такое, что count_weights(2*n, k) - count_weights(n, k) == m

. Это оказывается особенно простым, так как количество count_weights(2*n, k) - count_weights(n, k) монотонно увеличивается с n (для фиксированных k ), а точнее увеличивается либо на 0 или 1 каждый раз n увеличивается на 1 . Я оставлю доказательства тех вам факты, но вот демонстрация:

 >>> для n в диапазоне (10, 30): print(n, count_weights(n, 3))
...
10 1
11 2
12 2
13 3
14 4
15 4
16 4
17 4
18 4
195
20 5
21 6
22 7
23 7
24 7
25 8
26 9
27 9
28 10
29 10

Это означает, что мы гарантированно сможем найти решение.

Решений может быть несколько, поэтому мы постараемся найти наименьшее (хотя было бы так же легко найти и самое большое). Поиск пополам дает нам грубый, но эффективный способ сделать это. Вот код:

 defsolve(m,k):
    """
    Найдите наименьшее n >= 0 такое, что [n+1, 2n] содержит ровно
    m вес-k целых чисел.
    Предполагается, что m >= 1 (для m = 0 ответ тривиально n = 0).
    """
    определение большой_достаточно (n):
        """
        Целевая функция для нашего решателя поиска пополам.
        """
        diff = количество_весов (2*n, k) - количество_весов (n, k)
        вернуть разницу >= м
    низкий = 0
    утверждать, что недостаточно большой_достаточно (низкий)
    # Начальная фаза: расширить интервал, чтобы определить верхнюю границу.
    высокий = 1
    пока не большой_достаточно (высокий):
        высокий *= 2
    # Фаза деления пополам.
    # Инвариант цикла: big_enough(high) равно True, а big_enough(low) равно False
    пока высокий - низкий >
 
 1:
        середина = (высокая + низкая) // 2
        если большой_достаточно (средний):
            высокий = средний
        еще:
            низкий = средний
    вернуть высокий

Проверка решения:

 >>> n = решить(5853459801720308837, 27)
>>> н
407324170440003813446

Давайте еще раз проверим, что n :

 >>> count_weights(2*n, 27) - count_weights(n, 27)
5853459801720308837

Выглядит хорошо. И если мы правильно провели поиск, это должно быть самое маленькое n , который работает:

 >>> count_weights(2*(n-1), 27) - count_weights(n-1, 27)
5853459801720308836

Есть много других возможностей для оптимизации и очистки в приведенный выше код и другие способы решения проблемы, но я надеюсь, что это даст вам отправная точка.

ОП прокомментировал, что им нужно было сделать это на C, где мемоизация недоступна сразу без использования внешней библиотеки. Вот вариант count_weights , который не нуждается в запоминании. Это достигается за счет (а) настройки рекурсии в

count_weights таким образом, чтобы одни и те же n использовались в обоих рекурсивных вызовах, а затем (б) возврата для данного n значений count_weights(n, k ) для все к , для которого ответ отличен от нуля. По сути, мы просто перемещаем запоминание в явный список.

Примечание: как написано, приведенный ниже код требует Python 3.

 def count_all_weights(n):
    """
    Возвращает частоты весов всех целых чисел в [0, n],
    как список. К-я запись в списке дает количество
    целых чисел веса k в [0, n].
    Пример
    -------
    >
 
>> count_all_weights(16)
    [1, 5, 6, 4, 1]
    """
    если п == 0:
        возврат [1]
    еще:
        wm = count_all_weights((n-1)//2)
        веса = [wm[0], *(wm[i]+wm[i+1] для i в диапазоне (len(wm)-1)), wm[-1]]
        если n % 2 == 0:
            веса[бин(n).count('1')] += 1
        обратные веса

Пример вызова:

 >>> count_all_weights(7590)
[1, 13, 78, 286, 714, 1278, 1679, 1624, 1139, 559, 182, 35, 3]

Эта функция должна быть достаточно хороша даже для больших n : count_all_weights(10**18) на моей машине занимает меньше полмиллисекунды.

Теперь поиск пополам будет работать как раньше, заменив вызов count_weights(n, k) на count_all_weights(n)[k] (и аналогично для count_weights(2*n, k) ).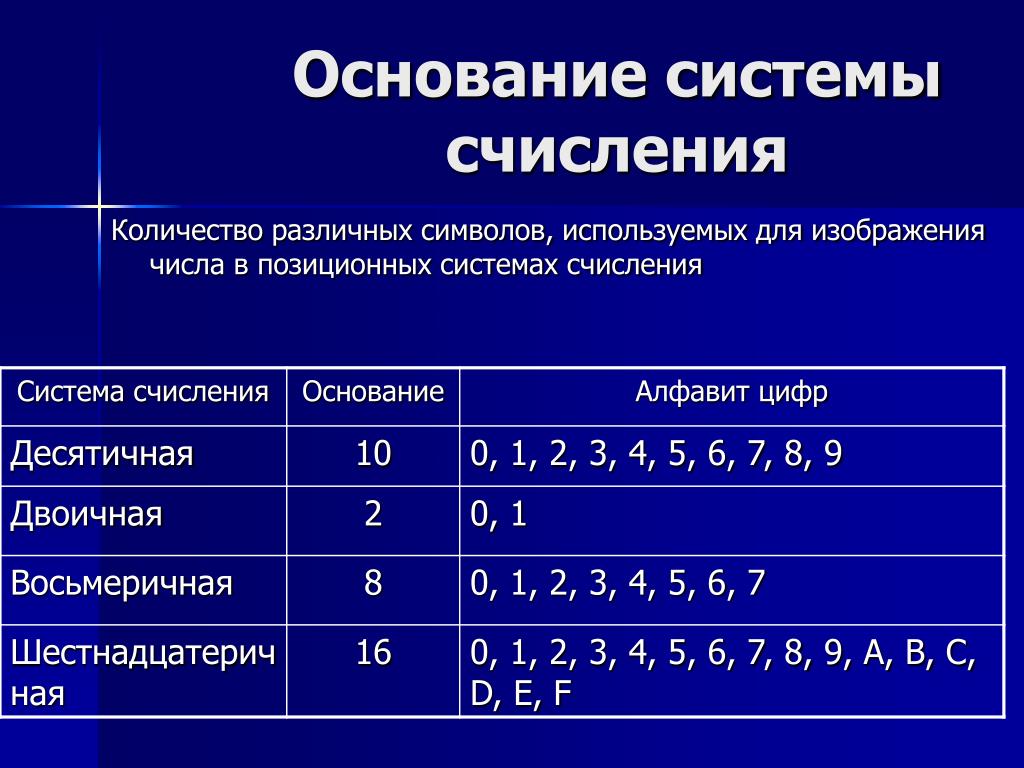

Наконец, еще одна возможность состоит в том, чтобы разбить интервал [0, n] на последовательность все меньших и меньших подинтервалов, где каждый подынтервал имеет длину, равную степени двойки. Например, мы разобьем интервал [0, 101] на [0, 63] , [64, 95] , [96, 99] и [100, 101] . Преимущество этого в том, что мы можем легко вычислить, сколько целых k целых чисел содержится в любом из этих подинтервалов, путем подсчета комбинаций. Например, в [0, 63] у нас есть все возможные 6-битные комбинации, поэтому, если нам нужны целые числа веса-3, мы знаем, что их должно быть ровно 6-выбор-3 (т. е. 20). И в [64, 95] мы знаем, что каждое целое число начинается с 1 -бит, а затем, после исключения этого 1 -бита, у нас есть все возможные 5-битные комбинации, поэтому мы снова знаем, сколько целых чисел там находятся в этом интервале с любым заданным весом.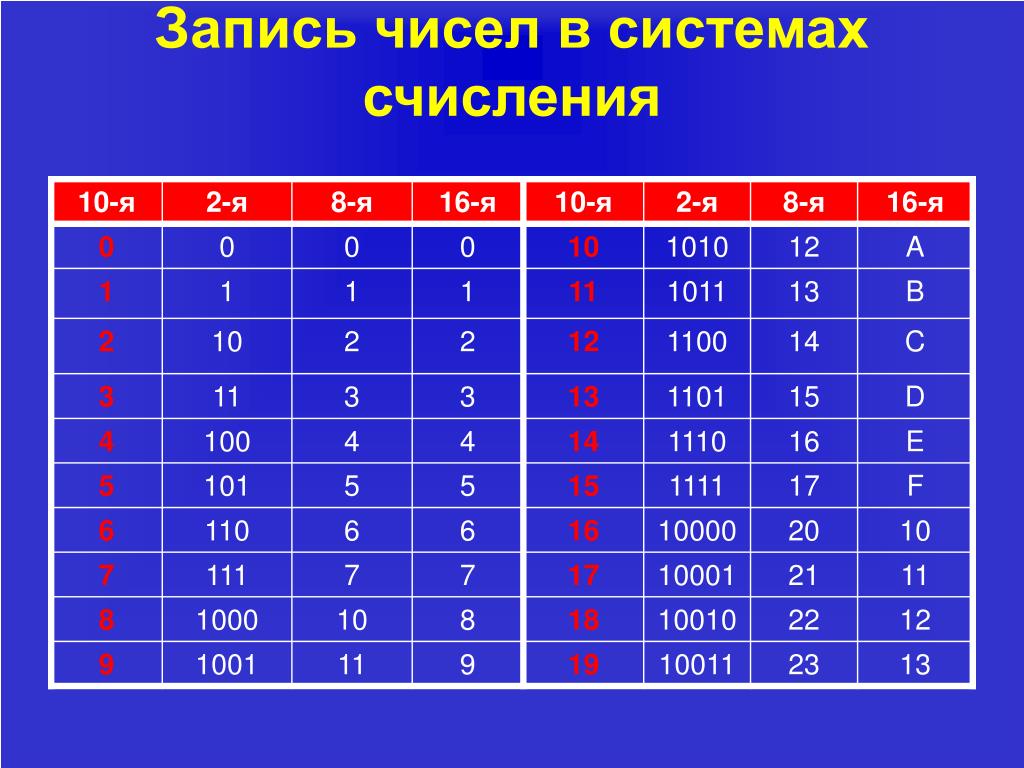

Применяя эту идею, вот полная, быстрая, все-в-одном функция, которая решает вашу первоначальную проблему. В нем нет рекурсии и мемоизации.

 по определению решить(м, к):
    """
    Даны неотрицательные целые числа m и k, найти наименьшее
    неотрицательное целое число n такое, что отрезок
    [n+1, 2*n] содержит ровно m целых чисел веса k.
    Обратите внимание, что для малых k решения может не быть:
    если k == 0, то у нас нет решения, кроме m == 0,
    и если k == 1, у нас нет решения, если m не равно 0 или 1.
    """
    # Работа с пограничными случаями.
    если k < 2 и k < m:
        поднять ValueError("Нет решения")
    элиф к == 0 или м == 0:
        вернуть 0
    к -= 1
    # Находим верхнюю границу n и генерируем подмножество
    # Треугольник Паскаля, как мы идем.
    строки = []
    высокий, строка = 1, [1] + [0] * k
    в то время как строка [k] < m:
        rows.append((высокая, строка))
        высокий, строка = высокий * 2, [1, * (строка [i] + строка [i + 1] для i в диапазоне (k))]
    # Делим пополам, чтобы найти первые n, которые работают. 
    низкий = mlow = вес = 0
    в то время как строки:
        высокий, строка = rows.pop()
        mmid = mlow + row[k - вес]
        если mmid < m:
            низкий, mlow, вес = низкий + высокий, mmid, вес + 1
    вернуть низкий + 1

математика - Почему десятичные числа не могут быть точно представлены в двоичном виде?

Десятичные числа могут быть точно представлены , если у вас достаточно места - только не плавающими двоичными точечными числами. Если вы используете десятичный тип с плавающей запятой (например, System.Decimal в .NET), то множество значений, которые не могут быть точно представлены в двоичном формате с плавающей запятой, могут быть точно представлены.

Давайте посмотрим на это с другой стороны - в системе счисления с основанием 10, с которой вам, вероятно, будет удобно, вы не сможете точно выразить 1/3. Это 0,3333333... (повторяющееся). Причина, по которой вы не можете представить 0,1 как двоичное число с плавающей запятой, по той же причине.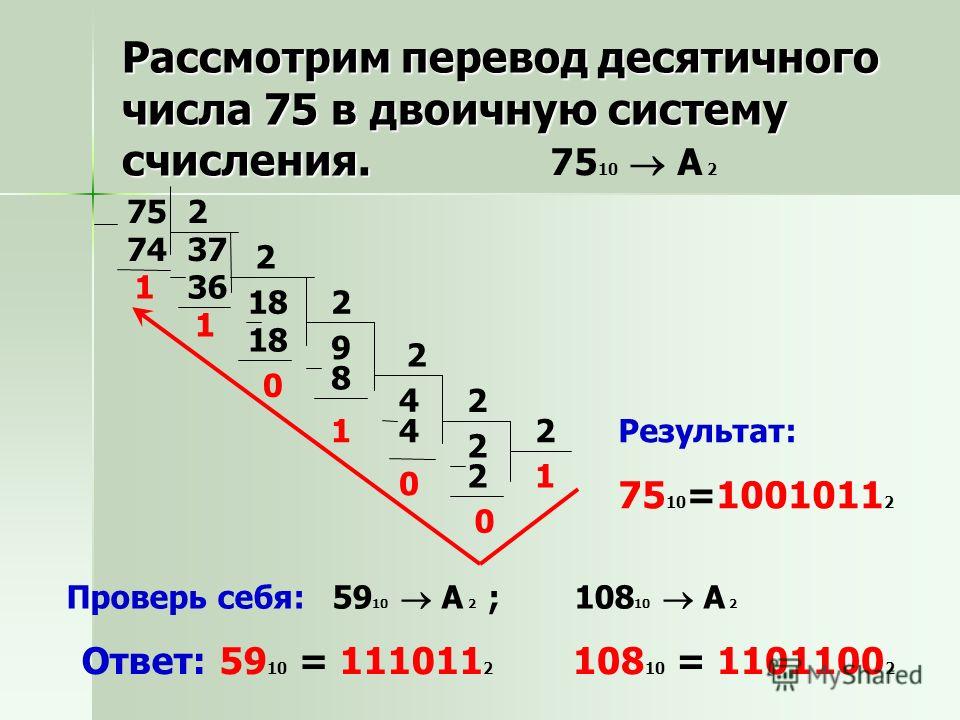 Вы можете представить 3 и 9, и 27 точно - но не 1/3, 1/9 или 1/27.

Проблема в том, что 3 — это простое число, которое не является множителем 10. Это не проблема, когда вы хотите умножить число на 3: вы всегда можете умножить на целое число, не сталкиваясь с проблемами. Но когда вы делите на число, которое является простым и не является множителем вашего основания, вы можете столкнуться с проблемой (и сделает это , если вы попытаетесь разделить 1 на это число).

Хотя 0,1 обычно используется в качестве простейшего примера точного десятичного числа, которое не может быть точно представлено в двоичном формате с плавающей запятой, возможно, 0,2 является более простым примером, поскольку это 1/5, а 5 — это простое число, которое вызывает проблемы между десятичными числами. и двоичный.

Дополнительное примечание для решения проблемы конечных представлений:

Некоторые типы с плавающей запятой имеют фиксированный размер, например System. Decimal другие, такие как java.math.BigDecimal , являются «произвольно большими», но они будут в какой-то момент достичь предела, будь то системная память или теоретический максимальный размер массива. Однако это совершенно отдельный момент от основного этого ответа. Даже если бы у вас было действительно произвольно большое количество битов для игры, вы все равно не могли бы точно представить десятичное число 0,1 в представлении с плавающей двоичной точкой. Сравните это с обратным: учитывая произвольное количество десятичных цифр, вы может точно представлять любое число, которое можно точно представить как плавающую двоичную точку.

0

Например, число 61,0 имеет точное двоичное представление, потому что целая часть любого числа всегда точна. Но число 6,10 не точное. Все, что я сделал, это передвинул десятичную дробь на одно место, и внезапно я перешел от Экзактопии к Инексактвиллю. С математической точки зрения между двумя числами не должно быть внутренней разницы — это просто числа 9.n = 22 , целое число. Однако x = 1/3 этого не делает, потому что какие бы n мы ни выбрали, мы не сможем избавиться от 3.

Этот второй пример побуждает нас задуматься о факторах, и мы можем видеть, что для любого Рациональное x = p/q (предполагается, что оно меньше всего), мы можем ответить на вопрос, сравнив простые факторизации b и q . Если q имеет какие-либо простые делители, не входящие в простую факторизацию числа b , мы никогда не сможем найти подходящий n , чтобы избавиться от этих факторов.

Таким образом, для основания 10 любое p/q , где q имеет простые делители, отличные от 2 или 5, не будет иметь завершающего представления.

Итак, теперь возвращаясь к основаниям 10 и 2, мы видим, что любое рациональное число с завершающим 10-представлением будет иметь вид p/q в точности тогда, когда q имеет только 2 с и 5 с в его простая факторизация; и это же число будет иметь завершающее 2-представление ровно тогда, когда q имеет только 2 с в простой факторизации.

Но один из этих случаев является подмножеством другого! Всякий раз

q имеет только 2 с в простой факторизации

это очевидно также правда что

q имеет только 2 с и 5 с в простой факторизации

или, другими словами, всякий раз, когда p/q имеет завершающее 2-представление, p/q имеет завершающее 10-представление . Обратное, однако, , а не , имеет место - всякий раз, когда q имеет 5 в своей простой факторизации, оно будет иметь завершающее 10-представление, но , а не - завершающее 2-представление. Это пример 0.1 , упомянутый в других ответах.

Итак, у нас есть ответ на ваш вопрос - , потому что простые делители числа 2 являются подмножеством простых делителей числа 10, все 2-конечные числа являются 10-конечными числами, но не наоборот. Дело не в 61 против 6.1, а в 10 против 2.

В заключение, если бы по какой-то причуде люди использовали (скажем) основание 17, а наши компьютеры использовали основание 5, ваша интуиция никогда бы не поддалась этому... не было бы и (ненулевых, нецелочисленных) чисел, которые завершались бы в обоих случаях!

6

Основная (математическая) причина в том, что когда вы имеете дело с целыми числами, они счетно бесконечны .

Это означает, что даже если их бесконечное количество, мы могли бы «отсчитать» все элементы в последовательности, не пропуская ни одного. Это означает, что если мы хотим получить элемент на 610000000000000 -й позиции в списке, мы можем вычислить это с помощью формулы.

Однако действительные числа несчетно бесконечны . Вы не можете сказать «дайте мне настоящий номер на позиции 610000000000000 » и получить ответ. Причина в том, что даже между 0 и 1 , существует бесконечное количество значений, когда вы рассматриваете значения с плавающей запятой. То же самое верно для любых двух чисел с плавающей запятой.

Дополнительная информация:

http://en.wikipedia.org/wiki/Countable_set

http://en.wikipedia.org/wiki/Uncountable_set

Обновление: Прошу прощения, я, кажется, неправильно понял вопрос. Мой ответ о том, почему мы не можем представить каждое реальное значение , я не понял, что числа с плавающей запятой автоматически классифицируются как рациональные.

6

Повторяю то, что я сказал в своем комментарии мистеру Скит: мы можем представлять 1/3, 1/9, 1/27 или любое рациональное число в десятичной системе счисления. Мы делаем это, добавляя дополнительный символ. Например, линия над цифрами, которые повторяются в десятичной записи числа. Что нам нужно для представления десятичных чисел в виде последовательности двоичных чисел, так это 1) последовательность двоичных чисел, 2) точка счисления и 3) какой-либо другой символ для обозначения повторяющейся части последовательности.

Цитата Hehner - способ сделать это. Он использует символ кавычек для обозначения повторяющейся части последовательности. Статья: http://www.cs.toronto.edu/~hehner/ratno.pdf и статья в Википедии: http://en.wikipedia.org/wiki/Quote_notation.

Ничто не говорит о том, что мы не можем добавить символ в нашу систему представления, поэтому мы можем точно представлять десятичные рациональные числа, используя двоичные кавычки, и наоборот.

3

BCD — двоично-десятичный — представление точное. Они не очень компактны, но в этом случае вам придется пойти на компромисс ради точности.

2

Хороший вопрос.

Весь ваш вопрос основан на том, "как мы представляем число?"

ВСЕ числа могут быть представлены в десятичной или двоичной форме (дополнение до 2). Все они!!

НО некоторые (большинство из них) требуют бесконечного числа элементов ("0" или "1" для двоичной позиции или "0", "1" до "9" для десятичного представления).

Как 1/3 в десятичном представлении (1/3 = 0,3333333... <- с бесконечным числом "3")

Как 0,1 в двоичном ( 0,1 = 0,00011001100110011.... <- с бесконечным числом "0011")

Все в этом понятии. Поскольку ваш компьютер может рассматривать только конечных набор цифр (десятичных или двоичных), только некоторые числа могут быть точно представлены в вашем компьютере...

И, как сказал Джон, 3 - это простое число, которое не является множителем 10, поэтому 1/3 не может быть представлено конечным числом элементов по основанию 10.

Даже при арифметических действиях с произвольной точностью система нумерации позиций по основанию 2 не может полностью описать 6. 1, хотя она может представлять 61.

Для 6.1 мы должны использовать другое представление (например, десятичное представление или IEEE 854, который допускает основание 2 или основание 10 для представления значений с плавающей запятой)

2

Если вы сделаете достаточно большое число с плавающей запятой (как это может быть с экспонентой), то вы получите неточность и перед десятичной запятой. Поэтому я не думаю, что ваш вопрос полностью обоснован, потому что предпосылка неверна; дело не в том, что сдвиг на 10 всегда будет создавать большую точность, потому что в какой-то момент число с плавающей запятой должно будет использовать показатели степени для представления величины числа и таким образом также потеряет некоторую точность. 91001b)

Обратите внимание, что мы сделали, чтобы умножить числа. Мы умножили мантиссы и сложили степени. Затем, поскольку мантисса закончилась больше двух, мы нормализовали результат, увеличив показатель степени. Это похоже на то, когда мы корректируем показатель степени после выполнения операции над числами в десятичной экспоненциальной системе счисления. В каждом случае значения, с которыми мы работали, имели конечное представление в двоичном виде, поэтому значения, выдаваемые базовыми операциями умножения и сложения, также давали значения с конечным представлением. 910b

Именно округление мантиссы приводит к потере точности, которую мы связываем со значениями с плавающей запятой. Даже когда мантисса может быть выражена точно (например, при простом сложении двух чисел), мы все равно можем получить числовые потери, если мантисса требует слишком много цифр для соответствия после нормализации показателя степени.

На самом деле мы постоянно делаем подобные вещи, когда округляем десятичные числа до приемлемого размера и просто даем первые несколько цифр. Поскольку мы выражаем результат в десятичном виде, это кажется естественным. Но если бы мы округлили десятичное число, а затем преобразовали его в другое основание, это выглядело бы так же уродливо, как и десятичные числа, которые мы получаем из-за округления с плавающей запятой.

Я удивлен, что никто еще не заявил об этом: используйте непрерывные дроби. Таким образом, любое рациональное число может быть представлено в конечной двоичной системе.

Некоторые примеры:

1/3 (0,3333...)

 0; 3

5/9 (0,5555...)

 0; 1, 1, 4

10/43 (0,232558139534883720930...)

 0; 4, 3, 3

9093/18478 (0,49209871198181621387596060179673...)

 0; 2, 31, 7, 8, 5

Отсюда существует множество известных способов хранения последовательности целых чисел в памяти.

Помимо хранения вашего числа с идеальной точностью, непрерывные дроби также имеют некоторые другие преимущества, такие как наилучшее рациональное приближение. Если вы решите прервать последовательность чисел в непрерывной дроби досрочно, оставшиеся цифры (при объединении в дробь) дадут вам наилучшую возможную дробь. Вот как находятся приближения к числу Пи:

Непрерывная дробь числа Пи:

 3; 7, 15, 1, 292. ..

Завершая последовательность на 1, получаем дробь: 9(лог(0,41)/лог(2))

Проблема в том, что вы не знаете, действительно ли это число равно 61.0. Рассмотрим это:

поплавок а = 60;
поплавок b = 0,1;
поплавок с = а + b * 10;

Каково значение с? Это не точно 61, потому что b на самом деле не .1, потому что .1 не имеет точного двоичного представления.

Число 61.0 действительно имеет точную операцию с плавающей запятой, но это неверно для всех целых чисел. Если вы написали цикл, добавляющий единицу к числу двойной точности с плавающей запятой и к 64-битному целому числу, в конечном итоге вы достигли бы точки, в которой 64-битное целое число идеально представляет число, а число с плавающей запятой — нет… потому что не хватает значащих битов. 9-1 равно 1/10, что определенно не является целым числом. Так вы окажетесь в Inexactville.

Параллель можно составить из дробей и целых чисел. Некоторые дроби, например 1/7, не могут быть представлены в десятичной форме без большого количества десятичных знаков. Поскольку число с плавающей запятой основано на двоичном коде, особые случаи меняются, но возникают те же проблемы с точностью.

Существует бесконечное число рациональных чисел и конечное число битов для их представления. См. http://en.wikipedia.org/wiki/Floating_point#Accuracy_problems. 9-4=0,0625

Двоичное представление с плавающей запятой:

знак Показатель степени    Дробь (думаю, к дроби добавляется невидимая единица)
B11  B10 B9 B8   B7 B6 B5 B4 B3 B2 B1 B0

Ответ с высокой оценкой выше прибил его .

Сначала вы смешивали основание 2 и основание 10 в своем вопросе, затем, когда вы ставите справа число, которое не делится на основание, возникают проблемы. Как 1/3 в десятичном виде, потому что 3 не входит в степень 10 или 1/5 в двоичном формате, который не входит в степень 2.

Еще один комментарий, хотя НИКОГДА не используйте equal с числами с плавающей запятой, точка. Даже если это точное представление, в некоторых системах с плавающей запятой есть числа, которые могут быть точно представлены более чем одним способом (IEEE плохо относится к этому, это ужасная спецификация с плавающей запятой для начала, так что ожидайте головной боли). Никакой разницы здесь нет: 1/3 НЕ РАВНА числу на вашем калькуляторе 0,3333333, сколько бы троек не было справа от запятой. Это или может быть достаточно близко, но не равно. поэтому вы ожидаете, что что-то вроде 2 * 1/3 не будет равно 2/3 в зависимости от округления. Никогда не используйте равные с плавающей запятой.

Как мы уже говорили, в арифметике с плавающей запятой десятичное число 0,1 не может быть идеально представлено в двоичном виде.

Представления с плавающей запятой и целыми числами обеспечивают сетки или решетки для представляемых чисел. По мере выполнения арифметических операций результаты выпадают из сетки и должны быть возвращены в сетку путем округления. Пример 1/10 в двоичной сетке.

Если мы будем использовать двоично-десятичное представление, как предложил один джентльмен, сможем ли мы хранить числа в сетке?

1

Для простого ответа: у компьютера нет бесконечной памяти для хранения дробей (после представления десятичного числа в виде научной записи). Согласно стандарту IEEE 754 для чисел с плавающей запятой двойной точности, у нас есть ограничение в 53 бита для хранения дроби. Для получения дополнительной информации: http://mathcenter.oxford.emory.edu/site/cs170/ieee754/

Я не буду повторять то, что уже подытожили другие 20 ответов, поэтому я просто отвечу кратко:

Ответ в вашем содержании:

Почему числа с основанием из двух не могут точно представлять определенные отношения?

По той же причине, по которой десятичных дробей недостаточно для представления определенных отношений, а именно, неприводимых дробей со знаменателями, содержащими простые множители, отличные от двух или пяти, которые всегда будут иметь неопределенную строку по крайней мере в мантиссе своего десятичного разложения.

Почему десятичные числа не могут быть точно представлены в двоичном виде?

Этот вопрос на первый взгляд основан на неправильном представлении о самих ценностях. Никакой системы счисления недостаточно, чтобы представить какое-либо количество или отношение таким образом, чтобы сама вещь говорила вам, что она является одновременно и количеством, и в то же время сама по себе давала интерпретацию внутренней ценности представления. Как таковые, все количественные представления и вообще модели носят символический характер и могут быть поняты только апостериори, а именно после того, как человек научится читать и интерпретировать эти числа.

Поскольку модели являются субъективными вещами, которые истинны, поскольку отражают реальность, нам не обязательно интерпретировать двоичную строку как сумму отрицательных и положительных степеней двойки. Вместо этого можно заметить, что мы можем создать произвольный набор символов, использующих основание два или любое другое основание для точного представления любого числа или отношения. Просто учтите, что мы можем обращаться ко всей бесконечности, используя одно слово и даже один символ, не «показывая бесконечность» как таковую.

В качестве примера я разрабатываю двоичное кодирование для смешанных чисел, чтобы иметь большую точность, чем число с плавающей запятой IEEE 754. На момент написания этой статьи идея состояла в том, чтобы иметь знаковый бит, обратный бит, определенное количество битов для скаляра, чтобы определить, насколько «увеличить» дробную часть, а затем оставшиеся биты делятся поровну между целая часть смешанного числа, а последнее число с фиксированной запятой, которое, если установлен обратный бит, должно интерпретироваться как единица, деленная на это число. Преимущество этого заключается в том, что я могу представлять числа с бесконечным десятичным разложением, используя их обратные числа, которые до имеют завершающие десятичные расширения или, альтернативно, как дробь напрямую, возможно, как приближение, в зависимости от моих потребностей.

Вы не можете точно представить 0,1 в двоичном формате по той же причине, по которой вы не можете измерить 0,1 дюйма с помощью обычной английской линейки.

Английские линейки, как и двоичные дроби, состоят из половинок. Вы можете измерить полдюйма или четверть дюйма (что, конечно же, составляет половину половины), восьмую, шестнадцатую и т. д.

Если вы хотите измерить десятую часть дюйма, вы не повезло. Это меньше одной восьмой дюйма, но больше шестнадцатой. Если вы попытаетесь уточнить, то обнаружите, что это чуть больше 3/32, но чуть меньше 7/64. Я никогда не видел настоящую линейку с градацией тоньше 64-х, но если вы посчитаете, то обнаружите, что 1/10 меньше 13/128, больше 25/256 и больше 51. /512. Вы можете идти дальше и дальше, к 1024-му, 2048-му и 409-му.6-й и 8192-й, но вы никогда не найдете точную маркировку, даже на бесконечно точной линейке с основанием 2, которая точно соответствует 1/10, или 0,1.

Впрочем, вы найдете кое-что интересное. Давайте посмотрим на все приближения, которые я перечислил, и для каждого явно запишем, больше или меньше 0,1:

дробь десятичный 0,1 это.

Related Posts

Leave A Comment