Максимальное растяжение — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Максимальное растяжение, которое может развить гидропривод, составляет 120000 Н ( 12 т), что достаточно для освобождения плунжера вплоть до принудительного аварийного обрыва ленты. [1]
Максимальное растяжение пружины динамометра х0 определяем по максимальному значению силы трения покоя JFn kxQ9 где k — жесткость пружины динамометра. После того как брусок срывается с места, он движется под действием равнодействующей двух сил: силы трения скольжения и силы упругости пружины динамометра. [2]
Максимальное растяжение обсадной колонны возникает в верхней части, поэтому критерий расчета — использование в этой части высокопрочной марки стали. Так как давления разрыва особенно велики в верхней части, обсадные трубы должны быть достаточно прочными вверху, чтобы противостоять разрыву. Однако при расчетах возможного смятия самые тяжелые условия встречаются на забое, поэтому толстостенные обсадные трубы необходимо устанавливать в нижней части, чтобы противостоять сминающему давлению.
Определить максимальное растяжение s пружины, если в начальный момент пружина была недеформирована, а груз отпущен без начальной скорости. [4]
Определить максимальное растяжение s пружины, если в начальный момент пружина была не деформирована, а груз отпущен без начальной скорости. [5]
При максимальном растяжении степень релаксации изменяется прямолинейно, подобно тому как и в предыдущем опыте, изображенном на левом графике этого рисунка. Однако по мере снижения начального удлинения остаточное удлинение сначала падает, а затем вовсе исчезает. [6]
При режиме / const максимальное растяжение е возрастает. Поэтому осуществить режим з — — — const можно только частичной разгрузкой образца, что соответствует более мягкому режиму испытания. Если число циклов до разрушения и долговечность достаточно велики, то можно считать практически, что истинное напряжение постоянно в процессе всего испытания.
[7]
Чтобы согласовать наблюдаемые и предсказываемые кинетической теорией максимальные растяжения жидкости, нужно принять гораздо меньшее поверхностное натяжение на границе зародышевых пузырьков, чем для плоской границы раздела. [8]
Через какое время / подставка оторвется от тела и каким будет максимальное растяжение лг, пружины. [9]
В дальнейшем удобно ввести величину LMaKC, представляющую собой длину аморфного волокна при максимальном растяжении. [10]
Для этого на установочном образце подбирают положение пальца в прорези диска так, чтобы максимальное растяжение между зажимами, соответствующее нижнему положению ползуна, обеспечивало расстояние между метками рабочего участка 75 мм, а минимальное, соответствующее верхнему положению ползуна, — 25 мм. [11]
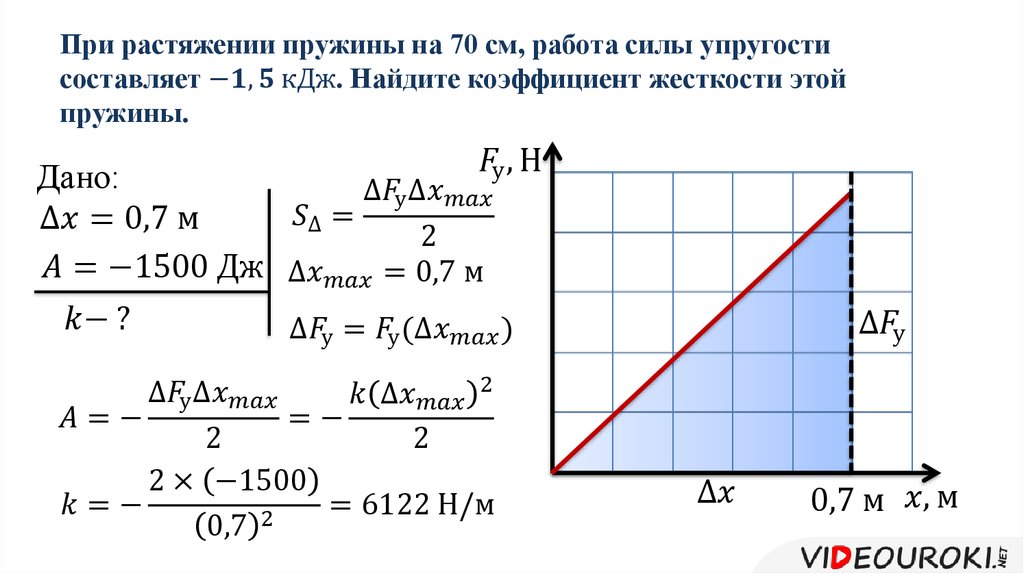[12]| Зависимость напряжение при сжатии — деформация эпокси-лавсанотекстолита ( а и эпоксикапроноволокнита ( длина волокон до. [13] |
Образцы органоволокнитов на основе жестких волокон при изгибе также не разламываются, но в зоне максимального растяжения иногда наблюдаются разрывы волокон. [14]
На лаке образуется система мелких кривых трещин, которые везде располагаются по нормали к направлению
Страницы: 1 2 3
3.3. Формулы расчета пружин растяжения
Основные понятия
Пружина растяжения — это спирально-цилиндрическая пружина, витки которой прилегают друг к другу. Пружина подвергается действию противоположно направленных усилий, приложенных вдоль ее оси.
Размеры
d | диаметр проволоки [мм, д] |
D | средний диаметр пружины [мм, д] |
D1 | наружный диаметр пружины [мм, д] |
D2 | внутренний диаметр пружины [мм, д] |
H | рабочая деформация [мм, д] |
t | шаг активных витков в ненагруженном состоянии [мм, д] |
o | высота ушка [мм, д] |
sx | деформация пружины [мм, д] |
Lx | длина пружины [мм, д] |
Fx | рабочая сила, действующая на пружину [Н, фунт] |
W8 | энергия деформации [Дж, фут фунт] |
x | индекс, обозначающий состояние пружины |
Навивка
Вправо (стандарт)
Влево (должна отображаться соответствующая надпись)
Состояния
Свободное: пружина не нагружена (индекс 0)
Предварительная нагрузка: пружина с минимальной рабочей нагрузкой (индекс 1)
Полная нагрузка: пружина с максимальной рабочей нагрузкой (индекс 8)
Предел: пружина вдавлена до касания витков (индекс 9).
Зацепы пружин растяжения
Высота зацепа пружины растяжения
Где:
L0 | длина пружины в свободном состоянии [мм] |
LZ | длина части пружины с витками [мм] |
Часто используемые зацепы пружин растяжения
Тип зацепа и информация о размерах | Изображение |
Половина
витка, o = 0,55…0,8 D |
|
Обычно d ≤ 6,3 мм, D >= 3,15 мм, i >= 9 | |
Полный
виток, o = 0,8. |
|
Используется без ограничений | |
Полный виток сбоку, o D2 |
|
Когда нагрузка не обязательно должна прикладываться по оси | |
Полный виток внутри, o = 1,05…1,2 D2 |
|
Обычно d ≥ 10 мм, i >= 7 | |
Поднятый зацеп, o = 1,2 D2 … 30 d |
|
Обычно для d = от 0,5мм до 4 мм, o ≤ 100 мм | |
Два полных витка, o D |
|
Используется без ограничений | |
Два полных витка сбоку, o D2 |
|
Когда нагрузка не обязательно должна прикладываться по оси | |
..1,1 D2Расчет пружин в метрических единицах
Общие формулы расчета
Коэффициент использования материала
Наружный диаметр пружины
D1 = D + d [мм]
Где:
| D | средний диаметр пружины [мм] |
| d | диаметр проволоки [мм] |
Внутренний диаметр пружины
D2 = D — d [мм]
Где:
| D | средний диаметр пружины [мм] |
| d | диаметр проволоки [мм] |
Рабочая деформация
H = L81= s81[мм]
Где:
| L8 | длина полностью нагруженной пружины [мм] |
| L1 | длина предварительно нагруженной пружины [мм] |
| s8 | деформация полностью нагруженной пружины [мм] |
| s1 | деформация предварительно нагруженной пружины [мм] |
Высота зацепа пружины
Где:
| L0 | длина пружины в свободном состоянии [мм] |
| LZ | длина части пружины с витками [мм] |
Индекс пружины
c = D/d [-]
Где:
| D | средний диаметр пружины [мм] |
| d | диаметр проволоки [мм] |
Поправочный коэффициент Валя
Где:
| c | индекс пружины [-] |
| LZ | длина части пружины с витками [мм] |
Начальное растяжение
Где:
| d | диаметр проволоки [мм] |
| 0 | напряжение в свободном состоянии [Мпа] |
| D | средний диаметр пружины [мм] |
| Kw | поправочный коэффициент Валя [-] |
Общая сила, действующая в пружине
Где:
| d | диаметр проволоки [мм] |
| G | напряжение
при кручении – это усилие на единицу
площади материала пружины при изгибе
[фн/кв. |
| D | средний диаметр пружины [мм] |
| Kw | поправочный коэффициент Валя [-] |
| G | модуль упругости материала пружины [МПа] |
материала пружины в общем случае
[МПа]Жесткость пружины
Где:
| d | диаметр проволоки [мм] |
| G | модуль упругости материала пружины [МПа] |
| D | средний диаметр пружины [мм] |
| n | количество активных витков [-] |
| F8 | рабочее усилие в полностью нагруженной пружине [МПа] |
| F1 | рабочее усилие в минимально нагруженной пружине [МПа] |
| H | рабочая деформация [мм] |
Расчет конструкции пружины
При
проектировании пружины подбирается
диаметр проволоки, количество витков
и длина свободной пружины L0 для
заданной нагрузки, материала и сборочных
размеров.
Если рассчитанная пружина не соответствует ни одному значению диаметра проволоки для данного напряжения 0 согласно формуле, расчет пружины повторяется с использованием скорректированного значения напряжения в свободном состоянии из рекомендуемого диапазона.
Пружине без начального растяжения соответствует средний рекомендуемый шаг витков t = 0,35 D [мм].
Если рассчитанная пружина не соответствует ни одному значению диаметра проволоки для выбранного шага, расчет пружины повторяется с использованием скорректированного значения шага из рекомендуемого диапазона 0,3 D ≤ t ≤ 0,4 D [мм].
Конструкция пружины определяется с учетом условия прочности 8≤ usA и рекомендуемых диапазонов некоторых геометрических параметров пружины: L0≤ D и L0≤ 31,5 д и 4 ≤ D/d ≤16 и n 2.
Задание нагрузки, материала и сборочных размеров пружины
Вначале
выполняется проверка входных величин
для расчета.
Затем вычисляется длина пружины в свободном состоянии.
После расчета выбирается диаметр проволоки, количество витков и диаметры пружины – так, чтобы высота зацепа соответствовала выбранному типу зацепа. Кроме того, должны выполняться упомянутые выше прочностные и геометрические условия. Конструкция пружины должна удовлетворять по диаметрам всем заданным начальным условиям. При отсутствии таких дополнительных условий предельный диаметр пружины устанавливается по геометрическим условиям для минимально/максимально допустимого диаметра проволоки.
Отбираются
все диаметры проволоки (от меньшего к
большему), которые проходят по прочностным
и геометрическим условиям. Проверяются
высота зацепа и количество витков. Если
все условия выполнены, расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Вычисленное значение высоты зацепа должно находиться в пределах d ≤ o ≤ 30 d. Комбинация диаметра проволоки, количества витков и диаметра пружины должна давать в итоге такую высоту зацепа, которая удовлетворяет его типу. Вначале в качестве типа зацепа берется полный виток, затем, если он не годится–полный виток внутри и т.д.
Задание нагрузки, материала и диаметра пружины
Вначале выполняется проверка входных величин для расчета.
После
проверки выбирается диаметр проволоки,
количество витков, длина пружины в
свободном состоянии и сборочные размеры
пружины – так, чтобы высота зацепа
соответствовала выбранному типу зацепа.
Кроме того, должны выполняться прочностные
и геометрические условия. Если сборочный
размер L1 или
L8 взят
из спецификации или значение рабочей
деформации пружины ограничено, конструкция
пружины должна соответствовать этому
условию. В остальных случаях предельные
значения сборочных размеров пружины и
ее длины в свободном состоянии определяются
геометрическими условиями для заданного
диаметра пружины и минимального/максимального
допустимого диаметра проволоки.
Формула для проектирования пружины по заданному диаметру проволоки.
где значение 8 = 0,85 A используется в качестве величины напряжения материала пружины при кручении в полностью нагруженном состоянии.
Если для данного диаметра проволоки не удается подобрать подходящую комбинацию размеров пружины, расчетная процедура оценивает другие диаметры проволоки. Они проверяются, начиная от меньшего к большему, до тех пор пока не будет достигнуто такое количество витков, при котором высота зацепа удовлетворяет всем условиям. Расчет конструкции завершается, и текущие значения параметров принимаются в качестве его результатов, независимо от того, как прошел бы расчет при других подходящих диаметрах проволоки. Таким образом, полученная пружина имеет минимально возможный диаметр проволоки и минимально возможное количество витков.
Вычисленное
значение высоты зацепа должно находиться
в пределах d ≤ o ≤ 30 d. Для
высоты, вычисленной таким способом,
выбирается соответствующий тип зацепа.
Комбинация диаметра проволоки, количества
витков, длины пружины в свободном
состоянии и сборочных размеров пружины
должна давать в итоге такую высоту
зацепа, которая удовлетворяет его типу.
Вначале в качестве типа зацепа берется
полный виток, затем, если он не
годится–полный виток внутри и т.д.
Задание максимального рабочего усилия, материала, сборочных размеров и диаметра пружины
Вначале выполняется проверка входных величин для расчета.
Затем подбирается диаметр проволоки, количество витков, длина свободной пружины и минимальное рабочее усилие F1 таким образом, чтобы высота зацепа пружины соответствовала выбранному типу зацепа. Кроме того, должны выполняться прочностные и геометрические условия.
Формула для проектирования пружины по заданному диаметру проволоки.
где значение 8 = 0,9 A используется в качестве величины напряжения материала пружины при кручении в полностью нагруженном состоянии.
Если
для данного диаметра проволоки не
удается подобрать подходящую комбинацию
размеров пружины, расчетная процедура
оценивает другие диаметры проволоки.
Они проверяются, начиная от меньшего к
большему, до тех пор пока не будет
достигнуто такое количество витков,
при котором высота зацепа удовлетворяет
всем условиям. Расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Проверочный расчет пружины
Расчет соответствующих значений сборочных размеров и рабочего отклонения для указанной нагрузки, материала и размеров пружины.
Сначала проверяются расчетные входные значения. Затем на основании приведенных ниже формул вычисляются сборочные размеры.
Длина предварительно нагруженной пружины
Длина полностью нагруженной пружины
Где:
| L0 | длина пружины в свободном состоянии [мм] |
| F1 | рабочая сила в минимально нагруженной пружине [мм] |
| D | средний диаметр пружины [мм] |
| n | количество активных витков [-] |
| G | модуль упругости материала пружины [МПа] |
| d | диаметр проволоки [мм] |
| F8 | рабочее усилие в полностью нагруженной пружине [МПа] |
Рабочая деформация
H = L18[мм]
Расчет рабочих сил
Расчет
соответствующих сил, действующих в
пружинах в рабочем состоянии для
указанного материала, сборочных размеров
и размеров пружины.
Сначала проверяются
и рассчитываются входные данные, а затем
выполняется расчет рабочих сил с помощью
следующих формул.
Минимальное рабочее усилие
Максимальное рабочее усилие
Расчет выходных параметров пружины
Эта часть является общей для всех типов расчета пружины. Расчет производится в следующем порядке.
Коэффициент высоты зацепа
Жесткость пружины
Длина части с витками
Пружина без начального растяжения | |
| Lz = t n + d [мм] |
Пружина с начальным растяжением | |
| Lz = 1,03 (n + 1) d [мм] |
Деформация предварительно нагруженной пружины
s1 = L1 — L0 [мм]
Полная деформация пружины
s8 = L8 — L0 [мм]
Напряжение при кручении материала пружины в состоянии предварительной нагрузки
Напряжение материала пружины при кручении при полном нагружении
Предельное усилие в пружине
Деформация в предельном состоянии
Где:
| k | жесткость пружины [Н/мм] |
| F9 | рабочее усилие в пружине, нагруженной до предела [Н] |
| F0 | начальное растяжение пружины [Н] |
Предельная длина пружины
L9 = L0 + s9 [мм]
Энергия деформации пружины
Длина развернутой проволоки
l
= 3. | |||
| Где длина развернутого зацепа l0: | ||
|
| для половины витка | |
|
|
| l0 = D + 4 o — 2 D — 2 d [мм] |
|
| для полного витка | |
|
|
| l0 = 2 ( D — 2 d) [мм] |
|
| для полного витка сбоку | |
|
|
| l0 = 2 ( D — 2 d) [мм] |
|
| для полного витка внутри | |
|
|
| l0 = 2 ( D — d) [мм] |
|
| для поднятого зацепа | |
|
|
| l0 = D + 2 o — D + 3 d [мм] |
|
| для двух полных витков | |
|
|
| l0 = 4 D [мм] |
|
| для двух полных витков сбоку | |
|
|
| l0 = 4 D [мм] |
|
| для неуказанного типа зацепа | |
|
|
| l0 = 0 [мм] |
2 D n + l0 [мм]Масса пружины
Собственная частота колебаний пружины
Проверка нагрузки пружины
8≤ us A
Обзор используемых переменных:
d | диаметр проволоки [мм] |
k | жесткость пружины [Н/мм] |
D | средний диаметр пружины [мм] |
D1 | наружный диаметр пружины [мм] |
D2 | внутренний диаметр пружины [мм] |
F | обобщенное усилие, приходящееся на пружину [Н] |
G | модуль упругости материала пружины при сдвиге [МПа] |
H | рабочая деформация [мм] |
c | индекс пружины [-] |
Kw | поправочный коэффициент Валя [-] |
l | длина развернутой проволоки [мм] |
L | обобщенная длина пружины [мм] |
LZ | длина части пружины с витками [мм] |
m | масса пружины [N] |
n | количество активных витков [-] |
o | высота зацепа пружины [мм] |
t | шаг активных витков в ненагруженном состоянии [мм] |
s | обобщенная деформация (растяжение) пружины [мм] |
us | коэффициент использования материала |
| плотность материала пружины [Н/мм3] |
| напряжение
при кручении – это усилие на единицу
площади материала пружины при изгибе
[фн/кв. |
A | допустимое напряжение материала пружины при кручении [МПа] |
материала пружины в общем случае
[МПа]домашнее задание и упражнения — Максимальное растяжение системы пружинных масс
спросил
Изменено 6 лет, 5 месяцев назад
Просмотрено 17 тысяч раз
$\begingroup$
Решая задачи простого гармонического движения, я наткнулся на эту задачу, которая меня запутала.
Неподвижная горизонтальная пружина растягивается с постоянной силой $F$. От меня требуется получить максимальное удлинение этой пружины. Но проблема в том, какой метод правильный, энергетический или силовой? Дайте мне знать неправильное представление на неправильном пути.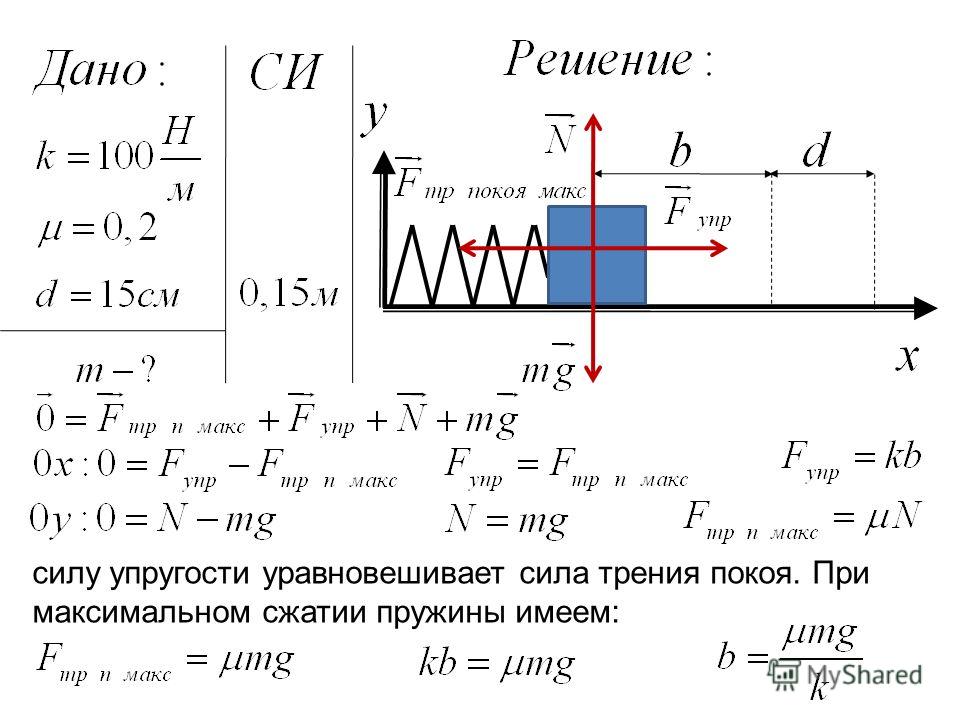
2
$$
Последнее, конечно, и есть потенциальная энергия пружины. Таким образом, уравнение «сохранения энергии» тривиально и не дает никакой новой информации.
$\endgroup$
10
$\begingroup$
Если вы используете постоянную силу на пути, пружина переместится за положение, где $F=kx$, потому что она достигнет этой точки с некоторой скоростью. Таким образом, использовать силовой метод так, как вы его использовали, некорректно, так как при максимальном расширении $v=0$, но $a\neq0$. Энергетический метод, который вы использовали, даст правильный ответ. Если вместо этого используется сила, чтобы удерживать пружину удлиненной в состоянии покоя, то силовой метод является правильным. Чтобы понять, почему прочитайте ответ Прахара.
$\endgroup$
1
Ньютоновская механика — Максимальное растяжение пружины
$\begingroup$
Предположим, что к пружине прикреплен груз $m$.
2+mg(-x)$. Вот в этом случае $x=\frac{2mg}{k}$. Где мы ошиблись тогда? Поскольку оба не равны.
- ньютоновская механика
- ньютоновская гравитация
- сохранение энергии
- пружина
- равновесие
$\endgroup$
4
$\begingroup$
Теперь, если отпустить массу, натяжение будет восстанавливающей силой пружины, а поскольку масса не поднимается и не опускается
Но в этот момент скорость (кинетическая энергия) отлична от нуля. Таким образом, утверждение, что оно не идет ни вверх, ни вниз, ложно.
В вашем заявлении о сохранении энергии у вас нулевая кинетическая энергия, и это происходит только при максимальном смещении, которое составляет $x=2mg/k$ (и $0$). И если вы подключите это (в основном $ 2x $, вы увидите, что проблем нет.
$\endgroup$
2
$\begingroup$
Если выпустить массу, она также будет иметь кинетическую энергию.
Leave A Comment