Максимальная кинетическая энергия груза: формула
Кинетическая энергия
Определение 1
Кинетическая энергия — внутренняя энергия движущегося тела, обусловленная его инертностью (массой) и скоростью. Она равна энергии, которую нужно затратить, чтобы снизить скорость этого тела до нуля.
Например, движущийся автомобиль невозможно остановить мгновенно. Для остановки необходимо затратить энергию трения тормозных колодок о тормозные диски колес и шин об асфальт.
Замечание 1
Кинетическая и потенциальная энергия измеряются в джоулях ($1 Дж = Н \cdot м$).
В некоторых физических системах происходят циклические преобразования потенциальной (запасенной) энергии в кинетическую и обратно. Такие системы называются маятниками. Например, для груза, подвешенного на нити, потенциальная энергия максимальна, когда он отклонен на максимальный угол от вертикали. Мгновенная скорость груза в этот момент равна нулю и, следовательно, нулю равна и кинетическая энергия. По мере движения вниз под действием силы тяжести, скорость груза нарастает и достигает максимума в нижней точке, после чего снова начинает запасаться по мере движения вверх.
Готовые работы на аналогичную тему
Проще всего изучать переход кинетической и потенциальной энергий друг в друга на примере пружинного маятника, где действует, если пренебречь силой трения, лишь сила упругости. Когда пружину сжимают, энергия запасается. Когда отпускают — потенциальная энергия, сохраненная в кристаллической решетке материала, высвобождается и превращается в кинетическую, разгоняя груз. Когда скорость груза достигает максимума, он продолжает движение по инерции, растягивая пружину в противоположном направлении, вновь запасая энергию и снижая скорость. Характеристики такого колебательного движения зависят только от материала пружины, толщины проволоки, из которой она намотана, диаметра и количества витков. Все эти факторы описываются единым параметром — коэффициентом упругости.
Максимальная кинетическая энергия груза
Для простого пружинного маятника полную энергию груза в любой момент времени можно выразить как
$E = E_p + E_k = \frac{m \cdot v^2}{2} + \frac{k \cdot x^2}{2}$, где:
- $E_p$ — потенциальная энергия,
- $E_k$ — кинетическая энергия,
- $m$ — масса,
- $v$ — моментальная скорость,
- $k$ — коэффициент упругости,
- $x$ — приращение длины пружины в данный момент.
Максимальную кинетическую энергию можно вычислить как
$(E_k)_{max} = \frac{m \cdot v_{max}^2}{2}$,
где $v_{max}$ — максимальная скорость груза. Однако измерить ее на практике сложно. Проще, опираясь на постоянство суммы кинетической и потенциальной энергий, определить максимальную потенциальную (когда кинетическая равна нулю). Поскольку справедливо и обратное, можно записать:
$(E_k)_{max} = (E_p)_{max} = \frac{k \cdot x_{max}^2}{2}$,
где $x_{max}$ — максимальное приращение растяжения пружины. Его легко измерить, а коэффициент упругости посмотреть в справочнике.
Пример 1
Компактный груз, массой 0,5 кг прикреплен к движущейся горизонтально пружине. Ее коэффициент упругости равен 2000 $\frac{Н}{м}$. Каково было начальное приращение длины пружины, если его максимальная скорость во время колебаний составляет 1 $\frac{м}{с}$?
Из условий задачи можно найти максимальную кинетическую энергию груза:
$(E_k)_{max} = \frac{0,5 \cdot 1^2}{2} = 0,25 Дж$
Выразив максимальную потенциальную энергию через приращение длины пружины, составим равенство:
$0,25 = \frac{2000 \cdot x_{max}^2}{2} \implies x_{max} = \sqrt{\frac{2 \cdot 0,25}{2000}} \approx 0,016 м$.
Ответ: $\approx 1,6 мм$.
Кинетическая энергия | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Кинетическая энергия — скалярная физическая величина, равная половине произведения массы тела на квадрат его скорости.
![Rendered by QuickLaTeX.com \[\LARGE W_k=\frac{m\upsilon ^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-903510ee357d0ffb6790e969240dd5d9_l3.png)
Что бы понять, что же такое кинетическая энергия тела, рассмотрим случай, когда тело массой m под действием постоянной силы (F=const) движется прямолинейно равноускоренно (а=const). Определим работу силы, приложенной к телу, при изменении модуля скорости этого тела от v1 до v2.
Кинетическая-энергия-тела
Как мы знаем, работа постоянной силы вычисляют по формуле
![Rendered by QuickLaTeX.com \[A=FScos\alpha\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-b7f11e89f095731ad60414040ced7d92_l3.png)
. Так как в рассматриваемом нами случае направление силы F и перемещения s совпадают, то
![Rendered by QuickLaTeX.com \[cos\alpha =1\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-79c9bc5a411f2441dc9800271ba8b80b_l3.png)
, и тогда у нас получается, что работа силы равна
![Rendered by QuickLaTeX.com \[А=Fs\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-4ff6eebc0fd47501e8f7b2a42c77fea1_l3.png)
. По второму закону Ньютона найдем силу F=ma. Для прямолинейного равноускоренного движения справедлива формула:
![Rendered by QuickLaTeX.com \[\large \upsilon _2^2=\upsilon _1^2+2aS\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-f4a6417a29ffbeaacffb47e58533524f_l3.png)
Из это формулы мы выражаем перемещение тела:
![Rendered by QuickLaTeX.com \[\large S=\frac{\upsilon _2^2-\upsilon _1^2}{2a}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-7757b1f76a8fe01e4454fb7caed6f83d_l3.png)
Подставляем найденные значения F и S в формулу работы, и получаем:
![Rendered by QuickLaTeX.com \[\large A=\frac{m\upsilon ^2}{2}-\frac{m\upsilon _1^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-f904f0f3bd35e6c5a859df88947d2867_l3.png)
Из последней формулы видно, что работа силы, приложенной к телу, при изменении скорости этого тела равна разности двух значений некоторой величины
![Rendered by QuickLaTeX.com \[\frac{m\upsilon ^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-dd7d19bb870c82f74ab69774ac2ed388_l3.png)
. А механическая работа это и есть мера изменения энергии. Следовательно, в правой части формулы стоит разность двух значений энергии данного тела. Это значит, что величина
![Rendered by QuickLaTeX.com \[\frac{m\upsilon ^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-dd7d19bb870c82f74ab69774ac2ed388_l3.png)
представляет собой энергию, обусловленную движением тела. Эту энергию называют кинетической. Она обозначается Wк.
![Rendered by QuickLaTeX.com \[\large W_k=\frac{m\upsilon ^2}{2} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-44e13af14375c997e0d60df42bf425b1_l3.png)
Если взять выведенную нами формулу работы, то у нас получится
![Rendered by QuickLaTeX.com \[\large A=W_{k2}-W_{k1}=\Delta W_k\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-acb2c752a264932cbe4e1a71f5bdb537_l3.png)
Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии этого тела
Так же есть :
Потенциальная энергия :
![Rendered by QuickLaTeX.com \[\large W_p=mgh \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-bb8cf55efe57b360c4712087ecf3fb02_l3.png)
В формуле мы использовали :
![Rendered by QuickLaTeX.com \[W_k\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-fdefdaf99ff1a5468ebee9f4a1013f0b_l3.png)
— Кинетическая энергия
m — Масса тела
![Rendered by QuickLaTeX.com \[ \upsilon\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-61a6a14986c7b1d45a6f39da48f3a43b_l3.png)
— Скорость движения тела
![Rendered by QuickLaTeX.com \[ \upsilon_1\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-3ee646ce78bdfdc2586537a0e204a975_l3.png)
— Начальная скорость тела
![Rendered by QuickLaTeX.com \[ \upsilon_2\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-36adf79a8c949e974e82bd707606d29e_l3.png)
— Конечная скорость тела
A — Работа тела
a — Ускорение тела
F — Сила, действующая на тело
S — Перемещение тела
Формула кинетической энергии в физике
Определение и формула кинетической энергии
ОпределениеКинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.
Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.
Встречаются следующие обозначения кинетической энергии: Ek,Wk,T.
Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:
Кинетическая энергия материальной точки и тела
Кинетическая энергия материальной точки равна:
где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.
Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:
где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела, v – скорость перемещения рассматриваемого элемента, — плотность участка, m–масса всего рассматриваемого тела, V – объем тела.
В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.
При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:
где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела, r – расстояние от элементарного участка тела до оси вращения, L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.
Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:
где – момент импульса рассматриваемого тела относительно точки О.
Единицы измерения кинетической энергии
Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:
[Ek]=Дж (джоуль),
в системе СГС –[Ek]= эрг.
При этом: 1 дж= 107 эрг.
Теорема Кенига
Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой,
кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения
системы со скоростью центра масс (v
где –суммарная масса системы материальных точек.
Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:
где Jc — момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении Jc=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.
Примеры решения задач
ПримерРешение. По определению изменение кинетической энергии равно работе (A’), которая производится над телом при силовом взаимодействии, то есть можно записать, что:
Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:
(Дж)
Ответ. A’=-2 Дж.
ПримерЗадание. Материальная точка движется по окружности, радиус которой равен R. Кинетическая энергия частицы связана c величиной пути (s), пройденного ей в соответствии с формулой: . Какое уравнение связывает силу (F), действующую на точку и путь s?
Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:
Но по условию задачи:
Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:
Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:
Энергия. Виды механической энергии. Работа и энергия. | |
Энергия — физическая величина, характеризующая состояние тела или системы тел по их движению и взаимодействию. В механике энергия тела или системы тел определяется взаимным положением тел или системы тел и их скоростями. При изменении состояния тела (изменении энергии) совершается механическая работа. Т.о. изменение энергии при переходе системы из одного состояния в другое равно работе внешних сил. Механическая работа — мера изменения энергии тела. |
|
В механике выделяют два вида энергии: кинетическую энергию и потенциальную энергию. |
|
Кинетическая энергия. Кинетическая энергия — энергия движущегося тела.(От греческого слова kinema — движение). По определению кинетическая энергия покоящегося в данной системе отсчета тела обращается в ноль. |
|
Пусть тело движется под действием постоянной силы Тогда:
Т.к. Т.к. движение равноускоренное, то: |
|
Следовательно: |
|
|
[Ek]=Дж. |
Кинетическая энергия — величина относительная, зависящая от выбора СО, т.к. скорость тела зависит от выбора СО. |
|
Т.о. |
|
Эта теорема справедлива для любого движения и для сил любой природы. Если тело разгоняется из состояния покоя, то Ek1=0. Тогда A = Ek2. Следовательно, кинетическая энергия численно равна работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости. |
|
Вывод: Работа силы равна изменению кинетической энергии тела, т.е. | A = ΔEk |
Окружающий мир пребывает в постоянном движении. Любое тело (объект) способно выполнить определенную работу, даже если оно в состоянии покоя. Но для совершения любого процесса требуется приложить некоторые усилия, порой немалые.
В переводе с греческого языка этот термин означает «деятельность», «сила», «мощь». Все процессы на Земле и за пределами нашей планеты происходят благодаря этой силе, которой обладают окружающие объекты, тела, предметы….
Виды энергии
Среди большого разнообразия выделяют несколько основных видов данной силы, отличающихся прежде всего своими источниками:
- механическая – данный вид характерен для движущихся в вертикальной, горизонтальной или другой плоскости тел,
- тепловая – выделяется в результате неупорядоченного движения молекул в веществах,
- электрическая – источником этого вида является движение заряженных частиц в проводниках и полупроводниках,
- световая – переносчиком ее являются частицы света – фотоны,
- ядерная – возникает вследствие самопроизвольного цепного деления ядер атомов тяжелых элементов.
В этой статье пойдет речь о том, что собой представляет механическая сила предметов, из чего она состоит, от чего зависит и как преобразуется во время различных процессов.
Благодаря этому виду предметы, тела могут находиться в движении либо в состоянии покоя. Возможность такой деятельности объясняется присутствием двух основных составляющих:
- кинетической (Ек),
- потенциальной (Еп).
Именно сумма кинетической и потенциальной энергий определяет общий численный показатель всей системы. Теперь о том, какие формулы используются для расчетов каждой из них, и в чем измеряется энергия.
Как рассчитать энергию
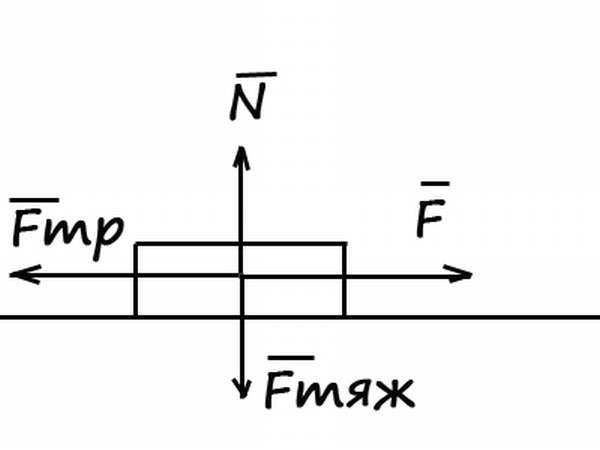 Кинетическая энергия – это характеристика любой системы, которая находится в движении. Но как найти кинетическую энергию?
Кинетическая энергия – это характеристика любой системы, которая находится в движении. Но как найти кинетическую энергию?
Сделать это несложно, так как расчетная формула кинетической энергии весьма проста:
Конкретное значение определяется двумя основными параметрами: скоростью перемещения тела (V) и его массой (m). Чем больше данные характеристики, тем большей значением описываемого явления обладает система.
Но если объектом не совершаются перемещения (т.е. v = 0), то и кинетическая энергия равна нулю.
Потенциальная энергия – это характеристика, зависящая от положения и координат тел.
Любое тело подвержено земному притяжению и воздействию сил упругости. Такое взаимодействие объектов между собой наблюдается повсеместно, поэтому тела находятся в постоянном движении, меняют свои координаты.
Установлено, чем выше от поверхности земли находится предмет, чем больше его масса, тем большим показателем данной величины оно обладает.
Таким образом, зависит потенциальная энергия от массы (m) , высоты (h). Величина g – ускорение свободного падения, равное 9,81 м/сек2. Функция расчета ее количественного значения выглядит так:
Eп = mgh, (2)
Единицей измерения этой физической величины в системе СИ считается джоуль (1 Дж). Именно столько нужно затратить сил, чтобы переместить тело на 1 метр, приложив при этом усилие в 1 ньютон.
Важно! Джоуль как единица измерения утвержден на Международном конгрессе электриков, который проходил в 1889 году. До этого времени эталоном измерения была Британская термическая единица BTU, используемая в настоящее время для определения мощности тепловых установок.
Основы сохранения и превращения
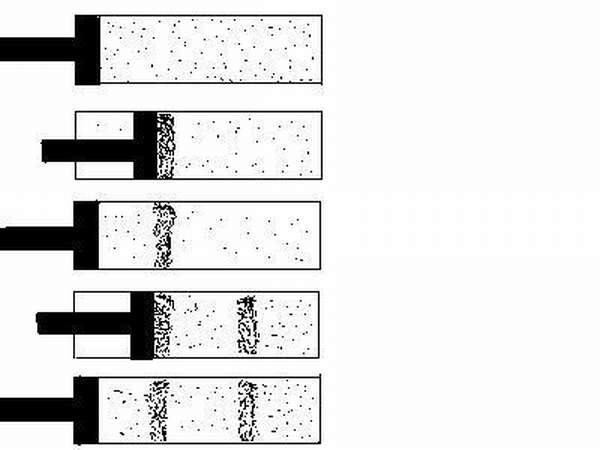 Из основ физики известно, что суммарная сила любого объекта, независимо от времени и места его пребывания, всегда остается величиной постоянной, преобразуются лишь ее постоянные составляющие (Еп) и (Ек).
Из основ физики известно, что суммарная сила любого объекта, независимо от времени и места его пребывания, всегда остается величиной постоянной, преобразуются лишь ее постоянные составляющие (Еп) и (Ек).
Переход потенциальной энергии в кинетическую и обратно происходит при определенных условиях.
Например, если предмет не перемещается, то его кинетическая энергия равна нулю, в его состоянии будет присутствовать только потенциальная составляющая.
И наоборот, чему равна потенциальная энергия объекта, например, когда он находится на поверхности Земли (h=0)? Конечно, она нулевая, а Е тела будет состоять только из ее составляющей Ек.
Но потенциальная энергия – это мощность движения. Стоит только системе приподняться на какую- то высоту, после чего его Еп сразу начнет увеличиваться, а Ек на такую величину, соответственно, уменьшаться. Эта закономерность просматривается в вышеуказанных формулах (1) и (2).
Для наглядности приведем пример с камнем либо мячом, которые подбрасывают. В процессе полета каждый из них обладает и как потенциальной, так и кинетической составляющей. Если одна увеличивается, то другая на такую же величину уменьшается.
Полет предметов вверх продолжается лишь до тех пор, пока хватит запаса и сил у составляющей движения Ек. Как только она иссякла, начинается падение.
 А вот чему равна потенциальная энергия предметов в самой верхней точке, догадаться нетрудно, она максимальная.
А вот чему равна потенциальная энергия предметов в самой верхней точке, догадаться нетрудно, она максимальная.
При их падении происходит все наоборот. При касании с землей уровень кинетической энергии равен максимуму.
Действие этого закона наблюдается не только в обычной жизни, но и в научных теориях. Кратко об одной из них.
Так как между многочисленными частицами идеального газа отсутствует какое-либо взаимодействие, то потенциальная составляющая описываемого явления молекул постоянно нулевая. Значит, вся внутренняя сила частиц идеального газа определяется, как средняя кинетическая, и рассчитывается по приведенной выше формуле (1).
Внимание! В наше время на письменных столах можно увидеть сувенир, называемый «маятником Ньютона». Этот прибор прекрасно демонстрирует процесс преобразования. Если крайний шарик отвести в сторону, а затем его отпустить, он после столкновения передает свой энергетический заряд следующему шарику, а тот своему соседу.
Виды энергии в физике
Кинетическая и потенциальная энергии, формулы
Вывод
На вопрос, например, как найти кинетическую энергию, ученые давно дали ответ. Уже в середине XIX в. английский механик Уильям Томсон использовал в своих опытах определение «кинетическая». Но современная жизнь заставила проводить глубокие исследования по части преобразования одного вида в другой.
Это интересно! Что показывает скорость при равномерном прямолинейном движении: формула
Кинетическая энергия — урок. Физика, 8 класс.
Энергию, которой обладают только движущиеся тела, называют кинетической энергией.
Если тело находится в состоянии покоя, его кинетическая энергия равна нулю.Кинетическая энергия тела (Eкин) зависит от массы тела (m) и от скорости его движения (v).
Кинетическая энергия прямо пропорциональна массе тела и квадрату его скорости.
Определяют кинетическую энергию по формуле:
Eкин=m⋅v22.
Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом:
m=2⋅Eкинv2 и v=2⋅Eкинm.
С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия.
Если масса увеличивается в \(2\) раза, тогда кинетическая энергия увеличивается также в \(2\) раза.
Зависимость кинетической энергии от массы можно отобразить на данном графике, если принять скорость тела постоянной и равной \(2 м/с\).
С увеличением скорости движения тела увеличивается также и его кинетическая энергия в квадратичной зависимости.
Если скорость увеличивается в \(2\) раза, тогда кинетическая энергия увеличивается в \(4\) раза.
Зависимость кинетической энергии от скорости движения можно отобразить на данном графике, если принять массу тела постоянной и равной \(2 кг\).
Пример:
Автомобиль, масса которого \(1400 кг\), из состояния покоя развивает скорость до значения \(5 м/с\).
Какова кинетическая энергия автомобиля на конечном этапе движения?
Eкин=m⋅v22=1400⋅522=17500Дж.
Источники:
E. Šilters, V. Regusts, A. Cābelis. «Fizika 10 klasei», Lielvārds, 2004, 256 lpp.
(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.)
Формула кинетической энергии
– кинетическая энергия движущегося тела, – его масса, – скорость его движения.
Условное обозначение —
Единица измерения энергии — Дж (джоуль).
Кинетическая энергия характеризует движение тела. Это векторная физическая величина. Она равна нулю, когда тело неподвижно. Кинетическую энергию подразделяют на энергию поступательного и вращательного движения. Указанная формула имеет смысл только для поступательного движения.
Примеры решения задач по теме «Кинетическая энергия»
| Понравился сайт? Расскажи друзьям! | |||

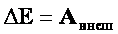
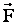 в направлении действия силы.
в направлении действия силы.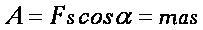 .
. 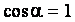 .
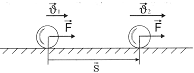
.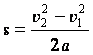 .
.
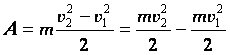 .
.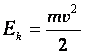
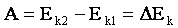 — эта формула выражает теорему о кинетической энергии: изменение кинетической энергии тела (материальной точки)за некоторый промежуток времени равно работе, совершенной силой, действующей на тело, за этот же промежуток времени
— эта формула выражает теорему о кинетической энергии: изменение кинетической энергии тела (материальной точки)за некоторый промежуток времени равно работе, совершенной силой, действующей на тело, за этот же промежуток времени
Leave A Comment