Решение неравенств, все формулы и примеры
Определение и формулы неравенств
Знаки > называются знаками строгого неравенства, а знаки — знаками нестрогого неравенства.
Если в неравенство входят только числовые величины, то такое неравенство называется числовым неравенством.
Неравенства называют равносильными, если они имеют одно и тоже множество решений.
Основные правила, применяемые при решении неравенств
- Если какое-либо слагаемое перенести из одной части неравенства в другую, изменив при этом его знак на противоположный, то получим неравенство, равносильное данному.
- Если обе части неравенства умножить (разделить) на одно и то же положительное число, то получим неравенство, равносильное данному.
- Если обе части неравенства умножить (разделить) на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получим неравенство, равносильное данному.
В зависимости от того, какие функции входят в неравенство, различают линейные, квадратные, дробно-рациональные, иррациональные, логарифмические, показательные неравенства, неравенства с параметром.
Если требуется все общие решения двух или нескольких неравенств, то решают систему неравенств. Как и систему уравнений, систему неравенств записывают с помощью фигурной скобки. Решение системы неравенств есть пересечение решений всех входящих в нее неравенств.
Одним из основных методов решения неравенств является метод интервалов.
Примеры решения неравенств
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Алгебра. Урок 8. Неравенства, системы неравенств.
Содержание страницы:
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
ax<bax≤bax>bax≥b
где a и b — любые числа, причем a≠0,x — переменная.
Примеры линейных неравенств:
3x<5x−2≥07−5x<1x≤0
Решить линейное неравенство — получить выражение вида:
x<cx≤cx>cx≥c
где c — некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
-
Если знак неравенства строгий
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥,≤, точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x<c | x∈(−∞;c) | |
| x≤c | x∈(−∞;c] | |
| x>c | x∈(c;+∞) | |
| x≥c | x∈[c;+∞) |
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
ax<bax≤bax>bax≥b
- Пусть получилось неравенство вида ax≤b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a>0 то неравенство приобретает вид x≤ba.
- Если a<0, то знак неравенства меняется на противоположный, неравенство приобретает вид x≥ba.
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3(2−x)>18.
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6−3x>18
−3x>18−6−3x>12|÷(−3)
Делим обе части неравенства на (-3) — коэффициент, который стоит перед x. Так как −3<0, знак неравенства поменяется на противоположный. x<12−3⇒x<−4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x∈(−∞;−4)
№2. Решить неравество 6x+4≥3(x+1)−14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6x+4≥3x+3−14
6x−3x≥3−14−4
3x≥−15 | ÷3 Делим обе части неравенства на (3) — коэффициент, который стоит перед x. Так как 3>0, знак неравенства после деления меняться не будет.
x≥−153⇒x≥−5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x∈[−5; +∞)
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6x−1≤2(3x−0,5).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6x−1≤6x−1
6x−6x≤−1+1
0≤0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
- x — любое число
- x∈(−∞;+∞)
- x∈ℝ
№2. Решить неравенство x+3(2−3x)>−4(2x−12).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x+6−9x>−8x+48
−8x+8x>48−6
0>42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x∈∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: ax2+bx+c>0ax2+bx+c≥0ax2+bx+c<0ax2+bx+c≤0 где a, b, c — некоторые числа, причем a≠0,x — переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение ax2+bx+c=0 и найти корни x1 и x2.
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий >,<, точки будут выколотые.
Если знак неравенства нестрогий ≥,≤, точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение ax2+bx+c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x2≥x+12.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
x2≥x+12
x2−x−12≥0
x2−x−12=0
a=1,b=−1,c=−12
D=b2−4ac=(−1)2−4⋅1⋅(−12)=1+48=49
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−1)±492⋅1=1±72=[1+72=82=41−72=−62=−3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x2−x−1=62−6−1=29>0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪.
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x∈(−∞;−3]∪[4;+∞)
№2. Решить неравенство −3x−2≥x2.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
−3x−2≥x2
−x2−3x−2≥0
−x2−3x−2=0
a=−1,b=−3,c=−2
D=b2−4ac=(−3)2−4⋅(−1)⋅(−2)=9−8=1
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−3)±12⋅(−1)=3±1−2=[3+1−2=4−2=−23−1−2=2−2=−1
x1=−2,x2=−1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
−x2−3x−2=−(0)2−3⋅0−2=−2<0
Это значит, что знак на интервале, в котором лежит точка 0 будет −.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥, выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x∈[−2;−1]
№3. Решить неравенство 4<x2+3x.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
4<x2+3x
−x2−3x+4<0
−x2−3x+4=0
a=−1,b=−3,c=4
D=b2−4ac= (−3)2−4⋅(−1)⋅4=9+16=25
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−3)±252⋅(−1)=3±5−2=[3+5−2=8−2=−43−5−2=−2−2=1
x1=−4,x2=1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
−x2−3x+4=−(2)2−3⋅2+4=−6<0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства <, выбираем в ответ интервалы со знаком −.
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x∈(−∞;−4)∪(1;+∞)
№4. Решить неравенство x2−5x<6.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
x2−5x<6
x2−5x−6<0
x2−5x−6=0
a=1,b=−5,c=−6
D=b2−4ac=(−5)2−4⋅1⋅(−6)=25+25=49
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−5)±492⋅1=5±72=[5+72=122=65−72=−22=−1
x1=6,x2=−1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x2−5x−6=102−5⋅10−6=100−50−6= 44>0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства >, выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x∈(−1;6)
№5. Решить неравенство x2<4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x2<4
x2−4<0
x2−4=0
(x−2)(x+2)=0⇔[x−2=0x+2=0 [x=2x=−2
x1=2,x2=−2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x2−4=32−4=9−4=5>0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства <, выбираем в ответ интервал со знаком −.
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x∈(−2;2)
№6. Решить неравенство x2+x≥0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x2+x=0.
x2+x≥0
x2+x=0
x(x+1)=0⇔[x=0x+1=0[x=0x=−1
x1=0,x2=−1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x2+x=12+1=2>0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥, выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x∈(−∞;−1]∪[0;+∞)
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x−1x+3<03(x+8)≤5×2−1x>0x+20x≥x+3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0
- Приравнять числитель дроби к нулю f(x)=0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g(x)=0. Найти нули знаменателя.
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x.
Вне зависимости от знака неравенства
при нанесении на ось xнули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x−1x+3>0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f(x)g(x)>0.
- Приравниваем числитель к нулю f(x)=0.
x−1=0
x=1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g(x)=0.
x+3=0
x=−3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):x−1x+3 = 2−12+3=15>0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства >, выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x∈(−∞;−3)∪(1;+∞)
№2. Решить неравенство 3(x+8)≤5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f(x)g(x)≤0.
3(x+8)≤5
3(x+8)−5\x+8≤0
3x+8−5(x+8)x+8≤0
3−5(x+8)x+8≤0
3−5x−40x+8≤0
−5x−37x+8≤0
- Приравнять числитель к нулю f(x)=0.
−5x−37=0
−5x=37
x=−375=−375=−7,4
x=−7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g(x)=0.
x+8=0
x=−8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f(x)g(x):
−5x−37x+8=−5⋅0−370+8=−378<0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤, выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x∈(−∞;−8)∪[−7,4;+∞)
№3. Решить неравенство x2−1x>0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f(x)g(x)>0.
- Приравнять числитель к нулю f(x)=0.
x2−1=0
(x−1)(x+1)=0⇒[x−1=0x+1=0[x=1x=−1
x1=1,x2=−1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g(x)=0.
x=0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):
x2−1x=22−12=4−12=32>0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства >, выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x∈(−1;0)∪(1;+∞)
Системы неравенств
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{x+4>02x+3≤x2
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств {2x−3≤57−3x≤1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2x−3≤5
2x≤8|÷2, поскольку 2>0, знак неравенства после деления сохраняется.
x≤4;
Графическая интерпретация:
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
7−3x≤1
−3x≤1−7
−3x≤−6|÷(−3), поскольку −3<0, знак неравенства после деления меняется на противоположный.
x≥2
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x∈[2;4]
№2. Решить систему неравенств {2x−1≤51<−3x−2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2x−1≤5
2x≤6|÷2, поскольку 2>0, знак неравенства после деления сохраняется.
x≤3
Графическая интерпретация:
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
1<−3x−2
3x<−1−2
3x<−3|÷3, поскольку 3>0, знак неравенства после деления сохраняется.
x<−1
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x∈(−∞;−1)
№3. Решить систему неравенств {3x+1≤2x−1x−7>5−x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
3x+1≤2x−1
3x−2x≤−1−1
x≤−1
Графическая интерпретация решения:
- Решаем второе неравенство системы
x−7>5−x
x+x>5+7
2x>12| ÷2, поскольку 2>0, знак неравенства после деления сохраняется.
x>6
Графическая интерпретация решения:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x∈∅
№4. Решить систему неравенств {x+4>02x+3≤x2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
x+4>0
x>−4
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
2x+3≤x2
−x2+2x+3≤0
Решаем методом интервалов.
−x2+2x+3=0
a=−1,b=2,c=3
D=b2−4ac=22−4⋅(−1)⋅3=4+12=16
D>0 — два различных действительных корня.
x1,2=−b±D2a=−2±162⋅(−1)=−2±4−2=[−2−4−2=−6−2=3−2+4−2=2−2=−1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪.
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x∈(−4;−1]∪[3;+∞)
Скачать домашнее задание к уроку 8.
epmat.ru
ШВЕЦОВ К.И., БЕВЗ Г.П. 
СОДЕРЖАНИЕ ДАННОЙ СТАТЬИ В данной области обе части неравенства неотрицательны, возводя их в квадрат, получим неравенство (х + 2)(х — 5) x)², или x ² — 3 x — 10 x + x ², откуда Решением первоначального неравенства будет пересечение областей -∞ x ≥ — 2, 5 ≥ x ≥ 8 и . Ответ. . Пример 2. Решить неравенство Решение. Определяем область существования каждого радикала: 9 — х ² ≥ 0, x ² ≤ 9, — 3 ≤ x ≤ + 3; 6 х — х ² ≥ 0, x (6 — х) ≥ 0, 0 ≤ х ≤ 6. Следовательно, область существования обоих радикалов будет 0 ≤ x ≤ 3. Далее решаем неравенство или или 6 x — 2 x ² > 0, x (3 — x) > 0, откуда 1) x > 0 и 3 — x > 0, значит, 0x x x Ответ. 0x 30. Тождественные неравенства 1. Определения. Всякое верное числовое неравенство, а также всякое буквенное неравенство, справедливое при всех допустимых значениях входящих в него букв, называется тождественным неравенством. Примеры тождественных неравенств: 2. Некоторые замечательные неравенства 1) , т.е. модуль суммы любых чисел не больше суммы их модулей. 2) Если a ₁, a ₂,…, a n — числа положительные, то т.е. среднее геометрическое нескольких положительных чисел не больше их среднего арифметического. Равенство имеет место лишь в том случае, когда все числа a ₁, a ₂,…, a n равны. 3) Если a ₁, a ₂,…, a n — числа положительные, то т.е. среднее арифметическое нескольких положительных чисел не больше их среднего квадратического. Равенство имеет место лишь в том случае, когда все числа a ₁, a ₂,…, a n равны. 4) Если a ₁, a ₂,…, a n — числа положительные, то т.е. среднее гармоническое несколько положительных чисел не больше их среднего геометрического. Равенство имеет место лишь в том случае, когда все числа a ₁, a ₂,…, a n равны. 5) какие бы ни были числа a ₁, a ₂,…, a n , b ₁, b ₂,…, b n . Знак равенства здесь имеет место лишь в том случае, когда a ₁: b ₁ — a ₂: b ₂ =… = a n : b n . ⇦ Ctrl предыдущая страница / страница 122 из 168 / следующая страница Ctrl ⇨мобильная версия страницы Смотрите также на этом сайте: ГАДАНИЯ, СОННИКИ, ЗАГОВОРЫ, НУМЕРОЛОГИЯ, ХИРОМАНТИЯ, ВУДУ, МАЯТНИК, ДЕНЕЖНАЯ МАГИЯ ВЯЗАНИЕ НА СПИЦАХ, КРЮЧКОМ, ТУНИССКОЕ ВЯЗАНИЕ, МОДЕЛИ ВЯЗАНОЙ ОДЕЖДЫ; ШИТЬЕ; МАШИННОЕ ВЯЗАНИЕ РАЗНООБРАЗНЫЕ КУЛИНАРНЫЕ РЕЦЕПТЫ; ГОРШОЧКИ, МИКРОВОЛНОВКА; КОНСЕРВИРОВАНИЕ СПРАВОЧНИКИ ПО ФИЗИКЕ, МАТЕМАТИКЕ, АНГЛИЙСКОМУ ЯЗЫКУ; ПОХУДЕНИЕ, АКУПУНКТУРА; НЕИСПРАВНОСТИ АВТОМОБИЛЯ МНОЖЕСТВО ИСТОРИЧЕСКИХ ФАКТОВ О СОБЫТИЯХ, ОРУЖИИ И ОБМУНДИРОВАНИИ ВТОРОЙ МИРОВОЙ ВОЙНЫ; АРМЕЙСКИЕ БОТИНКИ ВСЕХ ВРЕМЕН ПОПУЛЯРНЫЕ ПЕСЕННИКИ 1963-1987 гг.; ТОСТЫ, РОЗЫГРЫШИ, КОНКУРСЫ Пользуйтесь поиском вверху страницы! Все, что будет найдено со значком Ł — относится к данному сайту | 
|
cartalana.org
Двойные неравенства. 2 способа решения
Например:
\(5<11<17\)
\(-2\leq3x+5\leq2\)
\(2x-5\leq3x+7\leq8x\)
Двойное неравенство по своей сути – это система из двух неравенств, записанных в одну строку. Поэтому их всегда можно представить в виде системы.
Например:
\(-2\leq3x+5\leq2\Leftrightarrow\begin{cases}-2\leq3x+5\\3x+5\leq2\end{cases}\)
\(2x-5\leq3x+7\leq8x\Leftrightarrow\begin{cases}2x-5\leq3x+7\\3x+7\leq8x\end{cases}\)
Но делать это нужно не всегда.
2 способа решения двойного неравенства
1) Если в крайней левой и крайней правой частях двойного неравенства нет неизвестных, то удобнее оставить его как есть. При этом в процессе решения стремится равносильными преобразованиями привести неравенство к виду \([число]\)\(<\)\(x\)\(<\)\([число]\).
Пример: Решите двойное неравенство:
|
\(-2\leq3x+5\leq2\) \(|-5\) |
Здесь нет неизвестных по краям, поэтому к системе переходить не будем. Вместо этого делаем такие преобразования, чтоб в центре остался голый икс, а по краям — числа. |
|
|
\(-7≤3x≤-3\) \(|:3\) |
Теперь нам мешает \(3\). Поделим все три части неравенства на \(3\). |
|
|
\(-\)\(\frac{7}{3}\)\(\leq x \leq-1\) |
Готово, наш икс «голый». Можно записывать ответ. |
2) Если в крайних частях двойного неравенства есть неизвестные лучше перевести неравенство в систему и решать его как обычную систему неравенств.
Пример: Решите двойное неравенство:
|
\(2x-5<3x+7≤8x\) |
В крайней левой и крайней правой частях есть неизвестные –значит переходим к системе. |
|
\(\begin{cases}2x-5<3x+7\\3x+7\leq8x\end{cases}\) |
Решаем обычные линейные неравенства: все, что с иксами переносим в левую сторону, все что без иксов — в правую. |
|
\(\begin{cases}2x-3x<7+5\\3x-8x\leq-7\end{cases}\) |
Приводим подобные слагаемые |
|
\(\begin{cases}-x<12 \\-5x\leq-7 \end{cases}\) |
«Оголим» иксы, поделив верхнее неравенство на \((-1)\), нижнее на \((-5)\). Не забываем при этом перевернуть знаки сравнения, так как мы делим на отрицательное число. |
|
\(\begin{cases}x>-12 \\x\geq \frac{7}{5}\end{cases}\) |
Отметим на числовой оси оба решения |
|
Так как у нас система, то мы ищем значения иксов, которые подойдут обоим неравенствам, т.е. интервал, где есть двойная штриховка: и сверху, и снизу. Его и запишем ответ. |
Ответ: \([\)\(\frac{7}{5}\)\(;\infty)\)
Скачать статьюcos-cos.ru
Некоторые моменты о том, как выполняется решение неравенств :: SYL.ru
Одна из тем, которая требует от учеников максимума внимания и усидчивости, это решение неравенств. Такие похожие на уравнения и при этом сильно от них отличающиеся. Потому что к их решению нужен особый подход.
Свойства, которые потребуются для нахождения ответа
Все они применяются для того, чтобы заменить имеющуюся запись равносильной. Большая их часть похожа на то, что было в уравнениях. Но есть и отличия.
- Функцию, которая определена в ОДЗ, или любое число можно прибавить к обеим частям исходного неравенства.
- Аналогичным образом возможно умножение, но только на положительную функцию или число.
- Если это действие выполняется с отрицательными функцией или числом, то знак неравенства нужно заменить на противоположный.
- Функции, которые являются неотрицательными, можно возводить в положительную степень.
Иногда решение неравенств сопровождается действиями, которые дают посторонние ответы. Их нужно исключить, сравнив область ОДЗ и множество решений.
Использование метода интервалов
Его суть состоит в том, чтобы свести неравенство к уравнению, в котором в правой части стоит ноль.
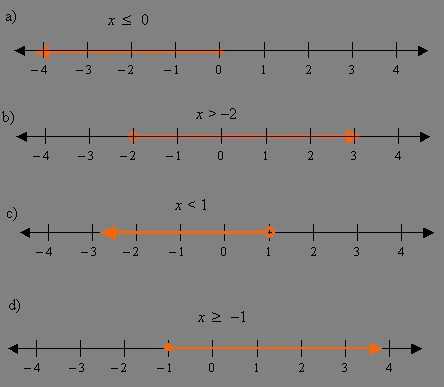
- Определить область, где лежат допустимые значения переменных, то есть ОДЗ.
- Преобразовать неравенство с помощью математических операций так, чтобы в его правой части стоял ноль.
- Знак неравенства заменить на «=» и решить соответствующее уравнение.
- На числовой оси отметить все ответы, которые получились во время решения, а также интервалы ОДЗ. При строгом неравенстве точки нужно нарисовать выколотыми. Если присутствует знак равенства, то их полагается закрасить.
- Определить знак исходной функции на каждом интервале, получившемся из точек ОДЗ и делящих его ответов. Если при переходе через точку знак функции не изменяется, то она входит в ответ. В противном случае — исключается.
- Граничные для ОДЗ точки нужно дополнительно проверить и только потом включать или нет в ответ.
- Ответ, который получается, нужно записать в виде объединенных множеств.
Немного о двойных неравенствах
Они используют в записи сразу два знака неравенства. То есть некоторая функция ограничена условиями сразу дважды. Такие неравенства решаются, как система из двух, когда исходное разбито на части. И в методе интервалов указываются ответы от решения обоих уравнений.
Для их решения также допустимо использовать свойства, указанные выше. С их помощью удобно приводить неравенство к равенству нулю.

Как обстоят дела с неравенствами, в которых имеется модуль?
В этом случае решение неравенств использует следующие свойства, причем они справедливы для положительного значения «а».
Если «х» принимает алгебраическое выражение, то справедливы такие замены:
- |х| < a на -a < х < a;
- |х| > a на х < -a или х > a.
Если неравенства нестрогие, то формулы тоже верны, только в них, кроме знака больше или меньше, появляется «=».
Как осуществляется решение системы неравенств?
Это знание потребуется в тех случаях, когда дано такое задание или имеется запись двойного неравенства или в записи появился модуль. В такой ситуации решением будут такие значения переменных, которые удовлетворяли бы всем имеющимся в записи неравенствам. Если таких чисел нет, то система решений не имеет.
План, по которому выполняется решение системы неравенств:
- решить каждое из них отдельно;
- изобразить на числовой оси все интервалы и определить их пересечения;
- записать ответ системы, который и будет объединением того, что получилось во втором пункте.
Как быть с дробными неравенствами?
Поскольку во время их решения может потребоваться изменение знака неравенства, то нужно очень тщательно и внимательно выполнять все пункты плана. Иначе может получиться противоположный ответ.
Решение дробных неравенств тоже использует метод интервалов. И план действий будет таким:
- Используя описанные свойства, придать дроби такой вид, чтобы справа от знака остался только ноль.
- Заменить неравенство на «=» и определить точки, в которых функция будет равна нулю.
- Отметить их на координатной оси. При этом числа, получившиеся в результате расчетов в знаменателе, всегда будут выколоты. Все другие — исходя из условия неравенства.
- Определить интервалы знакопостоянства.
- В ответ записать объединение тех промежутков, знак которых соответствует тому, который был в исходном неравенстве.
Ситуации, когда в неравенстве появляется иррациональность
Другими словами, в записи присутствует математический корень. Поскольку в школьном курсе алгебры большая часть заданий идет для квадратного корня, то именно он и будет рассмотрен.
Решение иррациональных неравенств сводится к тому, чтобы получить систему из двух или трех, которые будут равносильны исходному.
| Исходное неравенство | условие | равносильная система |
| √ n(х) < m(х) | m(х) меньше или равно 0 | решений нет |
| m(х) больше 0 | n(х) больше или равно 0 n(х) < (m(х))2 | |
| √ n(х) > m(х) | m(х) больше или равно 0 n(х) > (m(х))2 | |
или n(х) больше или равно 0 m(х) меньше 0 | ||
| √n(х) ≤ m(х) | m(х) меньше 0 | решений нет |
| m(х) больше или равно 0 | n(х) больше или равно 0 n(х) ≤ (m(х))2 | |
| √n(х) ≥ m(х) | m(х) больше или равно 0 n(х) ≥ (m(х))2 | |
или n(х) больше или равно 0 m(х) меньше 0 | ||
| √ n(х) < √ m(х) | n(х) больше или равно 0 n(х) меньше m(х) | |
| √n(х) * m(х) < 0 | n(х) больше 0 m(х) меньше 0 | |
| √n(х) * m(х) > 0 | n(х) больше 0 m(х) больше 0 | |
| √n(х) * m(х) ≤ 0 | n(х) больше 0 m(х) ≤0 | |
или n(х) равно 0 m(х) –любое | ||
| √n(х) * m(х) ≥ 0 | n(х) больше 0 m(х) ≥0 | |
или n(х) равно 0 m(х) –любое |
Примеры решения разных видов неравенств
Для того чтобы добавить наглядности в теорию про решение неравенств, ниже приведены примеры.
Первый пример. 2х — 4 > 1 + х
Решение: для того чтобы определить ОДЗ, достаточно просто внимательно посмотреть на неравенство. Оно образовано из линейных функций, поэтому определено при всех значениях переменной.
Теперь из обеих частей неравенства нужно вычесть (1 + х). Получается: 2х — 4 — (1 + х) > 0. После того как будут раскрыты скобки и приведены подобные слагаемые неравенство примет такой вид: х — 5 > 0.
Приравняв его к нулю, легко найти его решение: х = 5.
Теперь эту точку с цифрой 5, нужно отметить на координатном луче. Потом проверить знаки исходной функции. На первом интервале от минус бесконечности до 5 можно взять число 0 и подставить его в неравенство, получившееся после преобразований. После расчетов получается -7 >0. под дугой интервала нужно подписать знак минуса.
На следующем интервале от 5 до бесконечности можно выбрать число 6. Тогда получается, что 1 > 0. Под дугой подписан знак «+». Этот второй интервал и будет ответом неравенства.
Ответ: х лежит в интервале (5; ∞).
Второй пример. Требуется решить систему двух уравнений: 3х + 3 ≤ 2х + 1 и 3х — 2 ≤ 4х + 2.
Решение. ОДЗ этих неравенств тоже лежит в области любых чисел, поскольку даны линейные функции.
Дальше действовать нужно поэтапно. Сначала преобразовать первое из неравенств и приравнять его к нулю. 3х + 3 — 2х — 1 = 0. То есть х + 2 = 0. Таким образом, х равен -2.
Второе неравенство примет вид такого уравнения: 3х — 2 — 4х — 2 = 0. После преобразования: -х — 4 =0. Из него получается значение для переменной, равное -4.
Эти два числа нужно отметить на оси, изобразив интервалы. Поскольку неравенство нестрогое, то все точки нужно закрасить. Первый интервал от минус бесконечности до -4. Пусть будет выбрано число -5. Первое неравенство даст значение -3, а второе 1. Значит, этот промежуток не входит в ответ.
Второй интервал от -4 до -2. Можно выбрать число -3 и подставить его в оба неравенства. В первом и во втором получается значение -1. Значит, под дугой «-».
На последнем интервале от -2 до бесконечности самым лучшим числом является ноль. Его и нужно подставить и найти значения неравенств. В первом из них получается положительное число, а втором ноль. Этот промежуток тоже нужно исключить из ответа.
Из трех интервалов решением неравенства является только один.
Ответ: х принадлежит [-4; -2].
Третий пример. |1 — х| > 2 |х — 1|.
Решение. Первым делом нужно определить точки, в которых функции обращаются в ноль. Для левого этим числом будет 2, для правого — 1. их нужно отметить на луче и определить промежутки знакопостоянства.
На первом интервале, от минус бесконечности до 1, функция из левой части неравенства принимает положительные значения, а из правой — отрицательные. Под дугой нужно записать рядом два знака «+» и «-».
Следующий промежуток от 1 до 2. На нем обе функции принимают положительные значения. Значит, под дугой два плюса.
Третий интервал от 2 до бесконечности даст такой результат: левая функция — отрицательная, правая — положительная.
С учетом получившихся знаков нужно вычислить значения неравенства для всех промежутков.
На первом получается такое неравенство: 2 — х > — 2 (х — 1). Минус перед двойкой во втором неравенстве получился из-за того, что эта функция отрицательная.
После преобразования неравенство выглядит так: х > 0. Оно сразу дает значения переменной. То есть из этого интервала в ответ пойдет только промежуток от 0 до 1.
На втором: 2 — х > 2 (х — 1). Преобразования дадут такое неравенство: -3х + 4 больше ноля. Его нулем будет значение х = 4/3. С учетом знака неравенства получается, что х должен быть меньше этого числа. Значит, этот интервал уменьшается до промежутка от 1 до 4/3.
Последний дает такую запись неравенства: — (2 — х) > 2 (х — 1). Его преобразование приводит к такому: -х > 0. То есть уравнение верно при х меньшем ноля. Это значит, что на искомом промежутке неравенство не дает решений.
На первых двух промежутках граничным оказалось число 1. Его нужно проверить отдельно. То есть подставить в исходное неравенство. Получается: |2 — 1| > 2 |1 — 1|. Подсчет дает что 1 больше 0. Это верное утверждение, поэтому единица входит в ответ.
Ответ: х лежит в промежутке (0; 4/3).
www.syl.ru
ТЕОРИЯ
1. Справочный материал
2. Решение неравенств
Определение и основные свойства неравенств.
Определения:
Неравенствами называют выражения вида a<b (a≤ b) ,a>b (a≥b),
где a и b могут быть числами или функциями.
Символы <(≤), >(≥) называются знаками неравенства и читаются соответственно :
меньше(меньше или равно) ,больше(больше или равно).
Неравенства , которые записываются с помощью знаков > и <,называются строгими,
а неравенства, в записи которых участвуют знаки ≥ и ≤,- нестрогими.
Неравенства вида a<x<b (a≤x≤b) называются двойными неравенствами
и читаются соответственно :x больше a,но меньше b (x больше или равно a,но меньше или равно b ).
Различают два вида неравенств: числовые (2>0,7 ;½<6) и неравенства с переменной (5x-40>0 ; x²-2x<0).
Свойства числовых неравенств :
- Если a>b , то b<a; если a<b, то b>a.
- Если a<b и b<c, то a<c.
- Если a<b и c-любое число, то a +c<b+c.
- Если a<b и c>0,то ac<bc. Если a<b и c<0,то ac>bc.
- Если a<b и c<d,то a +c<b +d.
- Если a<b и c<d,где a, b, c, d-положительные числа, то ac<bd.
Числовые промежутки
Вверх
Основные определения и свойства.
Определения:
Решением неравенства с одной переменной называется значение переменной,
которое обращает его в верное числовое неравенство.
Решить неравенство — значит найти все его решения или доказать, что решений нет.
Неравенства, имеющие одни и те же решения, называются равносильными.
Неравенства, не имеющие решений, также считают равносильными.
При решении неравенств используются следующие свойства:
1) Если из одной части неравенства перенести в
другую слагаемое с противоположным знаком,
то получится равносильное ему неравенство.
2) Если обе части неравенства умножить или
разделить на одно и то же положительное число,
то получится равносильное ему неравенство.
3) Если обе части неравенства умножить или
разделить на одно и то же отрицательное число,
изменив при этом знак неравенства на противоположный,
то получится равносильное ему неравенство.
Многие неравенства в процессе преобразований сводятся к линейным неравенствам.
Неравенства вида ах>b ( ах <b ,ax≤b или ax≥b), где а и b — некоторые числа,
называют линейными неравенствами с одной переменной.
Если a>0 ,то неравенство ax>b равносильно неравенству
и множество решений неравенства есть промежуток
Если a<0 ,то неравенство ax>b равносильно неравенству
и множество решений неравенства есть промежуток
неравенство примет вид 0∙x>b, т.е. оно не имеет решений ,если b≥0,
и верно при любых x ,если b<0.
Аналитический способ решения неравенств с одной переменной.
Алгоритм решения неравенства с одной переменной
- Преобразовать обе части неравенства.
- Привести подобные слагаемые.
- Привести неравенства к простейшему виду, на основании свойств неравенств.
- Записать ответ.
Приведем примеры решения неравенств .
Пример 1. Решить неравенство 3x≤15.
Решение:
Обе части неравенства
разделим на положительное число 3 (свойство 2) : x≤5.
Множество решений неравенства представляет собой числовой промежуток (-∞;5].
Ответ :(-∞;5]
Пример 2. Решить неравенство -10x≥34.
Решение:
Обе части неравенстваразделим на отрицательное число -10 ,
при этом знак неравенства изменим на противоположный (свойство 3) : x≤-3,4.
Множество решений неравенства представляет собой промежуток (-∞;-3,4].
Ответ : (-∞;-3,4].
Пример 3. Решить неравенство 18+6x>0.
Решение:
Перенесем слагаемое 18 с противоположным знаком в левую часть неравенства (свойство 1): 6x>-18.
Разделим обе части на 6 (свойство 2) :
x>-3.
Множество решений неравенства представляет собой промежуток (-3;+∞).
Ответ : (-3;+∞).
Пример 4.Решить неравенство 3(x-2)-4(x+2)<2(x-3)-2.
Решение:
Раскроем скобки : 3x-6-4x-8<2x-6-2.
Перенесем члены ,содержащие неизвестное ,в левую часть ,
а члены не содержащие неизвестное , в правую часть (свойство 1):
3x-4x-2x<6+8-6-2.
Приведем подобные члены: -3x<6.
Разделим обе части на -3 (свойство 3) :
x>-2.
Множество решений неравенства представляет собой промежуток (-2;+∞).
Ответ : (-2;+∞).
Пример 5. Решить неравенство
Решение:
Умножим обе части неравенства на наименьший общий знаменатель дробей,
входящих в неравенство, т. е. на 6 (свойство 2).
Получим:
,2x-3x≤12.
Отсюда , —x≤12 , x≥-12.
Ответ : [-12;+∞).
Пример 6. Решить неравенство 3(2-x)-2>5-3x.
Решение:
Упростим неравенство ,раскрыв скобки:
6-3x-2>5-3x, 4-3x>5-3x, -3x+3x>5-4.
Приведем подобные члены в левой части неравенства и запишем результат в виде 0∙x>1.
Полученное неравенство не имеет решений, так как при любом значении x
оно обращается в числовое неравенство 0 < 1, не являющееся верным.
Значит, не имеет решений и равносильное ему заданное неравенство.
Ответ : решений нет.
Пример 7.Решить неравенство 2(x+1)+5>3-(1-2x).
Решение:
Упростим неравенство ,раскрыв скобки:
2x+2+5>3-1+2x, 2x+7>2+2x,2x-2x>2-7, 0∙x>-5.
Полученное неравенство является верным при любом значении x,
так как левая часть при любом x равна нулю, а 0>-5.
Множеством решения неравенства является промежуток (-∞;+∞).
Ответ : (-∞;+∞).
Пример 8. При каких значениях x имеет смысл выражение:
a)
b)
Решение:
а)По определению арифметического квадратного корня
должно выполнятся следующее неравенство 5x-3≥0.
Решая, получаем 5x≥3, x≥0,6.
Итак, данное выражение имеет смысл при всех x из промежутка [0,6;+∞).
Ответ : [0,6;+∞).
б)С учетом свойств арифметического квадратного корня и знаменателя дроби
должно выполнятся следующее неравенство 2-3x>0.
Отсюда ,-3x>-2 (свойство 3), x<2/3.
Данное выражение имеет смысл при всех x из промежутка (-∞;2/3).
Ответ :(-∞;2/3).
Пример 9.При каких значениях a квадратное уравнение x-8x2-4a=0 имеет два корня ?
Решение:
Квадратное уравнение будет иметь два корня ,если дискриминант D будет больше нуля.
D=(-8)2-4∙(-4a)=64+16a,
64+16a>0,
16a>-64,
a>-4.
Таким образом , при всех значениях a из промежутка (-∞;-4)
данное квадратное уравнение будет иметь два корня.
Ответ : при всех a из промежутка (-∞;-4) .
Пример 10.Решите задачу:
В одном бассейне налито 100 л воды, а во втором 150 л воды.
Каждый час в первый бассейн вливается 15 л воды, а во второй — 5 л воды.
В какие моменты времени в первом бассейне будет больше воды, чем во втором?
Решение:
Пусть за x ч в первый бассейн вольется 15x л воды и в нем станет 100+15x л воды.
Тогда через x ч во втором бассейне будет 150+5x л воды.
Надо найти такие значения x , для которых выполняется неравенство
100+15x>150+5x.
Преобразовав ,получаем
15x-5x>150-100,
10x>50,
x>5.
Итак ,в первом бассейне окажется больше воды ,чем во втором, при x>5,
т.е. после 5ч с начала вливания воды.
Ответ : после 5ч с начала вливания воды.
Пример 11. При каких значениях x значения функции Y=-1/3x+8 принадлежит промежутку (-1,1)?
Решение: -1<-1/3x+8<1,
-9<-1/3x<7,
27>x>21,
21<x<27.
Ответ : (21;27).
Вопросы.
1. Что называется неравенством первой степени с одним неизвестным?
2. Что называется решением неравенства с одним неизвестным?
3. Что значит решить неравенство с одним неизвестным?
4. Каким способом можно решить неравенство первой степени с одним неизвестным?
.Графический способ решения неравенств с одной переменной.
Покажем, как можно, применяя графический метод, решить неравенства вида
kx+ b> 0 (1)
или
kx + b<0, (2)
где k и b — заданные числа и k≠0.
В декартовой системе координат Оху рассмотрим прямую
y = kx + b. (3)
На рис. 1 изображена такая прямая при k> 0, а на рис. 2 изображена такая прямая при k<0.
рис1. рис.2.
Решить неравенство (1) — это значит найти все решения х,
для которых прямая y = kx-b расположена выше оси х.
Здесь важную роль играет точка А пересечения прямой (3) с осью х.
Абсциссу точки А обозначим через xo. Так как ее ордината равна нулю, то xo удовлетворяет уравнению
O = kxo + b, откуда
xo=-b/k.
Обратимся к рис. 1, соответствующему случаю k> 0. Мы видим , что прямая y = kx+bрасположена выше оси х для всех х, находящихся правее точки xo, т. е. для всех х из интервала (-∞, + ∞), и расположена ниже оси х для всех х, находящихся левее точки xo, т. е. для всех х из интервала (—∞,xo).
Итак, при k> 0 неравенство (1) выполняется на интервале (xo, + ∞), а неравенство (2) —на интервале (—∞,xo).
При k<0, как это видно из рис. 2, неравенство (1) выполняется на интервале (—∞,xo),
а неравенство (2) — на интервале (xo, + ∞).
Пример 1. Решить, применяя графический метод, неравенства
2X+1 >0, (4)
2X+1 <0. (5)
Решение :
Начертим в декартовой системе координат Оху прямую
у = 2X+1. (6)
рис3.
Для этого нужно знать две ее точки. В качестве первой точки возьмем точку пересечения прямой с осью х. Она все равно будет нужна. Полагая в формуле (6) у = 0, получим уравнение
0 = 2х+1.
Его решение есть абсцисса точки А пересечения прямой с осью х. Итак, А ( —1/2 ,0).
В качестве второй точки можно взять точку В пересечения прямой с осью у. Ее абсцисса X=0, а ордината
y=2∙0+1, y=1.
Итак, В(0, 1).
Через точки А и В проводим прямую. Это и есть прямая y=2X+1 (рис. 3).
Из рис. 3 видно, что неравенство (4) выполняется на интервале ( — 1/2 , + ∞) а (5) — на интервале (— ∞, —1/2).
Вопрос.
Как можно решать неравенства первой степени, применяя графический метод?
kalach-gimnazia.narod.ru
❶ Что такое неравенства ? как решить графически неравенство ? Математика
Понятием «неравенство» пользовались еще в Древней Греции. Так, в III в. до н.э. Архимед, вычисляя длину окружности, установил, что периметр круга равен «утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых». Другими словами, он установил границы для числа π: 3 10/71b означает, что число a больше числа b. Если записано aэто значит, что a меньше b. Для нестрогих неравенств: a≥b означает, что число a больше или равно числу b, a≤b – число a меньше или равно числу b. В нестрогих неравенствах числа могут совпадать.Простейшие неравенства могут быть линейными, содержащими модули, рациональными, иррациональными. Более сложные неравенства – показательные, логарифмические, тригонометрические, смешанные. Особый вид задач – неравенства с параметрами.Графически решение неравенства изображается полупространством, которое может быть ограниченным и неограниченным. Чтобы найти решение, полезно знак неравенства заменять знаком равенства, решать полученное уравнение и строить график.Чтобы решить иррациональное неравенство, надо перенести все дроби в левую часть, привести к общему знаменателю, разложить числитель и знаменатель на множители, применить метод интервалов.Для решения показательных уравнений необходимо использовать свойства степеней, логарифмических – свойства логарифмов. В конечном счете, все сложные неравенства решаются сведением их к простейшим. При решении все переходы должны быть равносильными.Решение всех неравенств начинайте с нахождения ОДЗ, области допустимых значений. Следите за равносильностью преобразований. То есть, каждый ваш шаг не должен сужать или расширять ОДЗ.Приступая к решению логарифмических неравенств, выучите определение логарифма, свойства логарифмов, формулы преобразования. Набейте руку в решении логарифмических уравнений. Учитывайте, что свойства логарифмов различаются в зависимости от основания: когда оно больше единицы, и когда от нуля до одного.www.kakprosto.ru

Leave A Comment