Как найти объем шестиугольной пирамиды – Объем шестиугольной пирамиды - формулы, примеры расчетов

Объем шестиугольной пирамиды — формулы, примеры расчетов

Шестиугольной пирамидой называется многогранник, в основании которого лежит правильный шестиугольник, а боковые грани образуются одинаковыми равнобедренными треугольниками.

Такие пирамиды обладают множеством уникальных свойств:

Все стороны основания одинаковой длины;
Все боковые ребра равны между собой;
Все углы в основании равны, а также двугранные углы, образующиеся ребрами равны;
Каждая боковая грань одинаковой площади.

Площадь шестиугольной пирамиды рассчитывается из площади ее основания и боковой развертки. Для расчета объема достаточно знать высоту пирамиды и площадь ее основания. Для начала разберемся с формулой площади правильного шестиугольника.
Одним из самых весомых отличий правильного шестиугольника от остальных фигур является равенство его стороны радиусу описанной окружности. Благодаря этому свойству площадь основания правильной шестиугольной пирамиды рассчитывается по формуле:

Для расчета можно использовать как радиус описанной окружности, так и длину стороны правильного шестиугольника.
Теперь вернемся к формуле объема шестиугольной пирамиды. Она представляет собой одну треть произведения площади основания на высоту пирамиды, опущенную к этому основанию:

Теперь рассмотрим пример расчета объема шестиугольной пирамиды.

Пусть дана правильная шестиугольная пирамида, высота которой равна h = 8 см. вокруг основания описана окружность с радиусом R = 6 см. Найдите объем.
В вычислении требуемого параметра не будет ничего сложного – ведь все необходимые величины заданы условиями. Поэтому найдем площадь основания нашего многогранника. Помним, что радиус описанной вокруг правильного шестиугольника окружности равен его сторонам. Подставим данные в формулу:

Теперь можем использовать найденную площадь для расчета объема нашей шестиугольной пирамиды:

Вот таким образом, зная свойства правильного шестиугольника и формулу объема для шестиугольной пирамиды, мы нашли все необходимые параметры.

2mb.ru

Правильная шестиугольная пирамида | Банк ЕГЭ

Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник.

Обозначения

$SABCDEF$ — правильная шестиугольная пирамида
$O$ — центр основания пирамиды
$a$ — длина стороны основания пирамиды
$h$ — длина бокового ребра пирамиды
$S_{\text{осн.}}$ — площадь основания пирамиды
$V_{\text{пирамиды}}$ — объем пирамиды

Площадь основания пирамиды

В основаниях пирамиды находится правильный шестиугольник со стороной $a$. По свойствам правильного шестиугольника, площадь основания пирамиды равна $$ S_{\text{осн.}}=\frac{3\sqrt{3}}{2}\cdot a^2 $$

Правильный шестиугольник в основании пирамиды

По свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF, FOA являются правильными треугольниками. Отсюда следует, что $$ AO=OD=EO=OB=CO=OF=a $$ Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём $AO=OE=a,\ \angle EOA=120^{\circ}$. По свойствам равнобедренного треугольника $$ AE=a\cdot\sqrt{2(1-\cos EOA)}=\sqrt{3}\cdot a $$ Аналогичным образом приходим к заключению, что $ AC=CE=\sqrt{3}\cdot a $, $FM=MO=\frac{1}{2}\cdot a$.

Находим $SO$

Прямая $SO$ является высотой пирамиды, поэтому $\angle SOF=90^{\circ}$. Треугольник $SOF$ прямоугольный, в нем $FO=a,\ FS=h$. По свойствам прямоугольного треугольника $$ SO=\sqrt{FS^2-FO^2}=\sqrt{h^2-a^2} $$

Объем пирамиды

Объем пирамиды вычисляется как треть произведения площади ее основания на ее высоту. Высотой правильной пирамиды является отрезок $SO$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{\text{пирамиды}}=\frac{1}{3}\cdot S_{\text{осн.}}\cdot SO=\frac{\sqrt{3}}{2}\cdot a^2 \cdot \sqrt{h^2-a^2} $$

Находим $ST$ и $TO$

Пусть точка $T$ является серединой ребра $AF$. Треугольник $AOF$ правильный, поэтому, по свойствам правильного треугольника $$ TO=\frac{\sqrt{3}}{2}\cdot a $$ Треугольник $STO$ прямоугольный, высота $SO$ равна $\sqrt{h^2-a^2}$. По теореме Пифагора $$ ST=\sqrt{SO^2+TO^2}=\sqrt{h^2-\frac{1}{4}\cdot a^2} $$

bankege.ru

Формула объема шестиугольной пирамиды: пример решения задачи

Вычисление объемов пространственных фигур является одной из важных задач стереометрии. В данной статье рассмотрим вопрос определения объема такого полиэдра, как пирамида, а также приведем формулу объема пирамиды шестиугольной правильной.

Пирамида шестиугольная

Для начала рассмотрим, что собой представляет фигура, о которой пойдет речь в статье.

Пусть у нас имеется произвольный шестиугольник, стороны которого не обязательно равны друг другу. Также предположим, что мы выбрали в пространстве точку, не находящуюся в плоскости шестиугольника. Соединив все углы последнего с выбранной точкой, мы получим пирамиду. Две разные пирамиды, имеющие шестиугольное основание, показаны на рисунке ниже.

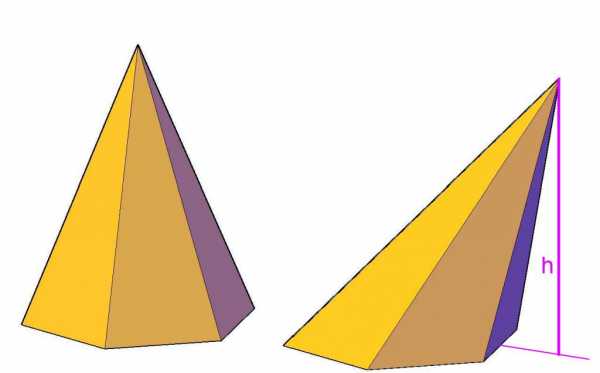
Видно, что помимо шестиугольника фигура состоит из шести треугольников, точка соединения которых называется вершиной. Различие между изображенными пирамидами заключается в том, что высота h правой из них не пересекает шестиугольное основание в его геометрическом центре, а высота левой фигуры попадает точно в этот центр. Благодаря этому критерию левая пирамида получила название прямой, а правая — наклонной.

Поскольку основание левой фигуры на рисунке образовано шестиугольником с равными сторонами и углами, то она называется правильной. Дальше в статье речь пойдет только об этой пирамиде.

Объем шестиугольной пирамиды

Для вычисления объема произвольной пирамиды справедлива следующая формула:

V = 1/3 * h * S_o

Здесь h — это длина высоты фигуры, S_o — площадь ее основания. Воспользуемся этим выражением для определения объема пирамиды шестиугольной правильной.

Поскольку в основании рассматриваемой фигуры лежит равносторонний шестиугольник, то для вычисления его площади можно воспользоваться следующим общим выражением для n-угольника:

S_n = n/4 * a²* ctg(pi/n)

Здесь n — целое число, равное количеству сторон (углов) многоугольника, a — длина его стороны, функцию котангенса высчитывают, используя соответствующие таблицы.

Применяя выражение для n = 6, получим:

S₆ = 6/4 * a²* ctg(pi/6) = √3/2 * a²

Теперь остается подставить это выражение в общую формулу для объема V:

V₆ = S_{6 *}h = √3/2 * h * a²

Таким образом, для вычисления объема рассматриваемой пирамиды необходимо знать два ее линейных параметра: длину стороны основания и высоту фигуры.

Пример решения задачи

Покажем, как можно использовать полученное выражение для V₆ для решения следующей задачи.

Известно, что правильной шестиугольной пирамиды объем равен 100 см³. Необходимо определить сторону основания и высоту фигуры, если известно, что они связаны друг с другом следующим равенством:

a = 2*h

Поскольку в формулу для объема входят только a и h, то можно подставить в нее любой из этих параметров, выраженный через другой. Например, подставим a, получаем:

V₆ = √3/2*h*(2*h)² =>
h = ∛(V₆/(2*√3))

Для нахождения значения высоты фигуры необходимо взять корень третей степени из объема, что соответствует размерности длины. Подставляем значение объема V₆

пирамиды из условия задачи, получаем высоту:

h = ∛(100/(2*√3)) ≈ 3,0676 см

Поскольку сторона основания в соответствии с условием задачи в два раза больше найденной величины, то получаем значение для нее:

a = 2*h = 2*3,0676 = 6,1352 см

Объем шестиугольной пирамиды можно найти не только через высоту фигуры и значение стороны ее основания. Достаточно знать два разных линейных параметра пирамиды для его вычисления, например апотему и длину бокового ребра.

fb.ru

Правильная шестиугольная пирамида. Формулы объема и площади поверхности. Решение геометрической задачи

Стереометрия, как раздел геометрии в пространстве, изучает свойства призм, цилиндров, конусов, шаров, пирамид и других объемных фигур. Данная статья посвящена подробному рассмотрению характеристик и свойств шестиугольной правильной пирамиды.

Какая пирамида будет изучаться

Правильная шестиугольная пирамида представляет собой фигуру в пространстве, которая ограничена одним равносторонним и равноугольным шестиугольником, и шестью одинаковыми треугольниками равнобедренными. Эти треугольники могут быть также равносторонними при определенных условиях. Эта пирамида ниже показана.

Здесь изображена одна и та же фигура, только в одном случае она повернута боковой гранью к читателю, а в другом — боковым ребром.

Правильная шестиугольная пирамида имеет 7 граней, которые были названы выше. Также ей принадлежат 7 вершин и 12 ребер. В отличие от призм, у всех пирамид имеется одна особая вершина, которая образована пересечением боковых треугольников. Для правильной пирамиды она играет важную роль, поскольку опущенный с нее на основание фигуры перпендикуляр является высотой. Далее высоту будем обозначать буквой h.

Показанная пирамида называется правильной по двум причинам:

в ее основании находится шестиугольник с равными длинами сторон a и с одинаковыми углами по 120^o;
высота пирамиды h пересекает шестиугольник точно в его центре (точка пересечения лежит на одинаковом расстоянии от всех сторон и от всех вершин шестиугольника).

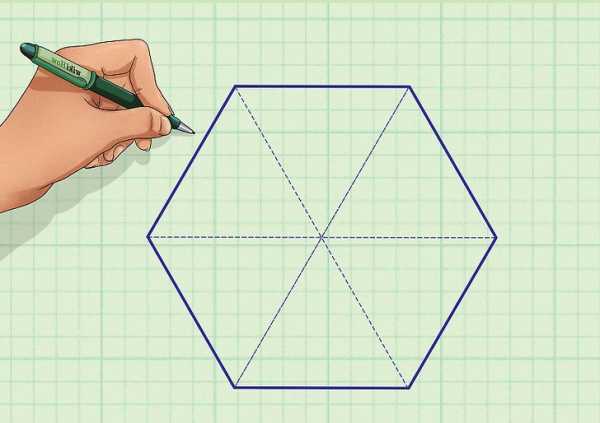
Площадь поверхности

Свойства правильной пирамиды шестиугольной начнем рассматривать с определения ее площади. Для этого сначала полезно привести развертку фигуры на плоскости. Схематическое ее изображение показано ниже.

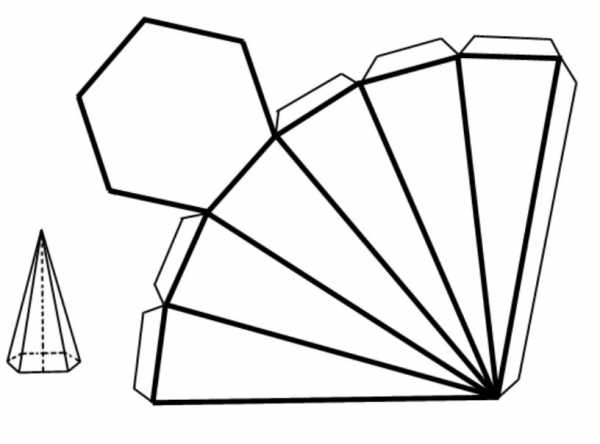
Видно, что площадь развертки, а значит, и всей поверхности рассматриваемой фигуры, равна сумме площадей шести одинаковых треугольников и одного шестиугольника.

Для определения площади шестиугольника S₆ воспользуемся универсальной формулой для правильного n-угольника:

S_n = n/4*a²*ctg(pi/n) =>
S₆ = 3*√3/2*a².

Где буквой a обозначена длина стороны шестиугольника.

Площадь треугольника S₃ боковой стороны найти можно, если знать величину его высоты h_b:

S₃ = 1/2*h_b*a.

Поскольку все шесть треугольников равны между собой, то получаем рабочее выражение для определения площади шестиугольной пирамиды с правильным основанием:

S = S₆ + 6*S₃ = 3*√3/2*a² + 6*1/2*h_b*a = 3*a*(√3/2*a + h_b).

Объем пирамиды

Так же, как и площадь, объем шестиугольной правильной пирамиды является важным ее свойством. Этот объем рассчитывается по общей формуле для всех пирамид и конусов. Запишем ее:

V = 1/3*S_o*h.

Здесь символом S_o названа площадь шестиугольного основания, то есть S_o = S₆.

Подставляя в формулу для V записанное выше выражение для S₆, приходим к конечному равенству для определения объема пирамиды шестиугольной правильной:

V = √3/2*a² *h.

Пример геометрической задачи

В шестиугольной пирамиде правильной боковое ребро в два раза больше длины стороны основания. Зная, что последнее равно 7 см, необходимо вычислить площадь поверхности и объем данной фигуры.

Как можно догадаться, решение этой задачи предполагает использование полученных выше выражений для S и V. Тем не менее сразу ими воспользоваться не получится, поскольку мы не знаем апофему и высоту правильной пирамиды шестиугольной. Займемся их вычислением.

Апофему h_bможно определить, рассмотрев треугольник прямоугольный, построенный на сторонах b, a/2 и h_b. Здесь b — длина бокового ребра. Используя условие задачи, получаем:

h_b = √(b²-a²/4) = √(14²-7²/4) = 13,555 см.

Высоту h пирамиды определить можно точно так же, как апофему, только рассматривать теперь следует треугольник со сторонами h, b и a, находящийся внутри пирамиды. Высота будет равна:

h = √(b² — a²) = √(14² — 7²) = 12,124 см.

Видно, что рассчитанное значение высоты меньше такового для апофемы, что справедливо для любой пирамиды.

Теперь можно воспользоваться выражениями для объема и площади:

S = 3*a*(√3/2*a + h_b) = 3*7*(√3/2*7 + 13,555) = 411,96 см²;
V = √3/2*a

2*h = √3/2*7²*12,124 = 514,48 см³.

Таким образом, для однозначного определения любой характеристики правильной шестиугольной пирамиды необходимо знать два любых ее линейных параметра.

fb.ru

Площадь шестиугольной пирамиды — формула, пример расчета

Пирамида, в основании которой лежит правильный шестиугольник, а боковые стороны образуются правильными треугольниками, называется шестиугольной.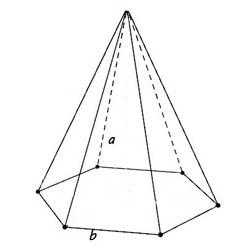

Этот многогранник отличается множеством свойств:

Все стороны и углы основания равны между собой;
Все ребра и двугранные угля пирамиды также равны между собой;
Треугольники, образующие боковые стороны одинаковы, соответственно, у них одинаковые площади, стороны и высоты.

Для расчета площади правильной шестиугольной пирамиды применяется стандартная формула площади боковой поверхности шестиугольной пирамиды:

где P – периметр основания, a – длина апофемы пирамиды. В большинстве случаев можно рассчитать боковую площадь по этой формуле, однако иногда можно воспользоваться и другим методом. Так как боковые грани пирамиды образованы равными треугольниками, можно найти площадь одного треугольника, а потом умножить его на количество боковых сторон. В шестиугольной пирамиде их 6. Но этот способ можно применять и при расчете площади треугольной пирамиды.Рассмотрим пример расчета площади боковой поверхности шестиугольной пирамиды.

Пусть дана правильная шестиугольная пирамида, в которой апофема равна a = 7 см, сторона основания b = 3 см. Рассчитайте площадь боковой поверхности многогранника.
Для начала найдем периметр основания. Так как пирамида правильная – в ее основании лежит правильный шестиугольник. Значит, все его стороны равны, а периметр рассчитывается по формуле:
Подставляем данные в формулу:
Теперь можем легко найти площадь боковой поверхности, подставив найденное значение в основную формулу:

Также немаловажным моментом является поиск площади основания. Формула площади основания шестиугольной пирамиды выводится из свойств правильного шестиугольника:

Рассмотрим пример расчета площади основания шестиугольной пирамиды, взяв за основу условия из прошлого примера.Из них мы знаем, что сторона основания b = 3 см. Подставим данные в формулу:

Формула площади шестиугольной пирамиды представляет собой сумму площади основания и боковой развертки:

Рассмотрим пример расчета площади шестиугольной пирамиды.

2mb.ru

Формула объема шестиугольной правильной пирамиды

В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна ? | Печать |. Подробности: Категория: Задачи по планиметрии. В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна 14v6. Найдите sin

Объем шестиугольной пирамиды

Такие пирамиды обладают множеством уникальных свойств:

Все стороны основания одинаковой длины; Все боковые ребра равны между собой; Все углы в основании равны, а также двугранные углы, образующиеся ребрами равны; Каждая боковая грань одинаковой площади.

Одним из самых весомых отличий правильного шестиугольника от остальных фигур является равенство его стороны радиусу описанной окружности. Благодаря этому свойству площадь основания правильной шестиугольной пирамиды рассчитывается по формуле:

Для расчета можно использовать как радиус описанной окружности, так и длину стороны правильного шестиугольника.

Теперь вернемся к формуле объема шестиугольной пирамиды. Она представляет собой одну треть произведения площади основания на высоту пирамиды, опущенную к этому основанию:

Теперь рассмотрим пример расчета объема шестиугольной пирамиды.

В вычислении требуемого параметра не будет ничего сложного – ведь все необходимые величины заданы условиями. Поэтому найдем площадь основания нашего многогранника. Помним, что радиус описанной вокруг правильного шестиугольника окружности равен его сторонам. Подставим данные в формулу:

Теперь можем использовать найденную площадь для расчета объема нашей шестиугольной пирамиды:

Формула объема шестиугольной правильной пирамиды

Объем шестиугольной пирамиды

Такие пирамиды обладают множеством уникальных свойств:

Теперь рассмотрим пример расчета объема шестиугольной пирамиды.

Теперь можем использовать найденную площадь для расчета объема нашей шестиугольной пирамиды:

Формула объема шестиугольной правильной пирамиды

Объем правильной шестиугольной пирамиды, формула

Правильная шестиугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный шестиугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр правильного шестиугольника — основания из вершины.

Объем правильной шестиугольной пирамиды равен одной трети произведения площади правильного шестиугольника, являющегося основанием S (ABCDEF) на высоту H (OS)

H — высота правильной шестиугольной пирамиды

poiskvstavropole.ru

Объем правильной шестиугольной пирамиды

Задачи с пирамидами. В данной статье продолжим рассматривать задачи с пирамидами. Их нельзя отнести к какому-то классу или типу заданий и дать общие (алгоритмы) рекомендации для решения. Просто здесь собраны оставшиеся задачи, не рассмотренные ранее.

Перечислю теорию, которую необходимо освежить в памяти перед решением: формула объёма пирамиды, свойства подобия фигур и тел, свойства правильных пирамид, теорема Пифагора, формула площади треугольника (в этой статье она вторая). Рассмотрим задачи:

От треугольной пирамиды, объем которой равен 80, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Объём пирамиды равен одной трети произведения площади её основания и высоты:

Данные пирамиды (исходная и отсечённая) имеют общую высоту, поэтому их объемы соотносятся как площади их оснований. Средняя линия от исходного треугольника отсекает треугольник площадь которого в четыре раза меньше, то есть:

Подробнее об этом можно посмотреть здесь.

Это означает, что объём отсечённой пирамиды будет в четыре раза меньше.

Таким образом, он будет равен 20.

Ответ: 20

*Посмотрите решение аналогичной задачи, использована формула площади треугольника.

Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.

Постоим пирамиду, обозначим вершины. Отметим на ребре AS точку Е, так чтобы AE была в два раза больше ES (в условии сказано, что ES относится к AE как 1 к 2), и построим указанную плоскость проходящую, через ребро АС и точку Е:

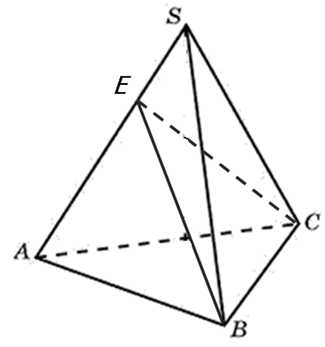
Проанализируем объём какой пирамиды будет больше: EABC или SEBC?

*Объём пирамиды равен одной трети произведения площади её основания и высоты:

Если рассмотреть две полученные пирамиды и в обеих принять за основание грань ЕВС, то становится очевидно, то объём пирамиды АЕВС будет больше объёма пирамиды SEBC. Почему?

Расстояние от точки А до плоскости ЕВС больше чем расстояние от точки S. А это расстояние играет у нас роль высоты.

Итак, найдём объём пирамиды ЕАВС.

Объём исходной пирамиды нам дан, основание у пирамид SАВС и ЕАВС общее. Если мы установим соотношение высот, то без труда сможем определить объём.

Из отношения отрезков ES и AE следует, что АЕ равно две третьих ES. Высоты пирамид SАВС и ЕАВС находятся в такой же зависимости — высота пирамиды ЕАВС будет равна 2/3 высоты пирамиды SАВС.

Таким образом, если

То

Ответ: 10

Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.

В правильной пирамиде вершина проецируется в центр основания. Выполним дополнительные построения:

Найти боковое ребро мы можем из прямоугольного треугольника SOC. Для этого нужно знать SO и ОС.

SO это высота пирамиды, её мы можем вычислить используя формулу объёма:

Вычислим площадь основания. это правильный шестиугольник со стороной равной 1. Площадь правильного шестиугольника равна площади шести равносторонних треугольников с такой же стороной, подробнее об этом изложено здесь (п.6), итак:

Значит

ОС = ВС = 1, так как в правильном шестиугольнике отрезок соединяющий его центр с вершиной равен стороне этого шестиугольника.

Таким образом, по теореме Пифагора:

Ответ: 7

Объем тетраэдра равен 200. Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра.

Объем указанного многогранника равен разности объемов исходного тетраэдра V₀ и четырех равных тетраэдров, каждый из которых получается отсечением плоскостью, проходящей через середины рёбер, имеющих общую вершину:

Определим, чему равен объём отсеченного тетраэдра.

Отметим, что исходный тетраэдр и «отсечённый» тетраэдр являются подобными телами. Известно, что отношение объёмов подобных тел равно k³, где k — коэффициент подобия. В данном случае он равен 2 (так как все линейные размеры исходного тетраэдра в два раза больше соответствующих размеров отсечённого):

Вычислим объём отсечённого тетраэдра:

Таким образом, искомый объём будет равен:

Ответ: 100

Площадь поверхности тетраэдра равна 120. Найдите площадь поверхности многогранника, вершинами которого являются середины ребер данного тетраэдра.

Первый способ:

Искомая поверхность состоит из 8 равносторонних треугольников со стороной, вдвое меньшей ребра исходного тетраэдра. Поверхность исходного тетраэдра состоит из 16-ти таких треугольников (на каждой из 4 граней тетраэдра по 4 треугольника), поэтому искомая площадь равна половине площади поверхности данного тетраэдра и равна 60.

Второй способ:

Так как известна площадь поверхности тетраэдра, то мы можем найти его ребро, затем определить длину ребра многогранника и далее вычислить площадь его поверхности.

Площадь поверхности тетраэдра состоит из четырёх равных по площади правильных треугольников. Пусть сторона такого треугольника (ребро тетраэдра) равна а, тогда можем записать:

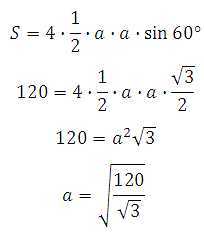
Ребра многогранника равны его половине ребра тетраэдра, то есть:

*Они проходят через середины рёбер тетраэдра.

Многогранник имеет восемь равных граней являющихся правильными треугольниками, значит его площадь поверхности будет равна:

*Данное решение алгебраическое и рациональным его назвать никак нельзя, представлено как альтернативный вариант.

Ответ: 60

27115. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Посмотреть решение

27175. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

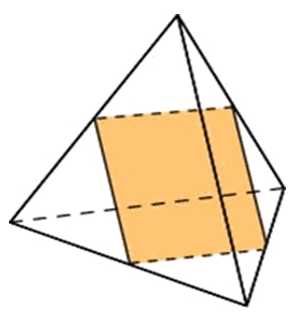
Посмотреть решение

27214. Объем тетраэдра равен 1,9. Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра.

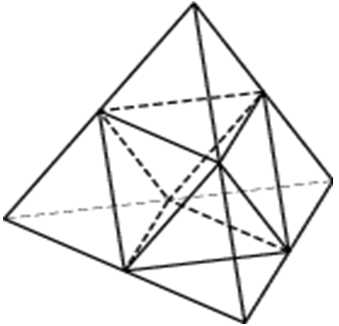
Посмотреть решение

На этом всё. Успеха Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Объем шестиугольной пирамиды — формулы, примеры расчетов