Куда направлена скорость тела движущегося по окружности: Ошибка 403

Движение тела по окружности | Частная школа. 9 класс

Конспект по физике для 9 класса «Движение тела по окружности». Куда направлена мгновенная скорость тела при его движении по окружности. Куда направлено ускорение тела при его движении по окружности и как вычислить его значение.

Конспекты по физике Учебник физики Тесты по физике

Одним из простейших видов криволинейного движения является движение тела по окружности. Рассмотрим такое движение при постоянной по модулю скорости.

Согласно второму закону Ньютона направление ускорения совпадает с направлением равнодействующей всех сил, действующих на тело. Сообщим шарику, лежащему на столе и закреплённому на нити, начальную скорость в направлении, перпендикулярном нити. Он начнёт двигаться по окружности. Сила тяжести, действующая на него, уравновешивается силой упругости стола, а сила трения качения мала, и ею можно пренебречь. Получается, что сила, обусловливающая движение шарика по окружности, — сила упругости нити, направленная по радиусу окружности.

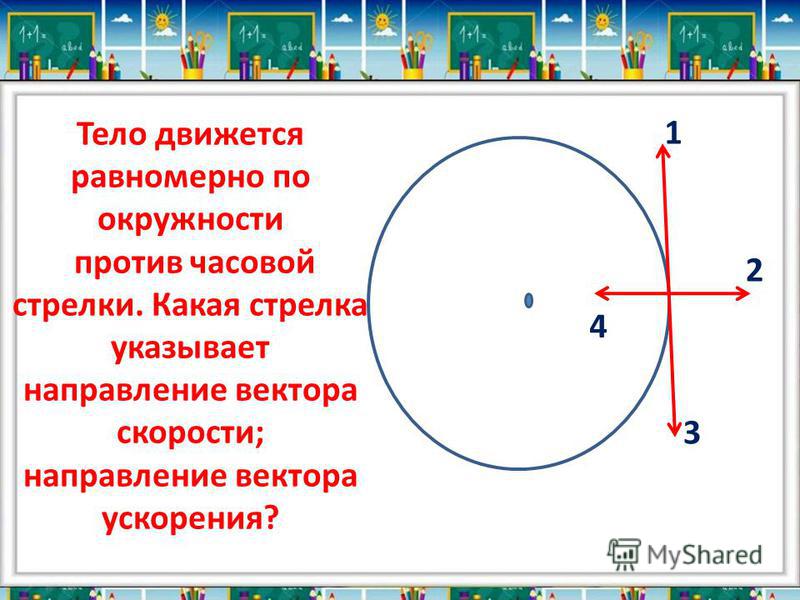
Поэтому ускорение должно быть направлено так же, т. е.по радиусу окружности в направлении к центру.

НАПРАВЛЕНИЕ ВЕКТОРА МГНОВЕННОЙ СКОРОСТИ

При движении тела по окружности при неизменном модуле скорости в каждый момент времени скорость меняет своё направление. Как направлен вектор мгновенной скорости?

Для ответа на этот вопрос представим себе движение некоторого тела, закреплённого на верёвке и раскрученного в горизонтальной плоскости.

Если верёвка оборвётся, то тело начнёт двигаться по прямой. Эта прямая — касательная к окружности, являющейся траекторией движения тела. При этом направление движения тела совпадает с направлением скорости тела в момент разрыва верёвки.

Таким образом, мгновенная скорость тела в любой точке траектории направлена по касательной к траектории в этой точке.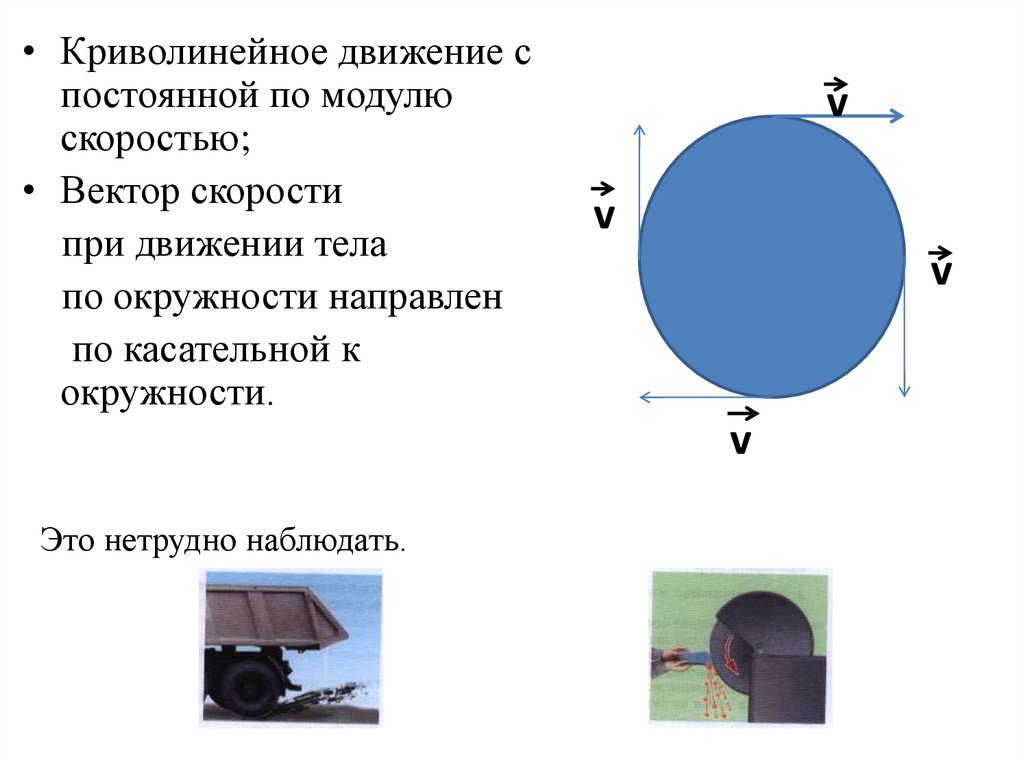

НАПРАВЛЕНИЕ ВЕКТОРА УСКОРЕНИЯ ТЕЛА, ДВИЖУЩЕГОСЯ ПО ОКРУЖНОСТИ

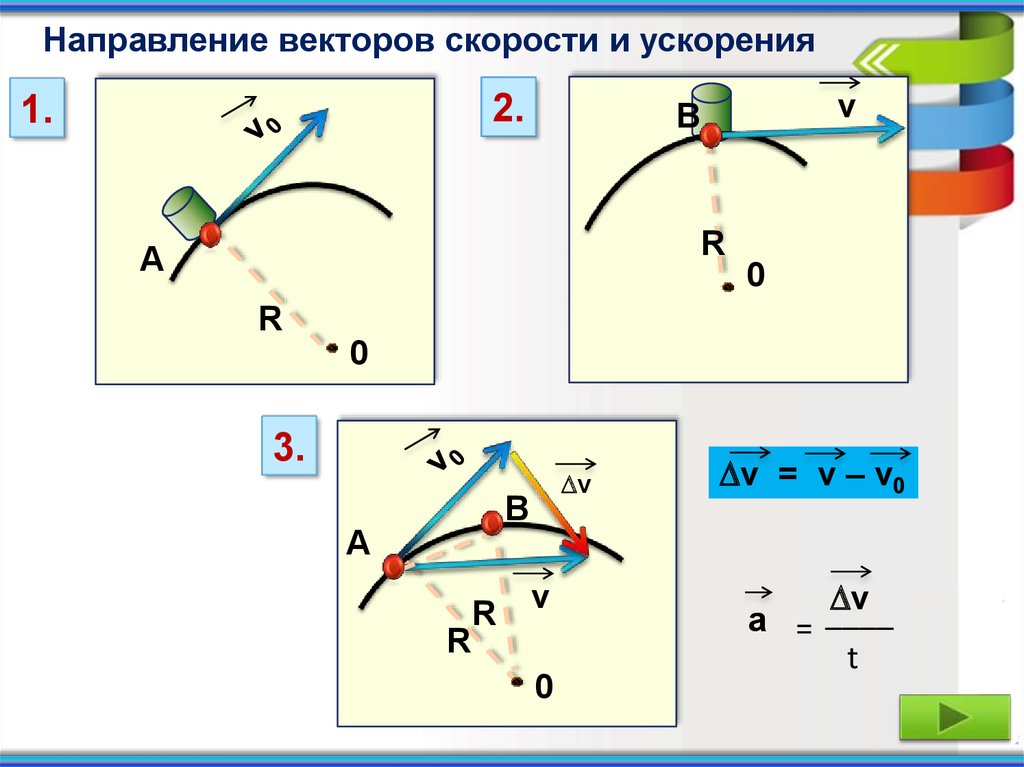
При движении по окружности с постоянной по модулю скоростью в каждый момент времени направление скорости изменяется. Значит, такое движение является движением с ускорением. Рассмотрим движение тела по окружности радиуса R. Обозначим скорость тела в точке А через ʋ₁, а его скорость в точке В через ʋ₂. Тогда ускорение, с которым тело движется, можно найти по формуле

В числителе этой формулы стоит векторная физическая величина, а в знаменателе — скалярная. Поэтому направление вектора ускорения должно совпадать с направлением вектора, равного разности векторов скоростей:

Для того чтобы изобразить вектор, являющийся разностью двух векторов, используют правило треугольника. Сначала векторы изображают исходящими из одной точки (при этом перемещать их можно только при помощи параллельного переноса). Затем проводят отрезок так, чтобы получился треугольник.

В нашем случае направленный отрезок, соединяющий конец вычитаемого вектора ʋ₁ с концом уменьшаемого вектора ʋ₂, и будет их векторной разностью.

Из рисунка видно, что вектор Δʋ и, следовательно, вектор a направлены внутрь окружности. Для того чтобы понять, как направлено ускорение в определённой точке траектории представим, что промежуток времени от момента нахождения тела в точке А до момента, когда тело стало находиться в точке В, становится всё меньше и меньше. Тогда точки А и В стягиваются в одну точку А. При этом направление вектора Δʋ приближается к направлению вектора AO.

Получается, что ускорение тела, движущегося по окружности с постоянной по модулю скоростью, направлено по радиусу окружности к её центру. Именно поэтому оно называется центростремительным и обозначается а_ц.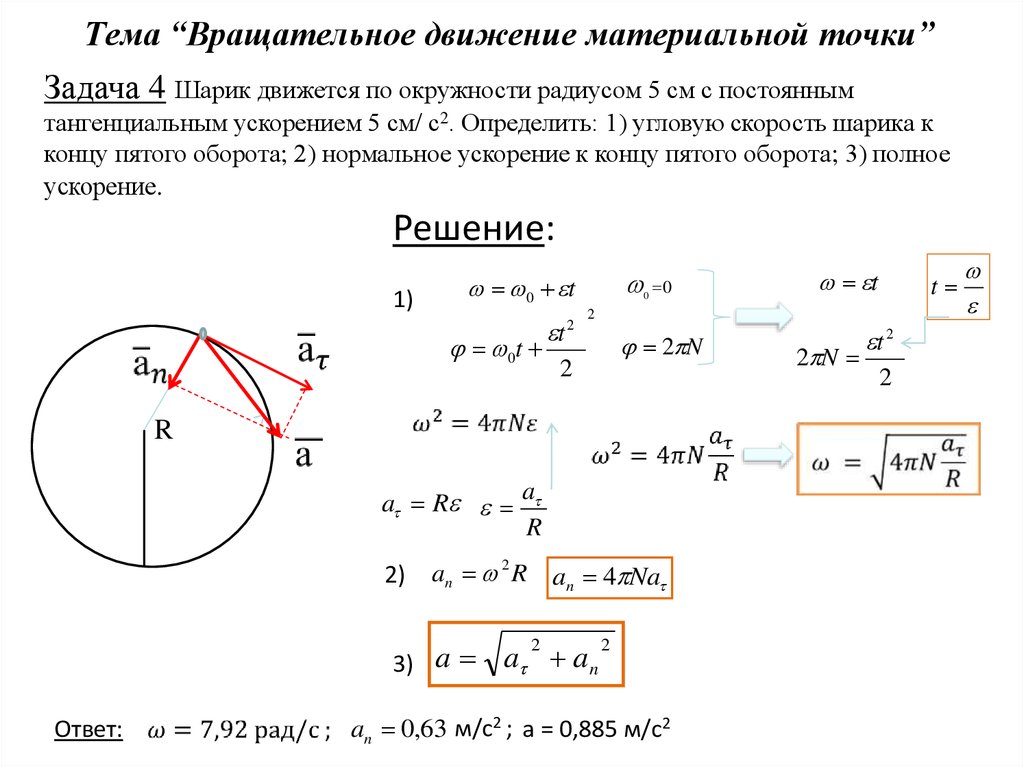

Так как касательная к окружности перпендикулярна радиусу, проведённому в точке касания, то векторы скорости ʋ и центростремительного ускорения а_ц перпендикулярны друг другу.

МОДУЛЬ ЦЕНТРОСТРЕМИТЕЛЬНОГО УСКОРЕНИЯ ТЕЛА

Для нахождения модуля центростремительного ускорения вновь обратимся к рисунку.

Вы смотрели Конспект по физике для 9 класса «Движение тела по окружности».

Вернуться к Списку конспектов по физике (Оглавление).

Движение по окружности с постоянной по модулю скоростью

Понятия и определения

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

Траектория движения тела есть окружность.
Вектор скорости всегда направлен по касательной к окружности.
Направление скорости постоянно меняется под действием центростремительного ускорения.
Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Определение и формулы

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Определение и формулы

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Полезные факты

Радиан

— угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂ .
У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Определение и формула

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_{ц.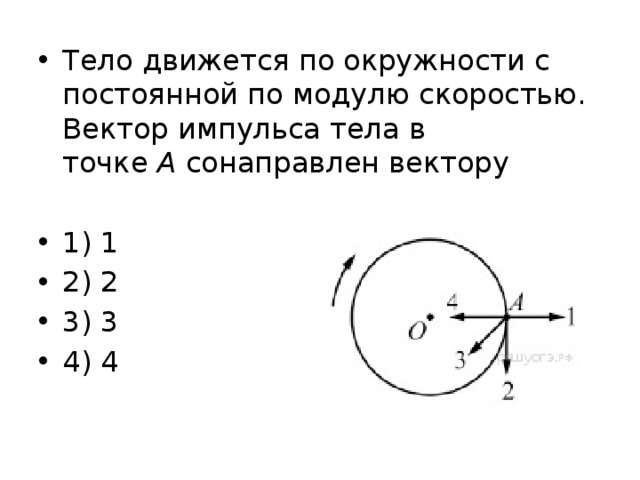 с.}. Единица измерения — метры на секунду в квадрате (м/с²). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10³ секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10

6. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Задание EF18273 Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…

Алгоритм решения

Записать исходные данные.
Записать формулу для определения искомой величины.
Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

Радиус окружности, по которой движется автомобиль: R = 100 м.
Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Ответ: 4

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17763

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

Записать исходные данные.
Определить, что нужно найти.
Записать формулу зависимости центростремительного ускорения от частоты.
Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Радиус окружности R₁ = R

.
Радиус окружности R₂ = 4R.
Центростремительное ускорение: a_ц.с.= a₁ = a₂.

Найти нужно ν₂.

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Или:

Отсюда:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое.

Верный ответ: «б».

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 21k

Скорость тела, движущегося по окружности радиусом 15 см, изменяется от 180об/мин→600об/мин11с. Тогда угловое ускорение тела составит

Вопрос

Обновлено на: 25/03/2020

Nikita Publication-Circular-Circular Moltiple Choice Вопрос

20 Видео

Текстовое решение

1RAD/S2. Ответ

Правильный ответ: D

Решение

α=ω2−ω1t=2π(n2−n1)t

Ответ

Пошаговое решение, разработанное экспертами, чтобы помочь вам в сомнениях и получить отличные оценки на экзаменах.

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

Похожие видео

Если маховик совершает 120 об/мин, то его угловая скорость будет

15599912

Угловая скорость вращения колеса двигателя 9(-1) за 10 с, то его угловое ускорение будет

18707850

Маховик вращается со скоростью 100 об/мин, к маховику приложен крутящий момент в течение 10 с. (-1) . Чему равен момент инерции маховика?

327884545

Частица движется по окружности радиусом 25 м с постоянной угловой скоростью 12 об/мин. тогда угловое ускорение частицы равно

365717940

Угловая скорость автомобильного двигателя увеличивается с постоянной скоростью от 1200 об/мин до 3200 об/мин за 12 с. а) Чему равно его угловое ускорение в оборотах в минуту в квадрате? б) Сколько оборотов сделает двигатель за эти 12 с?

557531707

За время, когда компакт-диск разгоняется из состояния покоя до постоянной скорости вращения 477 об/мин, он совершает угловое смещение 0,250 об/мин. Каково угловое ускорение компакт-диска?

557532078

Маховик вращается со скоростью 100 об/мин, к маховику прикладывается крутящий момент в течение 10 с. Если крутящий момент увеличивает скорость до 200 об/мин, то угловое ускорение маховика будет

643020980

, то его угловое ускорение будет

643192002

Если маховик совершает 120 об/мин, то его угловая скорость будет

643989448

Угловая скорость колеса двигателя, совершающего 90″ об//»мин» равна

6439009 частица вращается по окружности радиусом 25 м с постоянной угловой скоростью 12 об/мин. тогда угловое ускорение частицы равно

644374124

કોણીય ઝડપ 120об/мин = ……… .

645056881

Скорость тела, движущегося по окружности в радикальном направлении: Kaysons Education

Видеолекции

Доступ к более чем 500 часам видеолекций в режиме 24/7, охватывающих полную программу подготовки к ЕГЭ.

Онлайн-поддержка

Отработайте более 30000+ вопросов, начиная с базового уровня и заканчивая продвинутым уровнем JEE.

Сеанс устранения сомнений в реальном времени

Задавайте свои сомнения в прямом эфире каждый день. Присоединяйтесь к нашему сеансу устранения сомнений в прямом эфире, проводимому нашими экспертами.

Национальные пробные испытания

Проведите тесты, чтобы проанализировать свой прогресс и оценить, на каком уровне вы находитесь с точки зрения подготовки к ЕГЭ.

Организованное обучение

Правильное планирование завершения учебного плана является ключом к получению достойного рейтинга в JEE.

Серия тестов/Ежедневные задания

ПОГОВОРИТЬ С КОНСУЛЬТАНТОМ? НАЖМИТЕ ЗДЕСЬ

Загрузить вопросник и решение JEE Загрузить Важные вопросы JEE Загрузить полную программу по математике, физике, химии

Скорость тела, движущегося по окружности в радикальном направлении, равна

0
Скорость тела
v ² / Р
Ничего из вышеперечисленного

легкий

Раствор

Правильный вариант

Поскольку скорость направлена по касательной, ее составляющая вдоль радиального направления равна нулю.

Загрузить вопросник и решение ЕГЭ Загрузить ЕГЭ Важные вопросы Загрузить полную программу по математике, физике, химии