Прямая функции параллельна касательной к графику функции: Прямая параллельна касательной к графику функции

Прямая параллельна касательной к графику функции

Рассмотрим задания из №7 ЕГЭ, в которых данная прямая параллельна касательной к графику функции.

№1

Прямая y=9x+5 параллельна касательной к графику функции y=x²-5x+54. Найти абсциссу точки касания.

Решение:

Прямые y=k₁x+b₁ y=k₂x+b₂ параллельны,если их угловые коэффициенты равны: k₁=k₂.

y=9x+5, отсюда k₁=9.

Угловой коэффициент касательной равен значению производной в точке касания: k₂=f'(x_o).

f'(x)=(x²-5x+54)’=2x-5;

f'(x_o)=2x_o-5.

Таким образом, 2x_o-5=9; 2x_o=14; x_o=7.

Ответ: 7.

№2

Прямая y=14-2x является касательной к графику функции y=x³+1,5x²-8x+4. Найти абсциссу точки касания.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(x_o).

f'(x)=(x³+1,5x²-8x+4)’=3x²+3x-8;

f'(x_o)=3x_o²+3x_o-8.

По условию, y=14-2x. Отсюда k=-2.

3x_o²+3x_o-8=-2

3x_o²+3x_o-6=0

x_o²+x_o-2=0

x_o=1 либо x_o=-2.

Точка касания принадлежит и касательной, и графику функции.

x_o³+1,5x_o²-8x_o+4=14-2x_o.

Проверяем, выполняется ли равенство при x_o=1:

1³+1,5·1²-8·1+4=14-2·1?

-1,5≠12.

При x_o=-2:

(-2)³+1,5·(-2)²-8·(-2)+4=14-2·(-2)

18=18.

Абсцисса точки касания равна x_o=-2.

Ответ: -2.

№3

Прямая y=11x+8 является касательной к графику функции y=ax²+7x-2. Найти a.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(x_o).

f'(x)=(ax²+7x-2)’=2ax+7;

f'(x_o)=2ax_o+7.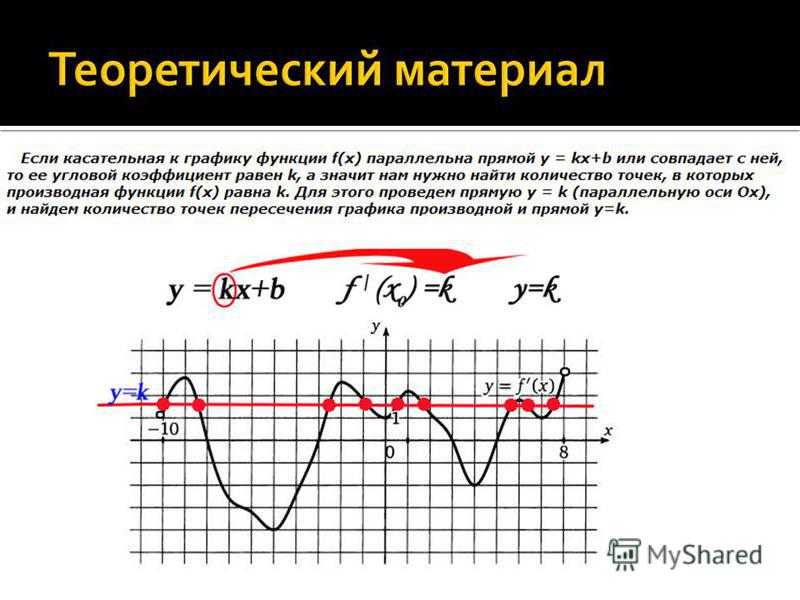

По условию, уравнение касательной y=5x+1, поэтому k=5.

Имеем: 2ax_o+7=11, откуда ax_o=2.

Точка касания принадлежит и касательной, и графику функции, поэтому

ax_o²+7x_o-2=11x_o+8. Подставив в это равенство ax_o=2, получим

2x_o+7x_o-2=11x_o+8, откуда x

o=-5.

ax_o=2

-5_a=2

a=-0,4.

Ответ: 0,4.

№4

Прямая y=-6x+7 является касательной к графику функции y=6x²+bx+13. Найти b, учитывая, что абсцисса точки касания меньше 0.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(x_o).

f'(x)=(6x²+bx+13)’=12x+b;

f'(x_o)=12x_o+b.

По условию, уравнение касательной y=-6x+7, поэтому k=-6.

Имеем: 12x_o+b=-6, откуда b=-12x_o-6.

Точка касания принадлежит и касательной, и графику функции.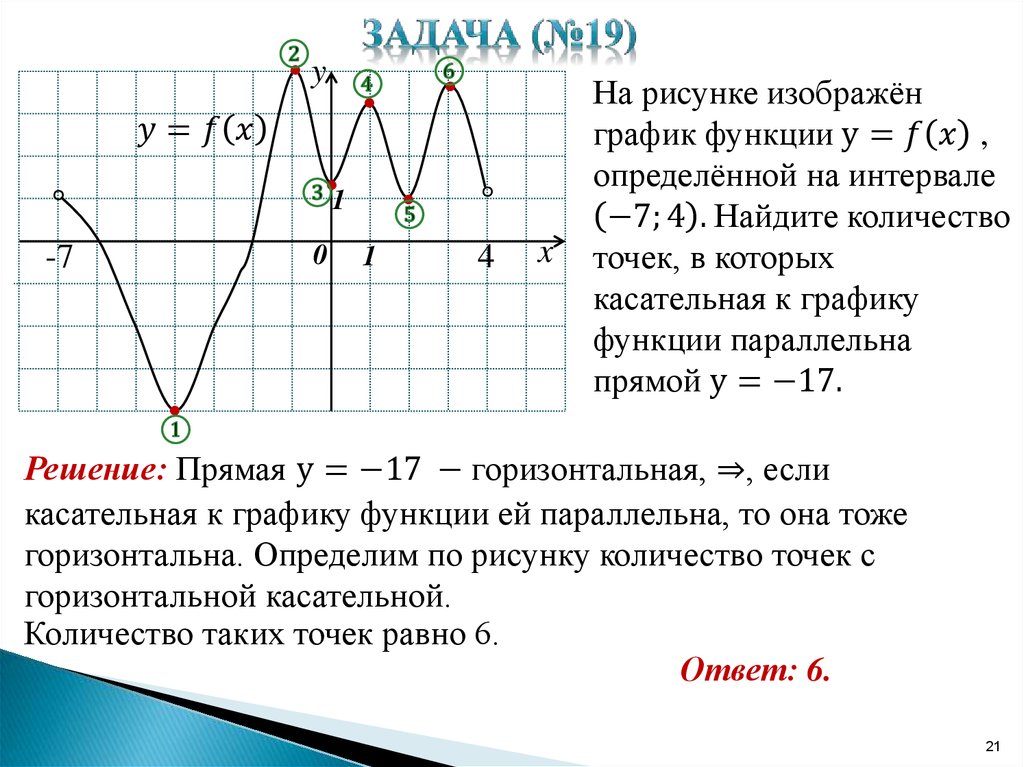

6x_o²+bx_o+13=-6x_o+7

6x_o²+(-12x_o-6)x_o+13=-6x_o+7

6x_o²-12x_o²-6x_o+13+6x_o-7=0

-6x_o²+6=0

x_o=1 либо x_o=-1.

По условию, x_o<0, следовательно, x_o=-1.

b=-12·(-1)-6=6.

Ответ: 6.

№5

Прямая y=2x+4 является касательной к графику функции y=x²-4x+c. Найти c.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(x_o).

f'(x)=(x²-6x+c)’=2x-6;

f'(x_o)=2x_o-6.

По условию, уравнение касательной y=2x+4, поэтому k=2.

Имеем: 2x_o-6=2, откуда x_o=4.

Точка касания принадлежит и касательной, и графику функции, поэтому

x_o²-4x_o+с=2x_o+4. Подставив в это равенство x_o=4, получим

16-16+с=8+4

с=12.

Ответ: 12.

Прямая является касательной к графику функции

Бизнес с Oriflame — рост и РАЗВИТИЕ!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2013-04-11

   Продолжаем рассматривать задачи входящие в состав экзамена по математике. В курсе алгебры есть группа задач, где задаётся уравнение функции и уравнение прямой — касательной к графику данной функции или прямой параллельной этой касательной.

Задачи несложные, но они требуют чёткого понимания геометрического смысла производной. Это теоретическая основа для решения подобных задач (и подобных им), и без этой основы никак нельзя. Рекомендую ознакомиться со статьями «Геометричесий смысл произвоной. Часть 1» и «Геометрический смысл производной. Часть 2».

Рассмотрим две задачи:

Прямая у = 4х + 8 параллельна касательной к графику функции

у = х² – 5х + 7 

Найдите абсциссу точки касания.

Из геометрического смысла производной мы знаем, что значение производной  в точке касания равно угловому коэффициенту касательной.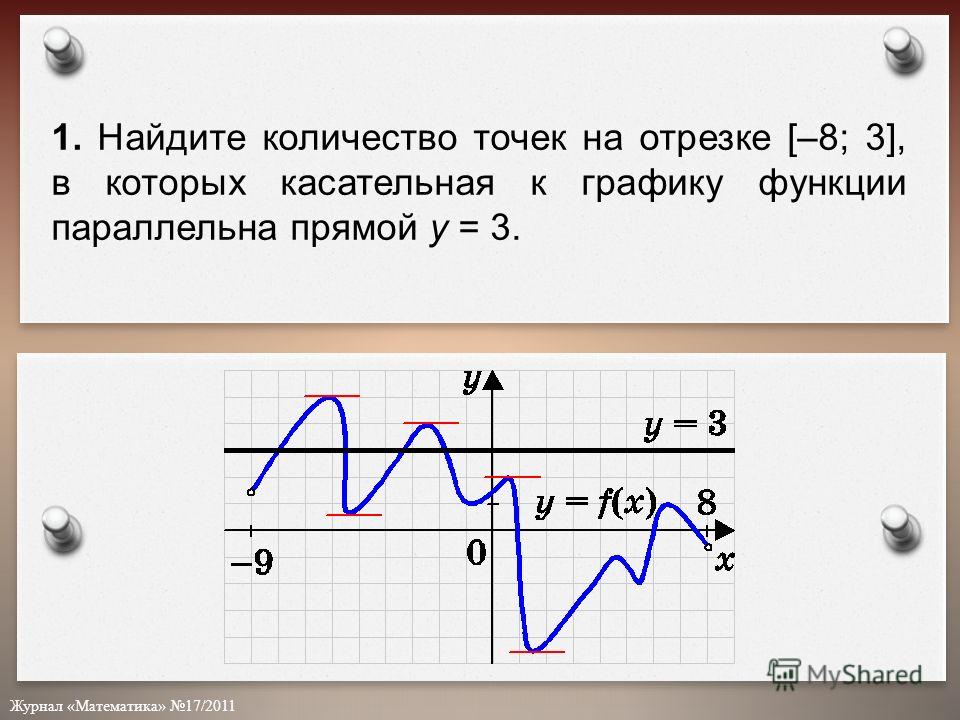

Известно, что угловые коэффициенты параллельных прямых равны, значит  угловые коэффициенты прямой  у = 4х + 8 и касательной равны 4.

Угловой коэффициент прямой  вида у = kх + b это число  k.

Таким образом, абсцисса точки касания находится из уравнения:

Значит,

Ответ: 4,5

Второй способ: 

Он предельно прост, но не всегда работает. Строим на координатной плоскости график у = х² – 5х + 7, строим прямую у = 4х + 8, далее строим (параллельным переносом) параллельную ей прямую касающуюся параболы, и в некоторых задачах вы визуально сможете определить абсциссу точки касания.

Отмечу, что таким способом можно решить задачу, если абсцисса целое число или целое  с половиной, например  1,5; – 2,5; –3,5  и так далее. Если же точка пересечения «непонятна», то есть, нельзя точно и уверенно определить абсциссу (например, визуально сложно определить 3,2; 5,7 …), то точное решение  даст  первый способ. 

Если вы  решили задачу этим способом  и уверены в правильности решения, обязательно сделайте проверку. Подставьте полученную абсциссу в оба исходных уравнения, должны получится равные значения функций (ордината точки пересечения).

Решите самостоятельно:

Прямая у = 7х – 8 параллельна касательной к графику функции

у = х² + 6х – 8

Найдите абсциссу точки касания.

Посмотреть решение

Прямая у = 6х + 4  является касательной к графику функции 

у = х³ – 3х² + 9х + 3

Найдите абсциссу точки касания.

Из геометрического смысла производной функции известно, что  она (производная)  равна угловому коэффициенту касательной.

Известно, что угловой коэффициент прямой  вида у = kх + b это число  k.

Значит, угловой коэффициент прямой  у = 6х + 4   равен 6. Таким образом,

Решая квадратное уравнение, получим:

Получили два равных корня.  Таким образом, абсцисса точки касания равна 1.

Ответ: 1

Решите самостоятельно:

Прямая у = – 4х – 11  является касательной к графику функции

у = х³ + 7х² + 7х – 6 

Найдите абсциссу точки касания

Посмотреть решение

В данной рубрике продолжим рассматривать задачи, не пропустите! 

На этом все.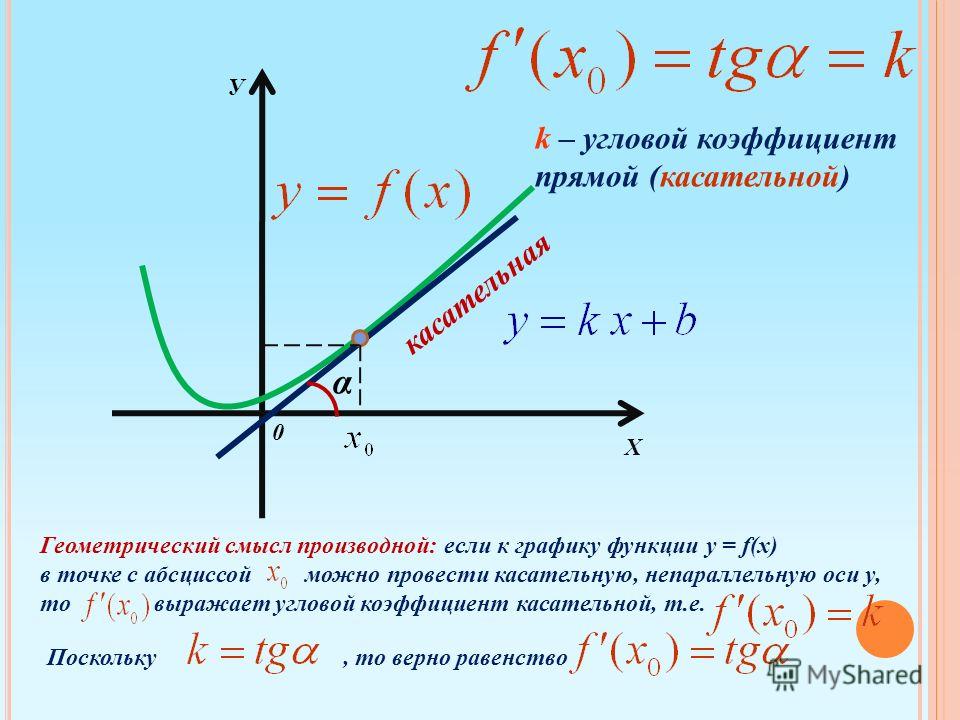 Успехов Вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Производная Графики | ЕГЭ-№7Производная

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Найти уравнение прямой, касательной к кривой в заданной точке

Все ресурсы для предварительного исчисления

12 Диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

Precalculus Help » Вводный расчет » Касательные к кривой » Найдите уравнение прямой, касательной к кривой в заданной точке

Найдите уравнение прямой, касательной к графику

в точке в форме пересечения наклона.

Возможные ответы:

Правильный ответ:

Пояснение:

Начнем с того, что вспомним, что одним из способов определения производной функции является наклон касательной функции в данной точке. Следовательно, нахождение производной нашего уравнения позволит нам найти наклон касательной. Поскольку две вещи, необходимые для нахождения уравнения прямой, — это наклон и точка, мы на полпути.

Мы вычисляем производную по степенному правилу.

Однако нам нужен наклон касательной не в любой точке, а именно в этой точке. Чтобы получить это, мы просто подставляем наше значение x 1 в производную.

Следовательно, наклон нашей касательной равен .

Теперь нам нужна точка на нашей касательной. Наш выбор довольно ограничен, так как единственная точка на касательной, которую мы знаем, — это точка, в которой она пересекает наш исходный график, а именно точка .

Таким образом, мы можем подставить эти координаты вместе с нашим наклоном в общую форму точка-наклон, чтобы найти уравнение.

Решение для даст нам форму пересечения наклона.

 

Сообщить об ошибке

Найти уравнение касательной к функции

at .

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение касательной в точке  зависит от производной в этой точке и значения функции.

Производная в этой точке равна

 с использованием степенного правила

, что означает

Производная равна нулю, поэтому касательная будет горизонтальной.

Он пересекает ее в точке  since , так что эта линия .

Сообщить об ошибке

По заданной функции найдите уравнение касательной в точке .

Возможные ответы:

Правильный ответ:

Объяснение:

Перепишите  в форме пересечения наклона, , , чтобы определить наклон.

Наклон данной функции равен 2.

Подставьте наклон и заданную точку в форму наклона и точки пересечения, чтобы определить точку пересечения по оси y.

Подставьте это и наклон обратно в уравнение пересечения наклона.

Уравнение касательной:  

Сообщить об ошибке

Используя предельное определение производной, найдите уравнение касательной к кривой  в точке .

Возможные ответы:

Правильный ответ:

Объяснение:

Начнем с нахождения уравнения производной, используя определение предела:

Определим  и  следующим образом:

Затем мы можем определить их разницу:

Затем мы делим на h, чтобы подготовиться к пределу:

Тогда предел даст нам уравнение производной .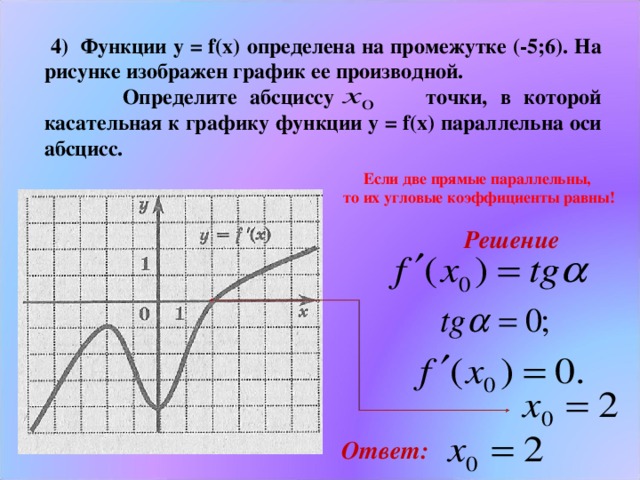

Теперь мы должны понять, что наклон линии, касательной к кривой в данной точке, эквивалентен производной в этой точке. Итак, если мы определим нашу касательную линию как: , то это m определяется следующим образом:

Следовательно, уравнение касательной к кривой в данной точке:

Сообщить об ошибке

Напишите уравнение касательной к кривой в точке .

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала найдите наклон этой касательной, взяв производную:

Подставив 1 вместо x:

Итак, наклон равен 4

Теперь нам нужно найти координату y, когда x равен 1, поэтому подставьте 1 к исходному уравнению:

варианты ответа:

распределите 4

добавьте 2 к обеим сторонам

Сообщите об ошибке

Напишите уравнение для касательной к точке .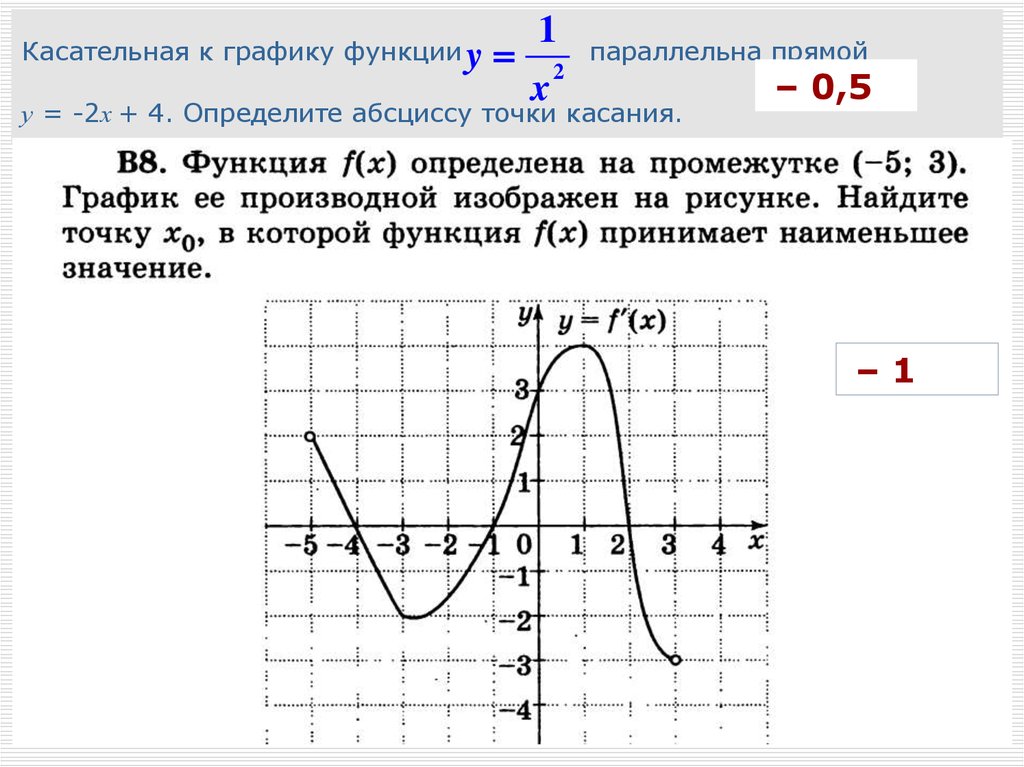

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала найдите наклон касательной, взяв первую производную:

Чтобы завершить определение наклона, подставьте значение x, 2:

, наклон равен 6

Теперь найдите y -координата, где x равно 2, подставив 2 к исходному уравнению:

Чтобы написать уравнение, начните в форме точки-наклона, а затем используйте алгебру, чтобы преобразовать его в наклон-пересечение, как варианты ответа.

распределите 6

добавьте 8 к обеим сторонам

Сообщите об ошибке

Напишите уравнение касательной для точки .

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала возьмите первую производную, чтобы найти наклон:

 

Чтобы продолжить поиск наклона, подставьте значение x, -2:

Затем найдите координату y, подставив — 2 в исходное уравнение:

Координата y равна

Теперь напишите уравнение в форме точки-наклона, а затем алгебраически обработайте его, чтобы оно соответствовало одной из форм пересечения наклона вариантов ответа.

распределить -5

добавить в обе стороны

 

 

Сообщить об ошибке

Напишите уравнение для касательной к точке .

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала распространите файл . Это облегчит получение производной:

Теперь возьмите производную уравнения:

Чтобы найти наклон, подставьте значение x -3:

Чтобы найти координату y точки, подставьте значение x в исходное уравнение:

Теперь напишите уравнение в виде точка-наклон, затем используйте алгебру, чтобы преобразовать его в наклон-пересечение, как варианты ответа:

 распределить

вычесть из обеих сторон

записать как смешанное число

 

Сообщить об ошибке

Уведомление об авторских правах

Все Precalcul ресурсы США

12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

Теорема о среднем значении

Теорема о среднем значении

Секущая — это линия, проведенная через две точки на кривой.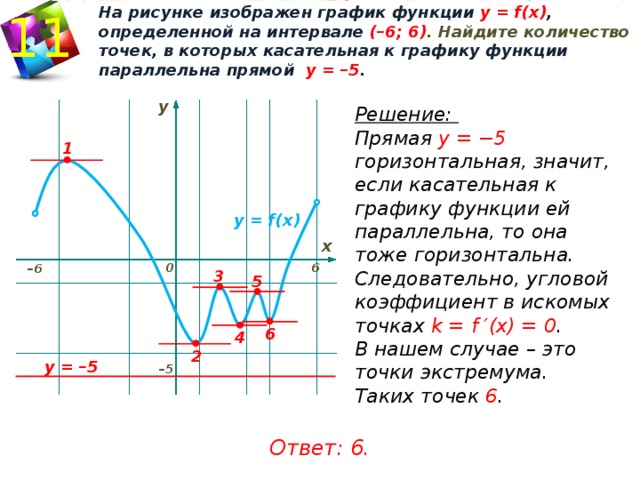

Теорема о среднем значении связывает наклон секущей с наклон касательной.

Теорема. (Среднее значение Теорема) Если f непрерывна на и дифференцируема на , то существует число c такое, что

Я не буду приводить здесь доказательства, но на рисунке ниже показано, почему это делает смысл. Я провел секущую через точки и . Среднее значение Теорема утверждает, что где-то между a и b есть точка c на кривая, где касательная имеет тот же наклон, что и секущая линия.

Прямые с одинаковым наклоном параллельны. Чтобы найти точку, где касательная параллельна секущей, возьмите секущую и «сдвиньте» его (не меняя наклона), пока он не станет касательной к кривой.

Если вы поэкспериментируете с некоторыми кривыми, вы обнаружите, что всегда это возможно (при условии, что кривая непрерывна и дифференцируема, как указано в теореме).

---

Пример. Для функции на интервале найти число (или числа), удовлетворяющее заключение теоремы о среднем значении.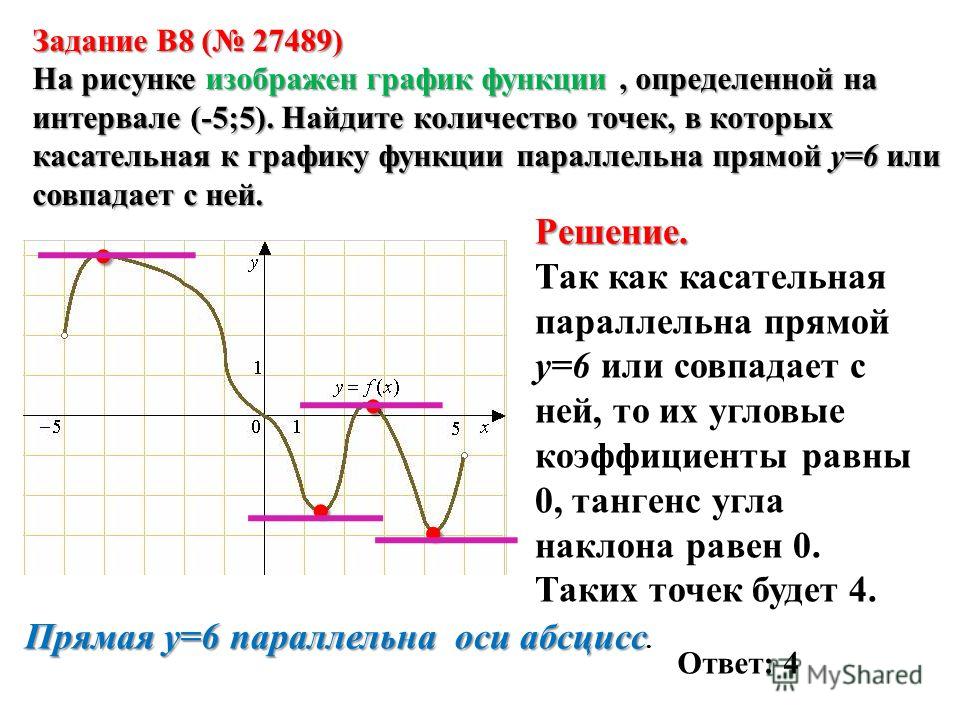

Поскольку f полином, f непрерывен на и дифференцируем на . Более того,

Следовательно, существует число c — может быть больше одного — между -5 и 1 такой, что . Я постараюсь найти один.

, так . Приравняйте к 9 и решите для с:

это , а не в интервале — это конечная точка — но есть. число, удовлетворяющее заключение теоремы о среднем значении.

---

Замечание. Математики часто говорят «есть номер» как сокращение от «есть по крайней мере одно число». Таким образом, теорему о среднем значении следует интерпретировать как означают «существует хотя бы одно число c», удовлетворяющее заключение теоремы. Там может быть много номеров, которые работают — даже бесконечное их количество!

Кроме того, нахождение значения c, которое работает, может быть затруднено. Но теорема гарантирует только то, что такое c существует , а не то, что вы сможете найти его.

Пример. Рассмотрим на интервале . Затем

Однако , и не имеет решения. Почему это не противоречит теореме о среднем значении? Это не противоречит среднему Теорема о ценности, потому что f не определено в точке , которая находится в середине интервала .

---

Пример. Кальвин Баттербол бежит 100 ярдов рывок за 20 секунд. Предположим, что функция, задающая его положение относительно начального линия непрерывна и дифференцируема. Покажите, что Кальвин должен иметь бегал со скоростью 5 ярдов в секунду во время своего бега.

Когда , он на стартовой линии, так что . Когда , он на финише, так что . Применение теоремы о среднем значении к s для , я нахожу, что есть точка c между 0 и 20 таких, что

То есть скорость Кальвина была равна 5 ярдам в секунду. Во-вторых, это то, что я хотел показать.

---

Вы знаете, что производная константы равна нулю. Среднее значение Теорему можно использовать, чтобы показать, что верно и обратное.

Теорема. Если f непрерывна на замкнутом интервал и для всех x в открытом интервале, то f постоянна на закрытом интервале.

Доказательство. Позвольте d быть любым числом таким, что . Теорема о среднем значении применяется к f на интервале , значит, существует число c такое, что и

По предположению, . Поэтому,

Поскольку d было произвольным числом таким, что , следует, что для всех x в . Это означает, что f постоянна на интервал.

Мы воспользуемся этой идеей, когда будем обсуждать . первообразные . Вот набросок идеи.

я знаю это

Если любая другая функция такая, что , то

По теореме , где c — константа. Поэтому, . Другими словами, единственный функции, производные которых являются функциями типа

Когда я буду обсуждать первообразные, я буду выражать этот факт, написав

---

Следствие. ( Ролль Теорема ) Пусть f непрерывна на и дифференцируема на и, кроме того, что . Тогда существует число c такое, что

Доказательство. Примените теорему о среднем значении, чтобы получить

Но, значит, и левая сторона равна 0 — что дает заключение теоремы Ролля.

Частным случаем, когда гипотеза верна, является случай, когда a и b являются корнями f, так как тогда

В этой ситуации теорема Ролля говорит, что существует по крайней мере один горизонтальная касательная между каждой парой корней.

На рисунке выше есть три критические точки между корни в a и b.

---

Пример. По теореме о среднем значении функция имеет критическое значение точки — места, где — от 0 до 20, от 20 до 200 и от 200 до 2000.

---

Пример. Докажите, что функция имеет ровно один корень.

Шаг 1. Так как и , и поскольку f непрерывно, из теоремы о промежуточном значении следует, что есть корень между -10 и 10. Таким образом, f имеет по крайней мере один корень.

Шаг 2. Предположим, что f имеет более одного корня. Предположим, в частности, что a и b — два корня f.

По теореме Ролля f должна иметь горизонтальную касательную между a и b. То есть для .

Однако производная есть. Поскольку четные степени неотрицательны, для всех x. Это противоречит.

Это противоречие показывает, что двух корней быть не может, поэтому не может быть более одного корня.

Шаг 1 показывает, что есть хотя бы один корень. Шаг 2 показывает, что не может быть больше одного. Следовательно, должен быть ровно один корень.

---

Определение. Функция f равна строго увеличивая на интервале, если для всех p и q таких, что ,

Если последнее неравенство заменить на , то f равно увеличение .

Функция f есть , строго убывающая на интервал, если для всех p и q таких, что ,

Если последнее неравенство заменить на , то f равно уменьшение .

Предложение. Предположим, что f дифференцируема на .

(a) Если на , то f есть строго возрастает на .

(б) Если на , то f есть строго убывает на .

Доказательство. Возьмите p и q между a и b; сказать . Я хочу показать . По теореме о среднем значении существует число c, такое это и

Но так

Это доказывает, что f строго возрастает на отрезке.

Доказательство (b) аналогично.

Примечание. В (а) если вместо этого предположить, что на , то то же самое доказательство показывает, что f возрастает на . Аналогично, в (b), если вы предполагаете, что на , то f равно уменьшается на .

---

Пример.