Идеальный газ получил количество теплоты 300: Идеальный газ получил количество теплоты равное 300 Дж и совершил работу равную 100 Дж.Как изменилась...

Задачи на первый закон термодинамики

Первый закон термодинамики .

\( Q=\Delta U+A \)

\(Q\) — Количество теплоты, полученное газом

Если \(\; Q>0 \; ,\) то газ получает тепло

Если \(\; Q < 0 \; , \) то газ отдает тепло

\( \Delta U \)-Изменение внутренней энергии газа

\(A\) — Работа газа

\(A=P \Delta V \)

\( \Delta V \)- Изменение объема газа

Если изменение объема газа равно нулю \(( \Delta V =0) \), то и работа газа равна нулю

Если газ расширяется , то \(\; A>0 \; ,\) (газ совершает положительную работу)

Если газ сужается , то \(\; A < 0 \; , \) и говорят:»Внешние силы совершают работу над газом « или » Работа газа отрицательна »

Задача 1.

Внутренняя энергия идеального газа возрастает на 300 Джоулей \((\Delta U=300 Дж) \; , \) при этом газ совершает работу \(A=200 Дж \; .

\) Какое количество теплоты получил газ?
Показать ответ Показать решение Видеорешение

Ответ: \( Q=500 Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\(\Delta U=300 Дж\)

\(A=200 Дж \)

\(Q-? \)

\( Q=\Delta U+A \)

\( Q=300 Дж+200 Дж=500 Дж \)

Ответ: \( Q=500 Дж \)

Задача 2.

Газ получает из внешней среды \(Q=500 Дж \; , \) при этом газ совершает работу \(A=200 Дж \; . \) Найти изменение внутренней энергии \( \Delta U \; .\)
Показать ответ Показать решение Видеорешение

Ответ: \( \Delta U= 300 Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\(Q=500 Дж \)

\(A=200 Дж \)

\(\Delta U-? \)

\( Q=\Delta U+A \)

\( \Delta U=Q-A \)

\( \Delta U= 500 Дж- 200 Дж=300 Дж \)

Ответ: \( \Delta U= 300 Дж \)

Задача 3.

Газ получает из внешней среды \(Q=700 Дж \; , \) при этом внутренняя энергия газа возрастает на 150 Джоулей \( (\Delta U=150 Дж) \; .\) Какую работу совершает газ?
Показать ответ Показать решение Видеорешение

Ответ: \( A= 550 Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\(Q=700 Дж \)

\( \Delta U=150 Дж \)

\(A-? \)

\( Q=\Delta U+A \)

\( A=Q-\Delta U \)

\( A= 700 Дж-150 Дж=550 Дж \)

Ответ: \( A= 550 Дж \)

Задача 4.

Газ получает из внешней среды \(Q=1700 Дж \; , \) при этом внутренняя энергия газа возрастает на 250 Джоулей \( (\Delta U=250 Дж) \; .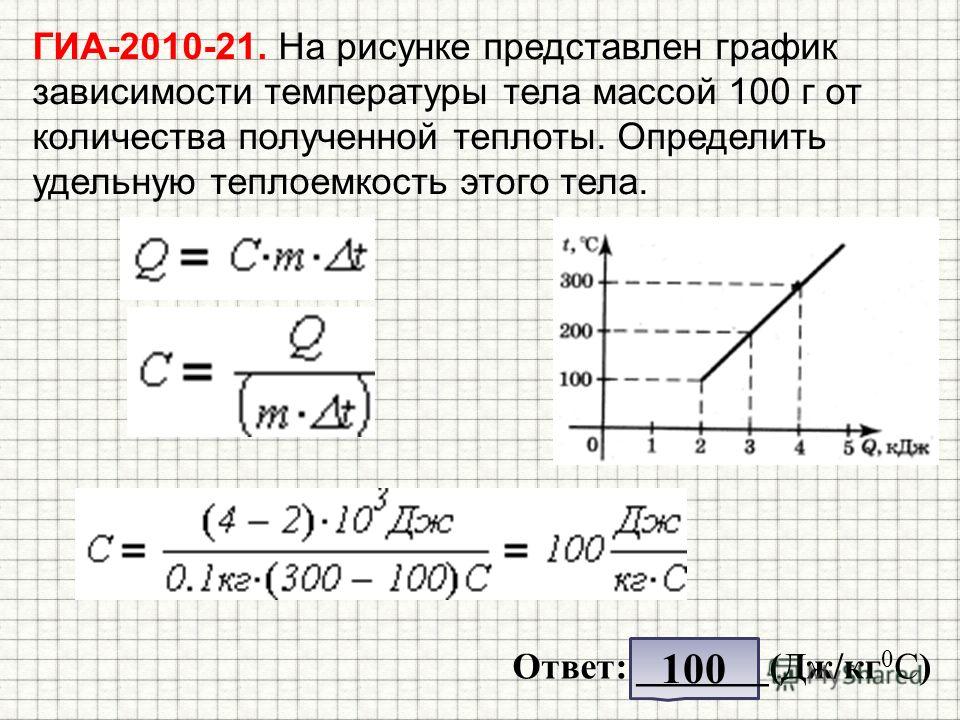

\) Какую работу совершает газ?
Показать ответ Показать решение Видеорешение

Ответ: \( A= 1450 Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\(Q=1700 Дж \)

\( \Delta U=250 Дж \)

\(A-? \)

\( Q=\Delta U+A \)

\( A=Q-\Delta U \)

\( A= 1700 Дж-250 Дж=1450 Дж \)

Ответ: \( A= 1450 Дж \)

Задача 5.

Внутренняя энергия идеального газа уменьшается на 300 Джоулей \((\Delta U=-300 Дж) \; , \) при этом газ совершает работу \(A=500 Дж \; . \) Какое количество теплоты получил газ?
Показать ответ Показать решение Видеорешение

Ответ: \( Q=200Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\(A=500 Дж \)

\( \Delta U=-300 Дж \)

\(Q-? \)

\( Q=\Delta U+A \)

\( Q=-300 Дж+500 Дж=200Дж \)

Ответ: \( Q=200Дж \)

Задача 6.

Внутренняя энергия идеального газа уменьшается на 400 Джоулей \((\Delta U=-400 Дж) \; , \) при этом газ совершает работу \(A=450 Дж \; . \) Какое количество теплоты получил газ?
Показать ответ Показать решение Видеорешение

Ответ: \( Q=50Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\(A=450 Дж \)

\( \Delta U=-400 Дж \)

\(Q-? \)

\( Q=\Delta U+A \)

\( Q=-400 Дж+450 Дж=50Дж \)

Ответ: \( Q=50Дж \)

Задача 7.

Внутренняя энергия идеального газа уменьшается на 500 Джоулей \((\Delta U=-500 Дж) \; , \) при этом газ совершает работу \(A=500 Дж \; .

\) Какое количество теплоты получил газ?
Показать ответ Показать решение Видеорешение

Ответ: \( Q=0Дж \;\;\;\;\;\;\;\; \) Газ не получил тепло

Запишем уравнение Первого закона термодинамики:

Дано:
\(A=500 Дж \)

\( \Delta U=-500 Дж \)

\(Q-? \)

\( Q=\Delta U+A \)

\( Q=-500 Дж+500 Дж=0 Дж \)

Ответ: \( Q=0Дж \)

Газ не получил тепло , это адиабатный процесс, процесс идущий без теплообмена с окружающей средой

Задача 8.

Внутренняя энергия идеального газа уменьшается на 500 Джоулей \((\Delta U=-500 Дж) \; , \) при этом газ совершает работу \(A=200 Дж \; . \)
Какое количество теплоты получил(или отдал) газ?
Показать ответ Показать решение Видеорешение

Ответ: \( Q=-300Дж \;\;\;\;\;\;\;\; \) Газ не получил тепло,а отдал во внешнюю среду

Запишем уравнение Первого закона термодинамики:

Дано:
\(A=200 Дж \)

\( \Delta U=-500 Дж \)

\(Q-? \)

\( Q=\Delta U+A \)

\( Q=-500 Дж+200 Дж=-300 Дж \)

Ответ: \( Q=-300Дж \)

Газ не получил тепло , а отдал во внешнюю среду 300 Джоулей

Задача 9.

Внутренняя энергия идеального газа уменьшается на 1200 Джоулей \((\Delta U=-1200 Дж) \; , \) при этом газ совершает работу \(A=400 Дж \; . \)
Какое количество теплоты получил(или отдал) газ?
Показать ответ Показать решение Видеорешение

Ответ: \( Q=-800Дж \;\;\;\;\;\;\;\; \)
Газ не получил тепло,а отдал во внешнюю среду

Запишем уравнение Первого закона термодинамики:

Дано:
\(A=400 Дж \)

\( \Delta U=-1200 Дж \)

\(Q-? \)

\( Q=\Delta U+A \)

\( Q=-1200 Дж+400 Дж=-800 Дж \)

Ответ: \( Q=-800Дж \)

Газ не получил тепло , а отдал во внешнюю среду 800 Джоулей

Задача 10.

Газ отдал во внешнюю среду 40 Джоулей \( (Q=-40 Дж ) \; , \) при этом внутренняя энергия газа уменьшается на 120 Джоулей \((\Delta U=-120 Дж) . \)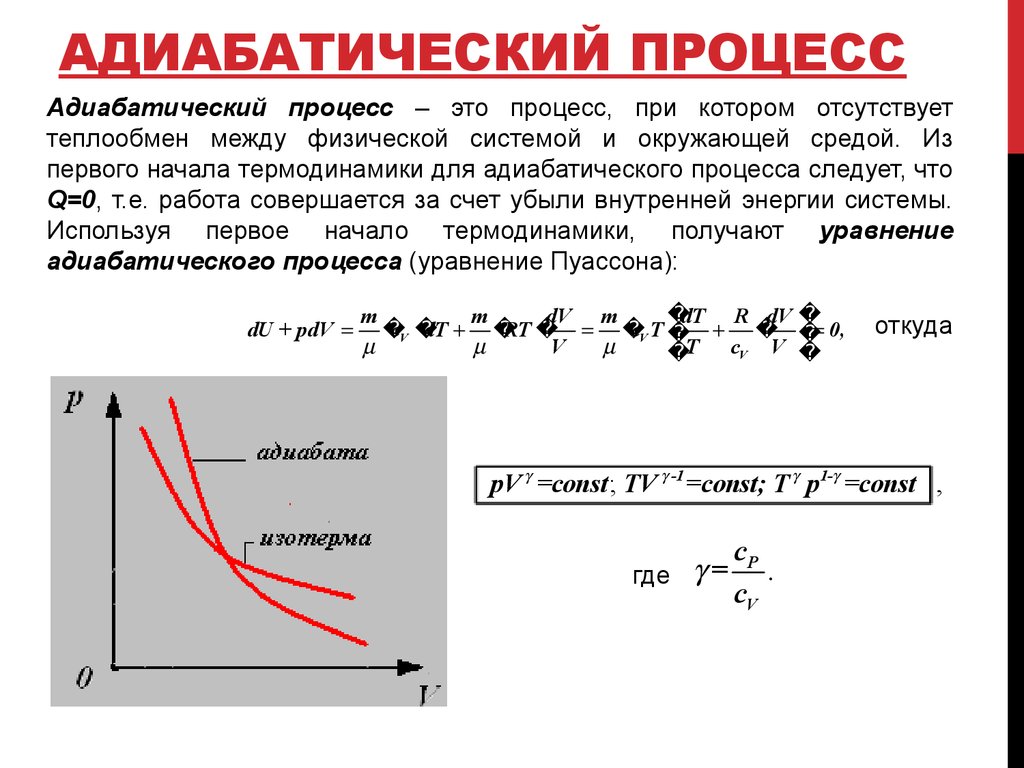
Найти совершенную газом работу.
Показать ответ Показать решение Видеорешение

Ответ: \( A=80 Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\(Q=-40 Дж \)

\( \Delta U=-120 Дж \)

\(A-? \)

\( Q=\Delta U+A \)

\(-40 Дж =-120 Дж+A \)

\(-40 Дж +120 Дж=A \)

\(A=80 Дж \)

Ответ: \( A=80 Дж \)

Задача 11.

Газ отдал во внешнюю среду 85 Джоулей \( (Q=-85 Дж ) \; , \) при этом внутренняя энергия газа уменьшается на 135 Джоулей \((\Delta U=-135 Дж) . \)
Найти совершенную газом работу.
Показать ответ Показать решение Видеорешение

Ответ: \( A=50 Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\(Q=-85 Дж \)

\( \Delta U=-135 Дж \)

\(A-? \)

\( Q=\Delta U+A \)

\(-85 Дж =-135 Дж+A \)

\(-85 Дж +135 Дж=A \)

\(A=50 Дж \)

Ответ: \( A=50 Дж \)

Задача 12.

Газ отдал во внешнюю среду 180 Джоулей \( (Q=-180 Дж ) \; , \) при этом внутренняя энергия газа уменьшается на 100 Джоулей \((\Delta U=-100 Дж) . \)
Найти совершенную газом работу.
Показать ответ Показать решение Видеорешение

Ответ: \( A=-80 Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\(Q=-180 Дж \)

\( \Delta U=-100 Дж \)

\(A-? \)

\( Q=\Delta U+A \)

\(-180 Дж =-100 Дж+A \)

\(-180 Дж +100 Дж=A \)

\(A=-80 Дж \)

Работа газа отрицательна, значит газ сжался (объем газа уменьшился), Внешние силы совершили работу над газом \(A_{внешних сил}= 80 Дж \)

Ответ: \( A=-80 Дж \)

Задача 13.

Работа внешних сил над газом равна 200 Дж \( (A=-200 Дж) \) при этом внутренняя энергия газа увеличивается на 300 Джоулей \((\Delta U=300 Дж) . \)
Какое количество теплоты получил газ?
Показать ответ Показать решение Видеорешение

Ответ: \( Q= 100 Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\( A=-200 Дж \)

\( \Delta U=300 Дж \)

\(Q -? \)

\( Q=\Delta U+A \)

\(Q= -200 Дж + 300 Дж \)

\( Q= 100 Дж \)

Газ получил 100 Джоулей

Ответ: \( Q= 100 Дж \)

Задача 14.

Внешние силы совершают над газом работу 800 Дж \( (A=-800 Дж) \) при этом внутренняя энергия газа увеличивается на 800 Джоулей \((\Delta U=800 Дж) . \)
Какое количество теплоты получил газ?
Показать ответ Показать решение Видеорешение

Ответ: \( Q= 0 Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\( A=-800 Дж \)

\( \Delta U=800 Дж \)

\(Q -? \)

\( Q=\Delta U+A \)

\(Q= -800 Дж + 800 Дж \)

\( Q= 0 Дж \)

Ответ: \( Q= 0 Дж \)

Газ не получил тепло , это адиабатный процесс, процесс идущий без теплообмена с окружающей средой

Задача 15.

Газ получает количество теплоты 500 Джоулей, при этом его внутрення энергия возрастает на 500 Джоулей.
Какую работу совершает газ?
Показать ответ Показать решение Видеорешение

Ответ: \( A= 0 Дж \)

Запишем уравнение Первого закона термодинамики:

Дано:
\( Q=500 Дж \)

\( \Delta U=500 Дж \)

\(A -? \)

\( Q=\Delta U+A \)

\(500 Дж= 500 Дж + A \)

\( A= 0 Дж \)

Газ не совершает работу

Ответ: \( A= 0 Дж \)

Тесты для педагогов по всем школьным предметам с ответами

#2 класс
#Чтение
#Проверочная работа

Тест «проектная работа по рассказам»

В прошлой теме «форуме» я говорила,что готовля для вас тест по рассказам из учебника 2 класса.

3 марта 2023Фидаша

#2 класс
#Чтение
#Проверочная работа

То, что мы пройдём, кто уже знает

А кто же из первоклашек и второклашек знает программу которую, мы будем проходить.

1 марта 2023Фидаша

#6 класс
#Природоведение
#Проверочная работа
#Проверочная работа за четверть
#Итоговое тестирование

Вода в природе

Тест по природоведению предназначен для обучающихся 6 класса коррекционной школы VIII вида.

28 февраля 2023Фролова Елена Николаевна

#1 класс
#Проверочная работа

Тест по бравл старсу

Добро пожаловать! Тут тест по всем известной игре Бравл старс

25 февраля 2023

#8 класс
#Русский язык
#Проверочная работа

Тест по русскому языку. 8 класс. «Проверь себя!» . Тема урока «Отличительные черты обстоятельства».

Данный тест используется на уроке по русскому языку в 8 классе по теме «Отличительные черты обстоятельства» на этапе закрепления учебного материала. Цель: уметь применять новые знания на практике; установить правильность и осознанность изученного материала. Тренировать способность к самоконтролю и самооценке. Тест состоит из 5 заданий. Задание для обучающихся: выполните тестовую работу, выберите правильные варианты ответов.

14 февраля 2023Юркина Людмила Владимировна

#5 класс
#Литература
#Проверочная работа

Биография М.Ю. Лермонтова

Тест может быть использован в виде проверочной работы по биографии поэта

9 февраля 2023Татьяна Сергеевна Корепанова

#9 класс
#Обществознание
#Подготовка к ОГЭ

Тест по обществознанию (ОГЭ-2023)

В тест вошли вопросы 1 части пробников (9238, 9239, 9240)

8 февраля 2023Уразалеев Руслан Фаритович

#10 класс
#История
#Проверочная работа

Латинская Америка в первой половине ХХ в.

В тест для 10-го класса вошли такие темы, как «Особенности общественного развития», «Мексика», «Кубинская революция 1933-1934 гг.», «Демократии и диктатуры».

4 февраля 2023Уразалеев Руслан Фаритович

#8 класс
#Обществознание
#Проверочная работа

Современный работник

Тест по обществознанию составлен для учащихся 8 класса и включает в себя такие темы, как «Профессионализм», «Проблемы занятости», «Выбор жизненного пути», «Готовимся выбирать профессию».

21 января 2023Уразалеев Руслан Фаритович

#8 класс
#История
#Проверочная работа

Причины нестабильности политического строя.

В тест по истории России вошли такие темы, как «Причины и сущность дворцовых переворотов», «Екатерина I», «Пётр II», «Верховники».

21 января 2023Уразалеев Руслан Фаритович

#3 класс
#Русский язык
#Проверочная работа

«Слово в языке и речи»

Тест по русскому языку (3 класс)

17 января 2023Семирунняя Светлана Сергеевна

#5 класс
#Русский язык
#Проверочная работа

Тест по русскому языку «Разделы русского языка»

Тест по русскому языку «Разделы русского языка» для 5 класса

14 января 2023Александр Владимирович Жуковский

#9 класс
#Труд
#Проверочная работа

Пастбища. Виды пастбищ

Тест предназначен для учеников коррекционных школ, 9 класс, сельскохозяйственный труд

11 января 2023Павлова Елена Николаевна

#9 класс
#Труд
#Проверочная работа

Болезни и вредители огурца

Тест предназначен для проверки знаний обучающихся с ОВЗ 9 класса коррекционной школы

11 января 2023Павлова Елена Николаевна

#8 класс
#Информатика и ИКТ
#Проверочная работа

Основы алгоритмизации

Подготовка к контрольной работе

7 января 2023Иванова Марина

#1 класс
#Математика
#Проверочная работа

Счёт в пределах 20.

Классический тест на проверку вычислительных навыков в пределах 20.

7 января 2023Рита

#6 класс
#Математика
#Проверочная работа

Десятичные дроби и проценты

Тест состоит из 10 вопросов.

26 декабря 2022Костицина Инна Геннадьевна

#11 класс
#Русский язык
#Подготовка к ЕГЭ

Тест по русскому языку 11 класс

Задание 10 ЕГЭ русский язык

25 декабря 2022Цыбульникова Ольга Михайловна

#10 класс
#Правоведение
#Проверочная работа
#Проверочная работа за четверть

Тест по дисциплине «Правовое обеспечение профессиональной деятельности»

Тест по основам трудового и гражданского права

12 декабря 2022Татьяна Алексеевна

#9 класс
#Геометрия
#Проверочная работа

Соотношение в прямоугольном треугольнике

11 декабря 2022Ахременко Марина Анатольевна

Второй закон термодинамики

Одним из первых ученых, заинтересовавшихся тепловыми двигателями, был француз. инженер по имени Сади Карно (1796-1832). Тепловая машина использует теплопередачу совершать работу в циклическом процессе. После каждого цикла двигатель возвращается в исходное состояние и готов повторить процесс преобразования (неупорядоченный —> упорядоченная энергия) снова.

Карно предполагал, что идеальный двигатель, преобразующий максимальное количество теплового энергии в упорядоченную энергию, будет двигатель без трения. Это также было бы реверсивный двигатель . Само по себе тепло всегда исходит от объекта более высокой температуры к объекту с более низкой температурой. Реверсивный двигатель это двигатель, в котором теплопередача может менять направление, если температура один из объектов изменяется на крошечную (бесконечно малую) величину. Когда реверсивный двигатель заставляет тепло поступать в систему, оно течет в результате бесконечно малые перепады температур, или потому что существует бесконечно малая работа, совершаемая системой. Если бы такой процесс мог быть реально реализуемый, он будет характеризоваться непрерывным состоянием равновесие (т. е. отсутствие перепадов давления или температуры) и будет происходит с такой скоростью, что требует бесконечного времени. Импульс любой компонент обратимого двигателя никогда не изменяется скачком в неупругом столкновение, так как это привело бы к необратимому, внезапному увеличению неупорядоченная энергия этого компонента. Настоящий двигатель всегда включает в себя по крайней мере небольшое количество необратимости. Тепло не будет течь без перепад температур и трение не могут быть полностью устранены.

Карно показал, что если идеальная обратимая машина, называемая двигателем Карно , улавливает количество теплоты Q ₁ из резервуара при температуре T ₁ , преобразует часть его в полезную работу и отдает количество теплоты Q ₂ в пласт при температуре T ₂ , тогда Q ₁ /T ₁ = Q ₂ /T ₂ . Здесь T – абсолютная температура, измеренная в Кельвина, а резервуар тепла — это система, такая как озеро, которая настолько велика, что его температура не меняется при выделении тепла, участвующего в рассматриваемом процессе течет в водохранилище или из него. Для преобразования теплоты в работу необходимо при не менее двух мест с разной температурой. Если вы возьмете Q ₁ в температура T ₁ необходимо сбросить не менее Q ₂ при температуре T ₂ .

Карно постулировал, что теплота не может быть поглощена при определенной температуре без другие изменения в системе и преобразованы в работу. Это один из способов указать второй закон термодинамика.

Реверсивные двигатели

Пример идеализированного двигателя без трения, в котором все процессы обратимы, представляет собой идеальный газ в цилиндре, снабженном поршень. Цилиндр попеременно входит в контакт с одним из двух тепловых резервуары при температуре Т ₁ и Т ₂ соответственно, с Т ₁ выше Т ₂ .

(1) Мы начинаем с точки a на диаграмме PV. Ставим цилиндр контакт с пластом на Т ₁ и _{нагреть газ и
в то же время расширяйте его по кривой, отмеченной (1). Чтобы сделать
процесс обратимый, мы вытягиваем поршень очень медленно по мере поступления тепла в
газа и следим за тем, чтобы температура газа оставалась примерно равной T ₁ .
Если бы мы медленно вталкивали поршень обратно, то температура была бы только
быть бесконечно мало больше, чем T ₁ , и тепло будет течь
обратно из газа в резервуар. Изотермическое расширение ,
когда делается достаточно медленно, может быть обратимым процессом.
Кривая, отмеченная (1) от точки а до точки b, говорит нам, как
давление и объем изменяются, если температура остается фиксированной на значении T ₁ . Для идеального газа эта кривая имеет вид PV = NkT ₁ .
По мере увеличения объема давление падает.
Как только мы достигнем точки b на диаграмме, количество теплоты Q ₁ будет
переводится из резервуара в газ. С момента расширения
изотермическая, температура газа не изменилась, ΔU = 0 и ΔQ ₁ = ΔW.}

ΔQ ₁ = ΔW = ∫ _a ^b PdV = ∫ _a ^b (Nk _B T ₁ /V) = Nk _B T ₁ пер(V _b /V _a ).

ΔQ ₁ = Q ₁ положителен, тепло поступает в газ в цилиндр.
(2) Отнимем цилиндр от резервуара в точке b и продолжим медленно, обратимое расширение без поступления тепла в цилиндр. Расширение сейчас адиабатический . По мере расширения газа температура падает, так как в цилиндр не поступает тепло. Мы пусть газ расширяется, следуя кривой, отмеченной (2), пока температура не упадет до T ₂ в точке с пометкой c . Адиабатическая кривая имеет более отрицательный наклон, чем изотермическая кривая. Для адиабатического расширения идеального газа, состоящего из точечных частиц, мы имеем ΔU = -ΔW, так как ΔQ = 0. Следовательно,

dU = -dW = -PdV.

Но у нас тоже есть

U = Н½м 2 >,

, поскольку внутренняя энергия представляет собой случайную кинетическую энергию атомов газа. Используя, из кинетическая теория, PV = (2/3)N½m 2 > у нас есть

U = (3/2)PV.

Тогда из исчисления имеем

dU = (3/2)(PdV + VdP).

Приравнивая наши два выражения для dU, мы получаем

-ПдВ = (3/2)(ПдВ + ВдП),
(-5/2)PdV = (3/2)VdP,
dP/P + (5/3)dV/V = 0,

Мы можем интегрировать, чтобы получить lnP + (5/3)lnV = lnC, где lnC — постоянная интегрирования. Это дает

PV ^5/3 = C = константа

для адиабатического расширения идеального газа. С PV = NkT мы можем записать PV ^5/3 = NkTV ^2/3 = C или TV ^2/3 = константа. Поэтому

T ₁ В _b ^2/3 = T ₂ В _c ^2/3 или V _b /V _c = (T ₂ /T ₁ ) ^-2/3 .

(3) Когда газ достигает температуры T ₂ мы связались с резервуар на Т ₂ . Теперь мы медленно сжимаем газ изотермически при этом он находится в контакте с резервуаром в точке T ₂ , по отмеченной кривой (3). Температура газа не повышается и выделяется количество теплоты ΔQ ₂ из баллона в резервуар при температуре T ₂ . Для изотермических процесс у нас есть

ΔQ ₂ = ΔW = ∫ _в ^d PdV = ∫ _в ^d (Nk _B T ₂ /V) dV = Nk _B T ₂ ln(V _d /V _c ).

ΔQ ₂ = -Q ₂ отрицательна, теплота отводится от газа в цилиндр.
(4) В точке d извлекаем цилиндр из резервуара в точке T ₂ и сжать его еще больше, не выпуская тепла. Во время этого адиабатический процесс температура повышается, а давление следует кривой, отмеченной (4). Если мы несем правильно проделав каждый шаг, мы можем вернуться в точку a при температуре T ₁ где мы начали, и повторите цикл. Для адиабатического процесса из точки d в точку а имеем

T ₂ V _d ^2/3 = T ₁ V _a ^2/3 или V _a /V _d = (T ₂ /T ₁) ^-2/3.

Поэтому

V _a /V _d = V _b /V _c , V _b /V _a = V _c /V _d , и ln(V _b /V _a )= ln(V _c /V _{d)
= -ln(V _d /V _c ).}

При переходе из точки а в точку с газ расширяется и совершает работу. При переходе из точки c Вернемся к точке, над которой совершается работа над газом. Совершенная работа всегда равна площади под кривой на диаграмме ПВ. Суммарная работа, выполненная газом, обозначена желтой областью рисунка. Поскольку все, что мы сделали, обратимо, мы могли бы пойти и вспять. форвардов по циклу. Тогда площадь под кривой будет представлять собой чистая сумма работы, выполненной над газом.

За один цикл мы вложили в газ количество теплоты Q ₁ при температуры T ₁ и отдали количество теплоты Q ₂ при температура T ₂ . Из приведенных выше уравнений мы видим, что

Q ₁ /Q ₂ = (T ₁ ln(V _b /V _a ))/(T ₂ ln(V _{d _{/V 9))
= Т ₁ /Т ₂ или}}

Q ₁ /T ₁ = Q ₂ /T ₂ .

Мы показали, что если наш идеальный обратимый двигатель наберет количество теплоты Q ₁ из резервуара при температуре T ₁ и отдает количество теплоты Q ₂ в пласт при температуре T ₂ , тогда Q ₁ /T ₁ = Q ₂ /T ₂ . Работа, проделанная двигатель на своем окружении W = Q ₁ — Q ₂ = Q ₁ (1 — T ₂ / Т ₁ ).

Теперь предположим, что у нас есть другой двигатель, который принимает Q ₁ при T ₁ , работает W’ и отдает некоторое количество тепла при T ₂ . Если бы W’ было больше, чем работа W нашего обратимого двигателя, то мы могли бы использовать W, чтобы запустить наш обратимый двигатель в обратном направлении. и поместите Q ₁ обратно в резервуар по адресу T ₁ . Тогда все, что мы хотели бы эффективно сделать, запустив оба двигателя, это отобрать тепло из резервуара на Т ₂ и полностью превратил ее в полезную работу W’ — W. Но согласно второму закону термодинамики невозможно получить полезные работа от резервуара при одной температуре без каких-либо других изменений. Тепло не может быть поглощено при определенной температуре без каких-либо других изменений в системы и преобразуется в работу. Следовательно, ни один двигатель, поглощающий заданное количество тепла от более высокой температуры T ₁ и подает при более низкой температуре T ₂ может выполнять больше работы, чем реверсивный двигатель, работающий при той же температуре условия. Если наш второй двигатель тоже реверсивный, то W’ должно быть равно W, или мы могли бы обратить приведенный выше аргумент вспять. Если оба двигателя реверсивные, они оба должны выполнять одинаковую работу, и Q ₁ /T ₁ = Q ₂ /T ₂ для обоих двигателей. Если двигатель реверсивный, то не имеет значения, как он устроен. Количество работы, которую он совершает, поглощая заданное количество теплоты при температуре T ₁ и отдает тепло при другой температуре T ₂ не отдает зависит от конструкции двигателя. Это достояние мира, не является свойством конкретного двигателя.

Полезная работа, совершаемая любой тепловой машиной, поглощающей тепло при температуре T ₁ и отдавать тепло при температуре T ₂ равно
W = Q ₁ — Q ₂ (энергосбережение). W положителен, если T ₁ больше T ₂ .
Все обратимые тепловые машины, поглощающие тепло при температуре T ₁ и отдают тепло при температуре T ₂ делают столько же полезная работа,

Вт _макс. = Q ₁ — Q ₂ = Q ₁ — Q ₁ T ₂ / T ₁ = Q ₁ (1 — T ₂ / Т ₁ ).

Любой реальный двигатель выделяет больше тепла Q ₂ на водохранилище Т ₂ чем обратимый и, следовательно, совершает меньшую полезную работу.

максимальный объем работы вы можете поэтому выйти из тепловой машины — это то количество, которое вы получите от идеального, реверсивный двигатель.

КПД тепловой машины – это отношение полученной работы к тепловой энергии, вложенной при высокой температуре, e = W/Q _{высокий} . Максимально возможная эффективность e _макс таких двигатель

e _макс = W _макс /Q _{высокий} = (1 — T _низкий /T _{высокий} ) = (T _{высокий} — T _низкий )/T высокий .

Предположим, у вас есть резервуар с горячей водой с температурой T ₁ . Можете ли вы взять количество теплоты Q ₁ из этого резервуара и преобразовать это в работу? Нет! Вы можете преобразовать часть теплоты в работу, если у вас место при более низкой температуре Т ₂ куда можно сбросить часть жара. Двигатель, работающий за счет отвода тепла от резервуара с одной температуры быть не может.

Тепло не может быть поглощено при определенной температуре без каких-либо других изменений в системе и превращается в работу. Это один из способов сформулировать второй закон термодинамики.

Теплота сама по себе не может передаваться от холодного к горячему предмету. способ сформулировать второй закон термодинамики.

Если бы это было возможно, то тепло, сбрасываемое на T ₂, могло бы просто утекать обратно в водохранилище на T ₁ и чистый эффект будет количество тепла ΔQ = Q ₁ — Q ₂ a T ₁ и преобразуется в тепло без каких-либо других изменений в системе.

Проблема:

Определенный бензиновый двигатель имеет КПД 30,0%. Что бы температура горячего резервуара должна быть для двигателя Карно с таким КПД, если работает при температуре холодного пласта 200 ^или С?

Решение:

Рассуждение:
Для двигателя Карно Q ₁ /T ₁ = Q ₂ /T ₂ .
Двигатель Карно имеет максимальный КПД e _max = (T _high — T _low )/T _high .
Детали расчета:
Если e _max = 0,3, то 0,3 = 1 — (473 K)/T _high . Т _{высокий} = 473/0,7 = 675,7 К = 402,7·^или С.

Проблема:

Изобретатель продает устройство и утверждает, что оно потребляет 25 кДж тепла при 600 К, передает в окружающую среду теплоту 300 К и совершает работу 12 кДж. Стоит ли инвестировать в это устройство?

Решение:

Рассуждение:
Двигатель Карно, потребляющий 25 кДж тепла и работающий при температуре от 600 до 300 К. может выполнить объем работы
Вт _макс. = Q _{высокий} (1 — T _низкий / T _{высокий} ) = 25 кДж*(1 — 300/600) = 25 кДж/2 = 12,5 кДж.
Утверждается, что эффективность устройства составляет 96% от e _max . Нет известный двигатель приближается к e _max. Трение и прочее потери снижают эффективность. Так что пока не запрещено вторым закона, маловероятно, что устройство будет работать так, как заявлено.

Примечание:
Неупорядоченная энергия не может быть полностью преобразована обратно в упорядоченную энергию.
Максимальный КПД тепловой машины, преобразующей тепловую энергию в упорядоченную, равен 100%*(T _{высокий} — T _низкий )/T _{высокий} .
Здесь T _high и T _low — самая высокая и самая низкая температура. доступным для двигателя.

С другой стороны, упорядоченная энергия может быть полностью преобразована в другие формы энергии. Максимальный КПД двигателя, использующего упорядоченную энергию составляет 100%.

Цикл Карно — Химия LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 1962

В начале 19 века паровые машины стали играть все более важную роль в промышленности и на транспорте. Однако систематический набор теорий преобразования тепловой энергии в движущую силу паровыми двигателями еще не был разработан. Николя Леонар Сади Карно (1796-1832), французский военный инженер, опубликовал в 1824 году «Размышления о движущей силе огня ». известный как цикл Карно. Карно разработал основу второго закона термодинамики, и его часто называют «отцом термодинамики».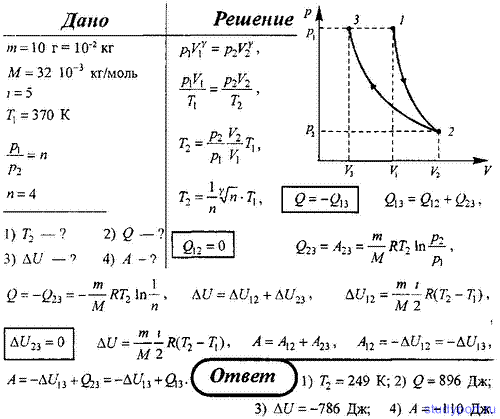

Цикл Карно

Цикл Карно состоит из следующих четырех процессов:

Процесс обратимого изотермического расширения газа. В этом процессе идеальный газ в системе поглощает количество тепла \(q_{in}\) от источника тепла при высокой температуре \(T_{high}\), расширяется и совершает работу с окружающей средой.
Процесс обратимого адиабатического расширения газа. При этом система теплоизолируется. Газ продолжает расширяться и совершать работу с окружающей средой, что приводит к охлаждению системы до более низкой температуры, \(T_{low}\).
Процесс обратимого изотермического сжатия газа. В этом процессе окружающая среда совершает работу с газом при \(T_{low}\) и вызывает потерю тепла, \(q_{out}\).
Процесс обратимого адиабатического сжатия газа. При этом система теплоизолируется. Окружающая среда продолжает совершать работу с газом, из-за чего температура снова поднимается до \(T_{high}\).

Рисунок \(\PageIndex{1}\): Модель идеального газового поршня цикла Карно.

(CC BY 4.0; XiSen Hou через колледж Хоуп)

Диаграмма PV

Диаграмма PV цикла Карно показана на рисунке \(\PageIndex{2}\). В изотермических процессах I и III ∆U=0, так как ∆T=0. В адиабатических процессах II и IV q=0. Работа, теплота, ∆U и ∆H каждого процесса в цикле Карно суммированы в таблице \(\PageIndex{1}\).

Рисунок \(\PageIndex{2}\): PV-диаграмма цикла Карно.

Таблица \(\PageIndex{1}\): работа, теплота, ∆U и ∆H на диаграмме P-V цикла Карно.
Процесс	ш	q	ΔU	ΔН
Я	\(-nRT_{высокий}\ln\left(\dfrac{V_{2}}{V_{1}}\right)\)	\(nRT_{high}\ln\left(\dfrac{V_{2}}{V_{1}}\right)\)	0	0
II	\(n\bar{C_{v}}(T_{низкий}-T_{высокий})\)	0	\(n\bar{C_{v}}(T_{низкий}-T_{высокий})\)	\(n\bar{C_{p}}(T_{низкий}-T_{высокий})\)
III	\(-nRT_{low}\ln\left(\dfrac{V_{4}}{V_{3}}\right)\)	\(nRT_{low}\ln\left(\dfrac{V_{4}}{V_{3}}\right)\)	0	0
IV	\(n\bar{C_{v}}(T_{высокий}-T_{низкий})\)	0	\(n\bar{C_{v}}(T_{высокий}-T_{низкий})\)	\(n\bar{C_{p}}(T_{высокий}-T_{низкий})\)
Полный цикл	\(-nRT_{высокий}\ln\left(\dfrac{V_{2}}{V_{1}}\right)-nRT_{low}\ln\left(\dfrac{V_{4}}{V_ {3}}\справа)\)	\(nRT_{высокий}\ln\left(\dfrac{V_{2}}{V_{1}}\right)+nRT_{low}\ln\left(\dfrac{V_{4}}{V_{ 3}}\справа)\)	0	0

Диаграмма T-S

Диаграмма T-S цикла Карно показана на рисунке \(\PageIndex{3}\). В изотермических процессах I и III ∆T=0. В адиабатических процессах II и IV ∆S=0, так как dq=0. ∆T и ∆S каждого процесса в цикле Карно показаны в таблице \(\PageIndex{2}\).

Рисунок \(\PageIndex{3}\): T-S диаграмма цикла Карно. (CC BY 4.0; XiSen Hou через колледж Хоуп)

Таблица \(\PageIndex{1}\): работа, теплота и ∆U на диаграмме T-S цикла Карно.
Процесс	ΔТ	ΔS
Я	0	\(-nR\ln\left(\dfrac{V_{2}}{V_{1}}\right)\)
II	\(T_{низкий}-T_{высокий}\)	0
III	0	\(-nR\ln\left(\dfrac{V_{4}}{V_{3}}\right)\)
IV	\(T_{высокий}-T_{низкий}\)	0
Полный цикл	0	0

Эффективность

Цикл Карно является наиболее эффективным из возможных двигателей, основанным на допущении об отсутствии побочных расточительных процессов, таких как трение, и допущении об отсутствии теплопроводности между различными частями двигателя при разных температурах. КПД двигателя Карно определяется как отношение выходной энергии к подводимой энергии. 9{C_{V}/R}=\dfrac{V_{4}}{V_{1}}\]

И так как T ₁ = T ₂ и T ₃ = T ₄ ,

\[\dfrac{V_{3}}{V_{4}}=\dfrac{V_{2}}{V_{1}}\]

Следовательно,

\[ \text{эффективность}=\dfrac{nRT_{высокий}\ln\left(\dfrac{V_{2}}{V_{1}}\right)-nRT_{low}\ln\left(\dfrac{V_{ 2}}{V_{1}}\right)}{nRT_{high}\ln\left(\dfrac{V_{2}}{V_{1}}\right)}\]

\[\boxed{ \text{эффективность}=\dfrac{T_{высокий}-T_{низкий}}{T_{высокий}}}\]

Резюме

Цикл Карно имеет максимально возможный КПД двигателя (хотя другие циклы имеют такой же КПД) на основе предположения об отсутствии побочных расточительных процессов, таких как трение, и предположения об отсутствии теплопроводности между различными частей двигателя при различных температурах.

Проблемы

Сейчас вы работаете с двигателем Карно с КПД 40%, который отводит тепло в радиатор при температуре 298 К. Если вы хотите увеличить КПД двигателя до 65%, до какой температуры вам придется поднять резервуар для тепла?
Двигатель Карно поглощал 1,0 кДж тепла при температуре 300 К и выделял 400 Дж тепла в конце цикла. Какая температура в конце цикла?
Внутренний обогреватель, работающий по циклу Карно, нагревает дом со скоростью 30 кДж/с, поддерживая внутреннюю температуру на уровне 72 ºF. Какова мощность нагревателя, если температура наружного воздуха 30 ºF?

Ссылки

Goldstein, M. J. Chem. Образовательный , 1980 , 57, 114-116
Bader, M. J. Chem. Образовательный , 1973 , 50 , 834
В. Ф. Людер. J. Chem. Образовательный , 1944 , 21 , 600-601
Salter, C. J. Chem. Образовательный , 2000 , 77, 1027-1030

Цикл Карно распространяется под лицензией CC BY 4.

Задачи на первый закон термодинамики

Тесты для педагогов по всем школьным предметам с ответами