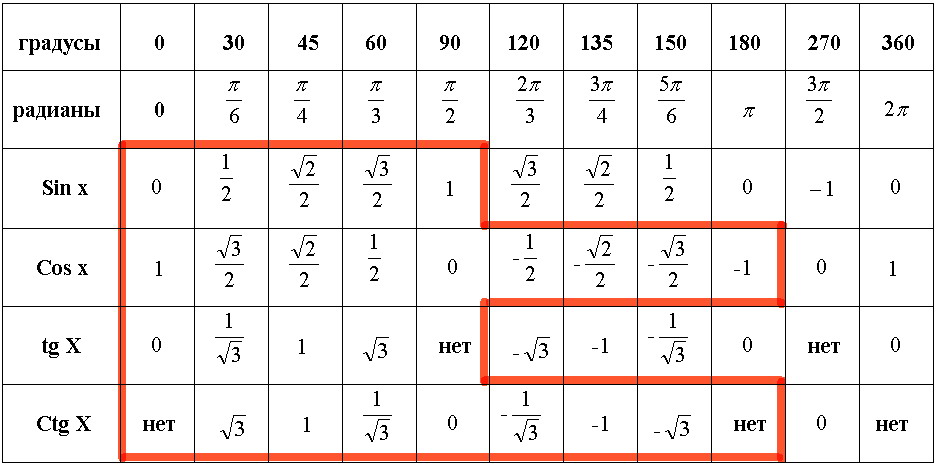
Таблица косинусов (полная, градусы и значения)
В данной таблице представлены значения косинусов от 0° до 360°. Таблица косинусов нужна, чтобы узнать, чему равен косинус угла. Нужно только найти его в таблице. Для начала короткая версия таблицы.
https://uchim.org/matematika/tablica-kosinusov — uchim.org
Таблица косинусов для 0°-180°
|
|
|
Таблица косинусов для 181°-360°
|
|
|
Как легко запомнить таблицу косинусов (видео)
Существуют также следующие таблицы тригонометрических функций: таблица синусов, таблица тангенсов и таблица котангенсов.
Всё для учебы » Математика в школе » Таблица косинусов (полная, градусы и значения)
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim. org/matematika/tablica-kosinusov
org/matematika/tablica-kosinusov
Тригонометрические тождества
Возможно, сначала вы захотите прочитать о тригонометрии!
Прямоугольный треугольник
Тригонометрические тождества — это уравнения, которые верны для прямоугольных треугольников. (Если это не прямоугольный треугольник, перейдите на страницу «Тождества треугольников».)
Каждая сторона прямоугольного треугольника имеет имя:
И Противоположный угол находится напротив угла
Скоро мы будем играть со всевозможными функциями, но помните, что все возвращается к простому треугольнику с:
- Угол θ
- Гипотенуза
- Смежный
- Напротив
Синус, косинус и тангенс
Три основные функции в тригонометрии — это синус, косинус и тангенс.
Они просто длины одной стороны разделить еще на
Для прямоугольного треугольника с углом θ :
Функция синуса: | sin( θ ) = Противоположность / Гипотенуза |
Функция косинуса: | cos( θ ) = Смежный / Гипотенуза |
Касательная функция: | tan( θ ) = Противоположный / Смежный |
Для заданного угла θ каждое отношение остается одним и тем же
независимо от того, насколько велик треугольник или мал
Когда мы делим синус на косинус, мы получаем: (θ) = противоположность/гипотенуза соседний/гипотенуза = противоположность соседний
, так что мы можем сказать:
Tan (θ) = SIN (θ) 11112 COS111 2 COS (θ) = SIN (θ) 111112 COS111 2 COS112.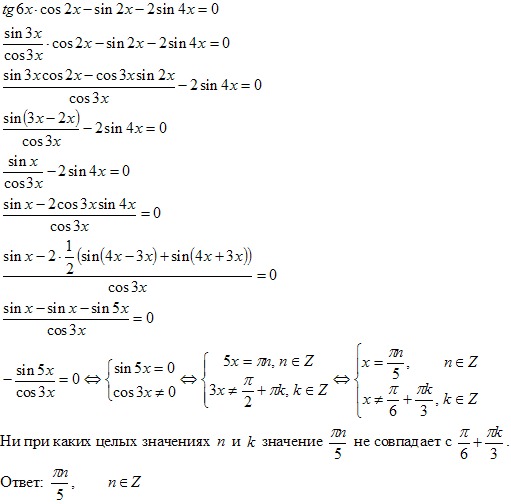 θ)
θ)
Это наша первая тригонометрическая идентичность .
Cosecant, Secant и Cotangent
Мы также можем разделить «Другой путь» (например, прилегающий/противоположный вместо напротив/соседнего ):
Функция: | |
. | csc( θ ) = гипотенуза / напротив |
| сек( θ ) = Гипотенуза / Смежный | |
Функция котангенса: | детская кроватка( θ ) = рядом / напротив |
Пример: когда Противоположность = 2 и Гипотенуза = 4, тогда
sin(θ) = 2/4 и csc(θ) = 4/2
Из-за всего, что мы можем сказать:
sin(θ) = 1/csc(θ)
cos(θ) = 1/сек(θ)
tan(θ) = 1/cot(θ)
И наоборот:
csc(θ) = 1/sin(θ)
sec(θ) = 1/cos(θ)
cot(θ) = 1/tan(θ)
А также имеем:
cot(θ) = cos(θ)/sin(θ)
Теорема Пифагора
Следующие тригонометрические тождества начнем с теоремы Пифагора:
Теорема Пифагора утверждает, что в прямоугольном треугольнике, квадрат a плюс квадрат b равен квадрату c: а 2 + б 2 = в 2 |
Деление на c 2 дает
и 2
Можно упростить до:
( и с ) 2 + ( б в ) 2 = 1
Сейчас A / C — противоположность / гипотенуза , который составляет SIN (θ)
и B / C — , находящийся в состоянии / гипотенсию , что составляет COS (COS (COS (COS (COS (COS (COS (COS (COS (COS (COS (COS (COS (COS (COS (COS (COS ( θ)
Итак (a/c) 2 + (b/c) 2 = 1 также можно записать:
sin 2 θ + cos 2 θ1 = 1 9000
- sin 2 θ означает найти синус θ, затем возвести результат в квадрат и
- sin θ 2 означает возведение в квадрат θ, затем выполняет функцию синуса
Пример: 32°
Использование Только 4 знака после запятой :
- sin(32°) = 0,5299.
 ..
.. - cos(32°) = 0,8480…
Теперь вычислим sin 2 θ + cos 2 θ :
0,5299 2 + 0,8480 2
= 0,2808… + 0,7191…
Мы получаем очень близко к 1, используя только 4 знака после запятой. Попробуйте это на ваш калькулятор , вы можете получить лучшие результаты!
Связанные идентификаторы включают в себя:
SIN 2 θ = 1 — COS 2 θ
COS 2 θ = 1 — SIN 2 θ
TAN 2 θ + 10232. 2 2 2 310231 2 3153153115 2 θ 31315315315 3 θ 315315315 2 θ 3. 2 θ . загар 2 θ = сек 2 θ — 1
COT 2 θ + 1 = CSC 2 θ
COT 2 θ = CSC 2 θ — 1
Но подождите.
 .. Это еще не все!
.. Это еще не все!Идентификаций гораздо больше… вот некоторые из наиболее полезных:
Тождества противоположных углов
sin(−θ) = −sin(θ)
cos(−θ) = cos(θ)
tan(−θ) = −tan(θ)
Тождества двойного угла
Тождества половинных углов
Обратите внимание, что «±» означает, что может быть либо одно , в зависимости от значения θ/2
Тождества суммы и разности углов , и средства для использования противоположного знака.
sin(A B) = sin(A)cos(B) cos(A)sin(B)
cos(A B) = cos(A)cos(B) sin(A)sin(B)
tan(A B) = tan(A) tan(B) 1 tan(A)tan(B)
кроватка(A B) = кроватка(A)кроватка(B) 1 кроватка(B) кроватка(A)
Тождества треугольников
Существуют также тождества треугольников, которые применимы ко всем треугольникам (не только прямоугольным). Треугольники)
Сводка тригонометрических тождеств
Сводка тригонометрических тождествВы видели довольно много тригонометрических тождеств на последних нескольких страницах.
 Удобно иметь их сводку для справки. Эти тождества в основном относятся к одному углу, обозначенному t, , но есть несколько из них, включающих два угла, и для них другой угол обозначается
Удобно иметь их сводку для справки. Эти тождества в основном относятся к одному углу, обозначенному t, , но есть несколько из них, включающих два угла, и для них другой угол обозначается Более важные личности
Вам не нужно знать все личности навскидку. Но это вы должны.- Определение отношений тангенса, котангенса, секанса и косеканса через синус и косинус.
тан т = sin t
cos tдетская кроватка т = 1
тан т= cos t
sin tсек t = 1
cos тcsc т = 1
sin t- Формула Пифагора для синусов и косинусов.

sin 2 t + cos 2 t = 1
- Тождества, выражающие триггерные функции через их дополнения
cos t = sin(/2 t ) sin t = cos(/2 t )
детская кроватка t = загар(/2 т ) загар t = кроватка (/2 t )
csc t = сек(/2
- Периодичность триггерных функций. Синус, косинус, секанс и косеканс имеют период 2, а тангенс и котангенс имеют период.
sin ( t + 2) = sin t
cos ( t + 2) = cos т
тангенс ( t +) = тангенс t
- Тождества для отрицательных углов. Синус, тангенс, котангенс и косеканс — нечетные функции, а косинус и секанс — четные функции.
sin t = sin t
cos t = cos t
тан t = тангенс t
- Формулы сумм для синуса и косинуса
sin ( s +
cos ( s + t ) = cos s cos t sin s sin t
- Формулы двойного угла для синуса и косинуса
sin 2 t = 2 sin t cos t
соз 2 t = cos 2 t sin 2 t = 2 cos 2 t 1 = 1 2 sin 2 t
Менее важные личности
Вы должны знать, что эти личности есть, но они не так важны, как упомянутые выше. Все они могут быть получены из приведенных выше, но иногда для этого требуется некоторая работа.
Все они могут быть получены из приведенных выше, но иногда для этого требуется некоторая работа.- Формула Пифагора для тангенсов и секансов.
сек 2 t = 1 + танк 2 t
- Тождества, выражающие триггерные функции через их дополнения
sin( t ) = sin t
cos( t ) = cos t
тангенс( t ) = тангенс t
- Разностные формулы для синуса и косинуса
sin ( s t ) = sin s cos t cos s sin t
cos ( s t ) = cos s cos t + sin s sin t
- Формулы суммы, разности и двойного угла для тангенса
тангенс ( s + t ) = желто-коричневый s + + желто-коричневый t
1 желто-коричневый s желто-коричневый tтангенс ( с t ) = коричневый s коричневый t
1 + коричневый s коричневый tтангенс 2 t = 2 коричневый t
1 коричневый 2 t- Формулы половинного угла
sin t /2 = ±((1 cos t ) / 2)
cos t /2 = ±((1 + cos т ) / 2)
tan t /2 = sin t
1 + cos t= 1 cos t
sin t
Действительно неясные тождества
Они просто здесь для извращенности.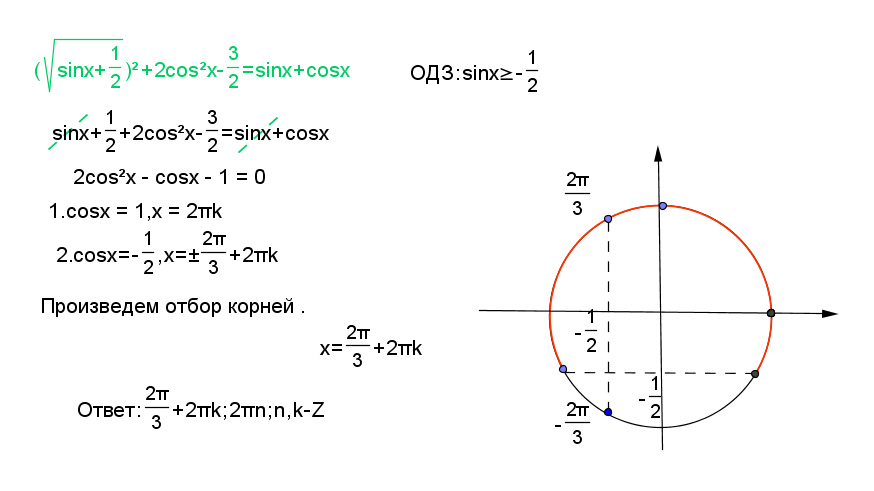 Да, конечно, у них есть кое-какие приложения, но обычно это узкие приложения, и о них вполне можно было бы забыть до тех пор, пока они не понадобятся.
Да, конечно, у них есть кое-какие приложения, но обычно это узкие приложения, и о них вполне можно было бы забыть до тех пор, пока они не понадобятся.- Тождества суммы произведений
sin s + sin t = 2 sin s + t
2cos s t 7 sin s sin t = 2 cos s + t
2sin s t
2cos s + cos t = 2 COS S + T
2COS S T
2cos s cos t = 2 SIN S + T
2SIN S T
2- Личность продукта.

sin s cos t = sin ( s + t ) + sin ( s t )
2cos с cos t = cos ( s + t ) + cos ( s t )
2sin с sin t = cos ( с t ) cos ( s + t )
2В стороне: как ни странно, эти идентификаторы продуктов использовались до логарифмов для выполнения умножения. Вот как можно использовать второй. Если вы хотите умножить x на y, используйте таблицу, чтобы найти угол s , косинус которого равен x , и угол t , косинус которого равен y.  Найдите косинусы суммы с + т, и разница с т. Среднее значение этих двух косинусов. Вы получаете товар xy ! Три поиска в таблице и вычисление суммы, разности и среднего, а не одного умножения. Тихо Браге (1546-1601), среди прочих, использовал этот алгоритм, известный как prosthaphaeresis. )
Найдите косинусы суммы с + т, и разница с т. Среднее значение этих двух косинусов. Вы получаете товар xy ! Три поиска в таблице и вычисление суммы, разности и среднего, а не одного умножения. Тихо Браге (1546-1601), среди прочих, использовал этот алгоритм, известный как prosthaphaeresis. )- Формулы тройного угла. Вы можете легко реконструировать их по формулам сложения и двойного угла.
- sin 3 t = 3 sin t 4 sin 3 t
cos 3 t = 4 cos 3 t 3 cos t
7 Еще формулы полууглов. (Они используются в исчислении для особого вида подстановок в интегралах, иногда называемых Вейерштрассом 9).тан 3 т = 3 тангенс t тангенс 3 t
1 3 тангенс 2 t 0009 т -замена.)
0009 т -замена.)sin t = 2 коричневый t /2
1 + коричневый 2 t /2
cos t = 1 желто-коричневый 2 t /2
1 + желтовато-коричневый 2 t /2
тангенс t = 2 коричневый t /2
1 коричневый 2 т /2
Оглавление.
© 1996, 1997.
Дэвид Э. Джойс
Кафедра математики и информатики
Университет Кларка
Вустер, Массачусетс 01610
Электронная почта: [email protected]
Краткий триггерный курс Дейва находится по адресу http://aleph0.

 9703
9703 7771
7771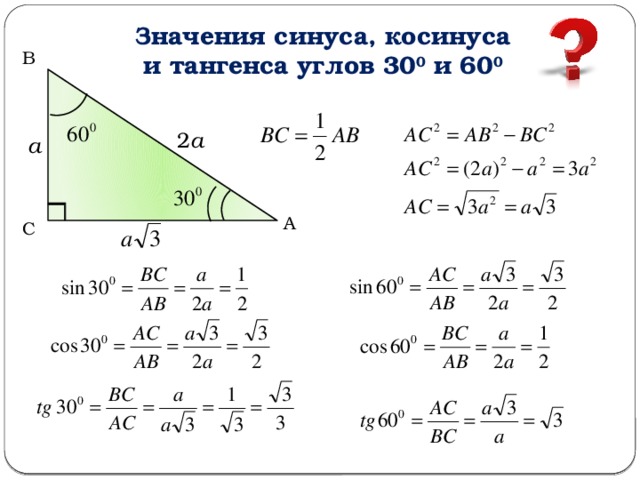 454
454 0349
0349 3746
3746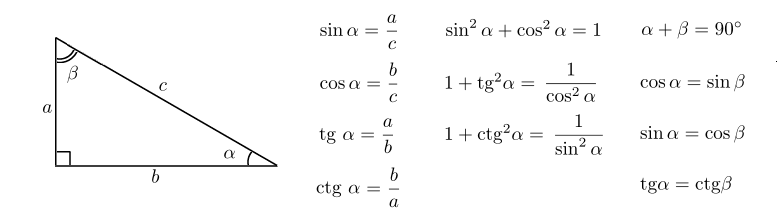 7071
7071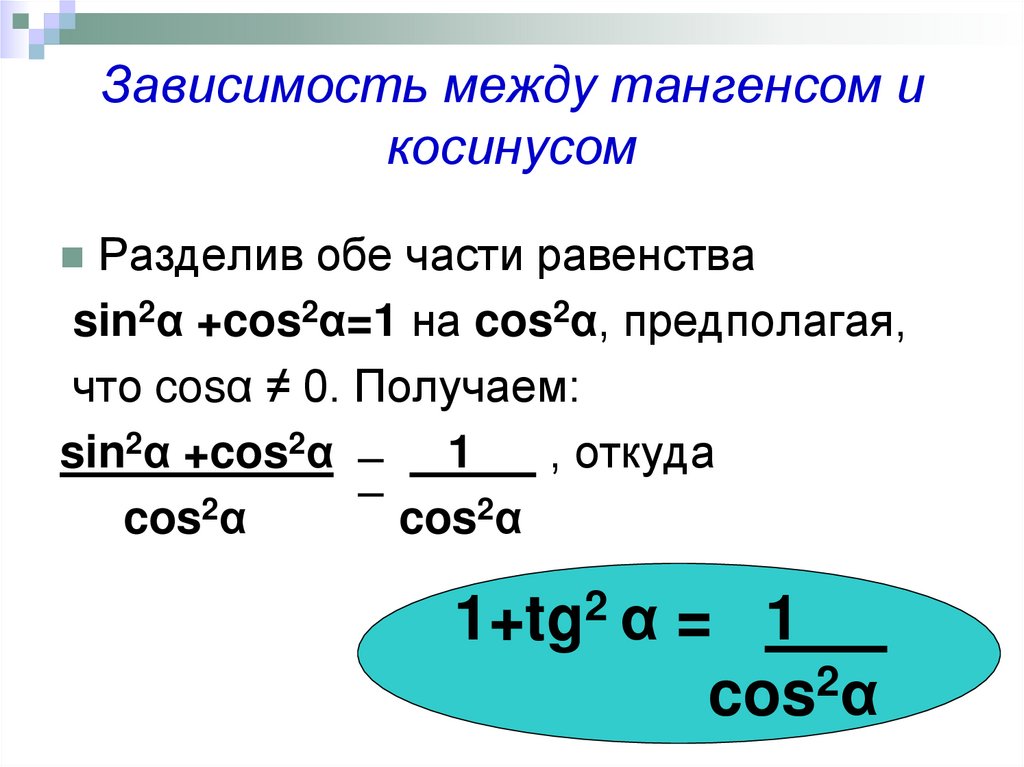 9336
9336 9998
9998 9063
9063 6561
6561 309
309 1045
1045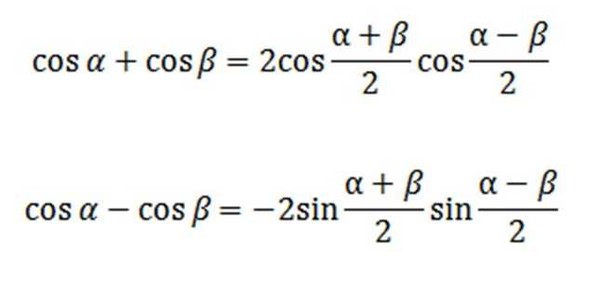 5
5 809
809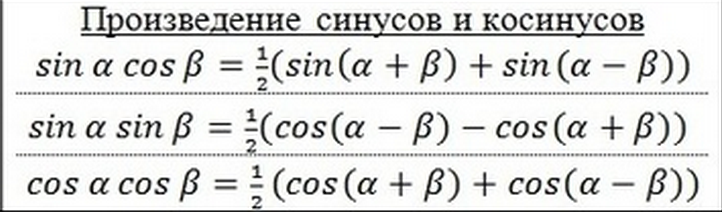 9781
9781 ..
..

 Найдите косинусы суммы с + т, и разница с т. Среднее значение этих двух косинусов. Вы получаете товар xy ! Три поиска в таблице и вычисление суммы, разности и среднего, а не одного умножения. Тихо Браге (1546-1601), среди прочих, использовал этот алгоритм, известный как prosthaphaeresis. )
Найдите косинусы суммы с + т, и разница с т. Среднее значение этих двух косинусов. Вы получаете товар xy ! Три поиска в таблице и вычисление суммы, разности и среднего, а не одного умножения. Тихо Браге (1546-1601), среди прочих, использовал этот алгоритм, известный как prosthaphaeresis. ) 0009 т -замена.)
0009 т -замена.)
Leave A Comment