Координаты вектора / Метод координат / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Метод координат
- Координаты вектора
Прямоугольная система координат (декаротова система координат) — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.
На рисунке выше оси и перпендикулярны. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом. В дальнейшем под длиной отрезка мы будем понимать это число. Так, единичный вектор — это вектор, длина которого равна 1.
Отложим от начала координат О единичные векторы и так, чтобы их направления совпадали с направлениями осей и соответственно.
Векторы и называют координатными векторами.
Координатные векторы не коллинеарны, поэтому любой вектор можно разложить по координатным векторам, т.е. представить в виде , причем коэффициенты разложения и определяются единственным образом. Коэффициенты разложения вектора по координатным векторам называются координатами вектора в данной системе координат.
Координаты вектора записывают в фигурных скобках после обозначения вектора: .
На рисунке выше .
Нулевой вектор
Если векторы и равны, то и . Значит, координаты равных векторов соответственно равны.
Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число:10. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов. |
Доказательство
Дано: , , .
Доказать: .
Доказательство:
По условию и , тогда и .
Сложим последние два равенства и применим свойства сложения векторов и умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. .
| 20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. |
Доказательство
Дано: , , .
Доказать: .
Доказательство:
По условию и , тогда (1) и . (2)
Вычтем из равенства (1) равенство (2) и применим свойства сложения векторов и умножения вектора на число, получим: , следовательно, координаты вектора равны , т.
| 30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. |
Доказательство
Дано: , — число, .
Доказать: .
Доказательство:
По условию , значит, .
Умножим последнее равенство на число и используя свойства умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. .
Данные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
ПримерНайти координаты вектора , если известно, что .
Решение:
По правилу 30 вектор будет иметь координаты , т.е. , вектор координаты , т. е. .
е. .
Так как , то координаты вектора можно найти по правилу 10: , т.е. .
Ответ: .
Советуем посмотреть:
Разложение вектора по двум неколлинеарным векторам
Связь между координатами вектора его начала и конца
Простейшие задачи в координатах
Уравнение линии на плоскости
Уравнение окружности
Уравнение прямой
Взаимное расположение двух окружностей
Метод координат
Правило встречается в следующих упражнениях:
7 класс
Задание 927, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 928, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 930, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 944, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 945, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 4, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1008, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Сумма ⭐ двух векторов: определение, правило, координаты
Основные понятия
Определение 1Направленный отрезок, то есть отрезок, который имеет длину и определенное направление, носит название вектора.
Обозначается буквенным символом со стрелкой над ним:
Определение 2
Сонаправленные векторы — это векторы, направления которых совпадают (одинаковые по направлению).
Определение 3Противоположно направленные векторы — это векторы, которые направлены в разные стороны.
С векторами можно производить такие операции, как:
- сложение;
- вычитание;
- умножение на число.
Для начала, рассмотрим подробно сложение.
Сложение (сумма) векторов «a + b» — это операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:
c=a+b
Вычитание (разность) векторов «a — b» — это операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:
c=a-b
Сложение векторов может осуществляться по трем правилам:
- Правило параллелограмма.
 Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов.
Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов. - Правило многоугольника. Из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее. Когда все векторы отложены, соединим начальную точку с концом последнего вектора и получим сумму нескольких векторов.
- Правило треугольника.
Сумма сонаправленных и противоположно направленных векторов, правило треугольника
Правило треугольника заключается в следующем: для того чтобы сложить два сонаправленных вектора, необходимо из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго. Конечный вектор и будет суммой двух векторов.
Чертеж поможет наглядно объяснить правило:
a+b=AB+BC=AC
AC — сумма векторов.
Разность векторов a и b является суммой векторов a и -b.
Как вычислить координаты суммы двух векторов, пояснение на примерах
Кроме геометрического способа сложения (вычитания) векторов (правила треугольника, параллелограмма, многоугольника), существует способ сложения координат векторов.
Для того чтобы найти координаты суммы двух векторов, нужно сложить их соответствующие координаты по следующей формуле:
Пример 1Найти сумму векторов a(7;5) и b(3;8)
Решение: a+b=(7+3;5+8)=(10;13)
Пример 2Найти сумму координат векторов a(-7;2), b(-3;6), c(6;-5)
Решение: a+b+c=(-7-3+6;2+6-5)=(-4;3)
Примеры решения задач
Пример 3Найти сумму векторов a(1;2), b(7;9)
Решение:a+b=(1+7;2+9)=(8;11)
Пример 4Найти разность координат векторов a(4;-6), b(5;-1)
Решение: a-b=(4-5;-6-(-1))=(-1;-5)
Нахождение суммы двух векторов — Криста Кинг Математика
Что значит найти сумму двух векторов?
Когда мы хотим найти комбинацию двух векторов, мы просто совмещаем начальную точку второго вектора с конечной точкой первого вектора, а затем рисуем новый третий вектор из начальной точки первого в конечный пункт второго.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Другими словами, сочетание серого и синего — фиолетовый:
По сути, объединение двух векторов дает нам тот же результат, что и сложение векторов. В приведенном выше примере серый + синий = фиолетовый. Мы также можем вычитать векторы. Если вычитается вектор, мы движемся точно в направлении, противоположном исходному вектору. В приведенном ниже примере серый — синий = фиолетовый. Сплошной синий вектор — исходный вектор, но поскольку мы вычитаем, мы движемся в противоположном направлении.
Когда нам заданы числовые значения для векторов, мы просто суммируем ???x???-координаты, чтобы получить новую ???x???-координату, и суммируем ???y???? ?-координаты, чтобы получить новую ???y???-координату.
Как найти сумму векторов, в том числе, когда векторы заданы в разных формах
Пройти курс
Хотите узнать больше о Calculus 3? У меня есть пошаговый курс для этого.
 🙂
🙂Еще два примера суммирования векторов
Пример
Найти сумму векторов.
???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???
???u=2i-3j??? и ???v=6i+2j???
Для ???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???:
Суммировать векторы ???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???, мы просто суммируем ???x???-координаты, чтобы получить новую ???x???-координату, а затем делаем то же самое для ???y???-координат. Мы можем назвать наш новый вектор ???w???.
???w=\langle2+(-1),1+5\rangle???
???w=\langle1,6\rangle???
По сути, объединение двух векторов дает нам тот же результат, что и сложение векторов.
Для ???u=2i-3j??? и ???v=6i+2j???:
Суммировать векторы ???u=2i-3j??? и ???v=6i+2j???, коэффициенты возьмем от нашего ???i??? и ???j??? слагаемых, и складываем их вместе, чтобы найти коэффициенты при этих слагаемых для вектора ???w???.
???w=(2+6)i+(-3+2)j???
???w=8i-j???
Мы могли бы также написать вектор ???w=\langle8,-1\rangle???.
Получить доступ к полному курсу Calculus 3
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление iii, исчисление 3, исчисление iii, вычисление 3, векторное исчисление, сумма векторов, добавление векторов, добавление векторов, добавление векторов, вычитание векторов, вычитание векторов
0 лайковСложение и вычитание векторов
Горячая математикаЧтобы добавить или вычесть два вектора, добавьте или вычтите соответствующие компоненты.
Позволять
ты
→
«=»
〈
ты
1
,
ты
2
〉
и
в
→
«=»
〈
в
1
,
в
2
〉
быть два вектора.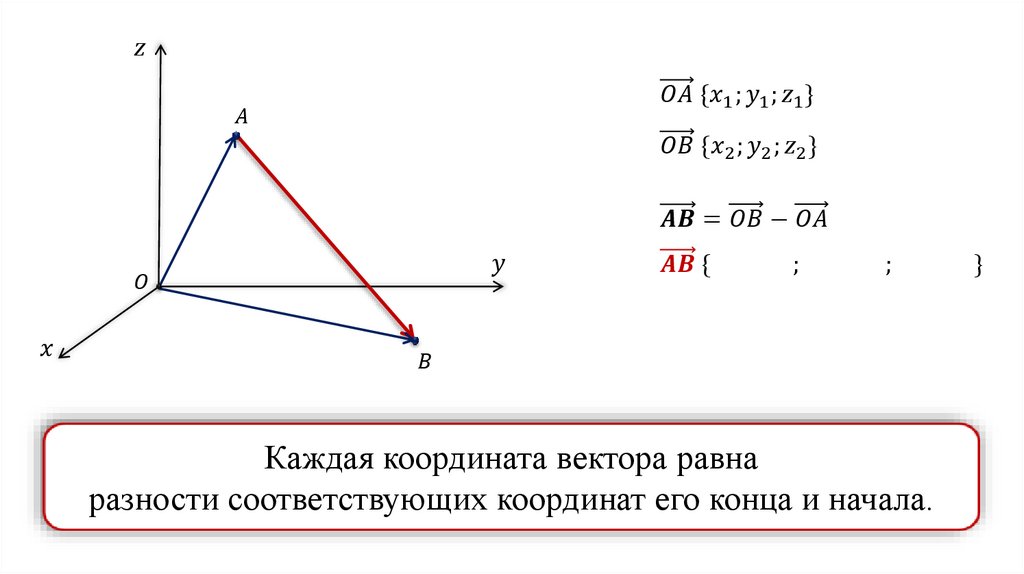
Тогда сумма ты → и в → это вектор
ты → + в → «=» 〈 ты 1 + в 1 , ты 2 + в 2 〉
Разница ты → и в → является
ты → − в → «=» ты → + ( − в → ) «=» 〈 ты 1 − в 1 , ты 2 − в 2 〉
Сумма двух и более векторов называется равнодействующей. Результат двух векторов можно найти с помощью метод параллелограмма или метод треугольника .
Результат двух векторов можно найти с помощью метод параллелограмма или метод треугольника .
Метод параллелограмма:
Нарисуйте векторы так, чтобы их начальные точки совпадали. Затем нарисуйте линии, чтобы сформировать полный параллелограмм. Диагональ из начальной точки в противоположную вершину параллелограмма является равнодействующей.
Добавление вектора:
- Поместите оба вектора ты → и в → в той же начальной точке.
- Завершите параллелограмм. Результирующий вектор ты → + в → является диагональю параллелограмма.
Вычитание векторов:
- Завершите параллелограмм.

- Проведите диагонали параллелограмма из начальной точки.
Метод треугольника:
Нарисуйте векторы один за другим, помещая начальную точку каждого последующего вектора в конечную точку предыдущего вектора. Затем проведите равнодействующую от начальной точки первого вектора до конечной точки последнего вектора. Этот метод также называют метод «голова к хвосту» .
Добавление вектора:
Вычитание векторов:
Пример:
Найди)
ты
→
+
в
→
и (б)
ты
→
−
в
→
если
ты
→
«=»
〈
3
,
4
〉
и
в
→
«=»
〈
5
,
−
1
〉
.
Подставить заданные значения ты 1 , ты 2 , в 1 и в 2 в определение сложения векторов.
ты → + в → «=» 〈 ты 1 + в 1 , ты 2 + в 2 〉 «=» 〈 3 + 5 , 4 + ( − 1 ) 〉 «=» 〈 8 , 3 〉
Перепишите разницу
ты
→
−
в
→
как сумма
ты
→
+
(
−
в
→
)
. Нам нужно определить компоненты
−
в
→
.
Нам нужно определить компоненты
−
в
→
.
Напомним, что − в → является скалярным множителем − 1 раз в . Из определения скалярного умножения имеем:
− в → «=» − 1 〈 в 1 , в 2 〉 «=» − 1 〈 5 , − 1 〉 «=» 〈 − 5 , 1 〉
Теперь добавьте компоненты
ты
→
и
−
в
→
.

 Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов.
Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов.
Leave A Comment