Подготовка к ОГЭ, Задание 16.
Задание №16
Задача №1
Четырехугольник АВСD вписан в окружность. ∠ АВС равен 38°, ∠ САD равен 33°. Найдите угол АВD. Ответ дайте в градусах.
Дано: ∠АВС = 38°, ∠САD = 33°.
Найти: ∠АВD.
Решение:
1) ∠DBC = ∠CAD = 33°, так как вписанные углы, опирающиеся на одну и ту же дугу DC .
2) ∠АВD = ∠AВC – ∠DBC = 38° – 33° = 5°
Ответ: 5.
Задача №2
Площадь круга равна 69. Найдите площадь сектора этого круга, центральный угол которого равен 120°.
Дано: S круга = 69, угол кругового сектора равен 120°.
Найти: S сектора .
Решение:
Ответ: 23.
Задача №3
Угол А четырехугольника АВСD, вписанного в окружность, равен 33°. Найдите угол С этого четырехугольника. Ответ дайте в градусах.
Дано: АВСD вписан в окружность, ∠А = 33°.
Найти: ∠С.
Решение:
∠ C = 180° – ∠A = 180° – 33° = 147°, так как сумма противоположных углов вписанного четырехугольника равна 180°.
Ответ: 147.
Задача №4
Отрезки АС и BD – диаметры окружности с центром О. Угол АСВ равен 53°. Найдите угол АОD. Ответ дайте в градусах.
Дано: АС и BD – диаметры окружности,
∠ АСВ = 53°.
Найти: ∠ АОD.
Решение:
1) АCВ = 53° – вписанный угол, опирающийся
на ᴗ АВ, поэтому ᴗ АВ = 53° 2 = 106°, так как вписанный угол измеряется половиной дуги, на которую он опирается.
2) BD – диаметр, значит ᴗ ВАD = 180°.
3) ∠ АОD – центральный угол, опирающийся на ᴗ АD, следовательно ∠ АОD = ᴗ АD = 180° – 106° = 74°.
Ответ: 74.
Задача №5
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 20,5. Найдите ВС, если АС = 9.
Дано: АВ – d; r = 20,5; АС = 9.
Найти: ВС.
Решение:
1) ∠C = 90°, так как угол, опирающийся на диаметр, значит треугольник АВС прямоугольный.
2) r = 20,5, следовательно АВ = 20,5 2 = 41
3) По теореме Пифагора: АВ 2 = АС 2 + ВС 2
41 2 = 9 2 + ВС 2 ВС 2 = 1681 – 81
ВС 2 = 1600 ВС = 40
Ответ: 40.
Задача №6
Точка О – центр окружности, на которой лежат точки А, В и С. Известно, что ∠АВС = 61° и ∠ОАВ = 8°. Найдите угол ВСО. Ответ дайте в градусах.
Дано: ∠АВС = 61°, ∠ОАВ = 8°.
Найти: ∠ ВСО.
Решение:
1) Проведем радиус ОВ, АО = ВО = СО = r.
2) Треугольник АОВ – равнобедренный, значит ∠А = ∠АВО = 8°.
3) Треугольник ВОС – равнобедренный, значит
∠ ВСО = ∠ОВС= 61° – 8° = 53°.
Ответ: 53.
Задача №7
На окружности с центром О отмечены точки А и В так, что : ∠АОВ = 45°. Длина меньшей дуги равна 91. Найдите длину большей дуги.
Дано: ∠АОВ = 45°, длина меньшей дуги
равна 91.
Найти: длину большей дуги.
Решение:
Ответ: 637.
Задача №8
Угол А четырехугольника АВСD, вписанного в окружность, равен 33°. Найдите угол С этого четырехугольника. Ответ дайте в градусах.
Дано: АВСD вписан в окружность,
∠ А = 77°.
Найти: ∠С.
Решение:
∠ C = 180° – ∠A = 180° – 77° = 103°, так как сумма противоположных углов вписанного четырехугольника равна 180°.
Ответ: 103.
Задача №9
Четырехугольник АВСD описан около окружности, АВ = 8, ВС = 12, СD = 13. Найдите АD.
Дано: АВСD описан около окружности,
АВ = 8, ВС = 12, СD = 13.
Найти: АD.
Решение:
- АD + ВС = АВ + СD, так как суммы
противоположных сторон описанного четырехугольника равны.
2) АD + 12 = 8 + 13
АD = 21 – 12
АD = 9
Ответ: 9.
Задача №10
Треугольник АВС вписан в окружность с центром О. Точки О и С лежат в одной полуплоскости относительно прямой АВ. Найдите угол АСВ, если угол АОВ равен 73°.
Дано: треугольник АВС вписан в
окружность, ∠АОВ = 73°.
Найти: ∠АСВ.
Решение:
- ∠ АОВ = 73° – центральный угол, опирающийся на ᴗ АВ, следовательно ᴗ АВ = 73°.
2) ∠АСВ = 73° : 2 = 36, 5° , так как вписанный
угол измеряется половиной дуги, на которую он
опирается.
Ответ: 36,5.
Задача №11
Радиус окружности, вписанной в трапецию, равен 12. Найти высоту этой трапеции.
Дано: трапеция вписана в окружность, r = 12.
Найти: h.
Решение:
Высота трапеции равна диаметру вписанной
окружности, поэтому h = 2 r = 2 12 = 24 .
Ответ: 24.
Задача №12
Сторона АВ треугольника АВС проходит через центр описанной около него окружности .
Найдите ∠ А, если ∠В = 44°. Ответ дайте в градусах.
Дано: треугольник АВС вписан в окружность,
∠ В = 44 °.
Найти: ∠А.
Решение:
1)∠C = 90°, так как угол, опирающийся на диаметр, значит треугольник АВС прямоугольный.
2)По теореме о сумме углов треугольника
∠ А = 180° – (90° + 44°) = 46°
Ответ: 46.
Задача №13
Четырехугольник АВСD вписан в окружность. Угол АВD равен 37°, а угол САD равен 58°. Найдите угол АВС. Ответ дайте в градусах.
Дано: АВСD вписан в окружность,
∠ АВD = 37°, ∠САD = 58°.
Найти: ∠АВС.
Решение:
- ∠ АВD = 37° – вписанный угол, опирающийся на ᴗ АD,
поэтому ᴗ АD = 37° 2 = 74°.
2) ∠САD = 58° – вписанный угол, опирающийся на ᴗ СD,
поэтому ᴗ СD = 58° 2 = 116°.
- ᴗ АDС = ᴗ АD + ᴗ DС = 74° + 116° = 190°,
значит ∠АВС = 190° : 2 = 95°.
Ответ: 95.
Задача №14
Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ = ВС и ∠АВС = 107°.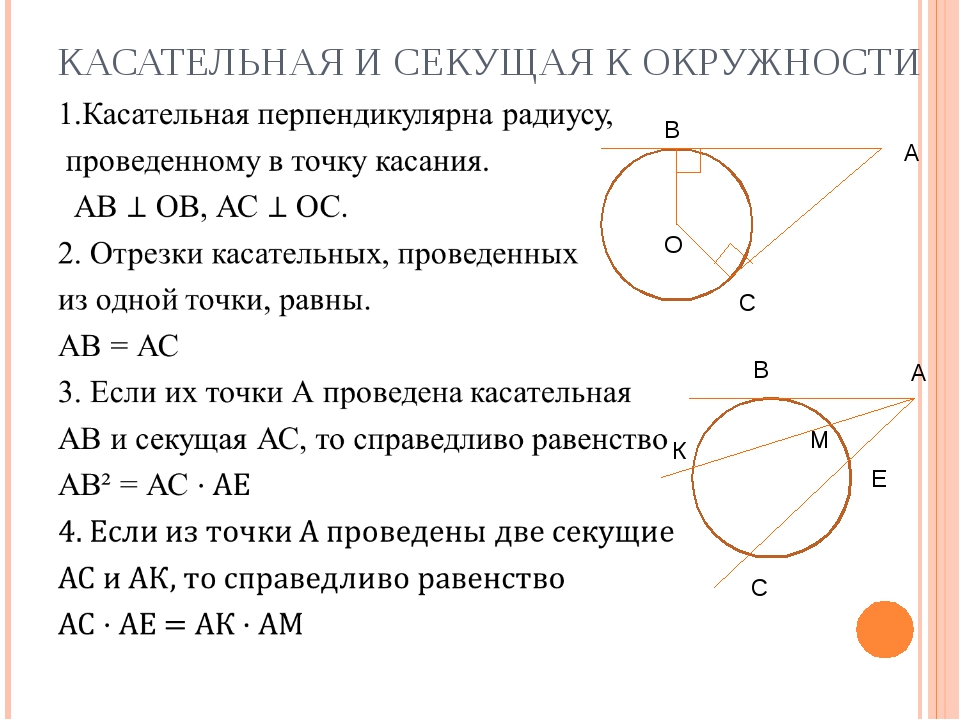
Дано: АВС вписан в окружность,
АВ = ВС, ∠АВС = 107°.
Найти: ∠ВОС.
Решение:
1)Треугольник АВС равнобедренный, поэтому в нем углы при основании равны, то есть
∠ А = ∠АСВ = (180° – 107°) : 2 = 36,5°.
2)∠ВАС = 36,5° – вписанный угол, опирающийся на ᴗ ВС, поэтому ᴗ ВС = 36,5° 2 = 73°.
3)∠ ВОС – центральный угол, опирающийся
на ᴗ ВС, следовательно ∠ ВОС = ᴗ ВС = 73°.
Ответ: 73.
Задача №15
Радиус окружности, вписанной в равносторонний треугольник, равен 6.
Найдите высоту этого треугольника.
Дано: треугольник АВС описан около окружности, r = 6.
Найти: h.
Решение:
1) В равностороннем треугольнике любая высота является медианой и биссектрисой и все они пересекаются в одной точке, которая является центром вписанной и описанной окружности.
2) Медианы треугольника точкой пересечения делятся в отношении 2: 1, считая от вершины,
значит h = 6 3 = 18.
Ответ: 18.
Задача №16
Через точку А, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке К.
Другая прямая пересекает окружность в точках В и С, причем АВ = 2, АК = 4. Найдите АС.
Дано: АК – касательная, АС – секущая,
АВ = 2, АК = 4
Найти: АС.
Решение:
АК 2 = АВ АС
4 2 = 2 АС
АС = 16 : 2
АС = 8
Ответ: 8.
Задача №17
Касательные в точках А и В к окружности с центром О пересекаются под углом 82°. Найдите угол АВО. Ответ дайте в градусах.
Дано: касательные в точках А и В пересекаются под углом 82°.
Решение:
1)Обозначим точку пересечения касательных буквой С .
2)Отрезки касательных СА и СВ равны, значит треугольник АСВ равнобедренный,
∠ САВ = ∠СВА = (180° – 82°) : 2 = 49°.
3)Радиус окружности, проведенный в точку касания, перпендикулярен касательной, поэтому ∠АВС = 90°.
4)∠АВО = 90° – 49° = 41°
Ответ: 41.
Карточки ОГЭ 9 класс
Карточки ОГЭ 9 класс| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека
▪Учебно-дидактические материалы
▪Контрольные / проверочные работы
Материал опубликовала
0
#9 класс #Математика #ФГОС #Учебно-дидактические материалы #Контрольные / проверочные работы #Все учителя #Школьное образование #УМК А.
Г. Мордковича
1 ВАРИАНТ | 2 ВАРИАНТ |
Найдите значение выражения | Найдите значение выражения |
Решите уравнение (x + 2)2 = (x − 4)2. | Решите уравнение . |
Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. | Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. |
Найдите площадь параллелограмма | Площадь параллелограмма ABCD равна 5. Точка Е – середина стороны АD. Найдите площадь трапеции АЕСВ. |
На клетчатой бумаге с размером клетки 1см х 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах | Касательные в точках А и В к окружности с центром О пересекаются под углом 680. Найдите угол АВО. Ответ дайте в градусах. |
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 12. | Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 9. |
1 ВАРИАНТ | 2 ВАРИАНТ |
Найдите значение выражения | Найдите значение выражения |
Решите уравнение (x + 2)2 = (x − 4)2. | Решите уравнение . |
Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. | Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. |
Найдите площадь параллелограмма | Площадь параллелограмма ABCD равна 5. Точка Е – середина стороны АD. Найдите площадь трапеции АЕСВ. |
На клетчатой бумаге с размером клетки 1см х 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах | Касательные в точках А и В к окружности с центром О пересекаются под углом 680. Найдите угол АВО. Ответ дайте в градусах. |
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 12. | Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 9. |
Какое расстояние прошёл человек, если l = 80 см,n = 1600? Ответ выразите в километрах.
Какое расстояние прошёл человек, если l = 80 см,n = 1600? Ответ выразите в километрах.
1 ВАРИАНТ | 2 ВАРИАНТ |
Найдите значение выражения | Найдите значение выражения |
Упростите выражение , | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответ запишите меньший из корней |
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле , где — длительность поездки, выраженная в минутах . Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки. | В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле , где — длительность поездки, выраженная в минутах . |
Касательные в точках А и В к окружности с центром О пересекаются под углом 560. Найдите угол АВО. Ответ дайте в градусах. | В треугольнике АВС АС=ВС. Внешний угол при вершине В равен 14. Найдите угол С. Ответ дайте в градусах. |
На клетчатой бумаге с размером клетки 1см*1см изображена трапеция. Найдите ее площадь. Ответ дайте в квадратных сантиметрах | Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ=ВС и угол Авс равен 1240. Найдите величину угла ВОС. Ответ дайте в градусах. |
Катеты прямоугольного треугольника равны 6 и 8. | В треугольнике АВС угол С прямой, ВС=2, sin A =0,4. Найдите АВ. |
1 ВАРИАНТ | 2 ВАРИАНТ |
Найдите значение выражения | Найдите значение выражения |
Упростите выражение , | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответ запишите меньший из корней |
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле , где — длительность поездки, выраженная в минутах . | В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле , где — длительность поездки, выраженная в минутах . Пользуясь этой формулой, рассчитайте стоимость 10-минутной поездки. |
Касательные в точках А и В к окружности с центром О пересекаются под углом 560. Найдите угол АВО. Ответ дайте в градусах. | В треугольнике АВС АС=ВС. Внешний угол при вершине В равен 14. Найдите угол С. Ответ дайте в градусах. |
На клетчатой бумаге с размером клетки 1см*1см изображена трапеция. Найдите ее площадь. Ответ дайте в квадратных сантиметрах | Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ=ВС и угол Авс равен 1240. |
Катеты прямоугольного треугольника равны 6 и 8. Найти гипотенузу данного треугольника | В треугольнике АВС угол С прямой, ВС=2, sin A =0,4. Найдите АВ. |
Пользуясь этой формулой, рассчитайте стоимость 10-минутной поездки.
Найти гипотенузу данного треугольника
Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
Найдите величину угла ВОС. Ответ дайте в градусах.1 ВАРИАНТ | 2 ВАРИАНТ |
Решите неравенство | Решите неравенство |
Решите уравнение | Решите уравнение |
На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет. | На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. |
Основания трапеции равны 17 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей | П ериметр квадрата равен 32. Найдите площадь этого квадрата |
В треугольнике АВС угол С прямой, ВС=2, sin A =0,4. Найдите АВ. | Катеты прямоугольного треугольника равны 6 и 8. Найти гипотенузу данного треугольника |
В окружности с центром О АС и ВD – диаметры. | В окружности с центром О АС и BD – диаметры. Центральный угол AOD равен 860. Найдите вписанный угол АСВ. Ответ дайте в градусах. |
Центральный угол AOD равен 380. Найдите вписанный угол АСВ. Ответ дайте в градусах.1 ВАРИАНТ | 2 ВАРИАНТ |
Решите неравенство | Решите неравенство |
Решите уравнение | Решите уравнение |
На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет. | На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. |
Основания трапеции равны 17 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей | П ериметр квадрата равен 32. Найдите площадь этого квадрата |
В треугольнике АВС угол С прямой, ВС=2, sin A =0,4. Найдите АВ. | Катеты прямоугольного треугольника равны 6 и 8. Найти гипотенузу данного треугольника |
В окружности с центром О АС и ВD – диаметры. Центральный угол AOD равен 380. Найдите вписанный угол АСВ. Ответ дайте в градусах. | В окружности с центром О АС и BD – диаметры. |
Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Центральный угол AOD равен 860. Найдите вписанный угол АСВ. Ответ дайте в градусах.1 ВАРИАНТ | 2 ВАРИАНТ |
Найдите значение выражения | Найдите значение выражения |
Вычислить | Вычислить |
В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке. | Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,11. |
Н айдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно. | Прямая касается окружности в точке К. Точка О – центр окружности. Хорда КМ образует с касательной угол, равный 40. Найдите величину угла ОМК. Ответ дайте в градусах. |
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 27. Найдите площадь этого треугольника. | Н а клетчатой бумаге размером клетки 1х1 изображён треугольник АВС. |
К асательная в точках А и В к окружности с центром в точке О пересекается под углом 480. Найдите угол АВО. Ответ дайте в градусах | Основания трапеции равны 21 и 33. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей |
Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Найдите длину его средней линии, параллельной стороне АС.1 ВАРИАНТ | 2 ВАРИАНТ |
Найдите значение выражения | Найдите значение выражения |
Вычислить | Вычислить |
В каждой десятой банке кофе согласно условиям акции есть приз. | Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,11. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо. |
Н айдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно. | Прямая касается окружности в точке К. Точка О – центр окружности. Хорда КМ образует с касательной угол, равный 40. Найдите величину угла ОМК. Ответ дайте в градусах. |
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 27. Найдите площадь этого треугольника. | Н а клетчатой бумаге размером клетки 1х1 изображён треугольник АВС. Найдите длину его средней линии, параллельной стороне АС. |
К асательная в точках А и В к окружности с центром в точке О пересекается под углом 480. Найдите угол АВО. Ответ дайте в градусах | Основания трапеции равны 21 и 33. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей |
Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке.
1 ВАРИАНТ | 2 ВАРИАНТ |
Найдите значение выражения 0,3 — | Найдите значение выражения 2 + · |
Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле , где — угловая скорость (в с-1), R – радиус окружности (в метрах). | Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле , где — угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 6 с-1, а центростремительное ускорение равно 216 м/с2. Ответ дайте в метрах. |
Длину окружности можно вычислить по формуле , где — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать ). | Площадь ромба можно вычислить по формуле , где — диагонали ромба (в метрах). |
П ериметр квадрата равен 68. Найдите площадь квадрата | Н айдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно |
Н а клетчатой бумаге размером клетки 1х1 изображён треугольник АВС. Найдите длину его средней линии, параллельной стороне АС. | С торона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника. |
Найдите площадь треугольника, изображенного на рисунке. | Четырехугольник ABCD вписан в окружность. Угол АВС равен 1120, угол САD равен 700. Найдите угол АВD. Ответ дайте в градусах |
Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 4 с-1, а центростремительное ускорение равно 48 м/с2. Ответ дайте в метрах.
Пользуясь этой формулой, найдите диагональ , если диагональ равна 30 м, а площадь ромба 120 м2.
1 ВАРИАНТ | 2 ВАРИАНТ |
Найдите значение выражения 0,3 — | Найдите значение выражения 2 + · |
Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле , где — угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 4 с-1, а центростремительное ускорение равно 48 м/с2. | Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле , где — угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 6 с-1, а центростремительное ускорение равно 216 м/с2. Ответ дайте в метрах. |
Длину окружности можно вычислить по формуле , где — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать ). | Площадь ромба можно вычислить по формуле , где — диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ , если диагональ равна 30 м, а площадь ромба 120 м2. |
П ериметр квадрата равен 68. Найдите площадь квадрата | Н айдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно |
Н а клетчатой бумаге размером клетки 1х1 изображён треугольник АВС. Найдите длину его средней линии, параллельной стороне АС. | С торона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника. |
Найдите площадь треугольника, изображенного на рисунке. | Четырехугольник ABCD вписан в окружность. |
Ответ дайте в метрах.
Угол АВС равен 1120, угол САD равен 700. Найдите угол АВD. Ответ дайте в градусахОпубликовано
Чтобы написать комментарий необходимо авторизоваться.
Закрыть
угол APB = 5 : 1, тогда мера угла APB: видео бина kisi ad ki rukaavat ke!
Обновлено: 27-06-2022
Текстовое решение
Ответ
Правильный ответ A
Похожие видео
В окружности с центром O предположим, что A, P, B являются тремя точками на ее окружности, так что P является серединой малой дуги AB. Предположим, что угол AOB=theta (Площадь(треугольник AOB))/(Площадь(треугольник APB))=sqrt (5)+2 Если угол AOB удвоить до 2theta, то отношение (площадь (треугольник AOB))/(площадь(треугольник APB)) составляет
इस चित्र में Ϫaob एक समकोण है तब ϪAPB =
111936404
Два касательных, нарисованных в точке A и B на кругу, пересекают друг друга в точке P.
Если ▲ 60∘ , то ∠PAB=
112616261
Два касательных из внешней точки P к окружности с центром в точке O — это PA и PB. Если ∠APB=70∘, то значение ∠AOB равно
159832316
Две касательные из внешних точек P к окружности с центром в точке O равны PA и PB. Если ∠APB=70∘, то значение ∠AOB равно
159832354
Две касательные PA и PB проведены к окружности с центром O из внешней точки P. Докажите, что ∠APB=2∠OAB
27 73800305 9@ Если, угол APB И угол APO Рассчитайте значение
5820
На данном рисунке O является центром окружности, ∠AOB=90∘. Найдите ∠APB :
643372717
O — центр круга. AC и BD — две хорды окружности, пересекающиеся в точке P. Если ∠AOB=15∘и∠APB=30∘, то tan2∠APB+cot2∠COD равно :
643372777
Text Solution
In данный круг. Дуги APB и BQC находятся в соотношении 2:5, а O является центром окружности.
9@ тогда мера угла POQ
645189057
На рисунке APB является касательной к окружности с центром O в точке.
PA и PB — касательные к окружности с центром O, такие, что ∠APB=42∘. Каково будет значение ∠AOB?
647583434
геометрия — Найти расстояние между точками двух касательных по окружности
спросил
Изменено 2 года, 9 месяцев назад
Просмотрено 263 раза
$\begingroup$
У меня следующая проблема: есть окружность с $R = 5$ и центром окружности с координатой $(0, 0)$. У меня есть две точки $A(6,8)$ и $B(-4,-6)$. Из точек проведены касательные к окружности. Это лучше проиллюстрировано как:
Обозначим точки, в которых пересекаются касательные и окружность, как $E, F, G, H$ (для лучшего понимания см.
рисунок выше). Итак, нам нужно найти расстояние между E и F по окружности.
- геометрия
- аналитическая геометрия
- окружности
- касательная
$\endgroup$
$\begingroup$
\begin{align} |OE|=|OF|= R&=5 ,\четверка |ОА|=10 ,\четверка |OB|=2\sqrt{13} ,\четверка |АВ|=2\кв{74} ,\\ \ треугольник АОЕ: \ четырехугольник |AE|&=5\sqrt3 ,\\ \треугольник BFO:\quad |BF|&=3\sqrt3 . \end{выравнивание} 92}{2\cdot|ОА|\cdot|ОБ|} «=» \pi-\arccos(\tfrac{18}{65}\sqrt{13}) ,\\ \угол AOE&= \arccos\frac{|OE|}{|OA|} =\tfrac\pi3 ,\\ \угол FOB&= \arccos\frac{|OF|}{|OB|} =\arccos(\tfrac5{26}\sqrt{13}) ,\\ \угол EOF&= \tfrac{2\pi}3-\arccos(\tfrac{18}{65}\sqrt{13}) -\arccos(\tfrac5{26}\sqrt{13}) \приблизительно 1,234262917 . \end{align}
Итак, расстояние между $E$ и $F$ по окружности, то есть длина дуги $FE$ равна
\begin{align}
R\cdot\угол EOF&=
5\cdot(\tfrac{2\pi}3-\arccos(\tfrac{18}{65}\sqrt{13})
-\arccos(\tfrac5{26}\sqrt{13}))
\приблизительно 6.
Leave A Comment