Касательная производная: Уравнение касательной к графику функции

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Справочник по математике

Элементы математического анализа

Производная функции

Секущая графика функции. Уравнение секущей графика функции

Касательная к графику функции

Производная функции

Уравнение касательной к графику функции

Геометрический смысл производной

Секущая графика функции. Уравнение секущей графика функции

      Рассмотрим график некоторой функции   y = f (x),   точки   A= (x₀;  f (x₀))   и   B = (x₁;  f (x₁))   на графике, прямую, проходящую через точки   A   и   B,   и произвольную точку   C = (x; y)   на этой прямой (рис. 1).

Рис.1

      Определение 1. Прямую, проходящую через две произвольные точки графика функции, называют секущей графика функции.

      В соответствии с определением 1 прямая, проходящая через точки   A   и   B   графика функции   y = f (x),   является секущей этого графика.

      Выведем уравнение секущей графика функции.

      Для этого рассмотрим векторы и , координаты которых имеют вид:

      Поскольку векторы и лежат на одной прямой, то справедливо равенство

(1)

где   k   – некоторое число.

      Переписывая равенство (1) в координатах, получим систему (2):

(2)

      Исключая из системы (2) переменную   k ,  получим систему (3):

(3)

второе уравнение которой можно записать в следующем виде

(4)

      Уравнение (4) и является уравнением секущей графика функции   y = f (x),   проходящей через точки   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁))   этого графика.

Касательная к графику функции

      Проведем секущую графика функции   y = f (x),   проходящую через точки   A   и   B   этого графика, и рассмотрим случай, когда точка   A   неподвижна, а точка   B   неограниченно приближается к точке   A   по графику функции   y = f (x)   (рис. 2).

Рис.2

      Неограниченное приближение точки   B   к точке   A   принято обозначать

B → A

и произносить   «B   стремится к   A».

      Заметим, что, если   B → A   для точек   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁))  графика функции  y = f (x),   то это означает, что   x₁ → x₀ .

      Определение 2.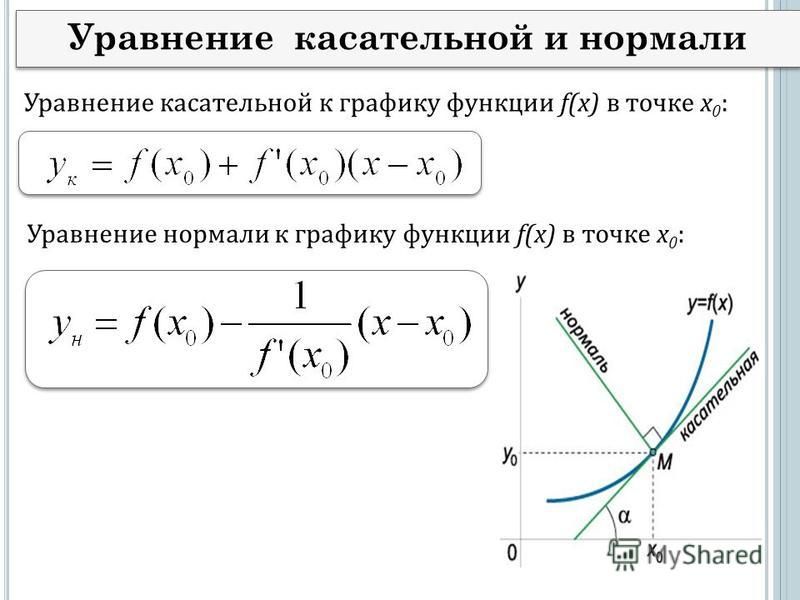 Если при   x₁ → x₀   существует предельное положение секущей графика фукнкции   y = f (x),   то это предельное положение секущей называют касательной к графику функции   y = f (x)   в точке   A = (x₀;  f (x₀))  (рис. 3) .

Рис.3

Производная функции

      Определение 3. Если при   x₁ → x₀   отношение

(5)

входящее в формулу (4), стремится к некоторому числу, то это число называют производной функции   y = f (x) в точке   x₀ ,   обозначают   f ′(x₀)   или и записывают так:

(6)

Уравнение касательной к графику функции

      Из формул (4) и (6) вытекает следующее

      Утверждение. Если у функции   y = f (x)   существует производная в точке   x₀ ,   то к графику функции   y = f (x)   в точке с координатами  (x₀;  f (x₀))   можно провести касательную, а уравнение этой касательной имеет вид:

y = f′(x0) (x – x0) + f (x0)

(7)

Геометрический смысл производной

      Рассмотрим сначала возрастающую функцию   y = f (x)   и проведем секущую графика этой функции, проходящую через точки   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁)) (рис. 4).

Рис.4

      Обозначим буквой   φ   угол, образованный секущей и положительным направлением оси   Ox,   отсчитываемый против часовой стрелки.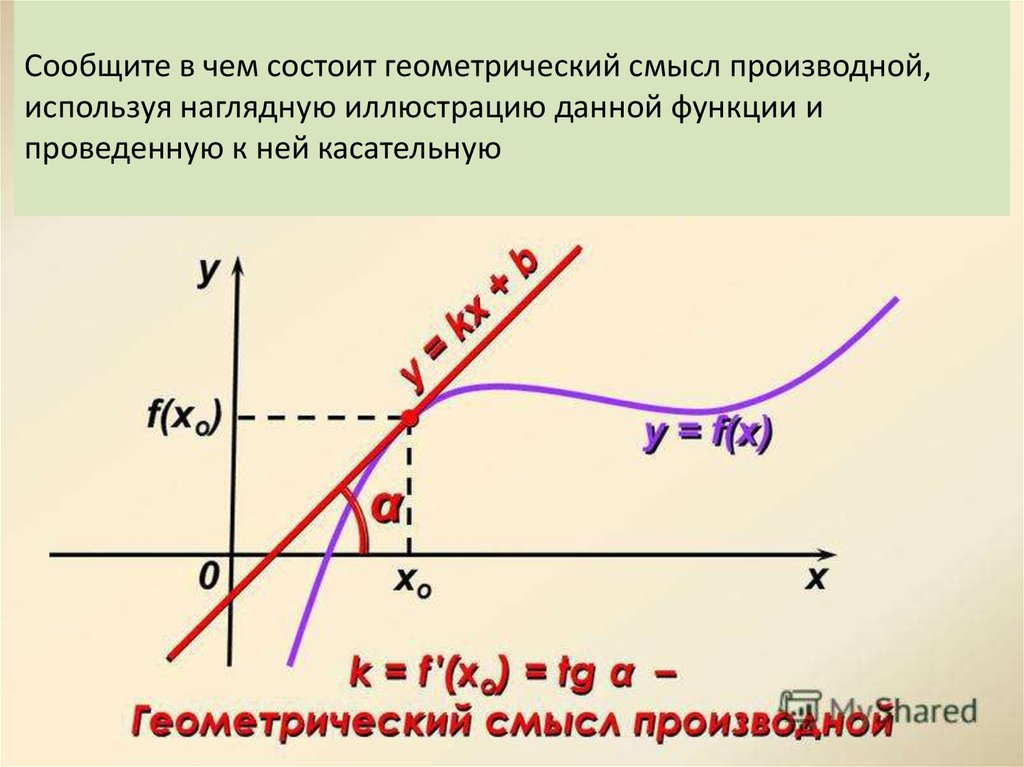 Тогда угол   BAD   в треугольнике   ABD   на рисунке 4 равен   φ ,   и по определению тангенса угла получаем равенство

(8)

причем по определению углового коэффициента прямой   tg φ   является угловым коэффициентом секущей графика функции   y = f (x),   проходящей через точки   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁))   этого графика.

      Случай, когда функция   y = f (x)   убывает, изображен на рисунке 5

Рис.5

      В этом случае угол   φ  является тупым, причем

то есть формула (8) справедлива и для случая, когда функция   y = f (x)   убывает.

      Отсюда в соответствии с определением производной функции вытекает соотношение:

где буквой   α   обозначен угол, образованный касательной к графику функции   y = f (x)   в точке   A = (x₀;  f (x₀))   с положительным направлением оси   Ox   (рис. 6).

Рис.6

      Таким образом, если у функции   y = f (x)   в точке   x₀   существует производная, то эта производная равна тангенсу угла наклона касательной к графику функции   y = f (x)   в точке   (x₀;  f (x₀)) :

f′(x₀) = tg α ,

где угол наклона   α   образован касательной и положительным направлением оси   Ox   и отсчитывается в положительном направлении (то есть против часовой стрелки).

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Определения и понятия

Определение 1

Угол наклона прямой y=kx+b называется  угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.

На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Определение 2

Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.

• Угол наклона прямой равняется 0 только при параллельности ох и  угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
• Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
• Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
• Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.

Определение 3

Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α — красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.

Определение 4

Получаем формулу для нахождения секущей вида:

k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) — это значения функции в этих точках.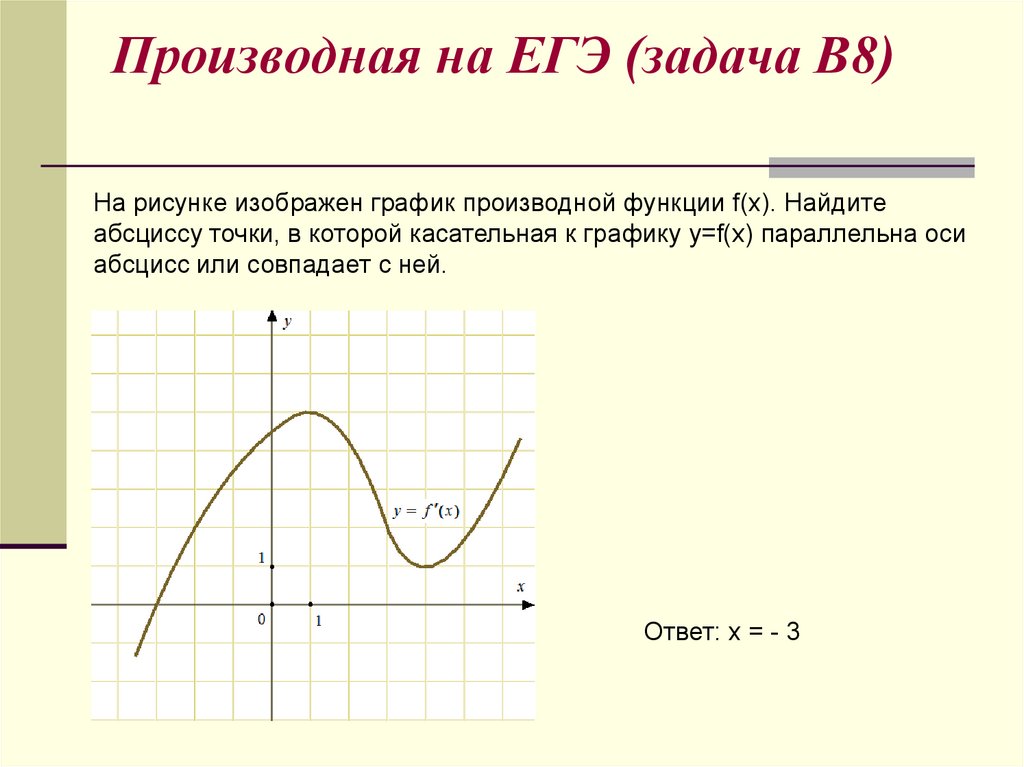

Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или

y=f(xA)-f(xB)xA-xB·x-xB+f(xB).

Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Определение 5

Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0),  с наличием отрезка, который имеет множество значений х, близких к x0.

Пример 1

Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке  с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y=2x сливается с прямой у=х+1.

Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.

Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.

Определение 6

Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Геометрический смысл производной функции в точке

Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.

Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.

То есть получаем, что f’(x) может существовать  в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной  в точке равняется производной  в точке x0. Тогда получаем, что kx=f'(x0).

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.

Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).

Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).

Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0). При параллельности к оси ох получаем, что kk=0, при параллельности к оу — kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.

Пример 2

Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке  с координатами (1; 3) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.

Необходимо найти производную в точке со значением -1. Получаем, что

y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33

Значение f’(x) в точке касания является  угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда kx=tg αx=y'(x0)=33

Отсюда следует, что αx=arctg33=π6

Ответ: уравнение касательной приобретает вид

y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает  в увеличенном виде.

Пример 3

Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.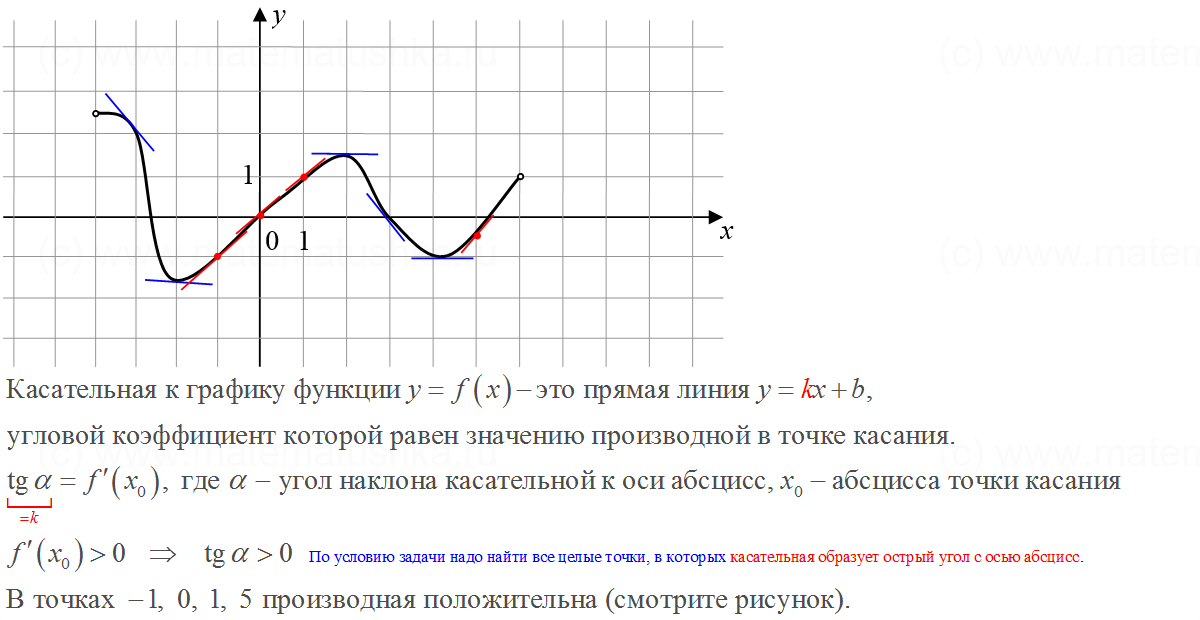

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45

Если x0=1, тогда f’(x) не определена, но пределы записываются как  limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).

Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.

Для наглядности изобразим графически.

Пример 4

Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где

1. Касательная не существует;
2. Касательная располагается параллельно ох;
3. Касательная параллельна прямой y=85x+4.

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что

y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)

Необходимо продифференцировать функцию. Имеем, что

y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)

Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:

limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3

Вычисляем значение функции в точке х=-2, где получаем, что

1. y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.
2. Касательная параллельна ох, когда угловой коэффициент равняется нулю. Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции  обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.

Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.

Решим:

-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2   15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞

Вычисляем соответствующие значения функции

y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43

Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

3. Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0

Другое уравнение имеет два действительных корня, тогда

15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞

Перейдем к нахождению значений функции. Получаем, что

y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83

Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.

Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные  в точках -1; 415, 5; 83.

Возможно существование бесконечного количества касательных для заданных функций.

Пример 5

Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой  и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.

Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной  в точке
x0 получаем, что kx=y'(x0).  Из данного равенства найдем значения х для точек касания.

Получаем, что

y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk

32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk

x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z

Z- множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у:

y0=3cos32x0-π4-13

y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13

y0=3·1—192-13 или y0=3·-1—192-13

y0=45-13 или y0=-45+13

Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.

Ответ: необходимы уравнения запишутся как

y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Для задания окружности  с центром  в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.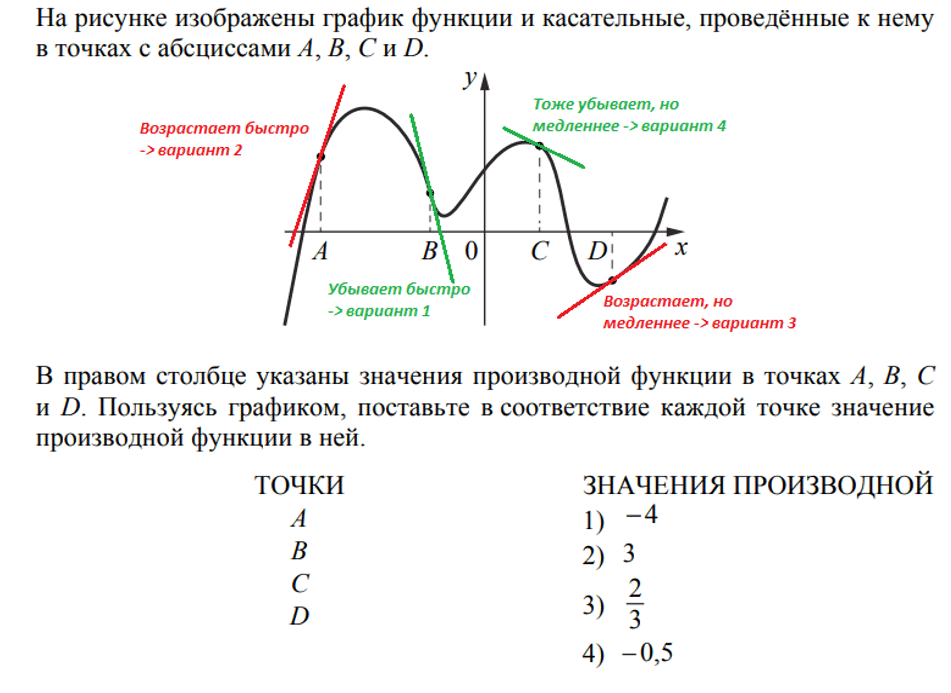

Данное равенство может быть записано как объединение двух функций:

y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности  в точке x0; y0, которая располагается  в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.

Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а  в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.

Касательная к эллипсу

Когда эллипс имеет центр  в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter

Если  касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.

Пример 6

Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.

Решение

Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что

x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5

Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что

x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32

Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид

y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5

Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид

y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5

Графически касательные обозначаются  так:

Касательная к гиперболе

Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.

Гипербола может быть представлена в виде двух объединенных функций вида

y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter

В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Пример 7

Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.

Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

Получаем, что

y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3

Ответ: уравнение касательной можно представить как

y=-3·x-7-33-3=-3·x+43-3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0). Такая касательная в вершине параллельна ох.

Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что

x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a

Графически изобразим как:

Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна оу относительно параболы.

Пример 8

Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4

Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.

Получаем:

kx=y'(x0)=tg αx=tg 150°=-13

Отсюда определим значение х для точек касания.

Первая функция запишется как

y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.

Вторая функция запишется как

y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34

Имеем, что точки касания — 234; -5+34.

Ответ: уравнение касательной принимает вид

y=-13·x-234+-5+34

Графически изобразим это таким образом:

Производная тангенса х — формула, доказательство, примеры

Производная тангенса х есть квадрат сек х. Прежде чем доказывать это, напомним некоторые факты о tan x. Тангенс х в прямоугольном треугольнике представляет собой отношение стороны, противоположной х, к стороне, примыкающей к х, и поэтому его можно записать как (sin x)/(cos x). Мы используем это при дифференцировании тангенса х.

Давайте изучим дифференцирование тангенса х вместе с его доказательством различными методами, а также решим несколько примеров, используя производную тангенса х.

1.	Что такое производное Tan x?
2.	Производная Tan x Доказательство по первому принципу
3.	Производная Tan x Доказательство по цепному правилу
4.	Производная Tan x Доказательство по частному правилу
5.	Часто задаваемые вопросы о производном Tan x

Что такое производное Tan x?

Производная тангенса х по х обозначается d/dx (тангенс х) (или) (тангенс х)’ и ее значение равно сек ² х. Tan x дифференцируем в своей области определения. Чтобы доказать, что дифференцирование tan x равно sec ² x, мы используем существующие тригонометрические тождества и существующие правила дифференцирования. Мы можем доказать это следующими способами:

• Доказательство по первому принципу
• Доказательство по цепному правилу
• Доказательство по правилу частных

Производная формулы Tan x

Формула дифференцирования тангенса x is,

• d/dx (tan x) = sec ² x (или)
• (tan x)’ = сек ² x

Теперь мы докажем это различными методами в следующих разделах.

Производная Tan x Доказательство по первому принципу

Чтобы найти производную от тангенса х, предположим, что f(x) = тангенс х. Тогда по первому принципу его производная дается следующим пределом.

f'(x) = limₕ→₀ [f(x + h) — f(x)] / h … (1)

Так как f(x) = tan x, то f(x + h ) = тангенс (х + ч).

Подставляя их в (1),

f'(x) = limₕ→₀ [tan(x + h) — tan x] / h

= limₕ→₀ [ [sin (x + h) / cos ( x + h)] — [sin x / cos x] ] / h

= limₕ→₀ [ [sin (x + h ) cos x — cos (x + h) sin x] / [cos x · cos(x + ч)] ]/ ч

По формулам суммы и разности sin A cos B — cos A sin B = sin (A — B).

f'(x) = limₕ→₀ [sin (x + h — x)] / [h cos x · cos(x + h)]

= limₕ→₀ [sin h] / [h cos x · cos(x + h)]

= limₕ→₀ (sin h)/ h · limₕ→₀ 1 / [cos x · cos(x + h)]

По предельным формулам limₕ→₀ (sin h)/ h = 1.

f'(x) = 1 [ 1 / (cos x · cos(x + 0))] = 1/cos ² x

Мы знаем, что обратное значение cos равно сек. Итак,

f'(x) = сек ² х.

Отсюда доказано.

Производная Tan x Доказательство по цепному правилу

Докажем дифференцирование формулы tan x по цепному правилу. Для этого заметим, что мы можем записать y = tan x как y = 1 / (cot x) = (cot x) ^-1 . Теперь, по степенному правилу и цепному правилу,

y’ = (-1) (cot x) ^-2 · d/dx (cot x)

Мы имеем d/dx (cot x) = -csc ² х. Кроме того, по свойству показателей а ^-т = 1/а ^м .

y’ = -1/cot ² x · (-csc ² x)

y’ = tan ² x · csc ² x

Теперь, tan x/ (cos x) и csc x = 1/(sin x). Таким образом,

y’ = (sin ² x)/(cos ² x) · (1/sin ² x)

= 1/cos ² x

. сек х. Итак,

у’ = сек ² х

Отсюда доказано.

Производная Tan x Доказательство по частному правилу

Мы можем применить правило частных, чтобы вывести формулу производной от tan x. Для этого нам нужно записать тангенс х в виде дроби. Мы знаем, что tan x = (sin x)/(cos x). Итак, мы предполагаем, что y = (sin x)/(cos x). Тогда по правилу частных

y’ = [cos x · d/dx (sin x) — sin x · d/dx (cos x)] / (cos ² x)

= [cos x · cos x — sin x (-sin x)] / (cos ² x)

= [cos ² x + sin ² x] / (cos ² x)

По одному из тождеств Пифагора, cos ² x + sin ² x = 1. Итак,

y’ = 1 / (cos ² x) = sec ² x

Отсюда доказано. Это доказательство является самым простым среди всех других доказательств производных от tan x.

Распространенные заблуждения, связанные с производной Tan x:

Вот некоторая ясность в отношении некоторых распространенных заблуждений относительно дифференциации Tan x.

• d/dx (tan x) НЕ равно d/dx (sin x) / d/dx (cos x). Вместо этого мы должны использовать правило частных, чтобы найти производную от tan x (записав ее как (sin x)/(cos x)).
• d/dx (tan x) НЕ является кроваткой x. кроватка х есть просто величина, обратная тангенсу х.
• Производные tan x и tan ^-1 x НЕ совпадают.
  d/dx(тангенс х) = сек ² х
  d/dx(тангенс ^-1 х) = 1/(1 + х ² )

Темы, относящиеся к дифференциации Tan x:

Вот некоторые темы, которые могут вас заинтересовать при изучении производной Tan x.

• Расчетные формулы
• Расчетный калькулятор
• Производные формулы
• Калькулятор производных

Часто задаваемые вопросы о производном Tan x

Какая производная от Tan x относительно x?

Производная tan x по x равна квадрату sec x. т. е. d/dx(tan x) = sec ² x. Его также можно записать как (tan x)’ = sec ² x.

Как найти производную формулы Tan x?

Пусть y = tan x. У нас есть tan x = sin x/cos x. По правилу частных y’ = [cos x · d/dx (sin x) — sin x · d/dx (cos x)] / (cos ² x) = [cos ² x + sin ² x] / (cos ² x) = 1/(cos ² x) = сек ² x.

Какая производная от Tan x

² ?

Мы знаем, что d/dx(tan x) = sec ² x. Итак, d/dx(tan x ² ) = sec ² x ² d/dx(x ² ) = 2xsec ² x ² (по цепочке).

В чем отличие Tan x от Cos x?

Мы знаем, что производная от tan x равна sec ² x. Кроме того, sec x = 1/(cos x). Итак, d/d(tan x) = 1/cos ² x.

Что такое производная tan x

^-1 ?

Используя производную от tan x и цепное правило, d/dx(tan x ^-1 ) = sec ² x ^-1 d/dx(x ^-1 ) = sec ² x ^-1 (-1 х ^-2 ) = (-сек ² х ^-1 )/(х ² ).

Равна ли производная Tan x производной Tan

^-1 x?

Нет, производные tan x и tan ^-1 x различны. Производная tan x равна sec ² x, тогда как производная tan⁻¹x равна 1/(1 + x ² ).

В чем разница между производной Tan x и первообразной Tan x?

Производная тангенса x сек ² х. Первообразная tan x есть не что иное, как интеграл от tan x и ∫ tan x dx = ln |sec x| + C.

Модуль 8 — Производная функции

Модуль 8. Производная функции

Введение | Урок 1 | Урок 2 | Урок 3 | Самооценочный тест

Урок 8.1: Производная в точке

В Модуле 7 вы видели, что скорости соответствуют склонам. Средняя скорость соответствует наклону Секущая – это линия, проведенная через две точки кривой. секущая линия которая соединяет две точки, а мгновенная скорость соответствует наклону линии, касательной к кривой. Производная функции в точке — это наклон касательной в этой точке. В этом уроке вы будете использовать несколько различных функций TI-89.найти производные. Формальное определение производной Производная функции f при x = a равна при условии, что предел существует. Секущие линии сходятся к касательной, если одна точка на кривой фиксирована, а вторая точка приближается к этой фиксированной точке. Иллюстрация схождения секущих линий Следующая процедура найдет значение производной функции f ( x ) = 2 x x 2 в точке (0,5, 0,75), используя метод, аналогичный тому, который вы использовали. используется для нахождения мгновенных скоростей. Во-первых, вы найдете наклоны нескольких секущих и используете их для оценки наклона касательной на х = 0,5. Затем вы возьмете предел наклонов секущей, чтобы найти производную. График ниже иллюстрирует f ( x ) = 2 x x 2 в окне [-1, 3] x [-1, 2], с тремя секущими линиями, которые приближаются к касательная в точке (0,5, 0,75). Нахождение наклонов секущих линий На главном экране выберите NewProb в меню F6:Clean Up. Определить f ( x ) = 2 x x 2 Наклон секущей, проходящей через точки (0,5, f (0,5)) и (0,5 + h , f (0,5 + h )) можно найти, вычислив частное разности Нас интересуют значения h , которые малы, так что две точки находятся близко друг к другу, а результирующая секущая будет аппроксимировать касательную. Оцените этот разностный коэффициент для ч = 0,1, используя команду with, введя (f(0,5+h)-f(0,5))/h | ч=0,1. Команда «с» (вертикальная черта) находится слева от ключ. Наклон секущей, содержащей (0,5, f (0,5)) и (0,6, f (0,6)) равен 0,9. Использование меньших значений h Когда точка (0,5 + h , f (0,5 + h )) приближается к точке (0,5, f (0,5)), h приближается к 0, а секущие сходятся к касательной. Оцените коэффициент разности для меньших значений ч . Измените значение h в строке редактирования с 0,1 на 0,01 и оцените коэффициент разности. Наклон соответствующей секущей равен 0,99. Оцените коэффициент разности с ч = 0,001 и с ч = 0,0001 Наклон секущих равен 0,999 и 0,9999 соответственно. 8.1.1 Предсказать наклон касательной в точке (0,5, f(0,5)). Щелкните здесь, чтобы получить ответ. Оцените коэффициент разности с ч = -0,01 и ч = -0,001 Наклоны соответствующих секущих равны 1,01 и 1,001. Одна секущая проходит через (0,499, f(0,499)) и (0,5, f(0,5)), другая через (0,4999, f(0,4999)) и (0,5, f(0,5)). Затем вычислите частное разности без указания значения для h . Обратите внимание, что мы получаем формулу для разностного отношения, когда значение для 9 не указано.0386 ч . Нахождение производной в точке Производная, представляющая собой наклон касательной, определяется как предел Оцените это выражение, введя команду limit((f(0.5+h)-f(0.5))/h,h,0) Производная от f ( x ) = 2 x x 2 при x = 0,5 равно 1. Использование производной команды Вы также можете вычислить производную функции f при x = 0,5, используя команду производной d (, которая находится выше , а также в меню Calc. Синтаксис для нахождения производной в точке: d (выражение,переменная) | переменная=значение. Вставьте d ( в строку редактирования, нажав [ д ] Вычислить производную от f в точке с x = 0,5, введя выражение d (f(x),x)|x=0,5 Рисование касательной линии Теперь, когда точка на кривой и производная в этой точке известны, Уравнение прямой, проходящей через точку (x1, y1) с уклоном м , равно y y 1 = м ( x x 1 ). точечно-наклонная форма уравнения прямой можно найти уравнение касательной. Если наклон касательной в точке (0,5, 0,75) равен 1, то уравнение для касательной имеет вид y = 1 · ( x 0,5) + 0,75. График функции f и его касательная в точках (0,5, 0,75). Установите y1 = f(x) Установите y2 = (x0,5) + 0,75 График функции и касательной в окне [-1, 3] x [-1, 2] с xscl и yscl = 1 Линия кажется касательной к кривой при x = 0,5. Использование квадратного окна Иногда полезно визуализировать значение наклона касательной, нарисовав график в квадратном окне просмотра, где единица по оси x имеет ту же ширину, что и единица по оси y . Отобразите графики в квадратном окне просмотра, нажав F2:Zoom и выбрав 5:ZoomSqr. Share This Story, Choose Your Platform! FacebookTwitterLinkedInRedditWhatsappGoogle+TumblrPinterestVkEmail Related Posts Насморк при прорезывании зубов у детей: причины, симптомы и лечение Насморк при прорезывании зубов у детей: причины, симптомы и лечение Как развивать ребенка в 10 месяцев: игры и занятия для малыша Как развивать ребенка в 10 месяцев: игры и занятия для малыша Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов Когда и как вводить прикорм грудному ребенку: рекомендации педиатров Когда и как вводить прикорм грудному ребенку: рекомендации педиатров Leave A Comment Отменить ответ Comment Save my name, email, and website in this browser for the next time I comment.