Равнопеременное движение. Формулы. Ускорение. Конечная
Прямолинейное равнопеременное движение — движение тела вдоль прямой, характеризующееся постоянным по модулю и направлению линейным ускорением.
Траектория такого движения — прямая, поэтому в задачах равнозначными являются понятия пути и модуля перемещения. Такое движение может быть описано несколькими соотношениями:
- вектор скорости тела при равнопеременном движении
(1)
- где
- — вектор конечной скорости движения
- — вектор начальной скорости движения
- — вектор ускорения
- — время движения
- вектор перемещения тела при равнопеременном движении
(2)
- где
- — вектор перемещения тела
Однако это векторные уравнения, с которыми работать достаточно сложно, а иногда, просто не хочется. Попробуем, анализируя условия задачи, составить уравнения скалярного вида, спроецировав вектора на некую ось.
Рис. 1. Равноускоренное движение 1
Пример 1. Тело движется прямо с начальной скоростью и ускоряется. По задаче выставляем вектора на ось OX (движение прямолинейное) (рис. 1). Сказано, что тело движется вдоль оси (вектор направлен по оси) и ускоряется (вектор также направлен вдоль оси). Осталось зафиксированные вектора спроецировать:
- Для уравнения (1):
- Для уравнения (2):
В общем случае, мы не можем предугадать направления векторов и , соответственно, мы не можем указать точный знак проекции этих векторов на выбранную ось. Но не заморачиваемся: в результате решения задачи мы получим одно и то же по модулю число, даже если ошибёмся. Т.е. выбираем направления как хотим, а потом анализируем ответ.
Рис. 2. Равноускоренное движение-2
Пример 2. Тело движется в положительном направлении оси и затормаживает. По задаче тело движется вдоль оси (вектор направлен по оси), а торможение говорит о том, что вектор ускорения () направлен против оси OX (рис. 2). Проецируем:
2). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Рис. 3. Равноускоренное движение-3
Пример 3. Тело движется в отрицательном направлении оси и затормаживает. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а торможение говорит о том, что вектор ускорения () направлен против движения, а значит, по оси OX (рис. 3). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Рис. 4. Равноускоренное движение-4
Пример 4. Тело движется в отрицательном направлении оси и ускоряется. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а ускорение говорит о том, что вектор ускорения () направлен в сторону движения, а значит, против оси OX (рис. 4). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Вывод: только что мы получили восемь различных формул, применимых для решения задач. Очень не хотелось бы их помнить. К счастью, есть выход: запомнить и понять векторный вид этих уравнений (1) и (2), а далее, применительно к данной вам задаче, просто адаптировать их, используя проекции.
Очень не хотелось бы их помнить. К счастью, есть выход: запомнить и понять векторный вид этих уравнений (1) и (2), а далее, применительно к данной вам задаче, просто адаптировать их, используя проекции.
Кроме формул (1) и (2), имеется ещё одна расчётная формула, которая чаще всего используется, когда в задаче на нужно найти время или его не дано. Воспользуемся уже имеющимися (1) и (2), считая движение тела равноускоренным. Выделим из (1) время:
(3)
Подставим (3) в (2) при условии :
= = =
(4)
Таким образом, мы получили формулу, в которой нет параметра времени.
Равнопеременное прямолинейное движение | Физика для всех
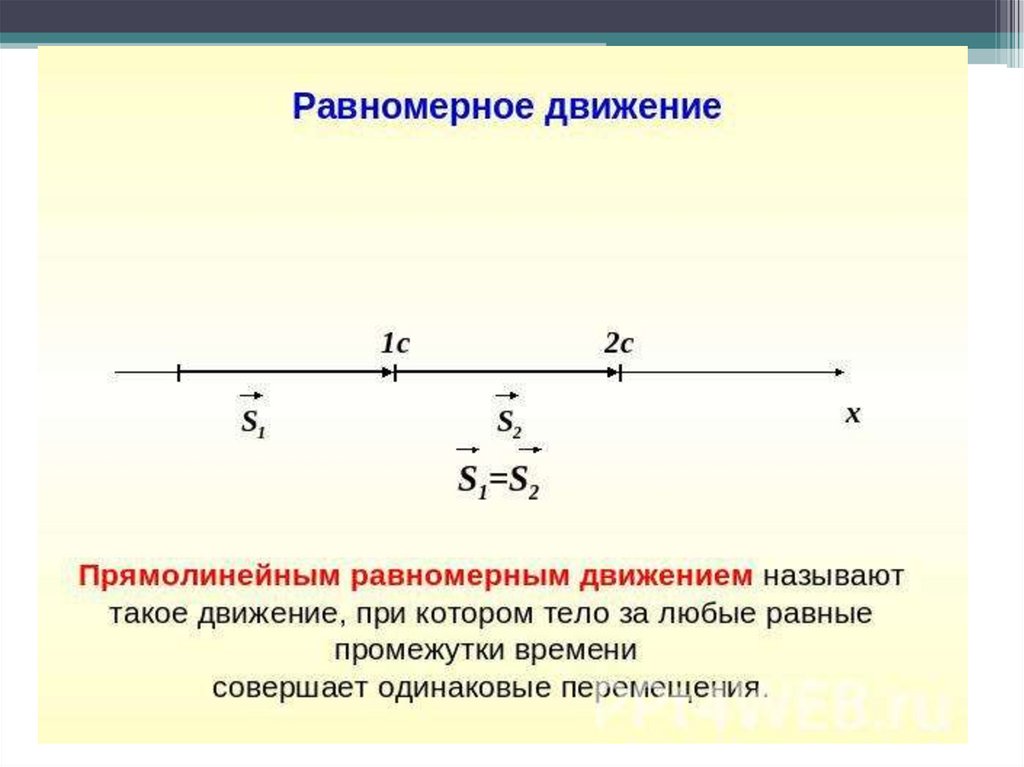
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.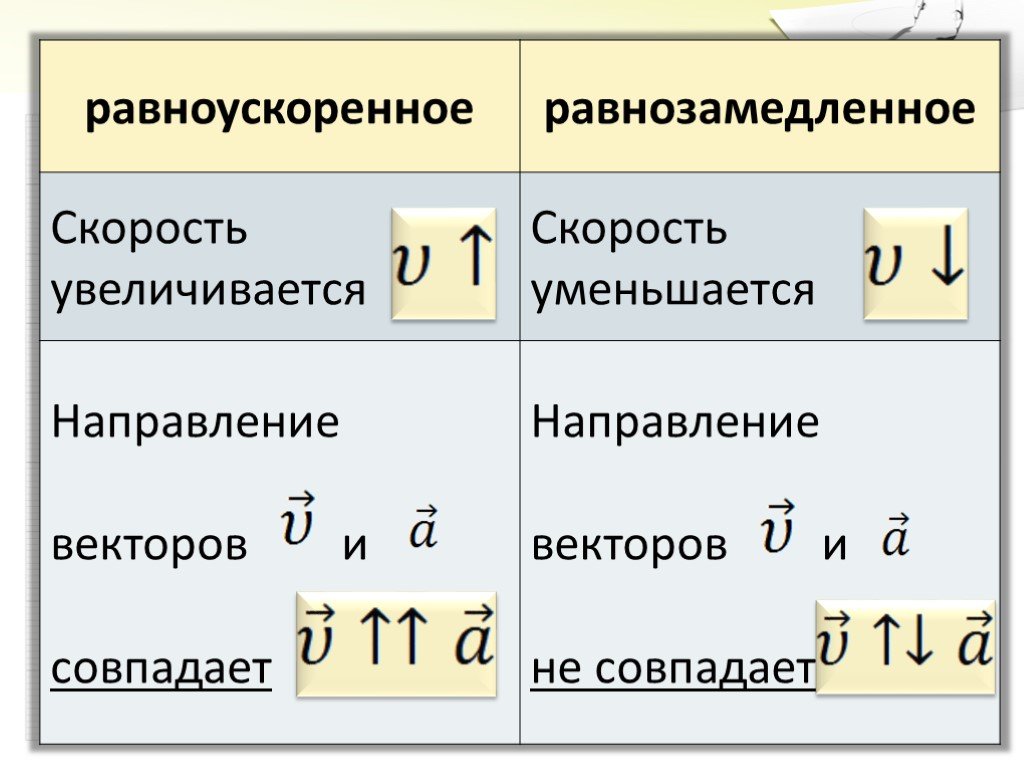
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
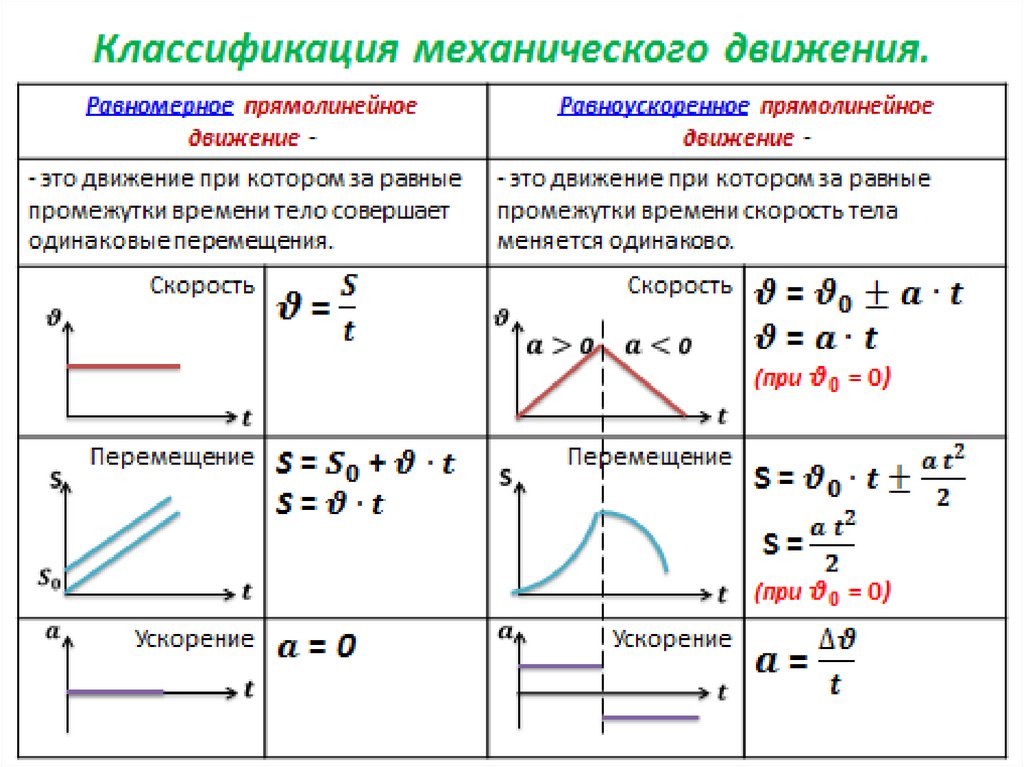
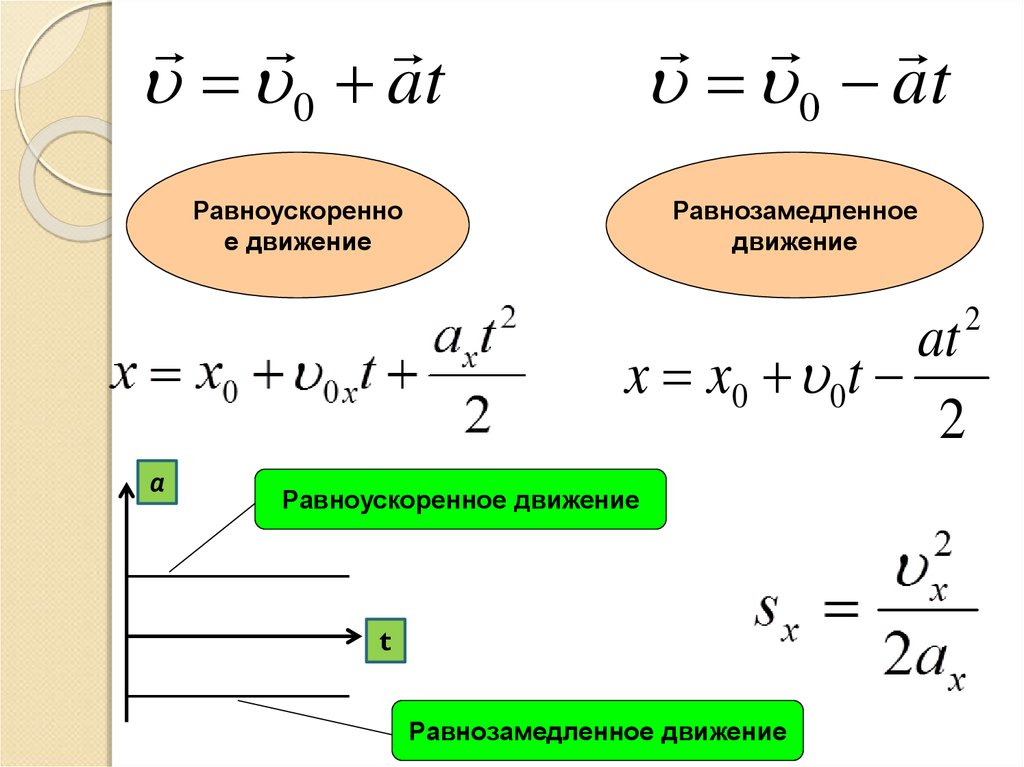
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
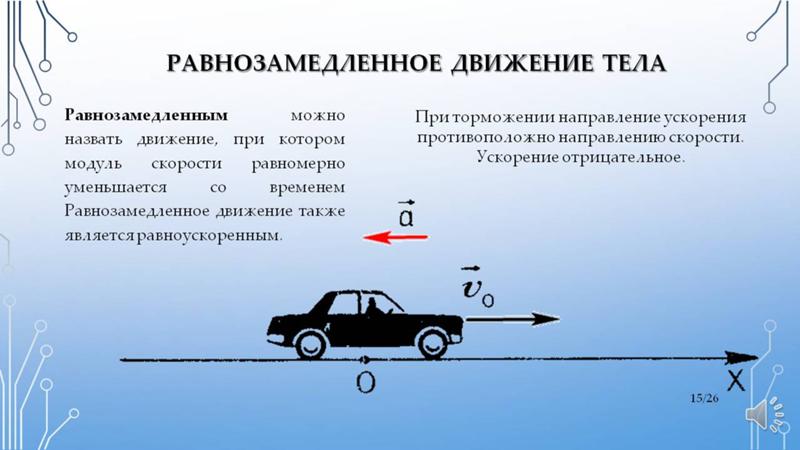
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.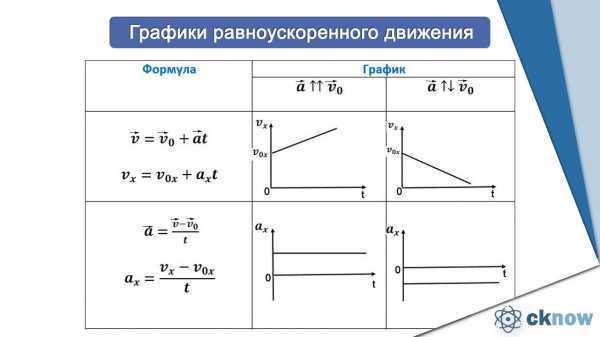
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
vcp = s / t
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
vx = x’
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
vx = v0x ± axt
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис.
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v0 bc = v
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
График зависимости скорости тела от времени при различных ускорениях показан на рис.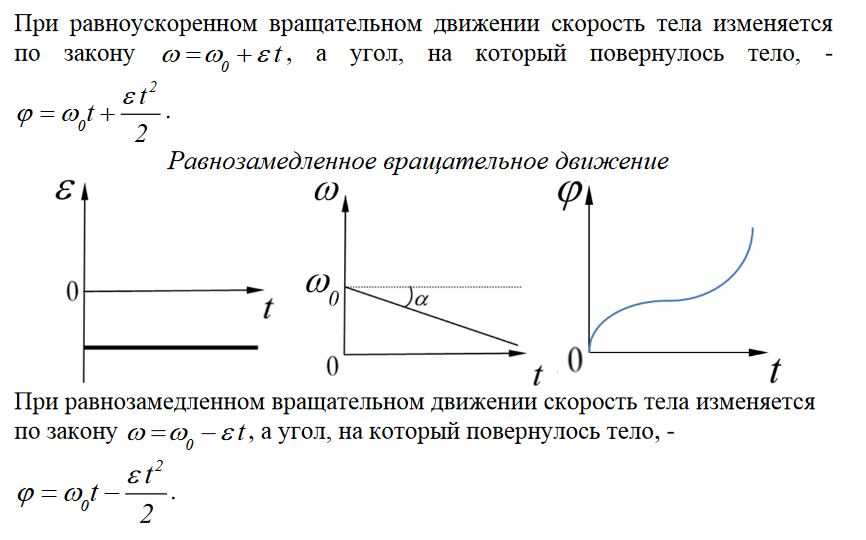 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат.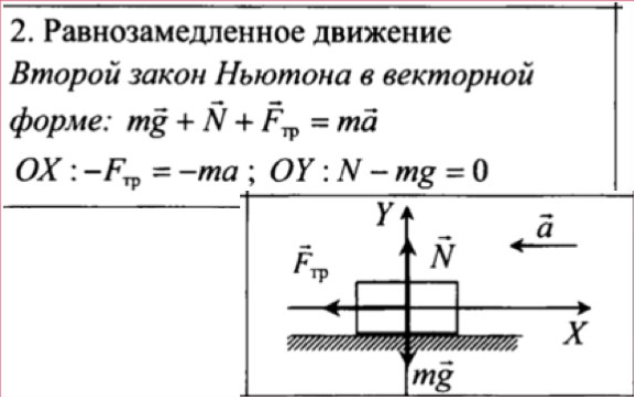
Линейное движение: определение, вращение, уравнение, примеры
В повседневной жизни мы обычно думаем о движении как о перемещении из одного места в другое. Но для физиков это не так просто. Хотя движение — это движение из одной точки в другую, в физике важную роль играет тип движения и его плоскость.
Движение может быть одномерным, двухмерным или трехмерным. Для этого объяснения мы рассмотрим движение в одном измерении, а именно движение (или движение) i n прямой.
Линейное движение — это изменение положения от одной точки к другой по прямой в одном измерении . Вождение автомобиля по прямому шоссе является примером движения в одном измерении.
Линейное движение: смещение, скорость и ускорение
Рассмотрим смещение, скорость и ускорение более подробно.
Смещение
Объект может двигаться только в двух направлениях по прямой линии, а именно, в нашем случае вперед или назад. Если мы изменим положение объекта в определенном направлении, мы вызовем смещение .
Если мы изменим положение объекта в определенном направлении, мы вызовем смещение .
Рисунок 1. Смещение может быть в любом направлении в зависимости от положительного или отрицательного знака.
Поскольку смещение является векторной величиной , что означает, что оно имеет величину и направление, оно может быть положительным или отрицательным. Вы можете принять любое опорное направление как положительное или отрицательное, но имейте в виду, какое направление вы выберете как положительное или отрицательное. Для расчета водоизмещения воспользуемся следующим уравнением, где Δx — водоизмещение, x f — конечная позиция, а x i — начальная позиция.
\[\Delta x = \Delta x_f — \Delta x_i\]
См. наше объяснение, Скаляр и Вектор, для получения дополнительной информации о скалярных и векторных величинах.
Скорость
Скорость — это изменение смещения во времени .
Мы можем рассчитать скорость, используя следующее уравнение, где v — скорость, Δx — изменение положения, а Δt — изменение во времени.
\[v = \frac{\Delta x}{\Delta t}\]
Вышеупомянутое уравнение предназначено специально для средней скорости , что означает, что оно является вычислением скорости для всего смещения , деленного на общее время . Но что, если вы хотите узнать скорость в определенный момент времени, а не за весь период? Здесь в игру вступает понятие мгновенной скорости.
Мгновенная скорость
Мы можем вычислить мгновенную скорость, используя среднюю скорость, но мы должны сузить время так, чтобы оно приближалось к нулю в этот конкретный момент. Теперь, если вы думаете, что для того, чтобы вычислить это, вам нужно знать некоторые вычисления, вы правы! Тем не менее, давайте сначала обсудим несколько сценариев.
Если скорость одинакова на всем протяжении смещения , то средняя скорость равна мгновенной скорости в любой момент времени.
Рис. 2. Мгновенная скорость будет одинаковой в течение всего времени перемещения, если скорость постоянна.
Итак, мгновенная скорость для приведенного выше примера составляет 7 м/с (метров в секунду), так как она не меняется ни в какой момент времени.
Градиент графика смещения-времени
Градиент в любой момент времени графика перемещение-время есть скорость в этот момент.
Посмотрите на приведенный ниже график смещение-время со смещением по оси Y и временем по оси X. Кривая на графике изображает смещение во времени .
Рис. 3. Градиент графика перемещение-время есть скорость
Рассчитать мгновенную скорость в точке p 1 , мы берем градиент кривой смещения-времени и делаем его бесконечно малым, чтобы он приближался к 0. Вот расчет, где x 2 — конечное перемещение, x 1 — начальное перемещение, т 2 — время конечного перемещения, t 1 — время начального перемещения.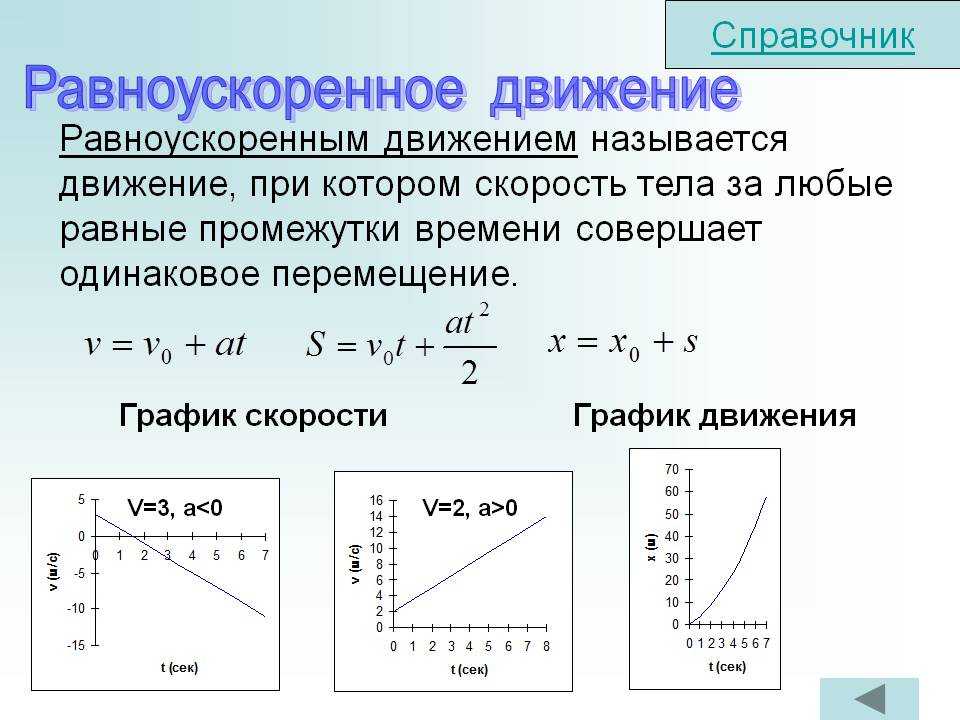
Мгновенная скорость в точке p 1 \(= \lim_{x \to 0} \frac{\Delta x}{\Delta t} = \frac{x_2-x_1}{t_2-t_1} \)
Если ускорение является постоянным , мы можем использовать одно из кинематических уравнений (уравнения движения) для нахождения мгновенной скорости . Взгляните на уравнение ниже.
\[v = u +at\]
В приведенном выше уравнении u — начальная скорость, а v — мгновенная скорость в любой момент времени t при условии, что ускорение остается постоянным в течение всего времени движения.
Ускорение
Ускорение скорость изменения скорости .
Мы можем рассчитать ускорение следующим образом:
\[a = \frac{\Delta v}{\Delta t}\]
Как и средняя скорость, приведенное выше уравнение для среднего ускорения . Так что, если вы хотите рассчитать ускорение в любой момент времени, а не за период? Рассмотрим мгновенное ускорение.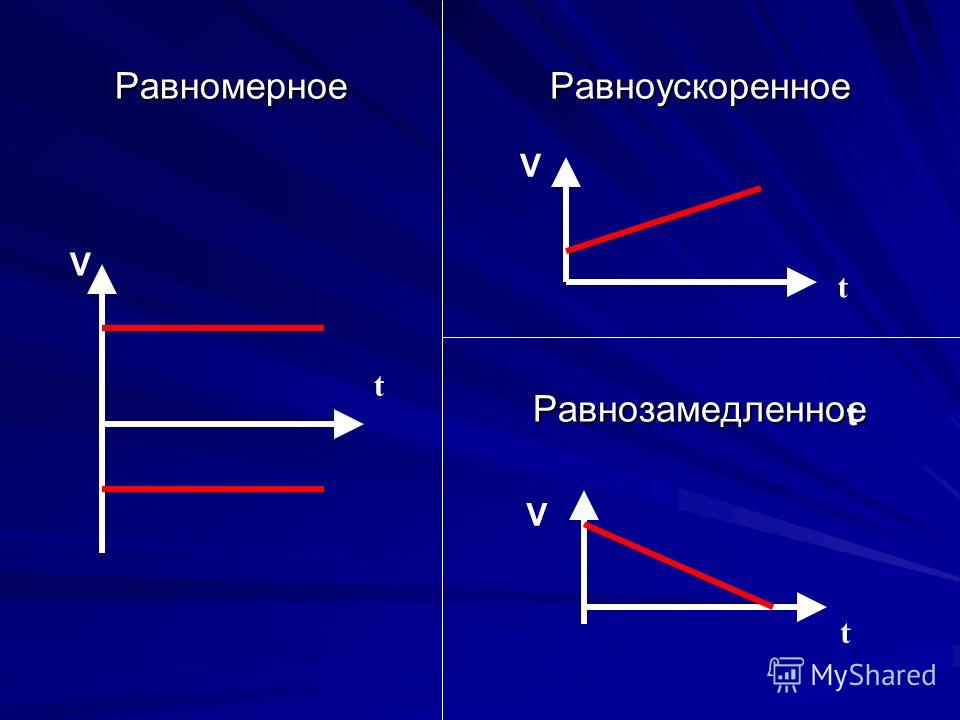
Мгновенное ускорение
Изменение скорости в любой момент времени является мгновенным ускорением . Расчет мгновенного ускорения аналогичен мгновенной скорости.
Если скорость движущегося тела одинакова на протяжении всего перемещения , то мгновенное ускорение равно нулю в любой момент времени.
Каково мгновенное ускорение тела, если на протяжении всего пути оно движется с постоянной скоростью 7 м/с?
Решение
Мгновенное ускорение в данном случае равно 0 м/с 2 , так как нет изменения скорости. Таким образом, мгновенное ускорение тела с постоянной скоростью равно 0.
Градиент графика зависимости скорости от времени
Градиент в любой момент времени графика скорости представляет собой ускорение в этот момент времени. мгновенный.
Рис. 4. Градиент графика скорость-время представляет собой ускорение.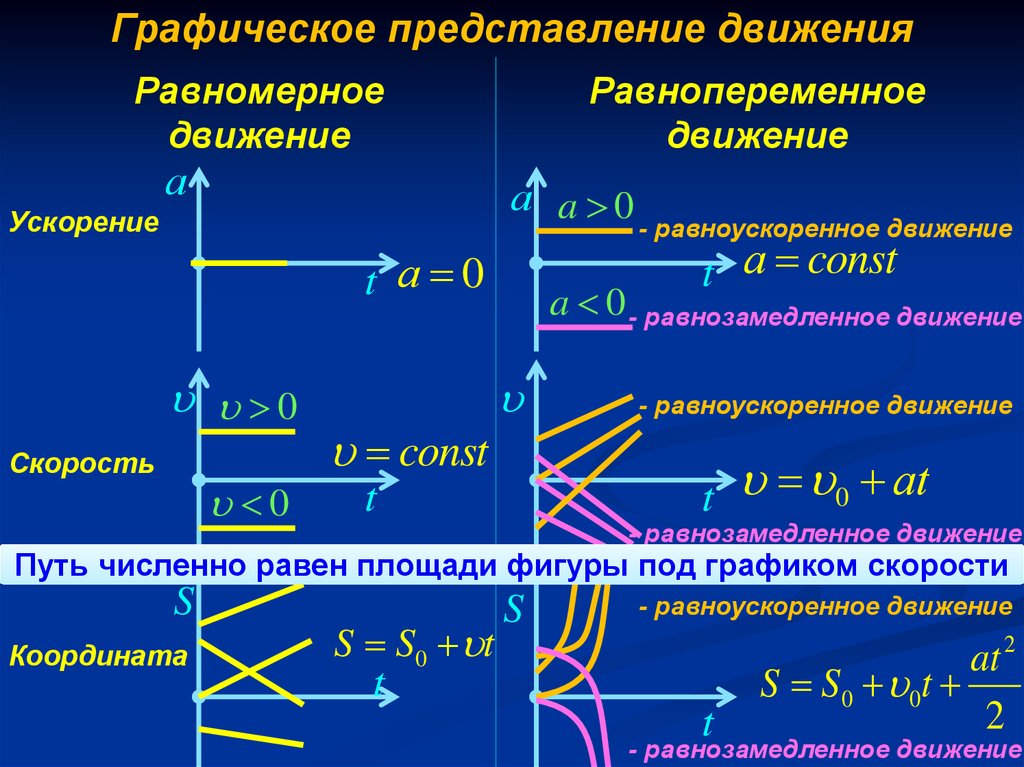
На приведенном выше графике скорость-время (скорость отложена по оси y, а время по оси x) 9Кривая 0005 — это скорость . Допустим, вы хотите рассчитать ускорение в точке p 1 . Градиент в точке p 1 — это мгновенное ускорение, и его можно рассчитать следующим образом, где v 2 — конечная скорость, v 1 — начальная скорость, t 2 — время достижения конечной скорости , а t 1 – время движения с начальной скоростью.
Мгновенное ускорение в точке p 1 \(= \lim_{v \to 0} \frac{\Delta v}{\Delta t} = \frac{v_2-v_1}{t_2-t_1}\) 9{-2}\]
С помощью вычислений и производных вы можете найти мгновенное ускорение в точке p 1 .
Уравнения линейного движения: что такое уравнения движения?
Уравнения движения управляют движением объекта в одном, двух или трех измерениях. Если вы когда-нибудь захотите рассчитать положение, скорость, ускорение или даже время, то эти уравнения — то, что вам нужно.
Первое уравнение движения равно
\[v = u +at\] 92 + 2as\]
В этих уравнениях v — конечная скорость, u — начальная скорость, a — ускорение, t — время, s — перемещение.
Важно! Вы не можете использовать эти уравнения для всех движений! Приведенные выше три уравнения работают только для объектов с равномерным ускорением или замедлением.
Равномерное ускорение: когда объект увеличивает свою скорость с постоянной (постоянной) скоростью.
Равномерное замедление: , когда объект снижает свою скорость с постоянной (устойчивой) скоростью.
Графики ниже определяют равномерное ускорение и равномерное замедление объекта.
Рис. 5. Равномерный график ускорение-время. Usama Adeel – StudySmarter Original
Рис. 6. Равномерный график зависимости замедления от времени. Usama Adeel — StudySmarter Original
Также обратите внимание, что для объектов, движущихся с постоянной скоростью и скоростью, вам не нужно использовать приведенные выше уравнения — достаточно простых уравнений скорости и перемещения .
Расстояние = скорость ⋅ время
Перемещение = скорость ⋅ время
Примеры линейного движения
Девушка бросает мяч вертикально вверх с начальной скоростью 20 м/с, а через некоторое время ловит его. Вычислите время, за которое мяч вернется на ту же высоту, с которой он был выпущен.
Решение
Мы примем любое движение вверх как положительное в данном случае.
Расстояние, пройденное в положительном и отрицательном направлениях, компенсируется, поскольку мяч возвращается в исходное положение. Следовательно, смещение равно нулю .
Конечная скорость — это скорость, с которой девочка ловит мяч. Поскольку девочка ловит мяч на той же высоте (и при условии, что воздух оказывает незначительное влияние на мяч), конечная скорость будет равна -20 м/с (направление вверх положительное, направление вниз отрицательное).
Для ускорения, когда мяч подбрасывается вверх, он замедляется из-за гравитационного притяжения, но поскольку направление вверх считается положительным, мяч замедляется в положительном направлении.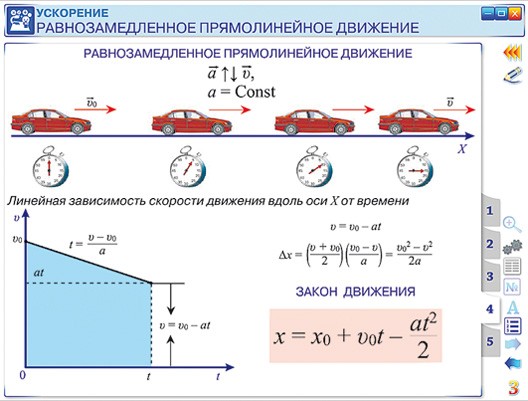 Когда мяч достигает максимальной высоты и движется вниз, он ускоряется в отрицательном направлении. Таким образом, при движении вниз ускорение будет равно -9,81 м/с 2 , что является константой для гравитационного ускорения.
Когда мяч достигает максимальной высоты и движется вниз, он ускоряется в отрицательном направлении. Таким образом, при движении вниз ускорение будет равно -9,81 м/с 2 , что является константой для гравитационного ускорения.
Используем первое линейное уравнение движения: v = u+at 92) \cdot t \rightarrow t = 4.08 \пробел s\)
Линейное движение — Ключевые выводы
Линейное движение — это изменение положения от одной точки к другой по прямой линии в одном измерении.
Перемещение является векторной величиной и представляет собой расстояние, пройденное в заданном направлении от начального положения до конечного положения.
Изменение смещения во времени называется скоростью.
Средняя скорость рассчитывается за все время движения, а мгновенная скорость рассчитывается для определенного момента времени.
Градиент в любой момент времени графика смещения-времени представляет собой скорость.

Изменение смещения в любой момент времени является мгновенной скоростью.
Скорость изменения скорости есть ускорение.
Изменение скорости в определенный момент времени является мгновенным ускорением.
Градиент графика скорость-время есть ускорение.
Когда объект увеличивает свою скорость с постоянной (устойчивой) скоростью, мы говорим, что он движется с равномерным ускорением.
Когда объект уменьшает свою скорость с постоянной (устойчивой) скоростью, мы говорим, что он замедляется с равномерным замедлением.
Уравнение движения графическим методом
Известный британский ученый Исаак Ньютон вывел три уравнения движения, которые описывают наиболее фундаментальные понятия движения объекта. Эти уравнения управляют движением объекта в одном, двух и трех измерениях. Эти уравнения легко использовать для вычисления значений или выражений для положения, скорости или ускорения объекта в различные моменты времени. Давайте сначала разберемся с основной концепцией движения и различными терминами, связанными с ним.
Давайте сначала разберемся с основной концепцией движения и различными терминами, связанными с ним.
Что такое движение?
Движение можно описать как изменение положения объекта во времени. Положение можно измерить, используя опорную точку и рассчитав расстояние объекта от опорной точки. Время можно рассчитать с помощью часов скорости, которые определят время, необходимое для изменения положения. Есть много великих ученых, которые работали и вывели некоторые уравнения или теории для изучения движения, такие как Галилео Галилей и Исаак Ньютон.
Движение автомобиля на временном интервале
Прежде чем обсуждать уравнение движения, давайте сначала повторим основные термины, относящиеся к движению объекта. Движение объекта можно описать с помощью четырех различных терминов, а именно:
Расстояние Фактическая мера общего изменения положения объекта (в определенный период времени) называется Расстоянием. .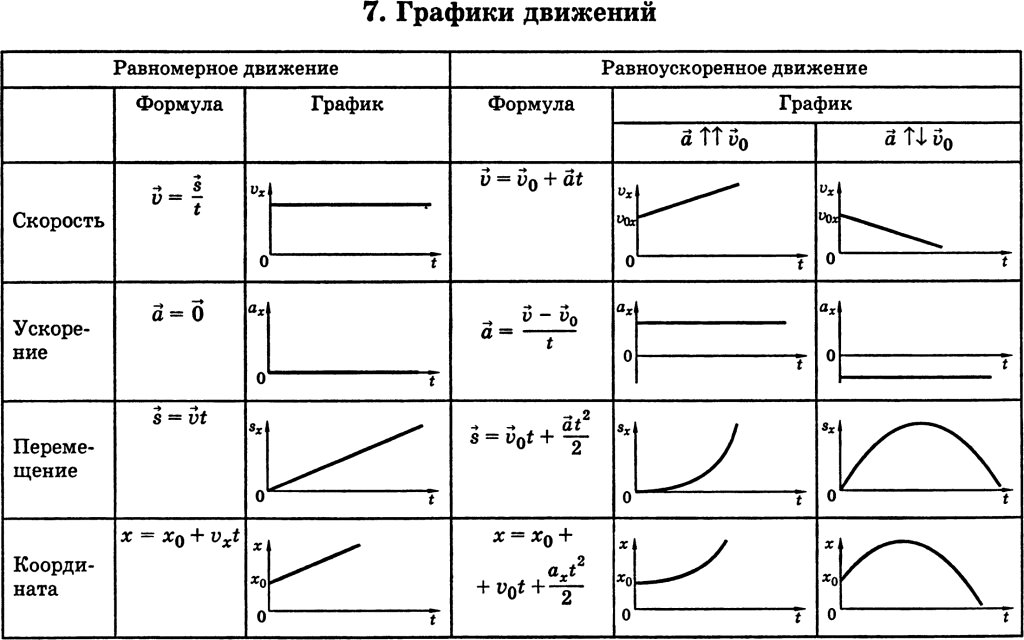
Расстояние (d) является скалярной величиной и, следовательно, дает только величину.
напр. Рассмотрим рисунок ниже: автомобиль движется из положения А в положение В. Спидометр в автомобиле покажет расстояние, пройденное из пункта А в пункт В. чистого изменения положения объекта (за определенный интервал времени) называется перемещением .
Перемещение является векторной величиной и, следовательно, дает как величину, так и направление.
Скоростьнапр. Рассмотрим рисунок ниже, есть автомобиль, движущийся из положения A в положение B. Перемещение равно расстоянию, пройденному в определенном направлении движения.
Водоизмещение автомобиля
Скорость объекта — это мера, определяющая, насколько быстро или медленно объект движется или меняет свое положение.
Скорость равна скорости изменения во времени расстояния, пройденного объектом.
Скоростьнапр. Предположим, что вентилятор работает очень быстро, но быстро относительно вашего стационарного состояния. Если вы также будете вращаться с той же скоростью, что и вентилятор, вы увидите, что он даже не движется.
Математически скорость объекта определяется как:
Поскольку и время, и расстояние являются скалярными величинами, следовательно, скорость также является скалярной величиной.
Единицей скорости в системе СИ является м/с.
Скорость изменения смещения объекта во времени или скорость изменения положения называется скорость .
Графически это наклон функции смещения. Это векторная величина, поэтому она дает как величину, так и направление.
УскорениеМатематически скорость определяется как:
Единица измерения скорости в системе СИ такая же, как и скорость, т. е. м/с. Разница между скоростью и скоростью объекта заключается в том, что скорость — это скалярная величина, а скорость — векторная величина.
Изменение скорости объекта в единицу времени или скорость изменения функции скорости во времени определяется как ускорение.
Графически это наклон функции скорости. Ускорение является векторной величиной и поэтому дает как величину, так и направление.
Математически ускорение определяется как:
Каковы уравнения движения?
Уравнения, которые объясняют природу и поведение физической системы с точки зрения ее движения как функции времени, называются уравнениями движения. Есть три уравнения движения, которые можно использовать для расчета компонентов движения, таких как расстояние, смещение, скорость (начальная и конечная), время (t) и ускорение (a) объекта. Ниже приведены три уравнения движения:
- Первое уравнение движения: v = u + at
- Второе уравнение движения: s = ut + 1/2(at 2 )
- Третье уравнение движения: v 2 = u 2 – 2as
, где v и u — начальная и конечная скорости, a — ускорение, t — затраченное время, а s — перемещение объекта.
Вывод уравнений движения
Исходя из цели применения различных компонентов в различных решениях, существует три различных способа вывода этих уравнений:
- Вывод уравнений движения алгебраически , используя определение и различные формулы составляющие движения.
- Вывод уравнений движения графически , используя графическое представление расстояния, скорости и ускорения объекта.
- Вывод уравнений движения интегральным методом .
Здесь, в настоящей статье, вывод трех уравнений движения обсуждается графически как:
Вывод первого уравнения движения графически:
объект. Следовательно, это уравнение применимо, когда перемещение не задано, и поэтому оно также известно как 90 374 соотношение скорости и времени 9.0377 .
Рассмотрим график зависимости скорости от времени, как показано ниже, скорость тела изменяется от A до C за время t с постоянной скоростью.
Расстояние от A до оси x — это конечная скорость, а OC — это общее время t.
Из В в ОС проведен перпендикуляр, из А в D проведена параллельная линия, а из В в ОЕ проведена еще одна перпендикулярная линия (обозначена пунктирными линиями).
График показывает, что объект имеет переменную скорость, которая увеличивается от u до v по мере того, как наклон положителен, скорость увеличивается в положительном направлении.
График зависимости скорости от времени
Теперь мы рассчитаем ускорение, используя этот график движения. Ускорение — это тангенс угла на графике v-t.
Графический вывод второго уравнения движения:
Ниже v-t график показывает зависимость скорости и времени объекта с начальной скоростью u м/с и конечной скоростью v м/с. Поскольку мы знаем, что площадь графика v-t дает смещение объекта, поэтому мы рассчитаем площадь графика и выясним уравнение смещения. Тот же график мы использовали в предыдущем выводе, но здесь подход будет другим, раньше мы использовали наклон для расчета ускорения, а теперь будем использовать площадь.
v-t Motion Graph
Смещение объекта (d) = площадь треугольника ABC + площадь прямоугольника BCOT
Здесь площадь треугольника ABC = 1/2 × основание × высота
= 1/2 × t × (v-u)
А площадь прямоугольника BCOT = Длина × Ширина
0002 Следовательно, смещение объекта, d = 1/2 × t × (v-u) + u × t ……(1) 9(1) ut + (1/2)at 2
Вывод третьего уравнения движения графически:
У нас есть разные способы вычисления площадей, такие как деление любой формы на мелкие части и последующее сложение площади преобразования задачи к хорошо известной нам форме. В этом выводе площадь прямоугольной формы преобразуется, а смещение рассчитывается с использованием площади прямоугольника. Это уравнение используется, когда время не указано.
От исходного графика к выделенному графику
Здесь P — центральная точка, поэтому скорость объекта равна (v + u)/2.
Следовательно, перемещение объекта (d) = площади треугольника ABC + площадь прямоугольника ACTO = площадь прямоугольника OPQT
Перемещение объекта, d = длина × ширина u) / 2 ……(2)
Также из первого уравнения движения v – u = at или t = (v – u) / a
Следовательно, уравнение (2) принимает вид:
d = (v – u) / a × ( v + u) / 2
v 2 = u 2 – 2ad
Примеры задач
.
График скорость-время
Решение:
Расчет расстояния с использованием площади под графиком скорость-время.
Площадь под заданной кривой.
Расстояние, пройденное частицей за 40 мин = Площадь под заданной кривой.
Форма, сформированная под кривой, представляет собой прямоугольник, поэтому площадь под кривой = длина × ширина.
Здесь длина формы эквивалентна затраченному времени, т.
е. 40 мин или 40 мин × 60 с/1 мин = 2400 с.
Точно так же ширина формы эквивалентна скорости, т. е. 15 км/ч или 15 км/ч × 1 ч/3600 с × 1000 м/1 км = 4,17 м/с.
Таким образом, площадь под кривой или расстояние, пройденное за 40 минут, определяется как:
⇒ 2400 с × 4,17 м/с = 10000 м или 10 км.
Следовательно, расстояние, пройденное частицей за 40 мин, равно 10 км.
Задача 2: Для приведенного ниже графика вычисляется расстояние, пройденное частицей в интервале времени от 20 до 40 минут.
График скорость-время
Решение:
Расстояние, пройденное частицей с момента времени t = 20 мин до 40 мин, равно площади под заданной кривой между заданным интервалом времени.
Выделенная область графика скорость-время
Форма, сформированная под кривой, представляет собой прямоугольник, поэтому площадь под кривой = длина × ширина.
Здесь длина формы эквивалентна затраченному времени, т.
е. (40 – 20) мин или 20 мин × 60 с/1 мин = 1200 с.
Точно так же ширина формы эквивалентна скорости, т. е. 15 км/ч или 15 км/ч × 1 ч/3600 с × 1000 м/1 км = 4,17 м/с.
Таким образом, площадь под кривой или расстояние, пройденное с момента времени t = 20 мин до 40 мин, определяется как:
⇒ 1200 с × 4,17 м/с = 5004 м или 5,004 км.
Следовательно, расстояние, пройденное частицей с момента времени t = 20 мин до 40 мин, равно 5,004 км.
Задача 3. Найти расстояние, пройденное частицей за интервалы времени t = 0 с и t = 4 с, для которых приведен график зависимости скорости от времени:
График зависимости скорости от времени Решение:
График скорость-время
Расстояние, пройденное частицей за время t = 0 с и t = 4 с, равно площади под кривой. Форма, образованная под кривой, представляет собой треугольник, следовательно, площадь под кривой = 1/2 × основание × высота.
Здесь основание формы эквивалентно затраченному времени, т.е. 4 с.
Точно так же высота формы эквивалентна скорости, т.е. 20 м/с.
Следовательно, площадь под кривой или расстояние, пройденное за t = 0 с и t = 4 с, определяется как:
⇒ 1/2 × 4 с × 20 м/с = 40 м.
Следовательно, расстояние, пройденное частицей за время t = 0 с и t = 4 с, равно 40 м.
Задача 4. На приведенном ниже рисунке показан график зависимости пути от времени трех объектов A, B и C. Определите:
(a) какой объект движется с большей скоростью?
б) какой объект движется с меньшей скоростью?
График расстояние-время
Решение:
Данный график представляет собой график расстояния и времени, а наклон дает нам значение скорости, т.е. чем больше наклон, тем больше скорость.
Как видно из данного графика, A имеет максимальный наклон, поэтому движется с большей скоростью, а C имеет наименьший наклон, поэтому движется с наименьшей скоростью.



 Расстояние от A до оси x — это конечная скорость, а OC — это общее время t.
Расстояние от A до оси x — это конечная скорость, а OC — это общее время t.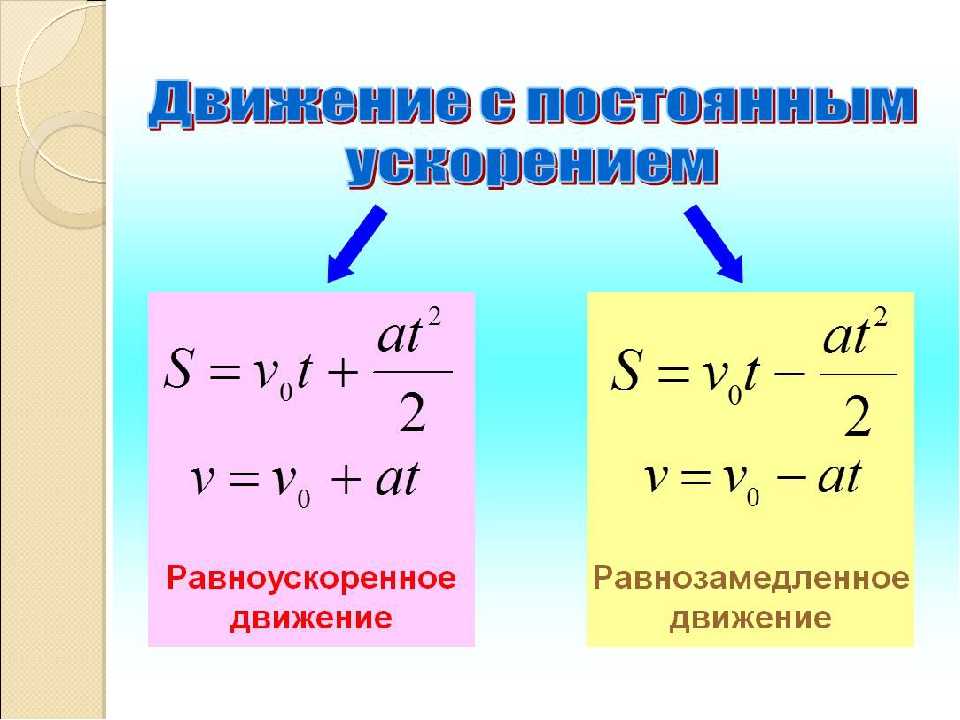
 е. 40 мин или 40 мин × 60 с/1 мин = 2400 с.
е. 40 мин или 40 мин × 60 с/1 мин = 2400 с. е. (40 – 20) мин или 20 мин × 60 с/1 мин = 1200 с.
е. (40 – 20) мин или 20 мин × 60 с/1 мин = 1200 с.
Leave A Comment