Углы равнобедренной трапеции

Бизнес с Oriflame — рост и РАЗВИТИЕ!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2015-10-14

   Углы равнобедренной трапеции. Здравствуйте! В этой статье речь пойдёт о решении задач с трапецией. Данная группа заданий входит в состав экзамена, задачки простые. Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса?

Работать будем с равнобедренной трапецией. У неё равны боковые стороны и углы при основаниях. О трапеции есть статья на блоге, посмотрите.

Отметим небольшой и важный нюанс, который в процессе решения самих заданий подробно расписывать не будем. Посмотрите, если у нас дано два основания, то большее основание высотами, опущенными к нему, разбивается на три отрезка – один равен меньшему основанию (это противолежащие стороны прямоугольника), два других равны друг другу (это катеты равных прямоугольных треугольников):

Простой пример: дано два основания равнобедренной трапеции 25 и 65. Большее основание разбивается на отрезки следующим образом:

*И ещё! В задачах не введены буквенные обозначения. Это сделано умышленно, чтобы не перегружать решение алгебраическими изысками. Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.

Рассмотрим задачи:

27439. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.

Для того чтобы найти угол необходимо построить высоты. На эскизе обозначим данные в условии величины. Нижнее основание равно 65, высотами оно разбивается на отрезки 7, 51 и 7:

В прямоугольном треугольнике нам известна гипотенуза и катет, можем найти второй катет (высоту трапеции) и далее уже вычислить синус угла.

По теореме Пифагора указанный катет равен:

Таким образом:

Ответ: 0,96

27440. Основания равнобедренной трапеции равны 43 и 73.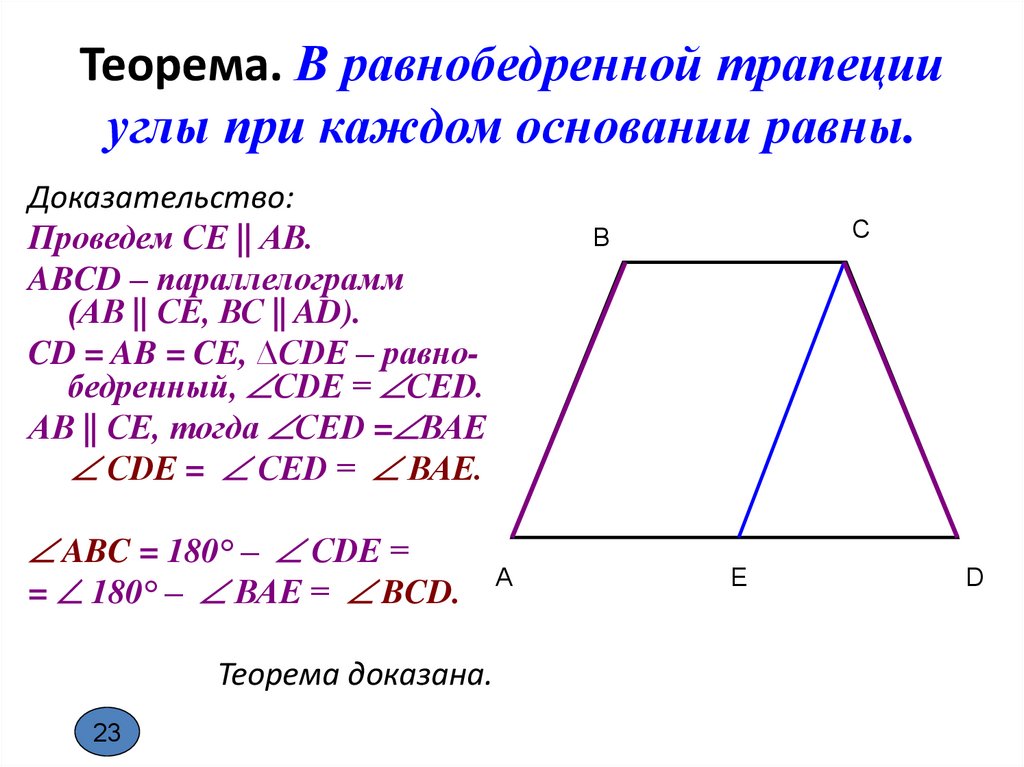 Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.

Построим высоты и отметим данные в условии величины, нижнее основание разбивается на отрезки 15, 43 и 15:

Ответ: 21

27441. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.

Построим высоты. Для того чтобы найти меньшее основание нам необходимо найти чему равен отрезок являющийся катетом в прямоугольном треугольнике (обозначен синим):

Можем вычислить высоту  трапеции, а затем найти катет:

По теореме Пифагора вычисляем катет:

Таким образом, меньшее основание равно:

Ответ: 22

27442. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.

Построим высоты и отметим данные в условии величины. Нижнее  основание разбивается на отрезки:

Что делать? Выражаем тангенс известного нам угла при основании в прямоугольном треугольнике:

Ответ: 10

27443.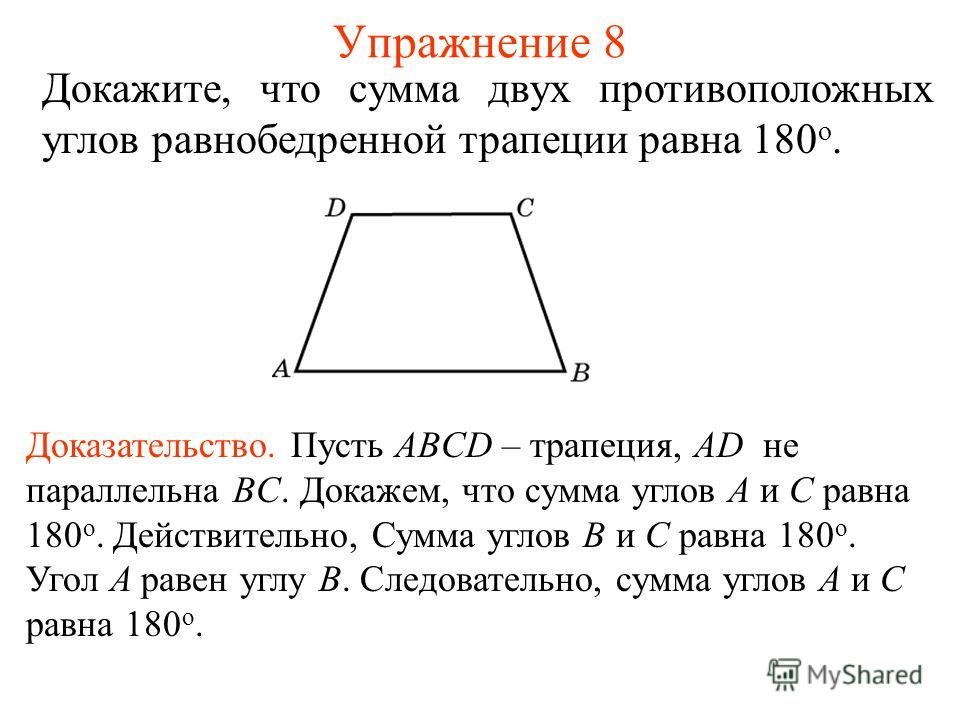 Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.

Строим высоты и вычисляем чему равен катет:

Таким образом большее основание будет равно:

Ответ: 71

27444. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.

Строим высоты и отмечаем известные величины на эскизе. Нижнее основание разбивается на отрезки 35, 17, 35:

По определению тангенса:

Ответ: 0,4

77152. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.

Построим эскиз, построим высоты и отметим известные величины, большее основание разбивается на отрезки 3, 6 и 3:

Выразим гипотенузу обозначенную как х через косинус:

Из основного тригонометрического тождества найдём cosα

Таким образом:

Ответ: 5

27818.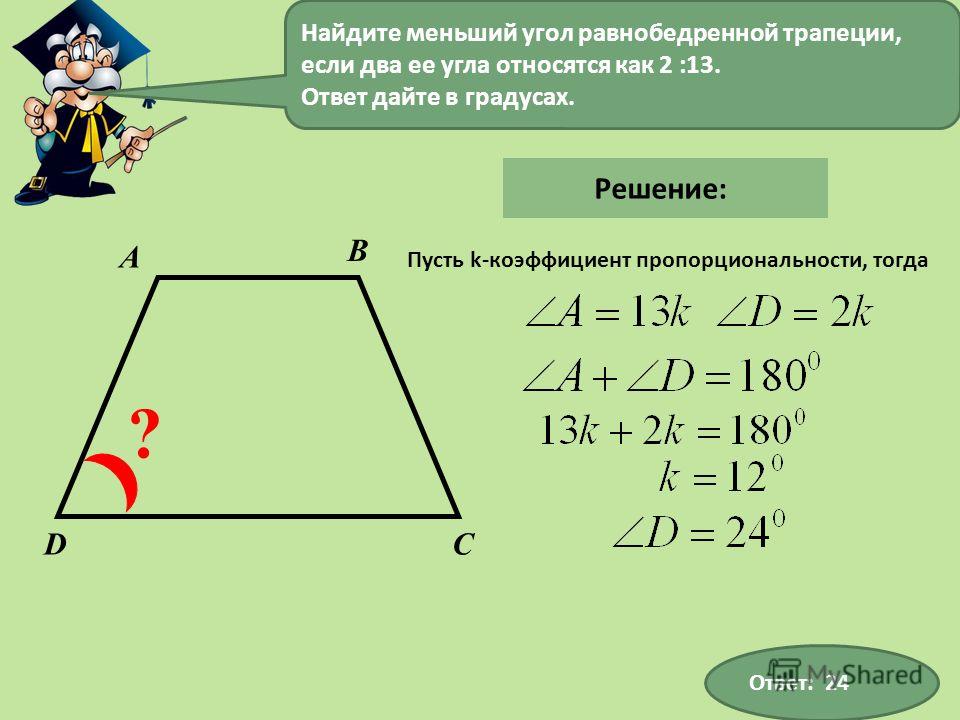 Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 500? Ответ дайте в градусах.

Из курса геометрии нам известно, что если имеем две параллельные прямые и секущую, что сумма внутренних односторонних углов равна 1800.  В нашем случае это

C условии сказано, что разность противолежащих углов равна 500, то есть

Так как у равнобедренной трапеции углы  при основании равны, то есть угол А равен углу В, то можем записать

Имеем два уравнения с двумя  неизвестными, можем решить систему:

*Конечно, эту задачу можно было легко решить просто перебирая пары углов )

27833. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 600. Найдите меньшее основание.

Построим высоты DE и CF:

Меньшее основание равно отрезку EF, так как DC и EF это противолежащие стороны прямоугольника. Отрезок EF мы можем найти если вычислим АЕ. Выразим этот катет прямоугольного треугольника ADE через функцию косинуса:

Так как AE=FB=5, то EF=25–5–5=15. Следовательно и DC=15.

Ответ: 15

27837. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 450. Найдите высоту трапеции.

Из точек D и C опустим две высоты:

Как уже сказано выше они разбивают большее основание на три отрезка: один равен меньшему основанию, два других равны друг другу.

В данном случае они равны 3, 9 и 3 (в сумме 15). Кроме того, отметим что высотами отсекаются прямоугольные треугольники, причём они являются равнобедренными, так как углы при основании равны по 450. Отсюда следует, что высота трапеции будет равна 3.

Ответ: 3

На этом всё! Успеха вам!

С уважением, Александр.

P.S: Расскажите о сайте в социальных сетях!


Категория: Четырёхугольники | ЕГЭ-№1ТрапецияУглы

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.


Трапеция. — Царство математики

Трапеция. — Царство математики

Трапеция — четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются её основаниями, а две другие — боковыми сторонами.

Трапеция называется равнобедренной, если её боковые стороны равны.

Трапеция называется прямоугольной, если у нее два угла прямые.

Основные свойства трапеции:

  1. Сумма углов при каждой боковой стороне трапеции равна 180°.
  2. Средняя линия трапеция параллельна её основаниям и равна их полусумме.
  3. В любой трапеции следующие точки лежат на одной прямой: точка пересечения продолжений боковых сторон, середины оснований и точка пересечения диагоналей.
  4. Треугольники, образованные отрезками диагоналей и основаниями трапеции, подобны.
  5. Треугольники, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
  6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
  7. Если сумма углов, при любом основании трапеции, равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
  8. Биссектриса любого угла трапеции отсекает от нее равнобедренный треугольник.
  9. Биссектрисы углов, при боковой стороне трапеции, перпендикулярны.
  10. Если в трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
  11. Отрезок, заключенный между боковых сторон трапеции, параллельный основаниям трапеции и проходящий через точку пересечения ее диагоналей — среднее гармоническое оснований трапеции.

Свойства равнобедренной трапеции:

  1. Диагонали равны.
  2. Углы при основании равны.
  3. Сумма противоположных углов равна 180°.
  4. Около равнобедренной трапеции можно описать окружность.
  5. Высота, опущенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на два отрезка, больший из которых равен полусумме оснований, а меньший — полуразности оснований.

Описанная трапеция:

  1. Если вокруг трапеции можно описать окружность, то трапеция равнобедренная.
  2. Радиус вписанной окружности равен среднему геометрическому длин отрезков, на которые радиус вписанной окружности делит боковую сторону, точкой касания.
  3. Радиус вписанной окружности равен половине высоты трапеции.

Вписанная трапеция:

  1. Трапецию можно вписать в окружность,если сумма длин оснований равна сумме длин боковых сторон.

Площадь трапеции:

  1. Формула площади трапеции через основания и высоту: S=0,5·(a+b)·h.
  2. Формула площади трапеции через диагонали и угол между ними: S=0,5·d1·d2·sinφ
    .

0

Оставьте комментарий! Напишите, что думаете по поводу статьи.x

Как найти угол в трапеции

Все ресурсы по геометрии среднего уровня

8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Промежуточная справка по геометрии » Плоская геометрия » Четырехугольники » Трапеции » Как найти угол в трапеции

В приведенной ниже трапеции найдите градусную меру .

Возможные ответы:

Правильный ответ:

Объяснение:

В трапеции углы на одном катете (называемые смежными) являются дополнительными, то есть их сумма составляет  градусы.

 и градусы измерения угла являются смежными углами, которые являются дополнительными.

Сообщить об ошибке

В приведенной ниже трапеции найдите угол  .

Возможные ответы:

Правильный ответ:

Пояснение:

В трапеции сумма всех внутренних углов составляет  градусы.

— это градусы.

Сообщить об ошибке

В приведенной ниже трапеции найдите значение угла .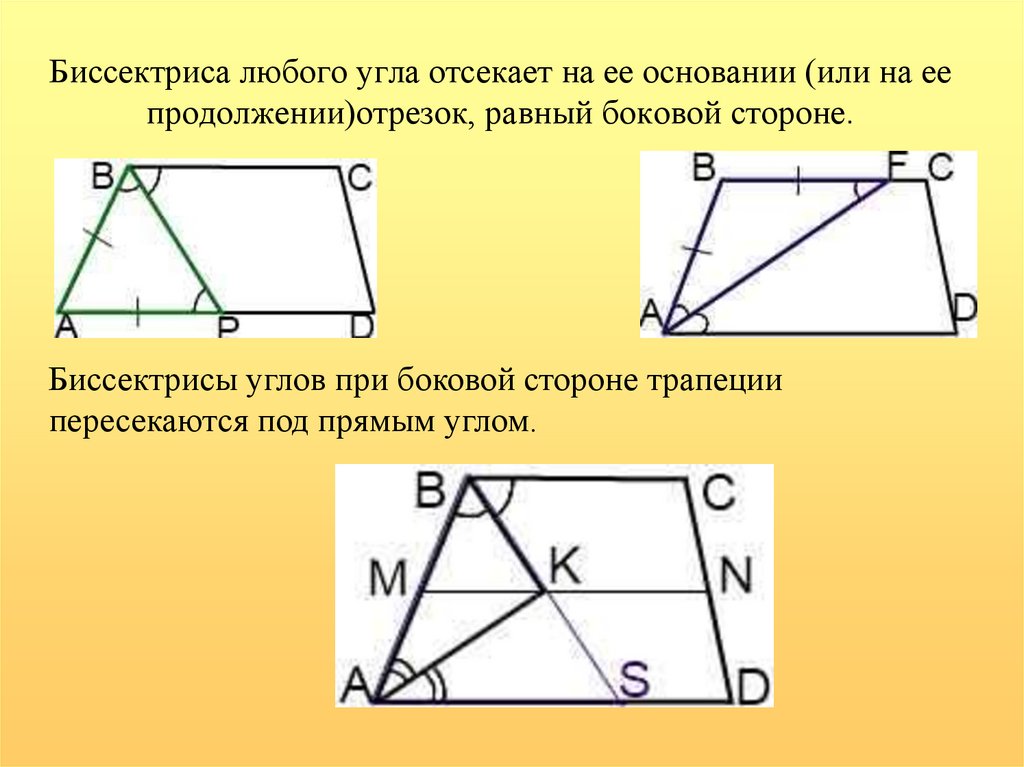

Возможные ответы:

Правильный ответ:

Пояснение:

Все внутренние углы трапеции в сумме равны .

— это градусы.

Сообщить об ошибке

В приведенной ниже трапеции найдите значение угла .

Возможные ответы:

Правильный ответ:

Пояснение:

Все внутренние углы трапеции в сумме равны .

— это градусы.

Сообщить об ошибке

В приведенной ниже трапеции найдите градусное измерение .

Возможные ответы:

Невозможно определить по данной информации.

Правильный ответ:

Объяснение:

В трапеции углы на одном катете (называемые смежными) являются дополнительными, то есть их сумма составляет  градусы.

 и градусы измерения угла являются смежными углами, которые являются дополнительными.

Сообщить об ошибке

В трапеции ниже найдите градусы .

Возможные ответы:

Невозможно определить по предоставленной информации.

Правильный ответ:

Объяснение:

В трапеции углы на одном катете (называемые смежными) являются дополнительными, то есть их сумма составляет  градусы.

 и градусы измерения угла являются смежными углами, которые являются дополнительными.

Сообщить об ошибке

В трапеции ниже найдите градусы .

Возможные ответы:

Правильный ответ:

Объяснение:

В трапеции углы на одном катете (называемые смежными) являются дополнительными, то есть их сумма составляет  градусы.

 и градусы измерения угла являются смежными углами, которые являются дополнительными.

Сообщить об ошибке

В трапеции ниже найдите градусы .

Возможные ответы:

Правильный ответ:

Объяснение:

В трапеции углы на одном катете (называемые смежными) являются дополнительными, то есть их сумма составляет  градусы.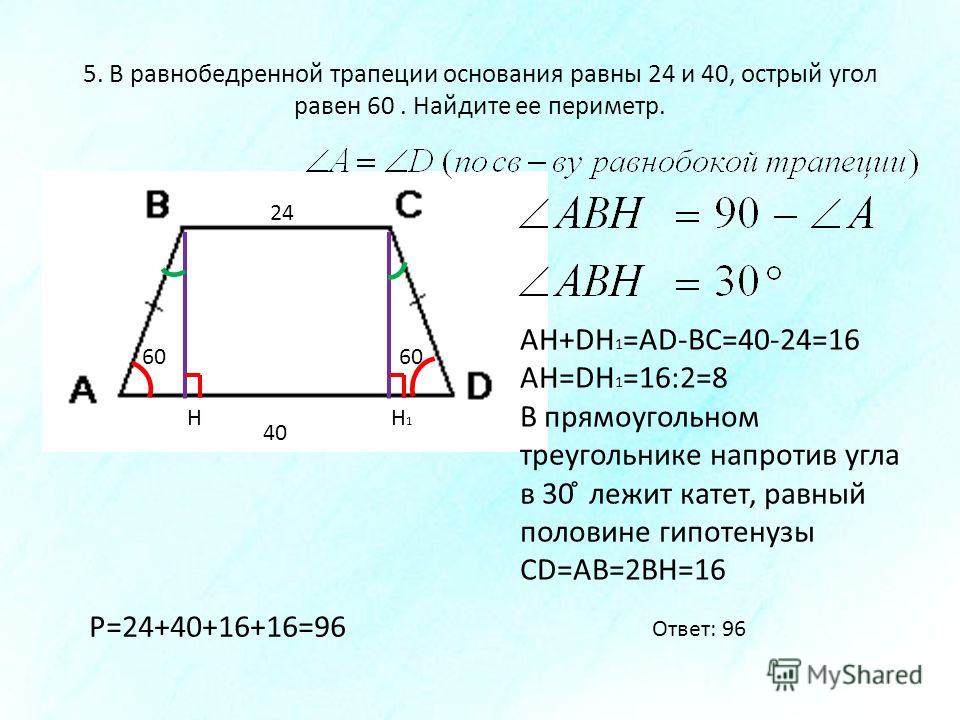

 и градусы измерения угла являются смежными углами, которые являются дополнительными.

Сообщить об ошибке

В трапеции ниже найдите градусы .

Возможные ответы:

Правильный ответ:

Объяснение:

В трапеции углы на одном катете (называемые смежными) являются дополнительными, то есть их сумма составляет  градусы.

 и градусы измерения угла являются смежными углами, которые являются дополнительными.

Таким образом, мы можем написать следующее уравнение и решить для a.

Сообщить об ошибке

В трапеции ниже найдите градусы .

Возможные ответы:

Правильный ответ:

Объяснение:

В трапеции углы на одном катете (называемые смежными) являются дополнительными, то есть их сумма составляет  градусы.

 и градусы измерения угла являются смежными углами, которые являются дополнительными.

Таким образом, мы можем написать следующее уравнение и решить для z.

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах 250 практических тестов Вопрос дня Карточки Учитесь по концепции

Калькулятор углов трапеции

Создано Komal Rafay

Отзыв от Davide Borchia

Последнее обновление: 02 февраля 2023 г. 0317 Типы трапеций

  • Как вычислить углы трапеции?
  • Калькулятор трапеции на Omni
  • Часто задаваемые вопросы

    • Вы ищете калькулятор угла трапеции? Потому что вы пришли в нужное место. Наш калькулятор угла трапеции — это инструмент, специально разработанный для всех вас, любителей геометрии. Он определяет углы трапеции: будь то равнобедренная или прямоугольная трапеция, мы обеспечим вас.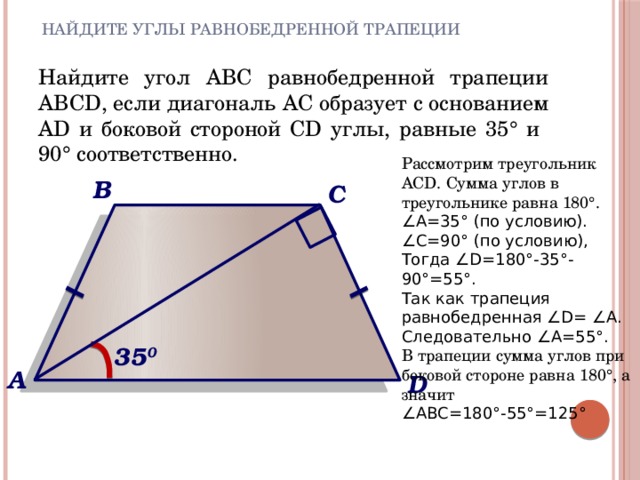 Не беспокойтесь, мы объясним, как вычислить углы трапеции.

    Углы трапеции

    У трапеции четыре угла:

    1. Альфа α;
    2. Бета β;
    3. Гамма γ; и
    4. Дельта δ.

    Как и во всех других четырехугольниках, сумма углов трапеции составляет 360 градусов (или 2π радиан).
    Так как у них есть пара параллельных сторон, у трапеции есть дополнительное условие. Пара углов вдоль одного из катетов являются дополнительными углами, а значит, их сумма должна быть равна 180 градусам (или π радианам).
    Это выглядит так:

    α + β = 𝛾+ δ = 180°

    Знание углов трапеции пригодится для определения ее высоты, а высота помогает определить площадь трапеции.

    Калькулятор углов трапеции

    Наш калькулятор углов трапеции — это удобный инструмент, который позволяет вычислять различные углы между сторонами трапеции.
    Вы можете ввести значение любого угла и получить значение его дополнительного партнера. Да, это действительно так просто.

    Например,
    , если ввести
    α=55°α = 55°α=55°
    , то инструмент определяет
    β=125°β = 125°β=125°

    и, если
    γ= 95°γ = 95°γ=95°
    , затем
    δ=85°δ = 85°δ=85°

    В инструменте можно также выбрать другую единицу измерения для преобразования углов.

    Типы трапеций

    Сейчас самое время обсудить два наиболее важных типа трапеций с точки зрения углов.

    • Угол равнобедренной трапеции
      Трапеция, у которой стороны и оба угла при основании равны по размеру, называется равнобедренной трапецией. Углы равнобедренных трапеций не зависят от формы и рассчитываются так же, как и у правильной трапеции.

    • Угол прямой трапеции
      Трапеция, у которой одна сторона перпендикулярна основаниям , является прямой трапецией. У него есть хотя бы один прямой угол.

    🙋 Интересно, что если одна из сторон перпендикулярна одному из оснований, то она перпендикулярна и другой, так как стороны параллельны.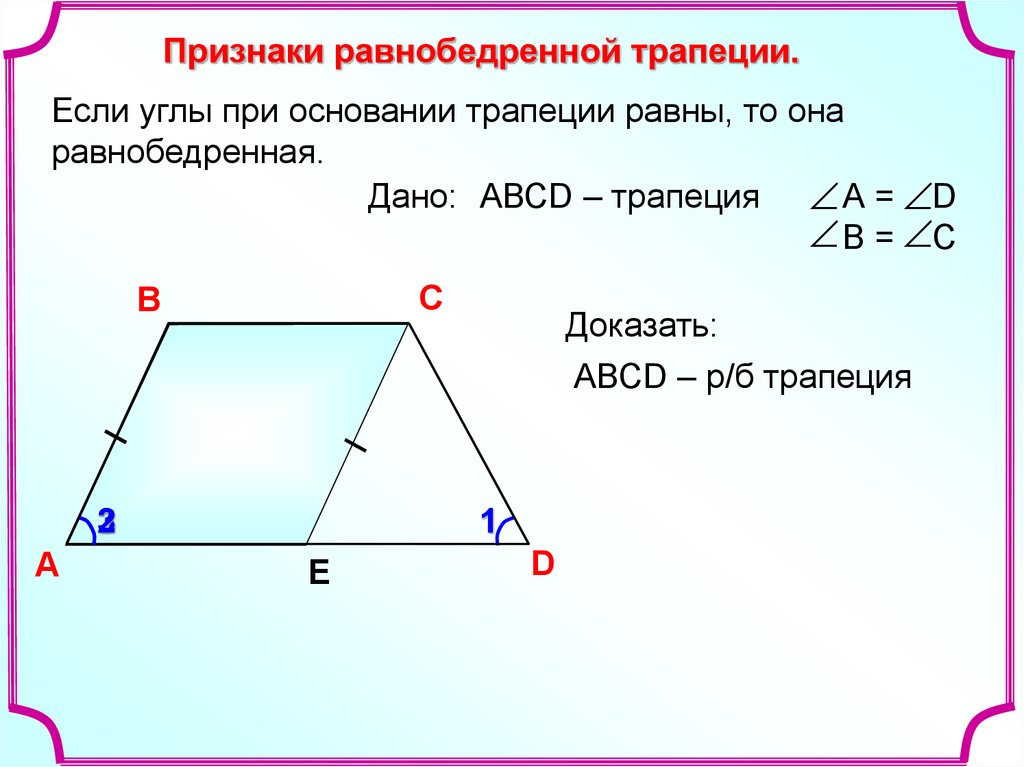 Итак, скорее всего, ваша правая трапеция имеет два прямых угла.

    Как вычислить углы трапеции?

    Теперь мы понимаем, что углы являются дополнительными, и можем вычислять их попарно.
    Формула:
    ∠α+∠β=π\угол α +\угол β = \pi∠α+∠β=π

    ∠γ+∠δ=π\угол γ + \угол δ = \pi∠ γ+∠δ=π

    Рассмотрим пример, у вас есть ∠α = 75°, тогда для определения ∠β вычтите 75 из 180, и у вас будет 105°.

    Формула для вычисления всех четырех углов вместе:

    ∠α+∠β+∠γ+∠δ=2π\угол α + \угол β + \угол γ + \угол δ = 2\pi∠α+∠ β+∠γ+∠δ=2π

    Например, α = 75° , β = 85° и γ = 95° . Чтобы определить δ , выполните следующие действия:

    1. Суммируйте значения α , β и 𝛾 . Вы получите 255°
    2. Затем вычтите полученное значение из 360 ( 2π ). Вы получите 105° .
    3. Это значение угла δ .

    Трапециевидные калькуляторы на Omni

    • Калькулятор трапеций
    • Калькулятор площади трапеции
    • Калькулятор периметра трапеции
    • Калькулятор стороны трапеции
    • Калькулятор высоты трапеции
    • Средняя часть трапеции
    • Калькулятор равнобедренной трапеции
    • Калькулятор площади равнобедренной трапеции
    • Калькулятор правой трапеции
    • Калькулятор площади правой трапеции
    • Калькулятор площади неправильной трапеции

    FAQ

    Чему равен угол 4ᵗʰ прямой трапеции, если первый угол равен 85°?

    Значение четвертого угла 95° .
    Прямоугольная трапеция означает, что пара ее углов равна 90° . Это облегчает определение углов. Если два угла равны 90° и 90° , и вы знаете третий угол, вы можете вычесть значение третьего угла из 180° .

    Как вычислить углы трапеции?

    Для вычисления дополнительных углов в парах используется следующая формула:

    ∠α + ∠β = π

    ∠γ + ∠δ = π

    где:

    6

    16

    1 180° .